Раскрытие модуля в функциях: Графики функций с модулем

Содержание

Презентация «Модуль в выражениях, линейных уравнениях и линейных функциях»

«Модуль в выражениях, линейных уравнениях и линейных функциях»

Работу выполнила Возная Татьяна, учащаяся 8А класса, УВК-школы-гимназии №5.

Руководитель Солохина Л.Н., учитель математики.

Содержание

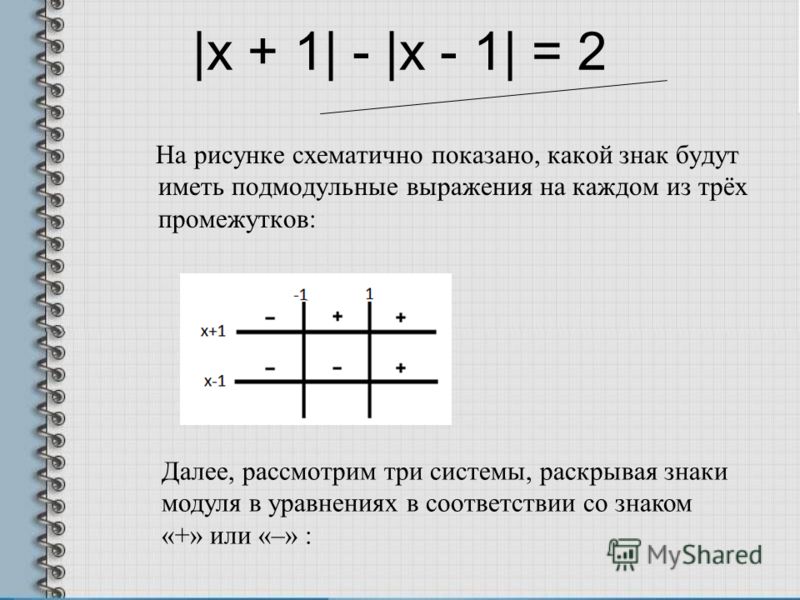
Введение

Глава 1. Модуль в выражениях

1.1. Определение модуля. Свойства модуля

1.2. Раскрытие модуля. Упрощение выражений, содержащих переменную под знаком модуля

Глава 2. Модуль в уравнениях

2.1. Основные методы решения уравнений с модулем. Раскрытие модуля по определению, переход от исходного уравнения к равносильной системе, возведение в квадрат обеих частей уравнения, метод интервалов, графический метод, использование свойств модуля.

2.2. Решение уравнений вида |f(x)| = а, |f(x)| = g(x), |f(x)| = |g(x)| и |f 1 (x)| + |f 2 (x)| + |f 3 (x)| + … + |f n (x)| = g(x), где f(x) и g(x) – линейные выражения, а Є R

2. 3. Решение уравнений «модуль в модуле»: ||f(x)| + а| = b. Способ последовательного раскрытия модуля при решении уравнений, содержащих «модуль в модуле».

Глава 3. Модуль в функциях

3.1. Построение графиков функций вида у =|(kх + b)|, у = k|х| + b

3.2. Построение графиков с модулями дробно- линейной функции у = |f(x)| + |g(x)|.

3.3. Графики функций, аналитическое выражение которых содержит знак модуля в олимпиадных заданиях

Заключение

Список использованной литературы

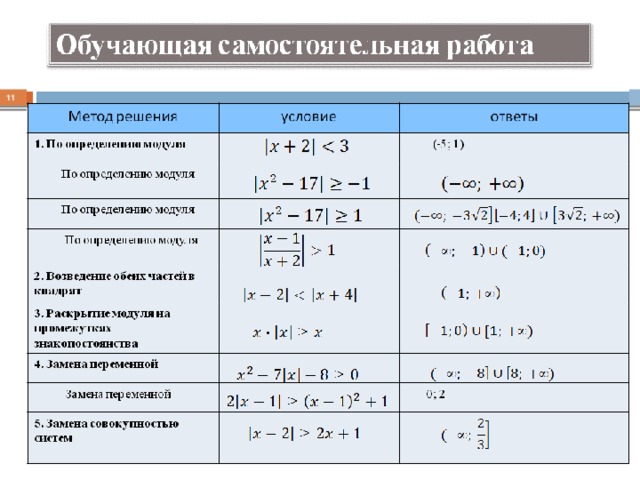
Изучение темы направлено на достижение следующих целей:

Обобщить и систематизировать, расширить и углубить знания методов и приёмов к решению задач с модулем.

Продолжить работу по интеллектуальному развитию, формированию определённого уровня логического мышления. Развивать исследовательскую и познавательную деятельности.

Углубить самостоятельную творческую работу.

основные задачи:

углубить знания по математике, формировать устойчивый интерес к предмету;
развить свои математические способности;
расширить математические представления о приёмах и методах решения задач с модулями;
повысить уровень математического и логического мышления;
сформировать навыки работы со справочной литературой и компьютером;
развить навыки исследовательской деятельности;
обеспечить подготовку к поступлению в вуз и продолжению образования;
обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.

Модулем неотрицательного действительного числа a называют само это число:

| | =

Модулем отрицательного

действительного числа х называют противоположное число:

| | = —

Короче это записывают так:

Модулем числа называют расстояние (в единичных отрезках) от начала координат до точки А() .

0 | | = | — |, = , при у = , ·уу | + у| | | + | у | | ·q| = q·| | , где q — положительное число | | 2 = 2 «

На практике используют свойства модуля

| | ≥ 0, | |
| · | = | | · | у |
|| = , при у
| | n = n , n є Z, 0, n 0
| | = | — |,
= , при у

= , ·уу

| + у| | | + | у |
| ·q| = q·| | , где q — положительное число
| | 2 = 2

Раскрытие модуля.
Упрощение выражений, содержащих переменную под знаком модуля
Раскрытие модуля. Упрощение выражений, содержащих переменную под знаком модуля

Пример 1. Раскрыть модуль:

| —

Пример 2. Вычислить:

Глава 2. Модуль в уравнениях. 2.1. Основные методы решения уравнений с модулем:

раскрытие модуля по определению;
переход от исходного уравнения к равносильной системе;
возведение в квадрат обеих частей уравнения;
метод интервалов;
графический метод;
использование свойств модуля.

1 Решение уравнений вида |f(x)| = а, где f(x) – линейное выражение, а Є R.

Уравнение вида  f(x)  = а , где а действительное число,

при а  0 решений не имеет;
при а= 0 равносильно уравнению f(x) = 0 ;
при а  0 равносильно совокупности уравнений f(x) = а, f(x) = — а.

– 0,5 12х + 6 = 30х – 4, 12х – 30х = – 4 – 6, – 18х = – 10, х = [– 0,5; + ∞), значит, – корень. «

Решение уравнений вида |f(x)| = g(x), где f(x) и g(x) – линейные выражения, а Є R.

Решить уравнение |12х + 6| = 30х –4.

Решение: Буду решать данное уравнение методом разбиения на промежутки .

12х + 6 = 0,

12х = –6, а) х

х = – 0,5 – (12х + 6) = 30х – 4,

– 12х — 6 = 30х – 4,

– 12х – 30х = – 4 + 6,

– 42х = 2,

х = — (–∞; -0,5), значит, -не является корнем.

б) х – 0,5

12х + 6 = 30х – 4,

12х – 30х = – 4 – 6,

– 18х = – 10,

х = [– 0,5; + ∞), значит, – корень.

Решение уравнений вида |f(x)| = |g(x)|, где f(x) и g(x) – линейные выражения, а Є R.

Решить уравнение  3х-5  =  5-2х  .

(3х-5) 2 =(5-2х) 2 .

9х²-30х+25 = 4х²-20х+25, 5х²-10х = 0,

Получили неполное квадратное уравнение, решая которое находим х 1 = 0, х 2 = 2.

Ответ: 0; 2.

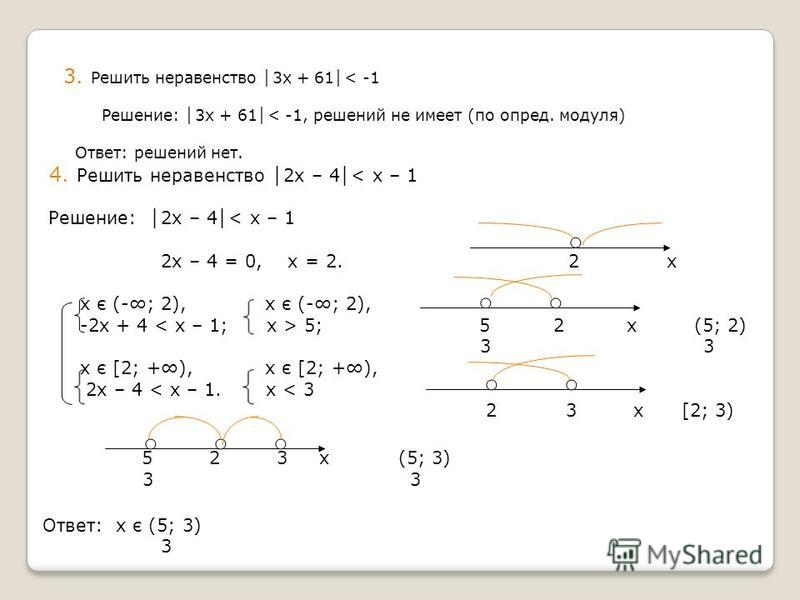
Решение уравнений вида |f1 (x)| + |f2 (x)| + |f3 (x)| + … + |fn (x)| = а, где (x) – линейные выражения, а Є R.

Решить уравнение |х + 8| – |х – 4| = 10.

Найдём подмодульные корни.

1) х + 8 = 0, х – 4 = 0,

х = – 8. х = 4.

Отметим их на координатных прямых и раскроем модули.

4 х + 8 – (х – 4) = 10, х + 8 – х + 4 = 10, 12 = 10 — неверно, значит, корней нет на промежутке [4; ∞). Ответ: 3. «

3) а) х

– (х + 8) – (– х + 4) = 10,

– х – 8 + х – 4 = 10,

– 12 = 10 — неверно, значит, корней нет на промежутке (–∞; – 8).

б) – 8 х

х + 8 – (– х + 4) = 10,

х + 8 + х – 4 = 10,

2х + 4 = 10 ,

2х = 6,

х = 3, 3 [– 8; 4), значит, 3 является корнем уравнения.

в) х 4

х + 8 – (х – 4) = 10,

х + 8 – х + 4 = 10,

12 = 10 — неверно, значит, корней нет на промежутке [4; ∞).

Ответ: 3.

Решение уравнений вида |f1 (x)| + |f2 (x)| + |f3 (x)| + … + |fn (x)| = g(x), где (x) и g(x) – линейные выражения, а Є R.

Решить уравнение |х + 3| + |х + 4| = х.

Найдём подмодульные корни.

1) х +3 = 0, х + 4 = 0.

х = – 3. х = – 4.

Раскроим модули.

– 3 х + 2 + х + 3 = х, 2х + 5 = х, 2х – х = – 5, х = – 5, – 5 ∉ [– 2;+ ∞), значит, – 5 не является корнем. Ответ: нет корней. «

3) а) х

– (х + 3) – (х + 4) = х,

– х – 3 – х – 4 = х,

– 2х – 7 = х,

– 2х – х = 7,

– 3х = 7,

х = –2, ∉(–∞; – 4), значит –2 – не является корнем.

б) – 4 ≤ х

– (х + 3) + х +4 = х,

– х – 3 + х + 4 = х,

– х = – 1,

х = 1, 1 ∉ [– 4; – 3), значит, 1 не является корнем.

в) х – 3

х + 2 + х + 3 = х,

2х + 5 = х,

2х – х = – 5,

х = – 5, – 5 ∉ [– 2;+ ∞), значит, – 5 не является корнем.

Ответ: нет корней.

Решение уравнений «модуль в модуле», ||f(x)| + а| = b.

Решить уравнение |7 + |7 + х|| = 10.

1) 7 + х = 0

х = – 7.

– 7 | 7 + (7 + х) |= 10, | 7 + 7 + х | = 10, |1 4 + х | = 10, х = – 14 – подмодульный нуль. 1. х х 14 + х = 10, х = – 4; – 4 [– 14; + ∞) Ответ: – 4; – 10. «

3) а) х

|7 – (7 + х)| = 10,

| 7 – 7 – х | = 10,

| –х | = 10, | х | = 10.

Так как, х

б) х – 7

| 7 + (7 + х) |= 10,

| 7 + 7 + х | = 10,

|1 4 + х | = 10,

х = – 14 – подмодульный нуль.

1. х

х 14 + х = 10,

х = – 4; – 4 [– 14; + ∞)

Ответ: – 4; – 10.

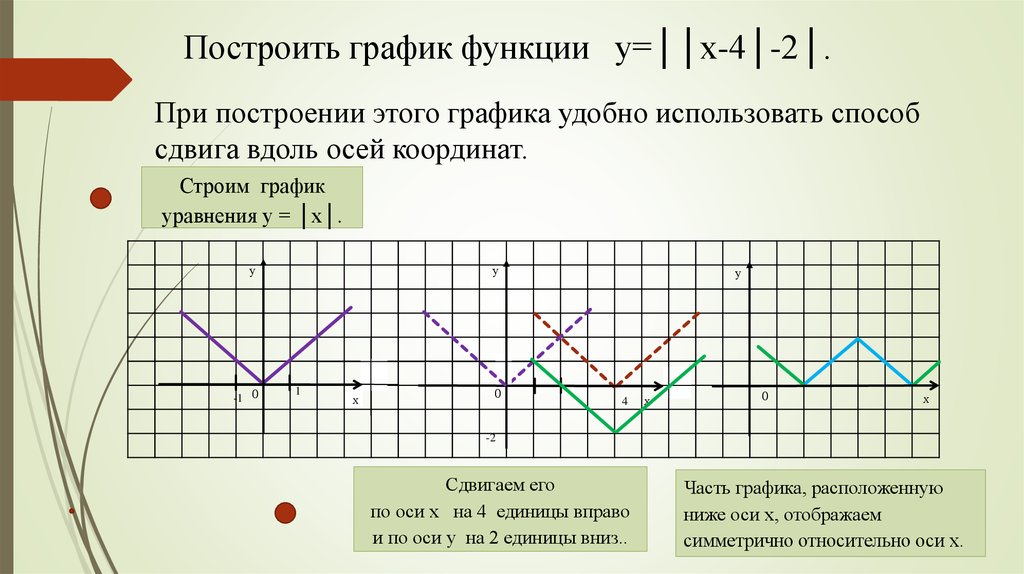
Глава 3. Модуль в функциях 3.1. Построение графиков функций вида у =|(kх + b)|, у = k|х| + b.

Построить график функции у= |2x-3|.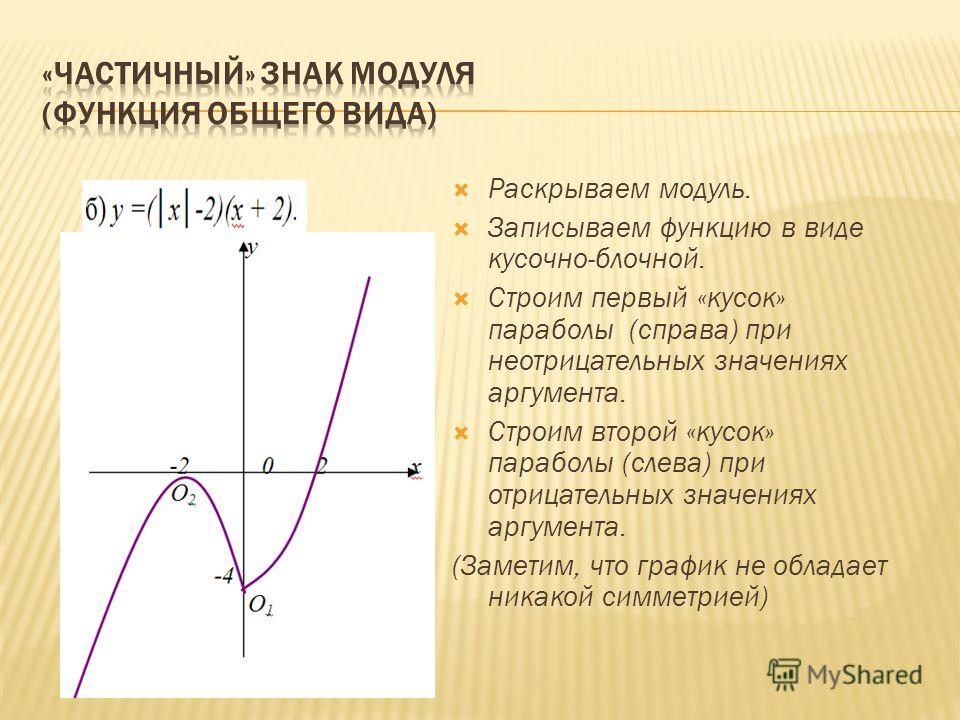

|2х-3| =

Построить график функции у = 2|х|+3.

Построение графиков с модулями дробно- линейной функции у = |f(x)| + |g(x)|.

Постройте график функции у=|х+2|+|х+3|.

Графики функций, аналитическое выражение которых содержит знак модуля в олимпиадных заданиях .

Решить уравнение х – 6 = .

2. Постройте график функции

у = | х — 1 | — | 2 — х | + 2.

Список литературы

Макарычев Ю.Н. Миндюк Н.Г. Алгебра 8. Алгебра 9. Дополнительные главы к школьному учебнику. Москва. «Просвещение». 2001год.
Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре 8-9. Москва. «Просвещение». 2001год.

Алгебра для 8-9 класса: пособие для учащихся школ и классов с углублённым изучением математики. Н.Я. Виленкин, Г.С. Сурвилло, А.С. Симонов, А.И. Кудрявцев, под редакцией Н.Я. Виленкина — М.: Просвещение, 1998 г.

Спасибо за внимание.

Геометрический смысл модуля

Билет №1: линейные уравнения вида ax=b.

а) a=0, b 0

a*x=b 0=b

нет решения

б) a 0 b=0

a*x=0 x=0

в) a=0 b=0

OX=0 0=0

X-любое число x R

г) a 0 b 0

ax=b x= – единственный корень уравнения.

Пример:

a -bx+c=0

a(x- )(x- )=0

если = , то

a +bx+c= a(x- )(x- )= a(x-

Билет №2:линейная функция, график, свойства.

Г рафиком линейной функции – является прямая. Для постоения прямой необходими иметь две точки.

Y=ax+b, a 0

2 ) y=ax+b, a 0 3) y=b, x R

4 )x=a, y R a

Билет №3: квадратичная функция (график свойства).

Квадратичной функцией называется функция, которую можно задать формулой вида

a +bx+c=0,

Многие свойства квадратичной функции зависят от значения дискриминанта (фор-ла дискриминанта D= -4ac)

График квадратичной функции называется парабалой. Координаты вершины параболы:

m = — , n= — , где D- дискриминан. Нули функции определяются формулой = . Прямая x=m является осью симметрии графика квадратичной функции. При a 0 ветви направлены вниз, при а 0 вверх.

а 0 a 0

Билет №4:Дробнорациональные уравнения, методы решения.

Решения уравнений сводится к решению системы.

Методы решения:

Биквадратные уравнения решаются путем замены и введения новых переменных. Этот метод применяется для понижения степени и упрощения решения. Решив уравнения относительно новых переменных , найдем значение «x».
При решении уравнений часто применяется теорема Виета:

= ;

Биквадратное уравнение решается путем замены:

Если , корней нет; Если x=0; Если , (x- )(x+ )=0? X=-

Билет №5: Решение рациональных уравнений, методы решения:

(x+1)( -5x)-6(x+1)=0

(x+1)( -5x+6)=0

X+1=0

-5x+6=0

X+1=0 -5x+6=0

X=-1 D=(-5 -4*6=25-24=1

=3, =2

Билет№ 5: Системы рациональных уравнений. Методы решения.

МЕТОД СЛОЖЕНИЯ:

Метод состоит в том, что уравняв коэффициенты при одной из переменных при сложении или вычитании в результате получается уравнение относительно одной из переменных. Полученные значения переменной при решении уравнения подставить в любое уравнение системы и найти значение второй переменной. При решении любым методом ответ записывается: (x; y)

МЕТОД ПОДСТАНОВКИ:

Необходимо выразить из любого уравнения системы более удобную переменную и подставить в другое уравнение. При этом получается уравнение относительно одной переменной. Найдем ее значение и, подставив в любое уравнение, получим значение второй переменной.

ГРАФИЧЕСКИЙ МЕТОД:

Состоит в том, что из каждого уравнения необходимо получить функцию, т. е. выразить переменную «у», которая будет зависеть от переменной «х». При построении графика функций необходимо учитывать область определения (Д(у)).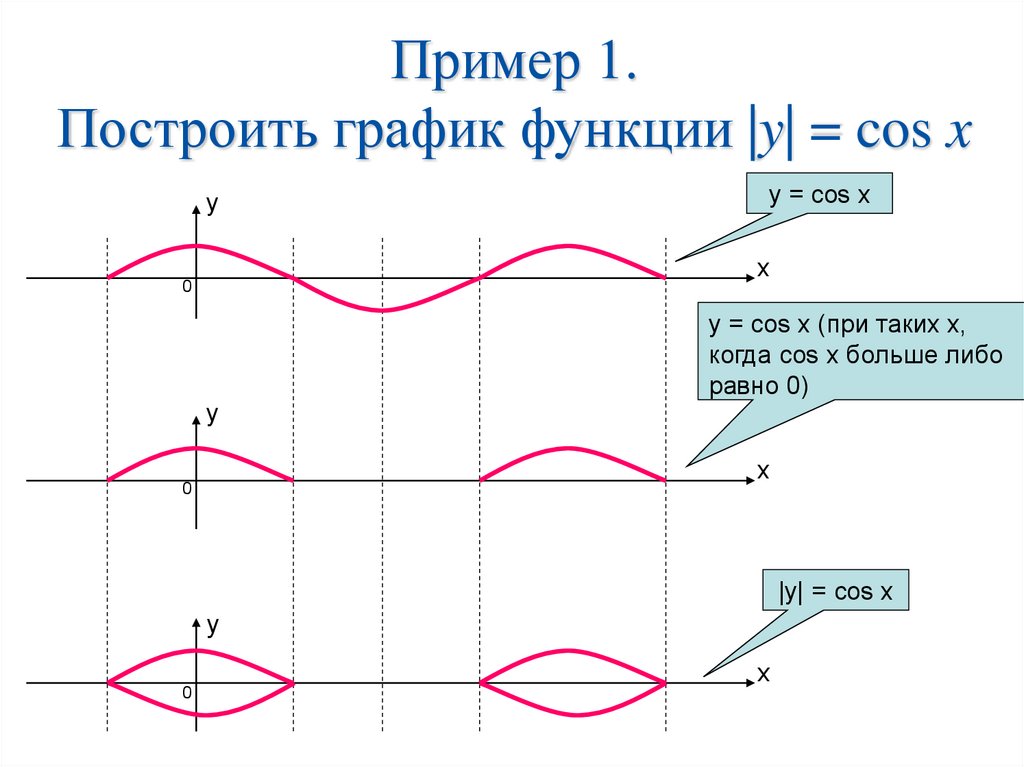 Решением системы будут координаты точек пересечения графиков функций.

ГРАФИЧЕСКИЙ МЕТОД:

Применяется для понижения степени и упрощения решения. При введении новых переменных мы получаем систему относительно новых переменных, а затем перейдем к решению и нахождению исходных переменных.

Билет№6: Модуль числа, определение, свойства.

Модуль действительного числа — это абсолютная величина этого числа.

Попросту говоря, при взятии модуля нужно отбросить от числа его знак.

Модуль числа a обозначается |a|. Обратите внимание: модуль числа всегда неотрицателен: |a|≥ 0.

|6| = 6, |-3| = 3, |-10,45| = 10,45

Определение модуля

Свойства модуля

1. Модули противоположных чисел равны
2. Квадрат модуля числа равен квадрату этого числа
3. Квадратный корень из квадрата числа есть модуль этого числа
4. Модуль числа есть число неотрицательное
5. Постоянный положительный множитель можно выносить за знак модуля	,
6. Если , то
7. Модуль произведения двух (и более) чисел равен произведению их модулей
8.

Модуль числа — это расстояние от нуля до данного числа.

Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.

Рассмотрим простейшее уравнение |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения: x = 3 и x = -3.

Пример 1.

|x — 3| = 4.

Это уравнение можно прочитать так: расстояние от точки до точки равно . С помощью графического метода можно определить, что уравнение имеет два решения: и .

Пример 2.

Решим неравенство: |x + 7| < 4.

Можно прочитать как: расстояние от точки до точки меньше четырёх. Ответ: (-11; -3).

Пример 3.

Решим неравенство: |10 — x| ≥ 7.

Расстояние от точки 10 до точки больше или равно семи. Ответ: (-∞; 3]υ [17, +∞)

График функции y = |x|

Для x≥ 0 имеем y = x. Для x < 0 имеем y = -x.

При решении задач, содержаних модуль вещественного числа, основным приемом является раскрытие знака модуля в соответствии с его свойствами.

Таким образом, если под знаком модуля стоит выражение, зависящее от переменной, мы раскрываем модуль по определению:

В некоторых случаях модуль раскрывается однозначно. Например: , так как выражение под знаком модуля неотрицательно при любых и . Или , так как выражением под модулем не положительно при любых .

Билет№7: Алгоритм освобождения от знака модуля.

Прировнять выражения стоящих под знаком, т. е. найти нули модуля, решив полученные уравнения.
Расположить в порядке возрастания нули модулей на числовой прямой, которые разобьют ее на интервалы.
Определить знак выражения, стоящего под знаком модуля в каждом интнрвале.
Если выражение под знаком модуля положительное, то убирая модуль, знак, стоящий перед выражением, необходимо сохранить. Если выражение отрицатольное, то убирая модуль, необходимо знак, стоящий перед выражением, изменить на противоположный.

Билет№8: Методы решения уравнений (неравенств) содержащих знак модуля.

Метод возведения обоих частей уравнения в квадрат. Этот метод применяется в том случае если обе части уравнения положительные при любых значениях, например |x+2|=3.
Универсальный метод заключается в том, что необходимо найти нули модуля и отметить на координатной прямой полученные точки. Определить знак модуля в каждом интервале, решить уравнения в каждом интервале.

Билет№9: Решение неравенств методом интнрвалов.

План решения неравенства методом интервалов.

Переносим все члены неравенства в одну сторону (например, влево)

Не производя абсолютно никаких преобразований, находим область определения функции стоящей в левой части неравенства, после чего в области определения функции с целью упрощения допускается выполнение тождественных преобразований.

Находим нули функций.

Рисуем пунктиром числовую ось, после чего сплошной линией обводим промежутки оси, принадлежащие области определения функции. На них точки, в которых функция терпит разрыв, отмечаем “пустыми” (не заштрихованными), отмечаем на оси нули (корни) функции:

— “пустыми” (не заштрихованными), точками, если неравенство строгое полными (черными), заштрихованными точками, если неравенство не строгое.

Определяем знак функции на каждом из полученных интервалов (например, подстановкой в выражении функции какого-либо значения из соответствующего интервала).

выбираем для ответа нужные интервалы в соответствии со знаком неравенства.

Записываем ответ.

Билет№10: Функция y=sinx. График, свойства.

y = sin x

график — синусоида

Свойства функции

Область определения: R
Область значений: [-1; 1]
Четность, нечетность: функция нечетная
Нули: sin x = 0 при x = πn, n Z
Промежутки знакопостоянства: sin x > 0 при x (2 π n; n + 2 π n), n Z sin x < 0 при x (- π + 2 π n; 2 π n), n Z
Экстремумы: x_min = + 2 π n, n Z; y_min = -1 x_max = + 2 π n, n Z; y_min = 1
Промежутки монотонности:
Функция переодическая с наименьшим положительным периудом 2 π

Билет№11: Функция y=cosx.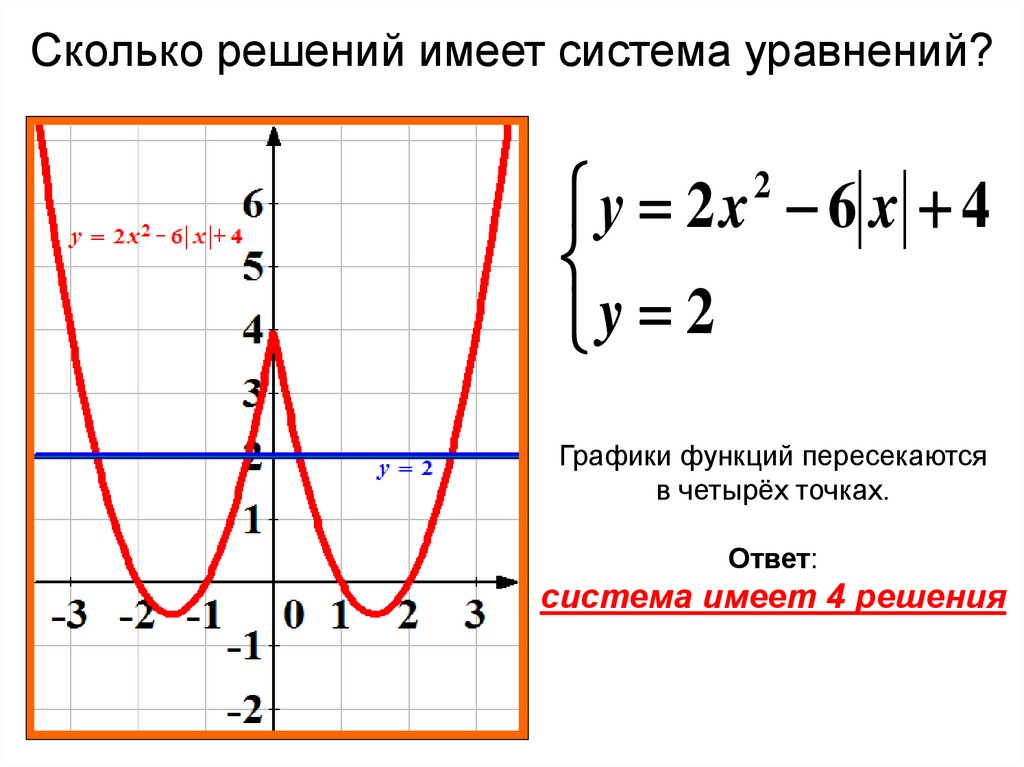 График, свойства.

y = cos x

график — косинусоида

Свойства функции

Область определения: R
Область значений: [-1; 1]
Четность, нечетность: функция четная
Период: 2
Нули:
Промежутки знакопостоянства:
Экстремумы: x_min = + 2 n, n Z; y_min = -1 x_max = 2 n, n Z; y_min = 1
Промежутки монотонности: < LI>

Преобразования графиков y = sinx и y = cosx : Графики функций y = sinx и y = cosx можно получить друг из друга путем параллельных переносов вдоль оси x на /2: <>

Билет№12: Функция y=tgx. График, свойства.

y = tg x

график — тангенсоида

Свойства функции

Область определения: объединение интервалов
Область значений: R
Четность, нечетность: функция нечетная
Период:
Нули: y = 0 при x = n, n Z
Промежутки знакопостоянства:
Экстремумов нет
Промежутки монотонности: функция возрастает на каждом интервале области определения
Асимптоты: x = + n, n Z

Билет№13: Функция y=сtgx. График, свойства.

y = ctg x

график — катангенсоида

Свойства функции

Область определения: объединение интервалов
Область значений: R
Четность, нечетность: функция нечетная
Период:
Нули:
Промежутки знакопостоянства:
Экстремумов нет
Промежутки монотонности: функция убывает на каждом интервале области определения
Асимптоты: x = n, n Z

Преобразования графика y = ctgx : График функци y = ctgx получается из графика у =tgx путем отражения относ. любой из координатныхосей и последующим параллельным переносом вдоль оси x на /2.

Билет№14: Определение тригонометрических функций по окружности и по треугольнику.

Синус угла — отношение противолежащего катета к гипотенузе: Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны. Косинус угла — отношение прилежащего катета к гипотенузе: Так как синус одного острого угла в треугольнике равна косинусу второго, и наоборот. Тангенс угла — отношение противолежащего катета к прилежащему: Котангенс угла — отношение прилежащего катета к противолежащему:

По окружности:

Так как длина отрезка OA равна 1, то Косинусом угла называется отношение абсциссы точки A к длине отрезка OA. Обозначают Так как длина отрезка OA равна 1, то Тангенсом угла называется отношение ординаты точки A к абсциссе точки A. Обозначают (в англоязычной литературе Так как и то Котангенсом угла называется отношение абсциссы точки A к ординате точки A. Обозначают Так как и то Котангенс равен обратному значению тангенса.

Билет №15: y=arccos, y=arcsin определение, свойства.

1.Функция y = arcsin х.

Арксинусом числа m называется такое значение угла x, для которого

Функция y = sin x непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.

extensions — Модуль классов и функций расширения — документация pyjsgf 1.9.0

Этот модуль содержит классы для компиляции и сопоставления правила JSpeech Grammar Format расширения.

Классы

класс jsgf.expansions. Альтернативный набор ( *расширения )

Класс для набора расширений, одно из которых может быть произнесено.

генерировать ()

Создайте соответствующую строку для этого альтернативного набора.

Каждая альтернатива имеет равные шансы быть выбранной для генерации строки.

Если заданы веса, то вероятность альтернативы равна ее весу свыше сумма всех весов:

 p = вес / сумма (веса)

set_weight ( ребенок , вес )

Установить вес ребенка.

Вес определяет вероятность произнесения альтернативы.

Более высокие значения более вероятны, более низкие значения менее вероятны. Ценность 0 означает, что альтернатива никогда не будет сопоставлена. Отрицательный веса не допускаются.

Примечание : веса составляются как числа с плавающей запятой с точностью до 4 десятичные знаки, например. 5.0001.

Параметры:	child ( Expansion\|int\|str ) — дочерний/списочный индекс/скомпилированный дочерний элемент, для которого устанавливается вес. вес ( float\|int ) – значение веса должно быть >= 0

гири

Словарь альтернатив их весам.

Тип возврата:	dict

класс jsgf. expansions. Дочерний список ( расширение , seq=() )

Класс-оболочка списка для расширенных дочерних списков.

Атрибут parent каждого дочернего элемента будет установлен соответствующим образом, когда они добавлены или удалены из списков.

прозрачный (): Удалить все расширения из этого списка и отменить их родительские атрибуты.

дети-сироты (): Установите для каждого дочернего родителя значение «Нет».

класс jsgf.expansions. Расширение ( детей )

Расширение базового класса.

_make_matcher_element ()

Метод, используемый свойством matcher_element для создания ParserElements.

Подклассы должны реализовать этот метод для функциональности сопоставления речи.

детей

Список детей.

Возвраты:	Список дочерних элементов

collect_leaves ( порядок = 0 , мелкий = ложь )

Соберите всех потомков расширения, у которых нет потомков. Это может включать себя, если у него нет детей. RuleRefs также считаются листья.

Параметры:	порядок – порядок обхода дерева (по умолчанию 0: предзаказ) мелкое – не собирать ли листья с деревьев указанных правил
Возвращает:	список

скомпилированный_тег

Получите скомпилированный тег для этого расширения, если он есть. Пустая строка возвращается, если тег не установлен.

Возврат:	стр

копия ( мелкий = Ложь )

Сделайте копию этого расширения. Это возвращает глубокую копию по умолчанию. Ни упомянутые правила, ни их расширения не будут глубоко скопированы.

Параметры:	small – создавать ли мелкую копию (по умолчанию: False)
Возвращает:	Расширение

текущий_матч

В настоящее время соответствует значению речи для этого расширения.

Если расширение не было сопоставлено, это будет None (если требуется) или ‘’ (если необязательно).

Возвраты:	ул \| Нет

генерировать (): Создайте строку, соответствующую этому расширению.

имел_соответствие

Имеет ли это расширение значение current_match , отличное от ‘’ или None. Это также проверит, было ли это расширение частью полного повторения, если у него есть предок Repeat или KleeneStar.

Возвращает:	bool

invalidate_calculations ()

Недействительные вычисления, хранящиеся в таблицах поиска, которые включают это расширение. Это влияет только на взаимоисключающих_из и is_descendant_of , ни один из которых не используется при компиляции или сопоставлении правила.

Должен вызываться, если к расширению добавляется дочерний элемент или если родитель расширения изменен вне того, что JointTreeContext делает.

Некоторые изменения могут также потребовать аннулирования потомков, т. е. Функция map_expansion может использоваться с этим методом для достижения этого:

 map_expansion(я, Expansion.invalidate_calculations)

invalidate_matcher ()

Метод аннулирования элемента анализатора, используемого для сопоставления с этим расширением. Этот метод вызывается автоматически, когда установлен родительский элемент или список дочерних элементов. изменен. При необходимости элемент анализатора будет воссоздан заново.

Это необходимо вызывать вручную только при изменении дерева расширения после сопоставление с расширением Диктовки.

is_alternative

Независимо от того, имеет ли это расширение предка AlternativeSet с более чем один ребенок.

Возвраты:	bool

is_descendant_of ( другое )

Является ли это расширение потомком другого расширения.

Параметры:	прочее – Расширение
Возвращает:	bool

is_Optional

Независимо от того, имеет ли это расширение необязательный предок.

Возвраты:	bool

листов

Параметры:	порядок – порядок обхода дерева (по умолчанию 0: предзаказ) мелкое – не собирать ли листья с деревьев указанных правил
Возвратов:	список

листья_после

Генераторная функция для листьев после этого (если есть).

Возврат:	генератор

статический make_expansion ( e )

Возьмите объект, превратите его в Расширение, если это не так, и верните его.

Параметры:	e – ул \| Расширение
Возвращает:	Расширение

matchable_leaves_after

Генераторная функция, выдающая все листья после себя, которые не взаимно исключая его.

Возврат:	генератор

matcher_element

Ленивая инициализация pyparsing ParserElement используется для сопоставления речи с расширения. Он также установит значений current_match .

Возвраты:	pyparsing.ParserElement

совпадений ( речь )

Сопоставьте речь с этим расширением, установите current_match на первое совпавшее подстроку и вернуть остаток строки.

Соответствие неоднозначным расширениям правил не поддерживается , потому что это не стоит производительность хит. Неоднозначные расширения правил определяются как некоторые необязательные литерал x, за которым следует требуемый литерал x. Например, успешно соответствие 'test' для следующего правила не поддерживается:

 <правило> = [тест] тест;

Параметры:	речь – стр
Возврат:	стр

match_slice

Фрагмент последней речевой строки совпал. Первоначально это будет None .

Тип возврата:	срез

взаимоисключающие_из ( прочие )

Нельзя ли говорить об этом расширении с другим расширением.

Параметры:	прочее – Расширение
Возвращает:	bool

родитель

Родитель этого расширения, если он есть.

Установка родителя вызовет Expansion.invalidate_matcher по мере необходимости на новых и старых родителей.

Возвращает:	Расширение \| Нет

repeat_ancestor

Ближайший предок этого дополнения Repeat или KleeneStar, если он есть.

Возвращает:	Расширение

reset_for_new_match (): Вызовите reset_match_data для этого расширения и всех его потомков.

reset_match_data ()

Сбросить все элементы или свойства, которые это расширение использует для сопоставления речи, то есть значений current_match .

Это делает , а не недействительным matcher_element .

root_expansion

Перейти к корневому расширению r и вернуться к нему.

Возвращает:	Расширение

тег

Тег JSGF для этого расширения.

Возврат:	стр

validate_compilable ()

Убедитесь, что расширение компилируется. Если это не так, этот метод должен поднимите CompilationError .

Поднимает:	Ошибка компиляции

класс jsgf.expansions. JointTreeContext ( root_expansion )

Класс, который временно объединяет дерево расширения с деревьями расширения всех ссылочные правила, устанавливая родительские отношения.

Это полезно, когда необходимо просмотреть дерево расширения и деревья упомянутых правил как одно большее дерево. Например. при определении взаимных эксклюзивность двух расширений, если расширение является необязательным или используется для повторение в контексте других деревьев и т. д.

Примечание : этот класс уменьшит производительность сопоставления при использовании, но только быть заметным с большими грамматиками.

На __exit__ деревья будут рекурсивно отсоединены.

Этот класс можно использовать с оператором Python with .

статический detach_tree ( x )

Если x является NamedRuleRef, отсоедините расширение ссылочного правила от этого дерево.

Параметры:	x – Расширение

статический дерево_объединения ( x )

Если x является NamedRuleRef, присоедините расширение указанного правила к этому дереву.

Параметры:	x – Расширение

класс jsgf.expansions. KleeneStar (расширение )

JSGF Оператор звездочки Клини для разрешения ноль или более повторений расширения.

Например:

  = (пожалуйста)* не сбой;

генерировать ()

Создайте строку, соответствующую этому расширению.

Этот метод может генерировать ноль или более повторений дочернего расширения, ноль повторений означает, что будет возвращена пустая строка ( «» ).

Тип возврата:	стр

класс jsgf.expansions. Литерал ( текст , с учетом регистра = Ложь )

Класс расширения для литералов.

с учетом регистра

Чувствительность к регистру, используемая при сопоставлении и компиляции правила Literal расширения.

Это свойство может быть Верно или Ложно . Сопоставление и компиляция будут be с учетом регистра if True и без учета регистра if False . значение по умолчанию False .

Тип возврата:	bool
Возвращает:	чувствительность к регистру

генерировать ()

Сгенерируйте строку, соответствующую тексту этого расширения.

Это просто вернет значение text .

Тип возврата:	стр

соответствие_regex_pattern

Шаблон регулярного выражения для соответствия этому расширению.

Это свойство оставлено для обратной совместимости. Метод Expansion.matches теперь использует свойство matcher_element . вместо.

Возвраты:	объект шаблона регулярного выражения

текст

Текст для сопоставления/компиляции.

Это вернет текст в нижнем регистре, если с учетом регистра не Правда .

Тип возврата:	стр
Возвращает:	текст

validate_compilable ()

Убедитесь, что расширение компилируется. Если это не так, этот метод должен поднимите CompilationError .

Поднимает:	Ошибка компиляции

класс jsgf.expansions. NamedRuleRef ( имя )

Класс, используемый для ссылки на правила по имени.

генерировать ()

Создать строку, соответствующую расширению указанного правила.

Тип возврата:	стр

referenced_rule

Найдите и верните правило, на которое ссылается это расширение в грамматике.

Это вызывает ошибку, если указанное правило не может быть найдено с помощью self.rule.grammar или если нет ссылки на грамматику.

Поднимает:	GrammarError
Возврат:	Правило

класс jsgf.expansions. NullRef

Расширение ссылки для специального правила NULL .

Правило NULL всегда соответствует речи. Если эта ссылка используется правило, эта часть расширения правила не требует совпадения речевой подстроки.

класс jsgf.expansions. Дополнительная группа (расширение )

Класс для расширений, которые можно дополнительно произнести в правиле.

генерировать (): Создайте строку, соответствующую этому расширению.

класс jsgf.expansions. Повторить ( расширение )

Оператор JSGF plus для разрешения одного или нескольких повторов расширения.

Например:

 <повторить> = (пожалуйста)+ не сбой;

генерировать ()

Создайте строку, соответствующую этому расширению.

Этот метод может генерировать одно или несколько повторений дочернего расширения.

Тип возврата:	стр

get_expansion_matches ( и )

Получить список дополнений current_match значений для каждого повторения.

Возвращает:	список

get_expansion_slices ( и )

Получить список значений match_slice расширения для каждого повторения.

Возвращает:	список

Repeats_matched

Количество последних совпавших повторений.

Возвращает:	целое число

reset_match_data ()

Это делает , а не недействительным matcher_element .

класс jsgf.expansions. RequiredGrouping ( * расширения ): Подкласс Последовательность для заключения нескольких расширений в круглые скобки.

класс jsgf. expansions. RuleRef ( referenced_rule )

Подкласс NamedRuleRef для ссылки на другое правило с помощью объекта Rule.

Параметры:	referenced_rule –

класс jsgf.expansions. Последовательность ( *расширения ): Класс для последовательного произнесения расширений.

класс jsgf.expansions. VoidRef

Расширение ссылки для специального правила VOID .

ПУСТОТА 9Правило 0009 никогда нельзя произносить. Если эта ссылка используется правилом, то он не будет совпадать, если ссылка не является необязательной.

Функции

jsgf.расширения. filter_expansion ( e , func=<функция <лямбда>> , порядок=0 , мелкое=ложь )

Найти все расширения в дереве расширений, для которых func(x) == True.

Параметры:	e — Расширение func – вызываемая (по умолчанию: тождественная функция, f(x)->x) заказ – вн. small – не обрабатывать ли деревья правил, на которые ссылаются (по умолчанию False)
Возвращает:	список

jsgf.расширения. find_expansion ( e , func=<функция <лямбда>> , порядок=0 , мелкий=ложь )

Найти первое расширение в дереве расширения, для которого функция func(x) имеет значение True и вернуть его. В противном случае вернуть None.

Эта функция прекратит поиск, как только будет найдено соответствующее расширение, в отличие от другие функции верхнего уровня в этом модуле.

Параметры:	e – Расширение func – вызываемая (по умолчанию: тождественная функция, f(x)->x) заказ – вн. small – не обрабатывать ли деревья правил, на которые ссылаются (по умолчанию False)
Возвращает:	Расширение \| Нет

jsgf.расширения. flat_map_expansion ( e , func=<функция <лямбда>> , порядок=0 , мелкий=ложь )

Вызовите map_expansion с аргументами и верните один плоский список.

Параметры:	e – Расширение func – вызываемая (по умолчанию: тождественная функция, f(x)->x) заказ – вн. small – не обрабатывать ли деревья правил, на которые ссылаются (по умолчанию False)
Возвращает:	список

jsgf.расширения. map_expansion ( e , func=<функция <лямбда>> , порядок=0 , мелкое=ложь )

Обход дерева расширения и вызов функции для каждого расширения, возвращающего кортеж Структура с результатами.

Параметры:	e – Расширение func – вызываемая (по умолчанию: тождественная функция, f(x)->x) заказ – вн. small – не обрабатывать ли деревья правил, на которые ссылаются (по умолчанию False)
Возвращает:	кортеж

jsgf. расширения. match_overlap ( m1 , м2 )

Проверить, не перекрываются ли два совпадения регулярных выражений.

Возвраты:	bool

jsgf.расширения. restore_current_matches ( e , значений , override_none=True )

Обход дерева расширения и восстановление совпадающих данных с помощью словаря значений.

Параметров:	e – Расширение значений – дикт override_none — логическое значение

jsgf.расширения. save_current_matches ( и )

Пройти по дереву расширения и вернуть словарь, заполненный каждым потомок Расширение и его данные соответствия.

Это также будет включать e .

Параметры:	e – Расширение
Возвращает:	дикт

extensions — Модуль классов и функций расширения — документация pyjsgf 1.9.0

Этот модуль содержит классы и функции расширения правил расширения.

Классы

класс jsgf.ext.expansions. Диктовка

Класс, представляющий ввод под диктовку, соответствующий любым произносимым словам.

Это в значительной степени основано на классе элементов Dictation в стрекозе Python. библиотека.

Диктовка расширения компилируются в специальную ссылку ( ), аналогично NullRef и VoidRef . См. Класс DictationGrammar , если вы хотите использовать этот тип расширения с CMU Карманный сфинкс.

Соответствующая реализация для 9Расширения 0010 Dictation ждут впереди возможные следующие литералы, чтобы избежать их сопоставления и сделать правило недействительным соответствовать. Он также будет искать литералы в возможных повторениях в будущем.

Это будет , а не , однако посмотрите на правила ссылок для следующего возможного литералы. Если из-за этого у вас возникают сбои в матче, используйте только Диктовка расширения в общедоступных правилах или используют класс JointTreeContext до сопоставление, если вы не возражаете против снижения производительности сопоставления.

соответствие_regex_pattern

Шаблон регулярного выражения для соответствия этому расширению.

Возвращает:	объект шаблона регулярного выражения

use_current_match

Соответствует ли current_match значение в следующий раз вместо совпадения одно или несколько слов.

Используется методом SequenceRule.graft_sequence_matches .

Возвраты:	bool

validate_compilable ()

Убедитесь, что расширение компилируется. Если это не так, этот метод должен поднимите CompilationError .

Поднимает:	Ошибка компиляции

Функции

jsgf.ext.expansions. calculate_expansion_sequence ( расширение , should_deepcopy = True )

Разделить расширение на 2*n расширений, где n — количество Диктовка расширений в дереве расширений.

Если нет Диктовка расширений, результатом будет оригинал расширение.

Презентация «Модуль в выражениях, линейных уравнениях и линейных функциях»

Геометрический смысл модуля

extensions — Модуль классов и функций расширения — документация pyjsgf 1.9.0

Классы

Функции

extensions — Модуль классов и функций расширения — документация pyjsgf 1.9.0

Классы

Функции

Добавить комментарий Отменить ответ