Калькулятор расстояния между точками
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор нахождения длины отрезка поможет вычислить расстояние между заданными точками и дать подробное решение как в пространстве размерности 2d, так и в 3d.
Укажите размерность пространства 23
Задайте координаты точек
Координаты точки А: ( ; )
Координаты точки В: ( ; )
Как найти расстояние между точками плоскости и пространства
Расстояние между двумя точками в Евклидовом пространстве вычисляется по теореме Пифагора c2 = a2 + b2 и выражается формулой:
|AB| = √(Bx — Ax)2 + (By — Ay)2 — для вычисления длины отрезка плоскости
|AB| = √(Bx — Ax)2 + (By — Ay)2 + (Bz — Az)2 — для вычисления длины отрезка пространства
Расстояние между точками в Евклидовом пространстве – называется Евклидовой метрикой, либо Евклидовым расстоянием.
Пример 1. Найдем расстояния между точками плоскости с координатами A(x; y) и точки B(x; y), где A(1; 9) и B(4; 7).
Тогда согласно формуле:
Bx = 4;
Ax = 1;
By = 7;
Ay = 9;
Подставим значения в формулу и вычислим расстояние между точками A и B:
|AB| = √(Bx — Ax)2 + (By — Ay)2
=
√(4 — 1)2 + (7 — 9)2
=
√32 + (-2)2
=
√
√13 = 3.60555127546399
Пример 2. Найдем расстояния между точками пространства с координатами A(x; y; z) и точки B(x; y; z), где A(5; 2; 9) и B(3; 6; 7).
Тогда согласно формуле
Bx = 3;
Ax = 5;
By = 6;
Ay = 2;
Bz = 7;
Az = 9;
Подставим значения в формулу и вычислим расстояние между точками A и B
|AB| = √(Bx — Ax)2 + (By — Ay)2 + (Bz — Az)2
=
√(3 — 5)2 + (6 — 2)2 + (7 — 9)2
=
√4 + 16 + 4 =
√24 = 2 √6 = 4.89897948556636
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Расстояние между двумя точками онлайн
С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить».
Теоретическую часть смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние между двумя точками на прямой
Пусть заданы на оси OX точки A с координатой xa и B с координатой xb (Рис.1). Найдем расстояние между точками A и B.
Расстояние между точками A и В равно:
| \( \small AB=OB-OA. \) | (1) |
Поскольку расстояние от O до В равна xb, а расстояние от O до A равна xa, получим:
| \( \small AB=x_b-x_a . \) | (2) |
На рисунке 2 точки A и В находятся по разные стороны начала координат O.
B этом случае рассояние между точками A и B равно:
| \( \small AB=OB+OA. \) | (3) |
Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:
| \( \small AB=x_b+|x_a|=x_b-x_a . \) | (4) |
На рисунке 3 точки A и В находятся c левой стороны начала координат O.
B этом случае рассояние между точками A и B равно:
| \( \small AB=OA-OB. \) | (5) |
Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:
| \( \small AB=|x_a|-|x_b|=x_b-x_a . \) | (6) |
Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).
Формулы (2),(4),(6) можно записать и так:
| \( \small AB=|x_b-x_a|= |x_a-x_b| . \) | (7) |
Пример 1. на оси Ox заданы точки \( \small A(x_a)=A(-4) \) и \( \small B(x_b)=B(7) \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):
| \( \small AB=|x_b-x_a|= |7-(-4)|=11 . \) | (7) |
Ответ: 11.
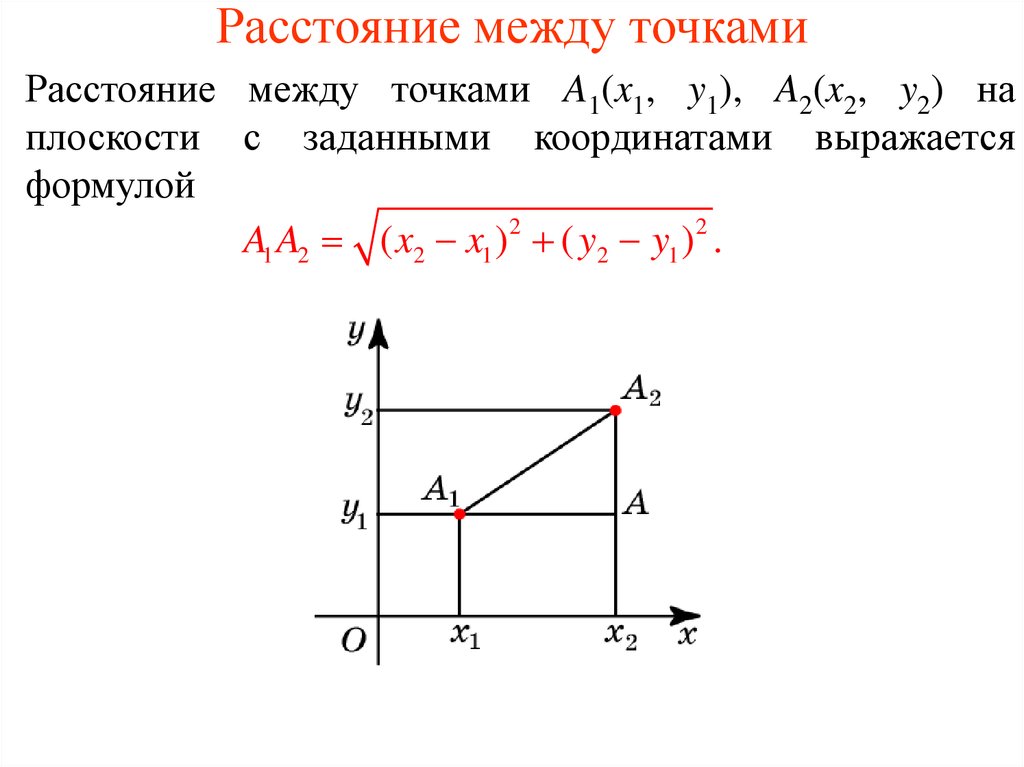
Расстояние между двумя точками на плоскости
Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (xa,ya), а B имеет координаты (xb,yb) (Рис.4).
Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:
\( \small AM=x_b-x_a,\;\; BM=y_b-y_a. 2}. \) | (9) |
Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки \( \small A(x_a; \ y_a)=A(-6;3) \) и \( \small B(x_b, \ y_b)=B(11,-4). \) . Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:
Ответ: .
Расстояние между двумя точками в пространстве
Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (xa,ya,za), а B имеет координаты (xb,yb,zb) (Рис.5).
AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника.
2}. \)
Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки \( \small A(x_a; \ y_a ;\ z_a)=A(5;1;0) \) и \( \small B(x_b, \ y_b, \ z_b)=B(-8,-4;21). \) Найти рассояние между этими точками.
Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:
Ответ: .
Калькулятор расстояния между двумя точками
Наш калькулятор расстояния между двумя точками может быстро найти расстояние между любыми двумя точками, ограниченными двумерной плоскостью.
В этом коротком тексте мы рассмотрим:
- Как найти расстояние между двумя точками ;
- Как использовать формулу расстояния между двумя точками; и
- Каково кратчайшее расстояние между двумя точками.
Начнем!
Предпочитаете смотреть , а не читать? Узнайте все, что вам нужно, за 90 секунд с помощью этого видео , которое мы сделали для вас :
youtube.com/embed/6_jGJuKyppY?rel=0&showinfo=0″ loading=»lazy»> Смотрите на YouTubeЧто такое расстояние? Определение расстояния между двумя точками
В простейшем определении расстояние между двумя точками на 2D плоскости равно длине соединяющего их отрезка .
Например, если нанести на график точки (0,4)(0,4)(0,4) и (4,4)(4,4)(4,4), провести линию между ними , и измерим длину этого отрезка, в результате получим 444.
Это определение получено из определения Евклидово расстояние , и мы также можем определить 1D , 3D , 4D и любое конечное измерение Евклидово расстояние.
Конечно, рисовать и измерять линии каждый раз, когда мы хотим найти расстояние между двумя точками, нецелесообразно . Вот где расстояние между двумя точками формула приходит на помощь.
Расстояние между двумя точками формула
9{2}}d=(x2−x1)2+(y2−y1)2
где:
- x1x_{1}x1 и y1y_{1}y1 – координаты любая из двух точек;
- x2x_{2}x2 и y2y_{2}y2 — координаты другой точки; и
- ddd — расстояние между ними.
💡 Это определение делает кратчайшее расстояние между двумя точками на двумерной плоскости всегда линией ! Не волнуйся . Мы не будем углубляться в математику в этом калькуляторе расстояния между двумя точками 😉.
Как найти расстояние между двумя точками?
Чтобы найти расстояние между двумя точками, просто выполните следующие действия:
Найти XY координаты первой точки (x₁, y₁) . Неважно, какую точку мы выберем, пока мы не смешиваем координаты между ними.
Найдите координаты XY другой точки (x₂, y₂) .
Замените эти значения в формуле расстояния между двумя точками:
√[(x₂ — x₁)² + (y₂ — y₁)²] .
Другие полезные инструменты
Если вам понравился этот калькулятор расстояния между двумя точками и вы хотите узнать больше о других определениях расстояния, проверьте любой из наших других инструментов расчета расстояния:
- Расстояние;
- 2D расстояние;
- Длина сегмента линии;
- Координатное расстояние; и
- Евклидово расстояние.
🙋 Попробуйте! Введите координаты любых двух точек в калькулятор расстояния между двумя точками, и он автоматически выведет расстояние между ними.
Часто задаваемые вопросы
Каково кратчайшее расстояние между двумя точками?
Кратчайшее расстояние между двумя точками — это прямая, соединяющая их . Это определение применимо только к плоским поверхностям или пространствам. Например, на сфере кратчайшее расстояние между двумя точками — это дуга, называемая расстоянием по большому кругу .
Какое расстояние между (5, 10) и (8, 9)?
3.16228 . Мы можем найти расстояние между точками (5, 10) и (8, 9) , заменив их в формуле расстояния между двумя точками:
√[(8 - 5)² + (9 - 10)²] = 3,16228 .
Расстояние между двумя точками калькулятор
Расстояние = 5,099
Генерировать работу
Отчет об этом
.
Создание работы
DSIATNCE между 2 очками — работа с шагами
Расчет двух очков . точки `A(x_A,y_A)` и `B(x_B,y_B)` в двумерной декартовой плоскости координат и найти длину отрезка `\overline{AB}`.
Для этого онлайн-инструмента геометрии требуются координаты 2 точек в двумерной декартовой координатной плоскости.
Необходимо выполнить следующие шаги:
- Введите координаты (`x_A`,`y_A`) и (`x_B`,`y_B`) двух точек `\text{A и B в рамке}`. Эти значения должны быть действительными числами или параметрами;
- Нажмите кнопку » GENERATE WORK «, чтобы произвести вычисления;
- Калькулятор расстояний выдаст длину отрезка линии `overline{AB}`.
Ввод: Две упорядоченные пары действительных чисел. Обратите внимание, что некоторые координаты могут быть переменными 92}`
Какое расстояние между двумя точками?
Для любых двух точек существует ровно один отрезок, соединяющий их.
Расстояние между двумя точками — это длина отрезка, соединяющего их. Обратите внимание, что расстояние между двумя точками всегда положительно. Сегменты, имеющие одинаковую длину, называются конгруэнтными сегментами.
| Расстояние между двумя точками | |||||
|---|---|---|---|---|---|
| (x A , y A ) и (x B , Y B ) | Расстояние | ||||
| (1, 2) и (3, 4) | 2,8284 | 9696.7082 | |||
| (1, 2) and (5, 5) | 5 | ||||
| (1, 2) and (7, 6) | 7.2111 | ||||
| (1, 1) and (7, -7) | 10 | ||||
| (13, 2) и (7, 10) | 10 | ||||
| (1, 3) и (5, 0) | 5 | ||||
| (1, 3) and (5, 6) | 5 | ||||
| (9, 6) and (2, 2) | 8. 0623 | ||||
| (5, 7) and ( 7, 7) | 2 | ||||
| (8, 2) and (3, 8) | 7.8102 | ||||
| (8, -3) and (4, -7) | 5.6569 | ||||
| ( 8, 2) и (6, 1) | 2,2361 | ||||
| (-6, 8) и (-3, 9) | 3,1623 | ||||
| (7, 11) и (-91, 91)0236 | 10 | ||||
| (-6, 5) and (-3, 1) | 5 | ||||
| (-6, 7) and (-1, 1) | 7.8102 | ||||
| (5, -4) и (0, 8) | 13 | ||||
| (5, -8) и (-3, 1) | 12,0416 | ||||
| (-5, 4) и (2, 6) | 6 7.2801 | ||||
| (4, 7) и (2, 2) | 5,3852 | ||||
| (4, 2) и (8, 5) | 5 | 3||||
| 9). 7) | 1,4142 | ||||
| (-3, 7) и (8, 6) | 11,0454 | ||||
| (-3, 4) и (5, 4) | 8 | (-3, 4) и (5, 4) | 8 | (3 29236 2920236.36236. (3, 4) и (5, 4).10 | |
| (-3, 4) и (1, 6) | 4,4721 | ||||
| (-2, 4) и (3, | 35.71111111113131313131313131313131313131131313131313113131313131313131131313131313. | . | |||
| (-2, 4) и (4, 7) | 6,7082 | ||||
| (-2, 5) и (5, 2) | 7,6158 | ||||
| 24.0832 | |||||
| (-1, 5) и (0, 4) | 1,4142 | ||||
| (-1, 4) и (4, 1) | 3335 (-1, 4) и (4, 1) | 533335 (-1, 4) и (4, 1) | 5333333335335.92335 (4) и (4, 1). и (4, 4) | 5 | |
| (0, 5) и (12, 3) | 12.1655 | ||||
| (0, 1) и (6, 3,5) | 6.5.95.9236.9236.9236 | (0, 1) и (6, 3,5). 0, 8) и (4, 5)5 | |||
| (0, 0) и (3, 4) | 5 | ||||
| (0, 0) и (1, 1) | 1,4142 | ||||
| (0, 1) и (4, 4) | 5 | ||||
| (0, 5) и (12, 3) | 12. 1655 | 36363613613613613613613613613613613613613613613613613613613613613613613613636136136363636363636133636363636363636er9) и (12, 3). 5, 7) | 5 | ||
| (2, 5) и (-4, 7) | 6.3246 | ||||
| (2, 3) и (1, 7) | 4.12335 (2, 3) и (1, 7) | 4.123335 (2, 3) и (7) | 4.1233123319236923692369236.92319236 923136.92319235.92319235. | 5,831 | |
| (3, 2) и (-1, 4) | 4,4721 | ||||
| (3, 12) и (94, 2)0236 | 14,8661 | ||||
| (3, 7) и (6, 5) | 3,6056 | ||||
| (3, 4) и (0, 0) | 5 | (3, 4) и (0, 0) | 5 | (3, 4) и (0, 0)5 | (3, 4). 2 балла? Длина сегмента обычно обозначается конечными точками без надчеркивания. Например, `\text{длина AB}` обозначается `\overline{AB}` или иногда `m\overline{AB}`. Расстояние также можно измерить с помощью масштаба на карте.
Расстояние между двумя точками, работа с шагами, показывает полный пошаговый расчет для нахождения длины отрезка, имеющего 2 конечные точки `A` с координатами `(5,3)` и `B` с координатами `(9, 6)`. Реальные задачи с использованием длины между двумя точкамиЕсли мы сравниваем длины двух или более отрезков, мы используем формулу для расстояния между двумя точками. Обычно мы используем формулу расстояния для нахождения длин сторон многоугольников, если нам известны координаты их вершин. В этом случае мы можем исследовать природу полигонов. Это также может помочь нам найти площадь и периметр многоугольника. Калькулятор расстояния между двумя точками используется почти во всех областях математики. Например, расстояние между двумя комплексными числами `z_1 = a + ib` и `z_2 = c + id` в комплексной плоскости равно расстоянию между точками `(a,b) и (c,d)`, то есть 92}` В физике длина пути между двумя точками `A и B` при их движении называется расстоянием. |
и (5, 8)
Линейка обычно используется для определения расстояния между двумя точками. Если мы поместим отметку «0» в левой конечной точке, а отметка, на которую падает другая конечная точка, будет расстоянием между двумя точками. В общем, нам не нужно измерять от отметки 0. Согласно постулату линейки, расстояние между двумя точками является абсолютным значением между числами, показанными на линейке.
С другой стороны, если две точки `A и B` находятся на оси x, то есть координаты `A и B` равны `(x_A,0)` и `(x_B,0)` соответственно, то расстояние между двумя точками `AB = |x_B −x_A|`. Тот же метод можно применить, чтобы найти расстояние между двумя точками на оси Y. Формула расстояния между двумя точками в двумерной декартовой плоскости координат основана на 92}`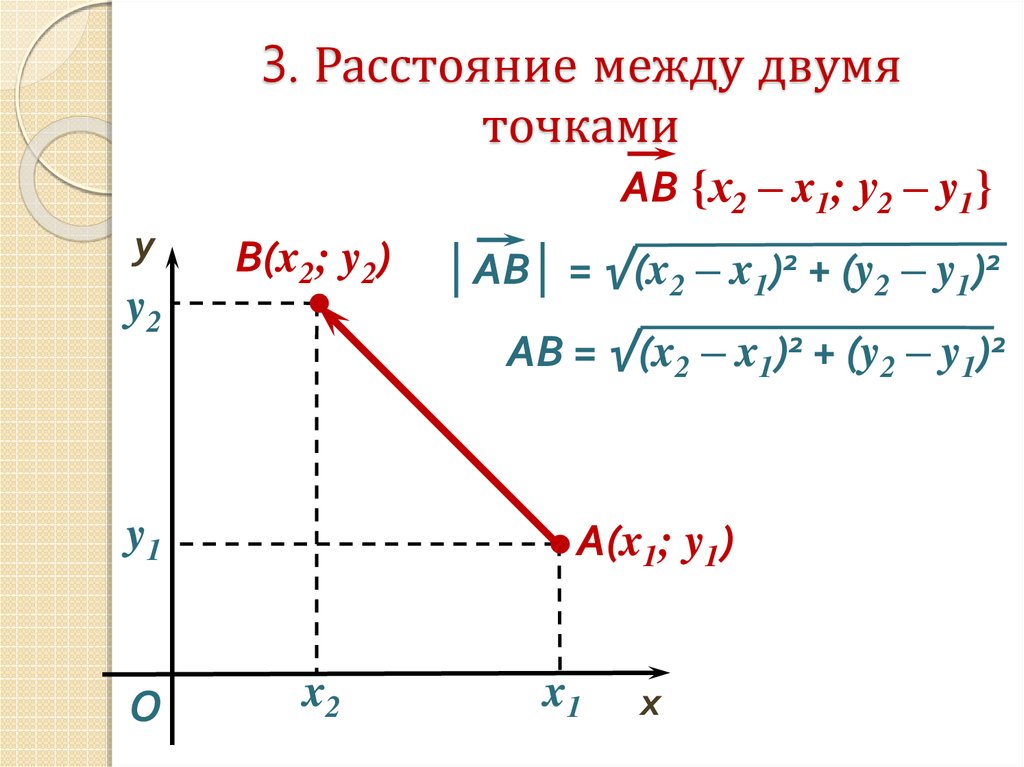
Для любых других комбинаций конечных точек просто укажите координаты 2 конечных точек и нажмите кнопку «СОЗДАТЬ РАБОТУ». Учащиеся начальной школы могут использовать этот калькулятор расстояний для создания работы, проверки результатов или эффективного решения домашних заданий.