Свойства средняя линия в трапеции: Средняя линия — урок. Геометрия, 8 класс.

Исследовательская работа по математике «Вторая средняя линия трапеции»

Министерство образования Республики Башкортостан

Муниципальное казенное учреждение  Управление образования Администрации муниципального района Белебеевский район Республики Башкортостан

муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа с.Усень-Ивановское муниципального района Белебеевский район Республики Башкортостан

                                                        

                                                                             452033

                                                                             Республика Башкортостан

                                                                             Белебеевский район

                                                                             с.Усень-Ивановское

                                                                              ул.

Комсомольская, д.70        

                                                                              т. 2-73-15

  МАОУ СОШ

                                                                              с.Усень-Ивановское

                                                                              «Интеллект будущего»

 

                                                                                  Секция: «математика»

 

  «Нужно ли изучать вторую среднюю линию трапеции?»

                                                                  

                                                   

                                                               Автор:  Подтеребкова Виктория

                                                               ученица 11 класса,

                                                               Научный руководитель:

                                                               Булатова Флюра Минниахметовна,

                                                               учитель   математики,

                                                               МАОУ СОШ с. Усень-Ивановское.

 

 

 

 

 

Белебей

 

Оглавление

 

1.      Введение                                                                                        3 стр.

2.      Основная часть

2.1    Определение второй средней линия трапеции                           4 стр.                                                                                                       

2.2    Свойства второй средней линии трапеции                                 5 стр.

2.3   Задачи ОГЭ и ЕГЭ                                                                          8 стр.

2.4   Задачи  составленные мною                                                          9 стр

3. Заключение                                                                                         12 стр.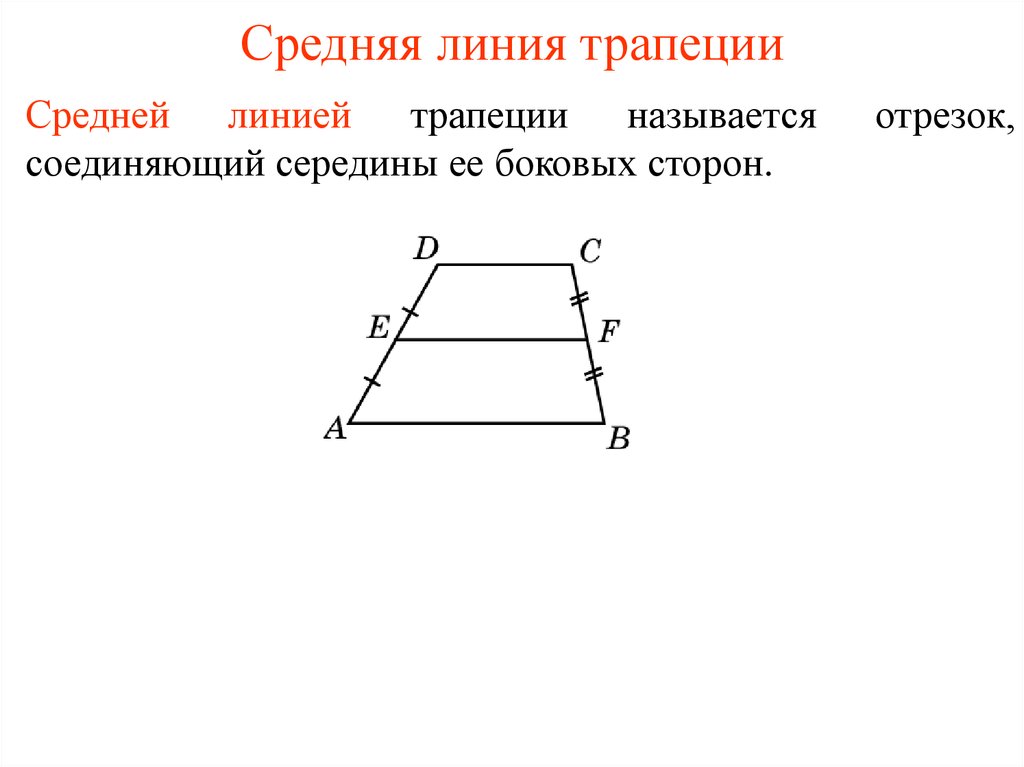

4. Список  литературы                                                                           13 стр.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение.

         На консультации по математике решая вариант ЕГЭ я столкнулась  с  геометрической задачей, которую не могла решить. За помощью обратилась учительнице. Она мне напомнила урок геометрии в 9 классе, когда изучая, тему средняя линия трапеции задали вопрос: а почему у трапеции только отрезок соединяющая середины боковых сторон называется средней линией трапеции, ведь можно так же соединить середины основании трапеции (по аналогии определения средней линии треугольника). Наша учительница сказала, что существует вторая средняя линия трапеции, но данная тема не изучается в школьном курсе.   Но если знать свойства второй средней линии трапеции данная задача ЕГЭ решается очень просто.

            Я заинтересовалась, а что же такое вторая средняя линия трапеции? После окончания школы я собираюсь поступать в ВУЗ, значит, мои знания должны быть шире школьной программы.  Чтобы расширить свои знания по теме трапеция я в интернете, в журналах  и в книгах по математике  стала искать информацию о второй средней линии трапеции.

    Цель работы: исследовать вторую среднюю линию трапеции.

Задачи:

·        Собрать информацию о второй средней линии трапеции.

·        Изучить свойства второй средней линии трапеции.

·        Решить задачи, имеющиеся в литературе, КИМах ОГЭ и ЕГЭ.

·        Составить и решить свои собственные задачи

·        Проанализировать каталог заданий ОГЭ и ЕГЭ

Актуальность темы: все больше и больше геометрических задач встречается в КИМах ОГЭ и  ЕГЭ   по математике в 9 и 11 классах,   материалы данного исследования можно использовать при подготовке к экзаменам.

Много интересного я нашла в статье «Вторая средняя линия трапеции» в журнале  «Математика в школе» № 2, 1993.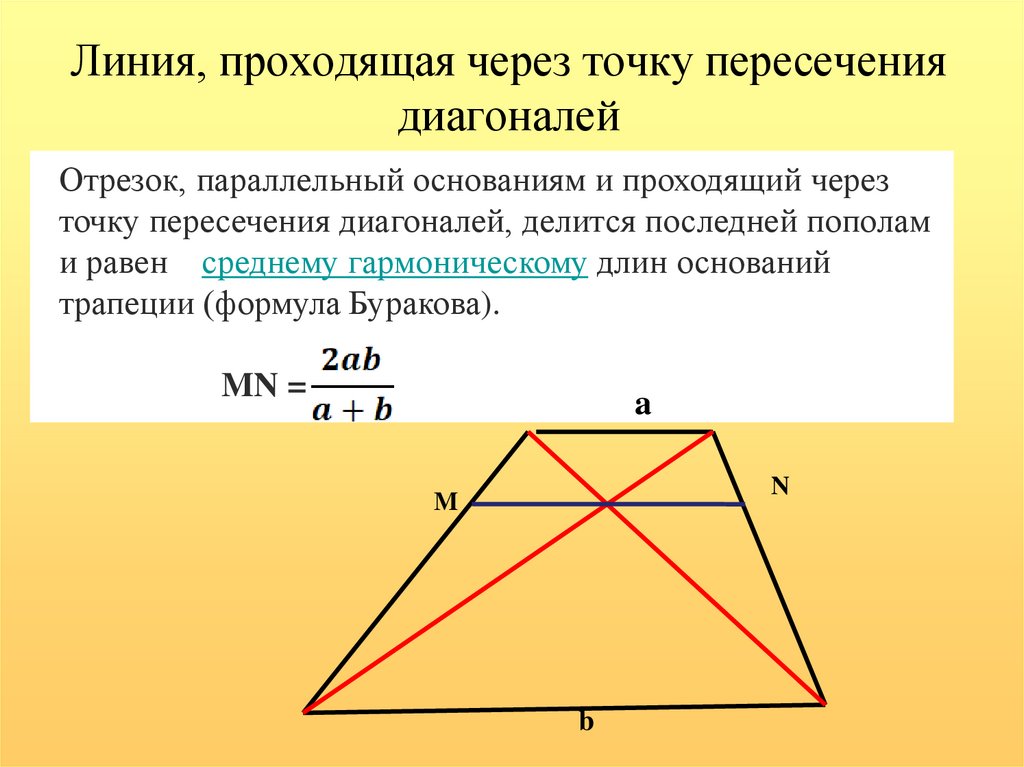 Автор статьи Кушнир И.А.

 

 

2.1 Основная часть

2.1 Определение второй средней линия трапеции.

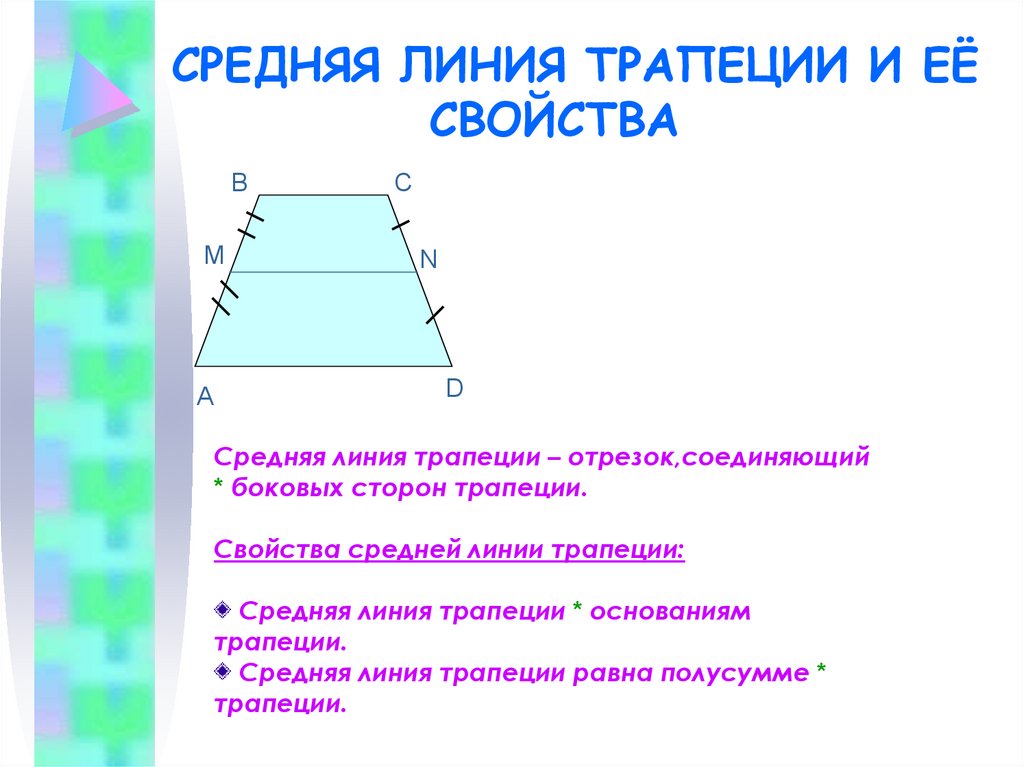
         Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон. Если же соединить отрезком середины оснований, получится вторая средняя линия трапеции. Итак, вторая средняя линия трапеции – это отрезок, соединяющий середины оснований трапеции.  

                                                       В          Е          С

 

 

 

 

                                   А                          К                     D

                                        ЕК – вторая средняя линия трапеции АВСD

             Как известно, средняя линия трапеции равна полусумме оснований. А есть ли связь между второй средней линией трапеции и её боковыми сторонами? Очевидно, что вторая средняя линия трапеции не равна полусумме боковых сторон, в чём можно убедиться, хотя бы растяжением одного из оснований:  

рис.1                             В         Е         С

 

 

 

              N              А                 К                   D                     M

 

сумма боковых сторон трапеции изменилась, а длина KS осталась прежней. И всё же связь между второй средней линией трапеции и боковыми сторонами есть. Воспользуемся векторным способом:

в трапеции АВСD (рис.1) ВС || АD, EK – вторая средняя линия.

 

EK = EB + BA +AК, с другой стороны,  ЕK = ЕC + CD + DК. Сложив оба равенства, получим:

                                                                

2ЕK = (ЕB + ЕC) + (BA + CD)+ (AК + DК)=0+(ВА+СD) + 0 = ВА + СD, т. е.

EK = (BA + CD)

Сделаем вывод: вектор второй средней линии трапеции равен полусумме векторов боковых сторон, взятых в одном порядке (сверху вниз).

Это утверждение можно доказать и вторым способом:

рис.2    О             

          В         Е     С                           В трапеции АВСD (ВС || АD) КS – вторая                    

                                                             средняя линия, О – произвольная точка

                                                         По формуле для середины отрезка:

    А              К               D                   ОЕ = (ОВ + ОС), OК = (OA + OD)

ЕК   =  OК – OЕ = ((OA – OB) + (OD – OC)),       ЕK = (BA + CD)

       При изучении данной темы, я узнала некоторые свойства средних линии трапеции.

2.2 Свойства средних линии трапеции.

1. Средние  линии трапеции пересекаются и в точке пересечения делятся пополам.

рис.3                                                                      Дано: АВСД- трапеция

                                                                              ЕК, MN— средние линии

                                                                             Доказать: MO=ON

                  B        Е        C                                  Доказательство: рассмотрим            

                В            Е          С                                  ВСD и    ABD: KN —

          M                                     N                          средняя линия       BCD                     

                              О                                                 EN || BD и EN=1/2 BD.

    А                      К                         D                 MK – средняя линия      ABD, MK || BD, MK=1/2BD. Аналогично, МE || АС, ME=1/2AC, NK || AC, NK=1/2AC. Таким образом, MENK – параллелограмм, (противоположные стороны четырехугольника параллельны) MN и EK – его диагонали, следовательно, KO = OE, MO = ON.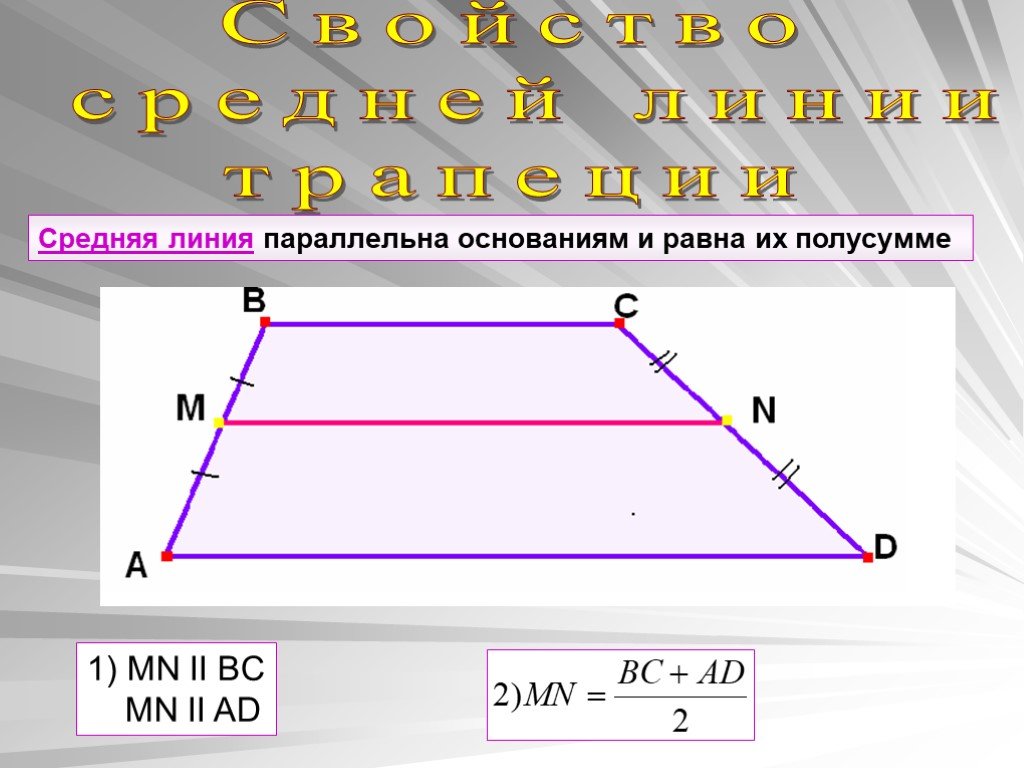

2. Если средние линии трапеции равны, то  диагонали трапеции перпендикулярны.

рис.4     В        Е      С            Дано: АВСD- трапеция                              

                                                   EK, MN- средние линии, ЕК=MN

          M                          N        АС, BD-диагонали                                                   

                                                   Доказать: AC┴BD

A                    K               D        Доказательство:

          МЕNK – параллелограмм (МЕ║АС, КN║AC, EN║BD, MK║BD), по условию MN=EK.Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник, ENME, т.к. EN||BD, ME||AC, то BDAC

Утверждение доказано.

Обратное утверждение: если диагонали трапеции перпендикулярны, то средние линии этой трапеции равны.

              В        Е      С            Дано: АВСD- трапеция                              

                                                   EK, MN- средние линии

          M                          N        АС, BD- диагонали,  AC┴BD                                               

                                                   Доказать: ЕК=MN

A                    K               D        Доказательство:

ACBD,  MEEN, MККN  MENК – прямоугольник  EК=MN

Применяя данное утверждение можно решить задачу ЕГЭ профильного уровня.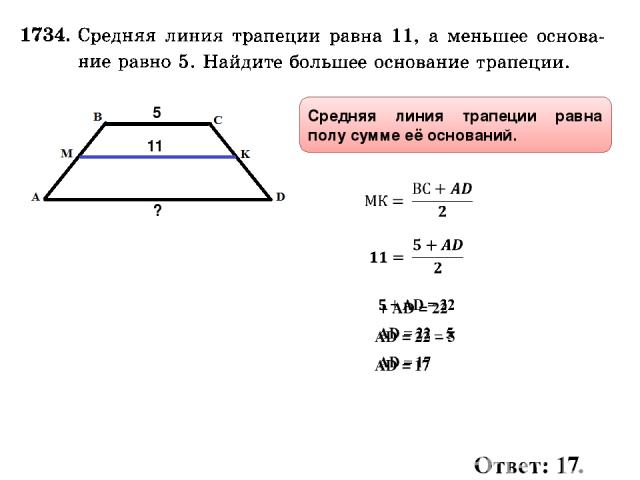

3. Вторая средняя линия трапеции проходит через точку пересечения диагоналей.  

рис.5     B        Е           C                              Дано:  АВСД — трапеция

                      О                                           АС, ВД – диагонали, АС ՌВD=O

                                                                    Е€ ВС,  ВЕ = ЕС, EOՌAD=К

      А                    К                    D            Доказать: AК = КD

     Доказательство:      как накрест лежащие при  ВС || AD и секущей BD. < ВОЕ=<КОD как вертикальные. ▲BOE∞ ▲KOD, аналогично,  ▲EOC∞AOK. BE/KD=OE/OK, EC/AK=OE/OK.

      Из этих равенств следует, что BE/KD=EC/AK, а т.к. BE = EC (по условию), то  AK = KD .  Значит, ЕК – вторая средняя линия трапеции и она проходит через точку пересечения диагоналей.        

4. Прямая, содержащая вторую среднюю линию трапеции, проходит через точку пересечения прямых, содержащих боковые стороны.

 

рис.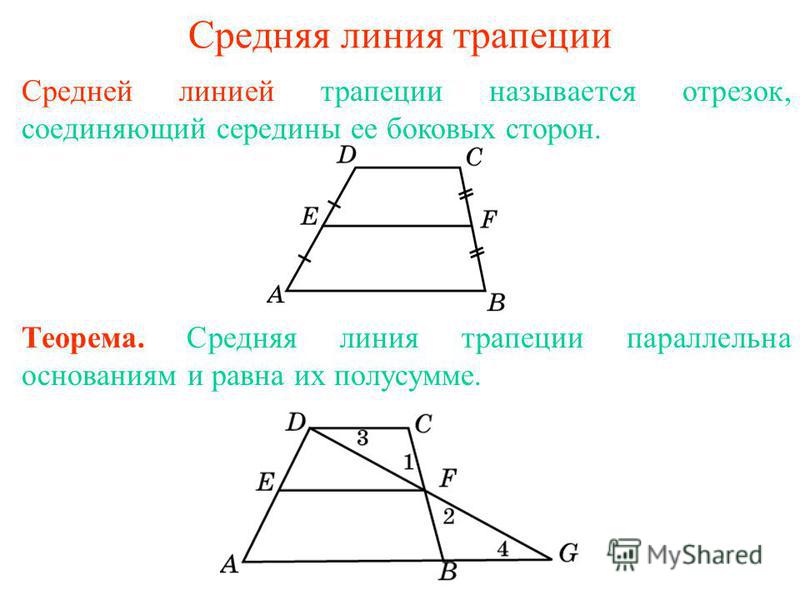 6             О              Дано: АВСD-трапеция

                                        ЕК- вторая средняя линия  

                                        Доказать: АВՌЕКՌСD=О

          B          Е      C      Доказательство:

                                        Рассмотрим ▲ВОС и  ▲AOD.    

                                        Они подобны по двум углам (<В=<А, <С=<D)

A               К            D                           ОА/ОВ=ОD/OC=k

                                                                

                      ODOC, OBOA,  OA =k ·OB,  OD = k ·OC.

                                               По формуле середины отрезка:

                               

OE = (ОВ+ОС),   OK = (OA+OD),   OK = (k ·OB + k ·OC)= k (OB+ OC)= = k ·OE   OE  коллинеарен  OK,  ОEK.

Обратное утверждение: если прямая проходит через точку пересечения прямых, содержащих боковые стороны и середину одного из оснований, то она является второй средней линией трапеции.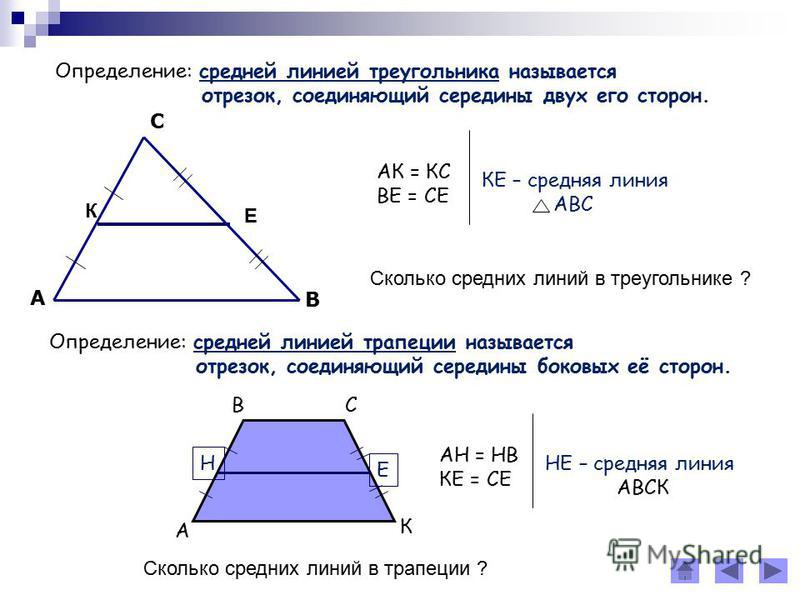

        Дано: трапеция- ABCD, АВՌDC=O, OК- прямая, К€АD, AK=KD.

       Доказать: ВЕ = ЕС

       Доказательство: (по рис.6)

∆ЕOC ~ ∆КOD  КD/EC=OK/OE  

∆ВОE ~ ∆AOK  AK/BE=OK/OE , т.к. АK = KD(по условию), то EС = ВE.

4. В равнобедренной трапеции средние линии перпендикулярны.

рис.7

      В       Е        С                                             Дано: ABCD — трапеция, АВ = CD,

                                                                            MN, ЕK – средние линии

М                             N                                         Доказать: MNЕK.

                                                 Доказательство:  

А             К               D                MЕ – средняя линия ∆АВС, МЕ||АС, МЕ=АС

 NК – средняя линия ∆ADC, NК||AC, NК =АС. Если противоположные стороны четырехугольника MЕNК равны и  параллельны, то по признаку MЕNК – параллелограмм  Т.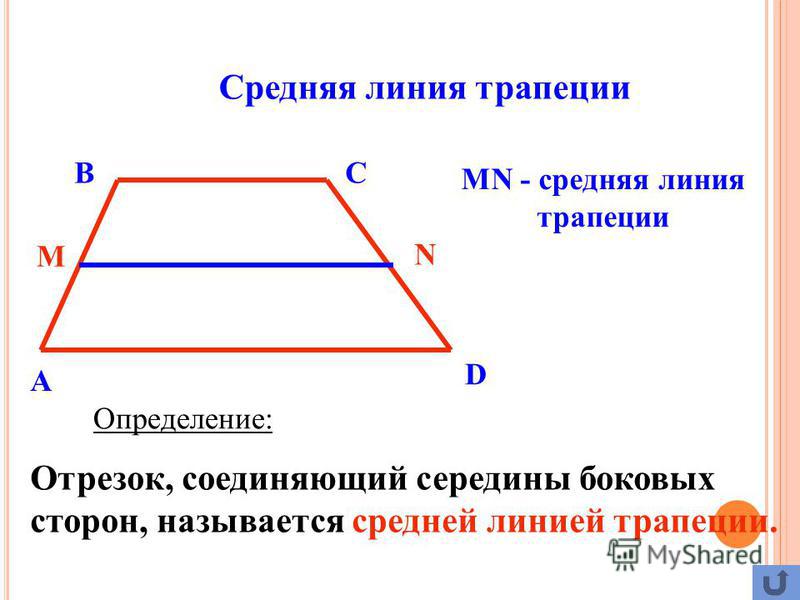 к. трапеция ABCD – равнобедренная, то AC = BD,

MЕ = АС,   ЕN = BD,  MЕ = ЕN,   MЕNК — ромб           

По свойству ромба, диагонали  MNЕK.

         Обратное утверждение: если средние линии трапеции перпендикулярны, то эта трапеция равнобедренная.

Доказательство (по рис.7) :

По теореме о средней линии трапеции MN||BC, MN||AD

По условию MNЕK,  BCЕK, ADЕK

BЕ=ЕC, AК=КD,  ЕK- ось симметрии трапеции ABCD,

AB и CD симметричны относительно ЕK,  AB=CD.

Из этого свойства, следует следующее:

          5. В равнобедренной трапеции вторая средняя линия перпендикулярна основаниям ( доказательство аналогичное)

2.3 Задачи по теме средние линии трапеции

         Приведу вашему вниманию задачи по теме вторая средняя линия трапеции .

ЕГЭ № 27844  В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию. (чертеж дан)                               

                 В        Е      С                                  

                                                  

                                                                  

                                                  

A                    K               D        Если диагонали перпендикулярны, то средние линии  трапеции равны, и в вторая средняя линия перпендикулярна основаниям.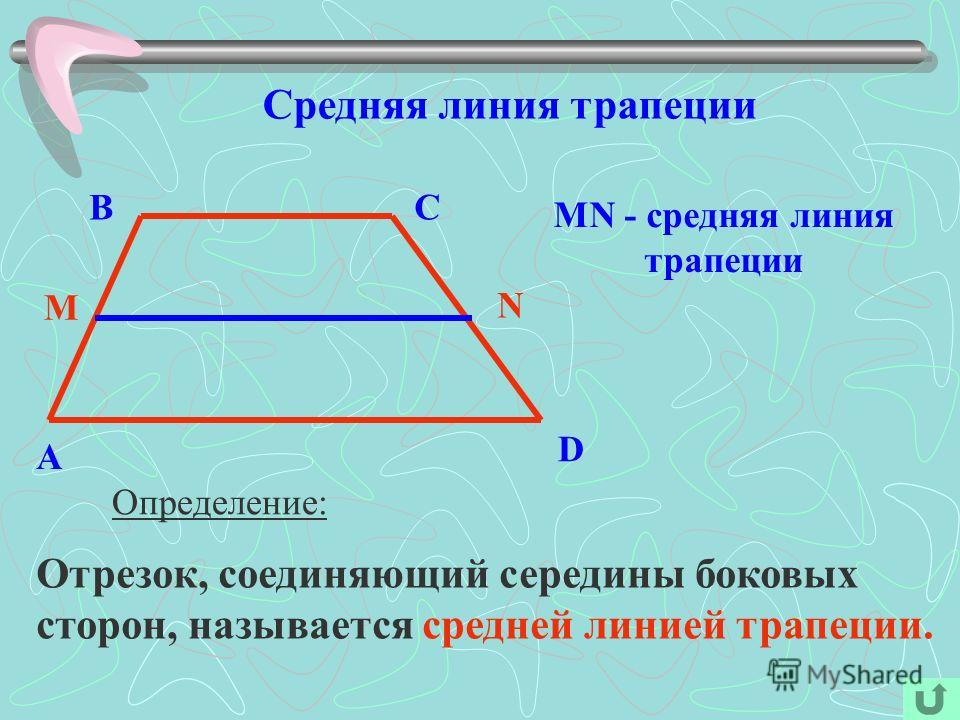 Следовательно, средняя линия равна 12. Ответ: 12.

Задача ОГЭ:

 Найти площадь равнобедренной трапеции, у которой диагонали взаимно перпендикулярны и высота равна 10 см. 

Sравн.трапеции=h²    если  d1 _┴ d2, высота трапеции будет равна средней линии трапеции. Ответ: 100см². 

В учебнике «Геометрия 7-9 » (автор Л.С.Атанасян) имеется задача №820, в разделе задачи повышенной трудности в главе V.

         Решим еще несколько задач.           

№1. Доказать, что площадь трапеции равна произведению второй средней линии на диагональ трапеции и на синус угла между ними.

             B      E        C

рис.9                                                                 Дано: ABCD – трапеция,

                                                                         EF – вторая средняя линия.

                       

                                                                          Доказать:

A                                F                          D

         Доказательство. Соединив точки А и E, С и F,  получим что площадь трапеции AECF,  , где  — угол между отрезками EF и AC.   и   . Значит, площадь трапеции ABCD равна удвоенной площади трапеции AECF, что и требовалось доказать.

№2. Доказать, что площадь трапеции равна произведению второй средней линии на сумму перпендикуляров, проведенных к этой средней линии (или её продолжению) из двух противоположных вершин трапеции.

               B      E    C

рис.10         N                                                Дано: ABCD – трапеция,

                                                                       EF – вторая средняя линия,

                               M                                     СNEF, AMEF.  

                                                                       Доказать:

A                               F                     D

Доказательство:  Рассмотрим треугольники AEF и ECF. , . Тогда . Т. к. , то .

№3. Как с помощью одной линейки провести в трапеции вторую среднюю линию?

         Решение:

1)    Провести диагонали.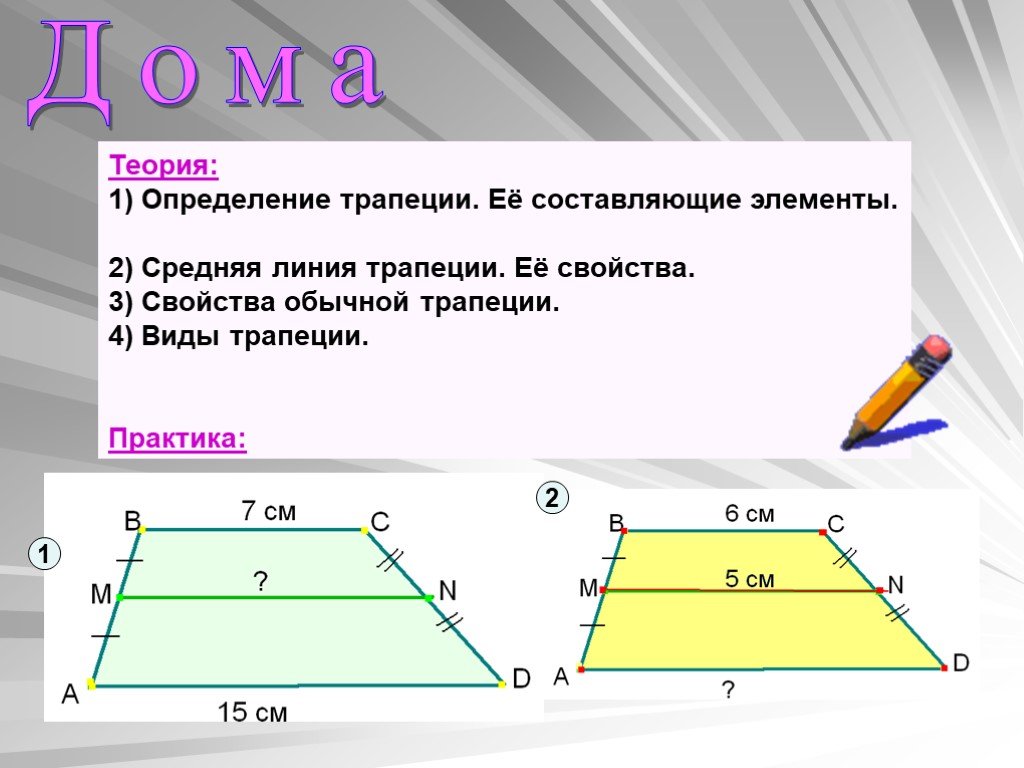

2)    Продолжить боковые стороны до их пересечения.

3)    Через точку пересечения диагоналей и точку пересечения продолжений боковых сторон провести прямую.

4)    Отрезок прямой, заключенный между основаниями трапеции – искомая вторая средняя линия трапеции.

№4. Можно ли построить трапецию, если известны её средние линии и угол между ними?

         Решение: можно; решений будет бесконечное множество. При построении нужно воспользоваться свойством 1.

№5.  (№820) Докажите, что прямая, проходящая через середины оснований равнобедренной трапеции, перпендикулярна к основаниям.

         Решение: см. доказательство свойства 4.

№6. В трапеции ABCD сумма углов при основании  AD равна 90º. Доказать, что отрезок, соединяющий середины оснований, равен полуразности оснований.

рис.11           M                                                           Решение: AF = FD, BN = NC

                                                                                   º, º,

                                                                                    AD – гипотенуза,

       B                   N                          C                         MF = AF = FD = AD

         А                      F                                        D        MN = BC

                                                                                     FN = MF – MN 

                                                                  FN = AD — BC = (AD – BC)

№7.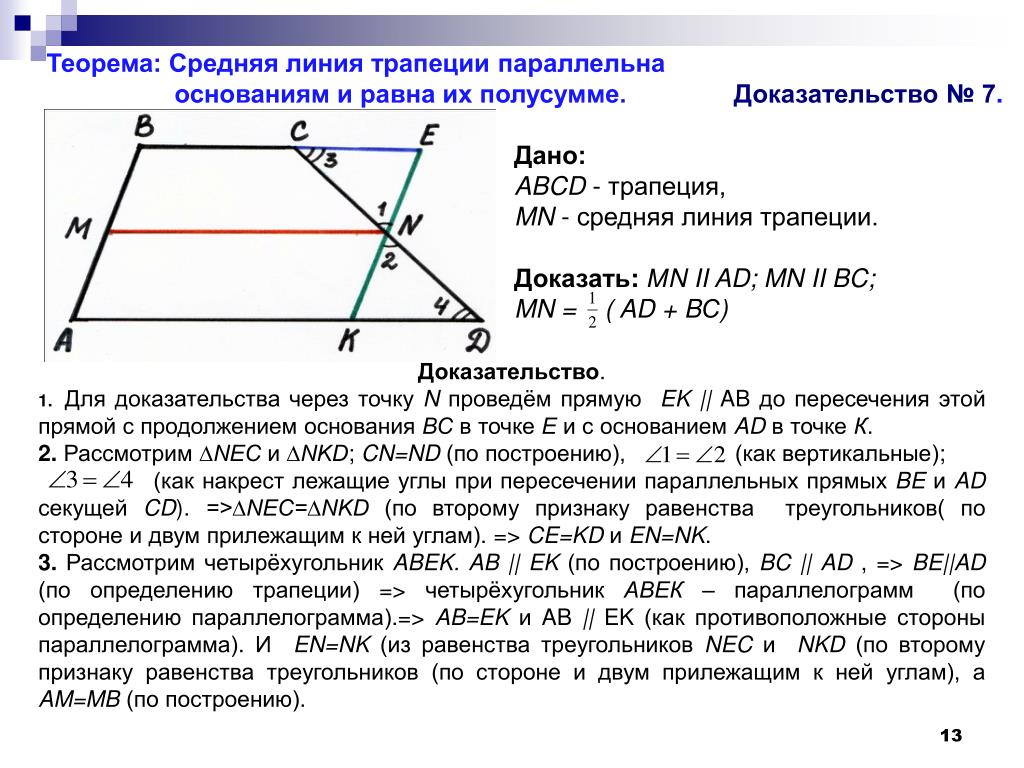 В трапеции ABCD сумма углов при меньшем основании равна 270º. Найти длину второй средней линии, если основания равны а и в (а >в).

         Решение: воспользуемся рис.11: в треугольнике AMD , значит, . Поэтому MN = , MF=.

NF = MF – MN = (a – b)/2.

Мне так же удалось составить несколько задач по данной теме.

№1.В равнобедренной трапеции АВСD   MN и KЕ средние линии. Они пересекаются в точке О. Известно КО=4см, МN=16 см. Найти среднюю линию КР и отрезок МО. (8см, 8см)

№2. В равнобедренной трапеции средняя линия трапеции равна 13см, а вторая средняя линия равна 6см. Найти площадь трапеции. (13*6=78 см²).

№3. Площадь равнобедренной трапеции равна 28см² . Вторая средняя линия равна 7см. Найти высоту трапеции. (7см).

№4.             B    E    C                              Дано: ABCD – трапеция,

                        N                                         EK – вторая средняя линия,

                               M                          СNEK, AMEK.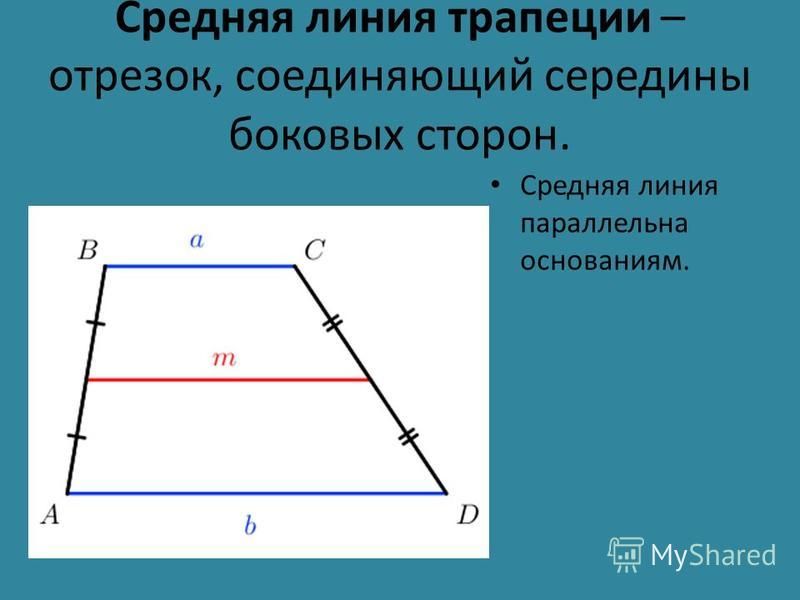 EK=10, CN=5, AM=8.

    А                           K                       D

                                                                    Найти : S_ABCD

Решение:      S_ABCD = EK*(CN+AM)= 10(5+8)= 130

№5. Верно ли утверждение: если прямая проходит через середину одного основания трапеции и точку пересечения диагоналей, то и другое основание она делит пополам?

         Решение: Да, см. свойство 2.

№6 Основания трапеции равны 10 см и 6 см, вторая средняя линия – 4 см, угол между средними линиями 30º. Найти площадь трапеции.

Решение:

    B            K            С

 

M                              O                        N

 

             A              H                 S                                   D

(соответственные), ,   КН = 2 см

   см².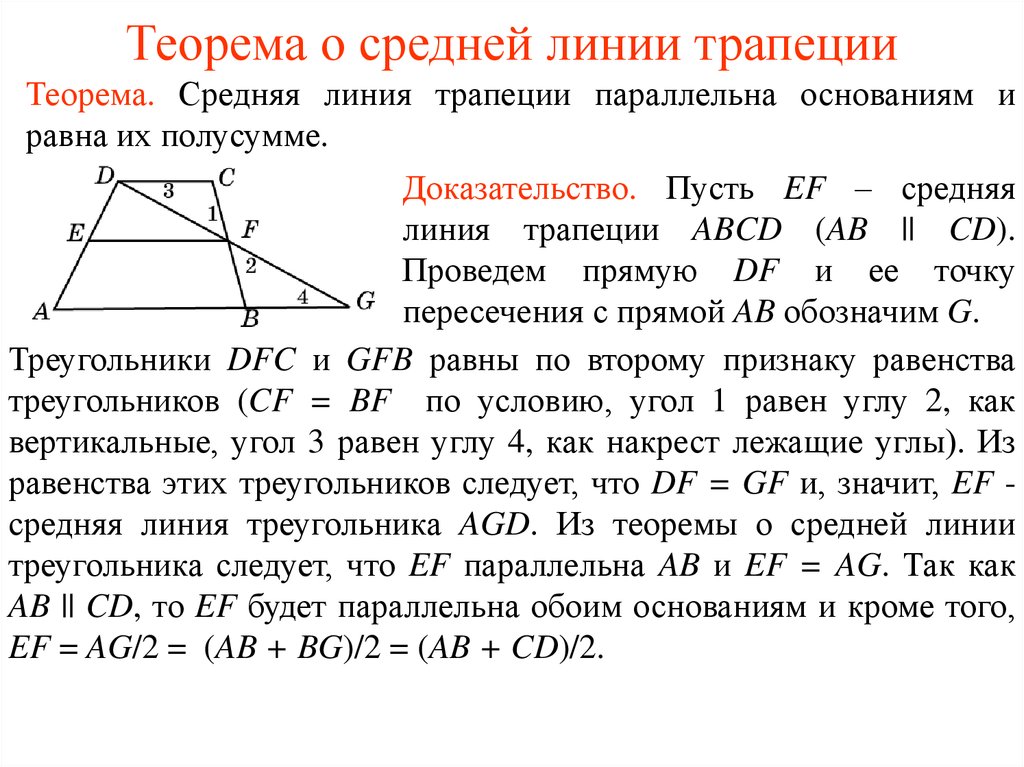

Заключение

 

         Развитие науки, необходимость мыслить по-новому, поиски нового — все эти требования современной жизни заставляют искать новые знания и методы, которые способны изменить решение тех или иных задач, расширить мышление.  В результате проделанной работы  узнала понятие второй средней линии трапеции, ее свойства. Так же доказала свойства второй средней линии, проанализировала КИМы ОГЭ и ЕГЭ, разобрала  задачи, связанные с этой линией, так  же составила свои задачи для закрепления свойств второй средней линии трапеции.

Выяснила, что вторая средняя линия трапеции используется в решении задач повышенной трудности.  Если знать свойства, которые мы доказали, то сложные задачи решаются просто и легко.  Все доказанные свойства собрала и сделала брошуру по данной теме.

         Учитель при изучении темы средняя линия трапеции и площадь трапеции сможет воспользоваться брошурой , где я собрала понятие и свойства второй средней линии трапеции.   Я надеюсь, что мои задачи помогут учащимся закрепить свойства второй средней линии, а мне решить планиметрические задачи ЕГЭ.

 

 

 

 

Литература

 

1.     Л. С. Атанасян и др. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006

2.     Википедия.- ru.wikipedia.org/wiki/средняя линия

3.     И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993.

4.     В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин «Задачи по элементарной математике» — М., Физматгиз, 1960.

5.     Научный форум dxdy. – dxdy.ru/topic20315.html

6.     В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 1986.

7.     И. Х. Сивашинский «Задачник по элементарной математике», — М., Наука, 1966.

8.     Фестиваль идей – portfolio.1september. ru/work

9.     К. У. Шахно «Сборник задач по элементарной математике повышенной трудности», — Минск, Высшая школа, 1966.

 

Самостоятельная работа средняя линия трапеции 25 вариантов | Материал для подготовки к ЕГЭ (ГИА) по геометрии (9 класс):

ВАРИАНТ 1

1.Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

2.Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

3.Боковые стороны трапеции равны 12 см и 16 см, а периметр равен 54 см. Найдите среднюю линию трапеции.

4.Дана равнобедренная трапеция АВСD. Перпендикуляр, проведенный из вершины  В к большему основанию АD, делит это основание на два отрезка, больший из которых равен 11 см. Найдите среднюю линию трапеции.

ВАРИАНТ 2

1.Большее основание трапеции равно 30 см, а средняя линия равна 25 см. Найдите меньшее основание трапеции

2.Средняя линия трапеции равна 12 см, а одно из оснований в 2 раза больше другого.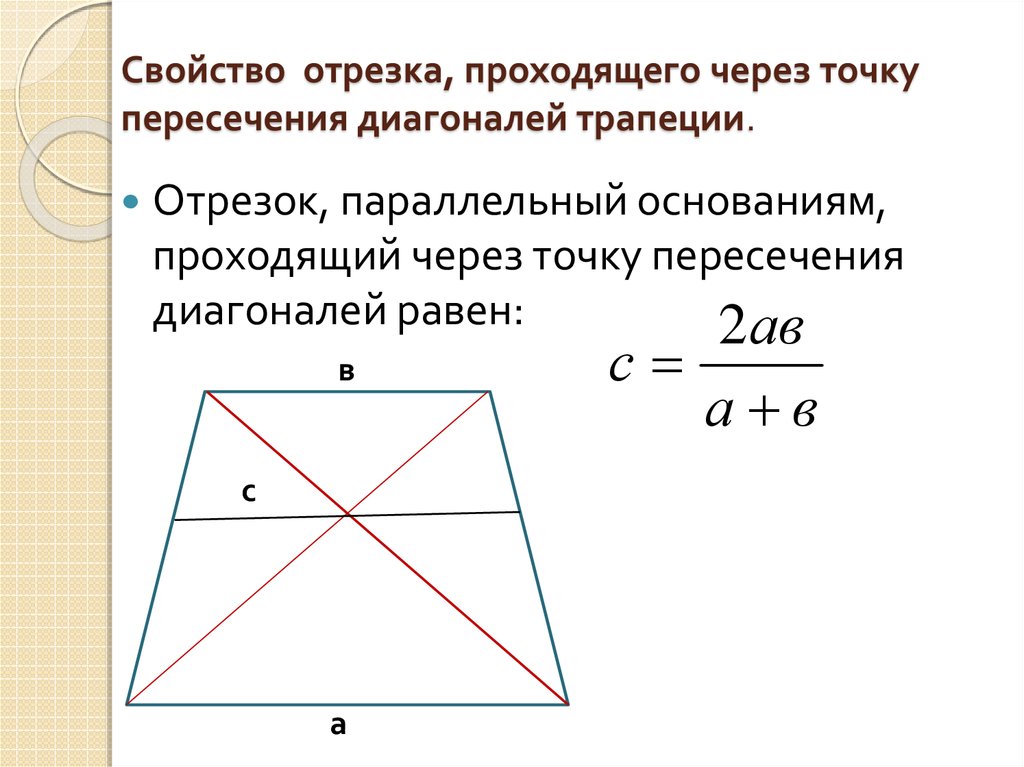 Найдите основания трапеции.

3.Боковые стороны трапеции равны 14 см и 18 см, а периметр равен 58 см. Найдите среднюю линию трапеции.угол =30.

4.Дана равнобедренная трапеция АВСD. Перпендикуляр, проведенный из вершины  В к большему основанию АD, делит это основание на два отрезка, больший из которых равен 15 см. Найдите среднюю линию трапеции.

ВАРИАНТ 3

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 30 И 16.

2.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 15 СМ, А ОДНО ИЗ ОСНОВАНИЙ В 3 РАЗА БОЛЬШЕ ДРУГОГО. НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИИ.

3.БОКОВЫЕ СТОРОНЫ ТРАПЕЦИИ РАВНЫ 16 СМ И 22 СМ, А ПЕРИМЕТР РАВЕН 74 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.УГОЛ =30.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШАЯ БОКОВАЯ СТОРОНА 12 СМ, А БОЛЬШАЯ СОСТАВЛЯЕТ С БОЛЬШИМ ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ ОСНОВАНИЕ ТРАПЕЦИИ, ЕСЛИ ЕЕ СРЕДНЯЯ ЛИНИЯ РАВНА 20 СМ.

ВАРИАНТ 4

1.Большее основание трапеции равно 40 см, а средняя линия равна 25 см. Найдите меньшее основание трапеции

2.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 10 СМ И 12 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 8 СМ.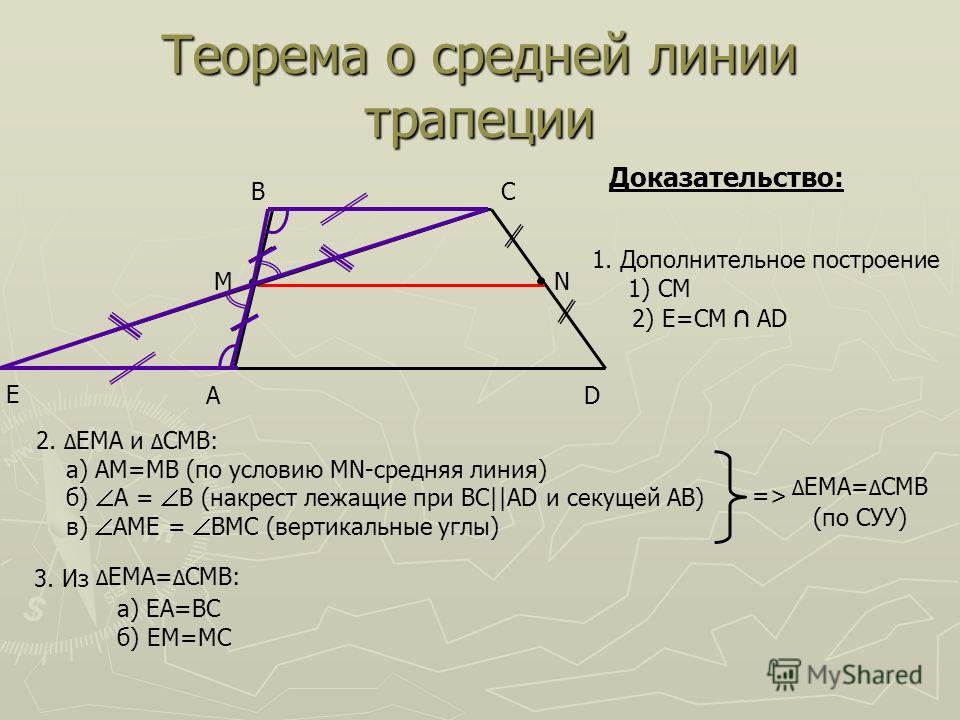 НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 25 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 12 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 5

1.В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 см и 12 см. Найдите среднюю линию трапеции.

2.В равнобедренной трапеции  один из углов равен 60о, боковая сторона равна 8 см, а меньшее основание  7 см. Найдите среднюю линию трапеции.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 9 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.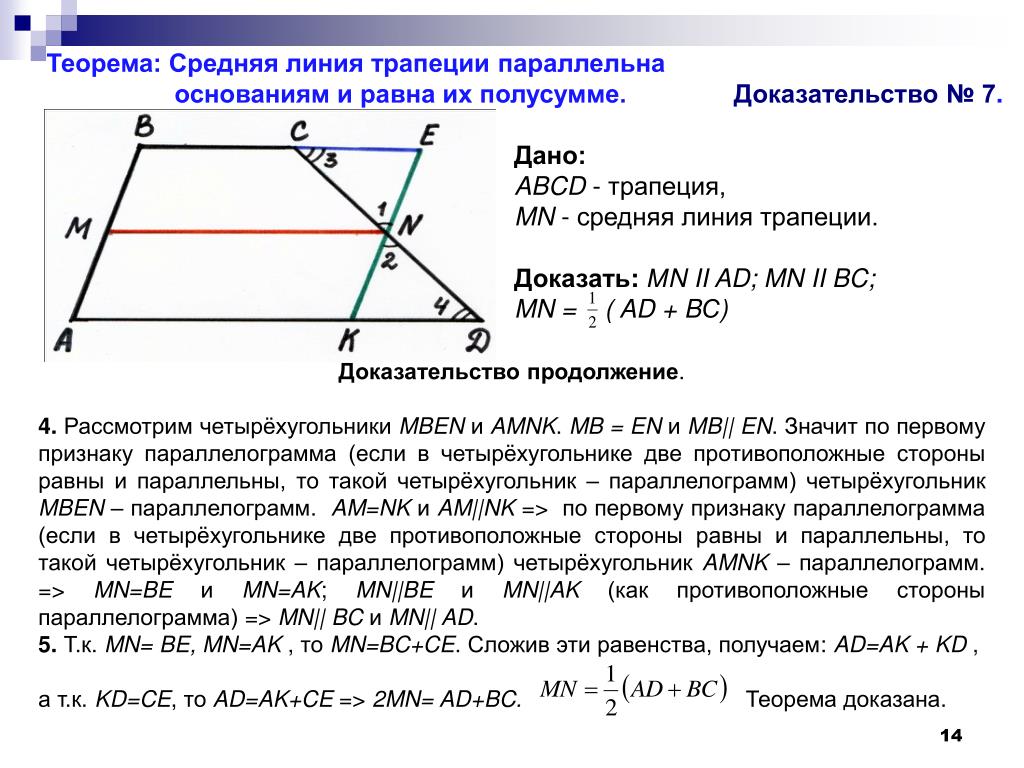  

ВАРИАНТ 6

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЫСОТА ДЕЛИТ БОЛЬШЕЕ ОСНОВАНИЕ НА ОТРЕЗКИ, РАВНЫЕ 15 СМ И 22 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 10 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ  17 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В ТРАПЕЦИИ MNKP , БОКОВЫЕ СТОРОНЫ РАВНЫ 8 СМ И 10 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 5 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 7

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ВЫСОТА ДЕЛИТ БОЛЬШЕЕ ОСНОВАНИЕ НА ОТРЕЗКИ, РАВНЫЕ 14 СМ И 19 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 18 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 4 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD СМ, А ВЫСОТА ТРАПЕЦИИ РАВНА 3 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.ДАНА РАВНОБЕДРЕННАЯ ТРАПЕЦИЯ АВСD. ПЕРПЕНДИКУЛЯР, ПРОВЕДЕННЫЙ ИЗ ВЕРШИНЫ  В К БОЛЬШЕМУ ОСНОВАНИЮ АD, ДЕЛИТ ЭТО ОСНОВАНИЕ НА ДВА ОТРЕЗКА, БОЛЬШИЙ ИЗ КОТОРЫХ РАВЕН 22 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 8

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 15 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 22 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

2.Средняя линия трапеции равна 21, а меньшее основание равно 5. Найдите большее основание трапеции. 

2.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 10 см и 17 см. Найдите среднюю линию трапеции. 

3.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 14 СМ И 16 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 8 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 10 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 9

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 15 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 12 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

2.Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции. 

3.Средняя линия трапеции равна 8 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 20 СМ И 22 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

ВАРИАНТ 10

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ БОКОВАЯ СТОРОНА РАВНА 18 СМ, А ЕЕ СРЕДНЯЯ ЛИНИЯ 10 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

2.Средняя линия трапеции равна 18, а меньшее основание равно 12. Найдите большее основание трапеции. 

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ДИАГОНАЛЬ РАВНА 14 СМ И СОСТАВЛЯЕТ С ОСНОВАНИЕМ УГОЛ 45О. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШЕЕ ОСНОВАНИЕ РАВНО МЕНЬШЕЙ БОКОВОЙ СТОРОНЕ, ОДИН ИЗ УГЛОВ 45О, А СРЕДНЯЯ ЛИНИЯ 10 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

ВАРИАНТ 11

1.НАЙДИТЕ БОКОВУЮ СТОРОНУ РАВНОБЕДРЕННОЙ ТРАПЕЦИИ, ПЕРИМЕТР КОТОРОЙ РАВЕН 38, А СРЕДНЯЯ ЛИНИЯ РАВНА 9.

2.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 3 см и 6 см. Найдите среднюю линию трапеции. 

3.В ТРАПЕЦИИ ABCD , БОКОВЫЕ СТОРОНЫ РАВНЫ 11 СМ И 13 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ 17 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

4.В ПРЯМОУГОЛЬНОЙ ТРАПЕЦИИ МЕНЬШЕЕ ОСНОВАНИЕ В 2 РАЗА МЕНЬШЕ БОКОВОЙ СТОРОНЫ, ОДИН ИЗ УГЛОВ РАВЕН 125О, А СРЕДНЯЯ ЛИНИЯ РАВНА 14 СМ. НАЙДИТЕ ПЕРИМЕТР ТРАПЕЦИИ.

ВАРИАНТ 12

1.Разность оснований трапеции равна 10 см, а средняя линия равна 22 см. Найдите основания этой трапеции.

2.В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 24.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 22, а меньшее основание BC равно 10

ВАРИАНТ 13

1. Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

2.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, CH — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 12, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 4.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 14.

4. В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 18, а меньшее основание BC равно 10

ВАРИАНТ 14

1.Средняя линия трапеции равна 30 см, а одно из оснований в два раза меньше другого. Найдите основания трапеции.

2.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, СН — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 16, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 6.

3. В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 14 см и 27 см. Найдите среднюю линию трапеции. 

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 18.

ВАРИАНТ 15

1.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 4 см и 7 см. Найдите среднюю линию трапеции. 

2.Разность оснований трапеции равна 10 см, а средняя линия равна 12 см. Найдите основания этой трапеции.

3.В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 20, а меньшее основание BC равно 6.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 . НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 16.

ВАРИАНТ 16

1.Средняя линия трапеции на 2 см меньше большего основания. Найдите среднюю линию трапеции, если меньшее основание равно 6 см. 

2.Разность оснований трапеции равна 12 см, а средняя линия равна 22 см. Найдите основания этой трапеции.

3.В ТРАПЕЦИИ АВСD БОКОВЫЕ СТОРОНЫ AB И CD РАВНЫ, СН — ВЫСОТА, ПРОВЕДЁННАЯ К БОЛЬШЕМУ ОСНОВАНИЮ AD. НАЙДИТЕ ДЛИНУ ОТРЕЗКА HD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ KM ТРАПЕЦИИ РАВНА 10, А МЕНЬШЕЕ ОСНОВАНИЕ BC РАВНО 5.

4.Средняя линия трапеции равна 16 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 17

1.Длина большего основания трапеции в 2 раза больше длины меньшего основания. Найдите длину меньшего основания, если длина средней линии равна 3 см. 

2.Боковые стороны равнобедренной трапеции равны по 25 см, а средняя линия этой трапеции 35 см. Найдите периметр этой трапеции.

3.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ СРЕДНЯЯ ЛИНИЯ РАВНА 10 СМ, А ПЕРИМЕТР 36 СМ. НАЙДИТЕ БОКОВЫЕ СТОРОНЫ ЭТОЙ ТРАПЕЦИИ.

4.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ ABCD С ОСНОВАНИЯМИ AD И BC

 DAC  60 .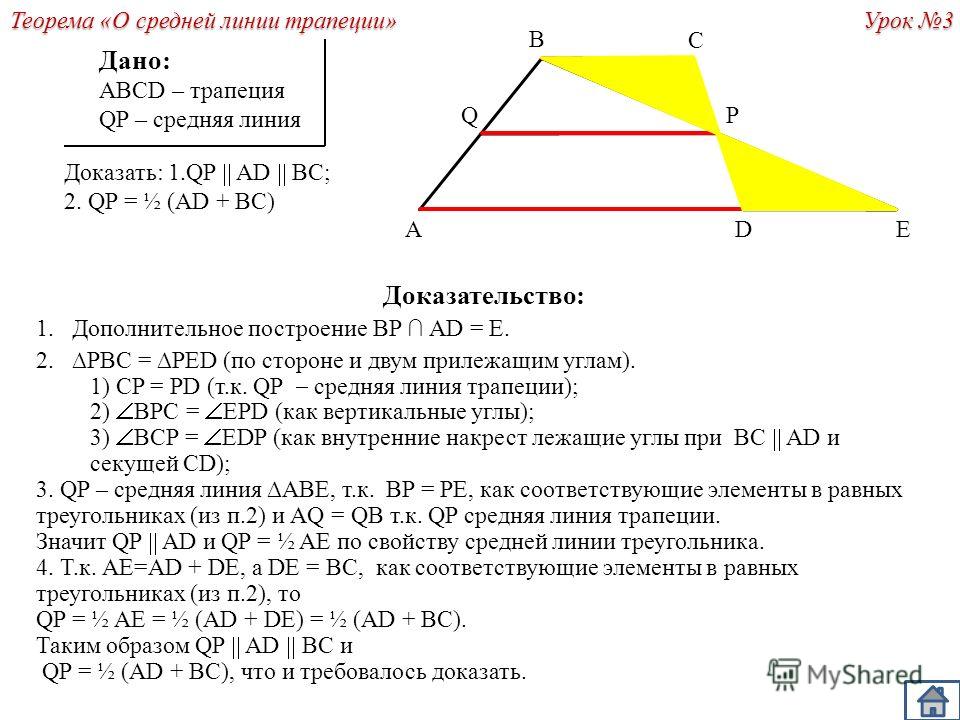 НАЙДИТЕ СРЕДНЮЮ ЛИНИИ ТРАПЕЦИИ, ЕСЛИ АС = 20.

ВАРИАНТ 18

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 10СМ И 14СМ.

2.Боковые стороны равнобедренной трапеции равны по 15 см, а средняя линия этой трапеции 25 см. Найдите периметр этой трапеции.

3.В равнобедренной трапеции средняя линия равна 10 см, а периметр 36 см. Найдите боковые стороны этой трапеции.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 12, а меньшее основание BC равно 4. 

ВАРИАНТ 19

1.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 30 СМ, А ОДНО ИЗ ОСНОВАНИЙ В ДВА РАЗА БОЛЬШЕ ДРУГОГО. НАЙДИТЕ ОСНОВАНИЯ ТРАПЕЦИИ.

2.Разность оснований трапеции равна 8см, а средняя линия равна 20см. Найдите основания этой трапеции.

3.В равнобедренной трапеции АВСD перпендикуляр, опущенный из вершины В на большее основание AD, делит его на отрезки, равные 2 см и 7 см. Найдите среднюю линию трапеции.  

4.Средняя линия трапеции равна 12 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 20

1.НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ, ЕСЛИ ЕЕ ОСНОВАНИЯ РАВНЫ 12СМ И 16СМ.

2.Боковые стороны равнобедренной трапеции равны по 14 см, а средняя линия этой трапеции 28 см. Найдите периметр этой трапеции.

3.Средняя линия трапеции равна 15 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .        Найдите среднюю линии трапеции, если высота трапеции равна 13.

ВАРИАНТ 21

1.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ СРЕДНЯЯ ЛИНИЯ РАВНА 20 СМ, А ПЕРИМЕТР 44 СМ. НАЙДИТЕ БОКОВЫЕ СТОРОНЫ ЭТОЙ ТРАПЕЦИИ.

2.Разность оснований трапеции равна 8см, а средняя линия равна 15см. Найдите основания этой трапеции.

3.Средняя линия трапеции равна 15 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .         Найдите среднюю линии трапеции, если высота трапеции равна 14.

ВАРИАНТ 22

1.Боковые стороны трапеции равны 18 см и 12 см, а периметр равен 50см. Найдите среднюю линию  трапеции.

2.Дана равнобедренная трапеция АВСД.  Перпендикуляр, проведённый из вершины В к большему основанию АД, делит это основание на  два отрезка, больший из которых равен 8 см. Найдите среднюю линию трапеции.

3.В равнобедренной трапеции ABCD с основаниями AD и ВС АВ = ВС = CD. Найдите среднюю линии трапеции, если AD = 18 и

 D  60 .

4.Средняя линия трапеции равна 20 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

ВАРИАНТ 23

1.Боковые стороны трапеции равны 24 см и 26 см, а периметр равен 70см. Найдите среднюю линию трапеции.

2.Дана равнобедренная трапеция АВСД. Перпендикуляр, проведённый из вершины В к большему основанию АД, делит это основание на два отрезка, больший из которых равен 9 см. Найдите среднюю линию трапеции

3. Средняя линия трапеции равна 10 см, а одно из оснований в два раза больше другого. Найдите основания трапеции.

4.В равнобедренной трапеции ABCD с основаниями AD и BC

 DAC  45 .        Найдите среднюю линии трапеции, если высота трапеции равна 10.

 ВАРИАНТ 24

1.СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 38, А МЕНЬШЕЕ ОСНОВАНИЕ РАВНО 18. НАЙДИТЕ БОЛЬШЕЕ ОСНОВАНИЕ ТРАПЕЦИИ.

2.В РАВНОБЕДРЕННОЙ ТРАПЕЦИИ  ОДИН ИЗ УГЛОВ РАВЕН 60О, БОКОВАЯ СТОРОНА РАВНА 8 СМ, А МЕНЬШЕЕ ОСНОВАНИЕ  10 СМ. НАЙДИТЕ СРЕДНЮЮ ЛИНИЮ ТРАПЕЦИИ.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 9 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4. 

ВАРИАНТ 25

1.НАЙДИТЕ        ПЕРИМЕТР        РАВНОБЕДРЕННОЙ        ТРАПЕЦИИ        С        БОКОВЫМИ СТОРОНАМИ РАВНЫМИ 7 И СРЕДНЕЙ ЛИНИЕЙ РАВНОЙ 10

2. В равнобедренной трапеции  один из углов равен 60о, боковая сторона равна 18 см, а меньшее основание  17 см. Найдите среднюю линию трапеции.

3.В ТРАПЕЦИИ ABCD  AB = CD, ВЫСОТА ВН ДЕЛИТ ОСНОВАНИЕ НА ДВА ОТРЕЗКА, МЕНЬШИЙ ИЗ КОТОРЫХ РАВЕН 5 СМ. НАЙДИТЕ AD, ЕСЛИ СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ РАВНА 10 СМ.

4.В трапеции АВСD боковые стороны AB и CD равны, CH — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 14. 

Как найти среднюю линию треугольника. Трапеция, средняя линия трапеции, треугольник

Как найти среднюю линию треугольника. Трапеция, средняя линия трапеции, треугольник

Средняя линия треугольника. Здравствуйте друзья! Сегодня теоретический материал связан с треугольником. В составе экзамена имеется группа заданий, использующих свойство его средней линии. И не только в задачах с треугольниками, но и с трапециями. Был такой, в котором я предлагал просто запомнить эти факты, теперь подробнее. ..

Что такое средняя линия треугольника и каковы ее свойства?

Определение. Средняя линия треугольника — это отрезок, соединяющий середины сторон треугольника.

Ясно, что в треугольнике три средние линии. Покажем их:

Без всяких доказательств вы, наверное, уже заметили, что все четыре образовавшихся треугольника равны. Это правда, но об этом мы поговорим позже.

Теорема . Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна половине ее.

Доказательство:

1. Рассмотрим треугольники BMN и BAC. По условию имеем BM=MA, BN=NC. Можно написать:

Следовательно, треугольники подобны по двум пропорциональным сторонам и углу между ними (второй признак подобия). Что из этого следует? А вот то что:

На основе параллельных линий MN||AC.

2. Из подобия треугольников также следует, что

То есть МН в два раза меньше. Доказано!

Решим типовую задачу.

В треугольнике ABC точки M, N, K являются серединами сторон AB, BC, AC. Найдите периметр треугольника ABC, если MN=12, MK=10, KN=8.

Раствор. Конечно, в первую очередь нужно проверить существование треугольника MNK (а значит, и существование треугольника ABC). Сумма двух меньших сторон должна быть больше третьей стороны, пишем 10+8>12. Выполнить, следовательно, треугольник существует.

Построим эскиз:

Таким образом, периметр треугольника ABC равен 24+20+16=60.

*Теперь подробнее о треугольниках, полученных при построении всех трех средних линий. Их равенство легко доказывается. Смотрите:

Они равны с трех сторон. Конечно, здесь применимы и другие признаки. Получаем, что

Как это свойство используется в заданиях, включенных в экзамен? Особо хотелось бы остановиться на задачах стереометрии. Есть виды, в которых речь идет о треугольной призме.

Например, говорят, что плоскость проходит через середины сторон основания и параллельна третьему краю основания. Ставятся вопросы об изменении площади поверхности призмы, ее объема и др.

Так. Зная и понимая изложенную выше информацию, вы сразу определите, что эта плоскость отсекает от основания одну четвертую часть указанной призмы и решите задачу устно. Вот с такими задачами.

Вот и все! Всего наилучшего!

Скачать материал статьи

С уважением, Александр Крутицких.

Как найти середину треугольника: задача по геометрии. Основные элементарные задачи евклидовой геометрии пришли к нам из древности. В них заключена самая первичная суть и необходимые базовые знания о восприятии человеком пространственных форм. Одной из таких задач является задача нахождения середины треугольника. Сегодня это задание рассматривается как метод обучения развитию интеллектуальных способностей школьников. В античном мире знания о том, как найти середину треугольника, применялись и на практике: в землеустройстве, при изготовлении различных механизмов и т. д. В чем суть этой геометрической головоломки?

Что такое медиана? Перед решением задачи необходимо ознакомиться с простейшей геометрической терминологией, касающейся треугольников. Во-первых, каждый треугольник имеет три вершины, три стороны и три угла, от чего и произошло название этой геометрической фигуры. Важно знать, как называются линии, соединяющие вершины с противоположными сторонами: высота, биссектриса и медиана.

Высота — линия, перпендикулярная стороне, противоположной вершине, из которой она проведена; биссектриса – делит угол пополам; медиана делит сторону, противоположную исходящей вершине, пополам. Для решения этой задачи необходимо знать, как найти координаты середины отрезка, ведь именно точка пересечения медиан треугольника является его серединой.

Найдите середины сторон треугольника. Нахождение середины отрезка — тоже классическая геометрическая задача, для решения которой нужен циркуль и линейка без делений. Ставим стрелку компаса в конечную точку отрезка и в середине последнего чертим полуокружность больше половины отрезка. То же самое делаем с другой стороны отрезка. Полученные полуокружности обязательно пересекутся в двух точках, потому что их радиусы больше половины исходного отрезка.

Соединяем две точки пересечения окружности прямой линией с помощью линейки. Эта линия пересекает исходный отрезок ровно посередине. Теперь, зная, как найти середину отрезка, проделываем это с каждой стороной треугольника. Найдя все середины сторон треугольника, вы готовы построить его собственную середину.

Строим середину треугольника. Соединив вершины треугольника с серединами их противоположных сторон прямыми линиями, получим три медианы. Это может кого-то удивить, но один из законов гармонии этой геометрической фигуры заключается в том, что все три медианы всегда пересекаются в одной точке. Именно эта точка и будет искомой серединой треугольника, найти которую не так уж и сложно, если знать, как построить середину отрезка.

Интересно также, что точка пересечения медиан является не только геометрической, но и «физической» серединой треугольника. То есть, если, например, вырезать из фанеры треугольник, найти его середину и поместить эту точку на острие иглы, то в идеале такая фигура будет балансировать и не падать. Элементарная геометрия таит в себе множество таких захватывающих «загадок», познание которых помогает постичь гармонию окружающего мира и природу более сложных вещей.

Четырехугольник только с двумя параллельными сторонами называется трапецией .

Параллельные стороны трапеции называются ее основаниями , а те стороны, которые не параллельны, называются сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.

Средняя линия трапеции

Срединная линия представляет собой отрезок, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.

Теорема:

Если прямая, проходящая через середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.

Теорема:

Длина средней линии равна среднему арифметическому длин ее оснований

МН || АБ || DC
AM=MD; БН=НЗ

MN средняя линия, AB и CD — основания, AD и BC — стороны

MN=(AB+DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин ее оснований.

Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат на середине оснований трапеции.

Средняя линия треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Он параллелен третьей стороне и его длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC и BN = NC =>

Применение свойств средней линии треугольника и трапеции

Деление сегмента на определенное количество равных частей.
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч, начало которого находится в точке A и который не лежит на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Соединим A 5 с B и проведем через A 4 , A 3 , A 2 и A 1 прямые, параллельные A 5 B. Они пересекают AB в точках B 4 , B 3 , B 2 и B 1 соответственно. Эти точки делят отрезок АВ на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Точно так же из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

А из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 Б 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных отрезки на луч p. А затем продолжить в порядке, описанном выше.

Понятие средней линии треугольника

Введем понятие средней линии треугольника.

Определение 1

Это отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис. 1. Средняя линия треугольника

Теорема о средней линии треугольника

Теорема 1

Средняя линия треугольника параллельна одной из его сторон и равна половине ее.

Доказательство.

Дан треугольник $ABC$. $MN$ — средняя линия (как на рис. 2).

Рис. 2. Иллюстрация к теореме 1

Так как $\frac(AM)(AB)=\frac(BN)(BC)=\frac(1)(2)$, то треугольники $ABC$ и $MBN$ подобны по второму критерию подобия треугольников. Означает

Также отсюда следует, что $\angle A=\angle BMN$ означает $MN||AC$.

Теорема доказана.

Следствия из теоремы о средней линии треугольника

Следствие 1: Медианы треугольника пересекаются в одной точке и делят точку пересечения в отношении $2:1$, начиная с вершины.

Доказательство.

Рассмотрим треугольник $ABC$, где $(AA)_1,\ (BB)_1,\ (CC)_1$ — его медиана. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (рис. 3). 9Рис. 3. Иллюстрация следствия 1 Следовательно, треугольники $ABM$ и $A_1B_1M$ подобны по первому критерию подобия треугольников. Тогда

Аналогично доказывается, что

Теорема доказана.

Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=\frac(1)(2)$.

Доказательство.

Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1,\ (\ A)_1C_1,\ B_1C_1$ (рис. 4)

Рис. 4. Иллюстрация следствия 2

Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то

Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму критерию подобия треугольников с коэффициентом подобия $k=\frac(1)(2)$.

Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, а также треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=\frac(1)(2)$.

Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1,\ (\A)_1C_1,\B_1C_1$ — средние линии треугольника, то

Следовательно, по третьему критерию подобия треугольников треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k =\ гидроразрыва (1) (2) $.

Теорема доказана.

Примеры задания на понятие средней линии треугольника

Пример 1

Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найдите периметр треугольника, вершины которого лежат на серединах сторон данного треугольника.

Раствор.

Так как вершины искомого треугольника лежат в середине сторон данного треугольника, то его стороны являются средними линиями исходного треугольника. По следствию 2 получаем, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.

Ответ: $20$ см.

Пример 2

Дан треугольник $ABC$. Точки $N\ и \ M$ являются серединами сторон $BC$ и $AB$ соответственно (рис. 5).

Рисунок 5

Периметр треугольника $BMN=14$ см. Найдите периметр треугольника $ABC$.

Раствор.

Так как $N\ и\ M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит

По теореме 1 $AC=2MN$. Получаем:

Трапециевидная мышца: Анатомия, происхождение, прикрепление, действия

Автор: Гордана Сендич, доктор медицины • Рецензент: Димитриос Митилинаиос, доктор медицины, доктор философии
Последнее рассмотрение: 06 октября 2022 г.
Время считывания: 10 минут

Трапециевидная мышца (Musculus trapezius)

Трапециевидная мышца представляет собой большую треугольную парную мышцу, расположенную на задней поверхности шеи и грудной клетки. Если смотреть вместе, эта пара образует форму ромба или трапеции, отсюда и ее название. Трапециевидная мышца имеет множество точек крепления, простирающихся от черепа и позвоночника до плечевого пояса.

Трапециевидная мышца относится к поверхностному слою наружных мышц спины вместе с широчайшей мышцей спины, большой и малой ромбовидной мышцей и мышцей, поднимающей лопатку. Трапециевидная мышца в значительной степени участвует в движениях плечевого пояса и поэтому функционально считается мышцей верхней конечности, а не спины.

В этой статье мы подробно обсудим анатомию и функцию трапециевидной мышцы.

Ключевые факты о трапециевидной мышце

Происхождение	Нисходящая часть (верхние волокна): медиальная треть верхней выйной линии, наружный затылочный выступ, выйная связка Восходящая часть (нижние волокна): остистые отростки и надостные связки позвонков T4-T12
Вставка	Нисходящая часть (верхние волокна): латеральная треть ключицы Поперечная часть (средние волокна): медиальный акромиальный край, верхний гребень ости лопатки Восходящая часть (нижние волокна): латеральная вершина медиального конца лопатки лопаточный отдел позвоночника
Иннервация	Моторный: добавочный нерв (CN XI) Моторный/сенсорный: передние ветви спинномозговых нервов С3-С4 (через шейное сплетение)
	Нисходящая часть (верхние волокна) — Лопаточно-грудной сустав: отводит лопатку верхомедиально — Атлантозатылочный сустав: разгибание головы и шеи, боковое сгибание головы и шеи (ипсилатеральное) — Альтантоаксиальный сустав: вращение головы (контралатерально) Поперечная часть (средние волокна) — Лопаточно-грудной сустав: отводит лопатку медиально Восходящая часть (нижние волокна) — Лопаточно-грудной сустав: отводит лопатку нижне-медиально
Кровоснабжение	Затылочная артерия (нисходящая часть), поверхностная или поперечная шейная артерия (поперечная часть), дорсальная лопаточная артерия (восходящая часть)

Содержимое

1. Происхождение и вставка
2. Структура и отношения
3. иннервация
4. Кровоснабжение
5. Функция
   1. Нисходящие (верхние) волокна
   2. Восходящие (нижние) волокна
   3. Поперечные (средние) волокна
6. Клинические заметки
7. Источники

+ Показать все

Происхождение и вставка

Верхняя выйная линия затылочной кости

Верхняя выйная линия затылочной кости

1/5

Трапециевидная мышца имеет несколько исходных точек вдоль средней линии задней части шеи и спины.

• Верхние волокна прикрепляются к медиальной трети верхней выйной линии, наружному затылочному выступу затылочной кости и выйной связке, которая прикрепляется к остистым отросткам позвонков C1-C6. Эти волокна имеют нисходящий путь к точке их прикрепления, поэтому эту часть трапеции называют 9-й. 0300 по убыванию часть .
• средних волокон берут начало от остистых отростков позвонков T1-T4 (в некоторых источниках указывается C7-T3) и промежуточных надостных связок. Эти волокна направлены горизонтально, бегут латерально к плечу. Таким образом, эти волокна представляют собой поперечную часть трапеции.
• нижних волокон берут начало от остистых отростков позвонков T4-T12 и соответствующих им надостных связок. Эти волокна идут вверх и латерально к точке их прикрепления и, следовательно, представляют собой восходящая часть трапециевидная.

Ось лопатки

Spina scapulae

1/3

По своему ходу все волокна трапециевидной мышцы сходятся латерально к верхнему углу лопатки, чтобы прикрепиться к соответствующим точкам прикрепления.

• верхних волокон прикрепляются к заднему краю латеральной трети ключицы.
• Средние волокна вводят на медиальный край акромиона лопатки, а также на верхний гребень ости лопатки.
• Нижние волокна прикрепляются через апоневроз к бугорку на латеральной вершине медиального конца ости лопатки.

Структура и отношения

По их креплениям, ходу и расположению, рассмотренным ранее, мы можем разделить трапеции на три функциональные части. Каждая часть задействована в различных движениях, которые мы рассмотрим более подробно далее в этой статье. К частям трапеции относятся:

• Нисходящая (верхняя) часть , состоящая из верхних волокон
• Поперечная (средняя) часть , состоящая из средних волокон
• Восходящая (нижняя) часть , состоящая из нижних волокон

Наряду с широчайших спины трапециевидная является самой поверхностной из поверхностных внешних мышц спины. Она покрывает остальные мышцы этой группы, а именно 9-ю.0300 ромбы и поднимающая лопатку . Глубоко к трапециевидной мышце мы также можем найти serratus posterior superior , которая принадлежит к промежуточному слою наружных мышц спины.

Кроме того, трапециевидная мышца покрывает несколько мышц поверхностного слоя внутренней группы мышц , таких как ременная мышца головы, шейная ременная мышца, спинальная, длиннейшая и подвздошно-реберная мышцы. Верхняя часть трапеции также лежит над 9.0300 подзатылочная область .

[Поверхностные мышцы спины]

Передний край трапециевидной мышцы образует заднюю границу заднего треугольника шеи . Более того, его свободный нижний край образует медиальную границу аускультативного треугольника , участка грудной клетки, не закрытого лопаткой и покрытого только тонким слоем мышц.

иннервация

Трапециевидная мышца — единственная мышца верхней конечности, не получающая своей иннервации от плечевого сплетения. Вместо этого двигательная иннервация трапециевидной мышцы передается добавочным нервом (CN XI) , а также передними ветвями спинномозговых нервов C3 и C4, , которые также содержат проприоцептивные/чувствительные волокна от мышцы.

Проверь свои знания о поверхностных мышцах спины!

Кровоснабжение

Затылочная артерия

Затылочная артерия

1/5

Артериальное кровоснабжение трапециевидной мышцы зависит от ее уровня.

• Нисходящая (верхняя) часть мышцы кровоснабжается поперечными мышечными ветвями, отходящими от затылочной артерии (ветви наружной сонной артерии), проходящей по глубокой поверхности мышцы.
• Поперечная (средняя) часть мышцы кровоснабжается поверхностной шейной артерией или ветвью поперечной шейной артерии.
• Восходящая (нижняя) часть кровоснабжается мышечными ветвями дорсальной лопаточной артерии, отходящей от подключичной артерии.

Функция

Основной функцией трапеции является стабилизация лопатки на ее анатомическом месте, а также управление ею при движениях плеча и верхней конечности. Бросок является распространенным маневром, при котором активна трапециевидная мышца, а также дельтовидная мышца и мышцы-вращатели манжеты плеча. Кроме того, трапеции также участвуют в движениях головы и шеи.

Хотите изучить прикрепления, иннервацию и функции трапециевидной мышцы в 10 раз быстрее и проще? Вам нужна наша таблица анатомии мышц стенки туловища !

Действия трапециевидной мышцы во многом зависят от направления сокращающихся волокон.

Нисходящие (верхние) волокна

Боковые сгибания шеи

Латеральные сгибания шеи

1/3

Синонимы: Латеральная сгибательная мышца шеи

Нисходящие (верхние) волокна взаимодействуют с мышцей, поднимающей лопатку, создавая подъем лопатки на 90–300 градусов в лопаточно-грудном суставе. Таким же образом они также поддерживают уровень плеч против силы тяжести, т.е. когда в руке несут тяжесть.

Когда мышца действует односторонне, нисходящие волокна производят ипсилатеральное латеральное сгибание на 90–300°.0301 головы и шеи, воздействуя на атланто-затылочный сустав и верхние шейные позвонки соответственно. Одностороннее сокращение может также привести к контралатеральному вращению головы на на в атлантоаксиальном суставе. Двустороннее сокращение нисходящей части трапециевидной мышцы (т. е. когда сокращаются и левая, и правая мышцы) вызывает разгибание головы и шеи на 90–30°.

Восходящие (нижние) волокна

Восходящие (нижние) волокна отвечают за углубление медиальной части лопатки и, таким образом, опускание плеча. Это действие особенно важно для действий, при которых плечи опускаются, преодолевая сопротивление, например, при помощи рук, чтобы помочь себе подняться из сидячего положения.

Вместе с нисходящей частью восходящие волокна также производят поворот лопатки на 90-300° вокруг оси, проходящей кпереди-назад через основание ости лопатки.

Поперечные (средние) волокна

Поперечные (средние) волокна действуют вместе с ромбовидными, вызывая ретракцию лопатки, подтягивая ее к средней линии. Трапециевидная мышца вместе с передней зубчатой ​​мышцей также отвечает за ротацию лопатки на вверх . Это позволяет нам поднять руку над головой выше уровня плеча.

Готовы ли вы расширить свои знания о поверхностных мышцах спины? Нажмите на учебный блок ниже, чтобы продолжить обучение и проверить себя!

Поверхностные мышцы спины Исследуйте учебный блок

Клинические заметки

Функцию трапециевидной мышцы можно проверить, положив руку на плечо пациента и оценив его способность поднимать или «пожимать» плечо, преодолевая сопротивление.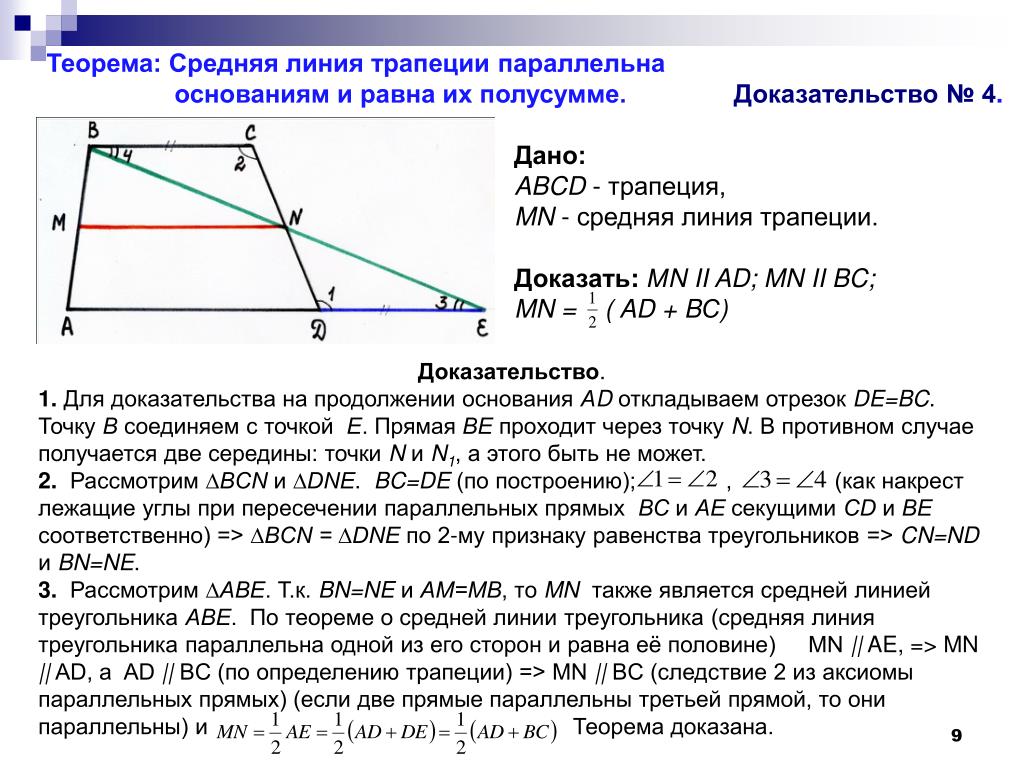 Этот тест в сочетании с тестом на функциональность грудино-ключично-сосцевидной мышцы можно использовать для оценки повреждений добавочного нерва .

Слабость трапециевидной мышцы при сохранном функционировании грудино-ключично-сосцевидной мышцы указывает на повреждение добавочного нерва в более дистальной точке, например, в заднем треугольнике шеи. Слабость как трапециевидной, так и грудино-ключично-сосцевидной мышц указывает на повреждение ближе к месту выхода добавочного нерва из основания черепа.

Поскольку трапециевидная мышца имеет обширное кровоснабжение, ее можно использовать в качестве места для лоскута кожно-мышечной ткани сбор в реконструктивных целях на других участках тела, например, для реконструкции молочной железы.

Источники

Весь контент, публикуемый на Kenhub, проверяется экспертами в области медицины и анатомии. Информация, которую мы предоставляем, основана на научной литературе и рецензируемых исследованиях.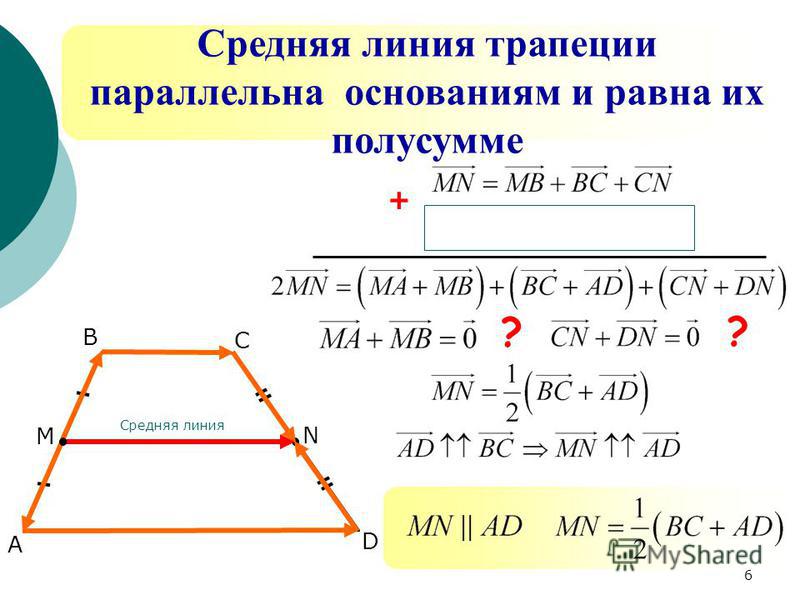 Kenhub не дает медицинских консультаций. Вы можете узнать больше о наших стандартах создания и проверки контента, прочитав наши рекомендации по качеству контента.

Каталожные номера:

• Паластанга, Н., Филд, Д., и Сомс, Р. (1989). Анатомия и движение человека: структура и функции. Оксфорд, Англия (6-е издание): Черчилль Ливингстон.
• Стэндринг, С. (2016). Анатомия Грея: анатомические основы клинической практики (41-е изд.). Эдинбург: Эльзевир Черчилль Ливингстон.
• Мур, К.Л., Далли, А.Ф., и Агур, А.М.Р. (2014). Клинически ориентированная анатомия (7-е изд.). Филадельфия, Пенсильвания: Липпинкотт Уильямс и Уилкинс.

Иллюстраторы:

• Трапециевидная мышца (Musculus trapezius) — Юсун Кох
• Поверхностные мышцы спины — Юсун Кох

Трапециевидная мышца: хотите узнать о ней больше?

Наши увлекательные видеоролики, интерактивные викторины, подробные статьи и HD-атлас помогут вам быстрее достичь наилучших результатов.