Равенство треугольников признаки равенства треугольников: Первый признак равенства треугольников — урок. Геометрия, 7 класс.

alexxlab / / Разное

Содержание

Равные треугольники – определение, свойства, признаки

4.5

Средняя оценка: 4.5

Всего получено оценок: 370.

4.5

Средняя оценка: 4.5

Всего получено оценок: 370.

Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Определение

Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.

Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.

Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$

Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.

Признаки равенства

Выделяют три признака равенства треугольников:

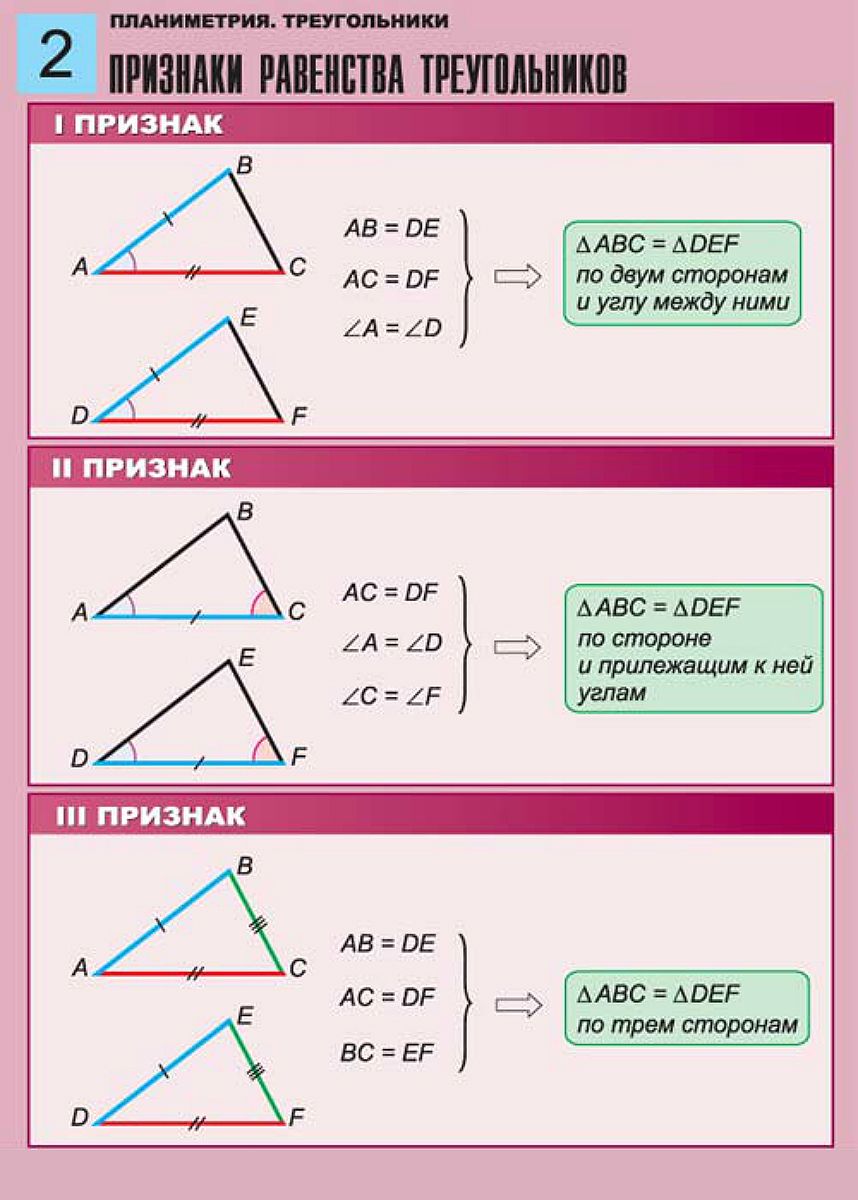
1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.

Рис. 1. Первый признак равенства

2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.

Рис. 2. Второй признак равенства

3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.

Кроме того, стоит выделить некоторые свойства:

  • Сумма двух внутренних углов треугольника будет всегда меньше 180
    0    .
  • Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
  • Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Алгоритм доказательства равенства фигур

  • Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
  • На рисунке отметить, все необходимые данные в условии задания.
  • Проверить есть ли у двух треугольников общая сторона либо угол.
  • Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
  • При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
  • При необходимости, можно сделать дополнительное построение.

Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.

Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.

Пример

Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.

Решение:
Стоит обратить внимание на рисунок

Рис. 3. Два треугольника

В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.

Что мы узнали?

Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

  • Анна Ножеева

    5/5

  • Ярик Яраслав

    5/5

  • Данила Салин

    5/5

  • Никита Ушаков

    5/5

Оценка статьи

4.5

Средняя оценка: 4.5

Всего получено оценок: 370.

А какая ваша оценка?

Равенство треугольников. Признаки равенства треугольников – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны

Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны, если выполняется одно из следующих условий:

  1. равны их катеты;
  2. катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
  3. гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
  4. катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
  5. катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

Стороны равной длины — определение, формы, примеры, факты

Стороны равной длины — введение

Математика — это не только числа, она также включает изучение различных форм, таких как круги, квадраты, овалы, цилиндры, треугольники, прямоугольники и многое другое.

Включает определение размеров сторон или точных углов фигур.

Сегодня мы обсудим фигуры, имеющие сторон одинаковой длины . Мы узнаем факторы, которые отличают их друг от друга, и их соответствующие названия. Давайте начнем!

Родственные игры

Что такое Стороны равной длины?

Стороны одинаковой длины означают, что их размеры одинаковы. Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.

Стороны, имеющие одинаковую длину, также называются конгруэнтными сторонами. Эти стороны могут быть частью одной формы или разных форм. Давайте посмотрим на несколько примеров фигур со сторонами одинаковой длины.

В прямоугольнике ниже противоположные стороны конгруэнтны друг другу.

В двух треугольниках ниже стороны конгруэнтны друг другу.

Связанные рабочие листы

Стороны равной длины в одной форме

Треугольники 

В зависимости от длины сторон треугольники можно разделить на разносторонние, равнобедренные и равносторонние.

  • Разносторонний треугольник:

Это треугольник, в котором каждая сторона имеет разную длину.

  • Равнобедренный треугольник:

Это треугольник, в котором две стороны имеют одинаковую длину. Угол, падающий между равными сторонами, называется углом при вершине. Углы, противолежащие двум равным сторонам треугольника, всегда будут равны. Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.

  • Равносторонний треугольник:

Это треугольник, в котором все три стороны имеют одинаковую длину. Каждый угол равностороннего треугольника равен 60°. Следовательно, его также называют равноугольным треугольником.

Итак, треугольники с равными сторонами могут быть либо равнобедренными, либо равносторонними.

Четырехугольники 

Четырехугольники — это многоугольники с четырьмя сторонами. Они также могут иметь равные все или некоторые из сторон. Различные категории перечислены ниже:

  1. Все стороны равны

В этих четырехугольниках все четыре стороны равны. Их еще называют правильными четырехугольниками. Примерами правильных четырехугольников являются квадрат и ромб.

  1. Три равные стороны

В этих четырехугольниках три стороны равны.

  1. Одна пара равных сторон

В этих четырехугольниках есть одна пара равных сторон. Стороны могут быть как противоположными, так и примыкающими друг к другу.

  1. Противоположные стороны равны: Примером этого является равнобедренная трапеция
  1. Смежные стороны равны: Примером этого является неправильный четырехугольник, у которого две смежные стороны равны.
  1. Две пары равных сторон 
  2. Равные стороны противоположны: Примеры: прямоугольник и параллелограмм.
  1. Равные стороны смежные: Пример — воздушный змей.

Многоугольники

Многоугольники — это двумерные замкнутые фигуры, состоящие только из прямых сторон. Многоугольники могут иметь любое количество сторон. Это означает, что треугольники и четырехугольники также являются многоугольниками. Многоугольники также могут иметь равные все или некоторые стороны.

  1. Правильные многоугольники:

Многоугольники, у которых все стороны и все внутренние углы равны, называются правильными многоугольниками. Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.

  1. Неправильные многоугольники:

Многоугольники, у которых все стороны не равны, называются правильными многоугольниками. У них могут быть некоторые стороны одинаковой длины, но не все. Таким образом, даже если прямоугольники и параллелограммы имеют равные противоположные стороны, они являются неправильными многоугольниками.

Стороны одинаковой длины в различных формах

При сравнении различных форм, если сторона одной формы равна стороне другой, говорят, что стороны равны.

Если все стороны одной фигуры равны всем сторонам другой фигуры и углы также одинаковы, то две фигуры называются конгруэнтными.

Например, два треугольника называются конгруэнтными, если все их соответствующие стороны и углы равны.

Критерии конгруэнтности треугольников

Нам не нужно измерять все стороны и углы двух треугольников, чтобы проверить, конгруэнтны они или нет. Если они соответствуют любому из заданных критериев, то они конгруэнтны.

  1. Критерии SSS (сторона-сторона-сторона)

Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критерию SSS, если их соответствующие стороны равны.

  • AB $=$ PQ
  • до н.э. $=$ QR
  • AC $=$ PR
  1. Критерии SAS (сторона-угол-сторона)

Два треугольника $\Delta{ABC}$ и $\Delta{PQR}$ называются конгруэнтными по критериям SAS, если две их соответствующие стороны и угол между ними равны.

  • AB $=$ PQ
  • ∠A $=$ ∠P
  • AC $=$ PR
  1. Критерии AAS (угол-угол-сторона)

Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критериям ААС, если любые два их соответствующих угла и любая одна сторона равны.

  • ∠A $=$ ∠P
  • ∠С $=$ ∠Р
  • AC $=$ PR
  1. RHS-критерий (правая сторона гипотенузы)

Два прямоугольных треугольника $\Delta\text{ABC}$ и $\Delta\text{XYZ}$ называются конгруэнтными по RHS-критерию, если их соответствующие гипотенуза и одна пара соответствующих сторон равны.

  • ∠B $=$ ∠Y (прямой угол)
  • AC $=$ XZ (гипотенуза)
  • AB $=$ XY (сторона)

Заключение

У некоторых фигур все стороны равны, а у других ни одна из сторон не равна. Кроме того, есть фигуры, у которых только несколько равных сторон. Мы можем сравнивать стороны и углы различных фигур, чтобы найти конгруэнтные стороны и конгруэнтные формы.

Решенные примеры 

1. Назовите три фигуры, все стороны которых имеют одинаковую длину.

Решение : Три фигуры, все стороны которых имеют одинаковую длину, это ромб, квадрат и равносторонний треугольник.

2. Найдите периметр правильного шестиугольника, если одна из его сторон равна 9 дм.

Решение: Правильный шестиугольник имеет 6 сторон одинаковой длины.

Поскольку сторона равна 9 дюймам, периметр будет: 

6$\умножить на 9 = 54$ дюймов.

3. Если две стороны треугольника равны, какой это треугольник?

Решение : Это равнобедренный треугольник. У равнобедренного треугольника две равные стороны.

4. Если одна сторона параллелограмма 10 дюймов, а другая сторона 6 дюймов, каков общий периметр?

Решение : В параллелограмме противоположные стороны равны друг другу.

Если одна сторона 10 дюймов, а другая сторона 6 дюймов, общий периметр будет:

10$ + 10 + 6 + 6 = 32$ дюймов.

Практические задачи

1

В $\Delta\text{ABC}$ ∠A $=$ 50°, ∠ B $=$ 80° и ∠ C $=$ 50°. Определите равные стороны.

AC $=$ BC

AB $=$ AC

AB $=$ BC

Стороны не равны

Правильный ответ: AB $=$ BC
Дано, что ∠A $=$∠ В $=$ 50°. Это означает, что стороны, противолежащие этим углам, также равны. То есть AB $=$ BC.

2

$\Delta\text{ABC}$ имеет стороны 6 дюймов, 8 дюймов и 10 дюймов. $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$. Что за треугольник $\Delta\text{DEF}$?

Разносторонний

Равносторонний

Равнобедренный

Невозможно определить

Правильный ответ: Разносторонний
Если $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$, стороны $\ Delta\text{DEF}$ также составляет 6 дюймов, 8 дюймов и 10 дюймов. Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.

3

Какие из следующих четырехугольников являются правильными многоугольниками?

Прямоугольник

Квадрат

Воздушный змей

Ромб

Правильный ответ: Квадрат
У правильного многоугольника все стороны равны и все углы равны. Квадрат – это единственный четырехугольник с равными сторонами и равными углами.

4

Определите фигуру, у которой не все стороны равны.

Равносторонний треугольник

Ромб

Прямоугольник

Правильный пятиугольник

Правильный ответ: Прямоугольник
В прямоугольнике смежные стороны имеют разную длину, а противоположные стороны равны.

Часто задаваемые вопросы

Возможны ли конгруэнтные формы с соответствующими сторонами разной длины?

Нет, конгруэнтные фигуры должны иметь стороны одинаковой длины.

Может ли быть неправильный многоугольник со сторонами одинаковой длины?

Да, если стороны равны, но углы разные, или равны только две или некоторые из сторон, то это будет неправильный многоугольник. Например, у ромба равные стороны, но разные углы.

Поскольку все углы равностороннего треугольника равны 60°, можем ли мы сказать, что все равносторонние треугольники конгруэнтны друг другу?

Нет, чтобы треугольники были равны, все их стороны и углы должны быть равны.

2.4: Доказательство равенства линий и углов

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    34127
    • Генри Африк
    • CUNY Технологический колледж Нью-Йорка через Технологический колледж Нью-Йорка в CUNY Академические работы

    Мы можем доказать равенство прямых и углов, если мы можем показать, что они являются соответствующими частями конгруэнтных треугольников. Мы считаем удобным представить эти доказательства в форме в два столбца с утверждениями в левом столбце и причиной каждого утверждения в правом.

    Пример \(\PageIndex{1}\)

    Дано \(AB || CD\) и \(AB = CD\) доказать \(AD = BC\)

    Решение

    903 60 Заявления
    Причины
    1. \(AB = CD\). 1. Дано.
    2. \(\угол ABD = \угол CDB\). 2. Альтернативные внутренние углы параллельных прямых \((AB || CD)\) равны.
    3. \(BD = DB\). 3. Личность.
    4. \(\треугольник ABD \cong \треугольник CDB\) 4. \(SAS = SAS\): \(AB, \угол B, BD\) из \(\треугольник ABD = CD\), \(\угол D\), \(DB\) из \(\ треугольник CDB\).
    5. \(АД = ВС\) 5. Соответствующие стороны равных треугольников равны,

    Объяснение: Каждое из первых трех утверждений говорит о том, что сторона или угол \(\треугольника ABD\) равна соответствующей стороне или углу \(\треугольника CDB\). Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0005

    Причины равенства линий

    1. Дано. Это означает, что в начале упражнения нас просят предположить, что строки равны. Например, в задаче будет указано «дано \(AB = CD\)» или \(AB\) и \(CD\) будут отмечены так же на схеме.
    2. Личность. Это означает, что в обоих треугольниках появляется один и тот же отрезок прямой. Например, \(BD\) и \(DB\) представляют один и тот же отрезок прямой. Конечно, длина отрезка равна самой себе.

    Причины равенства углов

    1. Дано.
    2. Личность.
    3. Альтернативные внутренние углы параллельных прямых равны. Чтобы применить эту причину, мы должны иметь в виду, что прямые параллельны.
    4. Соответствующие углы параллельных прямых равны.
    5. Вертикальные углы равны.

    Это не единственные возможные причины, но это все, что мы будем использовать в первую очередь.

    Мы также должны выбрать три пары равных сторон или углов, чтобы одну из причин \(SAS = SAS\), \(ASA = ASA\) или \(AAS = AAS\) можно было использовать для обоснования сравнения утверждение в утверждении 4. В разделах 2.6 и 2.7 мы приведем некоторые дополнительные причины конгруэнтности двух треугольников.

    Мы хотим доказать утверждение 5. Причина в том, что соответствующие стороны (или углы) конгруэнтных треугольников равны. Мы можем использовать эту причину здесь, потому что конгруэнтность треугольников уже доказана в утверждении 4,

    .

    Последнее замечание. Обратите внимание, что решение примера \(\PageIndex{1}\) согласуется с нашим первоначальным определением доказательства. Верность каждого нового утверждения подтверждается использованием предыдущих утверждений и уже установленных причин.

    Приведем другой пример:

    Пример \(\PageIndex{2}\)

    Учитывая \(QP || ST\) и \(QR = TR\) докажите \(PR = SR\).

    Решение

    Заявления Причины
    1. \(QR = TR\) 1. Дано.
    2. \(\угол Q = \угол T.\) 2. Альтернативные внутренние углы параллельных прямых (\(QP || ST\)) равны.
    3. \(\угол PRQ = \угол SRT\). 3. Вертикальные углы равны.
    4. \(\треугольник PQR \cong \треугольник STR\). 4. \(ASA = ASA: \угол Q, QR, \угол R\) из \(\треугольник PQR = \угол T\), \(TR, \угол R\) из \(\треугольник STR\) .
    5. \(PR = SR\). 5. Соответствующие стороны равных треугольников равны,

    1. Даны \(\угол A = \угол D\), \(\угол B = \угол E\), \(AB = DE\). Докажите \(AC = DF\).

    2. Даны \(AC=DF\), \(BC = EF\), \(\угол C = \угол F\).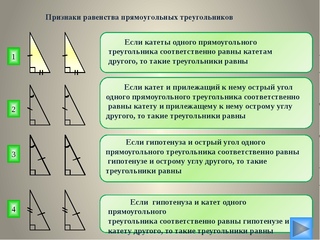 Докажите \(AB = DE\).

    3. Даны \(AC = EC\) и \(BC = DC\). Докажите \(AB = ED\).

    4. Даны \(AC = DC\), \(\угол A = \угол D\). Докажите \(BC = EC\).

    5. Даны \(\угол ABD = \угол CDB\) и \(\угол ADB = \угол CBD\). Докажите \(AB = CD\).

    6. Даны \(AB || CD\) и \(AD || CB\). Докажите \(AB = CD\).

    7. Даны \(AC = BC\) и \(\угол ACD = \угол BCD\). Докажите \(\угол А = \угол В\).

    8. Даны \(\угол A = \угол B\), \(\угол ACD = \угол BCD\). Докажите \(AC = BC\).

    9. Даны \(AB || CD\) и \(AB = CD\). Докажите \(AE = CE\). (Подсказка: покажите \(\треугольник ABE \cong \треугольник CDE\))

    10. Даны \(AE = CE\) и \(BE = DE\). Докажите \(\угол BAC = \угол CDB\).

    11. Даны \(\угол A = \угол D\), \(AC = DE\), \(AB || DC\). Докажите \(BC = CE\).

    12. Даны \(AB || DE\), \(AC || FE\) и \(DC = FE\). Докажите \(BE = EC\).

    13.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *