Разложение функций в ряды Тейлора и Маклорена
Разложение заданной функции f(x) в ряд Тейлора в окрестности точки распадается на два этапа
Сначала вычисляются значения функции f(x) и ее производных в точке и составляется ряд Тейлора для функции f(x). При этом предполагается, что функция f(x) бесконечное число раз дифференцируема.
Находится интервал, в котором составленный ряд Тейлора сходится к функции f(x), то есть устанавливается для каких значений х остаточный член ряда будет стремиться к нулю при . При этом можно воспользоваться следующей теоремой.
Теорема
Если в некотором интервале, окружающем
точку
,
абсолютные величины всех производных
функции f(x) ограничены одним и тем же числом, то
функция в этом интервале разлагается
в ряд Тейлора.
Доказательство
Нужно установить, что для всех точек интервала при .
По условию теоремы во всех точках интервала , где М – постоянная, не зависящая от n. Тогда в силу неравенства (***) . Но отношение при , то есть радиус сходимости . Следовательно, для всех точек х, рассматриваемого интервала, что и требовалось доказать.
Особенно часто используется разложение функции в ряд по степеням х. Полагая , получаем ряд . Такой ряд называется рядом Маклорена.
Разложение в ряды элементарных функций
Показательная функция
Разложим эту функцию в ряд Маклорена.
Все производные функции равны
и обращаются в 1 при х=0. По формуле
Тейлора .
Рассмотрим интервал [-N,N], где N – любое
фиксированное число. Для всех значений х из этого интервала . Следовательно, все производные в этом
интервале ограничены одним и тем же
числом и по доказанной теореме
.
По предположению N – любое число, следовательно, функция
разлагается в ряд Маклорена при всех
значениях х, то есть на всей числовой
оси.
Следовательно, все производные в этом
интервале ограничены одним и тем же
числом и по доказанной теореме
.
По предположению N – любое число, следовательно, функция
разлагается в ряд Маклорена при всех
значениях х, то есть на всей числовой
оси.
Итак
В частности при х=1 находим ряд для числа е
2. Тригонометрические функции sinx и cosx
Разложим в ряд Маклорена функцию sinx. Для этого последовательно находим значения ее производных в точке х=0
и т.д.
Значения производных повторяются и образуют периодическую последовательность
0,1,0,-1,0,1,0,-1,…

Итак
Аналогично для функции cosx
Биноминальный ряд
Рассмотрим функцию , где m – любое число. Разложим функцию в ряд Маклорена.
…
поэтому . Следовательно, ряд запишется в виде:
Установим область сходимости ряда. Найдем предел абсолютной величины отношения последующего элемента к предыдущему
согласно признака Даламбера ряд сходится, если |x|<1 и расходится, если |x}>1.
Исследуем , ограничившись случаем, когда 0<x<1. В этом интервале для всех n>m-1 имеем и поэтому Воспользуемся неравенством (***) . Правая часть неравенства есть абсолютная
величина (n+1)-го
члена степенного ряда, сходящегося при |x|<1.
Следовательно,
.
Соответствующее доказательство для
интервала
Правая часть неравенства есть абсолютная
величина (n+1)-го
члена степенного ряда, сходящегося при |x|<1.
Следовательно,
.
Соответствующее доказательство для
интервала
(-1,0) более сложное и оно не приводится.
Таким образом, биноминальный ряд представляет функцию в интервале (-1,1)
Если m – целое положительное число, то ряд справа содержит всего (m+1) слагаемых и превращается в форму бинома Ньютона. Заметим, что ряд сходится к функции во всем замкнутом интервале [-1,1].
Приведем биноминальные ряды, соответствующие значениям
(это геометрическая прогрессия)
Замечание
Разложение отдельных функций в ряды
могут быть получены из уже известных
разложений с помощью свойств степенных
рядов.
4. Функции ln(1+x) и arctgx
Для разложения в ряд Маклорена функции f(x)=ln(1+x) воспользуемся формулой для суммы геометрической прогрессии
Применим теорему об интегрировании степенных рядов и проинтегрируем ряд в пределах от 0 до х. Поскольку , то интегрируя поэлементно ряд, получим .
Совершенно аналогично получается разложение функции arctg x в ряд Маклорена. Для этого, заменим в формуле для суммы элементов геометрической прогрессии x на . Получим . Проинтегрируем ряд в пределах от 0 до х. Считая, что |x|<1 получаем
Замечание
Разложения (1)-(6) могут быть использованы для разложения в ряды других функций. Примеры:
Разложим в ряд Маклорена гиперболические функции chx и shx
Для ряда (1) заменим на получим . Далее, по правилу сложения и вычитания
рядов находим искомое разложение
Далее, по правилу сложения и вычитания
рядов находим искомое разложение
Разложим в ряд Маклорена функцию
Возьмем разложение функции и вместо , подставим получим
Разложим в ряд Маклорена функцию
Воспользуемся разложением биноминального ряда, где m=-1/2 и, для заменим x на , получим
Разложим в ряд Маклорена функцию
Так как . То разложение arcsinx получается интегрированием ряда (*)
Разложим в ряд Маклорена функцию
Так как ряды для и sinx сходятся абсолютно, то, перемножая их по правилу, рассмотренному ранее получим искомое разложение
(первые коэффициенты, так как закон подметить трудно).
Разложение основных элементарных функций в ряд Маклорена
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет.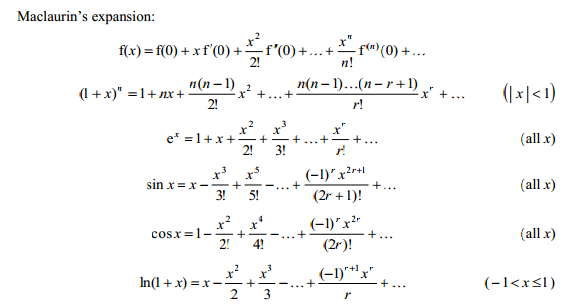 Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Конструирование Математика
- Главная /
- Статьи /
- Математика
(30.6.) Обозначим три основных этапа разложения бесконечно дифференцируемой в конкретной точке заданной функции в ряд Тейлора, представим особенности разложения определенной функции в ряд Маклорена.
Процесс разложения бесконечно дифференцируемой в т.функциив ряд Тейлора (частный случай, разложение функции в ряд Маклорена при) проходит в три этапа:
1) для функциизаписывается ряд Тейлора;
2) определяется интервал сходимости ряда;
3) осуществляется проверка того, что для записанного рядаесть сумма этого ряда.
30.6.1. Разложениев ряд Маклорена
1) Определяем производныеиначе выражаясь, , записываем ряд Маклорена для, используя формулу (30.7):
(30.10)
.
2) Находим интервал сходимости:
для ряда характерна абсолютная сходимость на промежутке.
3) Представимв форме Лагранжа (30.9):
(30.11)
Функциямонотонно возрастает, следовательноУчитывая то, что (30.10), в соответствии с признаком необходимости имеем
получается, что формула (30.11) является прооизведением ограниченной функции на б.м., следовательно.
Нравится
Твитнуть
Теги Математика
Сюжеты Математика
Понятие об автоматах, их задание графами
(38. 4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.
4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.
4099 0
Некоторые классы графов
(38.3.) Большинство графов, которые используются в приложениях (например, графы сортировок, классификаций) предполагают наличие диаграмм, именуемых деревьями. Связный неориентированный граф без циклов, в частности, предполагающий отсутствие петель и кратных ребер, именуют деревом. Несвязный неориентированный граф без цикла — лес, его связные компоненты являются деревьями.
10093 0
Маршруты, цепи и циклы
(38.2.) В рамках обозначенной темы рассмотрим случай определения связного неориентированного мультиграфа в качестве эйлерова и гамильтонова графа.
13605 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
расширений Тейлора
расширение Тейлора (c) Copyright Foundation Coalition (SA Fulling) 1998Классы 25.
 Т, 25.Р, 26.М, 27.М
Т, 25.Р, 26.М, 27.МПримечание. Поскольку Интернет еще не говорит на греческом языке легко, мы будем использовать Исландская буква Ð для «тета», знак фунта стерлингов £ для «лямбда», и знак цента ¢ для «эпсилон».
Вводный пример: пешеходный переход
[Вставить рисунок.]
Пешеходный переход проходит через прямую улицу между двумя светофорами. посты А и Б. Находится в 1000 метрах вниз по тротуару в точке C, инженер использует теодолит для измерения угла между А и В как ì = 2 градуса.
- Какой длины пешеходный переход?
- Насколько дальше от С до В, чем от С до А?
При подготовке к обсуждению этой задачи в классе используйте калькулятор, чтобы найти следующее по крайней мере до 2 значащих цифр:
- значение ì в радианах
- грех Р
- рыжевато-коричневый Р
- соз Ð
- 1 — cos Ð
Использование Maple для построения ì , sin ì , и tan Ð по тем же осям, в разных масштабах, около ì = 0. Затем сделайте то же самое для .
1 — cos Р и 1/2 Ð 2 .
Затем сделайте то же самое для .
1 — cos Р и 1/2 Ð 2 .
Вот что вы должны были заметить. (доступно после класса 25.Т)
Разложения Тейлора: основы
- Серия Taylor — ваши друзья! Нет причин бояться их или скучать по ним. Они позволяют аппроксимировать функции полиномами , которые легко вычислить. Немногие темы во всей последовательности исчисления более практичны!
- Ключевой факт: Для x рядом с и , f(x) примерно равно его N -й степени Полином Тейлора ,
Т Н (х) = [кликните сюда]. (PDF-версия)
Ошибка в этом приближении «ведет себя как» (х-а) N+1 (если у f достаточно производных).
Когда это утверждение становится более точным, оно становится Теорема Тейлора с остатком (Смотри ниже).
- Такое приближение известно под разными названиями: Разложение Тейлора, полином Тейлора, конечный ряд Тейлора,
усеченный ряд Тейлора, асимптотическое разложение, N аппроксимация го порядка ,
или (когда f определяется алгебраическим или дифференциальным уравнением
вместо явной формулы)
решение по теории возмущений (Смотри ниже).

Обычно мы можем расположить вещи так, чтобы базовая точка, и , 0 . Тогда разложение Тейлора называется Расширение Маклорена .
- Разложения Маклорена некоторых элементарных функции (версия в формате PDF)
Применение: уравнение маятника
Это будет предметом лаб 26.М. Прочтите это заранее. (PDF-версия)
Вычисления с полиномами Тейлора
Когда f является сложной функцией, формула Тейлора (с условиями f (j) /j !) обычно не самый лучший способ найти разложение Тейлора числа ф . Вместо этого пытаются найти ряд с помощью алгебры и исчисления из ранее известные разложения более простых функций. Начнем с двух простых примеров:
- Найдите первые 3 ненулевых члена в ряду Маклорена грех (2x) . (отвечать) (PDF-версия)
- Найдите первые 3 неисчезающих члена в ряду Маклорена x 2 e x .
 (отвечать)
(PDF-версия)
(отвечать)
(PDF-версия)А теперь попробуем что-нибудь посерьезнее: (Будьте готовы сделать это в классе в роли КРЫСЫ!)
- Найдите первые 3 члена разложения Маклорена е х е(х) ,
предположим, что все, что мы знаем о f , это то, что его серия Маклорена
начинается
f(x) = 1 + 3x + x 2 + … .
(ответ доступен после прохождения викторины) (PDF-версия)
Здесь нам нужно было перемножить два ряда Тейлора. При таком расчете есть две распространенные ошибки, которых следует избегать:
- Не забудьте крестики! Усеченные ряды Тейлора умножаются только как и любые другие многочлены: умножить на каждый член первой серии по каждый член второй серии. Затем объедините члены с одинаковым показателем степени.
- Члены высокого порядка (с большими показателями) похожи на
менее значащие цифры в десятичной арифметике:
Если вы сохраните один срок заказа x n ,
то вы должны сохранить все условий этого порядка, иначе ваш ответ будет
мусор.

Если вы знаете, что х = 3,5 приблизительно и г = 4,0962792966 точно, тут виднее чем писать х + у = 7,5962792966 ; вместо этого все, что вы можете сказать, это то, что x + y = 7,6 приблизительно.
Точно так же, если вы знаете, что
f(x) = 3 + x — x 2 + 5x 3 + 9x 4 + …
и что g(x) = 2 — x + … , где члены более высокого порядка в г не известны, значит не стоит писать
f(x) + g(x) = 5 — x 2 + 5x 3 + 9x 4 + … ;
все, что мы можем сказать, это то, что
f(x) + g(x) = 5 + O(x 2 ) .
(Обозначение O означает, что первый игнорируемый или неизвестный член имеет порядок х 2 . То есть линейное приближение к f + g фактически постоянно в этом случае, и у нас недостаточно информации для вычисления квадратичного приближение.
 )
)В случае, с которого началось это обсуждение, мы умножали два квадратичные полиномы Тейлора. Ваш ответ не должен содержать терминов более высокого порядка, чем второй, потому что в произведении есть члены третьего порядка, которые не могут быть определены из предоставленной информации.
- Найдите несколько первых членов ряда Маклорена
грех (2x + 1) .
Здесь есть еще одна ловушка, так что
мы разработаем это для вас.
(PDF-версия)
Можно также интегрировать и дифференцировать разложения Тейлора:
- Найти серию Maclaurin для ln (1 — x) путем интегрирования геометрического ряда. (отвечать) (PDF-версия)
Применение: Закон излучения черного тела
Это развитие упражнения 30 из гл. 10.12 Стюарт.
Для получения дополнительной информации об этой важной части истории физики см.
прочитать главу «Происхождение квантовой теории»
в FK Richtmyer et al., Введение в современную физику .
(Номер главы и имена соавторов варьируются от одного издания к
следующий. ) Обозначение:
) Обозначение:
- £ = длина волны
- T = температура
- k, h, c — некоторые физические константы.
В 19 веке было два конкурирующих теоретических предсказания для распределение энергии излучения в тепловом равновесии в идеально всасывающая полость.
- Закон Рэлея-Джинса ,
(первая формула)
Экспериментально проверено для длинных волн, но явно неверно на коротких волнах, где он предсказывает бесконечное количество энергии.
- Закон Вина ,
(вторая формула)
где константы C 1 и C 2 нужно было определить опытным путем. Это было экспериментально проверено для коротких волн. (Почему он там не бесконечен?)
В 1900 году была открыта правильная формула: Закон Планка ,
(третья формула)
[Здесь должен быть график из 3-х функций, но у меня еще не было
время произвести один. Так что вы, вероятно, захотите построить их в Maple!]
Так что вы, вероятно, захотите построить их в Maple!]
(версия формул в формате PDF)
Классное упражнение: Воспользуйтесь нашим список расширений Маклорена (PDF-версия) найти приближение к закону Планка, справедливое для больших £ и один действителен для небольших £. Покажите, что первый член каждого разложения согласуется с соответствующей формулой 19 века.
Прорыв в теории: открытие и обоснование теоремы Тейлора
Пришло время ответить на вопрос, что значит сказать, что Тейлор многочлен является хорошим приближением к функции, которую он представляет. Начнем со случая квадратичной аппроксимации и воспользуемся уже знакомым обозначение время-положение-скорость-ускорение для задействованных величин. (Кроме того, для упрощения обозначений мы возьмем точку расширения, и , быть 0 .)
ПРОЧИТАЙТЕ МЕНЯ! (PDF-версия)
Замечание по логике доказательства (PDF-версия)
Этот аргумент можно обобщить, чтобы доказать простейший и самый полезный
версия
Теорема Тейлора с остатком. (PDF-версия)
Другое доказательство (см. Stewart ed. 3, p. 662) доказывает
другая версия
(PDF-версия),
что немного точнее в отношении остаточного члена.
Прелесть этой версии в том, что формула для
остаток, Р Н ,
выглядит так же, как следующий член ряда, за исключением того, что
производная оценивается в неизвестной точке z вместо и .
(PDF-версия)
Другое доказательство (см. Stewart ed. 3, p. 662) доказывает
другая версия
(PDF-версия),
что немного точнее в отношении остаточного члена.
Прелесть этой версии в том, что формула для
остаток, Р Н ,
выглядит так же, как следующий член ряда, за исключением того, что
производная оценивается в неизвестной точке z вместо и .
(вернитесь к «Основам»)
Теорема о среднем значении и теорема Тейлора
Теорема Тейлора с остатком (во втором изложенном выше варианте) является обобщение теоремы о среднем значении; также используется теорема о среднем значении в его доказательстве. Хотя мы в спешке пропустили это, теорема о среднем значении появился еще в разделе 3.2 Стюарта и был тогда используется для доказательства многих элементарных свойств производных. Теперь мы можем присмотреться и лучше оценить оба теорема о среднем значении и теорема Тейлора.
Изучите (или повторите) теорему о среднем значении.
Посмотрите, что на самом деле говорит теорема Тейлора. (PDF-версия)
Пример: аппроксимация «невозможных» интегралов
ПРОЧТИТЕ МЕНЯ! (PDF-версия)
В практической работе многие люди привыкают использовать «правило большого пальца», согласно которому числовая ошибка при усечении ряд примерно равен первому слагаемому, которым пренебрегают. В нашей первой попытке в этом примере этот член был интегралом от х 4 /24 , что получилось 1/216 = 0,00463 (меньше запрошенного допуска 0,01 ). Обратите внимание, что это меньше, чем строгая ошибка связаны коэффициентом e . Если бы верхний предел интегрирования был намного больше, чем 1 , дополнительный коэффициент e c мог быть очень большой! Таким образом, эмпирическое правило может быть опасным при неосторожном использовании.
Однако при определенных особых обстоятельствах правило
палец точно правильный! Это так, когда ряд Тейлора удовлетворяет
«теорема об оценке переменного ряда» (Стюарт, стр. 632),
который используется Стюартом для решения задач этого типа.
Например, если показатель степени в подынтегральном выражении нашего примера был -х 2 (фактически более полезный интеграл из-за его связи с вероятностью!)
у нас был бы Пример 8 Стюарта, стр. 660-661.
632),
который используется Стюартом для решения задач этого типа.
Например, если показатель степени в подынтегральном выражении нашего примера был -х 2 (фактически более полезный интеграл из-за его связи с вероятностью!)
у нас был бы Пример 8 Стюарта, стр. 660-661.
Рекомендуемое назначение чтения
Не было обязательного задания по чтению текста Стюарта в начале эту веб-страницу. Причина в том, что подход Стюарта к разложениям Тейлора (как и во многих учебниках по математике) исходит из общей теории сходящихся бесконечных рядов, которые мы еще не изучали. Это делает соответствующие разделы, 10.9до 10.12, трудно понять контекста. Теперь, когда мы представили основные идеи о конечных рядах Тейлора и их приложений, возможно, вы готовы прочитать разделы 10.9–12 в первом чтении. Игнорируйте пока все обсуждения сходимости всей бесконечности ряд. Мы еще вернемся к этим разделам в конце курса.
Подход к разложениям Тейлора и связанным с ним вопросам, которые мы
нижеследующее во многом обязано статье Т. В. Такера,
«Переосмысление строгости исчисления: роль теоремы о среднем значении», American Mathematical Monthly , Vol. 104, стр. 231-240 (март 1997 г.).
В. Такера,
«Переосмысление строгости исчисления: роль теоремы о среднем значении», American Mathematical Monthly , Vol. 104, стр. 231-240 (март 1997 г.).
Теория возмущений: Решение уравнений в ряду Тейлора
Не удивительно, наиболее полезно иметь приближение Тейлора к функции когда нет точной формулы для функции. (Если вы точно знаете функцию, вас меньше интересует приближение.) Но в этой ситуации может быть сложно использовать формулу Тейлора. напрямую. (Как вычислить f (к) (а) если не знаешь ф ?) Если неизвестная функция определяется уравнением, которое нужно решить, можно предположить , что функция задается рядом Тейлора, с неизвестными коэффициентами и подставьте ряд в уравнение. Если повезет, результатом будет набор непротиворечивых уравнений, которые можно решить чтобы получить загадочные коэффициенты.
Простой, но нетривиальный пример дает алгебраическое уравнение. (PDF-версия)
(вернитесь к «Основам»)
Класс или домашнее задание: Давайте решим квадратных уравнений на этим методом и сравните результат с разложением Тейлора точного
решение, заданное квадратичной формулой.
- х 2 + 2 ¢ х + 1 =0
- ¢ x 2 + 2 x + 1 =0 (Что в этом случае происходит со вторым корнем в пертурбативной расчет?)
Классное упражнение: Давайте перечислим столько различных способов, сколько мы сможем придумать. найти ряд Маклорена функции г(х) = 1/(5-3х) . (Один из них должен быть «пертурбативным». Заполните детали нахождения первые несколько терминов таким образом.) (ответы доступно после занятий) (версия в формате PDF)
Приложение к дифференциальным уравнениям
Теория возмущений также может быть применена к дифференциальным уравнениям. Здесь есть сложность, что неизвестное есть функция секунды. переменная (независимая переменная дифференциального уравнения, скажем т ) а также малого параметра, скажем ¢. Частый недостаток метода состоит в том, что решение может терять точность при t увеличивается, даже если ¢ очень мало. Вот два примера:
- Атмосферное сопротивление падающему телу.
 (PDF-версия)
В лабораторной работе 27.М мы попытаемся обобщить это на два измерения и применить к ним.
к алгоритму наведения для вашей ракетницы для пинг-понга!
(PDF-версия)
В лабораторной работе 27.М мы попытаемся обобщить это на два измерения и применить к ним.
к алгоритму наведения для вашей ракетницы для пинг-понга! - Затухающий гармонический осциллятор. (PDF-версия) Подобно приведенному выше квадратному уравнению, эта задача имеет точное решение, которое можно быть разложена в ряд Тейлора, чтобы точно соответствовать пертурбативному решению.
Границы погрешности численного интегрирования
В качестве окончательного применения разложения Тейлора мы будем вывести формулы максимальной погрешности в знакомых правилах числового интеграция. Это незаконченное дело прошлого семестра. (Этот документ еще не написан. Если у нас будет время, мы вернемся к этому в конце семестра. См. также статью Такера, процитированную выше.)Аппроксимация рядов Тейлора высокого порядка для эффективного вычисления элементарных функций
- DOI:10.
 1049/iet-cdt.2014.0158
1049/iet-cdt.2014.0158 - Идентификатор корпуса: 13690993
@article{Chen2015HighorderTS,
title={Аппроксимация ряда Тейлора высокого порядка для эффективного вычисления элементарных функций},
автор={Чичан Чен},
журнал={Вычисление IET. цифра. Тех.},
год = {2015},
громкость = {9},
страницы = {328-335}
} - Chichyang Chen
- Опубликовано 26 октября 2015 г.
- Информатика
- IET Comput. цифра. Тех.
Предложен новый кусочно-полиномиальный метод вычисления элементарных функций с использованием тейлоровской аппроксимации высокого порядка. Предлагается аппроксимировать степенные члены ряда высокого порядка с помощью простого и быстрого поиска в таблице. Кроме того, сходство и регулярность коэффициентов Тейлора могут сделать возможным совместное использование справочных таблиц. Авторы разработали метод анализа ошибок для оценки максимальной ошибки предлагаемого подхода аппроксимации и сформулировали…
Просмотр через Publisher
Минимизация длины слова коэффициентов для кусочно-полиномиальной аппаратной оценки функции с точным или точным округлением
Описан новый метод минимизации длины слова полиномиальных коэффициентов с целью получения либо точного, либо достоверного округления при снижении стоимости оборудования.
Анализ и оптимизация для аппаратной реализации синуса/косинуса с точным округлением и монотонностью посредством кусочно-квадратичного полинома
Подробный анализ ошибок аппроксимации использовался для быстрого получения неравномерной сегментации и гарантии точного округления, а теоретический анализ показывает, что монотонность алгоритма, использующего сегментацию, согласуется с исходной функцией синуса и косинуса.
Усовершенствованный анализ точности на основе аффинной арифметики для оценки полиномиальной функции
- Рима Беллал, Эль-Седик Ламини, Х. Белбахир, С. Тагзоут, Адель Белоукрани
Информатика
IEEE Transactions on Computers
- 2019
В этой статье представлен анализ повышенной точности для полиномиального правила Горнера степени n, основанный на аффинной арифметике, и представлена формула распространения ошибки, учитывающая ошибку квантования всех соединений схемы, включая входы.
Прецизионный анализ с аналитическим процессом оптимизации разрядности для линейных схем с обратными связями
- Эль-Седик Ламини, С. Тагзоут, Х. Белбашир, А. Белухрани
Бизнес
IET Circuits Devices Syst.
- 2018
Описан метод аналитической оптимизации, учитывающий каждое соединение, который обеспечивает общее улучшение до 17% площади схемы по сравнению с существующими методами и выполняется за незначительное время независимо от заданной точности.
Методы компенсации ошибок при проектировании матричных умножителей фиксированной ширины — Технический обзор максимальная абсолютная ошибка, нормированная средняя ошибка и нормированная среднеквадратическая ошибка для оценки точности множителей фиксированной ширины.
Проектирование встроенного измерителя динамики TRA C: тематическое исследование
- L. G. León-Vega
Engineering
- 2018
PROYECTO FINAL DE GRADUACION (LICENCIATURARIARILIARILIARILIARILIARILIARILIARILIARILIARILIARILIARILIARILIE Electronica, 2018.
Разработка и внедрение в ПЛИС новой аппроксимации для снижения PAPR
ПОКАЗАНЫ 1–10 ИЗ 15 ССЫЛОК
0017
Elementary Functions Hardware Implementation Using Constrained Piecewise-Polynomial Approximations
- A. Strollo, D. D. Caro, N. Petra
Mathematics, Computer Science
IEEE Transactions on Computers
- 2011
A novel technique for designing кусочно-полиномиальные интерполяторы для аппаратной реализации элементарных функций и установлено, что увеличение погрешности аппроксимации из-за ограничений между полиномиальными коэффициентами легко преодолевается за счет увеличения дробных разрядов коэффициентов.
Метод таблиц и дополнений с эффективным использованием памяти для точного вычисления элементарных функций
В iATA математическая формулировка для вычисления элементарных функций выводится без использования формулировки центральной разности для экономии памяти, и в нее интегрированы три дополнительных метода. iATA для дальнейшего уменьшения объема памяти.
iATA для дальнейшего уменьшения объема памяти.
Аппроксимация элементарных функций с помощью симметричных двудольных таблиц
Этот метод выполняет поиск в двух параллельных таблицах для получения аппроксимации функции переноса-сохранения (заимствования-сохранения), которая либо преобразуется в число в дополнительном коде до двух, либо кодируется Бутом и имеет закрытый -form решение для записей таблицы.
Компромиссы аппаратной реализации полиномиальной аппроксимации и интерполяции
Результаты показывают, что степень экономии памяти, достигаемая с помощью интерполяции, значительно ниже, чем обычно считается, и доступность как основанных на интерполяции, так и основанных на аппроксимации проектов предлагает более богатый набор компромиссов при проектировании, чем то, что было доступно при использовании только интерполяции или аппроксимации.
Двухуровневая аппаратная функция оценки на основе коррекции нормированных кусочно-разностных функций
Экспериментальные результаты показывают, что предлагаемая архитектура, оптимизированная для ПЗУ, при использовании в многофункциональном анализаторе для вычисления нескольких элементарных арифметических функций на одном и том же оборудовании обеспечивает значительную экономию площади по сравнению с предыдущими подходами.
Эффективное начальное приближение для мультипликативного деления и извлечения квадратного корня умножением с изменением операнда
- Масаюки Ито, Н. Такаги, С. Ядзима
Математика, информатика
IEEE Trans. Компьютеры
- 1997
Предлагается эффективный метод начальной аппроксимации для мультипликативного деления и извлечения квадратного корня, модификация кусочно-линейной аппроксимации, требующая только побитовой инверсии и однобитового сдвига.
Алгоритмы поиска по таблицам для элементарных функций и их анализ ошибок
Показано, что при тщательном проектировании можно реализовать алгоритмы поиска по таблицам на аппаратном уровне, и единый подход к проведению тщательного анализа ошибок для таких реализаций представлены.
Новая стратегия неравномерной сегментации и переназначения адресов для аппаратно-ориентированных оценщиков функций на основе полиномиальной аппроксимации
Экспериментальные результаты показывают, что этот новый метод сегментации и переназначения адресов может эффективно уменьшить размер таблицы для некоторых элементарных арифметических функций, таких как log2x и 1/х.


 (отвечать)
(PDF-версия)
(отвечать)
(PDF-версия)
 )
)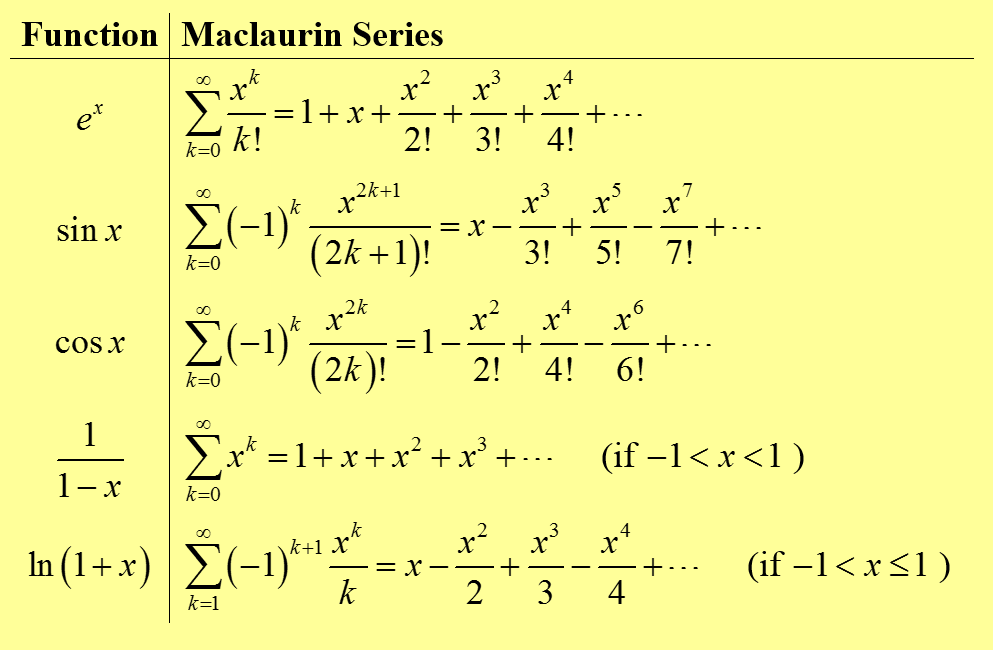 (PDF-версия)
В лабораторной работе 27.М мы попытаемся обобщить это на два измерения и применить к ним.
к алгоритму наведения для вашей ракетницы для пинг-понга!
(PDF-версия)
В лабораторной работе 27.М мы попытаемся обобщить это на два измерения и применить к ним.
к алгоритму наведения для вашей ракетницы для пинг-понга!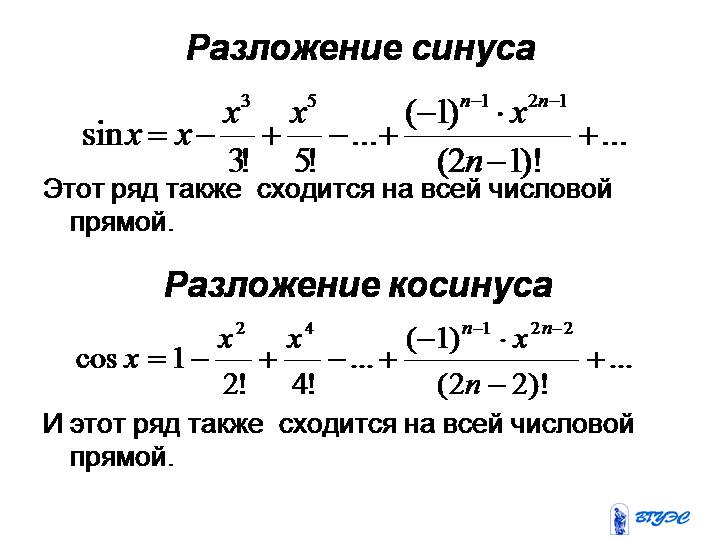 1049/iet-cdt.2014.0158
1049/iet-cdt.2014.0158