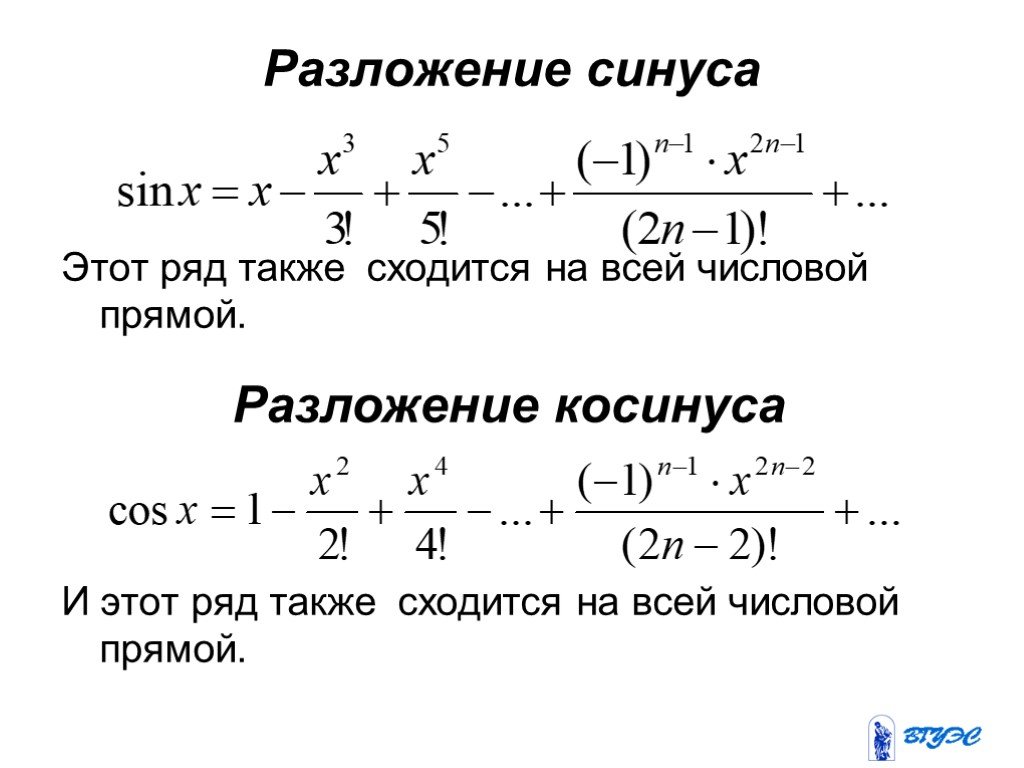
Разложение f(x) = cos x в ряд Маклорена. Разложение (1+x)? , m?R в ряд Маклорена (биномиальный ряд)
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
|
Конструирование Математика
- Главная /
- Статьи /
(30.6.3./30.6.4.) Обозначим особенности разложения заданной функции в ряд Маклорена, а также поэтапно запишем осуществление разложения (1+x)?, m ? R в биномиальный ряд.
В соответствии с формулой, запишем ряд дляпочленным дифференцированием (30.12):
Для ряда характерна абсолютная сходимость на интервале.
1) Следует найти производные
то есть
далее запишем дляряд Маклорена:
(30.13)
который именуют биномиальным рядом (в случае, когдаявляется натуральным числом, прикоэффициенты обращаются в нуль и образуется многочлен — это частный случай бинома Ньютона).
2) Выявляем интервал сходимости:
для ряда характерна абсолютная сходимость на интервале- ненатуральное число, ряд расходится на.
Нравится
Твитнуть
Теги Математика
Сюжеты Математика
Понятие об автоматах, их задание графами
(38.4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.
4093 0
Некоторые классы графов
(38.3.) Большинство графов, которые используются в приложениях (например, графы сортировок, классификаций) предполагают наличие диаграмм, именуемых деревьями. Связный неориентированный граф без циклов, в частности, предполагающий отсутствие петель и кратных ребер, именуют деревом. Несвязный неориентированный граф без цикла — лес, его связные компоненты являются деревьями.
10092 0
Маршруты, цепи и циклы
(38.
2.) В рамках обозначенной темы рассмотрим случай определения связного неориентированного мультиграфа в качестве эйлерова и гамильтонова графа.
13594 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
Ряд Тейлора, ряд Маклорена
Если функция f (x) разлагается в степенной ряд f (x)= с0+ с1(х-а)+с2(х-а)2+ с3(х-а)3+…+ск(х-а)к +… в некоторый окрестности точки а, т.е. в интервале (а-h,a+h), то коэффициенты этого ряда определяются по формулам: с0= F(a), ск=
Следовательно, f(x)=f(a)+
Ряд, сходящийся в правой части формулы называется рядом Тейлора для функции f(x)
Равенство
выполняется ряд Тейлора сходится к f(x)
в интервале (а-h,a+h),
если остаток ряда Тейлора r n(x)=
(f(x)-f(a)-
стремиться к нулю при неограниченном
возрастании n:
при всех х из интервала (а-h,a+h).
Формула (3) в частном случае при а=0 определяет разложение функции в ряд Маклорена:
f(x)= f(0)+
Лекция 5.
Рассмотрим разложение в ряд Маклорена элементарных функций.
Пусть f(x)=ex По формулам Тейлора:
+ Rn(x) ,
где Rn(x)=
Так как при фиксированном х величина ex ограничена (а значит, ограничены все производные) то Следовательно, при всех
+ ….
Аналогичным образом получаем разложение в ряд функций f(x)= sin x и f(x)= cos x (здесь также при всех х)
+ ….
….
Разложим в ряд Маклорена функцию f(x)= (1+x)m, где m- произвольное постоянное число.
Найдя f(0), f `(0), f (n)(0)… получим ряд (называемый биноминальным)
Определим радиус сходимости этого ряда
Так как Cn=
Cn+1= , то
Таким
образом биноминальный ряд сходится при
Х ε (-1,1) и расходится при Х<-1 и Х>1.
Сходится ли этот ряд при Х=1 и Х=-1,
необходимо исследовать в каждом случае
отдельно.
Осталось показать, что сумма этого ряда при Х ε (-1,1) действительно равна (1+x)m. Оценка остаточного члена в этом случае довольно сложна, поэтому доказательство опустим.
Итак , при Х ε (-1,1)
В частности при m= -1
Интегрируя это равенство от 0 до Х, где X<|1|, получим:
Откуда легко получить разложение функции:
это равенство справедливо в интервале (-1,1). Можно показать, что оно справедливо при Х=1
Положив в разложении х=t2, после интегрирования получим разложение в ряд функции
F(x)= arctg x. Справедливо при X<|1|,
Это верно при Х=1
Пусть в формуле m= -1/2, n= -t2
Интегрируя получаем, при Х ε (-1,1).
Геометрический ряд
Найти:
Заменив их разложениями в степенные ряды, получаем
Найти:
Используем разложение в степенные ряды, получаем:
С
помощью рядов Тейлора вычисляют значения
так называемых не берущиеся интегралы
.
Вычислить интеграл:
сначала
разложим подынтегральную функцию в
ряд, заменяя Х на –х
Интегрируя равенство, получаем:
(1) Таким образом, с помощью формулы (1) можно вычислить значение данного интеграла для любого Х с любой степенной точки.
Лекция 6 Дифференциальные уравнения.
Основные понятия.
Дифференциальным уравнением называется уравнения вида F(x,y,y`,y«,…,y(n))=0, где х- независимая переменная, y=f(x) искомая функция. y,y`,y«,…,y(n) — ее производные.
Решением дифференциального уравнения называется функция y=f(x),которая при подстановке ее и ее производных обращает равенство F(x,y,y`,y«,…,y(n))=0 в тождество.
Порядком дифференциального уравнения называется наибольший порядок n входящей в него производной.
Примеры:
Решить дифференциальное уравнение:
y`+sin x=0
Запишем
уравнение в виде y`=
— sin
x.
Поэтому решением данного уравнения имеют вид:
В общем виде для уравнения y`=f(x) решениями будут функции которые являются первообразными для f(x).
Интегрированием дифференциального уравнения называется процесс нахождения его решений.
Интегральной кривой называется график решения дифференциального уравнения.
Например: для уравнения y`= — sin x интегральные кривые являются графиками функции , полученным из графика сдвигом вверх (вниз) на константу С.
Общим решением дифференциального уравнения F(x,y,y`,y«,…,y(n))=0 порядка n называется такое решение y= f(x,C1, C2
Частным решением называется решение, получаемое из общего решения, при некоторых конкретных значениях постоянных C1, C2,… Cn.
Пример:
Для уравнения второго порядка y« =0 общее решение имеет вид y= C1х+ C2. Одним из частных решений будет решение y=x полученное при C1=1 ,C2=0.
Дифференциальные уравнения первого порядка.
Разрешенным относительно производной называется дифференциальное уравнение первого порядка F(x,y,y`)=0, которое можно записать в общем виде y`=f(x, y).
Уравнение с разделяющимися переменными.
Решением уравнения вида y`=f(x, y), сводящихся к нахождению неопределенных интегралов, если функция двух переменных f(x, y) представима в виде произведения двух функций одной переменной
f(x, y) =g(x)*h(y), заменяя y` на , получаем
Уравнением с разделяющимися переменными называется уравнение вида По-другому такие уравнения можно записать в виде:
М(х) dx+N(y) dy=0
или
М(х) dx= — N(y) dy
Интегрируя обе части последнего равенства, получаем:
Общее
решение Φ(x,y,C)=0
заданное в неявном виде,
называется интегралом этого уравнения.
Геометрически общее решение (и общий интеграл) представляется собой семейство интегральных кривых на плоскости, зависящее от одного параметра Сю
Частным
решением уравнения называется решение, полученное из общего
решения при фиксированном значении С:
y=
φ(x,C
Задача Коши.
Найдите решение y=f(x), дифференциального уравнения первого порядка, удовлетворявшее начальному условию y=y0 при x=x0. Другими словами, найти интегральную кривую этого уравнения , проходящую через точку М0 (x0, y0).
Лекция 7.
Примеры:
Пусть мы имеем уравнение
Функция y= sin x, y= 2cos x, y= 3sin x- cos x и вообще функция вида y= C1 sin x, y= C2 cos x, или
y=
C1 sin
x+
C2 cos
x
является решениями данного уравнения
при любом выбор постоянных C1 и C2,
в этом легко убедиться, подставив
заданные функции в уравнение.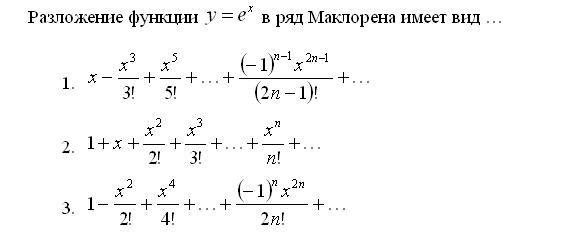
Наряду с
обыкновенными дифференциальными
уравнениями.
Рассмотрим уравнение y`x-x2-y=0. Его решениями будут все функции вида: y= x2+Cx, где С- любое постоянное. Действительно, дифференцируя функцию y=x2+Cx ,находим y`=2х+С. Подставляя выражения y и y` в исходное уравнение, получаем тождество (2х+С) x-x2— Cx=0
Каждое из уравнений, рассмотренных в примерах 1 и 2, имеет бесчисленное множество решений.
Рассмотрим уравнение y` =
Разделяя переменные, получаем: Интегрируя, имеем или Потенцируя, находим , что эквивалентно уравнению . Полагая окончательно получаем
Заметим,
что y=0
также решение уравнения (оно было
потеряно при делении на y).
Это решение можно включить в (9), если
считать что постоянная С принимает
значение С=0. Геометрическими общее
решение (9) представляет собой семейство
прямых проходящих через начало координат.
Пусть
требуется выделить из общего решения
(9) частное решение , удовлетворяющее
следующим начальным условиям: х0=1,
у0=2.
Подставляя эти значения в общее решение
вместо х и у, получаем 2=C•1, откуда С=2.
Таким образом , искомое частное решение
y =2x.
Для уравнения первого порядка общим уравнением будет семейство функций — это можно проверить простой подстановкой в уравнение. Найдем честное решение, удовлетворяющее следующему начальному условию: х0=2, у0=1. Подставляя эти значения : х0, у0 в формулу ,получаем или С=2. Следовательно, искомым частным решением будет функция
Рис.1
Дано семейство парабол:
Рис.2
Найдите
дифференциальное уравнение семейства
парабол y=Cx2.
Дифференцируя по х уравнение семейства,
найдем . Подставляя сюда значение найдем: из уравнения семейства получаем
дифференциальное уравнение данного
семейства, Это дифференциальное уравнение имеет
смысл при х≠0, т.
е.в точке любой области,
не содержащей точек на оси Оy/
исчисление — ряд Тейлора как приближение для cos(θ)
спросил
Изменено 5 лет, 4 месяца назад
Просмотрено 758 раз
$\begingroup$
Итак, я смотрел одну из лекций Уолтера Левина, и он записал, что… 92}{2L}$ (???Как он пришел к такому выводу???)
Вот набросок, который я нарисовал, чтобы наглядно представить себе ситуацию. Это связано с движением маятника, но, поскольку конкретная проблема связана с приближением Тейлора, здесь кажется подходящим местом для проблемы. Спасибо!
- исчисление
- разложение Тейлора
- треугольники
$\endgroup$
5
92}{2L}.
$$
Все это стандартная теория простого маятника.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Ряд Тейлора расширения cos x в python
Я хочу рассчитать сумму ряда cosx (при сохранении x в радианах). Это код, который я создал:
импортировать математику
определение косинуса (x, n):
сумма = 0
для i в диапазоне (0, n+1):
сумма += ((-1) ** i) * (x**(2*i)/math.factorial(2*i))
возвращаемая сумма
и я проверил это с помощью math.cos() .
Он отлично работает, когда я пробовал маленькие числа:
print("Результат: ", косинус(25, 1000))
печать (math.cos (25))
вывод:
Результат: 0,9912035409546670,9912028118634736
Номер все тот же. Но когда я попробовал большее число, то есть 40, он просто возвращает совершенно другое значение.
Результат: 1,2101433786727471-0,6669380616522619
Кто-нибудь знает, почему это происходит?
- python
- taylor-series
Погрешность расширения Тейлора тем больше, чем дальше вы находитесь от точки, о которой идет речь (в данном случае х_0 = 0 ).
Чтобы уменьшить ошибку, используйте периодичность и симметрию, оценивая только интервал [0, 2 * pi] :
def cosine(x, n):
х = х% (2 * пи)
всего = 0
для i в диапазоне (0, n + 1):
итог += ((-1) ** i) * (x**(2*i) / math.factorial(2*i))
общая сумма возврата
Это можно улучшить до [0, pi/2] :
по косинусу (x, n):
х = х% (2 * пи)
если х > пи:
х = абс (х - 2 * пи)
если х > пи/2:
вернуть -косинус (пи - х, п)
всего = 0
для i в диапазоне (0, n + 1):
итог += ((-1) ** i) * (x**(2*i) / math.factorial(2*i))
общая сумма возврата
Вопреки полученному вами ответу, этот ряд Тейлора сходится независимо от величины аргумента. Факториал в знаменателях терминов в конечном итоге приводит термины к 0.
Но до преобладает факториальная часть, термины могут становиться все больше и больше по абсолютной величине. Собственная плавающая запятая не имеет достаточной точности, чтобы сохранить достаточно информации для выживания младших битов.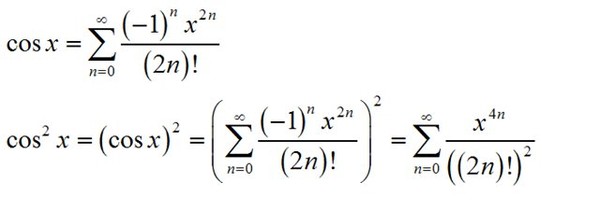
Вот способ, который не теряет ни капли точности. Это не практично, потому что медленно. Поверьте мне, когда я говорю вам, что обычно требуются годы опыта, чтобы научиться писать практичные, быстрые и высококачественные математические библиотеки.
определение mycos(x, nbits=100):
из дробей импорт дроби
x2 = - Фракция (x) ** 2
я = 0
число = 0
итог = срок = дробь (1)
пока верно:
количество записей += 1
срок = срок * x2 / ((i+1) * (i+2))
я += 2
всего += срок
if (total // term).bit_length() > nbits:
ломать
print("сходится к >=", nbits, "bits in", ntries, "steps")
общая сумма возврата
и далее ваши примеры:
>>> mycos(25) сошлись до >= 100 бит за 60 шагов Фракция (1779 г.902656315755268601372315751766446600474817729598222950654891626294219622069090604398951917221057277891721367319419730580721270980180746700236766890453804854224688235663001, 179569976498504495450560473003158183053487302118823494306831203428122565348395374375382001784940465248260677204774780370309486592538808596156541689164857386103160689754560975077376) >>> с плавающей запятой(_) 0,9912028118634736 >>> микос(40) сошлись до >= 100 бит за 82 шага Дробь(-41233919211296161511135381283308676089648279169136751860454289528820133116589076773613997242520904406094665861260732939711116309156993591792484104028113938044669594105655847220120785239949370429999292710446188633097549, 61825710035417531603549955214086485841025011572115538227516711699374454340823156388422475359453342009385198763106309156353690402915353642606997057282914587362557451641312842461463803518046090463931513882368034080863251) >>> с плавающей запятой(_) -0,6669380616522619
На что следует обратить внимание:
Для получения результатов с полной точностью требуется большое количество битов.
