Тождественные преобразования тригонометрических выражений
В тождественных преобразованиях тригонометрических выражений могут быть использованы следующие алгебраические приемы: добавление и вычитание одинаковых слагаемых; вынесение общего множителя за скобки; умножение и деление на одну и ту же величину; применение формул сокращенного умножения; выделение полного квадрата; разложение квадратного трехчлена на множители; введение новых переменных с целью упрощения преобразований.
При преобразованиях тригонометрических выражений, содержащих дроби, можно использовать свойства пропорции, сокращение дробей или приведение дробей к общему знаменателю. Кроме того, можно пользоваться выделением целой части дроби, умножением числителя и знаменателя дроби на одинаковую величину, а так же по возможности учитывать однородность числителя или знаменателя. При необходимости можно представлять дробь в виде суммы или разности нескольких более простых дробей.
Кроме того, применяя все необходимые методы преобразования тригонометрических выражений, необходимо постоянно учитывать облась допустимых значений преобразуемых выражений.
Рассмотрим несколько примеров.
Пример 1.
Вычислить А = (sin (2x – π) · cos (3π – x) + sin (2x – 9π/2) · cos (x + π/2))2+ (cos (x – π/2) · cos (2x – 7π/2) +
+ sin (3π/2 – x) · sin (2x – 5π/2))2
Решение.
Из формул приведения следует:
sin (2x – π) = -sin 2x; cos (3π – x) = -cos x;
sin (2x – 9π/2) = -cos 2x; cos (x + π/2) = -sin x;
cos (x – π/2) = sin x; cos (2x – 7π/2) = -sin 2x;
sin (3π/2 – x) = -cos x; sin (2x – 5π/2) = -cos 2x.
Откуда в силу формул сложения аргументов и основного тригонометрического тождества получаем
А = (sin 2x · cos x + cos 2x · sin x)2 + (-sin x · sin 2x + cos x · cos 2x)2 = sin2 (2x + x) + cos 2 (x + 2x) =
= sin2 3x + cos2 3x = 1
Ответ: 1.
Пример 2.
Преобразовать в произведение выражение М = cos α + cos (α + β) · cos γ + cos β – sin (α + β) · sin γ + cos γ.
Решение.
Из формул сложения аргументов и формул преобразования суммы тригонометрических функций в произведение после соответствующей группировки имеем
М = (cos (α + β) · cos γ – sin (α + β) · sin γ) + cos α + (cos β + cos γ) =
= 2cos ((β + γ)/2) · cos ((β – γ)/2) + (cos α + cos (α + β + γ)) =
= 2cos ((β + γ)/2) · cos ((β – γ)/2) + 2cos (α + (β + γ)/2) · cos ((β + γ)/2)) =
= 2cos ((β + γ)/2) (cos ((β – γ)/2) + cos (α + (β + γ)/2)) =
= 2cos ((β + γ)/2) · 2cos ((β – γ)/2 + α + (β + γ)/2)/2) · cos ((β – γ)/2) – (α + (β + γ)/2)/2) =
= 4cos ((β + γ)/2) · cos ((α +β)/2) · cos ((α + γ)/2).
Ответ: М = 4cos ((α + β)/2) · cos ((α + γ)/2) · cos ((β + γ)/2).
Пример 3.
Показать, что выражение А = cos2 (x + π/6) – cos (x + π/6) · cos (x – π/6) + cos2 (x – π/6) принимает для всех х из R одно и то же значение.
Найти это значение.
Решение.
Приведем два способа решения этой задачи. Применяя первый способ, путем выделения полного квадрата и пользуясь соответствующими основными тригонометрическими формулами, получим
А = (cos (x + π/6) – cos (x – π/6))2 + cos (x – π/6) · cos (x – π/6) =
= 4sin2 x · sin2 π/6 + 1/2(cos 2x + cos π/3) =
= sin2 x + 1/2 · cos 2x + 1/4 = 1/2 · (1 – cos 2x) + 1/2 · cos 2x + 1/4 = 3/4.
Решая задачу вторым способом, рассмотрим А как функцию от х из R и вычислим ее производную. После преобразований получим
А´ = -2cos (x + π/6) · sin (x + π/6) + (sin (x + π/6) · cos (x – π/6) + cos (x + π/6) · sin (x + π/6)) – 2cos (x – π/6) · sin (x – π/6) =
= -sin 2(x + π/6) + sin ((x + π/6) + (x – π/6)) – sin 2(x – π/6) =
= sin 2x – (sin (2x + π/3) + sin (2x – π/3)) =
= sin 2x – 2sin 2x · cos π/3 = sin 2x – sin 2x ≡ 0.
Отсюда в силу критерия постоянства дифференцируемой на промежутке функции заключаем, что
А(х) ≡ (0) = cos2 π/6 — cos2 π/6 + cos2 π/6 = (√3/2)2 = 3/4, x € R.
Ответ: А = 3/4 для x € R.
Основными приемами доказательства тригонометрических тождеств являются:
а) сведение левой части тождества к правой путем соответствующих преобразований;
б)
в) сведение правой и левой частей тождества к одному и тому же виду;
г) сведение к нулю разности левой и правой частей доказываемого тождества.
Пример 4.
Проверить, что cos 3x = -4cos x · cos (x + π/3) · cos (x + 2π/3).
Решение.
Преобразуя правую часть этого тождества по соответствующим тригонометрическим формулам, имеем
-4cos x · cos (x + π/3) · cos (x + 2π/3) =
= -2cos x · (cos ((x + π/3) + (x + 2π/3)) + cos ((x + π/3) – (x + 2π/3))) =
= -2cos x · (cos (2x + π) + cos π/3) =
= 2cos x · cos 2x — cos x = (cos 3x + cos x) – cos x = cos 3x.
Правая часть тождества сведена к левой.
Пример 5.
Доказать, что sin2 α + sin2 β + sin 2 γ – 2cos α · cos β · cos γ = 2, если α, β, γ – внутренние углы некоторого треугольника.
Решение.
Учитывая, что α, β, γ – внутренние углы некоторого треугольника, получаем, что
α + β + γ = π и, значит, γ = π – α – β.
Получим
sin2 α + sin2 β + sin2 γ – 2cos α · cos β · cos γ =
= sin2 α + sin2 β + sin2 (π – α – β) – 2cos α · cos β · cos (π – α – β) =
= sin2 α + sin2 β + sin2 (α + β) + (cos (α + β) + cos (α – β) · (cos (α + β) =
= sin2 α + sin2 β + (sin2 (α + β) + cos2 (α + β)) + cos (α – β) · (cos (α + β) =
= 1/2 · (1 – сos 2α) + ½ · (1 – cos 2β) + 1 + 1/2 · (cos 2α + cos 2β) = 2.
Исходное равенство доказано.
Доказать, что для того, чтобы один из углов α, β, γ треугольника был равен 60°, необходимо и достаточно, чтобы sin 3α + sin 3β + sin 3γ = 0.
Решение.
Условие данной задачи предполагает доказательство как необходимости, так и достаточности.
Вначале докажем необходимость.
Можно показать, что
sin 3α + sin 3β + sin 3γ = -4cos (3α/2) · cos (3β/2) · cos (3γ/2).
Отсюда, учитывая, что cos (3/2 · 60°) = cos 90° = 0, получаем, что если один из углов α, β или γ равен 60°, то
cos (3α/2) · cos (3β/2) · cos (3γ/2) = 0 и, значит, sin 3α + sin 3β + sin 3γ = 0.
Докажем теперь достаточность указанного условия.
Если sin 3α + sin 3β + sin 3γ = 0, то cos (3α/2) · cos (3β/2) · cos (3γ/2) = 0, и поэтому
либо cos (3α/2) = 0, либо cos (3β/2) = 0, либо cos (3γ/2) = 0.
Следовательно,
либо 3α/2 = π/2 + πk, т.е. α = π/3 + 2πk/3,
либо 3β/2 = π/2 + πk, т.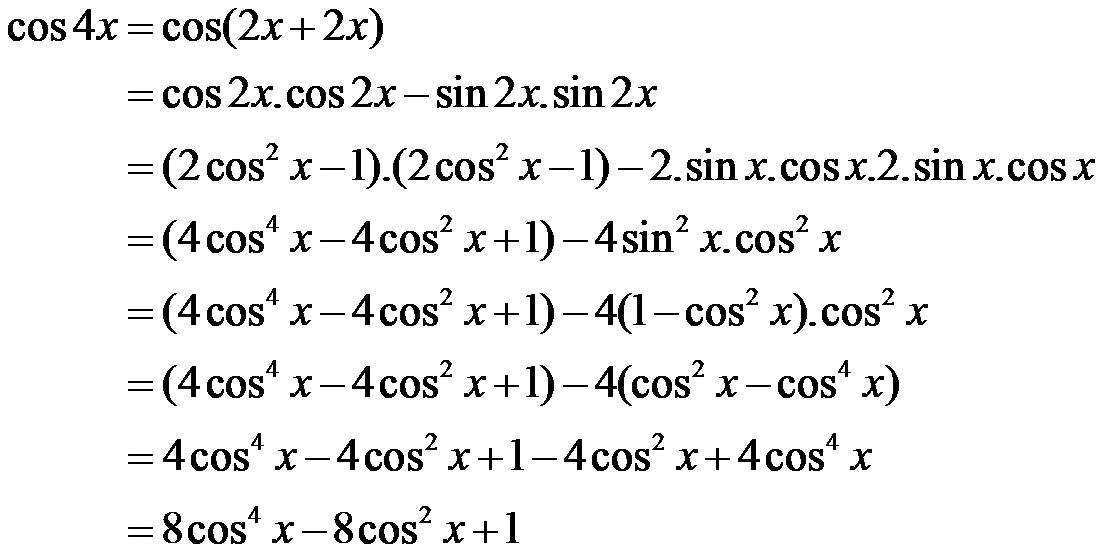
е. β = π/3 + 2πk/3, либо 3γ/2 = π/2 + πk,
т.е. γ = π/3 + 2πk/3, где k ϵ Z.
Из того, что α, β, γ – это углы треугольника, имеем
0 < α < π, 0 < β < π, 0 < γ < π.
Поэтому для α = π/3 + 2πk/3 или β = π/3 + 2πk/3 или
γ = π/3 + 2πk/3 из всех kϵZ подходит только k = 0.
Откуда следует, что либо α = π/3 = 60°, либо β = π/3 = 60°, либо γ = π/3 = 60°.
Утверждение доказано.
Остались вопросы? Не знаете, как упрощать тригонометрические выражения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |