Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена. Примеры решений
Продолжаем рассматривать теорию и практику степенных рядов. Материал несложный, но для его понимания необходимо уже более или менее хорошо ориентировать в теме. Если Вы только-только приступили к изучению рядов или чувствуйте себя чайником, пожалуйста, начните с урока Ряды для чайников. Примеры решений. Далее следует прочитать статьюСтепенные ряды. Область сходимости ряда, в частности, Вы должны хорошо понимать, что такое степенной ряд и его область сходимости. А для целей сегодняшнего урока потребуется методический материал Таблица разложений некоторых функций в степенные ряды, его можно раздобыть в кладовке Математические формулы и таблицы. По возможности, таблицу лучше распечатать, поскольку она потребуется не только сейчас, но и в оффлайне.
Понятие суммы степенного ряда
Начнем
подходить к теме с воспоминаний. Как мы
помним, любой числовой ряд может или
сходиться, или расходиться.
На уроке Степенные ряды. Область сходимости ряда мы рассматривали уже не числовые, а функциональные и степенные ряды. Возьмём тот самый подопытный степенной ряд, который всем понравился: . В ходе исследования было установлено, что этот ряд сходится при . Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда в его области сходимости является некоторая функция :
Еще раз подчеркиваю, что данный факт справедлив только для найденной области , вне этого промежутка степенной ряд будет расходиться.
Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:
Область сходимости ряда:
(По
какому принципу получены сами элементарные
табличные разложения, мы рассмотрим
чуть позже).
Теперь вспоминаем школьный график синуса :
Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел….
Теперь фишка. Если начертить график бесконечного многочлена , то получится… та же самая синусоида! То есть, наш степенной ряд сходится к функции . Используя признак Даламбера (см. статью Степенные ряды. Область сходимости ряда), легко проверить, что ряд сходится при любом «икс»: (собственно, поэтому в таблице разложений и появилась такая запись об области сходимости).
А
что значит вообще «сходится»? По
смыслу глагола – что-то куда-то идёт.
Если я возьму первые три члена ряда
и
начерчу график многочлена пятой степени,
то он лишь отдаленно будет напоминать
синусоиду. А вот если составить многочлен
из первых ста членов ряда:
и
начертить его график, то он будет с
синусоидой практически совпадать. Чем
больше членов ряда – тем лучше приближение.
И, как уже отмечалось, график бесконечного
многочлена – есть в точности синусоида.
Иными словами, ряд
сходится
к функции
при
любом значении «икс».
Рассмотрим более печальный пример, табличное разложение арктангенса: Область сходимости ряда:
Печаль заключается в том факте, что график бесконечного многочлена совпадает с графиком арктангенса только на отрезке (т.е. в области сходимости ряда):
Вне отрезка разложение арктангенса в ряд расходится, а график бесконечного многочлена пускается во все тяжкие и уходит на бесконечность.
Разложение функций в степенной ряд. Ряд Тейлора. Ряд Маклорена
Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.
Если функция в некотором интервале раскладывается в степенной ряд по степеням , то это разложение единственно и задается формулой: Примечания: Надстрочный индекс в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву .
Данная
формула получила имя некоего англичанина
Тейлора (ударение на первый слог).
На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда :
Это разложение в ряд обычно называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора по степеням .
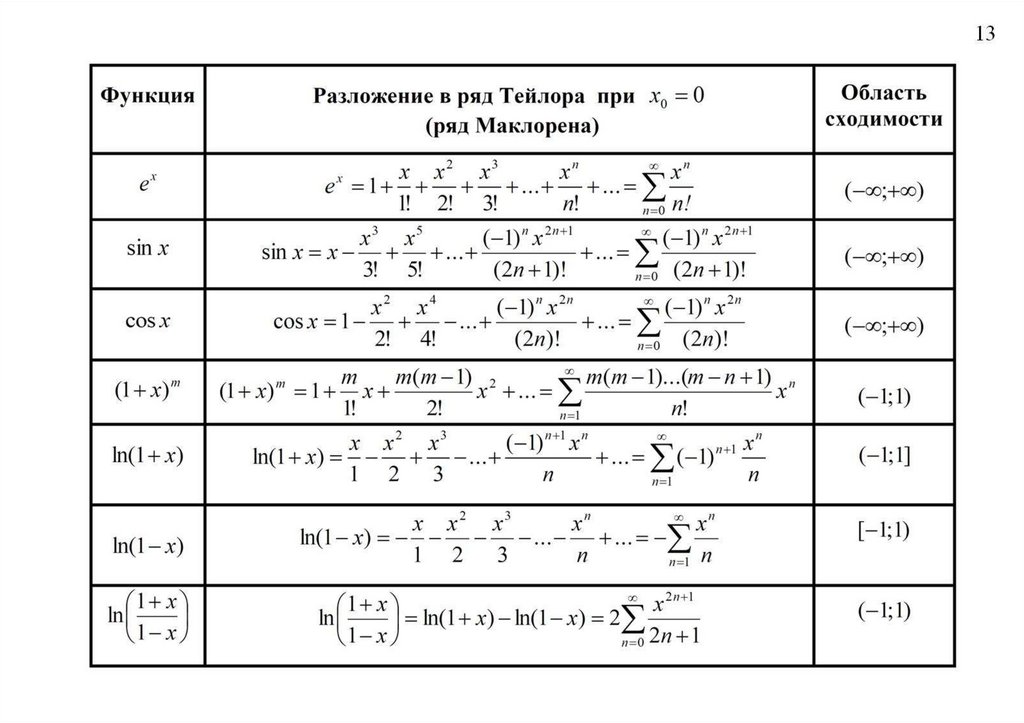
Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Как оно получилось? По формуле Маклорена: Рассмотрим функцию , тогда:
Теперь
начинаем находить
И так далее….
Совершенно очевидно, что
Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!
Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Примеры разложения функций в ряд Маклорена
В
данном параграфе мы рассмотрим типовую
задачу на разложение функции в ряд
Маклорена и определении области
сходимости полученного ряда.
Нет,
мучаться с нахождением производных не
придется, мы будем пользоваться таблицей.
Пример 1
Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.
! Эквивалентная формулировка: Разложить функцию в ряд по степеням
Решение незамысловато, главное, быть внимательным и не пропустить какую-нибудь степень, индекс.
Конструируем наш ряд. Плясать начинают, как правило, от функции, в данном случае – от косинуса. Используем элементарное разложение:
. Область сходимости ряда:
В данном случае
В числителях раскрываем скобки:
Теперь умножаем обе части на «икс»:
В итоге искомое разложение функции в ряд:
Как определить область сходимости? Разложение косинуса сходится при ЛЮБОМ значении «альфа»: , а значит и при . Домножение на «икс» не играет никакой роли в плане сходимости. Поэтому область сходимости полученного ряда:
Пример 2
Разложить
функцию в ряд по степеням
.
Найти область сходимости ряда.
Это пример для самостоятельного решения.
Я
не стал рассматривать простейшие
разложения вроде
,
или
,
поскольку это фактически задача в одно
действие. В нужные табличные разложения
вместо «альфы» необходимо подставить
,
,
и
немного причесать полученные
ряды.
А сейчас для разнообразия рассмотрим что-нибудь с минусами.
Пример 3
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
В таблице находим похожее разложение: Область сходимости ряда: , концы интервала нужно исследовать дополнительно.
Трюк прост: перепишем функцию немного по-другому:
Таким образом, и: Окончательно:
Теперь
нужно определить область сходимости.
Смотрим на табличное неравенство
.
У нас тут минус и «икс» в квадрате:
,
не факт, что область сходимости полученного
ряда будет именно такая.
В сомнительных случаях надежнее всего
подробно проанализировать полученный
степенной ряд.
Таким образом, область сходимости полученного ряда:
Интересно отметить, что простейшее разложение из учебника сходится ещё в одной точке, и область сходимости соответствующего ряда: . А разложение в ряд такого логарифма: – сходится на обоих концах интервала:
Таким образом, когда вам дан для разложения любой логарифм, следует быть предельно аккуратным и внимательным.
Пара примеров для самостоятельного решения:
Пример 4
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Пляска
традиционно начинается от функции, то
есть, начинать нужно с экспоненты.
Пример 5
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Здесь разложение не такое трудное, но могут возникнуть трудности с нахождением области сходимости полученного ряда.
Полные решения и ответы в конце урока.
Не редкость, когда перед разложением функции в ряд её необходимо предварительно преобразовать. Канонический случай – это разложение функции . Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы: . Решать я этот пример не буду, поскольку он довольно простой, к тому же что-то подобное мы недавно рассмотрели.
Пример 6
Разложить функцию в ряд по степеням . Найти область сходимости ряда.
Смотрим в таблицу и находим наиболее похожее разложение:
Во-первых, вверху нужно получить единицу, поэтому представляем функцию в виде произведения: Теперь нам нужно в знаменателе устроить , для этого выносим двойку за скобки: И сокращаем на два: В данном случае , таким образом:
В итоге искомое разложение:
Определим
область сходимости ряда.
Можно пойти
длинным и надежным путем, используя
признак Даламбера для полученного
степенного ряда
,
т.е. найти интервал сходимости ряда и
исследовать сходимость ряда на концах
найденного интервала.
А можно поступить проще. Из таблицы известно, что биномиальный ряд стопудово сходится при . В данном случае , поэтому: Умножаем все части неравенства на : – интервал сходимости полученного ряда. Что происходит с рядом на концах интервала? При При Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости ряда.
Таким образом, область сходимости полученного ряда:
Пример 7
Разложить функцию в ряд по степеням . Найти область сходимости ряда. Указание: предварительно функцию следует упростить, используя свойства логарифмов:
Это пример для самостоятельного решения.
Разложение
функций в ряд Маклорена необходимо
проводить в ряде других задач, например,
в задаче
приближенного вычисления определенного
интеграла.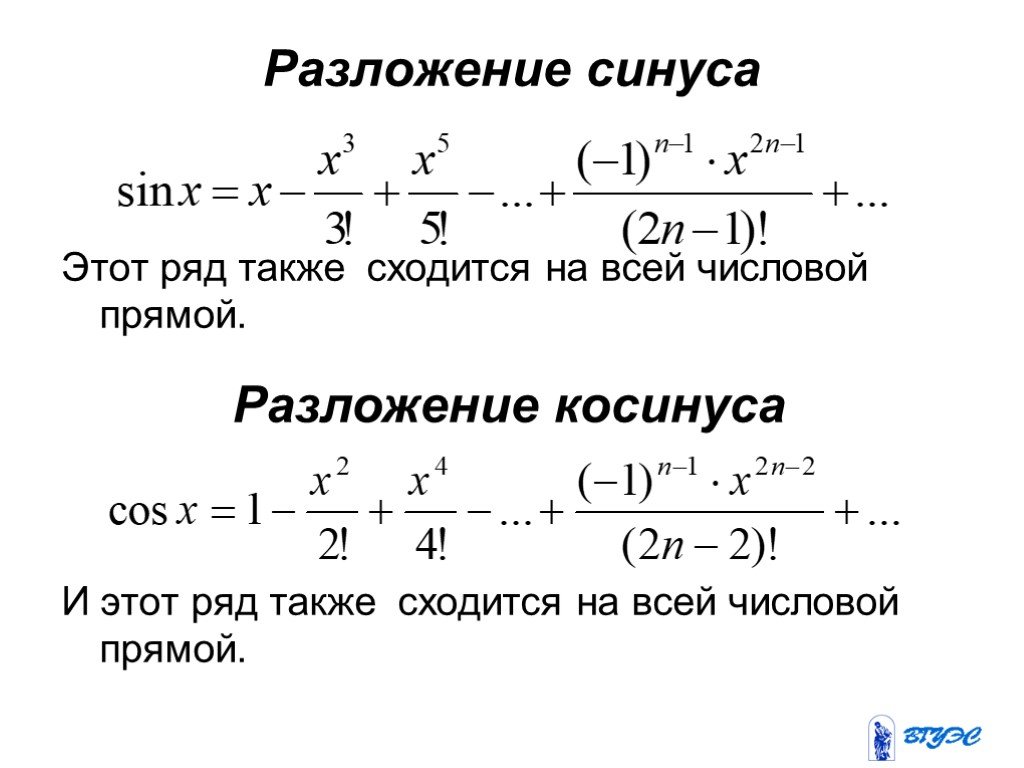
Кстати, там, помимо нового материала,
можно посмотреть примеры других
разложений, которые не поместились в
этот урок.
Примеры разложения функций в ряд Тейлора по степеням
Данное задание является более сложным и встречается значительно реже. Я сначала вообще не хотел включать задачу в урок, но всё-таки решил, что 2-3 примера не помешают. Пригодится.
Вытащим из чулана общую формулу Тейлора, о которой уже упоминалось:
Еще раз повторю, что вместо буквы «а» на практике часто можно встретить букву .
В чём сложность разложения функции по степеням ? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить производные.
Сразу небольшой Пример 8
Разложить функцию в ряд Тейлора по степеням
В данном случае , смотрим на формулу Тейлора, и становится уже всё понятнее. Теперь предстоит ручная работа по конструированию разложения:
,
все производные, начиная с четвёртой
производной, будут нулевыми.
Теперь подставляем весь найденный скарб в формулу Тейлора:
Готово. Для проверки можно раскрыть скобки: Получен исходный многочлен, что и требовалось проверить.
Рассмотрим более содержательные примеры.
Пример 9
Разложить функцию в ряд Тейлора по степеням . Найти область сходимости полученного ряда.
Решение: Используем разложение функции в ряд Тейлора по степеням
Хех, опять предстоит ручная работа….
В данном случае:
Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:
А теперь проанализируем найденные производные: , , . Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе растёт степень.
Теперь,
исходя из выявленной закономерности,
нужно составить производную «энного»
порядка. В данном случае она выглядит
так: Как
проверить, правильно ли составлена
энная производная? Подставьте в неё
значения
,
,
и
вас должны получиться в точности первая,
вторая и третья производные.
После того,
как мы убедились в том, что энная
производная составлена правильно,
подставляем в неё наше значение:
Теперь осталось все труды подставить в формулу Тейлора и аккуратно провести упрощения:
Далее необходимо найти область сходимости полученного степенного ряда . Это стандартная задача, которую мы многократно прорешивали на уроке Степенные ряды. Область сходимости ряда. Я сразу приведу ответ, поскольку умею решать почти все ряды устно =)
Область сходимости полученного степенного ряда:
И заключительный пример для самостоятельного решения:
Пример 10
Разложить функцию в ряд Тейлора по степеням . Найти область сходимости полученного ряда.
Если честно, то от рядов уже в глазах мельтешит, не злоупотребляйте! Пожалуйста, сообщите, если где заметили опечатку или ошибку.
Желаю успехов!
Решения и ответы:
Пример
2: Используем разложение: .
Данный ряд сходится при любом значении .
В
данном случае Область
сходимости ряда: .
Пример 4: Используем разложение: . Область сходимости ряда: . В данном случае Конструируем функцию дальше: Окончательно: Поскольку разложение экспоненты сходится при любом «альфа», то область сходимости полученного ряда:
Пример 5: Используем частный случай биномиального разложения: В данном случае Таким образом:
Само по себе разложение не слишком сложное, важно правильно найти область полученного сходимости ряда. Есть длинный путь и короткий.
Путь
короткий: из таблицы находим комментарий
к биномиальному разложению: «Область
сходимости ряда: .
Сходимость ряда в точках , исследуется
отдельно». В данном случае ,
то есть, ряд точно сходится при: .
Делим все части на 3 и извлекаем из всех
частей кубический корень: –
интервал сходимости ряда. Подставляем
концы интервала в полученный ряд . Если ,
то: При Оба
числовых ряда расходятся, так как не
выполнен необходимый признак сходимости
ряда. Окончательно.
Область сходимости полученного ряда:
Путь длинный (но более надежный и универсальный) состоит в исследовании полученного ряда с помощью признака Даламбера по стандартной схеме, рассмотренной на уроке Степенные ряды. Область сходимости ряда.
Пример
7: Преобразуем функцию: Используем
разложение: В
данном случае Таким
образом: Или
короче, в свёрнутом виде: Найдем
область сходимости полученного степенного
ряда. По таблице находим, что использованное
разложение сходится при .
В данном случае ,
поэтому: –
интервал сходимости исследуемого
степенного ряда. Исследуем
сходимость ряда на концах найденного
интервала: При –
расходится При –
сходится условно. Таким
образом, область сходимости полученного
степенного ряда:
Пример 10: Решение: Используем разложение функции в ряд Тейлора по степеням : В данном случае: … … Таким образом: Область сходимости полученного степенного ряда уже надоела. Ответ: ряд сходится при .
2.5.2. Разложение аналитической функции в ряд Тейлора
Естественные науки / Специальные главы высшей математики / 2.5.2. Разложение аналитической функции в ряд Тейлора
Используя интегральную формулу Коши, покажем, что всякую аналитическую функцию в круге сходимости можно представить в виде суммы степенного ряда.
Теорема. Пусть функция – аналитическая в области D. Если и R – расстояние z0до границы области D, то в круге она разлагается в ряд Тейлора.
Пусть ; рассмотрим круг (рис. 2.27).
Если Кr1– граница круга, то
. (2.98)
Разложим в ряд по степеням z-z0:
,
тогда
. (2.99)
При фиксированном z ряд (2.99) равномерно сходится относительно , так как
,
а мажорантный ряд также сходится. Следовательно, ряд (2.99) можно интегрировать почленно:
. (2.100)
Из (2.100) видно, что коэффициенты ряда
(2.101)
и не зависят от контура интегрирования.
Поэтому интеграл в (2.101) берут по контуру Кr.
Вывод: показали, что f(z) является суммой степенного ряда (Тейлора) в круге :
с коэффициентами:
. (2.102)
Методическое руководство
1) Если известны особые точки , то радиус сходимости ряда Тейлора можно найти так. Особые точки функции являются граничными для области ее аналитичности. Согласно теореме радиус сходимости ряда Тейлора не меньше, чем расстояние от точки z0 до ближайшей особой точки функции.
2) Имеет место свойство единственности разложения функции в ряд Тейлора. Это значит, что каким бы методом мы ни разлагали функцию в ряд Тейлора он единственный. Поэтому коэффициенты не обязательно находить по формуле (2.102).
Пример 1
Найти первые три члена разложения функции по степеням z + i и определить радиус сходимости ряда.
Решение. По условию должны записать ряд (z0 = – i):
Найдем последовательно
;
.
Тогда
.
Найдем особые точки данной функции, для чего знаменатель приравняем нулю (cos z = 0).
Отсюда – особые точки.
Для нахождения радиуса сходимости определим расстояние от точки —i до ближайшей особой точки (их две) (рис. 2.28). По теореме Пифагора:
– радиус сходимости ряда.
Пример 2
Разложить в ряд Тейлора функцию в окрестности точки z=0, не находя коэффициентов с помощью производных и применения формул (2.102)
Решение. Согласно свойства единственности, разложим cos z в ряд Маклорена и, проведя указанные действия, получим:
Задачи для упражнений
1) Найти три первых не равных нулю члена разложения функции по степеням и определить радиус сходимости ряда.
Ответ:
2) Найти несколько первых членов разложения по степеням z функции и определить радиус сходимости ряда.
Ответ:
3) Разложить в ряд Тейлора по степеням функцию .
Ответ: .
4) Разложить в ряд Тейлора по отношениям z функцию .
Ответ: .
5) Разложить в ряд Тейлора функцию в окрестности точки z0 = 0 (N = 1, 2,…) для N = 3.
Ответ: .
реальный анализ. Являются ли ряды Тейлора и степенные ряды одной и той же «вещью»?
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 59 тысяч раз
$\begingroup$
Мне просто интересно, используя жаргон математики, эти две «идеи» одинаковы? Я знаю, что у нас есть ряды Тейлора и их специализация — ряды Маклорена, но являются ли степенные ряды более общей концепцией? Как одна/все эти идеи относятся к производящим функциям? 9n$ (или иногда с $x$, переведенным на некоторый $x_0$, чтобы стать $(x — x_0)$).
Обычно
когда говорят ряд Тейлора , имеют в виду ряд Тейлора некоторой конкретной гладкой функции $f$. (Поэтому в математической речи обычно не говорят «рассмотрите как ряд Тейлора ». Вы можете сказать «рассмотрите степенной ряд» или
«рассмотрите как ряда Тейлора функции $f$». По крайней мере, таков мой опыт).{(n)}(x_0)/n!$, так что не каждый степенной ряд является рядом Тейлора (хотя каждый ряд Тейлора является степенным рядом) . Изменить : как заметил Мэтт, на самом деле каждый степенной ряд является рядом Тейлора, но ряды Тейлора связаны с определенной функцией, и если $f$, связанный с данным степенным рядом, не очевиден, вы, скорее всего, см. сериал, описанный как «серия мощности», а не как «серия Тейлора».
Оба этих типа рядов можно обобщить до форм, включающих большее количество переменных, и вы также можете придумать ряды, включающие отрицательные степени $x$.
Что касается производящих функций, то это более формальные объекты, при анализе которых вопрос сходимости не так важен, как при анализе степенного ряда или ряда Тейлора.
В этом случае коэффициенты кодируют информацию о некоторой последовательности чисел $\{a_n\}$, и мы формально исследуем ряд, чтобы собрать информацию об этой последовательности.
$\endgroup$
6
9n$, где $a_n$ — элементы некоторого кольца $R$ (например, $R=\mathbb{R}$ или $\mathbb{C}$). Вы можете выбрать любое $a_n$, которое вам нравится, и у вас по-прежнему будет четко определенный степенной ряд — вам не нужно заботиться о вопросах сходимости. Множество всех степенных рядов над кольцом $R$ само образует кольцо $R[[x]]$. Эти степенные ряды делают , а не , вообще говоря, определяют функции от $R$ до $R$; в общем случае нет способа понять бесконечную сумму элементов $R$, поэтому нет разумного способа заменить $x$ элементом $R$ в произвольном степенном ряду. 9{2x}!! в степенях !!(x-1)!! и был сбит с толку тем, что это значит, и в чем смысл этого. Я написал ответ, который мне понравился, который я воспроизвожу здесь.
3$$ 99$$Если мы сделаем это, то получим !!7.3887!!, что не так уж и далеко. Но это был много работы! И мы находим это как !!x!! отдаляется от нуля, т. серия выше становится все менее и менее точной. Например, возьмем !!x=3.1!!, формула с четырьмя членами дает нам !!66,14!!, что совершенно неверно. Даже если мы воспользуемся десятью терминами, мы получим !!444,3!!, до которого еще далеко. правильный ответ на самом деле !!492.7!!.
Что нам с этим делать? Просто добавить больше терминов? Это может быть много
работать, и это может привести нас не туда, куда нам нужно. (Некоторый Маклорен
серии просто перестают работать слишком далеко от нуля, и никакое количество
термины заставят их работать.) Вместо этого мы используем другую технику. 9я!! вместо этого, и когда !!x=3.1!!, они не маленькие, они очень большие! Они получают больше как !!i!!
увеличивается, и очень быстро. (Выигрывает !! i!!! в знаменателе,
в конце концов, но это происходит не во многих терминах.