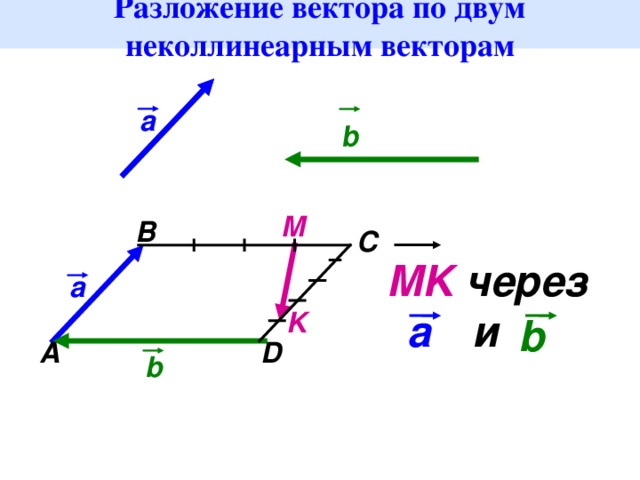
Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 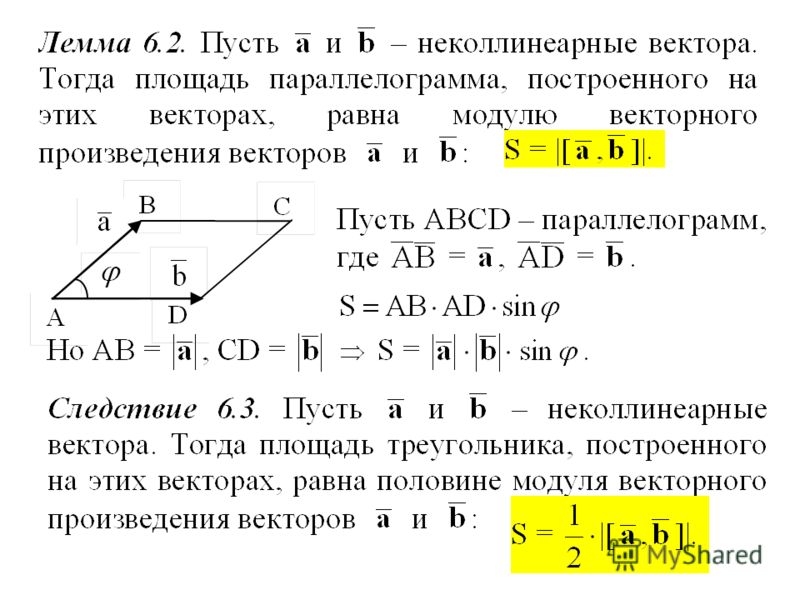 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 4. Векторные уравнения геометрических мест.  5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. 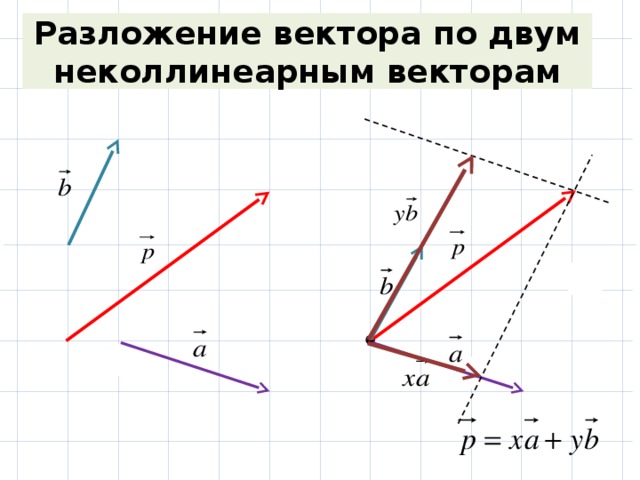 АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ§ 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).  § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
2.5. Разложение вектора по системе векторов
Пусть дана система n —мерных
векторов
выбираемn – произвольных чисел
.
Вектор называетсялинейной комбинацией векторов с коэффициентами.
Пусть теперь наряду с векторами дан ещеn-мерный вектор . Будем говорить, что векторлинейно выражается через векторы, если он равен некоторой линейной комбинации векторов, т.е. найдется такой набор чисел, что
. (5)
В этом случае будем говорить также, что вектор разлагается по векторам. Числаназываются коэффициентами разложения векторапо системе.
Разложение считается отличным от разложения (5), если различна хотя бы одна пара соответствующих коэффициентов разложения (т.е. хотя бы один).
Справедливы следующие утверждения:
1. Нулевой вектор разлагается по каждой системе векторов
.
2. Если вектор разлагается по части системы векторов, то он разлагается и по всей системе векторов.
Предположим, что
, где ,
тогда
.
3. Каждый -мерный векторразлагается по диагональной системе- мерных векторов:
с коэффициентами, которые равны координатам вектора .
В самом деле
.
4. Если вектор разлагается по системе векторов, а каждый вектор этой системы разлагается по системе векторов, то векторразлагается по системе векторов.
Из условия следует, что
После подстановки получаем:
Т.е. вектор разлагается по векторам.
2.6. Векторная форма записи системы линейных уравнений
Используя введенные операции над векторами, запишем систему линейных уравнений:
(1)
в векторной форме. Обозначим столбцы коэффициентов при неизвестных
, ,…,;.
Тогда систему (1) можно представить в виде:
(2)
Уравнение
(2) называется векторной формой системы
линейных уравнений (1).
Последовательность чисел называют решением системы (2), если– верное векторное равенство.
Пусть n-мерный вектор () является решением системы (1). Тогда ясно, что для разложения векторапо системедостаточно найти решение системы линейных уравнений (2).
Пример. Дана система векторов и вектор
;;;;.
Пример. Выяснить разлагается ли вектор по системе векторов.
Для этого необходимо решить систему уравнений
.
Имеем:
Получили систему уравнений:
,
которая эквивалентна исходной (т.е. имеет то же множество решений). Выразим главные неизвестные ичерез свободные.. Получим общее решение:
.
Достаточно положить свободным неизвестным ипроизвольные значения и получить разложение векторапо системе векторов.
Пример. , тогда,.
Следовательно:
.
Если же , тогда,
и
.
2.7. Задания
Найти разложение вектора В по диагональной системе (упражнение 1).
Найти разложение вектора В по системе А1, А2, А3 (упражнение 2).
Найти разложение вектора В по векторам А1, А2, А3 (упражнение 3).
Разложить каждый вектор системы А1, А2, …, Аn по векторам этой системы.
Доказать, что если векторы В1 и В2 разлагаются по системе векторов А1, А2, …, Аn, то векторы В1+В2, kB1, t1B1+t2B2 также разлагаются по системе векторов А1, А2, …, Аn (k, t1, t2 – константы).
Вектор В разлагается по системе векторов А1, А2, …, Аm. Доказать, что каждый вектор системы В+А1, В+А2,…, В+Аm разлагается по системе А1, А2, …, Аm.
Упражнения 1, 2, 3 выполняются по вариантам, остальные – без вариантов.
Таблица 1
№ варианта | Векторы А1, А2, А3, В | ||||
Упражнение 1 | Упражнение 2 | Упражнение 3 | |||
В | A1 A2 A3 | B | A1 A2 A3 | B | |
7 5 -3 4 | 0 0 1 1 0 1 0 1 1 | 1 3 0 | -1 -1 0 2 2 2 8 2 1 2 1 2 | 1 1 1 4 | |
-2 0 3 1 | 1 0 1 0 1 0 1 1 0 | -2 1 1 | -3 -1 5 5 2 3 5 2 1 2 1 2 | -5 5 1 4 | |
5 6 -3 2 | 1 -1 1 0 2 0 -2 2 0 | 0 4 1 | -2 -2 -2 0 2 3 0 2 1 2 1 2 | -3 3 1 4 | |
-5 7 -1 0 | 1 -1 1 0 1 0 -2 1 0 | 0 4 1 | -1 0 -4 3 2 3 0 2 1 2 1 2 | -2 3 1 4 | |
Окончание таблицы 1
№ варианта | Векторы А1, А2, А3, В | ||||
Упражнение 1 | Упражнение 2 | Упражнение 3 | |||
В | A1 A2 A3 | B | A1 A2 A3 | B | |
4 -5 1 1 | 1 0 1 1 1 1 0 1 1 | -2 5 1 | -1 0 0 1 2 5 1 2 1 2 1 2 | 0 4 2 4 | |
9 -10 3 1 | 1 0 1 0 0 1 0 1 0 | -8 4 6 | -1 0 0 1 2 3 0 2 1 2 1 2 | 0 1 2 4 | |
0 5 -12 8 | 1 0 1 1 1 2 0 1 0 | 0 6 2 | -1 -1 -2 0 2 3 0 2 1 2 1 2 | -3 3 1 4 | |
9 -10 3 1 | 1 0 1 0 0 1 0 1 0 | -8 4 6 | -1 0 0 1 2 3 0 2 1 2 1 2 | 0 1 2 4 | |
1 2 -3 7 | 1 0 1 1 2 2 1 2 0 | 0 2 4 | 4 2 0 0 2 3 0 0 1 3 0 0 | 0 0 1 1 | |
0 0 -1 8 | 1 0 1 1 1 3 0 1 3 | -1 1 2 | -1 0 0 0 0 2 2 0 2 2 1 0 3 1 2 1 | 0 3 1 4 | |
-3 5 5 -4 | 2 0 1 1 4 2 0 5 0 | 6 6 0 | -1 0 -2 0 2 3 0 2 2 2 1 2 | -3 3 2 4 | |
-2 0 -5 -1 | 5 0 1 1 4 3 0 5 1 | 10 2 0 | 1 4 4 0 1 3 2 1 4 0 1 0 | -1 2 1 1 | |
5 -6 -1 4 | 3 0 1 2 1 1 0 1 0 | -1 0 2 | -2 1 -2 0 1 2 0 2 3 2 2 1 | 0 2 1 1 | |
Глава 5 Векторная геометрия: углы, проекция и разложение
В этой главе вы познакомитесь с некоторыми дополнительными идеями геометрии векторов.
Опять же, хотя иллюстрация этих концепций ограничена двумерным пространством, все эти идеи могут быть расширены до n -мерностей.
5.1 Угол между векторами
Может оказаться весьма полезным определить угол между двумя векторами. Например, каков угол между вектором а и б где,
\[ \mathbf{a} = \begin{bmatrix} 2\3 \end{bmatrix} \quad \mathrm{and} \quad \mathbf{b}= \begin{bmatrix} -4\1 \end{bmatrix} \]
На рис. 5.1 показаны оба вектора, отображаемые в одной и той же двумерной базовой системе координат.
Рисунок 5.1: График, показывающий два вектора a (красный) и b (синий) в пространстве измерений R1–R2. Угол между ними обозначается как \(\theta\). Для удобства мы расположили хвосты обоих векторов в начале координат.
Угол между этими векторами обозначается как \(\theta\) и может быть найден с помощью следующего:
\[ \cos (\ theta) = \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert \rверт} \]
То есть косинус угла между двумя векторами равен скалярному произведению векторов, деленному на произведение их длин.
Чтобы найти угол (\(\theta\)), мы можем вычислить арккосинус этого отношения. В нашем примере 9{\circ}\). Ниже приведен синтаксис R для вычисления этого угла.
# Создание векторов a = матрица (данные = c (2, 3), ncol = 1) b = матрица (данные = c (-4, 1), ncol = 1) # Вычисление скалярного произведения между a и b a_dot_b = сумма (а * б) # Вычисление длин векторов l_a = sqrt (сумма (а * а)) l_b = sqrt (сумма (b * b)) # Вычислить тета (в радианах) acos(a_dot_b / (l_a * l_b))
[1] 1.91382
# Вычислить тета (в градусах) acos(a_dot_b / (l_a * l_b)) * 180 / pi
[1] 109,6538
Манипулирование формулой для вычисления угла между двумя векторами дает общую формулу для определения скалярного произведения между двумя векторами.
\[
\начать{разделить}
\ cos (\ theta) & = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert\rvert} \\[2ex]
\mathbf{a}\bullet\mathbf{b} &= \lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert\rvert \cos(\theta)
\конец{разделить}
\]
То есть скалярное произведение между векторами a и b равно произведению их модулей и косинуса угла между ними.
5.1.1 Ортогональные векторы 9\circ\) угол равен 0, если
a и b ортогональны, то\[ 0 = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \]
Например, рассмотрим следующие два элементарных вектора
\[ \mathbf{e}_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \qquad \mathbf{e}_2 = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \]
Скалярное произведение между этими двумя векторами равно 0, что означает, что косинус угла между ними также должен быть равен 0, указывая на то, что \(\mathbf{e}_1\) и \(\mathbf{e}_2 \) ортогональны. 9\circ\) угол равен 1, если a и b коллинеарны, то
\[ 1 = \ frac {\ mathbf {a} \ bullet \ mathbf {b}} {\ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \]
Например, рассмотрим следующие два вектора
\[ \mathbf{a} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 6 \\ 3 \end{bmatrix} \]
\[ \начать{разделить} \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\lvert\lvert\mathbf{b}\rvert\rvert} &= \frac {14}{\sqrt{5}\times\sqrt{45}} \\[2ex] &= \frac{14}{\sqrt{225}} \\[2ex] &= \frac{14}{14} \\[2ex] &= 1 \конец{разделить} \]
Это означает, что a и b лежат на одной прямой.
Два вектора коллинеарны, если один из них может быть записан как линейная комбинация другого. В нашем примере
\[ \mathbf{b} = 3\mathbf{а} \] Геометрически коллинеарные векторы параллельны друг другу (помните, что расположение в опорном пространстве удобно).
5.2 Ортогональная проекция
Ортогональная проекция вектора a на вектор b получается путем опускания перпендикулярной линии от конечной точки до до пересечения с x2.
Рисунок 5.2: Ортогональная проекция вектора a (красно-красный) на вектор b (черный). Обратите внимание, что проекция создает угол 90 градусов с вектором b . Результатом проекции является вектор p (синий).
Результатом является вектор p , который коллинеарен вектору b , но имеет другую длину. Чтобы вычислить длину p , мы используем тот факт, что проекция создает прямоугольный треугольник с гипотенузой a и смежный отрезок p до угла \(\theta\).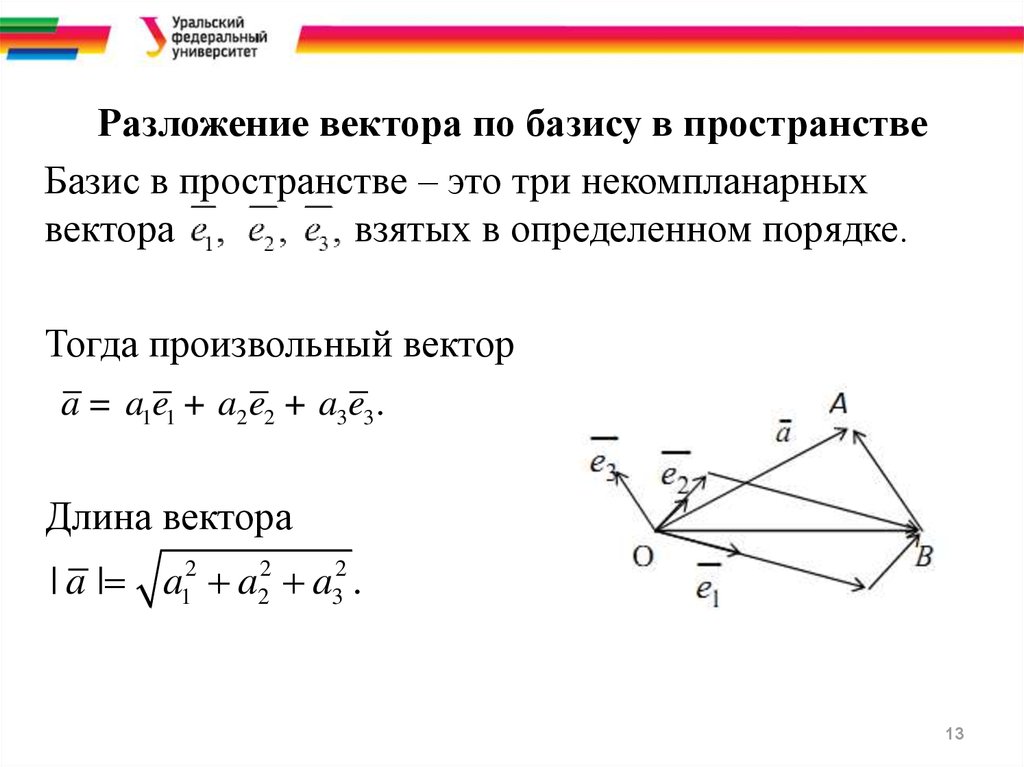
Затем
\[ \начать{разделить} \cos(\theta) &= \frac{\lvert\lvert\mathbf{p}\rvert\rvert}{\lvert\lvert\mathbf{a}\rvert\rvert} \\[2em] \lvert\lvert\mathbf{p}\rvert\rvert &= \lvert\lvert\mathbf{a}\rvert\rvert \times \cos(\theta) \конец{разделить} \]
Поскольку \(\theta\) — это угол между a и b ,
\[ \начать{разделить} \lvert\lvert\mathbf{p}\rvert\rvert &= \lvert\lvert\mathbf{a}\rvert\rvert \times \cos(\theta) \\[2em] &= \lvert\lvert\mathbf{a}\rvert\rvert\times\frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{a}\rvert\rvert\times\ lvert\lvert\mathbf{b}\rvert\rvert}\\[2em] & = \ гидроразрыва {\ mathbf {a} \ пуля \ mathbf {b}} {\ lvert \ lvert \ mathbf {b} \ rvert \ rvert} \конец{разделить} \]
То есть величина проекции p представляет собой отношение скалярного произведения векторов a и b к величине b . Рассмотрим следующие два вектора:
\[ \mathbf{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} \]
Проецирование a на b , геометрически,
Рисунок 5.
3: Ортогональная проекция вектора a (выделены красным) на вектор b (синий). Результатом проекции является вектор p (черный цвет).
Мы можем найти величину p , используя нашу формулу:
\[ \начать{разделить} \lvert\lvert\mathbf{p}\rvert\rvert &= \frac{\mathbf{a}\bullet\mathbf{b}}{\lvert\lvert\mathbf{b}\rvert\rvert} \\[2ex ] &= \frac{1}{\sqrt{5}} \\[2ex] &= 0,447 \конец{разделить} \]
# Создание векторов а = с (2, 3) б = с (2, -1) # Вычисление скалярного произведения a и b a_dot_b = сумма (а * б) # Вычислить длину b l_b = sqrt (сумма (b * b)) # Вычислить длину p l_p = a_dot_b / l_b л_п
[1] 0,4472136
В дальнейшем будем обозначать проекцию вектора a на вектор b как:
\[ \mathbf{p}_{\mathbf{a}\perp\mathbf{b}} \]
5.3 Ортогональное разложение
Ортогональное проецирование вектора приводит к геометрическому разложению вектора на две аддитивные компоненты.
На рис. 5.4 показано разложение вектора a на две аддитивные компоненты, \(\mathbf{p}_1\) и \(\mathbf{p}_2\). то есть
\[ \mathbf{a} = \mathbf{p}_1 + \mathbf{p}_2 \]
Рисунок 5.4: Две ортогональные проекции вектора a (киноварь). Первая ортогональная проекция — это вектор a на вектор b (горизонтальный черный), а вторая ортогональная проекция — вектор a на вектор o (вертикальный черный). Результатом проекций являются векторы \(\mathbf{p}_1\) (синяя горизонталь) и \(\mathbf{p}_2\) (синяя вертикаль).
Вектор \(\mathbf{p}_1\) является той же ортогональной проекцией из предыдущего примера, а именно \(\mathbf{p}_{\mathbf{a}\perp\mathbf{b}}\). Вектор \(\mathbf{p}_1\) является второй проекцией a на вектор o (\(\mathbf{p}_{\mathbf{a}\perp\mathbf{o}} \)). Вектор o по определению ортогонален вектору b .
Длины двух выступов соответствуют длинам сторон прямоугольного треугольника, где гипотенуза равна и . А именно 4 ,
\[ \начать{разделить} \ lvert \ lvert \ mathbf {p} _ {\ mathbf {a} \ perp \ mathbf {b}} \ rvert \ rvert & = \ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ cos (\ theta ) \\[2em] \ lvert \ lvert \ mathbf {p} _ {\ mathbf {a} \ perp \ mathbf {o}} \ rvert \ rvert & = \ lvert \ lvert \ mathbf {a} \ rvert \ rvert \ times \ sin (\ theta ) \конец{разделить} \]
В качестве примера мы можем разложить на Используя два наших предыдущих примера векторов:
\[ \mathbf{a} = \begin{bmatrix} 2 \\ 3 \end{bmatrix} \qquad \mathbf{b} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} \] 9\circ) \\[2em] &= 3,58 \конец{разделить} \]
# Вычислить длину l_a = sqrt (сумма (а * а)) # Вычислить тета (в радианах) тета = acos (a_dot_b / (l_a * l_b)) theta
[1] 1.446441
# Вычисление длины проекции a на o l_p2 = l_a * грех (тета) l_p2
[1] 3,577709
Мы можем использовать теорему Пифагора, чтобы проверить вычисление длин двух проекций.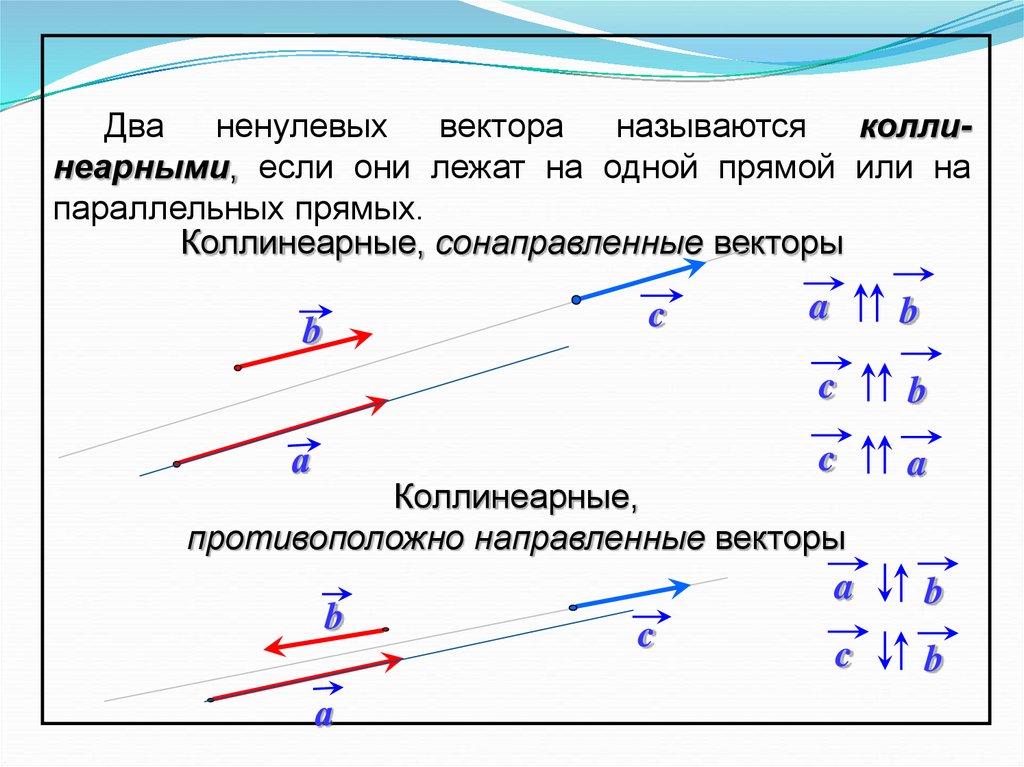
Так как квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его сторон, то 92
[1] TRUE
Окончательная система показана на рис. 5.5.
Рисунок 5.5: Ортогональная проекция вектора a (красный) на вектор b (синий). Результатом проекции является вектор \(\mathbf{p}_1\) (черный). Второй проекцией является вектор \(\mathbf{p}_2\) (черный) на вектор o , который ортогонален b .
Существуют и другие способы вычисления длины \(\mathbf{p}_{\mathbf{a}\perp\mathbf{o}}\). Например, с o ортогонален b , угол между o и a равен \(\phi=90-\theta\). Тогда \(\lvert\lvert\mathbf{p}_{\mathbf{a}\perp\mathbf{o}}\rvert\rvert=\lvert\lvert\mathbf{a}\rvert\rvert \times \cos( \фи)\).↩︎
Матрицы и линейная алгебра (математика)
Матрицы и линейная алгебра (математика)| Математика |
Разложение по сингулярным числам
A сингулярное значение и соответствующие сингулярные векторы прямоугольной матрицы A являются скаляром и парой векторов u и v , которые удовлетворяют
С сингулярными числами на диагонали диагональной матрицы и соответствующими сингулярными векторами, образующими столбцы двух ортогональных матриц U и V , мы имеем
Поскольку U и V ортогональны, это становится разложением по сингулярным числам
Полное разложение единственного значения M -BY — N MATRIX включает в себя M -BY — M U , M -BY — N и ANA M -BY -BY — N и AN .
n -by- n V . Другими словами, U и V квадратные и имеют тот же размер, что и А . Если A имеет намного больше строк, чем столбцов, результирующий U может быть довольно большим, но большинство его столбцов умножаются на нули в . В этой ситуации декомпозиция Economy экономит и время, и память, создавая m на n U , n на n и тот же самый V .
Разложение по собственным значениям является подходящим инструментом для анализа матрицы, когда она представляет собой отображение из векторного пространства в себя, как это делается для обыкновенного дифференциального уравнения. С другой стороны, разложение по сингулярным числам является подходящим инструментом для анализа отображения из одного векторного пространства в другое векторное пространство, возможно, с другой размерностью. Большинство систем одновременных линейных уравнений попадают во вторую категорию.
Если A является квадратным, симметричным и положительно определенным, то его разложения на собственные и сингулярные значения совпадают. Но по мере того, как A отклоняется от симметрии и положительной определенности, различие между двумя разложениями увеличивается. В частности, разложение по сингулярным числам вещественной матрицы всегда действительно, но разложение по собственным значениям вещественной несимметричной матрицы может быть сложным.
Для примера матрицы
А = 94 6 8 2 7
полное сингулярное разложение равно
[U,S,V] =
свд(А) У = -0,6105 0,7174 0,3355 -0,6646 -0,2336 -0,7098 -0,4308 -0,6563 0,6194 С = 14,9359 0 0 5.1883 0 0 В = -0,6925 0,7214 -0,7214 -0,6925
Вы можете убедиться, что U*S*V' равно A с точностью до ошибки округления. Для этой небольшой задачи разложение размера экономики лишь немного меньше.