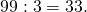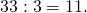| 1 | Вычислить | 6^3-4^3-7^2 | |
| 2 | Найти медиану | 11 , 13 , 5 , 15 , 14 | , , , , |
| 3 | Найти объем | сфера (5) | |
| 4 | Вычислить | квадратный корень 12 | |
| 5 | Преобразовать в десятичную форму | 3/8 | |
| 6 | Преобразовать в десятичную форму | 5/8 | |
| 7 | Найти длину окружности | окружность (5) | |
| 8 | Вычислить | 10^2 | |
| 9 | Вычислить | квадратный корень 75 | |
| 10 | График | y=2x | |
| 11 | Вычислить | квадратный корень 48 | |
| 12 | Найти площадь | окружность (5) | |
| 13 | Найти площадь | окружность (6) | |
| 14 | Вычислить | 3^4 | |
| 15 | Вычислить | 5^3 | |
| 16 | Вычислить | 2^4 | |
| 17 | Вычислить | квадратный корень 32 | |
| 18 | Вычислить | квадратный корень 18 | |
| 19 | Вычислить | квадратный корень 2 | |
| 20 | Вычислить | квадратный корень 25 | |
| 21 | Вычислить | квадратный корень 8 | |
| 22 | Найти площадь | окружность (4) | |
| 23 | Разложить на простые множители | 360 | |
| 24 | Вычислить | 3^-2 | |
| 25 | Вычислить | 2+2 | |
| 26 | Преобразовать в десятичную форму | 1/3 | |
| 27 | Вычислить | квадратный корень 9 | |
| 28 | Вычислить | квадратный корень 64 | |
| 29 | Преобразовать в десятичную форму | 3/5 | |
| 30 | Вычислить | квадратный корень 20 | |
| 31 | Вычислить | pi | |
| 32 | Вычислить | -3^2 | |
| 33 | Вычислить | 2^3 | |
| 34 | Вычислить | (-3)^3 | |
| 35 | Вычислить | квадратный корень 27 | |
| 36 | Вычислить | квадратный корень 5 | |
| 37 | Вычислить | квадратный корень 50 | |
| 38 | Вычислить | квадратный корень 16 | |
| 39 | Преобразовать в десятичную форму | 3/4 | |
| 40 | Преобразовать в десятичную форму | 2/3 | |
| 41 | Найти площадь | окружность (3) | |
| 42 | Вычислить | 3^2 | |
| 43 | Вычислить | -9^2 | |
| 44 | Вычислить | квадратный корень 72 | |
| 45 | Преобразовать в десятичную форму | 2/5 | |
| 46 | Вычислить | квадратный корень 100 | |
| 47 | Найти объем | сфера (3) | |
| 48 | Вычислить | 2^5 | |
| 49 | Множитель | x^2-4 | |
| 50 | Вычислить | -8^2 | |
| 51 | Вычислить | -6^2 | |
| 52 | Вычислить | -7^2 | |
| 53 | Вычислить | -3^4 | |
| 54 | Вычислить | (-2)^3 | |
| 55 | Множитель | x^2-9 | |
| 56 | Найти объем | сфера (6) | |
| 57 | Найти площадь | окружность (8) | |
| 58 | Вычислить | квадратный корень 81 | |
| 59 | Вычислить | кубический корень 64 | |
| 60 | Вычислить | кубический корень 125 | |
| 61 | Вычислить | квадратный корень 169 | |
| 62 | Вычислить | квадратный корень 225 | |
| 63 | Вычислить | квадратный корень 3 | |
| 64 | Преобразовать в десятичную форму | 1/4 | |
| 65 | Преобразовать в смешанную дробь | 5/2 | |
| 66 | Преобразовать в десятичную форму | 1/2 | |
| 67 | Множитель | x^2-16 | |
| 68 | Вычислить | 5^2 | |
| 69 | Вычислить | 4^-2 | |
| 70 | Вычислить | 8^2 | |
| 71 | Преобразовать в смешанную дробь | 13/4 | |
| 72 | Вычислить | квадратный корень 24 | |
| 73 | Вычислить | квадратный корень 28 | |
| 74 | Вычислить | кубический корень 27 | |
| 75 | Найти длину окружности | окружность (4) | |
| 76 | Найти площадь | окружность (7) | |
| 77 | Найти объем | сфера (2) | |
| 78 | График | y=3x | |
| 79 | Найти объем | сфера (4) | |
| 80 | Найти длину окружности | окружность (6) | |
| 81 | Вычислить | квадратный корень 150 | |
| 82 | Вычислить | квадратный корень 45 | |
| 83 | Вычислить | 4^3 | |
| 84 | Вычислить | 2^-3 | |
| 85 | Вычислить | 2^2 | |
| 86 | Вычислить | -(-3)^3 | |
| 87 | Вычислить | 3^3 | |
| 88 | Вычислить | квадратный корень 54 | |
| 89 | Вычислить | квадратный корень 10 | |
| 90 | Найти длину окружности | окружность (3) | |
| 91 | Преобразовать в смешанную дробь | 10/3 | |
| 92 | Преобразовать в десятичную форму | 2/5 | |
| 93 | Разложить на простые множители | 36 | |
| 94 | Вычислить | квадратный корень 144 | |
| 95 | Вычислить | (-7)^2 | |
| 96 | Множитель | x^2+5x+6 | |
| 97 | Вычислить | (-4)^3 | |
| 98 | Вычислить | (-5)^3 | |
| 99 | Вычислить | 10^2 | |
| 100 | Вычислить | 6^2 |
Разложение числа на простые множители
Вам также может пригодиться калькулятор разложения чисел на простые множители.
Основная теорема арифметики гласит:
Любое натуральное число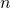 , большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
, большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.Как разложить число на множители?
Вот последовательность действий при разложении числа на простые множители:
- Берём самое маленькое простое число — 2 и по признакам делимости или обычным делением проверяем, делится ли наше число на 2.
- Если делится, то выписываем 2 в столбец с простыми множителями и делим наше число на 2 (получаем новое число). Далее снова проверяем, делится ли новое число на 2.
- Если не делится, то переходим к следующему простому числу — 3.
Эти три шага выполняются до тех пор, пока наше число не окажется равным 1.
Далее рассмотрим несколько примеров.
Разложить на простые множители число 54
- Число 54 делится на 2. Выписываем 2 в правый столбик.
 Записываем 27 в левый столбец.
Записываем 27 в левый столбец. - 27 не делится на 2, зато делится на 3. Выписываем 3 в правый столбик.
 Число 9 записываем в левую колонку.
Число 9 записываем в левую колонку. - 9 делится на 3. Снова выписываем 3 в правый столбик.
 В левый выписываем 3.
В левый выписываем 3. - Число 3 делится на 3,
 В правый столбик выписываем 3, в левый — 1. Разложение закончено.
В правый столбик выписываем 3, в левый — 1. Разложение закончено.
Разложить на простые множители число 65
- Число 65 не делится на 2 (так как оно оканчивается на нечётное число 5).
- 65 не делится на 3 (сумма цифр равна 11, а 11 не делится на 3).
- Зато 65 делится на 5. Выписываем число 5 в правую колонку.
 Теперь проверять мы будем уже число 13.
Теперь проверять мы будем уже число 13. - Число 13 — простое, его можно разделить только на 13. Выписываем в правую колонку 13, в левую — 1. Наше разложение закончено.
Разложить на простые множители число 99
- Число 99 не делится на 2, зато делится на 3.

- 33 также делится на 3.

- Число 11 — простое, поэтому разложение завершено.
Разложить на простые множители число 162
Разложить на простые множители число 1500
Разложение чисел на простые множители
Онлайн-калькулятор «Разложение числа на простые множители» позволит вам разложить любое составное число на простые множители. Для этого вам нужно ввести число в поле и нажать кнопку «Вычислить». Особенностью данного калькулятора является то, что он не просто выдаст ответ, но и представит подробное решение. С помощью нашего калькулятора Вы сможете быстро получить результат, а подробное решение поможет вам разобраться, как был произведен расчет.
Введите число:
Вычислить
Все натуральные числа можно разделить на две группы чисел: простые и составные.
Простое число
– это число, которые имеют только два делителя (единица и само это число), т.е. делится без остатка только на единицу и на само себя. Принято считать, что единица (1) не является простым числом. Пример простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 и т.д. Простых чисел бесконечное множество, ниже в таблице представлены простые числа до 1000.Составное число – это число, которые имеют более двух делителей. Любое составное число может быть представлено в виде произведенения простых чисел, например: 84 = 2 · 2 ·3 ·7.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 |
| 17 | 19 | 23 | 29 | 31 | 37 |
| 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 |
| 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 |
| 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 |
| 401 | 409 | 419 | 421 | 431 | 433 |
| 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 |
| 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 |
| 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 |
| 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 859 | 863 | |
| 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Разложение числа на простые множители онлайн
Любое натуральное число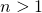 можно представить в виде произведения простых чисел. Это представление называется разложением числа
можно представить в виде произведения простых чисел. Это представление называется разложением числа 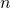 на простые множители.
на простые множители.Натуральное число 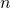 называется делителем целого числа
называется делителем целого числа 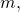
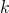 верно равенство
верно равенство 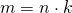 . В этом случае говорят, что
. В этом случае говорят, что 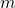 делится на
делится на 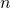 или что число
или что число 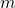 кратно числу
кратно числу 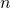 .
.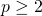 , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число
, делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число 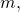 не равное
не равное 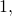 имеет как минимум два делителя:
имеет как минимум два делителя: 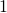 и
и 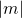 ). Например, числа
). Например, числа 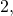
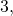
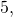
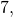
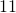 – простые, а числа
– простые, а числа 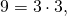
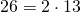 – составные. Основная теорема арифметики. Любое натуральное число
– составные. Основная теорема арифметики. Любое натуральное число 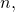 большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.Данная программа раскладывает число в произведение простых множителей онлайн. Разложить число на множители онлайн с её помощью очень просто.
Как разложить число на множители?
В школе на уроках математики разложение числа на множители обычно записывают столбиком (в две колонки). Делается это так: в левую колонку выписываем исходное число, затем
- Берём самое маленькое простое число — 2 и по признакам делимости или обычным делением проверяем, делится ли исходное число на 2.
- Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую колонку под исходным числом.
- Если не делится, то берём следующее простое число — 3.
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, разберём несколько примеров.
Пример. Разложить на множители число 84.Решение. Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2, то и 84 делится на 2 по признаку делимости. Записываем 2 в правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число 21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3, 21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
О калькуляторе
Программа раскладывает числа на множители методом перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие числа. Однако если число простое или имеет большие простые делители, разложение его на множители происходит очень медленно.
90000 Factors of 54 — Finding the Prime Factors by Division Method 90001 90002 90003 90004 90003 90002 90003 90008 Classes 90002 90003 Class 1 — 3 90004 90003 Class 4 — 5 90004 90003 Class 6 — 10 90004 90003 Class 11 — 12 90004 90018 90004 90003 90008 COMPETITIVE EXAMS 90002 90003 BNAT 90004 90003 90008 CBSE 90002 90003 90008 NCERT Books 90002 90003 NCERT Books for Class 5 90004 90003 NCERT Books Class 6 90004 90003 NCERT Books for Class 7 90004 90003 NCERT Books for Class 8 90004 90003 NCERT Books for Class 9 90004 90003 NCERT Books for Class 10 90004 90003 NCERT Books for Class 11 90004 90003 NCERT Books for Class 12 90004 90018 90004 90003 90008 NCERT Exemplar 90002 90003 NCERT Exemplar Class 8 90004 90003 NCERT Exemplar Class 9 90004 90003 NCERT Exemplar Class 10 90004 90003 NCERT Exemplar Class 11 90004 90003 NCERT Exemplar Class 12 90004 90018 90004 90003 90008 RS Aggarwal 90002 90003 RS Aggarwal Class 12 Solutions 90004 90003 RS Aggarwal Class 11 Solutions 90004 90003 RS Aggarwal Class 10 Solutions 90004 90 003 RS Aggarwal Class 9 Solutions 90004 90003 RS Aggarwal Class 8 Solutions 90004 90003 RS Aggarwal Class 7 Solutions 90004 90003 RS Aggarwal Class 6 Solutions 90004 90018 90004 90003 90008 RD Sharma 90002 90003 RD Sharma Class 6 Solutions 90004 90003 RD Sharma Class 7 Solutions 90004 90003 RD Sharma Class 8 Solutions 90004 90003 RD Sharma Class 9 Solutions 90004 90003 RD Sharma Class 10 Solutions 90004 90003 RD Sharma Class 11 Solutions 90004 90003 RD Sharma Class 12 Solutions 90004 90018 90004 90003 90008 PHYSICS 90002 90003 Mechanics 90004 90003 Optics 90004 90003 Thermodynamics 90004 90003 Electromagnetism 90004 90018 90004 90003 90008 CHEMISTRY 90002 90003 Organic Chemistry 90004 90003 Inorganic Chemistry 90004 90003 Periodic Table 90004 90018 90004 90003 90008 MATHS 90002 90003 Pythagoras Theorem 90004 90003 Prime Numbers 90004 90003 Probability and Statistics 90004 90003 Fractions 90004 90003 Sets 90004 90003 Trigonometric Functions 90004 90003 Relations and Functions 90004 90003 Sequence and Series 90004 90003 Multiplication Tables 90004 90003 Determinants and Matrices 90004 90003 Profit And Loss 90004 90003 Polynomial Equations 90004 90003 Dividing Fractions 90004 90018 90004 90003 90008 BIOLOGY 90002 90003 Microbiology 90004 90003 Ecology 90004 90003 Zoology 90004 90018 90004 90003 90008 FORMULAS 90002 90003 Maths Formulas 90004 90003 Algebra Formulas 90004 90003 Trigonometry Formulas 90004 90003 Geometry Formulas 90004 90018 90004 90003 90008 CALCULATORS 90002 90003 Maths Calculators 90004 90003 Physics Calculators 90004 90003 Chemistry Calculators 90004 90018 90004 90003 90008 CBSE Sample Papers 90002 90003 CBSE Sample Papers for Class 6 90004 90003 CBSE Sample Papers for Class 7 90004 90003 CBSE Sample Papers for Class 8 90004 90003 CBSE Sample Papers for Class 9 90004 90003 CBSE Sample Papers for Class 10 90004 90003 CBSE Sample Papers for Class 11 90004 90003 CBSE Sample Pa pers for Class 12 90004 90018 90004 90003 90008 CBSE Previous Year Question Paper 90002 90003 CBSE Previous Year Question Papers Class 10 90004 90003 CBSE Previous Year Question Papers Class 12 90004 90018 90004 90003 90008 HC Verma Solutions 90002 90003 HC Verma Solutions Class 11 Physics 90004 90003 HC Verma Solutions Class 12 Physics 90004 90018 90004 90003 90008 Lakhmir Singh Solutions 90002 90003 Lakhmir Singh Class 9 Solutions 90004 90003 Lakhmir Singh Class 10 Solutions 90004 90003 Lakhmir Singh Class 8 Solutions 90004 90018 90004 90003 90008 CBSE Notes 90002 90003 Class 6 CBSE Notes 90004 90003 Class 7 CBSE Notes 90004 90003 Class 8 CBSE Notes 90004 90003 Class 9 CBSE Notes 90004 90003 Class 10 CBSE Notes 90004 90003 Class 11 CBSE Notes 90004 90003 Class 12 CBSE Notes 90004 90018 90004 90003 90008 CBSE Revision Notes 90002 90003 CBSE Class 9 Revision Notes 90004 90003 CBSE Class 10 Revision Notes 90004 90003 CBSE Class 11 Revision Notes 9000 4 90003 CBSE Class 12 Revision Notes 90004 90018 90004 90003 90008 CBSE Extra Questions 90002 90003 CBSE Class 8 Maths Extra Questions 90004 90003 CBSE Class 8 Science Extra Questions 90004 90003 CBSE Class 9 Maths Extra Questions 90004 90003 CBSE Class 9 Science Extra Questions 90004 90003 CBSE Class 10 Maths Extra Questions 90004 90003 CBSE Class 10 Science Extra Questions 90004 90018 90004 90003 90008 CBSE Class 90002 90003 Class 3 90004 90003 Class 4 90004 90003 Class 5 90004 90003 Class 6 90004 90003 Class 7 90004 90003 Class 8 90004 90003 Class 9 90004 90003 Class 10 90004 90003 Class 11 90004 90003 Class 12 90004 90018 90004 90003 Textbook Solutions 90004 90018 90004 90003 90008 NCERT Solutions 90002 90003 90008 NCERT Solutions For Class 11 90002 90003 NCERT Solutions For Class 11 Physics 90004 90003 NCERT Solut 90004 90018 90004 90018 90004 90018 90004 90018 90004 90018 .90000 prime factorization of 54 | Find the Factors 90001 90002 How many squares are in this puzzle? Finding that answer is too tedious for me to pursue. There is 1 square that is bigger than all the rest, 169 of the smallest size squares, and some different number between 1 and 169 for each size square in between. Solving the actual puzzle will actually be less work and more fun. The actual puzzle challenges you to write the numbers 1 through 12 in the top row and again in the first column so that the answers you write and the clues inside the puzzle work together as a multiplication table.Use logic to find the unique solution to the puzzle. This week’s puzzles are available in an excel file here. If you have a spreadsheet program on your computer, you can access it. If you enable editing in excel, you can type your answers directly onto the puzzle, and you can also easily print the puzzles. Here are the factors from last week’s level 6 hook-shaped puzzle: Here is one way those factors can be found using logic. 90003 90002 54 is a composite number. 54 = 1 x 54, 2 x 27, 3 x 18, or 6 x 9.Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54. Prime factorization: 54 = 2 x 3 x 3 x 3, which can also be written 2 x 3³. 90003 90002 90003 90002 Sometimes 54 is a clue in the FIND THE FACTORS puzzles. Even though it has other factors, the only multiplication fact the puzzle uses is 6 x 9 = 54. 90003 .90000 Prime Factorization Calculator 90001 90002 Calculator Use 90003 90004 Use this prime numbers calculator to find all prime factors of a given integer number up to 1 trillion. This calculator presents: 90005 90006 90007 Prime factors of a number 90008 90007 Prime decomposition in exponential form 90008 90007 CSV (comma separated values) list of prime factors 90008 90007 Factorization in a prime factors tree 90008 90015 90004 For the first 5000 prime numbers, this calculator indicates the index of the prime number.The 90017 n 90018 th 90019 90020 prime number is denoted as Prime [n], so Prime [1] = 2, Prime [2] = 3, Prime [3] = 5, and so on. 90005 90004 The limit on the input number to factor is less than 10,000,000,000,000 (less than 10 trillion or a maximum of 13 digits). 90005 90024 What is Prime Factorization? 90003 90004 Prime factorization or integer factorization of a number is breaking a number down into the set of prime numbers which multiply together to result in the original number.This is also known as prime decomposition. 90005 90024 How to Find Prime Factorization of a Number 90003 90004 We cover two methods of prime factorization: find primes by trial division, and use primes to create a prime factors tree. 90005 90032 Prime Factorization by Trial Division 90033 90004 Say you want to find the prime factors of 100 using trial division. Start by testing each integer to see if and how often it divides 100 and the subsequent quotients evenly.The resulting set of factors will be prime since, for example, when 2 is exhausted all multiples of 2 are also exhausted. 90005 90032 Find the prime factors of 100: 90033 90038 90007 100 ÷ 2 = 50; save 90040 2 90041 90008 90007 50 ÷ 2 = 25; save 90040 2 90041 90008 90007 25 ÷ 2 = 12.5, not evenly so divide by next highest number, 3 90008 90007 25 ÷ 3 = 8.333, not evenly so divide by try next highest number, 4 90008 90007 25 ÷ 4 = 6.25, not evenly so divide by try next highest number, 5 90008 90007 25 ÷ 5 = 5; save 90040 5 90041 90008 90007 5 ÷ 5 = 1; save 90040 5 90041 90008 90061 90004 List the resulting prime factors as a sequence of multiples, 2 x 2 x 5 x 5 or as factors with exponents, 2 90018 2 90019 x 5 90018 2 90019. 90005 90032 Examples of Prime Decomposition: Factors and Exponents 90033 90038 90007 Prime factorization of 100 is 2 x 2 x 5 x 5 or 2 90018 2 90019 x 5 90018 2 90019 90008 90007 Prime factorization of 76 is 2 x 2 x 19 or 2 90018 2 90019 x 19 90018 1 90019 90008 90007 Prime factorization of 50 is 2 x 5 x 5 or 2 x 5 90018 2 90019 90008 90007 Prime factorization of 48 is 2 x 2 x 2 x 2 x 3 or 2 90018 4 90019 x 3 90018 1 90019 90008 90007 Prime factorization of 36 is 2 x 2 x 3 x 3 or 2 90018 2 90019 x 3 90018 2 90019 90008 90007 Prime factorization of 20 is 2 x 2 x 5 or 2 90018 2 90019 x 5 90018 1 90019 90008 90007 Prime factorization of 10 is 2 x 5 or 2 90018 1 90019 x 5 90018 1 90019 90008 90061 90032 Prime Factors Tree 90033 90004 Using a prime factorization tree to see the work, prime decomposition of 100 = 2 x 2 x 5 x 5 looks like this: 90005 90024 Related Calculators 90003 90004 For a list of the first 1000 prime numbers see our See 1000 Prime Numbers Table.90005 90024 References and Further Reading 90003 90004 Math is Fun: Prime Factorization. 90005 90004 Weisstein, Eric W. «Prime Number.» From 90125 MathWorld 90126 —A Wolfram Web Resource. 90005 90004 Weisstein, Eric W. «Direct Search Factorization.» From 90125 MathWorld 90126 —A Wolfram Web Resource. 90005 90004 Weisstein, Eric W. «Prime Factorization Algorithms.»From 90125 MathWorld 90126 —A Wolfram Web Resource. 90005 90004 Caldwell, Chris K. The Prime Pages. 90005 .90000 Prime Factorization 90001 90002 Prime Numbers 90003 90004 A Prime Number is: 90005 90004 a whole number greater than 1 that can 90007 not 90008 be made by multiplying other whole numbers 90005 90004 The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19 and 23, and we have a prime number chart if you need more. 90005 90004 If we 90007 can 90008 make it by multiplying other whole numbers it is a 90007 Composite Number 90008. 90005 90004 Like this: 90005 90020 90005 90004 2 is Prime, 3 is Prime, 4 is Composite (= 2 × 2), 5 is Prime, and so on… 90005 90002 Factors 90003 90004 «Factors» are the numbers you multiply together to get another number: 90005 90020 90005 90002 Prime Factorization 90003 90004 «Prime Factorization» is finding 90007 which prime numbers 90008 multiply together to make the original number. 90005 90004 Here are some examples: 90005 90038 Example 1: What are the prime factors of 12? 90039 90004 It is best to start working from the smallest prime number, which is 2, so let’s check: 90005 90020 12 ÷ 2 = 6 90005 90004 Yes, it divided exactly by 2.We have taken the first step! 90005 90004 But 6 is not a prime number, so we need to go further. Let’s try 2 again: 90005 90020 6 ÷ 2 = 3 90005 90004 Yes, that worked also. And 3 90007 is 90008 a prime number, so we have the answer: 90005 90020 90007 12 = 2 × 2 × 3 90008 90005 90004 90005 90004 As you can see, 90007 every factor 90008 is a 90007 prime number 90008, so the answer must be right. 90005 90004 90005 90004 Note: 90007 12 = 2 × 2 × 3 90008 can also be written using exponents as 90007 12 = 2 90072 2 90073 × 3 90008 90005 90038 Example 2: What is the prime factorization of 147? 90039 90004 Can we divide 147 exactly by 2? 90005 90020 147 ÷ 2 = 73½ 90005 90004 No it can not.The answer should be a whole number, and 73½ is not. 90005 90004 Let’s try the next prime number, 3: 90005 90020 147 ÷ 3 = 49 90005 90004 That worked, now we try factoring 49. 90005 90004 The next prime, 5, does not work. But 7 does, so we get: 90005 90020 49 ÷ 7 = 7 90005 90004 And that is as far as we need to go, because all the factors are prime numbers. 90005 90020 90007 147 = 3 × 7 × 7 90008 90005 90020 (or 90007 147 = 3 × 7 90072 2 90073 90008 using exponents) 90005 90038 Example 3: What is the prime factorization of 17? 90039 90004 Hang on… 90007 17 is a Prime Number 90008. 90005 90004 So that is as far as we can go. 90005 90020 90007 17 = 17 90008 90005 90002 Another Method 90003 90004 We showed you how to do the factorization by starting at the smallest prime and working upwards. 90005 90004 But sometimes it is easier to break a number down into 90007 any factors 90008 you can … then work those factor down to primes. 90005 90038 Example: What are the prime factors of 90? 90039 90004 Break 90 into 9 × 10 90005 90130 90131 The prime factors of 9 are 90007 3 and 3 90008 90134 90131 The prime factors of 10 are 90007 2 and 5 90008 90134 90139 90004 So the prime factors of 90 are 90007 3, 3, 2 and 5 90008 90005 90002 Factor Tree 90003 90004 And a «Factor Tree» can help: find 90007 any factors 90008 of the number, then the factors of those numbers, etc, until we can not factor any more.90005 90038 Example: 48 90039 90004 90005 90004 90007 48 = 8 × 6 90008, so we write down «8» and «6» below 48 90005 90004 Now we continue and factor 8 into 90007 4 × 2 90008 90005 90004 Then 4 into 90007 2 × 2 90008 90005 90004 And lastly 6 into 90007 3 × 2 90008 90005 90004 90005 90004 We can not factor any more, so we have found the prime factors. 90005 90004 Which reveals that 90007 48 = 2 × 2 × 2 × 2 × 3 90008 90005 90004 (or 90007 48 = 2 90072 4 90073 × 3 90008 using exponents) 90005 90002 Why find Prime Factors? 90003 90004 A prime number can only be divided by 1 or itself, so it can not be factored any further! 90005 90004 Every other whole number can be broken down into prime number factors.90005 90190 90191 90192 90193 90194 90193 90194 90193 90004 It is like the Prime Numbers are the 90007 basic building blocks 90008 of all numbers. 90005 90194 90203 90204 90205 90004 This idea can be very useful when working with big numbers, such as in Cryptography. 90005 90002 Cryptography 90003 90004 Cryptography is the study of secret codes. Prime Factorization is very important to people who try to make (or break) secret codes based on numbers.90005 90004 That is because factoring very large numbers is very hard, and can take computers a long time to do. 90005 90004 If you want to know more, the subject is «encryption» or «cryptography». 90005 90002 Unique 90003 90004 And here is another thing: 90005 90020 90007 There is only one (unique!) Set of prime factors for any number. 90008 90005 90004 Example The prime factors of 330 are 2, 3, 5 and 11: 90005 90020 330 = 2 × 3 × 5 × 11 90005 90004 There is no other possible set of prime numbers that can be multiplied to make 330.90005 90004 In fact this idea is so important it is called the 90007 Fundamental Theorem of Arithmetic 90008. 90005 90002 Prime Factorization Tool 90003 90004 OK, we have one more method … use our Prime Factorization Tool that can work out the prime factors for numbers up to 4,294,967,296. 90005 90004 90005 90004 90005 .
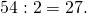 Записываем 27 в левый столбец.
Записываем 27 в левый столбец.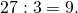 Число 9 записываем в левую колонку.
Число 9 записываем в левую колонку.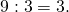 В левый выписываем 3.
В левый выписываем 3.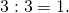 В правый столбик выписываем 3, в левый — 1. Разложение закончено.
В правый столбик выписываем 3, в левый — 1. Разложение закончено.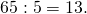 Теперь проверять мы будем уже число 13.
Теперь проверять мы будем уже число 13.