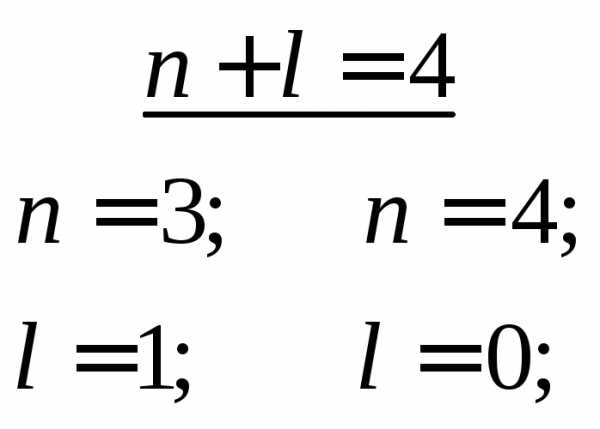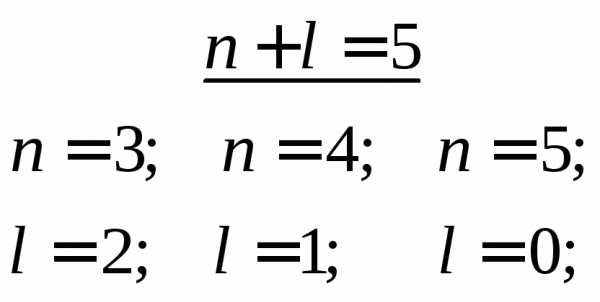Решение 3 6 – Сколько будет 3-3х6+2? Какой ответ?

3.6. Решение примера

3.6.1. Для системы, структурная схема которой показана на рис.3.1. Требуется, пользуясь критерием устойчивости Найквиста, исследовать устойчивость системы при К = 10 1/с, Т₁ = 2 с, Т₂ = 1 с, Т₃ = 0,2 с.

Решение

Для исследования на устойчивость по критерию Найквиста построим годограф по передаточной функции разомкнутой системы:

а) определим мнимую и вещественную части АФЧХ разомкнутой системы:

б) построение годографа

Для построения годографа будем изменять  от 0 до  . Данные сведем в табл.3.2, и по этим данным на комплексной плоскости можно построить годограф. Но этот путь трудоемкий, поэтому чаще строят годограф чисто асимптотически,задаваясь двумя значениями  (0, ) (см.табл.3.1), но зная при этом, какой сдвиг фаз дает каждое элементарное звено. В данном примере ПФ разомкнутой системы имеет на больших частотах (>>

c max) : интегрирующее звено — 90 ⁰ ;

три апериодических звена — 270 ⁰ ;

форсирующее звено + 90 ⁰,

значит, суммарный сдвиг фазы будет — 270 ⁰ . При этом годограф при  = , когда Re и Im части для выражения W(j) равны нулю, войдет в точку с координатами (0, 0) комплексной плоскости со стороны — 270 ⁰ , а значит, должен пересечь вещественную ось. Найдем эту точку “а”, пересечения годографа и вещественной оси (см.рис.3.7). Для этого нужно найти такое значение  , при котором мнимая часть выражения W(j) равна нулю.

Определим это значение  . Мнимая часть может быть равна нулю, когда числитель равен нулю:

— ⁴Т₁ Т₂² Т₃+²(Т₁ Т₃ + 2 Т₂ Т₃ + 2Т₁ Т₂ — Т₂² ) + 1 = 0.

Подставим в это выражение значения для Т₁ , Т₂ , Т₃:

— 0,4 ⁴ + 3,8 ² + 1 = 0 ;  = 3,12.

Второй корень отрицательный, и его не учитываем ( изменяется от 0 до ). Определяем теперь реальную часть при  = 3,12 , Re = — 1,3. Значит точка “а” имеет координаты (- 1,3; j0). Дополнительный годограф охватывает точку с координатами (- 1; j0) (см.рис.3.7), поэтому данная система неустойчива при К = 10 1/с.

Таблица 3.1

	Re	Im
0	— 2	
	0	0

Таблица 3.2

 Im	Re	Im		Re	Im
0	— 2		2,5
0 1 2 а — 1 — 2 0,6			3
Re 0,9			3,12	-1,3	0
1,3			3,5
1,9
2,0				0	0

Рис.3.7

3.6.2. Для системы, структурная схема которой показана на рис.3.1, требуется, пользуясь критерием устойчивости Найквиста (по ЛАХ и АФХ):

а) исследовать устойчивость системы при К = 10 1/с;

б) определить критическое значение К _кр общего общего коэффициента усиления разомкнутой системы;

в) определить значение К = К ₁ , при котором запас устойчивости системы по фазе равен 30 ⁰ ;

г) определить значение К = К ₂ , при котором запас устойчивости по амплитуде равен 6 дБ.

studfiles.net

2.3.6. Примеры решения задач по теме «Системы уравнений общего вида. Мет

Задача 1.

Указать базисный минор матрицы

Указание

Определите вначале ранг матрицы А, а затем найдите ненулевой минор, порядок которого равен R(A).

Решение

Определим R(A). Вторая и четвертая строки А равны, поэтому после вычитания из 4-й строки 2-й получаем:

Вычислим минор полученной матрицы, составленный из первых трех столбцов:

Таким образом, найден минор максимально возможного (3-го) порядка, не равный нулю. Следовательно, ранг матрицы А равен рангу преобразованной матрицы, то есть равен 3, а рассмотренный минор является базисным.

Ответ:

Задача 2.

Определить количество решений системы линейных уравнений

.

Указание

Сравните ранги матрицы системы и расширенной матрицы.

Решение

Сравним ранги матрицы системы

И расширенной матрицы

.

Для удобства вычислений будем искать ранг матрицы А1, отделив ее последний столбец вертикальной чертой. Тогда столбцы, стоящие слева от черты, образуют матрицу А, и мы одновременно найдем ранги обеих матриц.

А1 ~ .

Вычтем из второй строки удвоенную первую, а из третьей – первую, умноженную на 3:

А1 ~ ~ .

Таким образом, R(

A) = 2, a R(A1) = 3, следовательно, система не имеет решений.

Ответ: система несовместна.

Задача 3.

Найти общее решение линейной системы

.

Указание

Убедившись в том, что система совместна, определите базисные и свободные неизвестные и выразите базисные неизвестные через свободные.

Решение

Найдем R(A) и R(A1):

Итак, R = R(A) = R(A1) = 2, а число неизвестных П = 5. Следовательно, R < N, и система имеет бесконечно много решений (совместна, но не определена).

Число базисных неизвестных равно R, то есть двум. Выберем в качестве базисных неизвестных Х1 и Х2, коэффициенты при которых входят в базисный минор преобразованной матрицы А: .

Соответственно Х3, Х4, Х5 – свободные неизвестные.

Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:

И выразим базисные неизвестные через свободные:

.

Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: Х3 = Х4 = Х5 = 0. Тогда

Ответ:

Задача 4.

Найти общее решение системы, выразив в ответе первые неизвестные через последние:

Указание

Приведите расширенную матрицу к виду

Решение

Минор, состоящий из первых трех столбцов полученной матрицы,

Поэтому R(A) = R(A1) = 3, выбранный минор является базисным, а Х1, Х2, Х3, коэффициенты при которых составляют базисный минор, – базисными неизвестными. Тогда свободное неизвестное – Х4, и система, равносильная исходной, имеет вид:

Откуда

Ответ:

Задача 5.

Найти фундаментальную систему решений однородной линейной системы

Указание

Количество решений, образующих фундаментальную систему, равно числу

Свободных неизвестных. Задайте свободным неизвестным значения 1,0,0; 0,1,0; 0,0,1 и вычислите соответствующие значения базисных неизвестных.

Решение

Количество решений, образующих фундаментальную систему, равно числу Свободных неизвестных.

Матрица А1 отличается от матрицы А только добавлением нулевого столбца свободных членов, поэтому все ее ненулевые миноры являются минорами матрицы А, то есть R(A) = R(A1). Найдем R(A):

Выберем в качестве базисного минора

Значит,

R(A) = 2. Пусть Х4, Х5 – базисные неизвестные, Х1, Х2, Х3 – свободные неизвестные. Запишем для них новую систему:

Откуда

Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:

1) Х1 = 1, Х2 = Х3 = 0.

Тогда Х4 = -0,2, Х5 = 1,2, и решение можно записать в виде столбца

2) Х1 = 0, Х2 = 1, Х3 = 0.

При этом Х4 = 1,2, Х5 = 3,8, и следующее решение системы имеет вид

3) Х1 = Х2 = 0, Х3 = 1. Отсюда Х4 = -0,8, Х5 = -0,2, и последний столбец

Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется Нормальной. Поскольку столбцы свободных неизвестных , , линейно независимы, это гарантирует линейную независимость решений Х1, Х2, Х3.

Итак, в качестве фундаментальной системы решений можно выбрать

При этом любое решение данной системы имеет вид: Х = с1Х1 + С2Х2 + С3Х3, где С1, С2, С3 – произвольные постоянные. Эта формула задает общее решение системы.

Ответ:

Задача 6.

Составить однородную систему из двух уравнений, для которой столбцы

Образуют фундаментальную систему решений.

Указание

Пусть искомая система имеет вид:

Подставьте вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3 и решите полученную систему уравнений для коэффициентов Aij.

Решение

Существует бесконечно много систем однородных линейных уравнений, для каждой из которых фундаментальная система решений имеет указанный вид. Число уравнений в таких системах может быть различным. При этом можно указать их наименьшее требуемое количество, а увеличивать их число можно неограниченно.

Определим вначале, из какого наименьшего числа уравнений может состоять такая система.

Число элементов каждого столбца равно пяти, следовательно, в системе пять неизвестных (П = 5). Количество столбцов, составляющих фундаментальную систему, равно трем, то есть N – R = 3, поэтому R = 5 – 3 = 2. Значит, матрица А должна иметь по крайней мере 2 строки. Следовательно, система уравнений с заданной фундаментальной системой решений может состоять из двух и более уравнений.

Пусть искомая система имеет вид:

Подставим вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3. Получим:

Разобьем полученные 6 уравнений на две системы, одна из которых содержит A1I, а вторая – A2I:

Найдем какое-либо частное решение этой системы. Приведем ее матрицу к треугольному виду:

Откуда

Следовательно,

Выберем А14 = А15 = 4, тогда А11 = 0, А12 = 8, А13 = -4.

2) Так же выглядит общее решение системы для A2I:

Выберем свободные неизвестные так, чтобы получить решение, линейно независимое с предыдущим.

Пусть А24 = 4, А25 = 0, тогда А21 = 5, А22 = 5, А23 = -3.

Итак, используя найденные значения коэффициентов, можно составить линейную однородную систему:

Фундаментальная система решений которой имеет вид, приведенный в условии задачи.

Ответ:

Задача 7.

Найти общее решение неоднородной линейной системы

С помощью фундаментальной системы решений соответствующей однородной системы.

Указание

Убедитесь в том, что система совместна. Затем составьте соответствующую однородную систему и найдите для нее фундаментальную систему решений. Далее используйте то, что общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы.

Решение

Убедимся в том, что система совместна:

Итак, R(A) = R(A1) = 2 – система совместна.

Составим по преобразованной матрице однородную систему:

И найдем для нее фундаментальную систему решений:

Фундаментальная система решений может быть выбрана так:

Общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы.

Теперь найдем какое-нибудь частное решение неоднородной системы

Положим Х3 = Х4 = Х5 = 0, тогда . Следовательно,

и общее решение системы имеет вид:

Х = с1Х1 + С2Х2 + С3Х3 + Хчастн, где С1, С2, С3 – произвольные постоянные.

Ответ:

Задача 8.

Решить систему методом Гаусса:

.

Указание

Поменяйте местами 1-е и 2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице, а затем исключите Х из второго и третьего уравнений.

Решение

Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и

2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице:

Теперь исключим Х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2:

Далее можно легко исключить Z из третьего уравнения, если прибавить к нему второе:

Из последнего уравнения получаем, что У = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: Z = 3, Х = 1.

Ответ: Х = 1, У = 0, Z = 3.

При применении метода Гаусса совсем не обязательно приводить систему к «классическому» треугольному виду: . Достаточно, чтобы матрица коэффициентов, например, системы трех уравнений с тремя неизвестными содержала два нуля в одном столбце и одновременно два нуля в одной строке, причем один из нулей стоял на пересечении этих строки и столбца.

Задача 9.

Решить систему методом Гаусса:

Указание

Исключите Х2 из 2-го и 4-го уравнений, используя 1-е уравнение, а затем вычтите из 3-го уравнения 2-е, чтобы исключить Х3.

Решение

Исключим Х2 из 2-го и 4-го уравнений. Для этого из 2-го уравнения вычтем 1-е, а к 4-му прибавим 1-е, умноженное на 2:

Вычтем из 3-го уравнения 2-е, чтобы исключить Х3:

Теперь вычтем из 4-го уравнения удвоенное 3-е:

Из последнего уравнения находим . Тогда из 3-го уравнения Х1 = 0, из 2-го , из 1-го Х2 = 2.

Ответ:

< Предыдущая		Следующая >

matica.org.ua

6/2(2+1) Какой ответ правильный 1 или 9

Не мешало бы вместе с детьми немного размять застоявшиеся за время отдыха мозги и вспомнить школьную науку. Как говорится, знания за плечами не носить, так почему бы не стряхнуть пыль с собственных извилин?

Читайте также: загадка про 6 стаканов с водой ответ

Предлагаем тебе вспомнить математику третьего класса и решить простенький, на первый взгляд, пример. Как оказалось, на этой простенькой задачке обжигается больше половины взрослых!

Итак, сможешь ли ты решить этот пример?

Если у тебя получилось 1, то не спеши радоваться. Проверь результат на калькуляторе. Ответ будет 9!

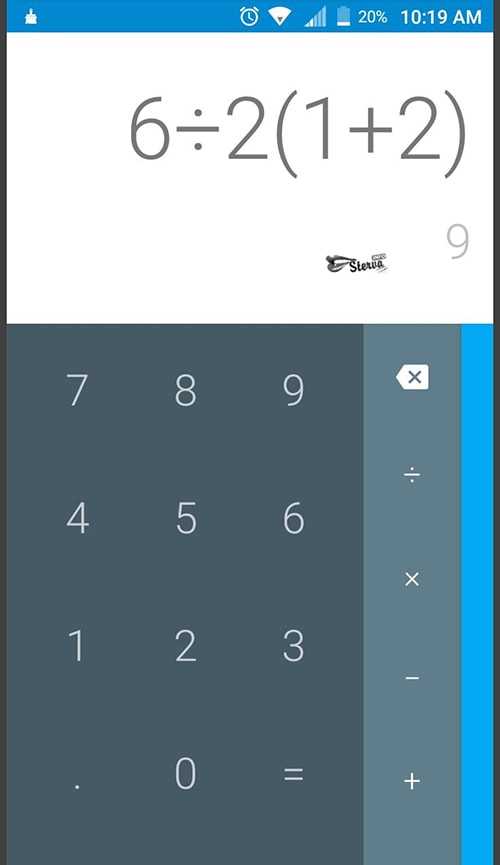
Несложно догадаться, что те, у кого в ответе получилась единица, сперва выполняли действие в скобках.

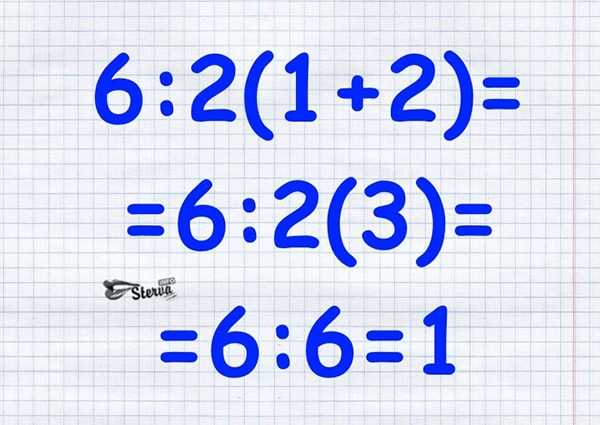
Затем умножали его на 2, и уже после этого делили 6 на то, что получилось.

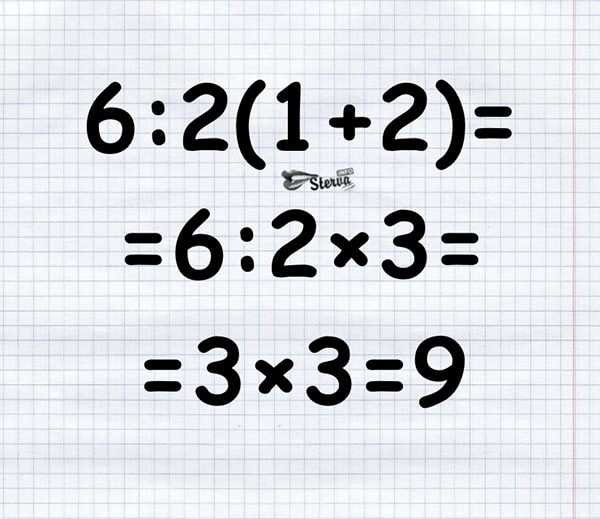
А вот бездушные калькуляторы решают пример по-другому. Они тоже первым делом выполняют действие в скобках, зато потом умножение и деление делают в строгом порядке — слева направо. Так какой же ответ правильный?

 

До революции в России была подобная шутка. Спрашивали на слух, чему равно 2+2*2. Не подумав, на слух говорили, что 8. Но написав на бумаге, видели, что 6.

Операции деления и умножения считаются равноправными по приоритетности. Поэтому последовательность умножений и делений выполняется слево направо.

6/2*(1+2) эквивалентно (6/2)*(1+2) = 9. У деления приоритет перед умножением только потому, что деление записано левее умножения.

6/2*(1+2) НЕ эквивалентно 6/(2*(1+2)). Здесь умножение записано правее деления, поэтому оно не должно выполняться перед делением. Умножение надо делать после деления.

Когда есть такого рода сомнения, то пишите эти арифметические выражения в устройствах или программах, которые понимают порядок действия. Это инженерные и научные калькуляторы, а также компьютерная программа Excel. Обычные простые калькуляторы и бухгалтерские калькуляторы не годятся, так как они не понимают пор

sterva.info

РЕШЕНИЕ 3-6/84

МИНИСТЕРСТВО ЭНЕРГЕТИКИИКИ И ЭI[ЕКТРИФИКАЦИИ СССР

ГЛАВНОЕ ТЕХНИЧЕСКОЕ УПРАВЛЕНИЕ ПО ЭКСПЛУАТАЦИИ ЭНЕРГОСИСТЕМ

РЕШЕНИЕ 3-6/84

г.Москва 30

30 мая 1984 г.

ОБ ИЗМЕНЕНИИ «ТИПОВОЙ ИНСТРУКЦИИ ПО СВАРКЕ
НЕИЗОЛИРОВАННЫХ ПРОВОДОВ С ПОМОЩЬЮ ТЕРМИТНЫХ
ПАТРОНОВ»

(М.: СПО Союзтехэнерго, 1982)

В целях повышения надежности соединений проводов ВЛ Главтехуправление решает внести в “Типовую инструкцию по сварке неизолированных проводов с помощью термитных патронов” следующие изменения:

1. Пункт 5.3.1 изложить в следующей редакции: «допускается соединение алюминиевых и сталеалюминиевых проводов сечением до 185 мм² в пролетах методом скрутки с последующей сваркой выпущенных концов (рис. 6), а проводов сечением 240 мм и более в шлейфах анкерных опор — сваркой концов проводов с последующим опрессованием в алюминиевых корпусах (рис. 7)» .

2. В подрисуночной подписи к рис. 7 заменить слово «пролетах» словом «шлейфах».

3. В п. 5.3.3 заменить в первом предложении слово «пролете» словом «шлейфе».

4. В п. 5.3.5 изъять второе предложение.

Заместитель начальника Главтехуправления, главный специалист-электрик

К. М. АНТИПОВ

 

files.stroyinf.ru

Математика 6 класс Виленкин, Жохов, Чесноков Номер 607

Учебник по математике 6 класс Виленкин

авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.

издательство: Мнемозина 2012 год

Выполните действия:
а)

23∗67:47

;
б)

1112:724∗2122

;
в)

1516:38∗34

;
г)

1314∗725:1325

;
д)

334∗(412:634)

;
е)

(227+117)∗116

;
ж)

(612−414):212

;
з)

(4815−113)∗178

;
и)

(223+156):112

;
к)

(316−2715):125

;
л)

(123+249):(42627−229)

;
м)

(6124−23):(312+178)

.

Решение а

23∗67:47=23∗67∗74=11∗11∗11=1

Решение б

1112:724∗2122=1112∗247∗2122=11∗11∗31=3

Решение в

1516:38∗34=1516∗83∗34=52∗11∗34=158=178

Решение г

1314∗725:1325=1314∗725∗2513=12∗11∗11=12

Решение д

334∗(412:634)=334∗(92:274)=334∗(92∗427)=334∗(11∗23)=154∗23=52∗11=212

Решение е

(227+117)∗116=337∗76=247∗76=241∗16=4

Решение ж

(612−414):212=(624−414):52=214∗25=94∗25=92∗15=910

Решение з

(4815−113)∗178=(4815−1515)∗178=3315∗158=4815∗158=61∗11=6

Решение и

(223+156):112=(246+156):32=396∗23=276∗23=93∗11=3

Решение к

(316−2715):125=(3530−21430):75=(23530−21430)∗57=2130∗57=36∗11=12

Решение л

(123+249):(42627−229)=(169+249):(42627−2627)=3109:22027=379:7427=379∗2774=11∗32=112

Решение м

(6124−23):(312+178)=(6124−1624):(348+178)=(52524−1624):4118=5924:438=12924∗843=33∗11=1

×

Нашли ошибку?

Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

Отправить

reshalka.com

Правильное решение примера

Дорогие читатели Фактора эволюции!

Спасибо за ваши честные комментарии. Мы и не подозревали, что задачка из начальной школы вызовет такой неподдельный интерес и бурные споры. Иногда дело доходило до сильных высказываний, которые пришлось удалять. Поэтому напоминаем вам: будьте терпимы к чужому мнению и высказывайтесь по поводу статей, не переходя на личности. Давайте относиться друг к другу с уважением.

Публикуя статью с задачкой, мы хотели, чтобы вы вспомнили своё детство и оценили, что даже несложные примеры вызывают у нас, опытных взрослых споры. Что же говорить о детях) Не ругайте их, лучше показывайте, что они сделали не так и объясняйте, как надо сделать.

В свою очередь мы хотим объяснить, почему же в примере 6:2(1+2) правильный результат 9.

Ещё раз напоминаем правило арифметики:

«Действия выполняются слева направо, причем сперва умножение и деление, а затем сложение и вычитание».

Если же в примере есть скобки, то действия в них выполняются в первую очередь, а затем по озвученному выше правилу.

И в советских школах, и в школах всех других странах эти правила одинаковы.

Поэтому:

Способ 1

1) Находим сумму в скобках: 1+2=3
2) Действуем по порядку, как говорит нам правило: 6:2=3
3) Теперь 3Х3 =9

Способ 2

Если вы хотите раскрыть скобки 6:2(a+b), где a=1, b =2 Действуем также по порядку
1) 6:2=3
2) Теперь уже раскрываем скобки: 3(a+b)= 3a + 3b
3) Подставляем значения a и b: 3Х1 + 3Х2 = 3+6=9

Число перед скобкой – это просто множитель (кто-то писал о коэффициенте) и на него распространяются всё те же правила арифметики.

Способ 3

Чтобы проверить правильность своего решения, можно придумать задачку, которая решалась бы этим выражением. Например, такую:
В одну канистру бензина входит 1 литр жидких продуктов пиролиза и два литра бензина. 6 таких канистр отправили на 2 бензозаправки поровну на каждую. Сколько литров разбавленного бензина получила каждая бензозаправка?

Решение:
1) 1+2=3 (л) разбавленного бензина в одной канистре.
2) 6:2= 3 (к.) разбавленного бензина получила каждая бензозаправка.
3) 3Х3=9 (л)

Ответ: 9 литров разбавленного бензина получила каждая бензозаправка.

У меня, после просмотра новостей, сама собой сложилась эта задачка. Вы же можете придумать свою более оптимистичную и жизнеутверждающую ситуацию.

Пример неправильно решенной задачи, когда вы получили в ответе 1:

На день рождения к Маше пришло 6 друзей. Для них она поставила две тарелочки угощения. На каждой тарелочке лежала 1 шоколадная конфета и 2 карамельки. Сколько конфет получит каждый ребёнок, если все дети воспитанные и не будут брать лишнюю конфету?

Выражение, которым решается эта задача, выглядит так:
6:(2Х(1+2))= 1 (к.)

Ответ: каждый ребёнок съест по 1 конфетке.

Обратите внимание, что появились ещё одни скобки, меняющие порядок действий.

Всем удачи! А мы уже приготовили для вас головоломную задачу начала 1 класса. Интересно, сколько наших читателей её осилят))))

factor-e.ru

3.6. Решение типовых задач

Пример 1. Определить последовательность заполнения электронами подуровней в атомах элементов, если их суммы п + l соответственно равны 4 и 5.

Решение. Напишем для каждого из случаев возможные значения:

Последовательность заполнения подуровней

Следует иметь в виду, что разница в энергии у орбиталей сравнительно невелика, благодаря чему последовательность заполненияможет быть нарушена (см.Cr и Cu). Различие энергетических состояний, по-видимому, еще меньше в случае (см.Nb, Mo, Ru, Rh, Pd, Ag) и особенно 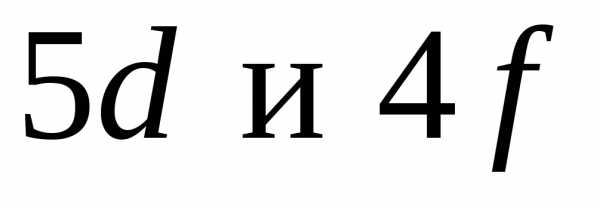(см. лантаноиды).

Пример 2. Написать электронные формулы атомов кальция и титана. К какому семейству элементов они относятся?

Решение. Кальций и титан – элементы IV периода и атомы их имеют 4 электронных слоя. У кальция (Z = 20), следующего через один элемент после аргона (Z = 18), заполняется двумя электронами подуровень . Электронная формула кальция

После заполнения подуровня электроны поступают в подуровеньи поэтому электронная формула титана, атомный номер которого на 2 единицы больше, чем у кальция, имеет вид:

Кальций – s –элемент, а титан -элемент.

Пример 3. Написать электронные формулы атомов хрома, меди и германия. К какому семейству элементов они относятся?

Решение. У элементов IV периода хрома (Z = 24) и меди (Z = 29), атомы которых имеют 4 электронных слоя, происходит, начиная от Sc, заполнение подуровня 3и поэтому следовало бы ожидать, что их формулы будут иметь вид

Структура атома Ar

Однако в действительности расположение электронов на внешних уровнях атомов этих элементов выражается соответственно формулам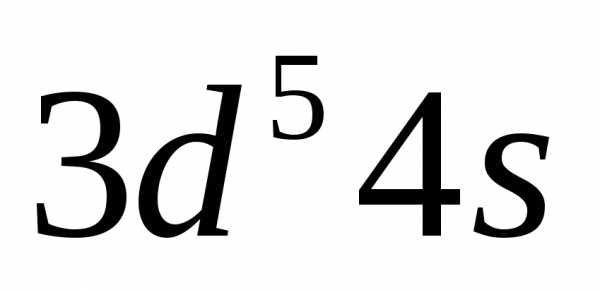и и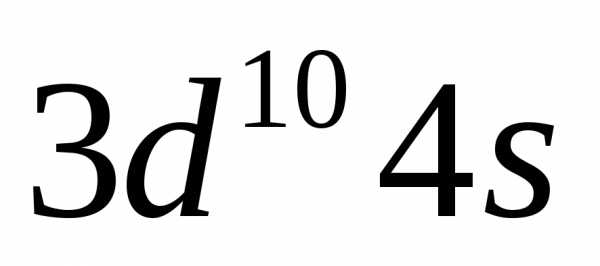, что объясняется провалом одного из электронов подуровняна подуровень. Атом германия (Z = 32) содержит сверх электронной структуры аргона (Z = 18) 14 электронов, заполнение которыми происходит в такой последовательности:

Электронная формула германия имеет вид

Хром и медь относятся к семейству -элементов, а германий – к семействур-элементов.

В электронно-графических формулах атомов два электрона, занимающих одну орбиталь, т.е. электроны с одинаковым значением п, l и т и различным спином 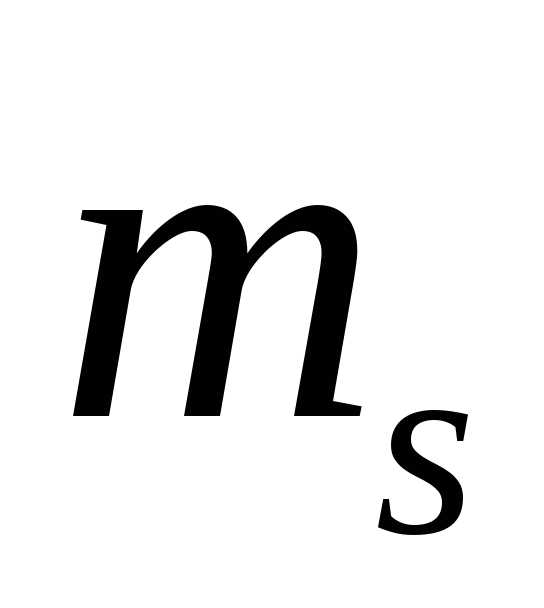, условно принято изображать в виде двух противоположно направленных стрелок.

Пример 4. Написать электронно-графические формулы атомов бериллия и бора в нормальном и в возбужденном состоянии.

Решение. Электронные формулы бериллия — 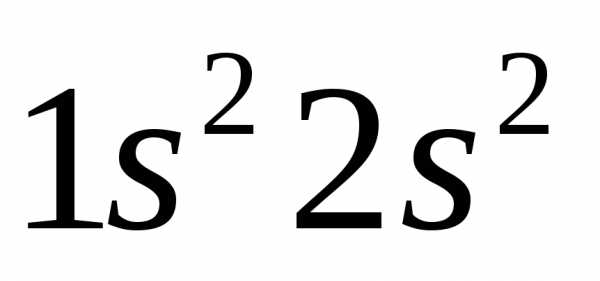и бора —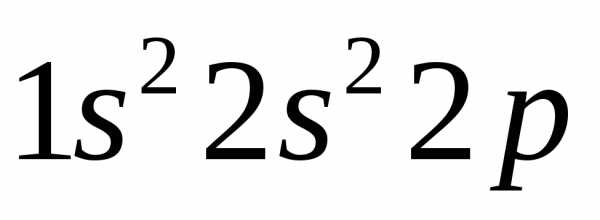могут быть представлены структурами:

бериллий бор

Такие электронные структуры соответствуют нормальному, т.е. невозбужденному, состоянию их атомов. Однако наличие на втором уровне вакантных орбиталей в подуровне 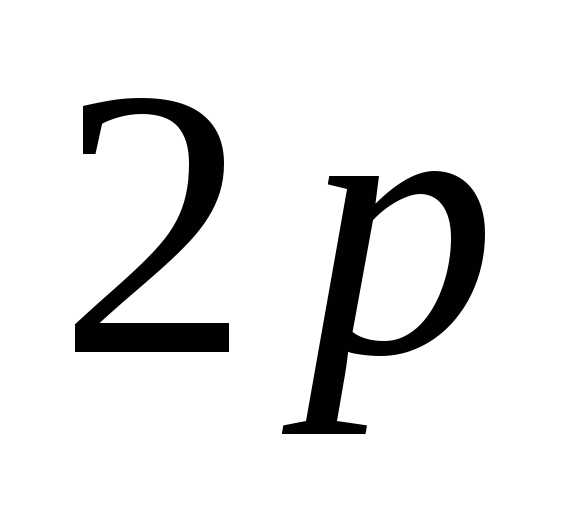делает возможным возбуждение этих электронов до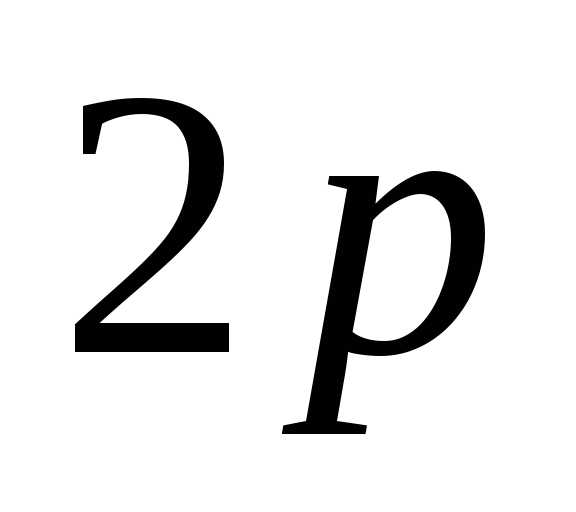-состояния с затратой сравнительно небольшого количества энергии, которое впоследствии полностью и даже с избытком компенсируется энергией, освобождающейся при образовании новых связей. Электронные формулы возбужденных атомов бериллия и бора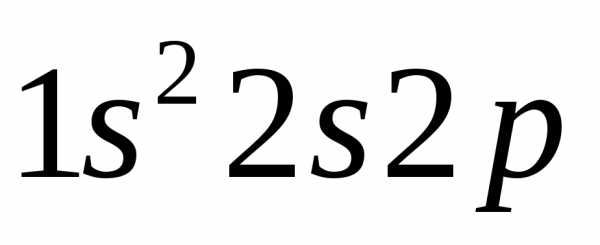и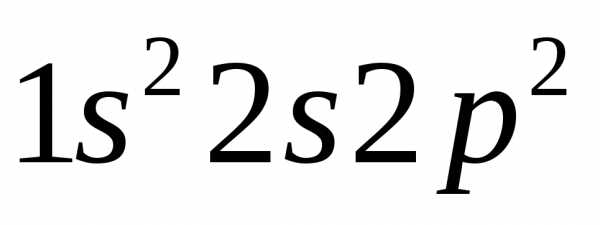, а их структуры имеют следующий вид:

бериллий бор

В таком состоянии валентность Ве и В равна соответственно двум и трем.

Пример 5. Написать электронно-графические формулы атомов азота и кислорода.

Решение. Электронные формулы атомов азота и кислорода:

и .

Возможны два варианта графических формул р-подуровня:

Из них обладают наименьшим запасом энергии, и, следовательно, энергетически более предпочтительны вторые варианты, отвечающие правилу Гунда, согласно которому наименьшим запасом энергии обладают атомы, у которых в пределах данного значения l электроны располагаются так, чтобы число неспаренных электронов с параллельными спинами было максимальным.

Пример 6. Написать электронную формулу атома железа. Как распределяются в нем электроны d-подуровня и какова высшая валентность железа?

Решение. В зависимости от значения п электроны по отдельным уровням K, L, M и т.д. распределяются в атоме железа (Z = 26) следующим образом: 2, 8, 14, 2, а электронная формула имеет вид

.

Энергетически наиболее выгодному распределению шести d-электронов отвечает схема

После возбуждения подуровня и перехода одногоs-электрона на подуровень 4р общее число непарных электронов равно 6, что и соответствует высшей валентности железа.

Пример 7. Написать электронные формулы трех последних квантовых уровней атомов церия и гадолиния. Как распределяются в них электроны подуровней ?

Решение. Электронная формула трех последних квантовых уровней имеет для атома ксенона (Z = 54) следующий вид:

.

Атомы церия (Z = 58) и гадолиния (Z = 64) обладают сверх этой структуры соответственно четырьмя и десятью электронами, которые распределяются следующим образом:

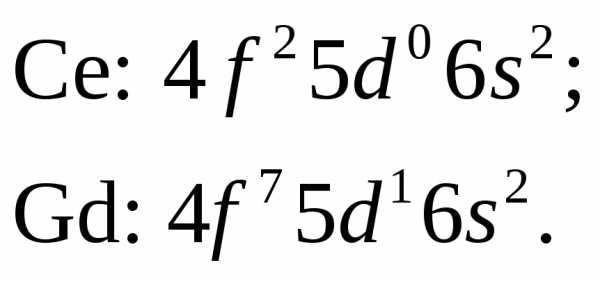
studfiles.net

No related posts.