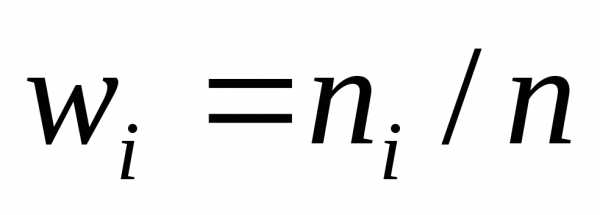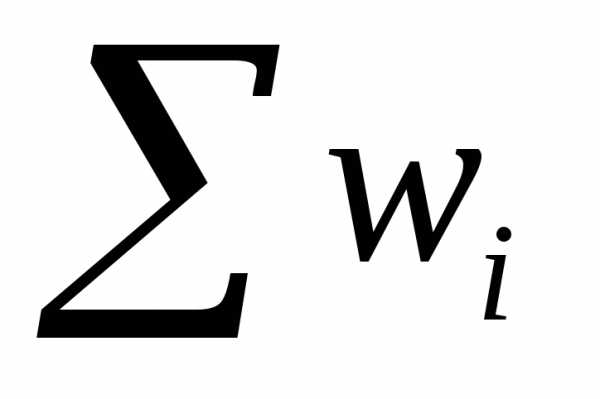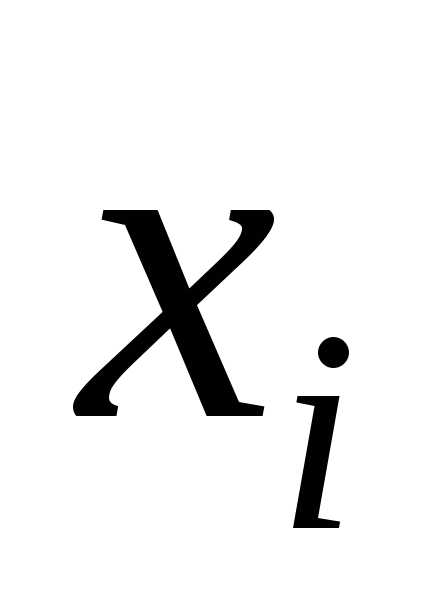Интервальный вариационный ряд — МегаЛекции
Если промежуток между наименьшей и наибольшей вариантами в выборке разбить на несколько интервалов одинаковой длины и каждому интервалу поставить в соответствие число выборочных значений, попавших в этот интервал, то получим интервальный вариационный ряд. Если случайная выборкаимеет большой объем (n ≥50), а генеральная совокупность имеет непрерывное распределение, то вместо обычного (дискретного) вариационного ряда составляют именно такой ряд.
Построение интервального вариационного ряда рассмотрим на следующем примере.
Пример 1. При измерении диаметра валиков после шлифовки получены следующие результаты:
6,75; 6,77; 6,77; 6,73; 6,76; 6,74; 6,70; 6,75; 6,71; 6,72; 6,77; 6,79; 6,71; 6,78;
6,73; 6,70; 6,73; 6,77; 6,75; 6,74; 6,71; 6,70; 6,78; 6,76; 6,81; 6,69; 6,80; 6,80;
6,77; 6,68; 6,74; 6,70; 6,70; 6,74; 6,77; 6,83; 6,76; 6,76; 6,82; 6,77; 6,71; 6,74;
6,77; 6,75; 6,74; 6,75; 6,77; 6,72; 6,74; 6,80; 6,75; 6,80; 6,72; 6,78; 6,70; 6,75;
6,78; 6,78; 6,76; 6,77; 6,74; 6,74; 6,77; 6,73; 6,74; 6,77; 6.74; 6,75; 6,74; 6,76;
6,76; 6,74; 6,74; 6,74; 6,74; 6,76; 6,74; 6,72; 6,80; 6,76; 6,78; 6,73; 6,70; 6,76;
6,76; 6,77; 6,75; 6,78; 6,72; 6,76; 6,78; 6,68; 6,75; 6,73; 6,82; 6,73; 6,80; 6,81;
6,71; 6,82; 6,77; 6,80; 6,80; 6,70; 6,70; 6,82; 6,72; 6,69; 6,73; 6,76; 6,74; 6,77;
6,72; 6,76; 6,78; 6,78; 6,73; 6,76; 6,80; 6,76; 6,72; 6,76; 6,76; 6,70; 6,73; 6,75;
6,77; 6,77; 6,70; 6,81; 6,74; 6,73; 6,77; 6,74; 6,78; 6,69; 6,74; 6,71; 6,76; 6,76;
6,77; 6,70; 6,81; 6,74; 6,74; 6,77; 6,75; 6,80; 6,74; 6,76; 6,77; 6,77; 6,81; 6,75;
6,78; 6,73; 6,76; 6,76; 6,76; 6,77; 6,76; 6,80; 6,77; 6,74; 6,77; 6,72; 6,75; 6,76;
6,77; 6,81; 6,76; 6,76; 6,76; 6,80; 6,74; 6,80; 6,74; 6,73; 6,75; 6,77; 6,74; 6,76;
6,77; 6,77; 6,75; 6,76; 6,74; 6,82; 6,76; 6,73; 6,74; 6,75; 6,76; 6,72; 6,78; 6,72;
6,76; 6,77; 6,75; 6,78.
Для построения интервального ряда необходимо определить величину частичных интервалов. Считая, что все частичные интервалы имеют одну и ту же длину, для каждого интервала следует установить его верхнюю и нижнюю границы, а затем в соответствии с полученной упорядоченной совокупностью частичных интервалов сгруппировать результаты наблюдении. Длину частичного интервала h следует выбрать так, чтобы построенный ряд не был громоздким и в то же время позволял выявить характерные черты изменения значений случайной величины.
При большом объеме выборки вычисления становятся громоздкими, и с целью упрощения вычислений, элементы выборки объединяют в группы (разряды). Для этого интервал, содержащий все множество элементов выборки, разбивают на k непересекающихся интервалов. При этом правый конец каждого интервала исключают из соответствующего множества, а левый – включают. Ради простоты интервалы обычно выбирают одинаковой длины
Просматривая результаты наблюдений, находим, что наибольшим значением случайной величины хнаиб является 6,83, а наименьшим хнаим = 6,68.
Найдем размах выборки R:
R = 6,83 – 6,68 = 0,15.
Выберем число интервалов. Для того чтобы вариационный ряд не был слишком громоздким, обычно число интервалов берут от 7 до 11. Положим предварительно k = 7, тогда длина частичного интервала
h = R/k = 0,15/7 ≈ 0,0214 ≈ 0,02.
За начало первого интервала рекомендуется брать величину
хнач = хнаим – 0,5h.
В нашем случае хнач = 6,67.
Конец последнего интервала должен удовлетворять условию
хнач – h ≤ хнаиб < хнач.
Промежуточные интервалы получают, прибавляя к концу предыдущего интервала длину частичного интервала h (у нас h = 0,02). Просматривая результаты наблюдений, определяем, сколько выборочных значений попало в каждый конкретный интервал.
В таблице частота ni показывает, в скольких наблюдениях случайная величина приняла значения, принадлежащие тому или иному интервалу, причем нижний конец интервала входит в него, а верхний – нет. Такие частоты обычно называют интервальными, а их отношение к общему числу наблюдений – интервальными относительными частотами или частостями. Для данного примера интервальный вариационный ряд приведен в таблице 1:
Таблица 1
| № | [аi; аi+ | ni | ni/n = | Плотность частоты ni/h | Плотность частности ni/nh | xi– середина интервала |
| 6,67–6,69 | 0,01 | 0,5 | 6,68 | |||
| 6,69–6,71 | 0,075 | 3,75 | 6,7 | |||
| 6,71–6,73 | 0,085 | 4,25 | 6,72 | |||
| 6,73–6,75 | 0,22 | 6,74 | ||||
| 6,75–6,77 | 0,26 | 6,76 | ||||
| 6,77–6,79 | 0,22 | 6,78 | ||||
| 6,79–6,81 | 0,07 | 3,5 | 6,8 | |||
| 6,81–6,83 | 0,055 | 2,75 | 6,82 | |||
| 6,83–6,85 | 0,005 | 0,25 | 6,84 | |||
| ∑ |
При вычислении интервальных относительных частот округление результатов следует проводить таким образом, чтобы общая сумма относительных частот была равна 1:
∑ni/n = 1.
По данным интервального ряда строят гистограмму частот или гистограмму относительных частот (частостей).
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h,а высоты равны отношению ni/h (плотность частоты).
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h,а высоты равны отношению ni/nh (плотность относительной частоты или частости).
На рисунке 1 построена гистограмма частостей для интервального вариационного ряда из примера 1:
Рис. 1
Пример 2.Построить гистограммы частот и относительных частот распределения, представленного таблицей.
Таблица 2
| Интервал [аi; аi+1) | Частота интервала ni |
| [0;2) | |
| [2;4) | |
| [4;6) | |
| [6;8] | |
| ∑ | n = 50 |
Как видим, объем выборки n = 50, а шаг h = 2.
Таблица 3
| Интервал [аi; аi+1) | Частота интервала ni | Плотность частоты ni/h | Плотность частости ni/nh | xi– середина интервала |
| [0;2) | 25/2 | 25/100 | ||
| [2;4) | 14/2 | 14/100 | ||
| [4;6) | 8/2 | 8/100 | ||
| [6;8] | 3/2 | 3/100 |
Построим гистограммы частот и относительных частот:

рис. 2

Рис. 3
Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки:
S = 2∙(12,5 + 7 + 4 + 1,5) = 50.
Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. 1:
S = 2∙(0,25 + 0,14 + 0,08 + 0,03) = 1.
С увеличением объема выборки n и уменьшением длины интервала гистограмма будет стремиться к кривой плотности распределения f(x), поэтому гистограмму используют в качестве аналога оценки для плотности распределения.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.
Для начала определим число интервалов по формуле Стержеса.
n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности.
n = 1 + 3, 322∙2 = 7,644
Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 5, 6, 7 и 8. Величину интервала определим по формуле:
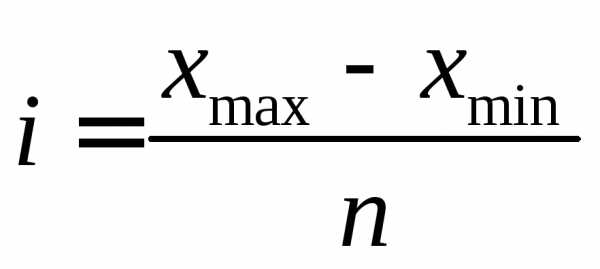
Тогда величина интервала для интервального ряда с 5 интервалами – 6,6, с 6 интервалами равна 5,5, с 7 интервалами – 4,72, с 8 интервалами – 4,125
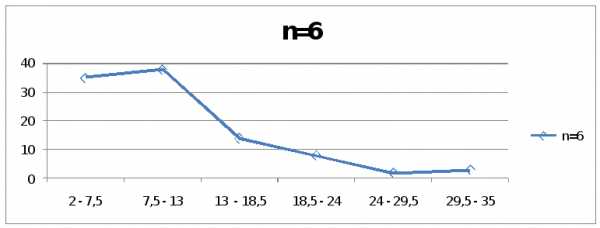
n=6 n=7 n=8
№ п/п | Значение интервала | Интервальная частота, f | 5,5 | |
1 | 2 – 7,5 | 35 | n=6 | |
2 | 7,5 – 13 | 38 | ||
3 | 13 – 18,5 | 14 | ||
4 | 18,5 – 24 | 8 | ||
5 | 24 – 29,5 | 2 | ||
6 | 29,5 – 35 | 3 | ||
| Итого: | 100 | ||
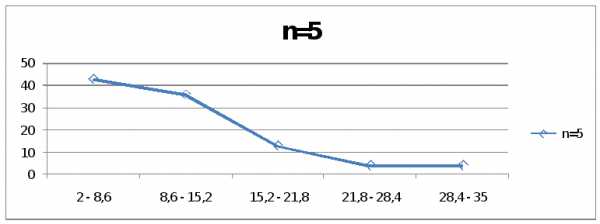
n=5
№ п/п | Значение интервала | Интервальная частота, f | 4,72 | |
1 | 2 – 6,72 | 29 | n=7 | |
2 | 6,72 – 11,44 | 37 | ||
3 | 11,44 – 16,16 | 15 | ||
4 | 16,16 – 20,88 | 11 | ||
5 | 20,88 – 25,6 | 3 | ||
6 | 25,6 – 30,32 | 3 | ||
7 | 30,32 – 35 | 2 | ||
| Итого: | 100 | ||
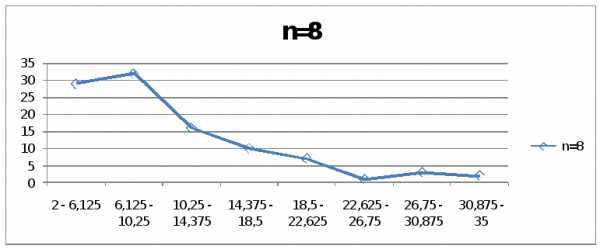
№ п/п | Значение интервала | Интервальная частота, f | 4,125 | |
1 | 2 – 6,125 | 29 | n=8 | |
2 | 6,125 – 10,25 | 32 | ||
3 | 10,25 – 14,375 | 16 | ||
4 | 14,375 – 18,5 | 10 | ||
5 | 18,5 – 22,625 | 7 | ||
6 | 22,625 – 26,75 | 1 | ||
7 | 26,75 – 30,875 | 3 | ||
8 | 30,875 – 35 | 2 | ||
| Итого: | 100 | ||
№ п/п | Значение интервала | Интервальная частота, f | 6,6 |
1 | 2 — 8,6 | 43 | n=5 |
2 | 8,6 — 15,2 | 36 | |
3 | 15,2 — 21,8 | 13 | |
4 | 21,8 — 28,4 | 4 | |
5 | 28,4 — 35 | 4 | |
| Итого | 100 |
По полученным данным видно, что наиболее лучший вариант группировки – это интервальный вариационный ряд с 5 интервалами, так как прослеживается тенденция в уменьшении частот, а так же отсутствие интервалов с нулевыми частотами.

№ п/п | Значение интервала | Центр интервала, xц | Интервальная частота, f | Накопленная частота |
1 | 2 – 8,6 | 5,3 | 43 | 43 |
2 | 8,6 – 15,2 | 12,05 | 36 | 79 |
3 | 15,2 – 21,8 | 18,5 | 13 | 92 |
4 | 21,8 – 28,4 | 25,1 | 4 | 96 |
5 | 28,4 – 35 | 31,7 | 4 | 100 |
| Итого |
| 100 |
|
1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).
Среднеарифметическая взвешенная.
Дискретный вариационный ряд.
 ,
где
,
где
Σxi∙fi – сумма произведений значений признака и их частот;
Σfi – сумма всех частот.
= 9,96
Интервальный вариационный ряд.
 ,
где
,
где
Σxцен∙fi – сумма произведений центров интервалов и их частот;
Σfi – сумма всех частот.
=
Мода.
Дискретный вариационный ряд.
Это вариант имеющий наибольшую частоту f.
Интервальный вариационный ряд.
, где
х0 – нижняя граница модального интервала;
i0 – величина модального интервала;
f1, f2, f3 – частота интервала предшествующего, модального и следующего за модальным.
=7,676
studfiles.net
Задание 1. Построить интервальный вариационный ряд распределения — МегаЛекции
Лабораторная работа №1
По математической статистике
Тема: Первичная обработка экспериментальных данных
2. Содержание работы.. 1
3. Оценка в баллах. 1
4. Содержание и форма отчета. 1
5. Контрольные вопросы.. 2
6. Методика выполнения лабораторной работы.. 3
7. Варианты заданий. 10
8. Рекомендуемая литература. 16
Цель работы
Приобретение навыков первичной обработки эмпирических данных методами математической статистики.
Содержание работы
На основе совокупности опытных данных выполнить следующие задания:
Задание 1. Построить интервальный вариационный ряд распределения.
Задание 2. Построить гистограмму частот интервального вариационного ряда.
Задание 3. Составить эмпирическую функцию распределения и построить график.
Задание 4. Рассчитать основные числовые характеристики вариационного ряда:
а) моду и медиану;
б) условные начальные моменты;
в) выборочную среднюю;
г) выборочную дисперсию, исправленную дисперсию генеральной совокупности, исправленное среднее квадратичное отклонение;
д) коэффициент вариации;
е) асимметрию;
ж) эксцесс;
Задание 5. Определить границы истинных значений числовых характеристик, изучаемой случайной величины с заданной надёжностью.
Задание 6. Содержательная интерпретация результатов первичной обработки по условию задачи.
Оценка в баллах
Задания 1-5 – 6 баллов
Задание 6 – 2 балла
Защита лабораторной работы (устное собеседование по контрольным вопросам и лабораторной работе) — 2 балла
Содержание и форма отчета
Работа сдается в письменной форме на листах формата А4 и включает:
1) Титульный лист (Приложение 1)
2) Исходные данные.
3) Представление работы по указанному образцу.
4) Результаты расчетов (выполненные вручную и/или с помощью MS Excel) в указанном порядке.
5) Выводы — содержательная интерпретация результатов первичной обработки по условию задачи.
6) Устное собеседование по работе и контрольным вопросам.
5. Контрольные вопросы
- Какая совокупность называется генеральной (выборочной)?
- Какая выборка называется репрезентативной?
- Какие способы формирования выборки вы знаете?
- Когда выборка называется повторной (бесповторной)?
- Какие вариационные ряды вы знаете?
- Можно ли от дискретного ряда перейти к интервальному и наоборот?
- От чего зависит число интервалов группировки?
- Как от простой статистической таблицы данных перейти к вариационному ряду?
- Как графически изобразить дискретный (непрерывный) вариационный ряд?
- Каким свойством обладает выборочное среднее?
- Как вычислить моду и медиану дискретного (интервального) вариационного ряда?
- Как вычислить дисперсию (среднее квадратичное отклонение) выборочной совокупности?
- Какими свойствами обладает дисперсия?
- Что характеризует коэффициент асимметрии?
- Что характеризует эксцесс?
- Какое число принимается в качество ложного нуля?
- По каким формулам от числовых характеристик, вычисленных в условных вариантах производится переход к числовым характеристикам в первоначальных вариантах?
- Какая оценка называется точечной?
- Что является несмещенной оценкой математического ожидания генеральной совокупности?
- Как вычисляется несмещенная оценка дисперсии генеральной совокупности?
- Какая оценка называется интервальной?
- Какая вероятность называется надежностью? Дайте пояснения на графике нормального закона распределения.
- По каким формулам находится доверительный (надежностный) интервал для генеральной средней и генерального среднеквадратичного отклонения?
- Как определить минимальный объем выборки, чтобы с заданной надежностью гарантировать определенную точность D вычисления генеральной средней?
- Как ведет себя предельная ошибка (точность оценки), если надежность увеличивается?
Методика выполнения лабораторной работы
Задание 1. Построить интервальный вариационный ряд распределения
Для того, чтобы статистические данные представить в виде вариационного ряда с равноотстоящими вариантами необходимо:
1.В исходной таблице данных найти наименьшее и наибольшее значения.
2.Определить размах варьирования:
3. Определить длину интервала h, если в выборке до 1000 данных, используют формулу: , где n – объем выборки – количество данных в выборке; для вычислений берут lgn).
Вычисленное отношение округляют до удобногоцелого значения.
4. Определить начало первого интервала для четного числа интервалов рекомендуют брать величину ; а для нечетного числа интервалов .
5. Записать интервалы группировок и расположить их в порядке возрастания границ
, ,………., ,
где — нижняя граница первого интервала. За берется удобное число не большее , верхняя граница последнего интервала должна быть не меньше . Рекомендуется, чтобы интервалы содержали в себе исходные значения случайной величины и выделять от 5 до 20 интервалов.
6. Записать исходные данные по интервалам группировок, т.е. подсчитать по исходной таблице число значений случайной величины, попадающих в указанные интервалы. Если некоторые значения совпадают с границами интервалов, то их относят либо только к предыдущему, либо только к последующему интервалу.
Замечание 1. Интервалы необязательно брать равными по длине. На участках, где значения располагаются гуще, удобнее брать более мелкие короткие интервалы, а там где реже — более крупные.
Замечание 2.Если для некоторых значений получены “нулевые”, либо малые значения частот , то необходимо перегруппировать данные, укрупняя интервалы (увеличивая шаг ).
Вариант №0
Даны результаты измерения роста (с точностью до см) 60 наудачу отобранных студентов:
178, 160, 154, 183, 155, 153, 167, 186, 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
179, 165, 156, 179, 158, 171, 175. 173, 164, 172
178, 160, 154, 183, 155, 153, 167, 186, 163, 155,
157, 175, 170, 166, 159, 173, 182, 167, 171, 169,
179, 165, 156, 179, 158, 171, 175. 173, 164, 172
Решение.
1. n=60;: .
Длина частичного интервала:
Примем h = 6. Начало первого интервала
Исходные данные разбиваем на 6 (m = 1 + log230 = 5,907 ≈ 6) интервалов:
[150,156), [156,162), [162,168), [168,174), [174, 180), [180, 186).
Подсчитав число студентов , попавших в каждый из полученных промежутков, получим интервальный вариационный ряд, который записывается в виде таблицы.
Таблица 1.
| Х | [150,156) | [156,162) | [162,168) | [168,174) | [174, 180) | [180, 186] |
| (частота) |
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
6. Методика выполнения лабораторной работы
Вариант №10.
Получены данные опроса населения (в тыс. чел.) относительно участия в голосовании :
551 | 550 | 550 | 562 | 550 | 550 | 550 | 551 | 562 | 550 | 538 | 558 | 544 | 554 | 546 |
542 | 539 | 537 | 543 | 540 | 530 | 542 | 535 | 556 | 546 | 545 | 558 | 564 | 545 | 550 |
548 | 533 | 558 | 560 | 558 | 556 | 556 | 534 | 548 | 540 | 559 | 558 | 558 | 548 | |
551 | 550 | 552 | 568 | 538 | 540 | 551 | 549 | 551 | 547 | 558 | 545 | 552 | 550 | |
546 | 552 | 550 | 557 | 547 | 552 | 559 | 557 | 552 | 554 | 558 | 557 | 556 | 546 | |
558 | 563 | 568 | 563 | 562 | 547 | 554 | 567 | 569 | 552 | 554 | 556 | 565 | 560 | |
560 | 550 | 539 | 549 | 539 | 554 | 549 | 545 | 547 | 540 | 550 | 558 | 566 | 554 |
Задание 1. Построить интервальный вариационный ряд распределения Краткие теоретические сведения
Для того, чтобы статистические данные представить в виде вариационного ряда с равноотстоящими вариантами необходимо:
1.В исходной таблице данных найти
наименьшее 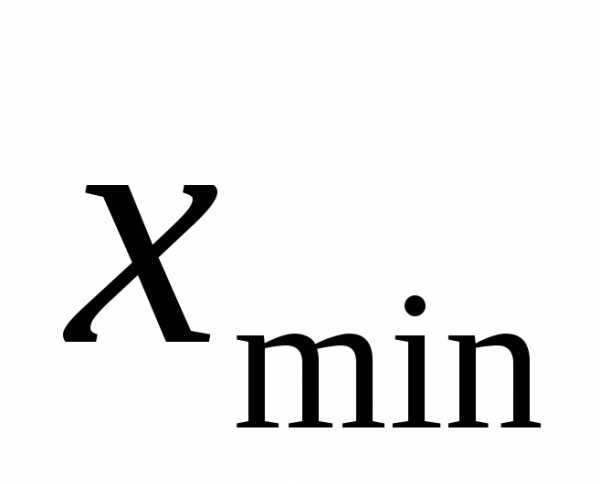 и наибольшее
и наибольшее значения.
значения.
2.Определить размах варьирования:
3. Определить длину интервала h, если в
выборке до 1000 данных, используют формулу: 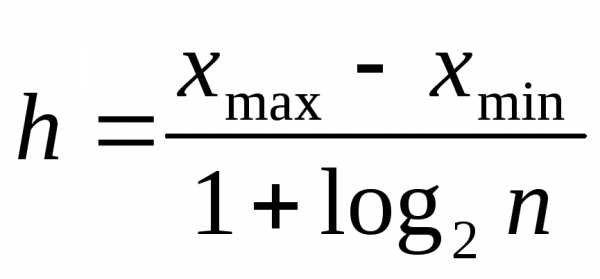 ,
где n – объем выборки – количество
данных в выборке; для вычислений берутlgn).
,
где n – объем выборки – количество
данных в выборке; для вычислений берутlgn).
Вычисленное отношение округляют до удобногоцелого значения.
4. Определить начало первого интервала
для четного числа интервалов рекомендуют
брать величину 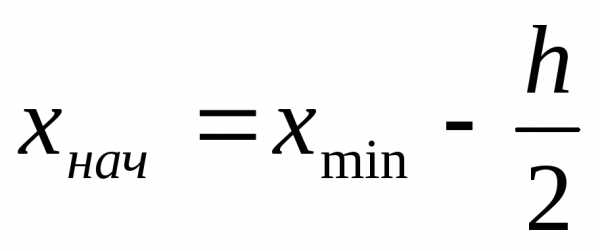 ;
;
а для нечетного числа интервалов 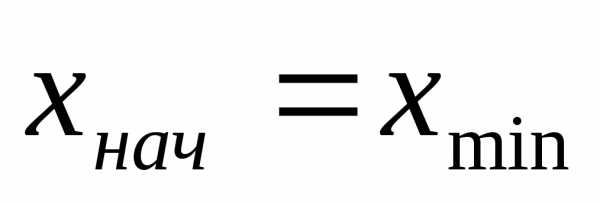 .
.
5. Записать интервалы группировок и расположить их в порядке возрастания границ
,,……….,,
где 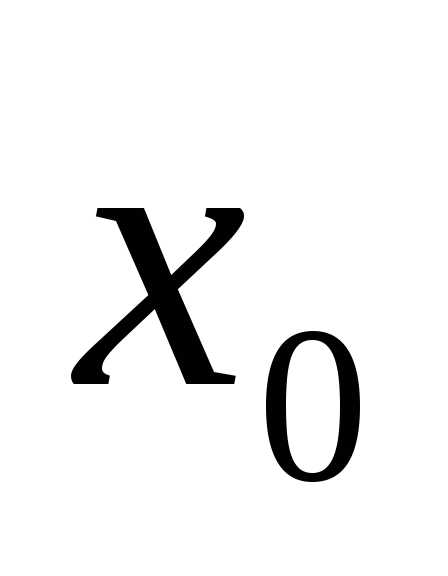 —
нижняя граница первого интервала. За
—
нижняя граница первого интервала. За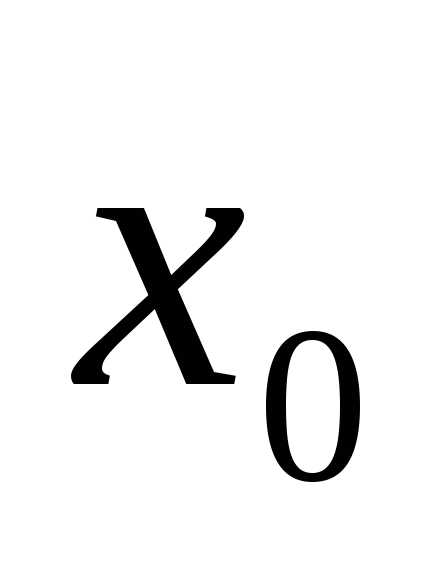 берется удобное число не большее
берется удобное число не большее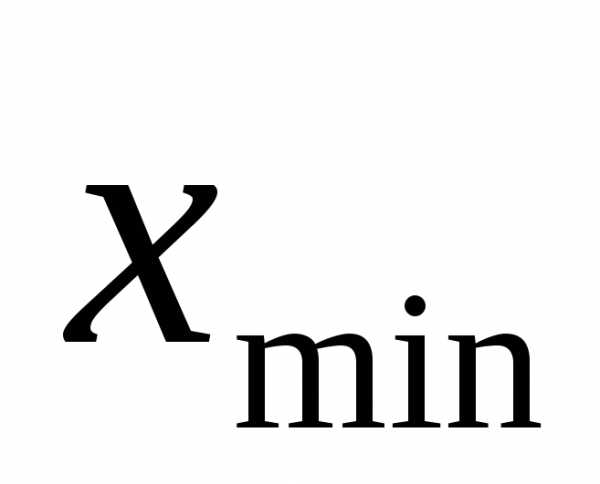 ,
верхняя граница последнего интервала
должна быть не меньше
,
верхняя граница последнего интервала
должна быть не меньше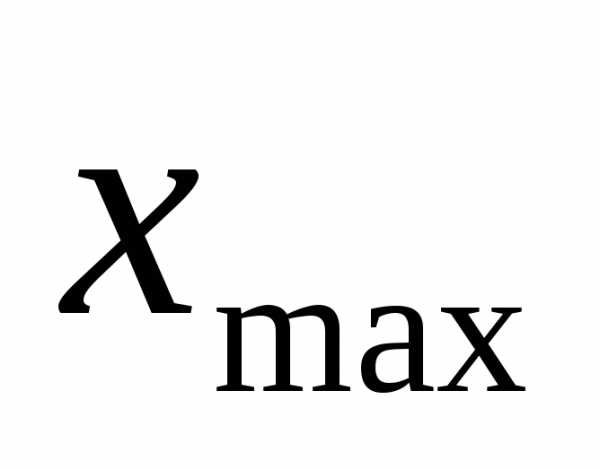 .
Рекомендуется, чтобы интервалы содержали
в себе исходные значения случайной
величины и выделять от5 до 20интервалов.
.
Рекомендуется, чтобы интервалы содержали
в себе исходные значения случайной
величины и выделять от5 до 20интервалов.
6. Записать исходные данные по интервалам группировок, т.е. подсчитать по исходной таблице число значений случайной величины, попадающих в указанные интервалы. Если некоторые значения совпадают с границами интервалов, то их относят либо только к предыдущему, либо только к последующему интервалу.
Замечание. Если для некоторых
интервалов получены “нулевые”, либо
малые значения частот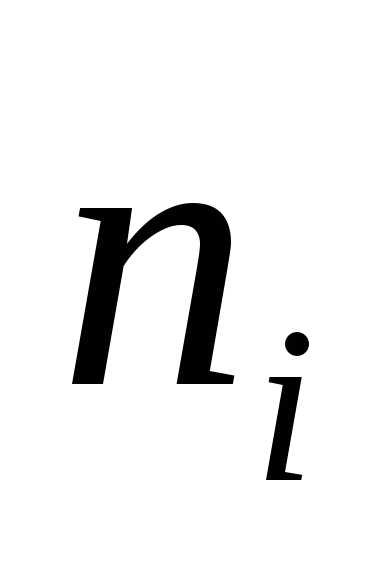 ,
то необходимо перегруппировать данные,
укрупняя интервалы (увеличивая шаг
,
то необходимо перегруппировать данные,
укрупняя интервалы (увеличивая шаг 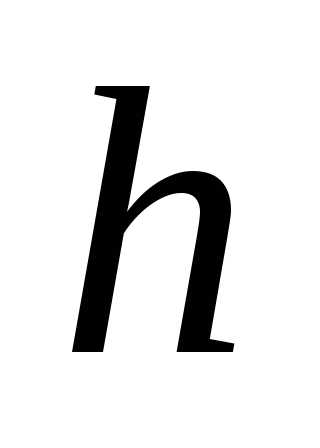 ).
).
Задание 1. Построить интервальный вариационный ряд распределения
Решение
1. n=100;:.
Длина частичного интервала:
Примемh = 5. Начало первого интервала
Исходные данные разбиваем на следующие равные интервалы:
(530, 535], (535, 540], (540, 545], (545, 550], (550, 555], (555, 560], (560, 565], (565, 570].
Подсчитаем 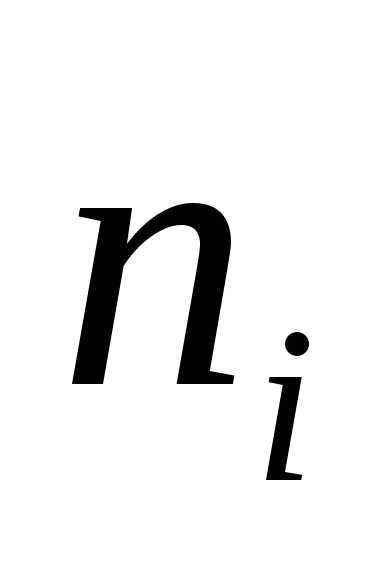 ,
— число студентов попавших в каждый из
полученных промежутков.
,
— число студентов попавших в каждый из
полученных промежутков.
Таблица 1.
Х | [530,535] | (535,540] | (540,545] | (545,550] | (550,555] | (555,560] | (560,565] | (565,570] |
| 4 | 10 | 8 | 26 | 17 | 23 | 7 | 5 |
studfiles.net
Задание 2. Построить гистограмму частот интервального вариационного ряда Краткие теоретические сведения
Гистограммой частотназывают
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых
служат частичные интервалы длиныh,
а высоты равны отношению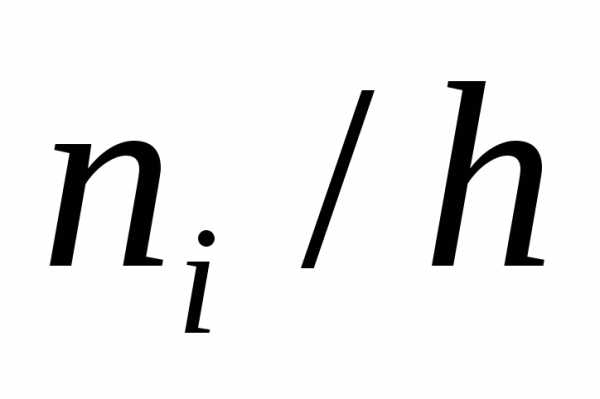 (плотность частоты).
(плотность частоты).
Для построения гистограммы на оси 0х отмечают интервалы. На оси 0у -плотность частоты. Над каждым интервалом проводят отрезки параллельные оси 0х
Площадь частичного i-го прямоугольника равнасумме частот вариант, попавших вi-й интервал. Площадь гистограммы частот равнасумме всех частот, т.е. объему выборки n.
Задание 2. Построить гистограмму частот интервального вариационного ряда Решение
Длина интервала h= 6. Найдем
плотность частоты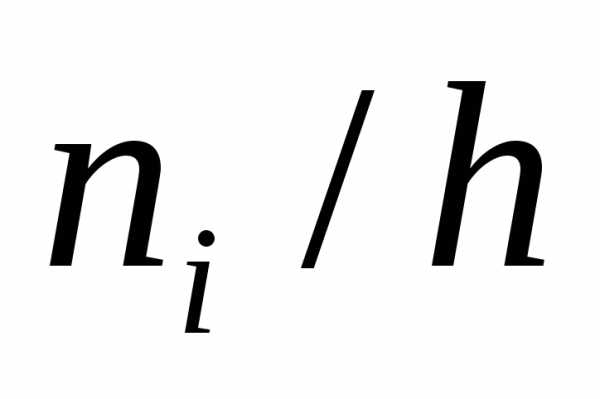 .
.
Таблица 2.
Х | [530,535] | (535,540] | (540,545] | (545,550] | (550,555] | (555,560] | (560,565] | (565,570] |
| 4 | 10 | 8 | 26 | 17 | 23 | 7 | 5 |
| 4/5 ≈ 0,8 | 10/5 ≈ 2 | 8/5 ≈ 1,6 | 26/5 ≈ 5,8 | 17/5 ≈ 3,4 | 23/5 ≈ 4,6 | 7/5 ≈ 1,4 | 5/5 ≈ 1 |
Задание 3. Записать эмпирическую функцию распределения и построить ее график
Краткие теоретические сведения
Эмпирическая функция распределения  ,определяет для каждого значения х
относительную частоту события Х <x.
,определяет для каждого значения х
относительную частоту события Х <x.
относительная частота (частость)
Для построения графика эмпирической
функции распределения переходят к
дискретному ряду распределения, для
этого в качестве вариант 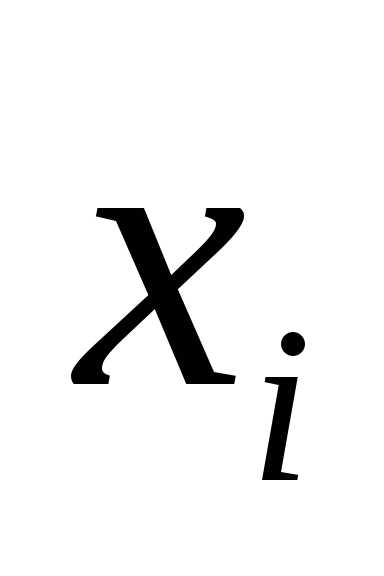 принимают середины частичных интервалов.
Частоты при этом не изменяются.
На оси 0х отмечают значения
принимают середины частичных интервалов.
Частоты при этом не изменяются.
На оси 0х отмечают значения 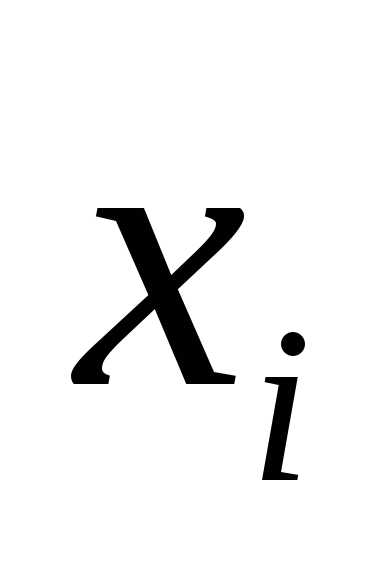 ,
на оси 0у – накопительные частоты.
,
на оси 0у – накопительные частоты.
Задание 3. Записать эмпирическую функцию распределения и построить ее график Решение
Вычислим:
— середину каждого интервала 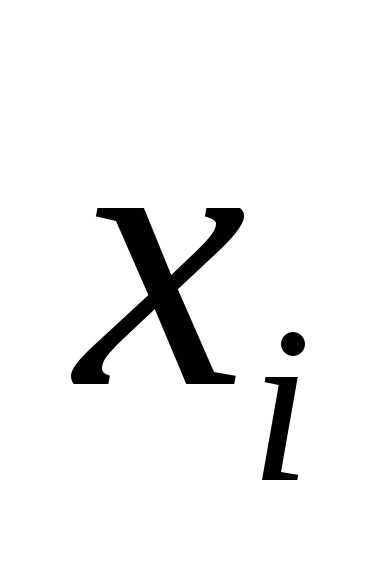 и запишем эти значения в первую
строку таблицы;
и запишем эти значения в первую
строку таблицы;
— относительные частоты 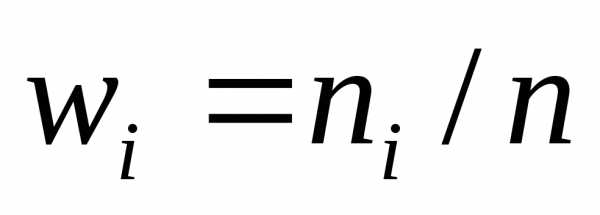 и запишем в третью строку таблицы;
и запишем в третью строку таблицы;
— накопительные частоты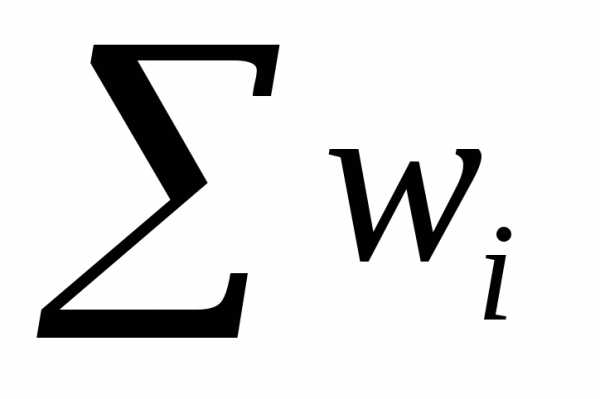 и запишем в четвертую строку таблицы.
и запишем в четвертую строку таблицы.
Таблица 3.
Значение
признака | 532,5 | 537,5 | 542,5 | 547,5 | 552,5 | 557,5 | 562,5 | 567,5 |
| 4 | 10 | 8 | 26 | 17 | 23 | 7 | 5 |
(частость) | 4/100 ≈ 0,04 | 10/100 ≈ 0,1 | 8/100 ≈ 0,08 | 26/100 ≈ 0,26 | 17/100 ≈ 0,17 | 23/100 ≈ 0,23 | 7/100 ≈ 0,07 | 5/100 ≈ 0,05 |
Накопительные относительные частоты
| 0,04 | 0,04+0,1= 0,14 | 0,04+0,1+0,08= 0,22 | 0,48 | 0,65 | 0,88 | 0,95 | 1 |
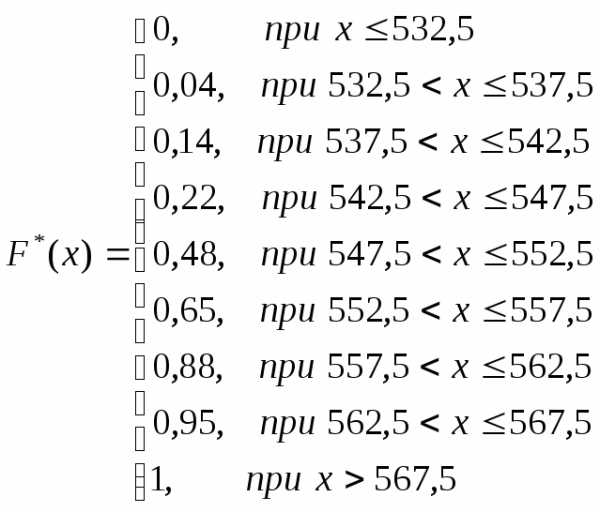
Задание 4. Рассчитать основные числовые характеристики вариационного ряда Решение
4А) Мода – это варианта, имеющая наибольшую частоту.
По данным Таблицы 3: 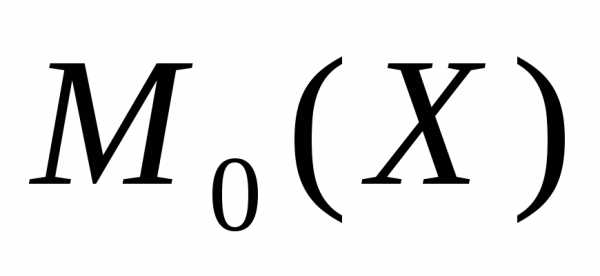 = 547,5.
= 547,5.
Медиана– это варианта, которая делит вариационный ряд на две части, равные по числу вариант.Если число интервалов четное, то медиана определяется как среднее арифметическое серединных значений интервалов, если нечетное, то медиана – это серединное значение медианного (среднего) интервала.
В нашем примере число интервалов четное
По данным Таблицы 3: (532,5+537,5+542,5+547,5+552,5+557,5+562,5+657,5)/8=550,
studfiles.net
2. Построение вариационного ряда
Пусть
изучается некоторая дискретная или
непрерывная случайная величина, закон
распределения которой известен.
Статистический материал, полученный в
результате измерений представляют в
виде таблицы, состоящей из двух строк,
в первой из которых находятся расположенные
в возрастающем порядке значения признаков
(для дискретной случайной величины) или
интервалов (для непрерывной случайной
величины), а во второй – их частота 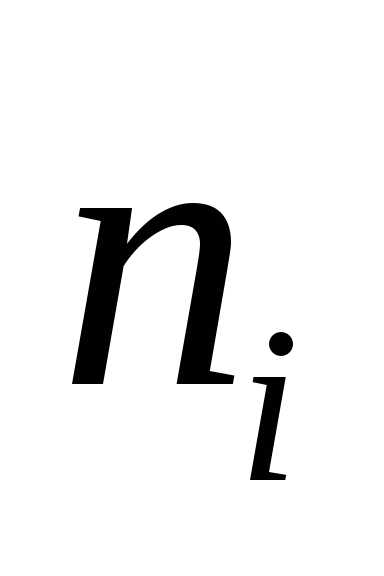 ;
(число одинаковых значений дискретной
случайной величины или число наблюдений
в i-м
интервале в случае непрерывной случайной
величины). Такое представление признака
и частот называется вариационным рядом.
;
(число одинаковых значений дискретной
случайной величины или число наблюдений
в i-м
интервале в случае непрерывной случайной
величины). Такое представление признака
и частот называется вариационным рядом.
На основе имеющейся выборки составляем интервальный статистический ряд.
Для
выбора оптимальной длины интервалов h воспользуемся формулой:  где
где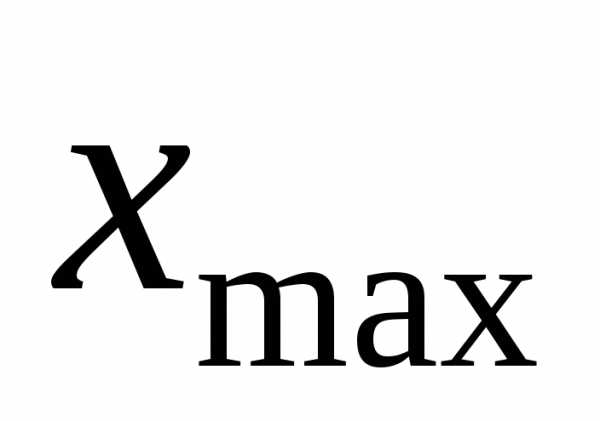 и
и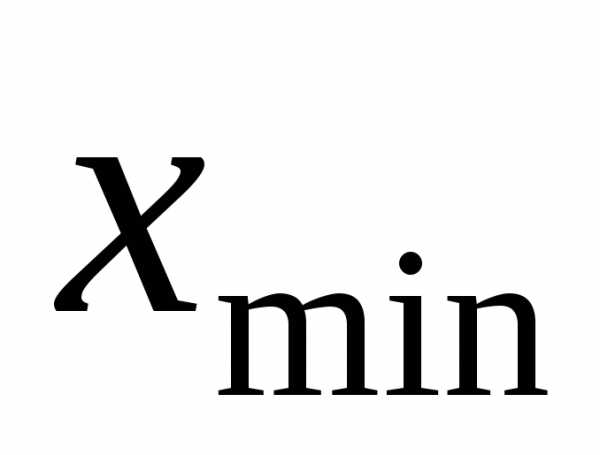 – соответственно максимальное и
минимальное значения признака
– соответственно максимальное и
минимальное значения признака 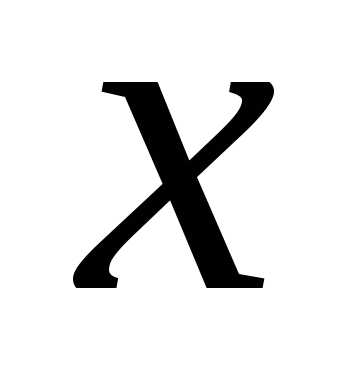 в выборке;l – количество
интервалов, причём в данной работе мы
будем использовать следующую формулу:
,
где n – объём
выборки.
в выборке;l – количество
интервалов, причём в данной работе мы
будем использовать следующую формулу:
,
где n – объём
выборки.
Для
нашего случая: 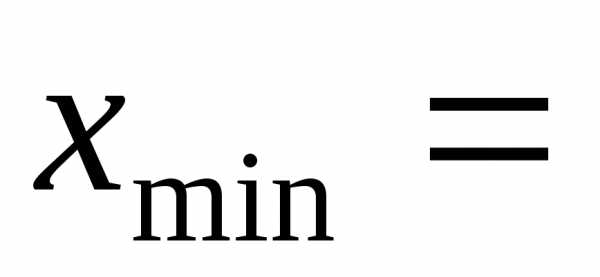 6,75,
6,75,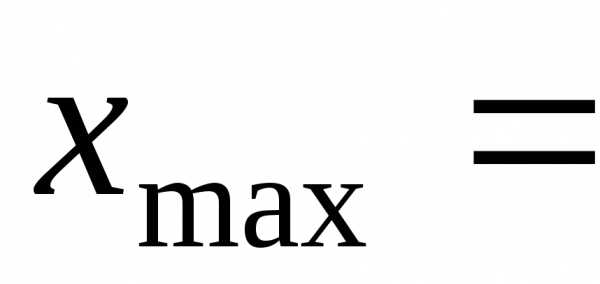 10,97
,
10,97
,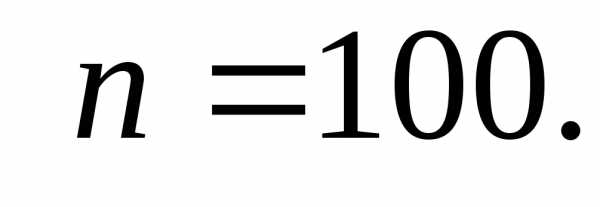
Найдём количество интервалов: .
Найдём
длину интервалов (шаг):  (10,97–6,75)/10=0,422
(10,97–6,75)/10=0,422 0,43.
0,43.
Нижнюю границу первого интервала принимаем 6,75.
Зная
нижнюю границу первого интервала 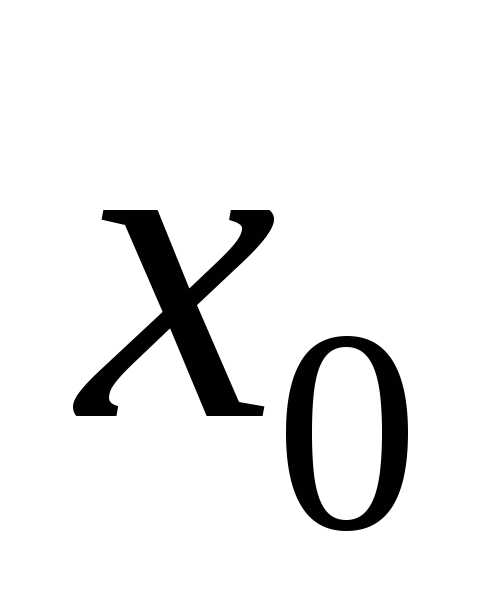 и длину интервала
и длину интервала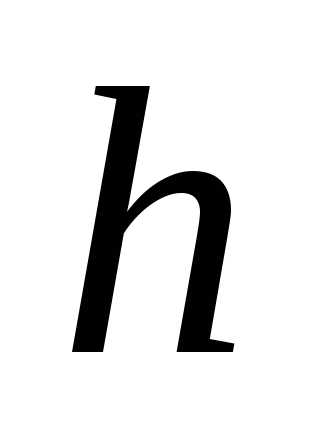 ,
построим весь интервальный ряд.
,
построим весь интервальный ряд.
Проанализируем
каждое значение имеющейся выборки на
факт попадания в определённый интервал,
а число значений, попавших в интервал,
запишем в столбец «Частота 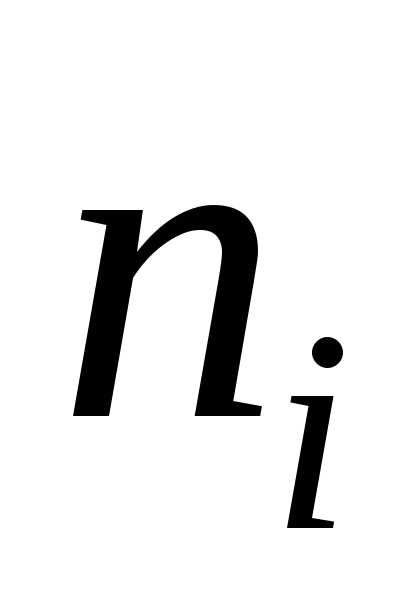 »
таблицы 1. Проведём проверку полученных
значений частот:
»
таблицы 1. Проведём проверку полученных
значений частот: .
.
Найдем
середину каждого интервала, используя
формулу: 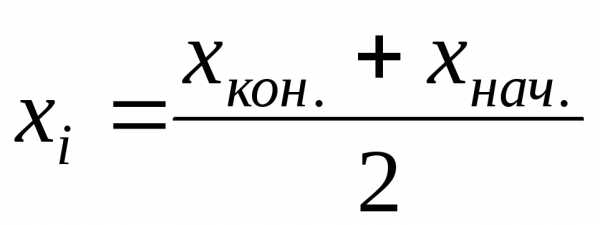 ,
где
,
где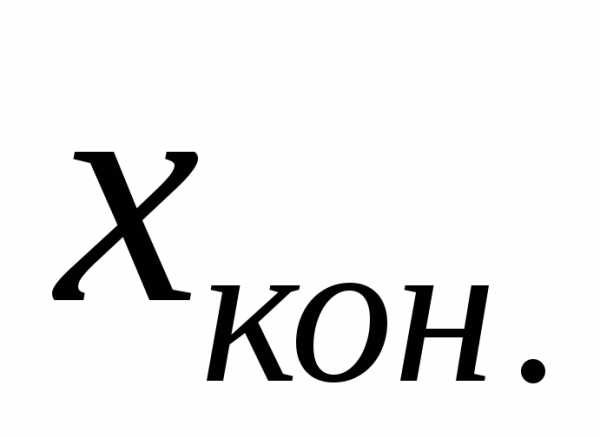 и
и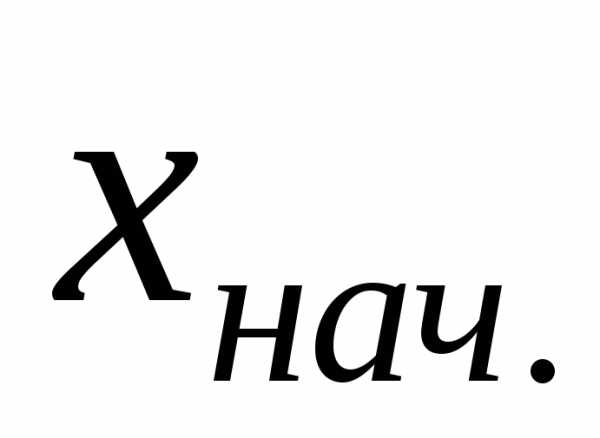 –
конечное и начальное значения определённого
интервала. Результаты занесем в таблицу
1.
–
конечное и начальное значения определённого
интервала. Результаты занесем в таблицу
1.
Таблица 1.
Интервалы | Середина
интервала | Частота | |
[6,75; 7,18) | 6,97 | *** | 3 |
[7,18; 7,61) | 7,40 | ****** | 6 |
[7,61; 8,04) | 7,83 | ** | 2 |
[8,04; 8,47) | 8,26 | ************** | 14 |
[8,47; 8,9) | 8,69 | ************** | 14 |
[8,9; 9,33) | 9,12 | ************************ | 24 |
[9,33; 9,76) | 9,55 | ************** | 14 |
[9,76; 10,19) | 9,98 | ************ | 12 |
[10,19; 10,62) | 10,41 | ********* | 9 |
[10,62; 11,05) | 10,84 | ** | 2 |
3. Графическое изображение вариационных рядов
Для наглядности статистические ряды представляют графиками, наиболее распространёнными являются полигон и гистограмма. Полигон применяется для изображения как дискретных, так и интервальных статистических рядов, гистограмма – для изображения только интервальных рядов. Покажем построение этих графиков на примере.
Для
построения гистограммы частот на оси
абсцисс откладываем частичные интервалы
значений случайной величины 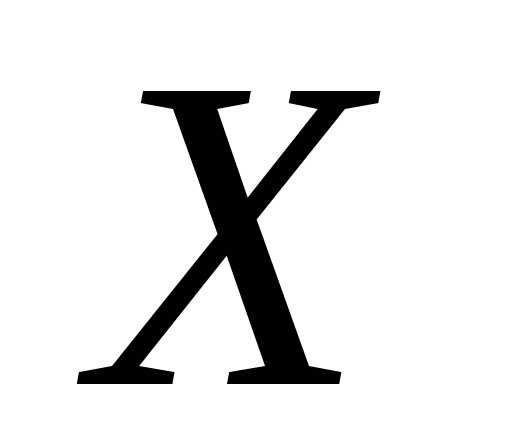 ,
на каждом из которых строим прямоугольник,
высота которого равна соответствующей
частоте интервала.
Если на гистограмме частот соединить
середины верхних сторон элементарных
прямоугольников, то полученная замкнутая
ломаная образует полигон распределения
частот (рис. 1). По гистограмме приближённо
определим моду (см. подраздел 5.1).
,
на каждом из которых строим прямоугольник,
высота которого равна соответствующей
частоте интервала.
Если на гистограмме частот соединить
середины верхних сторон элементарных
прямоугольников, то полученная замкнутая
ломаная образует полигон распределения
частот (рис. 1). По гистограмме приближённо
определим моду (см. подраздел 5.1).
Замечание:
в теории вероятностей гистограмме и
полигону относительных частот 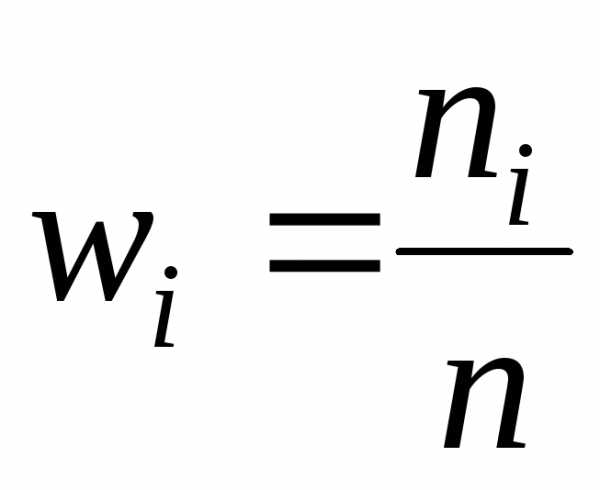 соответствует график функции плотности
распределения. По виду полигона делают
первоначальное предположение о законе
распределения исследуемой случайной
величины.
соответствует график функции плотности
распределения. По виду полигона делают
первоначальное предположение о законе
распределения исследуемой случайной
величины.
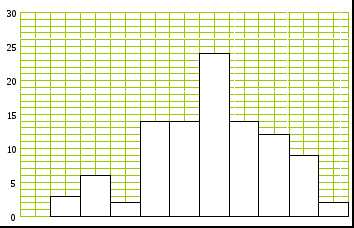
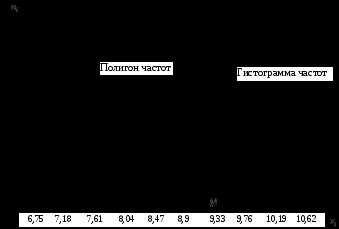
Рисунок 1. – Графическое изображение вариационного ряда.
studfiles.net
1.3.Построить дискретный вариационный ряд.
№ п/п | Значение варианты, х | Частота, f | № п/п | Значение варианты, х | Частота, f |
1 | 2 | 5 | 13 | 14 | 1 |
2 | 3 | 8 | 14 | 15 | 1 |
3 | 4 | 9 | 15 | 16 | 2 |
4 | 5 | 9 | 16 | 18 | 1 |
5 | 6 | 6 | 17 | 19 | 1 |
6 | 7 | 7 | 18 | 21 | 2 |
7 | 8 | 6 | 19 | 22 | 1 |
8 | 9 | 12 | 20 | 26 | 1 |
9 | 10 | 16 | 21 | 28 | 1 |
10 | 11 | 4 | 22 | 31 | 1 |
11 | 12 | 2 | 23 | Итого: | 100 |
12 | 13 | 4 |
|
1.4. Построить интервальный вариационный ряд, подобрав наилучшее число интервалов.
Для начала определим число интервалов по формуле Стержеса.
n = 1 + 3,322∙lgN, где n – число интервалов, N – общее число единиц совокупности.
n = 1 + 3, 322∙2 = 7,644
Исходя из этого, будем рассматривать интервальный ряд с количеством интервалов 6, 7 и 8. Величину интервала определим по формуле:
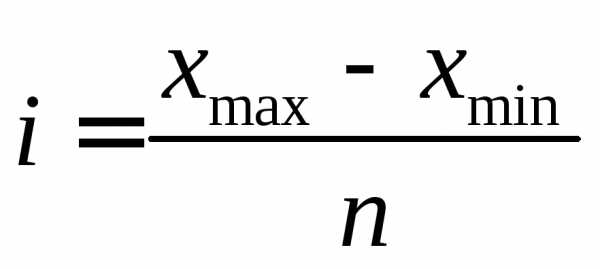
Тогда величина интервала для интервального ряда с 5 интервалами равна 5,8, с 6 интервалами – 4,83, с 7 интервалами – 4,14, c 8 интервалами – 3,63.
№ п/п | Значение интервала | Частота, f | № п/п | Значение интервала | Частота, f | ||
1 | 2 — 7.8 | 44 | 1 | 2 – 6.83 | 37 | ||
2 | 7.8 — 13.6 | 44 | 2 | 6.83 – 11.66 | 44 | ||
3 | 13.6 — 19.4 | 6 | 3 | 11.66 – 16.49 | 10 | ||
4 | 19.4 — 25.2 | 3 | 4 | 16.49 – 21.32 | 4 | ||
5 | 25.2 — 31 | 3 | 5 | 21.32 – 26.15 | 2 | ||
Итого: | 100 | 6 | 26.15 – 31 | 2 | |||
| Итого: | 100 |
№ п/п | Значение интервала | Частота, f |
1 | 2 – 6,14 | 37 |
2 | 6,14 – 10.28 | 41 |
3 | 10.28 – 14.42 | 11 |
4 | 14.42 – 18.56 | 4 |
5 | 18.56 – 22.7 | 4 |
6 | 22.7 – 26.84 | 1 |
7 | 26.84 – 31 | 2 |
| Итого: | 100 |
№ п/п | Значение интервала | Частота, f |
1 | 2 – 5.63 | 31 |
2 | 5.63 – 9.26 | 31 |
3 | 9.26 – 12.89 | 22 |
4 | 12.89 – 16.52 | 8 |
5 | 16.52 – 20.15 | 2 |
6 | 20.15 – 23.78 | 3 |
7 | 23.78 – 27.41 | 1 |
8 | 27.41 – 31 | 2 |
| Итого: | 100 |
По полученным данным видно, что наиболее лучший вариант группировки – это интервальный вариационный ряд с 5 интервалами, так как прослеживается тенденция в уменьшении частот, а так же отсутствие интервалов с нулевыми частотами.
№ п/п | Значение интервала | Центр интервала | Частота, f | Накопленная частота |
1 | 2 – 7,8 | 4,9 | 44 | 44 |
2 | 7,8 – 13,6 | 10,7 | 44 | 88 |
3 | 13,6 – 19,4 | 16,5 | 6 | 94 |
4 | 19,4 – 25,4 | 22,4 | 3 | 97 |
5 | 25,4 – 31 | 28,1 | 3 | 100 |
1.5.Для каждого из полученных рядов вычислить: среднюю арифметическую; моду; медиану; показатели вариации (размах вариации, среднее линейное и среднее квадратическое отклонение, дисперсию, коэффициент вариации).
Среднеарифметическая взвешенная.
Дискретный вариационный ряд.
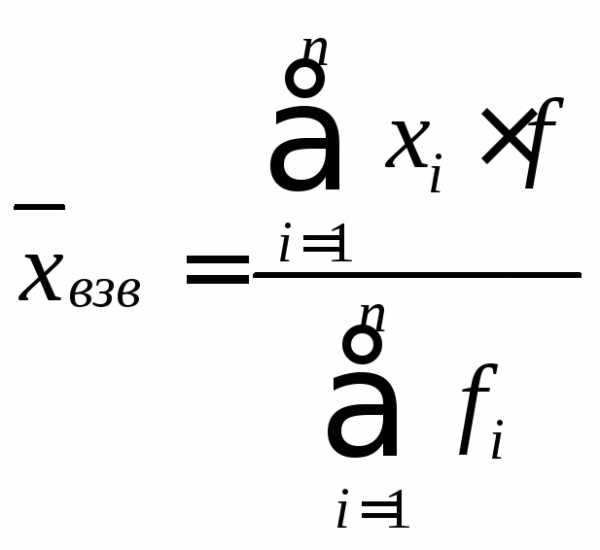 ,
где
,
где
Σxi∙fi – сумма произведений значений признака и их частот;
Σfi – сумма всех частот.
χ взв = 882/100=8,82
Интервальный вариационный ряд.
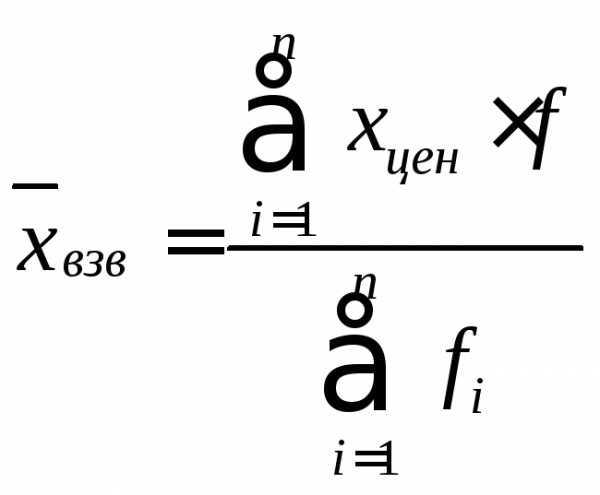 ,
где
,
где
Σxцен∙fi – сумма произведений центров интервалов и их частот;
Σfi – сумма всех частот.
χ взв = 963,52/100=9,64
Мода.
Дискретный вариационный ряд.
Это вариант имеющий наибольшую частоту f.
Интервальный вариационный ряд.
, где
х0 – нижняя граница модального интервала;
i0 – величина модального интервала;
f1, f2, f3 – частота интервала предшествующего, модального и следующего за модальным.
М0 = 2+5,8*((44-0)/(44-0)-(44-44))=7,8
Медиана.
Дискретный вариационный ряд.
Это вариант стоящий в центре ранжированного ряда.
Интервальный вариационный ряд.
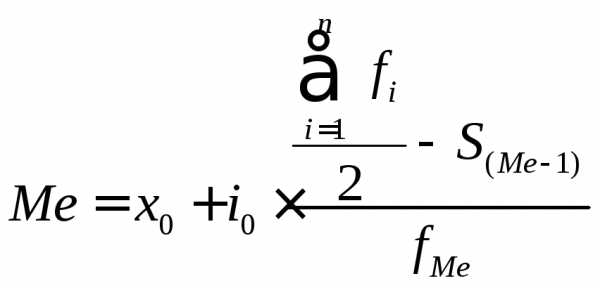 ,
где
,
где
х0 – нижняя граница медианного интервала;
i0 – величина медианного интервала;
Σfi – сумма всех частот;
S(Me – 1) – сумма накопленных частот интервалов, предшествующих медианному;
fMe – частота медианного интервала.
Размах вариации.
Дискретный вариационный ряд.
R=31 –2 = 29
Интервальный вариационный ряд.
R = 31 – 2 = 29
Среднее линейное отклонение.
Дискретный вариационный ряд.
l = (19,18+17,18+13,18+12,18+10,18+9,18+ 4,36+6,18+5,18+16,72+6,36+8,72+18,88+ 2,16+4,92+12,74+16,92+34,38+43,38+46,56+34,1)/100 = 374,82/100 = 3,75
Интервальный вариационный ряд.
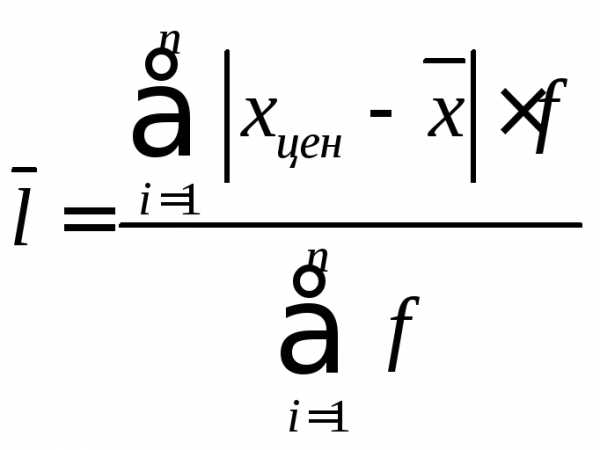
l = (172,48+82,72+46,08+40,74+57,84)/100 = 399,86/100 = 3,99
Дисперсия (средняя квадратов отклонений).
Дискретный вариационный ряд.
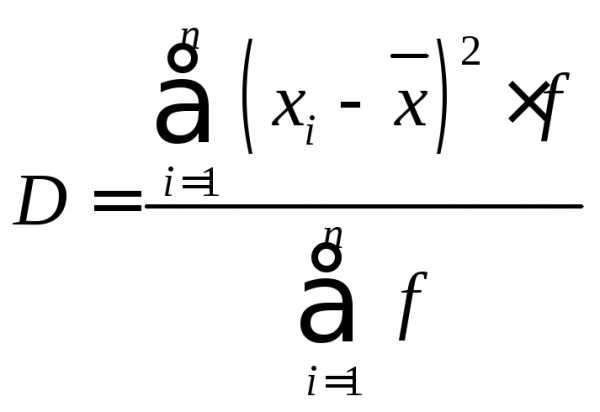
D = (232.56+270.98+209.09+131.33+47.7+
23.19+4.03+0.39+22.28+19+20.22+26.83+38.19+103.1+84.27+103.63+148.35+173.7+295.15+367.87+491.95)/100=2813.81/100=28.14
Интервальный вариационный ряд.
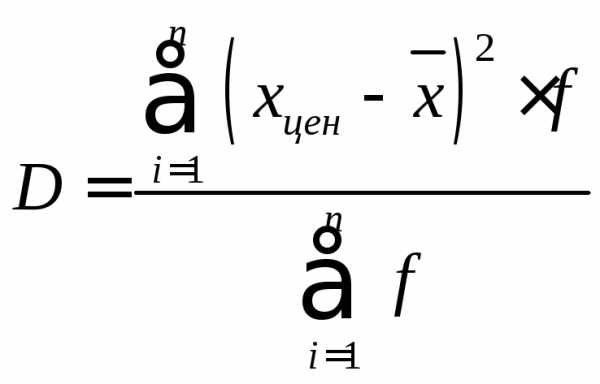
D = (672.12+155.5+353.89+553.25+1115.16)/
100=2853.92/100=28.54
Среднее квадратическое отклонение.
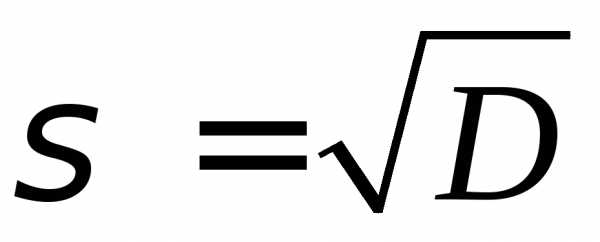
Дискретный вариационный ряд.
σ=√28.14=5.30
Интервальный вариационный ряд.
σ=√28.54=5.34
Коэффициент вариации.
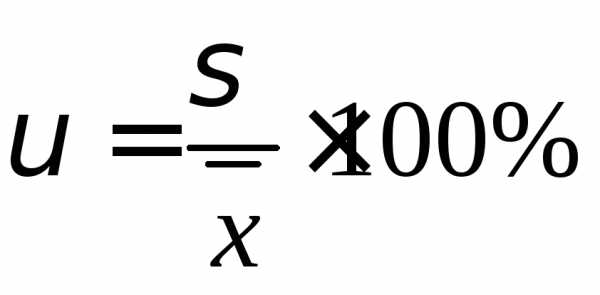
Дискретный вариационный ряд.
υ=(5.30/8.82)*100%=60.09%
Интервальный вариационный ряд.
υ=(5.34/8.82)*100%=60.54%
studfiles.net

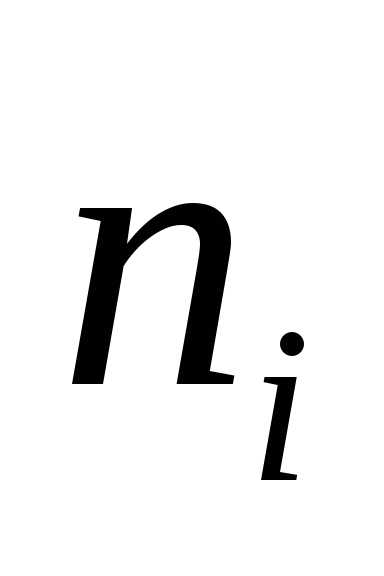 (частота)
(частота)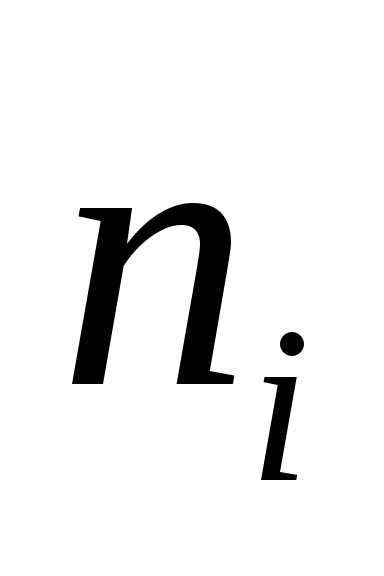 (частота)
(частота)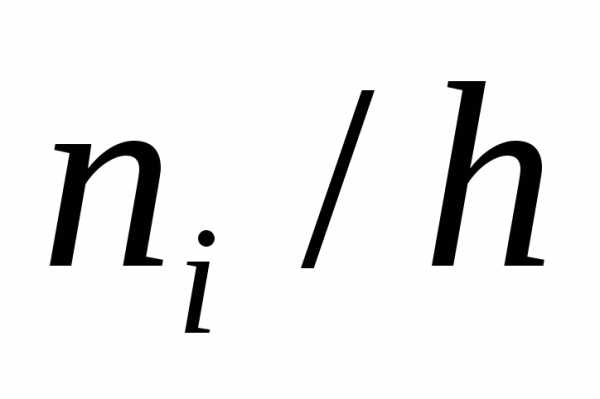
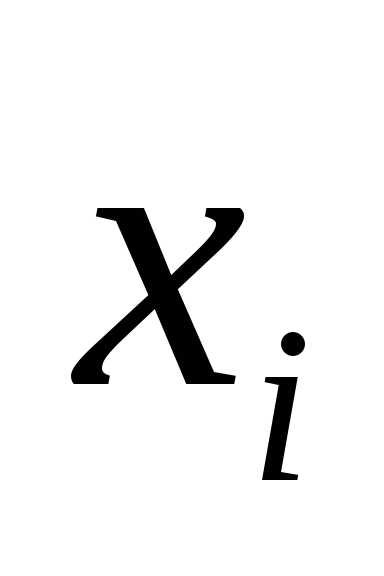 (середина интервала)
(середина интервала)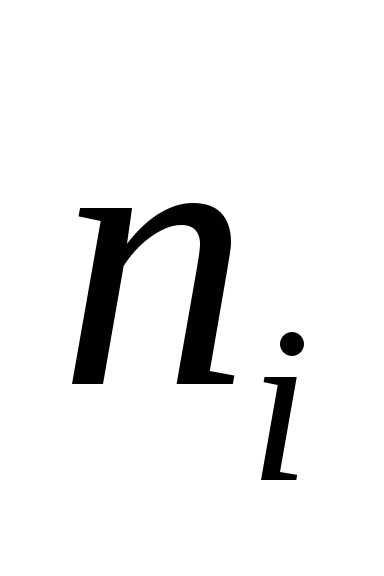 (частота)
(частота)