Решение интегралы определенные: Кусочно-заданная функция · Калькулятор Онлайн

Кусочно-заданная функция · Калькулятор Онлайн

Кусочно-заданная функция

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

при

На данной странице вы можете выполнить различные действия с кусочно-заданной функцией, а также для большинства сервисов — получить подробное решение.

• Производная кусочно-заданной функции
• Построить график
• Исследовать график
• Определённый интеграл
• Неопределённый интеграл от таких функций
• Предел кусочно-заданной
• Ряд Фурье (в примерах для нахождения ряда в основном используются кусочно-заданные функции)
• Ряд Тейлора

Сначала задайте соответствующую функцию.

Как задавать условия?

Приведём примеры, как задавать условия:

x≠0

x не равен нулю

x > pi

x больше, чем число Пи

-pi/2

x меньше или равно, чем Пи пополам, но нестрого больше, чем Пи пополам

true

означает «в любых других случаях»

Примеры

Для ряда Фурье

1 - x если -pi 
x если -2 
С параболой и модулем
8 - (x + 6)^2 если x = 5

Непрерывная функция

-5/x если x  -1

Функция с разрывом

x + 1 если x = 0

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Новости — Костромской автотранспортный колледж

Новости

Форма входа

Пароль

Запомнить меня

• Регистрация
• Забыли логин?
• Забыли пароль?

Версия для слабовидящих

Подробности

Опубликовано 24 Январь 2023

Важно! Важно помнить и знать свою историю! Оставаться благодарными за возможность жить!

С 23 января по 3 февраля 2023 года в России пройдёт ежегодная «Неделя памяти», посвящённая двум датам.

Подробнее…

Подробности

Опубликовано 30 Сентябрь 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее…

Подробности

Опубликовано 26 Сентябрь 2022

«С Днем среднего профессионального образования!» — такими теплыми словами впервые начнется праздничный концерт во Дворце творчества 01.10.2022 года. День среднего профессионального образования, объявленный Президентом страны 2 октября, должен коснуться каждого студента, преподавателя колледжа, мастера производственного обучения.

Подробнее…

Подробности

Опубликовано 29 Август 2022

График проведения 1 сентября 2022 г.

1 курс
11.30-12.00 — линейка
12.00-12.45 — классный час

2, 3, 4, 5 курс
8.40-9.40 — 1 пара
9.50-10.50 — 2 пара, согласно расписания
11.00-11.30 — классный час
11.30-12.00 — линейка

 

Подробности

Опубликовано 16 Август 2022

ОГБПОУ «Костромской автотранспортный колледж» продлевает прием документов на 2022-2023 учебный год по следующим образовательным программам:

Подробнее…

1. Кострома отмечает 78-ю годовщину образования Костромской области
2. Окончание учебного года в КАТК
3. Награждения участников IV Всероссийской летней Спартакиады «Юность России»
4. Свидетельства «Слесарь по ремонту автомобилей 1 разряда» вручены учащимся 8 и 9 классов
5. Фестиваль культур народов Костромской области

1.

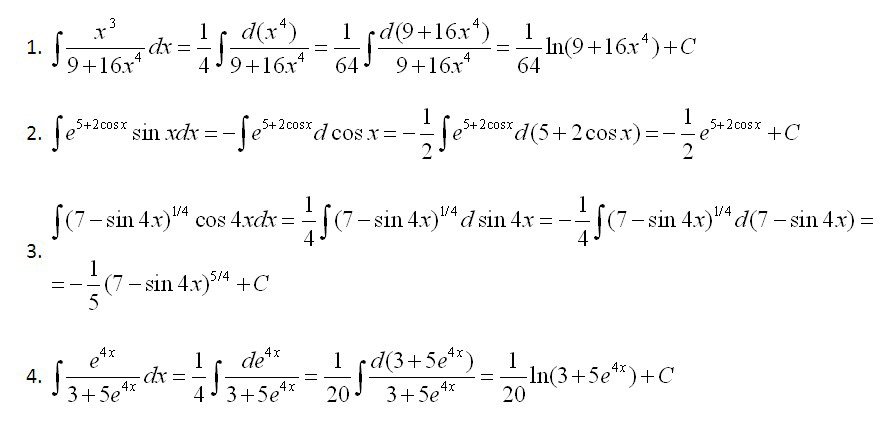1: Интегралы как решения — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

332

• Йиржи Лебл
• Университет штата Оклахома

ОДУ первого порядка представляет собой уравнение вида

\[\dfrac{dy}{dx}=f(x,y) \номер\]

или просто

\[y’=f(x,y) \номер\]

В общем, не существует простой формулы или процедуры, которой можно следовать, чтобы найти решение. В следующих нескольких лекциях мы рассмотрим частные случаи, когда решение получить несложно. В этом разделе предположим, что \(f\) является функцией только \(x\), то есть уравнение имеет вид

.

\[y’=f(x) \label{1. 1.1} \]

Мы могли бы просто проинтегрировать (антидифференцировать) обе части по \(x\).

\[\int y’ (x) dx = \int f(x) dx + C \nonumber \]

это

\[y(x)=\int f(x) dx + C \nonumber \]

Это \(y(x)\) на самом деле является общим решением. Итак, чтобы решить уравнение \(\ref{1.1.1}\), мы находим некоторую первообразную \(f(x)\), а затем добавляем произвольную константу, чтобы получить общее решение.

Сейчас самое время поговорить об обозначениях и терминологии исчисления. Учебники по математическому анализу мутят воду, говоря об интеграле прежде всего как о так называемом 9х f(t) dt + C \номер\]

Отсюда терминология «интегрировать», когда на самом деле мы можем иметь в виду «антидифференцировать». Интегрирование — это всего лишь один из способов вычисления первообразной (и этот способ работает всегда, см. следующие примеры). Интеграция определяется как площадь под графиком, это происходит только для вычисления первообразных. Ради согласованности мы будем продолжать использовать обозначение неопределенного интеграла, когда нам нужна первообразная, и вы всегда должны думать об определенном интеграле.

9{x_0} f(x) dx + y_0 = y_0\). Это!

Обратите внимание, что определенный интеграл и неопределенный интеграл (антидифференцирование) — совершенно разные звери. Определенный интеграл всегда дает число. Таким образом, уравнение \(\ref{1.1.2}\) представляет собой формулу, которую мы можем вставить в калькулятор или компьютер, и он будет рад рассчитать для нас определенные значения. Мы легко сможем построить решение и работать с ним, как и с любой другой функцией. Не так важно всегда находить замкнутую форму первообразной. 92} ds + 1. \nonumber \]

Решение

Вот хороший способ подшутить над своими друзьями, занимающимися исчислением во втором семестре. Скажите им найти решение в закрытой форме. Ха-ха-ха (плохая математическая шутка). Нельзя (в закрытом виде). Нет абсолютно ничего плохого в том, чтобы записать решение в виде определенного интеграла. Этот конкретный интеграл на самом деле очень важен в статистике.

Используя этот метод, мы также можем решать уравнения вида

\[y’ = f(y) \nonumber \]

Запишем уравнение в системе обозначений Лейбница.

\[\dfrac{dy}{dx} = f(y) \nonumber \]

Теперь мы используем теорему об обратной функции из исчисления, чтобы поменять местами \(x\) и \(y\), чтобы получить

\[\dfrac{dy}{dx} = \dfrac{1}{f(y)} \nonumber \]

То, что мы делаем, похоже на алгебру с \(dx\) и \(dy\). Заманчиво просто заняться алгеброй с \(dx\) и \(dy\), как если бы они были числами. И в этом случае это работает. Однако будьте осторожны, так как подобные расчеты могут привести к проблемам, особенно когда задействовано более одной независимой переменной. На данный момент мы можем просто интегрировать, 92} \nonumber \]

Интегрируем, чтобы получить

\[x = \dfrac{-1}{y} + C \nonumber \]

Находим \(y = \dfrac{1}{C-x} \). Таким образом, общее решение

\[y = \dfrac{1}{C-x} \,\ или\,\, y=0 \nonumber \]

Обратите внимание на особенности решения. Если например \(C=1\), то решение по мере приближения \(x=1\). См. рисунок \(\PageIndex{1}\). Как правило, по самому уравнению трудно сказать, как поведет себя решение. 2\) очень красивое и определено везде, но решение определено только на некотором интервале \((-\infty, C)\) или \((C, \infty)\) . Обычно, когда это происходит, мы рассматриваем только одно из них как решение. Например, если мы наложим условие \(y(0) = 1\), то решение будет \(y=\frac{1}{1-x}\), и мы будем рассматривать это решение только для \(x \) на интервале \((-\infty,1)\). На рисунке это левая часть графика. 92, \quad v(0) = 10 \nonumber \]

Как только мы найдем \(v\), мы можем проинтегрировать и найти \(x\).

---

Эта страница под названием 1.1: Интегралы как решения распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Йиржи Леблом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Йиржи Лебль

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. источник@https://www. jirka.org/diffyqs

Определение, правила, примеры и решение

Мы можем найти площадь под прямой на графике с помощью различных формул. Но задумывались ли вы когда-нибудь, как найти площадь под кривой? Потому что если да, не беспокойтесь, мы на одной волне.

Мы уже знаем, что можем вычислить наклон кривой путем дифференцирования. Теперь попробуем вычислить формулу площади под кривой.

Для лучшего понимания рассмотрите этот график.

 

Как можно рассчитать площадь под кривой от точки 0 до 3 на оси x и выше?

Согласно Риману, сумма площадей определенных прямоугольников под линией кривой дает приблизительную площадь под этой кривой. Что-то вроде этого:

 

Но этого недостаточно. Как насчет того, чтобы уменьшить ширину прямоугольных плит. И еще и еще. Может быть так:

 

Эта область будет относительно более точной, чем предыдущая. Но что, если… мы уменьшим его еще немного. Настолько, что почти ноль! Что-то щелкнуло в вашем сознании?

ДА, производные! Производные используются для расчета мгновенного наклона. Мы собираемся использовать эту концепцию, чтобы найти площадь под этой кривой. Это понятие называется интегралами.

Давайте узнаем, что такое интегралы? Каковы правила интегралов и как их решить?

Что такое интегралы?

Интегрирование — это процесс нахождения интегралов. Интегралы имеют множество применений, например, для нахождения объемов, массы и т. д. Но в этой статье мы обсудим площадь под кривой.

Определение интеграла:

«Если производная функции равна f’(x), то ее интеграл равен ∫f(x).dx + c».

Это можно объяснить на примере. Рассмотрим функцию и ее производную, т. е. f'(x) = 3. Но какова ее первообразная? Мы можем сделать некоторые предположения.

Если подумать, мы получим постоянный член как производную для функции с одним X. То есть:

= 3x

Итак, мы получаем исходную функцию 3x путем антидифференцирования.

Коэффициент интегрирования

Посмотрите на эти уравнения:

• 3x + 12
• 3x + 100

Производная всех этих уравнений также равна 3x . Итак, чтобы исправить любую ошибку, мы пишем:

= 3x + C        , где c может быть любым постоянным числом

Вот почему интеграл имеет все возможные первообразные этой функции.

Теперь, когда вы знаете, что такое интеграл, мы теперь изучим целочисленное представление.

Интегральная запись

У каждой операции есть свой оператор, символ. Для производных у нас есть обозначение d/dx. Точно так же для интегралов мы используем причудливые s .

∫ fx.dx + c

Интегралы и производные

Вы можете задаться вопросом: «Теперь я знаю, что такое интеграл, но как он связан с производными?».

Если быть точным, то первообразные (обратное дифференцирование) и неопределенные интегралы — это почти одно и то же. Но есть большая разница между определенными интегралами и первообразными.

Когда мы находим производные, мы уменьшаем разницу между двумя точками настолько, что она становится бесконечно малой. Но в интегралах мы делаем столько мелких деталей, что число этих достигает бесконечности.

Проще говоря, в производных мы применяем предел приблизительно нулевого значения, а в интегрировании применяем предел до бесконечности. Таким образом, мы можем сказать, что интегралы являются обратными производными.

Правила вычисления интегралов

Есть несколько правил, которые помогают решать интегралы так же, как мы используем правила дифференцирования. Правила интегралов очень похожи на правила, которые мы используем для решения производных.

Степенное правило

Когда функция возведена в некоторую степень, для интегрирования используется следующее правило:

∫ fx.dx = (xn+1)/n+1                     вытекает из правила мощности дифференциация. Давайте сначала докажем, что это правило является обратным степенному правилу дифференцирования.

Пример

Производная функции равна 6×2. Давайте пересмотрим процесс дифференциации и поступим наоборот.

• Из степени функции вычитается единица, поэтому, чтобы найти ее обратную, мы прибавляем единицу к степени, т.е. 6×2+1 = 6×3.
• Коэффициент такой же, как мощность, поэтому, чтобы обратить его, мы разделим на то же число, т.е. 6×3/3 = 2×3.

Итак, интеграл от 6×2 равен 2×3 (исходная функция). Чтобы проверить, равна ли производная 2×3 6×2, воспользуйтесь калькулятором производной.

Умножение на константу

Когда мы видим функцию, которая находится в умножении на некоторое постоянное число, мы применяем правило. Согласно этому правилу при интегрировании постоянный член выносится за интегральную запись.

∫k.fx dx =ck ∫fx dx

Пример                 

Функция f(y) = 6y ² + 12 лет. Вы видите постоянные числа 6 и 12. Возьмем 6 обычных.

= 6 ( y ² + 2y)

Применить интегрирование:

∫ 6y ² + 12y .dy = 6 ∫ y ² + 2y .dy    

Применение степенного правила:

=  6 ∫ у ² + 2у .dy 

=  6 { (у ²⁺¹ )/2+1 + 2у ¹⁺¹ /1+1 } 

=  6 { у ^{3 90 187 /3 + у 2 }}

= 2 года ³ + 6 лет ² + c

Правило суммы

Когда две функции добавляются, то при интеграции их можно интегрировать по отдельности, а затем добавить.

∫ (FX + GX) .dx = ∫ fx.dx + ∫ gx.dx

Пример

Найдите интеграл U ⁵ + 2U.

Решение:

  ∫u ⁵ + 2u.du = ∫u ⁵ .du + ∫2u.du

= (и ⁵⁺¹ / 5+1) + 2∫ у.ду

= u ⁶ /6 + 2u ¹⁺¹ /2

= u ⁶ /6 + u ² + c 9 0055

Правило разности

Аналогично сумме правило, когда функции находятся в вычитании, их можно интегрировать отдельно.

∫ (fx — gx).dx = ∫ fx.dx — ∫ gx.dx

Пример

Найдите интеграл от u ⁵ — 2u.

Решение:

  ∫u ⁵ + 2u.du = ∫u ⁵ .du — ∫2u.du

= (u ⁵⁺¹ / 5+1) — 2∫1u.du

= u ⁶ /6 — 2u ¹⁺¹ /2

= u ⁶ /6 — u ² + c

Из приведенного выше примера видно, что единственная разница между суммой и правило различия символ знака.

Интегрирование по частям

Это обратное правило дифференцирования произведения. Выведем его формулу.

Правило продукта:

(uv)’ = uv’ + u’v

Применить интегрирование с обеих сторон.

∫(uv)’.dx = ∫ uv’.dx + ∫ u’v.dx

uv = ∫ uv’.dx + ∫ u’v.dx

∫ uv’.dx = uv — ∫ u ‘v.dx

Пример

Вычислить ∫ x.cosx .dx

Решение:

Определить u и v’.

u = x  

v’ = cosx

Найдите значения u’ и v.

Для u’ найдите производную от u.

u = x

u’ = 1

Для v найдите интеграл от v’.

v = cosx

∫v.dx =  ∫ cosx.dx = sinx

Решить.

∫xcosx.dx = x.sinx —  ∫1.sinx.dx                

= x.sinx — cosx 900 32

Добавить константу.

= x.sinx — cosx + c

Правило подстановки

Это правило также известно как правило обратной цепочки . Это правило применяется в особых случаях. Иногда функцию можно настроить таким образом, чтобы можно было применить правило подстановки.

Правило:

∫ f((gx)).g’(x).dx = ∫f(u).du 

Чтобы понять эту формулу, посмотрите на задействованные операции.

g'(x) = d/dx g(x)   

Для удобства пусть

u = g(x)   тогда    du = g'(x)       

Следует отметить, что эта формула применима только когда в интегрируемой функции есть и и, и и’.

Пример

Найдите интеграл от (x + 1) ² .

Решение:

Понимая функцию, мы видим, что производная от x + 1 равна 1 . Это означает, что мы можем умножить 1, чтобы использовать правило подстановки.

∫ (x + 1) ² .dx = ∫ (x + 1) ² .1dx

Теперь у нас есть u и u ’, которые являются x + 1 и 1 соответственно. Используя формулу:

∫(x + 1) ² .1dx знак равно ∫ ты ² . du

= ∫ u ²⁺¹ / 3

= ∫u ³ /3

Возврат значения u:

= ∫(x+3) ³ / 3

Некоторые другие Правила

Функция	Интеграл
∫cos(x).dx 9003 2	sinx + c
∫sin(x).dx	-cosx + с
∫sec2(x).dx	tanx + c
∫(1/x). d х	ln|x| + c
∫ex . dx	ex + c
∫ln(x).dx	x ln(x) — x + c 9070 7

Типы интегралов: неопределенные и определенные интегралы

Существует два типа интегралов. Оба решаются по-разному и имеют разные приложения.

Неопределенные интегралы

Это обратная производная. Он вычисляет всю площадь под графиком кривой линии. Все примеры, которые вы видели в этой статье, относятся к неопределенной интеграции.

В этих интегралах нижняя, ни верхняя границы не применяются. Более того, в конце добавляется константа c , чтобы указать, что ответ включает в себя все возможные первообразные функции.

Давайте рассмотрим пример пула. Считайте, что вы наполняете бассейн с помощью водопроводной трубы. Поток воды время от времени меняется по какой-то причине.

Теперь, если скорость потока была постоянной, было бы легко вычислить объем воды в бассейне через некоторое время t .

 

Но проблема в том, что расход постоянно меняется и его нельзя измерить только в одной точке. Необходимо найти скорость потока в каждой точке, чтобы знать точный объем.

 

Для этого воспользуемся неопределенными интегралами. Скорость потока рассчитывается по производным и показывает, с какой скоростью наполняется бассейн в данный момент времени.0054 т .

d/d (x ² ) = 2x  (расход)

Интегрирование показывает, каков объем воды в бассейне через время t .

∫2x.dx = x ²   (объем)

Это также подтверждает тот факт, что интегралы являются первообразными.

А что, если в бассейне уже было немного воды c ? Это означает, что наш расчетный объем не является «чистым объемом». Чтобы получить правильный ответ, добавьте c в ответ.

= x ² + c

Определенные интегралы

Определенный интеграл находит объем за определенный интервал времени.