Решение квадратных уравнений примеры: 8.2.2. Решение полных квадратных уравнений.

alexxlab / / Разное
2 +b*x+c. Его еще называют квадратным трехчленом.

», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.

Содержание

Что называют квадратным уравнением

Важно!

Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.

Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.

Примеры квадратных уравнений

  • 5x 2 − 14x + 17 = 0
  • −x 2 + x + = 0
  • x 2 + 0,25x = 0
  • x 2 − 8 = 0

Важно! Общий вид квадратного уравнения выглядит так:

A x 2 + b x + c = 0

«a », «b » и «c » — заданные числа.

  • «a » — первый или старший коэффициент;
  • «b » — второй коэффициент;
  • «c » — свободный член.

Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».

Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.

5x 2 − 14x + 17 = 0 −7x 2 − 13x + 8 = 0 −x 2 + x + = 0 x 2 + 0,25x = 0
Уравнение Коэффициенты
  • a = 5
  • b = −14
  • с = 17
  • a = −7
  • b = −13
  • с = 8
  • a = −1
  • b = 1
  • с =
  • a = 1
  • b = 0,25
  • с = 0
x 2 − 8 = 0
  • a = 1
  • b = 0
  • с = −8

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .

Запомните!

Чтобы решить квадратное уравнение нужно:

  • привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
  • использовать формулу для корней:

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

X 2 − 3x − 4 = 0

Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .

Определим коэффициенты «a », «b » и «c » для этого уравнения.

x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =

С её помощью решается любое квадратное уравнение.

В формуле «x 1;2 = » часто заменяют подкоренное выражение
«b 2 − 4ac » на букву «D » и называют дискриминантом . Более подробно понятие дискриминанта рассматривается в уроке «Что такое дискриминант ».

Рассмотрим другой пример квадратного уравнения.

x 2 + 9 + x = 7x

В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».

X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0

Теперь можно использовать формулу для корней.

X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =

x = 3
Ответ: x = 3

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.

Видеоурок 2: Решение квадратных уравнений

Лекция: Квадратные уравнения

Уравнение

Уравнение — это некое равенство, в выражениях которого имеется переменная.

Решить уравнение — значит найти такое число вместо переменной, которое будет приводить его в верное равенство.

Уравнение может иметь одно решение или несколько, или же не иметь его вообще.

Для решения любого уравнения его следует максимально упростить до вида:

Линейное: a*x = b;

Квадратное: a*x 2 + b*x + c = 0.

То есть любые уравнение перед решением нужно преобразовать до стандартного вида.

Любое уравнение можно решить двумя способами: аналитическим и графическим.

На графике решением уравнения считаются точки, в которых график пересекает ось ОХ.

Квадратные уравнения

Уравнение можно назвать квадратным, если при упрощении оно приобретает вид:

a*x 2 + b*x + c = 0.

При этом a, b, c являются коэффициентами уравнения, отличающиеся от нуля. А «х» — корень уравнения. Считается, что квадратное уравнение имеет два корня или могут не иметь решения вообще. Полученные корни могут быть одинаковыми.

«а» — коэффициент, который стоит перед корнем в квадрате.

«b» — стоит перед неизвестной в первой степени.

«с» — свободный член уравнения.

Если, например, мы имеем уравнение вида:

2х 2 -5х+3=0

В нем «2» — это коэффициент при старшем члене уравнения, «-5» — второй коэффициент, а «3» — свободный член.

Решение квадратного уравнения

Существует огромное множество способов решения квадратного уравнения. Однако, в школьном курсе математики изучается решение по теореме Виета, а также с помощью дискриминанта.

Решение по дискриминанту:

При решении с помощью данного метода необходимо вычислить дискриминант по формуле:

Если при вычислениях Вы получили, что дискриминант меньше нуля, это значит, что данное уравнение не имеет решений.

Если дискриминант равен нулю, то уравнение имеет два одинаковых решения. В таком случае многочлен можно свернуть по формуле сокращенного умножения в квадрат суммы или разности. После чего решить его, как линейное уравнение. Или воспользоваться формулой:

Если же дискриминант больше нуля, то необходимо воспользоваться следующим методом:

Теорема Виета

Если уравнение приведенное, то есть коэффициент при старшем члене равен единице, то можно воспользоваться теоремой Виета .

Итак, предположим, что уравнение имеет вид:

Корни уравнения находятся следующим образом:

Неполное квадратное уравнение

Существует несколько вариантов получения неполного квадратного уравнения, вид которых зависит от наличия коэффициентов.

1.

Если второй и третий коэффициент равен нулю (b = 0, с = 0) , то квадратное уравнение будет иметь вид:

Данное уравнение будет иметь единственное решение. Равенство будет верным только в том случае, когда в качестве решения уравнения будет ноль.

В данной статье мы рассмотрим решение неполных квадратных уравнений.

Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах 2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным . Как мы видим коэффициент при х 2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.

Неполные квадратные уравнения бывают трех видов :

1) Если b = 0, с ≠ 0, то ах 2 + с = 0;

2) Если b ≠ 0, с = 0, то ах 2 + bх = 0;

3) Если b= 0, с = 0, то ах 2 = 0.

  • Давайте разберемся как решаются уравнения вида ах 2 + с = 0.

Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим

ах 2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х 2 = ‒с/а.

Если ‒с/а > 0 , то уравнение имеет два корня

x = ±√(–c/a) .

Если же ‒c/a

Давайте попробуем разобраться на примерах, как решать такие уравнения.

Пример 1 . Решите уравнение 2х 2 ‒ 32 = 0.

Ответ: х 1 = ‒ 4, х 2 = 4.

Пример 2 . Решите уравнение 2х 2 + 8 = 0.

Ответ: уравнение решений не имеет.

  • Разберемся как же решаются уравнения вида ах 2 + bх = 0.

Чтобы решить уравнение ах 2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах + b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах + b = 0. Решая уравнение ах + b = 0, получим ах = ‒ b, откуда х = ‒ b/a. Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a.

Посмотрите как выглядит на схеме решение уравнений этого вида.

Закрепим наши знания на конкретном примере.

Пример 3 . Решить уравнение 3х 2 ‒ 12х = 0.

х(3х ‒ 12) = 0

х= 0 или 3х – 12 = 0

Ответ: х 1 = 0, х 2 = 4.

  • Уравнения третьего вида ах 2 = 0 решаются очень просто.

Если ах 2 = 0, то х 2 = 0. Уравнение имеет два равных корня х 1 = 0, х 2 = 0.

Для наглядности рассмотрим схему.

Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.

Пример 4. Решить уравнение 7х 2 = 0.

Ответ: х 1, 2 = 0.

Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.

Пример 5. Решить уравнение

Умножим обе части уравнения на общий знаменатель, то есть на 30

Сократим

5(5х 2 + 9) – 6(4х 2 – 9) = 90.

Раскроем скобки

25х 2 + 45 – 24х 2 + 54 = 90.

Приведем подобные

Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный

Ответ: корней нет.

Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.

Если у вас появились вопросы по данной теме, записывайтесь на мои уроки , мы вместе решим возникшие проблемы.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

  1. Не имеют корней;
  2. Имеют ровно один корень;
  3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

  1. Если D
  2. Если D = 0, есть ровно один корень;
  3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

  1. x 2 − 8x + 12 = 0;
  2. 5x 2 + 3x + 7 = 0;
  3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом.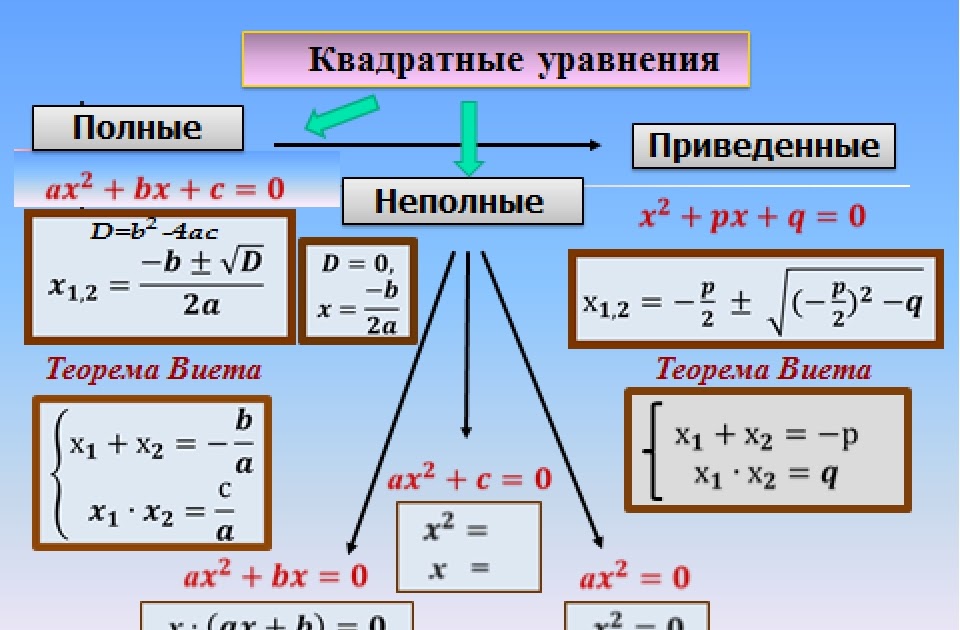 Наконец, если D

  1. x 2 − 2x − 3 = 0;
  2. 15 − 2x − x 2 = 0;
  3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

  1. x 2 + 9x = 0;
  2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

  1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
  2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

  1. x 2 − 7x = 0;
  2. 5x 2 + 30 = 0;
  3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Решение квадратных уравнений различными способами | План-конспект урока по алгебре (8 класс) на тему:

РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ РАЗЛИЧНЫМИ СПОСОБАМИ.

Обоснование выбора темы урока.

           С примерами применения различных формул учащиеся неоднократно встречаются как на уроках алгебры, геометрии, так и на других уроках.   Накопленный опыт позволяет восьмиклассникам довольно успешно применять для решения уравнений новые формулы, устанавливающие связь между коэффициентами и корнями квадратного уравнения.  

   Задача учителя при изучении темы «Квадратные уравнения» — добиться безусловного усвоения её каждым учащимся, поскольку умение решать квадратные уравнения относится к числу важнейших умений в курсе алгебры  8 класса. Без этого умения учащиеся не смогут усваивать материал следующих тем. Кроме того, умение решать квадратные уравнения необходимо и при решении тригонометрических, логарифмических, иррациональных, показательных уравнений и неравенств в курсе «Алгебра и начала анализа».

        Данный урок является уроком обобщения и систематизации знаний. В ходе его учащиеся предоставляют отчеты по исследовательским работам, которые были проведены учащимися в течение  двух недель; выполняют исследовательскую работу на наличие и величину корней квадратного уравнения в случае, когда сумма коэффициентов равна нулю, т.е. а+в+с=0; устно решают задания. На данном уроке проводится письменный и устный контроль знаний учащихся, заполняется специальная таблица по итогам прослушанных отчетов.         

Предметные знания

Обогащение  методологического аппарата   правомерностью использования новых формул для решения квадратных уравнений.

Предметные умения

  • Учить распознавать уравнения, сумма коэффициентов которых равна нулю.
  • Учить находить корни уравнений с помощью новых формул.

Межпредметные умения (ОУУН)

  • Учить выделять признаки объекта и на их основе проводить сравнение.
  • Учить выделять по общности признаков группы объектов.                                            
  • Учить выделять классификационный критерий на основе обобщения.
  • Учить формулировать на основе признаков вывод.
  • Учить выполнять умозаключения.

Развитие речи

  • Учить грамотно читать тексты, записанные на математическом языке.
  • Учить грамотно записывать фразы естественного языка с математическим содержанием на математическом языке.
  • Учить грамматически и логически правильно выражать свои мысли средствами как естественного, так и математического языков.

Развитие внимания

  • Концентрации.
  • Переключаемости.
  • Мобильности.

Развитие познавательного интереса

Развитие интереса к предмету и познавательного интереса через показ красоты и простоты нахождения корней квадратного уравнения новым способом.

Развитие личностных качеств

  • Целеустремлённости через потребности ставить перед собой цели и достигать их.
  • Чувства собственного достоинства через формирования адекватной самооценки у учащихся.

Формирование активной жизненной позиции

  • Формирование собственной точки зрения и умения её обосновывать.
  • Формирование собственных способов действий.

Тема: Решение квадратных уравнений. Способы решения.

Цель: 1.Актуализировать знания учащихся по изучаемой теме «Решение квадратных    

            уравнений».

           2.Содействовать формированию познавательной деятельности учащихся в

            обобщение способов решения квадратных уравнений.

           3.Способствовать формированию умения выделить главное в изучаемой теме,

            наиболее общее и существенное в способах решения квадратных уравнений.

           4.Содействовать умению осуществлять самоконтроль и самокоррекцию.

Задачи урока: 1.Обобщить изученные способы решения квадратных уравнений.

                         2.Систематизировать знания учащихся в умении решать квадратные

                         уравнения разными способами.

                         3.Проверить полученные знания средствами информатизации и

                          осуществить самоконтроль.

Тип урока: Урок обобщения и систематизации знаний, умений, навыков средствами

              информатизации.

 1. Организационный момент:

  1. Объявление темы и целей урока.

 Сегодня на уроке мы обобщим и систематизируем знания по теме « Квадратные уравнения и способы решения»

Задачи урока:

Информация о квадратных уравнениях:

Квадратные уравнения – это основа, фундамент, на котором покоится величественное здание – алгебра. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных уравнений, с которыми вам предстоит познакомиться в старших классах.

        На уроке мы с вами поговорим лишь о некоторых способах решения квадратных уравнений.

2. Актуализация знаний учащихся.

   

  1. Обобщающая работа по теме « Квадратные уравнения» Соломатина Алена.
  1. Кроссворд как проверка теоретических знаний учащихся

КВАДРАТНОЕ

                                          ПРИВИДЕННОЕ

                                  РАВНОСИЛЬНОЕ

                                               КОЭФФИЦИЕНТ

                                          КОРЕНЬ

                              УРАВНЕНИЕ

                                    АРИФМЕТИЧЕСКИЙ

                                            ДИОФАНТ

                                  НЕПОЛНОЕ

                                            РАЗЛИЧИТЕЛЬ

                               СВОБОДНЫЙ

                                       ВИЕТ

4. Тест как результат обобщения теоретических знаний, полученных из сообщения и устного опроса.

  1. Какое из данных уравнений является квадратным?

А) 3х2 – 4х = 6х3    б) 6х – 4 = 5 – 3х    в) 4х2 – 3х + 2 = 0      г) 4/х = х + 1

  1. Назовите коэффициенты квадратного уравнения -4х2 + х -5 = 0

           А) а=4   в=1   с=5    б) а= -4   в = 1  с= 5    в) а=-4  в =х  с= -5     г) а=-4  в=1  с= -5

  1. Уравнение 2х2 – 4х +6 = 0 сделайте приведенным:

А) х2 – 4х + 6 = 0    б) х2 – 2х + 3 = 0  в) –х2 + 4х – 6 = 0

           4.   Найдите дискриминант квадратного уравнения 2х2 -4х +1 = 0

           а) Д=24   б) Д=-8   в)  Д=8    г) Д=16

     

           5.   Определите количество корней квадратного уравнения из номера 4

            а) 2 корня    б) 1 корень    в) нет корней

           6.   Из данных уравнений выберите неполные квадратные уравнения

            а) х2 – 4х + 3 = 0  б) х2 – 5х= 0    в) х2 = 0     г) 2х – 3х2 +5 = 0

           

Ответы:              1     2    3     4     5    6

                           В     г     б     в     а    б, в

 

        5. Исследовательская работа на тему « КАК ЗАВИСЯТ ЗНАЧЕНИЯ КОРНЕЙ КВАДРАТНОГО УРАВНЕНИЯ ОТ ВЫБОРА СПОСОБА РЕШЕНИЯ ГРАФИЧЕСКИ» (Миронов Илья)

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 4х+3=0

Ответы:  а) 0 и 4/3  б) 0    2) 3 и 2

8. Исследовательская работа на наличие и величину корней уравнения в случае, когда а+в+с=0.

  •   Упражнение 1.. Даны квадратные уравнения  
  • 1) х2-5х+1=0;    
  • 2) 9х2-6х+10=0;
  • 3) х2+2х-2=0;    
  • 4) х2-3х-1=0;    
  • 5) х2+2х-3=0;      
  • 6) 5х2-8х+3=0;        

Найти сумму коэффициентов этих уравнений. ( ПРЕЗЕНТАЦИЯ « СВОЙСТВО КОРНЕЙ УРАВНЕНИЯ»)

Сумма коэффициентов

  • 1-5+1=-3.
  • 9-6+10=13.
  • 1+2-2=1.
  • 1-3-1=-3.
  • 1+2-3=0.
  •  5-8+3=0.

Упражнение 2.  Даны 4 уравнения  х2+4х-5=0    3х2+3х-6=0   5х2-8х+3=0  -7х2+2х+5=0

Найти сумму коэффициентов и решить одно из них.  Сделать вывод о величине корней.

ВЫВОД: Если сумма коэффициентов  квадратного уравнения равна 0, то

               Один из корней равен 1, а другой вычисляется по формуле  х= с / а

ДОМАШНЕЕ ЗАДАНИЕ: исследовать корни квадратного уравнения в случае, когда

а —  в + с = 0.

Доп. Задание:

         

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

7. Самостоятельная работа

1) решите уравнение алгебраически   а) 3х2 – 4 х=0  б) 6х2=0

2) Решите уравнение графически  х2 – 5х+6=0

Раздел 2.1: Решение квадратных уравнений

Результаты обучения

К концу этого раздела вы сможете:

  • Факторизировать квадратное уравнение для его решения.
  • Используйте свойство квадратного корня для решения квадратного уравнения.
  • Используйте теорему Пифагора и свойство квадратного корня, чтобы найти неизвестную длину стороны прямоугольного треугольника.
  • Заполните квадрат, чтобы решить квадратное уравнение.
  • Используйте квадратную формулу для решения квадратного уравнения.
  • Используйте дискриминант для определения количества и типа решений квадратного уравнения.

Левый компьютерный монитор на изображении ниже — это 23,6-дюймовая модель, а правый — 27-дюймовая модель. Пропорционально мониторы очень похожи. Если пространство ограничено и нам нужен максимально большой монитор, как нам решить, какой из них выбрать? В этом разделе мы узнаем, как решать такие проблемы, используя четыре различных метода. 9{2}-4=0[/latex] — квадратные уравнения. Они бесчисленным образом используются в инженерии, архитектуре, финансах, биологических науках и, конечно же, в математике.

Часто самым простым методом решения квадратного уравнения является факторизация . Факторинг означает нахождение выражений, которые можно перемножить, чтобы получить выражение на одной стороне уравнения.

Если квадратное уравнение можно разложить на множители, оно записывается как произведение линейных членов. Решение факторингом зависит от свойства нулевого произведения, которое гласит, что если [латекс]а\cdot b=0[/латекс], то [латекс]а=0[/латекс] или [латекс]b=0[/латекс] , где a и b — действительные числа или алгебраические выражения. Другими словами, если произведение двух чисел или двух выражений равно нулю, то одно из чисел или одно из выражений должно быть равно нулю, потому что ноль, умноженный на что-либо, равен нулю.

Умножение коэффициентов расширяет уравнение до строки членов, разделенных знаками плюс или минус. Таким образом, в этом смысле операция умножения отменяет операцию факторизации. Например, разложите факторизованное выражение [латекс]\влево(х — 2\вправо)\влево(х+3\вправо)[/латекс], перемножив два множителя. 9{2}+x — 6=0[/latex] имеет стандартную форму.

Мы можем использовать свойство нулевого произведения для решения квадратных уравнений, в которых мы сначала должны вынести наибольший общий делитель (НОД), а также для уравнений, которые имеют специальные формулы факторизации, такие как разность квадратов, оба из которых мы увидим позже в этом разделе.

Общее примечание: свойство нулевого произведения и квадратные уравнения текст{ или }b=0[/латекс], 9{2}[/latex], равно 1. У нас есть один метод факторизации квадратных уравнений в этой форме.

Как: Дано квадратное уравнение со старшим коэффициентом 1, разложить его на множители

  1. Найдите два числа, произведение которых равно c и сумма которых равна b .
  2. Используйте эти числа для записи двух множителей вида [латекс]\влево(х+к\вправо)\текст{ или }\влево(х-к\вправо)[/латекс], где k — одно из найденных чисел на шаге 1. {2}+2х+3х+3[/латекс], а затем разложим каждую часть выражения, чтобы получить [латекс]2х\влево(х+1\). вправо)+3\влево(x+1\вправо)[/латекс]. Затем мы извлекаем GCF [латекс]\влево(х+1\вправо)[/латекс], чтобы найти факторизованное выражение. 9\circ [/latex] угол, а [latex]c[/latex] относится к гипотенузе. Он имеет неизмеримое применение в архитектуре, технике, естественных науках, геометрии, тригонометрии и алгебре, а также в повседневных приложениях.

    Мы используем теорему Пифагора, чтобы найти длину одной стороны треугольника, зная длины двух других. Поскольку каждое из слагаемых в теореме возводится в квадрат, когда мы находим сторону треугольника, у нас получается квадратное уравнение. Мы можем использовать методы решения квадратных уравнений, которые мы изучили в этом разделе, чтобы найти недостающую сторону. 9{\ circ }[/latex] угол, а [latex]c[/latex] относится к гипотенузе.

    Пример 5. Нахождение длины недостающей стороны прямоугольного треугольника

    Найдите длину недостающей стороны прямоугольного треугольника.

    Показать раствор

    Попробуйте

    Используйте теорему Пифагора, чтобы решить задачу о прямоугольном треугольнике: Катет a измеряет 4 единицы, катет b измеряет 3 единицы. Найдите длину гипотенузы.

    Показать раствор

    https://ohm.lumenlearning.com/multiembedq.php?id=48710&theme=oea&iframe_resize_id=mom5

    Заполнение квадратной и квадратной формул

    Не все квадратные уравнения можно разложить на множители или решить в исходной форме с помощью свойство квадратного корня. В этих случаях мы можем использовать метод решения квадратного уравнения , известного как , дополняющего квадрат . Используя этот метод, мы добавляем или вычитаем члены с обеих сторон уравнения, пока у нас не получится идеальный квадратный трехчлен с одной стороны от знака равенства. Затем мы применяем свойство квадратного корня. Чтобы завершить квадрат, старший коэффициент, 9{2}-6x=13[/латекс].

    Показать раствор

    https://ohm.lumenlearning.com/multiembedq.php?id=1384&theme=oea&iframe_resize_id=mom1

    https://ohm.lumenlearning.com/multiembedq.php?id=79619&theme=oea&iframe_resize_id=mom2

    Использование Квадратная формула

    Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы , которая решит все квадратные уравнения. Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку при подстановке значений в формулу. Будьте внимательны при подстановке и используйте круглые скобки при вставке отрицательного числа. 9{2}+3x — 2=0[/латекс].

    Показать раствор

    https://ohm.lumenlearning.com/multiembedq.php?id=4014&theme=oea&iframe_resize_id=mom3

    https://ohm.lumenlearning.com/multiembedq.php?id=35639&theme=oea&iframe_resize_id=mom4

    Дискриминант

    Квадратная формула не только порождает решения квадратного уравнения, но и сообщает нам о характере решений, когда мы рассматриваем дискриминант или выражение под радикалом, [латекс]{b}^{2 }-4ac[/латекс]. Дискриминант говорит нам, являются ли решения действительными числами или комплексными числами, а также сколько решений каждого типа следует ожидать. В таблице ниже значение дискриминанта связано с решениями квадратного уравнения. 9{2}-10x+15=0[/латекс]

Показать решение

Попробуйте

https://ohm.lumenlearning.com/multiembedq.php?id=35145&theme=oea&iframe_resize_id=mom6

Основные понятия

  • Многие квадратные уравнения можно решить с помощью факторизации, если уравнение имеет старший коэффициент 1 или если уравнение представляет собой разность квадратов. Затем свойство нулевого фактора используется для поиска решений.
  • Многие квадратные уравнения со старшим коэффициентом, отличным от 1, могут быть решены путем факторизации с использованием метода группировки.
  • Другим методом решения квадратичных уравнений является свойство квадратного корня. Переменная возводится в квадрат. Мы выделяем квадрат члена и берем квадратный корень из обеих частей уравнения. Решение даст положительное и отрицательное решение.
  • Завершение квадрата — это метод решения квадратных уравнений, когда уравнение нельзя разложить на множители.
  • Очень надежным методом решения квадратных уравнений является формула квадратного уравнения, основанная на коэффициентах и ​​постоянном члене уравнения.
  • Дискриминант используется для указания характера решений, которые даст квадратное уравнение: действительные или комплексные, рациональные или иррациональные, а также их количество.
  • Теорема Пифагора, одна из самых известных теорем в истории, используется для решения задач о прямоугольных треугольниках и имеет приложения во многих областях. Чтобы найти длину одной стороны прямоугольного треугольника, нужно решить квадратное уравнение.

Глоссарий

заполнение квадрата
процесс решения квадратных уравнений, в котором члены добавляются или вычитаются из обеих частей уравнения, чтобы сделать одну сторону правильным квадратом
дискриминант
выражение под корнем в квадратной формуле, указывающее на природу решений, действительных или комплексных, рациональных или иррациональных, одинарных или двойных корней.
Теорема Пифагора
теорема, устанавливающая соотношение между длинами сторон прямоугольного треугольника, используемая для решения задач прямоугольного треугольника 9{2}[/latex] член изолирован, так что квадратный корень из обеих частей уравнения можно взять для решения для x
свойство нулевого продукта
свойство, которое формально утверждает, что умножение на ноль равно нулю, так что каждый множитель квадратного уравнения может быть установлен равным нулю для решения уравнений

 

Раздел 2.1 Домашнее задание Упражнения

1. Как распознать квадратное уравнение?

9{2}+280x-1000[/latex], где [latex]x[/latex] — количество товаров, проданных на аукционе, а [latex]p[/latex] — прибыль, полученная компанией, проводившей аукцион. . Сколько пунктов решения сделает эту прибыль максимальной? Решите это, нарисовав выражение в графической утилите и найдя максимум, используя 2nd CALC max . {2}-0,02А+120[/латекс]. Найдите возраст с точностью до года человека, у которого нормальное артериальное давление равно 125 мм рт. 9{2} + bx + c = 0$, где $a$, $b$, $c$ — вещественные числа и $a \ne 0$. Квадратные уравнения имеют два нуля или корня, которые могут быть действительными числами, мнимыми числами или и тем, и другим.

Существуют различные методы решения квадратных уравнений. Наиболее популярным методом является решение квадратных уравнений методом факторизации. Давайте разберемся с этими различными методами решения квадратных уравнений на примерах.

Методы решения квадратных уравнений

Решение уравнения — это процесс нахождения нулей (или корней) уравнения. Нули (или корни) также известны как решения уравнения. Это значения переменной, удовлетворяющей уравнению.

Поскольку квадратное уравнение является уравнением степени $2$, оно может иметь максимум $2$ действительных корней, т. е. квадратное уравнение может иметь любой из следующих

  • нулевой действительный корень
  • один действительный корень (или два равных действительных корня)
  • два действительных корня (или два неравных действительных корня)

Примечание: Термины «нет действительного корня» или «один действительный корень» не означают, что квадратное уравнение может иметь корни $0$ или $1$. Квадратное уравнение всегда имеет $2$ корней, где

  • оба настоящие
  • один реальный и один воображаемый
  • оба мнимые

Существуют разные способы решения квадратных уравнений. Наиболее распространенные методы:

  • Решение квадратных уравнений с помощью графика
  • Решение квадратных уравнений методом факторизации
  • Решение квадратных уравнений путем заполнения квадрата
  • Решение квадратных уравнений по квадратной формуле

Помимо этих методов, существуют и другие методы, которые используются только в особых случаях (когда в квадратном уравнении отсутствуют члены), которые также обсуждаются в следующих разделах.

СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:

Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.

Решение квадратных уравнений с помощью графика

$x$-пересечения уравнения – это точки, в которых его кривая пересекает ось $x$. {2} + bx + c$ 9{2} + 10  = 7x$ означает, что $4$ не имеет действительных корней.

Решение квадратных уравнений методом факторинга

Решение квадратных уравнений методом факторизации — один из популярных методов решения квадратных уравнений. Это этапы решения квадратных уравнений методом факторинга.

Шаг 1: Приведите уравнение к стандартной форме. т. е. получить все члены с одной стороны (обычно с левой стороны) уравнения так, что другая сторона равна $0$

Шаг 2: 9{2} = \frac {5}{2}$

Извлечение квадратного корня из обеих сторон

$=>x + 2 = \pm \sqrt{\frac {5}{2}}$

$=>x + 2 = \pm \frac{\sqrt{5}}{\sqrt{2}}$

$=>x + 2 = \pm \frac{\sqrt{10}}{2}$

$=>x = -2 \pm \frac{\sqrt{10}}{2}$

$=>x = -2 + \frac{\sqrt{10}}{2}$, $=>x = -2 — \frac{\sqrt{10}}{2}$

$=> x = \frac{-4 + \sqrt{10}}{2}$, $=> x = \frac{-4 – \sqrt{10}}{2}$

Решение квадратных уравнений по квадратичной формуле

Как видно из вышеизложенного, другие методы решения квадратных уравнений имеют некоторые ограничения, такие как метод факторизации полезен только тогда, когда квадратное выражение может быть факторизовано, метод построения графика полезен только тогда, когда квадратное уравнение имеет действительные корни и т. {2} + dx + e = 0$. Степень таких уравнений равна $4$. 9{2} + 12x + 7$

Часто задаваемые вопросы

В чем смысл решения квадратных уравнений?

Решение квадратных уравнений означает нахождение их решений или корней. т. е. это процесс нахождения значений переменной, удовлетворяющих уравнению.

Какие существуют четыре способа решения квадратных уравнений?

Четыре способа решения квадратных уравнений:
a) Решение квадратных уравнений путем построения графика
b) Решение квадратных уравнений путем факторизации
в) Решение квадратных уравнений путем заполнения квадрата
г) Решение квадратных уравнений по квадратной формуле

Какие способы решения квадратных уравнений наиболее популярны?

Существуют разные способы решения квадратных уравнений. Но самыми популярными способами являются «решение квадратных уравнений факторингом» и «решение квадратных уравнений по квадратной формуле».

Заключение

Решение квадратных уравнений означает нахождение их решений или корней.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *