Решение матриц онлайн методом жордана гаусса: Метод Жордана-Гаусса онлайн

Содержание

Метод Жордана-Гаусса

Определение 1

Метод Жордана-Гаусса – это метод решения линейных уравнений путём полного исключения неизвестных. Данный метод является модификацией метода Гаусса, только в случае метода Жордана-Гаусса элементарные преобразования проводятся дальше.

История возникновения метода

Исторически метод Гаусса возник достаточно давно. Решение систем уравнений подобным способом было изложено ещё в древнем китайском математическом трактате под названием “Математика в девяти книгах”, представляющим собой разрозненное собрание решений различных прикладных математических задач.

Некоторые главы этого трактата датируются 150 г. до н.э.

В Европе же первым, кто занимался изучением этого метода, был Исаак Ньютон. Учёный изучил много книг по алгебре того времени и обнаружил, что ни в одной из них не предложено решений систем уравнений со множеством переменных, после чего он предложил свой способ решения.

Его работа на эту тему была опубликована в 1707 г. , в это время Ньютон уже больше не работал в Кембридже. После этого в течение века метод появился во многих книгах и учебниках по алгебре.

В 1810 году известный немецкий учёный и математик К. Ф. Гаусс опубликовал свои дополнения к этому методу вместе с другими своими работами по линейной алгебре, после чего метод с получением верхней треугольной матрицы стал широко известен под его именем.

Затем в в конце XIX века геодезист и математик Жордан разработал на основе метода Гаусса свой усовершенствованный вариант с получением диагональной матрицы.

Примечательно, что он сделал это практически одновременно с другим учёным, тем не менее, в названии усовершенствованного метода отразилось только имя геодезиста Жордана.

Практическое применение метода Жордана-Гаусса

Метод Жордана и Гаусса используется для решения систем линейных уравнений, а также для получения обратных матриц и нахождения ранга матрицы. Также этот метод весьма полезен и часто применяем для решения технических задач со множеством неизвестных.

Для решения получаемых на основе технических задач систем уравнений выделяют наибольшие по модулю переменные для уменьшения ошибки погрешности, а затем производят поочередное удаление лишних переменных из строчек матрицы.

Для решения технических задач методом Жордана-Гаусса также используются реализации на различных языках программирования, они позволяют получать более точные значения переменных.

Объяснение сущности метода Жордана-Гаусса

Обычно матрица, полученная с помощью метода Жордана-Гаусса выглядит как диагональ с единицами, вот например:

$A = \begin{array}{ccc|c} 1& 0 &0 &a_1 \\ 0& 1 &0 &a_2 \\ 0 & 0 & 1 &a_3 \end{array}$

Разница между методом Гаусса и методом Жордана-Гаусса состоит в том, что в случае метода Гаусса необходимо привести только нижнюю часть матрицы к нулям, тогда как в случае метода Жордана-Гаусса в каждой строчке матрицы остаётся лишь один коэффициент при переменной.

С помощью метода Гаусса можно найти базисное и общее решение системы уравнений, также как и с помощью метода Жордана-Гаусса.

Базисное решение системы уравнений – это решение, при котором все свободные переменные равны нулю.

Общее решение системы уравнений – это решение, при котором основные переменные выражаются через свободные переменные.

Также методом Жордана-Гаусса производят получение обратных матриц.

Получение обратной матрицы методом Жордана-Гаусса

Обратная матрица – это такая матрица, при умножении на которую из исходной матрицы получается единичная матрица. Обратные матрицы существуют только для квадратных и невырожденных матриц.

Сущность метода нахождения обратной матрицы состоит в том, чтобы записать рядом исходную матрицу и единичную, и затем, производить элементарные преобразования по методу Жордана-Гаусса одновременно к двум матрицам.

В результате мы получим диагональную единичную матрицу из исходной, а рядом с ней будет её обратная матрица, полученная из единичной матрицы.

Получение обратной матрицы методом Жордана-Гаусса.

Исходная матрица:

$\begin{array}{cc} 1& 2 \\ 3 & 4 \\ \end{array}$

Запишем рядом единичную матрицу и исходную:

$ \begin{array}{cc|cc} 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end{array}$

Теперь к нижней строчке прибавляем верхнюю строчку, умноженную на $-3$:

$ \begin{array}{cc|cc} 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end{array}$

Прибавляем к верхней строчке нижнюю:

$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end{array}$

Делим вторую строку на $-2$:

$ \begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end{array}$

Обратной исходной будет следующая матрица:

$\begin{array}{cc} -2& 1 \\ 3/2 & -1/2 \\ \end{array}$

Чтобы решить СЛАУ методом Жордана-Гаусса, к матрице возможно применить те же элементарные преобразования, что и в случае решения методом Гаусса, а именно:

умножение любой строчки на константу, отличную от нуля;
вычитание или сложение двух любых строчек;
перестановка любых двух строчек местами;
удаление строчек, состоящих из одних нулей;
удаление лишних строк, пропорциональных друг другу.

Соответственно, чтобы решить систему линейных уравнений методом Гаусса-Жордана, необходимо выполнить ряд преобразований над получающейся после применения метода Гаусса матрицей.

Общий алгоритм решения системы уравнений методом Жордана-Гаусса

Выбирают строчку, в которой первый элемент имеет ненулевое значение максимально приближенное к единице и ставят её на место первой строки. Такой элемент называют также “разрешающим”
Приводят значение верхней левой ячейки к $1$ посредством деления или умножения всей верхней строки.
Из оставшихся строчек вычитают верхнюю строчку, помноженную на коэффициент, стоящий на первом месте в строчке, над которой ведутся преобразования.
Далее тоже самое проделывают необходимое количество раз с целью получения треугольной матрицы, в которой все элементы ниже главной диагонали, проходящей слева направо сверху вниз, равны нулю. Последовательность действий, описанных выше, называется прямым ходом преобразования матрицы.
После получения треугольной матрицы затем вычитают последнюю строку из предпоследней, помножив последнюю строку на элемент из предпоследней. На данном этапе в последней и предпоследней строке остаётся по одному коэффициенту. Эту операцию повторяют пока не дойдут до верха матрицы, получив диагональную матрицу. Эти действия носят название обратного хода преобразования матрицы.

Пример 1

Задача. Решить систему линейных уравнений методом Гаусса-Жордана

$\begin{cases} 3x_1 + 2x_2 – 5x_3 = -1 \\ 2x_1 – x_2 + 3x_3 = 13 \\ x_1 + 2x_2 – x_3 = 9 \end{cases}$

Теперь запишем эту систему в виде расширенной матрицы:

$ \begin{array}{ccc|c} 3& 2 & -5 & -1\\ 2 & -1& 3 & 13 \\ 1 & 2 & -1 & 9 \\ \end{array}$

Путём элементарных преобразований методом Гаусса получим следующую матрицу:

$ \begin{array}{ccc|c} 1& 2 & -1 & 9\\ 0 & 1& -1 & 1 \\ 0 & 0& 1 & 4 \\ \end{array}$

Теперь начнём использовать обратный ход и преобразуем эту матрицу чтобы получить диагональ из единиц.

Сначала к средней и верхней строчкам необходимо добавить последнюю строчку, получается:

$ \begin{array}{ccc|c} 1& 2 & 0 & 13\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$

А теперь к верхней строчке прибавим среднюю, умноженную на $-2$:

$ \begin{array}{ccc|c} 1& 0 & 0 & 3\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$

Получаем следующую систему:

$\begin{cases} x_1 = 3 \\ x_2 = 5 \\ x_3 = 4 \end{cases}$

Пример 2

Решить систему линейных уравнений методом Жордана-Гаусса:

$\begin{cases} x_1 – 8x_2 + x_3 — 9x_4 = 6 \\ x_1 – 4x_2 – x_3 — 5x_4 = 2 \\ -3x_1 + 2x_2 + 8x_3 + 5x_4 = 4 \\ 5x_1 + 2x_2 + 2x_3 + 3x_4 = 12 \end{cases}$

Сначала запишем систему в матричном виде:

$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ -1 & -4& -1 & -5 & 2 \\ -3 & 2 & 8 & 5 & 4 \\ 5& 2 & 2 & 3 & 12 \\ \end{array}$

Затем преобразуем до треугольной:

К самой верхней строчке прибавляем вторую строчку, домноженную на $-1$. К третьей строчке прибавляем утроенную самую верхнюю строчку, затем к последней строчке прибавляем самую верхнюю, помноженную на $-5$:

$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 4& -2 & 4 & -4 \\ 0 & -22 & 11 & -22 & 22 \\ 0& 42 & -3 & 48 & -18 \\ \end{array}$

Теперь вторую строчку необходимо поделить на $2$, третью строчку на на $11$, а самую нижнюю строку делим на 3:

$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0 & -2 & 1 & -2 & 2 \\ 0& 14 & -1 & 16 & -6 \\ \end{array}$

Удаляем третью строчку, так как она пропорциональна со второй. А к последней строке прибавляем вторую, предварительно домноженную на $-7$:

$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 6 & 2 & 8 \\ \end{array}$

Теперь сокращаем последнюю строчку с $2$:

$ \begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

В полученной матрице количество строк и столбцов неодинаково, а значит, она имеет бесконечное множество решений.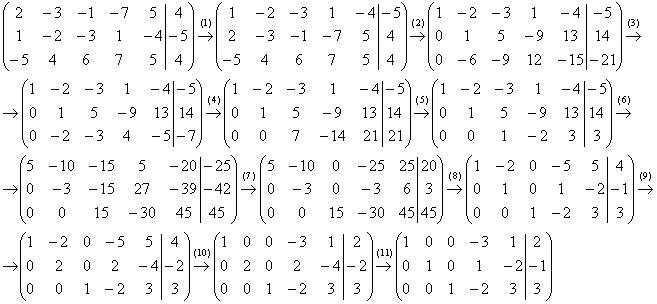 Продолжаем дальнейшее преобразование системы, для этого необходимо в третьем столбце получить числа с равным модулем, поэтому сначала верхнюю строку умножаем на $-3$, а среднюю на $3$:

$ \begin{array}{cccc|c} -3& 24 & -3 & 27 & -18 \\ 0 & 6& -3 & 6 & -6 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Складываем поочередно первую строчку с третьей, а затем вторую с третьей:

$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & 6 & 0 & 7 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Домножаем вторую строчку на $-4$ чтобы получить одинаковые по модулю числа во втором столбце нашей матрицы:

$ \begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Складываем верхнюю строчку со второй:

$ \begin{array}{cccc|c} -3& 0 & 0 & 0 & -6 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Теперь необходимо разделить верхнюю строчку на $-3$, среднюю строчку на $-24$, а последнюю строчку нужно разделить на 3:

$ \begin{array}{cccc|c} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 7/6 & -1/3 \\ 0& 0 & 1 & 1/3 & 4/3 \\ \end{array}$

Если переписать в виде системы, получим следующее:

$\begin{cases} x_1 = 2 \\ x_2 + \frac{7}{6}x_4 = -\frac{1}{3} \\ x_3 + \frac{1}{3}x_4 = \frac{4}{3} \\ \end{cases}$

А теперь просто выражаем базисные переменные:

$\begin{cases} x_1 = 2 \\ x_2 = -\frac{7}{6}x_4 — \frac{1}{3} \\ x_3 = -\frac{1}{3}x_4 + \frac{4}{3} \\ \end{cases}$

Данная система является общим решением уравнения.

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

Образовательные онлайн сервисы: теория и практика

Главная
Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
  Методы оптимизации
- Математика в экономике
  Экономическая статистика
Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование. Методы оптимизации
Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
  Методы оптимизации
- Математика в экономике
  Экономическая статистика
- Другое
Контакты

Полезные материалы:

Учебники
Справочники
Онлайн калькуляторы

Помощь в решении
Онлайн занятия в Zoom

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)

Пример из видеоурока в рукописном виде:

Пример 2.

Запишем систему в виде:

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
-2	4	-4	-2	-2	1	1
-1	1	0	-1	1	1	-2

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
0	0	0	-4	-4	5	9
0	-1	2	-2	0	3	2

Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	-1	-3	1	-2	2
0	0	0	-4	-4	5	9
0	0	1	-5	1	1	4

Разрешающий элемент равен (1).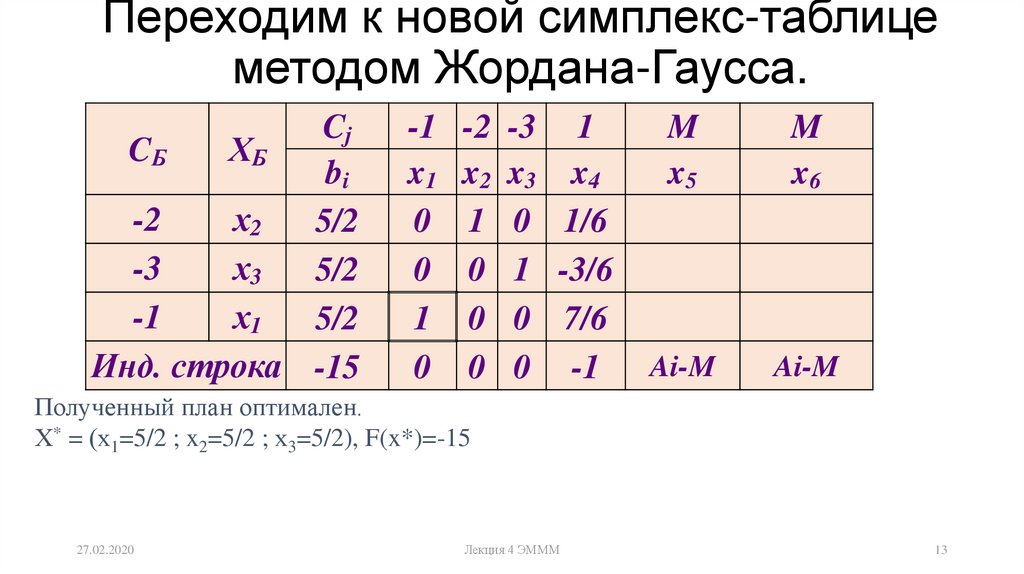 На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	0	-8	2	-1	6
0	0	1	-5	1	1	4
0	0	0	-4	-4	5	9

Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	0	8	-10.75	-7.75
0	1	0	0	10	-11	-12
0	0	1	0	6	-5. 25	-7.25
0	0	0	1	1	-1.25	-2.25

Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.

Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk. com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru

Метод Жордана-Гаусса для решения СЛАУ: основные понятия, примеры, определения

В данной статье мы рассмотрим метод Жордана-Гаусса для решения систем линейных уравнений, отличие метода Гаусса от метода Жордана-Гаусса, алгоритм действий, а также приведем примеры решений СЛАУ.

Основные понятия

Определение 1

Метод Жордана-Гаусса — один из методов, предназначенный для решения систем линейных алгебраических уравнений.

Этот метод является модификацией метода Гаусса — в отличие от исходного (метода Гаусса) метод Жордана-Гаусса позволяет решить СЛАУ в один этап (без использования прямого и обратного ходов).

Примечание

Матричная запись СЛАУ: вместо обозначения А в методе Жордана-Гаусса для записи используют обозначение Ã — обозначение расширенной матрицы системы.

Пример 1

Решить СЛАУ методом Жордана-Гаусса:

4×1-7×2+8×3=-232×1-4×2+5×3=-13-3×1+11×2+x3=16

Как решить?

Записываем расширенную матрицу системы:

Ã=4-78|-232-45|-13-3111|16

Напоминаем, что слева от черты записывается матрица системы А:

A=4-782-45-3111

Замечание 1

На каждом шаге решения необходимо выбирать разрешающие элементы матрицы. Процесс выбора может быть различным — в зависимости от того, как выбираются элементы, решения будут отличаться. Можно выбирать в качестве разрешающих элементов диагональные элементы матрицы, а можно выбирать произвольно.

В этой статье мы покажем оба способа решения.

Произвольный способ выбора разрешающих элементов

Первый этап:

Следует обратиться к 1-му столбцу матрицы Ã — необходимо выбрать ненулевой (разрешающий) элемент.

В 1-ом столбце есть 3 ненулевых элемента: 4, 2, -3. Можно выбрать любой, но, по правилам, выбирается тот, чей модуль ближе всего к единице. В нашем примере таким числом является 2.

Цель: обнулить все элементы, кроме разрешающего, т.е. необходимо обнулить 4 и -3:

4-782-45-3111

Произведем преобразование: необходимо сделать разрешающий элемент равным единице. Для этого делим все элементы 2-ой строки на 2. Такое преобразование имеет обозначение: II:2:

4-78|-232-45|-13-3111|16II÷2→4-78|-232-45/2|-13/2-3111|16

Теперь обнуляем остальные элементы: 4 и -3:

4-78|-232-45/2|-13/2-3111|16 I-4×IIIII-(-3)×II

Необходимо выполнить преобразования:

I-4×II и III-(-3)×II=III+3×II

Запись I-4×II означает, что от элементов 1-ой строки вычитаются соответствующие элементы 2-ой строки, умноженные на 4.

Запись III+3×II означает, что к элементам 3-ей строки прибавляются соответствующие элементы 2-ой строки, умноженные на 3.

I-4×II=4 -78 -23-41 -25/2 -13/2==4 -78 -23-4 -810 -26=0 1-2 3

Записываются такие изменения следующим образом:

4-78|-232-45/2|-13/2-3111|16I-4×IIIII-(-3)×II→01-2|31-25/2|-13/20517/2|-7/2

Второй этап

Необходимо обнулить 2-ой столбец, следовательно, нужно выбрать разрешающий элемент: 1, -2, 5. Однако 2-ую строку матрицы мы использовали в первом этапе, так что элемент -2 не может быть использован.

Поскольку необходимо выбирать число, чей модуль ближе всего к единице, то выбор очевиден — это 1. Обнуляем остальные элементы 2-го столбца:

01-2|31-25/2|-13/20517/2|-7/2II-(-2)×IIII-5×I

Итог:

01-2|31-25/2|-13/20517/2|-7/2II+2×IIII-5×I→01-2|310-3/2|-1/20037/2|-37/2

Третий этап

Теперь требуется обнулить элементы 3-го столбца. Поскольку первая и вторая строки уже использованы, поэтому остается только один вариант: 37/2. Обнуляем с его помощью элементы третьего столбца:

01-2|310-3/2|-1/20037/2|-37/2

Выполнив преобразования

I-(-2)×III=I+2×III и II-(-32)×III=II+32×II

получим следующий результат:

01-2|310-3/2|-1/2001|-1I+2×IIIII+3/2×III→010|1100|-2001|-1

Ответ: x1=-2; x2=1; x3=-1.

Полное решение:

4-78|-232-45|-13-3111|16II÷2→4-78|-232-45/2|-13/2-3111|16I-4×IIIII-(-3)×II→

→01-2|31-25/2|-13/20517/2|-7/2II-(-2)×IIII-5×I→01-2|310-3/2|-1/20037/2|-37/2III÷372→

→01-2|310-3/2|-1/2001|-1I+2×IIIII+3/2×III→010|1100|-2001|-1.

Выбор разрешающих элементов на главной диагонали матрицы системы

Определение 2

Принцип выбора разрешающих элементов строится на простом отборе соответствующих элементов: в 1-ом столбце выбирается элемент 1-го столбца, во 2-ом — второй, в 3-ем — третий и т.д.

Первый этап

В первом столбце необходимо выбрать элемент первой строки, т.е. 4. Но поскольку в первом столбце есть число 2, чей модуль ближе к единице, чем 4, то можно поменять местами первую и вторую строку:

4-78|-232-45|-13-3111|16→2-45|-134-78|-23-3111|16

Теперь разрешающий элемент — 2. Как показано в первом способе, делим первую строку на 2, а затем обнуляем все элементы:

4-78|-232-45|-13-3111|16I÷2→2-45/2|-13/24-78|-23-3111|16II-4×IIII+3×I→1-25/2|-13/201-2|30517/2|-7/2

Второй этап

На втором этапе требуется обнулить элементы второго столбца. Разрешающий элемент — 1, поэтому никаких изменений производить не требуется:

01-2|31-25/2|-13/20517/2|-7/2I+2×IIIII-5×II→01-2|310-3/2|-1/20037/2|-37/2

Третий этап

На третьем этапе необходимо обнулить элементы третьего столбца. Разрешающий элемент — 37/2. Делим все элементы на 37/2 (чтобы сделать равными 1), а затем обнуляем:

01-2|310-3/2|-1/20037/2|-37/2III÷372→10-3/2|-1/201-2|3001|-1I+2×IIIII+3/2×III→100|-2010|1001|-1

Ответ: x1=-2; x2=1; x3=-1.

4-78|-232-45|-13-3111|16I÷2→2-45/2|-13/24-78|-23-3111|16II-4×IIII+3×I→01-2|31-25/2|-13/20517/2|-7/2I+2×IIIII-5×II→

→01-2|310-3/2|-1/20037/2|-37/2III÷372→10-3/2|-1/201-2|3001|-1I+2×IIIII+3/2×III→100|-2010|1001|-1

Пример 2

Решить СЛАУ методом Жордана-Гаусса:

3×1+x2+2×3+5×4=-63×1+x2+2×4=-106×1+4×2+11×3+11×4=-27-3×1-2×2-2×3-10×4=1

Как решить?

Записать расширенную матрицу данной системы Ã:

3125|-63102|10641111|-27-3-2-2-10|1

Для решения используем второй способ: выбор разрешающих элементов на главной диагонали системы. На первом этапе выбираем элемент первой строки, на втором — второй строки, на третьем — третьей и т.д.

Первый этап

Необходимо выбрать разрешающий элемент первой строки, т. е. 3. Затем обнуляем все элементы столбца, разделяя на 3 все элементы:

3125|-63102|-10641111|-27-3-2-2-10|1I÷3→11/32/35/3|-23102|-10641111|-27-3-2-2-10|1II-3×IIII-6×IIV+3×I→

→11/32/35/3|-200-2-3|-40271|-150-10-5|-5

Второй этап

Необходимо обнулить элементы второго столбца. Для этого выделяем разрешающий элемент, но элемент первой строки второго столбца равен нулю, поэтому необходимо менять строки местами.

Поскольку в четвертой строке есть число -1, то меняем местами вторую и четвертую строки:

11/32/35/3|-200-2-3|-40271|-150-10-5|-5→11/32/35/3|-20-10-5|-50271|-1500-2-3|-4

Теперь разрешающий элемент равен -1. Делим элементы второго столбца на -1, а затем обнуляем:

11/32/35/3|-20-10-5|-50271|-1500-2-3|-4II÷(-1)→11/32/35/3|-20105|50271|-1500-2-3|-4I-1/3×IIIII-2×I→

→102/30|-11/30105|5007-9|-2500-2-3|-4

Третий этап

На третьем этапе необходимо также обнулить элементы третьего столбца. Для этого находим разрешающий элемент в третьей строке — это 7. Но на 7 делить неудобно, поэтому необходимо менять строки местами, чтобы разрешающий элемент стал -2:

102/30|-11/30105|5007-9|-2500-2-3|-4→102/30|-11/30105|500-2-3|-4007-9|-25

Теперь делим все элементы третьего столбца на -2 и обнуляем все элементы:

102/30|-11/30105|500-2-3|-4007-9|-25III÷(-2)→102/30|-11/30105|50013/2|2000-9|-25I-2/3×IIIIV-7×III→

100-1|-50105|50013/2|2000-39/2|-39

Четвертый этап

Обнуляем четвертый столбец. Разрешающий элемент — -392:

100-1|-50105|50013/2|2000-39/2|-39IV÷(-392)→100-1|-50105|50013/2|20001|2I+IVII-5×IVIII-3/2×IV→

→1000|-30100|-50010|-10001|2.

Ответ: x1=-3; x2=-5; x3=-1; x4=2

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Метод Жордана-Гаусса — 📙 Математика

1. Общие понятия
2. История появления метода Жордана-Гаусса
3. Использование метода Жордана-Гаусса на практике
4. Суть метода Жордана-Гаусса
5. Получение обратных матриц с применением метода Жордана-Гаусса

Методом Жордана-Гаусса является такой метод решения линейных уравнений, при котором полностью исключаются неизвестные. Этот метод есть производным от метода Гаусса, но в данной модификации элементарные преобразования производят дальше.

Возникновение метода Гаусса своими корнями уходит в далекие годя до нашей эры. Он описан еще в древней китайской книге, которая называется «Математика в девяти книгах», написанной примерно в 150 году до нашей эры. В этом трактате собраны различные математические задачи и методы их решения.

В Европе первым, кто занялся исследованием данного метода, стал Исаак Ньютон. Он изучал множество древних математических книг, но при этом не обнаружил ни одного способа решения систем уравнений с большим числом переменных, и предложил способ такого решения в своей работе, которая была обнародована в 1707 году. Его метод распространился на протяжении века в различных пособиях и справочниках по арифметике.

Немецким ученым К.Ф. Гауссом в 1810 году был усовершенствован данный метод и опубликован на ряду с другими его работами, после чего метод преобразования в треугольную матрицу нашел массовое распространение и был назван его именем.

Затем во второй половине ХІХ столетия ученый Жордан доработал метод Гаусса, трансформировав его в более совершенный метод приведения к диагональной матрице. Интересно, что на ряду с ним точно то же совершил еще один ученый, но все же название метода на сегодняшний день получило имена Гаусса и Жордана.

Метод Жордана-Гаусса имеет широкое применение для расчета систем линейных уравнений, создания обратных матриц, изучения рангов матриц. Зачастую именно с его помощью решаются инженерные задачи с большим количеством неизвестных.

При расчете полученных из инженерно-технических задач систем уравнений, сначала выбирают самые большие за модулем переменные для минимизации погрешности, далее поочередно удаляют не нужные переменные из матрицы.

Также при расчетах инженерно-технологических задач этим методом, пользуются различными алгоритмами программирования, что дает возможность получения результатов с меньшей погрешностью.

Применяя метода Жордана-Гаусса, мы получаем матрицу, диагональ которой состоит из единиц, а все остальные коэффициенты – нули, к примеру:

$A = \begin{array}{ccc|c} 1& 0 &0 &a_1 \\ 0& 1 &0 &a_2 \\ 0 & 0 & 1 &a_3 \end{array}$

Отличается данный метод от метода Гаусса тем, что в последнем к нулям приводится лишь нижняя часть матрицы, в то время, как при использовании метода Жордана-Гаусса к нулям приводится также и верхняя часть матрицы.

Оба метода применяют для определения базисного и общего решений системы уравнений.
Базисное решение являет собой такое решение системы уравнений, когда все свободные переменные равняются нулю.

Общее решение системы уравнений являет собой такое решение, когда основные переменные выражают через свободные.

Еще одним вариантом применения метода Жордана-Гаусса есть получение обратных матриц.

Обратной называют такую матрицу, результатом перемножения которой с заданной матрицей будет единичная матрица. Данная матрица может существовать исключительно для квадратных и невырожденных матриц.

Суть метода определения обратной матрицы состоит вот в чем: заданную и единичную матрицы одновременно преобразовывают элементарными действиями с использованием метода Жордана-Гаусса. В итоге получают две матрицы – единичную диагональную и обратную.

Рассмотрим последовательность действий для получения обратной матрицы с применением метода Жордана-

Гаусса на примере заданной квадратной матрицы:
$\begin{array}{cc} 1& 2 \\ 3 & 4 \\ \end{array}$
1) Записываем заданную и единичную матрицы:
$\begin{array}{cc|cc} 1& 2 & 1& 0\\ 3 & 4& 0 & 1 \\ \end{array}$
2) К последней строке плюсуем первую, перемноженную на -3:
$\begin{array}{cc|cc} 1& 2 & 1 & 0\\ 0 & -2 & -3 & 1 \\ \end{array}$
3) После этого к первой строчке добавляем последнюю:
$\begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & -2 & -3 & 1 \\ \end{array}$
4) Поделим вторую строчку на -2:
$\begin{array}{cc|cc} 1& 0 & -2 & 1\\ 0 & 1& 3/2 & -1/2 \\ \end{array}$
5) В итоге обратная матрица преобразуется в следующий вид:
$\begin{array}{cc} -2& 1 \\ 3/2 & -1/2 \\ \end{array}$

Для расчета систем линейных уравнений методом Жордана-Гаусса матрицу преобразуют при помощи тех же элементарных преобразований, как и при методе Гаусса, таких как:

перемножение любой строчки на число, не равное нулю;
прибавление или отнимание любых строк;
перестановка строк местами;
удаление строк, что состоят из одних нулей;
удаление пропорциональных строчек, которые можно считать лишними.

Таким образом, для расчета системы линейных уравнений методом Жордана-Гаусса, требуется провести череду элементарных преобразований матрицы, полученной после использования метода Гаусса.

Порядок действий во время расчета системы линейных уравнений методом Жордана-Гаусса:

Находят строку, у которой первый коэффициент не равняется нулю и максимально приближается по значению к единице. Эту строчку ставят в верхний ряд. Этот элемент имеет название «разрешающий».
Разрешающий элемент преобразуют до единицы делением или умножением всей первой строчки.
Из всех остальных строчек отнимают первую, перемноженную на коэффициент, что стоит вначале строки, которую изменяют.
Все то же проделывают до получения треугольной матрицы, иными словами, до тех пор, пока все элементы слева от главной диагонали станут равняться нулю. Эти все действия называют прямым ходом преобразования матрицы.
Затем отнимают нижнюю строчку от предпоследней, умножив нижнюю на последний коэффициент предпоследней строчки. Все то же повторяют снизу-вверх, получая диагональную матрицу. Эти действия называются обратным ходом преобразования матрицы.

Рассмотрим несколько задач по расчету системы линейных уравнений.

Задача 1. Задана система линейных уравнений:

$\begin{cases} 3x_1 + 2x_2 – 5x_3 = -1 \\ 2x_1 – x_2 + 3x_3 = 13 \\ x_1 + 2x_2 – x_3 = 9 \end{cases}$

Найти переменные.
Преобразуем систему в расширенную матрицу:

$\begin{array}{ccc|c} 3& 2 & -5 & -1\\ 2 & -1& 3 & 13 \\ 1 & 2 & -1 & 9 \\ \end{array}$

Применяя метод Гаусса, получаем матрицу следующего вида:

$\begin{array}{ccc|c} 1& 2 & -1 & 9\\ 0 & 1& -1 & 1 \\ 0 & 0& 1 & 4 \\ \end{array}$

Далее применяем обратный ход преобразования матрицы и получаем диагональную матрицу. Сперва к первой и средней строкам прибавим нижнюю:

$\begin{array}{ccc|c} 1& 2 & 0 & 13\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$

Затем среднюю строку перемножим на -2 и приплюсуем ее к верхней:

$\begin{array}{ccc|c} 1& 0 & 0 & 3\\ 0 & 1& 0 & 5 \\ 0 & 0 & 1 & 4 \\ \end{array}$

В итоге получим такую систему:

$\begin{cases} x_1 = 3 \\ x_2 = 5 \\ x_3 = 4 \end{cases}$

Эта система и будет являться решением.

Задача 2. Задана система линейных уравнений:

$\begin{cases} x_1 – 8x_2 + x_3 — 9x_4 = 6 \\ x_1 – 4x_2 – x_3 — 5x_4 = 2 \\ -3x_1 + 2x_2 + 8x_3 + 5x_4 = 4 \\ 5x_1 + 2x_2 + 2x_3 + 3x_4 = 12 \end{cases}$

Найти ее решение.

Записываем систему в форме матрицы:

$\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ -1 & -4& -1 & -5 & 2 \\ -3 & 2 & 8 & 5 & 4 \\ 5& 2 & 2 & 3 & 12 \\ \end{array}$

Преобразовываем матрицу прямым ходом до треугольной:

Ко второй строке добавляем первую, перемноженную на -1. К третьей строке добавляем первую, перемноженную на 3, а к нижней строке добавляем верхнюю, перемноженную на -5:

$\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 4& -2 & 4 & -4 \\ 0 & -22 & 11 & -22 & 22 \\ 0& 42 & -3 & 48 & -18 \\ \end{array}$

Разделим вторую строку на 2, третью – на 11, четвертую – на 3. Получаем следующее:

$\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0 & -2 & 1 & -2 & 2 \\ 0& 14 & -1 & 16 & -6 \\ \end{array}$

Убираем третью строку, так как она является пропорциональной ко второй, к нижней строке добавляем вторую, умноженную на -7:

$\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 6 & 2 & 8 \\ \end{array}$

Разделим на два нижнюю строку:

$\begin{array}{cccc|c} 1& -8 & 1 & -9 & 6 \\ 0 & 2& -1 & 2 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

В преобразованной матрице не равное число строк и переменных, это означает, что для нее существует бесконечное множество решений. Преобразовываем матрицу дальше. Нам необходимо получить в третьем столбике коэффициенты с равными модулями, для этого первую строчку умножаем на -3, а вторую на 3.

$\begin{array}{cccc|c} -3& 24 & -3 & 27 & -18 \\ 0 & 6& -3 & 6 & -6 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Добавляем к первой строке третью, а потом ко второй третью:

$\begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & 6 & 0 & 7 & -2 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Перемножаем на -4 вторую строку, чтобы уровнять модули чисел:

$\begin{array}{cccc|c} -3& 24 & 0 & 28 & -14 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Добавляем к верхней строке вторую:

$\begin{array}{cccc|c} -3& 0 & 0 & 0 & -6 \\ 0 & -24 & 0 & -28 & 8 \\ 0& 0 & 3 & 1 & 4 \\ \end{array}$

Разделим первую строку на -3, вторую – на -24, а третью на 3:

$\begin{array}{cccc|c} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 7/6 & -1/3 \\ 0& 0 & 1 & 1/3 & 4/3 \\ \end{array}$

Записываем в форме системы:

$\begin{cases} x_1 = 2 \\ x_2 + \frac{7}{6}x_4 = -\frac{1}{3} \\ x_3 + \frac{1}{3}x_4 = \frac{4}{3} \\ \end{cases}$

Выразим базисные переменные и получим общее решение заданной системы уравнений:

$\begin{cases} x_1 = 2 \\ x_2 = -\frac{7}{6}x_4 — \frac{1}{3} \\ x_3 = -\frac{1}{3}x_4 + \frac{4}{3} \\ \end{cases}$

Решение систем линейных алгебраических уравнений в системе MATLAB

Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

КАТЕГОРИИ:

Археология
Биология
Генетика
География
Информатика
История
Логика
Маркетинг
Математика
Менеджмент
Механика
Педагогика
Религия
Социология
Технологии
Физика
Философия
Финансы
Химия
Экология

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 3 из 6Следующая ⇒

Решение систем линейных алгебраических уравнений методом Жордана-Гаусса

Метод Жордана — Гаусса является одной из модификаций метода Гаусса, в котором матрица коэффициентов при неизвестных последовательно приводится к единичной матрице, а на месте столбца свободных членов в расширенной матрице в результате располагается решение системы линейных алгебраических уравнений:

где — коэффициенты системы, — свободные члены, — неизвестные.

Сущность этого метода заключается в том, что, начиная со второго шага, зануляются все элементы в соответствующем столбце, кроме элемента, стоящего на главной диагонали. Это достигается с помощью алгебраических преобразований аналогичных классическому методу Гаусса. Если имеется система линейных алгебраических уравнений — го порядка, то на каждом шаге прямого хода метода Гаусса в каждом столбце матрицы коэффициентов зануляется ровно коэффициент.

Стандартной функцией, которая реализует метод Жордана-Гаусса в системе MATLAB , является функция rref(). Аргументом у этой функции является расширенная матрица коэффициентов.

Пример: решить с помощью метода Жордана –Гаусса систему линейных алгебраических уравнений

>> A=[3 2 -1;2 -1 3;1 -2 2]; B=[4;9;3];

>> AB=[A B]

AB =

3 2 -1 4

2 -1 3 9

1 -2 2 3

>> rref(AB)

ans =

1 0 0 1

0 1 0 2

0 0 1 3

Для решения систем линейных алгебраических уравнений с помощью MATLAB можно применять оператор «\», который самостоятельно выбирает лучший метод для решения заданной системы уравнений. При этом решение системы линейных алгебраических уравнений любого порядка достигается одной командой:

Индивидуальные задания

· Решить систему линейных алгебраических уравнений методом Гаусса,

· решить систему линейных алгебраических уравнений методом Жордана— Гаусса в системе MATLAВ.

Таблица 4

№	Задание	№	Задание


5

Продолжение табл. 4

Окончание табл. 4

Содержание соответствующего раздела

В пояснительной записке

Данный раздел должен содержать:

· краткие теоретические сведения,

· исследование системы линейных алгебраических уравнений на совместность,

· аналитическое решение системы линейных алгебраических уравнений методом Гаусса,

· решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB,

· сравнение полученных результатов, найденных разными способами.

⇐ Предыдущая123456Следующая ⇒

Читайте также:

Коммуникативные барьеры и пути их преодоления

Рынок недвижимости. Сущность недвижимости

Решение задач с использованием генеалогического метода

История происхождения и развития детской игры

Последнее изменение этой страницы: 2016-12-28; просмотров: 990; Нарушение авторского права страницы; Мы поможем в написании вашей работы!

infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)

принцип, теорема и примеры решения задач

Содержание:

Историческая справка
Принцип метода Гаусса
Примеры решения систем уравнений

Историческая справка

Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 — 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.

Принцип метода Гаусса

Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный — методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.

Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений, которые не являются квадратными (чего не скажешь про метод Крамера и матричный метод). То есть метод Гаусса — наиболее универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет бесконечно много решений или несовместна.

Примеры решения систем уравнений

Пример

Задание. Решить СЛАУ $\left\{\begin{array}{l} 2 x_{1}+x_{2}+x_{3}=2 \\ x_{1}-x_{2}=-2 \\ 3 x_{1}-x_{2}+2 x_{3}=2 \end{array}\right. $ методом Гаусса.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся 1 (это мы делаем для упрощения вычислений):

$$\tilde{A}=A \mid B=\left(\begin{array}{rrr|r} 2 & 1 & 1 & 2 \\ 1 & -1 & 0 & -2 \\ 3 & -1 & 2 & 2 \end{array}\right) \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 2 & 1 & 1 & 2 \\ 3 & -1 & 2 & 2 \end{array}\right)$$

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 2 & 2 & 8 \end{array}\right)$$

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $\frac{1}{2}$ ):

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 3 & 1 & 6 \\ 0 & 1 & 1 & 4 \end{array}\right)$$

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 3 & 1 & 6 \end{array}\right)$$

От третьей строки отнимаем вторую, умноженную на 3:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & -2 & -6 \end{array}\right)$$

Умножив третью строку на $\left(-\frac{1}{2}\right)$ , получаем:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 1 & 4 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $a_{23}$, для этого от второй строки отнимем третью:

$$\tilde{A} \sim\left(\begin{array}{rrr|r} 1 & -1 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

$$\tilde{A} \sim\left(\begin{array}{ccc|c} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 3 \end{array}\right)$$

Полученной матрице соответствует система

$\left\{\begin{array}{l}x_{1}+0 \cdot x_{2}+0 \cdot x_{3}=-1 \\ 0 \cdot x_{1}+x_{2}+0 \cdot x_{3}=1 \\ 0 \cdot x_{1}+0 \cdot x_{2}+x_{3}=3\end{array}\right.$ или $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right.$

Ответ. $\left\{\begin{array}{l} x_{1}=-1 \\ x_{2}=1 \\ x_{3}=3 \end{array}\right. $

Читать дальше: однородные СЛАУ. Фундаментальная система решений.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Калькулятор исключения Гаусса Джордана с шагами

Введение в Калькулятор исключения Гаусса Джордана

Калькулятор Гаусса — это бесплатный онлайн-инструмент, используемый для преобразования матрицы в форму сокращенного эшелона. Он применяет операции со строками к матрице, чтобы найти обратную матрицу. Он может решить любую систему линейных уравнений методом исключения.

В математике всегда нужно решить систему линейных уравнений. Существует более двух методов решения системы линейных уравнений. Одним из таких методов является метод исключения Гаусса-Жордана.

Использование онлайн-инструмента — эффективный способ решить любую проблему. Итак, здесь мы представляем онлайн-инструмент, который является наиболее эффективным инструментом для поиска обратной матрицы.

Формула, используемая калькулятором метода исключения Гаусса

Исключение Гаусса-Жордана — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, сокращения ее с помощью операций со строками и представления системы в сокращенной строке- форма эшелона, чтобы найти решение.

Калькулятор Гаусса Жордана преобразует заданную матрицу в редуцированную ступенчатую форму для решения системы линейных уравнений и находит ее обратную. Сокращенную форму эшелона можно получить с помощью калькулятора исключения Гаусса, выполнив следующие шаги:

Преобразуйте все диагональные записи в 1, применяя операции со строками и столбцами.
Преобразование всех элементов, кроме диагоналей, в 0.

Сокращенная ступенчатая форма матрицы получается путем преобразования матрицы в единичную матрицу с помощью калькулятора исключения Жордана.

Как пользоваться калькулятором метода Гаусса-Жордана?

С помощью калькулятора Гаусса легко найти решение любой задачи, потому что он прост в использовании. Чтобы использовать этот инструмент, выполните следующие действия:

На первом этапе вам необходимо ввести количество строк и столбцов матрицы.
Теперь введите значения всех элементов матрицы.
Вы можете использовать случайную кнопку, чтобы выбрать случайный вариант.
Нажмите кнопку расчета.

Вы получите пошаговое решение через несколько секунд после нажатия на кнопку расчета.

Зачем использовать калькулятор исключения Гаусса?

Концепция исключения в матрицах важна, потому что она нам обычно нужна для формирования эшелонированной и редуцированной эшелонированной формы. Эти две формы являются ключом к решению системы линейных уравнений.

Но ручные расчеты иногда становятся сложными. Эффективный и простой способ решить эту проблему — использовать онлайн-инструмент. Вы можете использовать калькулятор метода исключения Гаусса, потому что он прост в использовании.

Преимущества использования Калькулятора метода исключения Гаусса по Жордану

В Интернете доступно множество математических инструментов, которые помогают решать многие задачи. Точно так же инструмент Gaussian преобразует матрицу в уменьшенную ступенчатую форму. Он имеет много полезных применений для улучшения ваших математических навыков. Вот некоторые из этих преимуществ:

Калькулятор исключения Гаусса с шагами может исключить любую матрицу за короткий промежуток времени.
Калькулятор исключения Гаусса может работать с матрицей до 4-го порядка.
Он предоставляет вам пошаговое решение, чтобы вы могли легко его понять.
надежен, потому что он экономит ваше время и дает точный ответ.
с шагами — это бесплатный онлайн-инструмент, поэтому вам не нужно подписываться на какой-либо платный план.

Другие связанные калькуляторы

Помимо этого калькулятора Гаусса, на этом веб-сайте есть много других связанных инструментов, которые вы можете использовать. Некоторые из бесплатных инструментов:

Добавление калькулятора матриц
Калькулятор вычитания матриц
Калькулятор матриц умножения
Определитель матричного калькулятора
Калькулятор транспонирования матрицы
Калькулятор обратной матрицы
Ранг матричного калькулятора
Матрица для калькулятора мощности
Калькулятор собственных векторов
Калькулятор собственных значений
Недействительность матричного калькулятора
Калькулятор матрицы трассировки
Калькулятор разложения Matrix Lu
Калькулятор формы эшелона с уменьшенным рядом
Калькулятор сопряженных матриц

Алан Уокер

Последнее обновление 02 июня 2022 г.

Изучает математические науки и технологии. Технический гик и автор контента. Помешанный на Википедии, который хочет знать все. Любит путешествия, природу, чтение. Математика и технологии сделали свое дело, и теперь пришло время извлечь выгоду из этого.

Исключение Гаусса-Джордана | Меньше пробелов

Часть: Последовательность алгебры
Краткое содержание: 1300 слов, 13 минут чтения.

Линейная алгебра — это математика векторов и матриц. Позвольте мне попытаться объяснить это как можно короче.

Операции с векторами

Если n — натуральное число, а ℝ — множество действительных чисел, то ℝ ⁿ — множество всех n-кортежей действительных чисел. Вектор v ∈ ℝ ⁿ является одним из таких n-наборов. Например,

Шесть векторных операций: сложение, вычитание, масштабирование, векторное произведение, скалярное произведение, норма (длина вектора). Для векторов u и v они определяются следующим образом:

Скалярное произведение и векторное произведение норма связаны с углом между двумя векторами. В частности,

Наконец, обратите внимание, что перекрестное произведение не является коммутативным: u x v != v x u.

Операции с матрицами

A матрица A ∈ ℝ ^{m x n} представляет собой прямоугольный массив действительных чисел с m строками и n столбцами. Например,

Важными матричными операциями являются сложение, вычитание, произведение, транспонирование и определение определителя:

Из вышеперечисленных операций произведение матриц имеет особое значение. Эта операция возможна только в том случае, если A имеет такое же количество столбцов, сколько B имеет строк.

Матрица как морфизм

Важно отметить, что матрицы с одной строкой или одним столбцом можно интерпретировать как векторы. Умножение матриц на вектор можно интерпретировать двумя способами. Изображение строки интерпретирует вывод как скалярное произведение, изображение столбца интерпретирует вывод как линейную комбинацию.

Возьмем A как матрицу 2 на 2 с векторами-строками (2, -1) и (-1,2), и пусть b = (0,3). Когда мы находим x, мы обнаруживаем, что есть два способа сделать это:

В приведенном выше примере мы установили b = (0,3). Но эта линейная комбинация может порождать любой вектор b. В общем, линейные комбинации могут генерировать все пространство (в данном случае двумерную плоскость).

В обоих представлениях мы говорим: Преобразование x → b. Если векторы представляют собой группы данных, 9Матрицы 0120 — это функции , которые работают с векторами. В частности, умножение на матрицу A ∈ ℝ ^{m x n} назовем линейным преобразованием , которое преобразует n-набор в m-набор T _A : ℝ ⁿ → ℝ ^m .

Симметрия между функциями и линейными преобразованиями укоренилась глубоко. Когда мы исследуем теорию категорий, мы обнаружим структуру, лежащую в основе этой связи. А пока рассмотрим следующие эквивалентности:

Особенно важным для матричных функций является понятие обратной матрицы . Подобно тому, как f ^-1 (x) = ln(x) отменяет действие f(x) = e ^x , обратная матрица A ^-1 отменяет действие A. Совокупный эффект применения A ^{— 1} после A является единичной матрицей A ^-1 A = 1 . Единичная матрица аналогична умножению на единицу или добавлению нуля: она алгебраически инертна.

Обратимыми могут быть только квадратные матрицы, так как обращение коммутативно AA ^-1 = А ^-1 А = 1 . Но не у всех квадратных матриц есть обратные. Определитель матрицы проверяет на обратимость. Det(A) != 0 тогда и только тогда, когда A обратим.

Инверсия матриц жизненно важна для решения систем линейных уравнений.

AX = B → умножьте обе части на A ^-1 справа → X = A ^-1 B
XA = B → умножьте обе части на A ^-1 справа → X = BA ^-1
ABXC = E → поставить C ^-1 справа и B ^-1 A ^-1 слева → X = B ^-1 A ^-1 EC ^-1

Исключение как обратный решатель

Чтобы решить Ax = b, мы должны найти обратную матрицу A ^-1 . Это можно сделать с помощью Gauss-Jordan Elimination . Этот метод позволяет выполнять три операции со строками:

Линейная комбинация: R _i += kR _j
Масштабирование: R _я *= к
Перестановка строк: R _i ⇆ R _j

После создания матрицы вида Ax = b мы можем найти x, создав расширенную матрицу вида [ A | b ] и преобразование левой части в единичную матрицу:

Чтобы найти x алгебраически, Ax = b → A ^-1 Ax = A ^-1 b → 𝟙 x = A ^-1 б. Таким образом, Гаусс-Жордан облегчает открытие обратной матрицы A ^-1. Мы можем явно показать это вычисление, установив расширенную матрицу вида [ A | 1 ]

Операции со строками — это функции, которые воздействуют на векторы. Так же и матрицы. Таким образом, неудивительно, что каждая из наших трех операций со строками соответствует элементарной матрице . Элементарная матрица аналогична единичной матрице; на картинке ниже расходится только заштрихованная область.

Теперь мы видим, что операции над строками исключения Гаусса-Жордана являются разновидностью факторизации: мы находим элементарные матрицы, лежащие в основе A ^-1 :

Thus E ₄ E ₃ E ₂ E ₁ = A ^-1 and Ax = b → (E ₄ E ₃ E ₂ E ₁) AX = (E ₄ E ₃ E ₂ E ₁) B → X = A ^-1 B

СПАСИСТалисные векторные пространства 9000

A 9 B

СПАСИСИСИНТЫ СПАКСИСТИКА 9000

A 9 VECTER 1201120112011201120112011120111012011201110111 гг. множество векторов и все линейные комбинации этих векторов. Множество всех линейных комбинаций называется 9.0120 диапазон . Например, векторное пространство S = span{ v ₁ , v ₂ } состоит из всех векторов вида v = ɑv ₁ + βv ₂ , где ɑ и β — действительные числа.

Векторные пространства можно охарактеризовать базисом : исходным набором векторов, линейная комбинация которых создает векторное пространство. Векторы любого базиса должны быть линейно независимыми или ортогональными . Вы можете проверить, являются ли два вектора ортогональными, подтвердив их скалярное произведение u · v = 0. 9Размерность 0120 векторного пространства — это мощность базиса (количество ортогональных векторов).

Напомним, что матрицы — это функции, которые проецируют векторы от ℝ ⁿ до ℝ ^m . Это соответствует проецированию из пространства строк в пространство столбцов следующим образом:

Мы раскроем все значения этого графика в другой раз. А пока достаточно понять, что обнаружение оснований этих подпространств — полезное упражнение.

Например, если мы покажем, что матрица имеет непустое ядро, это само по себе является доказательством необратимости. Почему? Потому что если Т _A отправляет вектор в нулевой вектор, нет T _A ^-1, которые могут отменить эту операцию.

Мы можем сказать больше. Для матрицы A размера n x n следующие утверждения эквивалентны:

A обратим
Определитель A отличен от нуля.
RREF A представляет собой единичную матрицу размера n x n
Ранг матрицы равен n
Пространство строки A равно ℝ ⁿ
Размер столбца A равен ℝ ⁿ
A не имеет пустого пространства (только нулевой вектор N(A) = {0} )

Исключение как базовый идентификатор

Мы видели, как исключение обнаруживает (и факторизует) обратную матрицу. Но что происходит, когда обратного не существует? Ну, у исключения есть естественная, уникальная точка остановки:

Матрицы в сокращенной эшелонированной форме строк (RREF) обладают следующими свойствами:

Строки со всеми нулями перемещаются вниз.
Первое ненулевое число слева ( опорная точка ) находится справа от опорной точки над ней.
Каждая опорная точка равна 1 и является единственной ненулевой записью в своем столбце

Исключение Гаусса-Жордана может заменить любую матрицу эквивалентной в форме rref. Обратите внимание, что мы видели несколько примеров исключения, создающих единичную матрицу 1 , когда A обратимо. Это возможно только потому, что 1 соответствует критериям ссылки.

После того, как матрица находится в форме rref, становится тривиальным открытие основы для трех ее фундаментальных пространств:

Базис R(A): все векторы-строки, отличные от нуля
Базис C(A): все векторы-столбцы, содержащие точку опоры.
Базис N(A): решение Ax = 0

Мы видим, что rank(A) + nullity(A) = 3 + 1 = 4, что действительно является количеством столбцов. Кроме того, пространство столбцов A равно пространству строк A ^T . Это не случайность, так как транспонирование просто меняет местами строки со столбцами.

Выводы

Векторы — это группы чисел; матрицы — это функции, которые действуют на векторы.
Мы можем решить линейные уравнения, проведя исключение Гаусса-Жордана.
Решение на основе исключения Гаусса-Жордана основано на поиске обратной матрицы A ^-1
Область определения матриц – это ее векторы-строки, ее кодовая область – это векторы-столбцы.
Даже если матрица необратима, исключение может найти ее наиболее сокращенную форму (RREF).
RREF могут использоваться для получения фундаментальных подпространств.

До следующего раза.

93 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2п 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)грех(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Метод исключения Гаусса Вопросы и ответы

Этот набор вопросов и ответов с множественным выбором численного анализа (MCQ) фокусируется на «Методе исключения Гаусса — 1».

1. Решите следующие уравнения методом исключения Гаусса.

 х+4y-z = -5
х+у-6z = -12
3x-y-z = 4

а) х = 1,64791, у = 1,14085, z = 2,08451
б) х = 1,65791, y = 1,14185, z = 2,08441
c) x = 1,64691, y = 1,14095, z = 2,08461
d) x = 1,64491, y = 1,15085, z = 2,09451
Просмотреть ответ Методом исключения получаем
$\begin{bmatrix}
1 & 4 & -1\\
1 & 1 & -6\\
3 & -1 & -1\\
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin{bmatrix}
-5\\
-12\\
4\\
\end {bматрица} $

By R ₂ -R ₁ и R ₃ -3R ₁
$\begin{bmatrix}
1 & 4 & -1\\
0 & -3 & -5 \\
0 & -13 & 2\\
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin{bmatrix}
-5\\
-7\\
19\\
\end{bmatrix} $

Примечание: Запишитесь на бесплатные занятия по санфаянсу в Telegram или Youtube

R ₃ -(-13/-3)*R ₂
$\begin{bmatrix}
1. 0000 & 4.0000 & -1.0000\\
0 & -3.0000 & -5.0000\\
0 6 & 06 & 7 23. \
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin{bmatrix}
-5\\
-7\\
49,33333\\
\end{bmatrix} $

x+4y-z = -5
-3y-5z = -7
23,6667z = 49,3333
Следовательно, z = 2,08451
-3y = — 7+5z
Следовательно, y = -1,14085
x = -4y+z-5
Следовательно, x = 1,64791.

2. Найдите значения x, y, z в следующей системе уравнений методом исключения Гаусса.

 2x + y – 3z = -10
-2у + г = -2
г = 6

а) 2, 4, 6
б) 2, 7, 6
в) 3, 4, 6
г) 2, 4, 5
Посмотреть ответ

Ответ: а
Объяснение: Методом исключения Гаусса получаем
$\begin{bmatrix}
2 & 1 & -3\\
0 & -2 & 1\\
0 & 0 & 1\\
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin{bmatrix}
-10\\
-2\\
6\\
\end{bmatrix} $
z = 6.
-2y+z = -2
Отсюда y = 4.
2x + y – 3z = -10
Отсюда z = 6.

3. Решить данную систему уравнений методом исключения Гаусса метод.

 3x + 4y – z = -6
-2г + 10г = -8
4у – 2з = -2

а) (-2, -1, -1)
б) (-1, -2, -1)
в) (-1, -1, -2)
г) (-1, -1, -1)
Посмотреть ответ

Ответ: d
Объяснение: Здесь,
$\begin{bmatrix}
3 & 4 & -1\\
0 & -2 & 10\\
0 & 4 & -2\\
\end {bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin{bmatrix}
-6\\
-8\\
-2\\
\end{bmatrix} $
Матрица почти представляет собой треугольную Матрицу. Умножая строку 2 на 2 и добавляя ее к строке 3, мы получаем верхнюю треугольную матрицу с 90 109 x, y, z = (-1, -1, -1).

4. Следующая система уравнений имеет:

 x – y – z = 4
2x - 2y - 2z = 8
5х – 5у – 5з = 20

a) Единственное решение
b) Нет решения
c) Бесконечное множество решений
d) Конечные решения
Просмотреть ответ

Ответ: c
Объяснение: Умножение строки 1 на -2, затем сложение строки 1 и строки 2 1-й строки матрицы уменьшается 0.
$\begin{bmatrix}
0 & 0 & 0\\
2 & -2 & -2 \\
5 & -5 & -5\\
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}$ = $ \begin {bmatrix}
0\\
8\\
20\\
\end{bmatrix} $
Следовательно, решений бесконечно много.

5. Решите эту систему уравнений и прокомментируйте характер решения, используя метод исключения Гаусса.

 х + у + г = 0
-х – у + 3z = 3
-х – у – г = 2

а) Единственное решение
б) Нет решения
в) Бесконечное множество решений
d) Конечные решения
Просмотреть ответ

Ответ: b
Объяснение: Методом исключения Гаусса мы складываем строки 1 и строки 3, чтобы получить следующую матрицу
$\begin{bmatrix}
1 & 1 & 1\\
— 1 & -1 & 3\\
0 & 0 & 0\\
\end{bmatrix} $ $ \begin{bmatrix}
x\\
y\\
z\\
\end{bmatrix}\ ) = \( \begin{bmatrix}
0\\
3\\
2\\
\end{bmatrix} $

Следовательно, матрица не имеет решения, так как 0 ≠ 2.

6. Цель шагов исключения в методе исключения Гаусса состоит в том, чтобы уменьшить матрицу коэффициентов до ____________
a) диагональ
b) тождество
c) нижний треугольник
d) верхний треугольник
Посмотреть ответ

Ответ: d
Объяснение: In Методом исключения Гаусса мы стремимся свести данную матрицу к матрице верхнего треугольника для решения x, y, z.

7. Деление на ноль при исключении по Гауссу системы уравнений [A] * [X]=[C] означает, что матрица коэффициентов [A] равна ______
a) Обратимый
b) Несингулярный
c) Нельзя определить, является ли он единственным или несингулярным единственное или нет.

8. В каком из следующих случаев обе части уравнения умножаются на ненулевую константу?
a) Метод исключения Гаусса
b) Гауссовская несогласованная процедура
c) Гауссовская непротиворечивая процедура
d) Гауссова замещающая процедура
View Answer

Ответ: a
Объяснение: Метод исключения Гаусса использует обе части уравнения для умножения на ненулевую константу. Затем матрица сводится к верхней треугольной матрице, чтобы получить значения соответствующих переменных.

9. В методе исключения Гаусса исходные уравнения преобразуются с помощью _____________
a) Операции со столбцами
b) Операции со строками
c) Математические операции
d) Операции с подмножествами
Просмотр ответа

Ответ: b
Объяснение: Операции со строками используются в методе исключения Гаусса, чтобы свести матрицу к верхней треугольной матрице и, таким образом, найти x, y, z.

10. Следующая информация касалась скорости и времени транспортного средства. Он подчиняется квадратному уравнению v(t)=at ² +bt+c. Следовательно, найдите матрицу, которая наиболее точно представляет уравнение.

Т	с	0	14	15	20	30	35
В	м/с	0	227,04	362,78	517,35	602,97	901,67

а) $\begin{bmatrix}
176 & 14 & 1\\
225 & 15 & 1\\
400 & 20 & 1\\
\end{bmatrix} $ $ \begin{bmatrix }
a\\
b\\
c\\
\end{bmatrix}$ = $ \begin{bmatrix}
227,04\\
362,78\\
517,35\\
\end{bmatrix} $
б) $\begin{bmatrix}
225 & 15 & 1\\
400 & 20 & 1\\
900 & 30 & 1\\
\end{bmatrix} $ $ \begin{bmatrix}
a \\
b\\
c\\
\end{bmatrix}$ = $ \begin{bmatrix}
362,78\\
517,35\\
602,97\\
\end{bmatrix} $
c) \ (\begin{bmatrix}
0 & 0 & 1\\
225 & 15 & 1\\
400 & 20 & 1\\
\end{bmatrix} \) $ \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}$ = $ \begin{bmatrix}
0\\
362,78\\
517,35\\
\end{bmatrix} $
d) $\begin{bmatrix}
400 & 20 & 1\\
900 & 30 & 1\\
1225 & 35 & 1\\
\end{bmatrix} $ $ \begin{bmatrix}
a\\
b\\
c\\
\end{bmatrix}$ = $ \begin{bmatrix}
517. 35\ \
602.97\\
901.67\\
\end{bmatrix} $
Просмотреть ответ

Ответ: b
Объяснение: Ближайшие к t=21 сек точки 15, 20, 30
V(t ₀ ) = 362,78 м/с = а(15) ² +b(15)+c
V(t ₁ ) = 517,35 м/с = a(20) ² +b(20)+c
V(t ₂ ) = 602,97 м/с s = a(30) ² +b(30)+c
Следовательно,
225a+15b+c = 362,78
400a+20b+c = 517,35
900a+30b+c = 602,97
Что приводит нас к $ \begin{bmatrix}
225 & 15 & 1\\
400 & 20 & 1\\
900 & 30 & 1\\
\end{bmatrix} $ $ \begin{bmatrix}
a\\
b \\
c\\
\end{bmatrix}$ = $ \begin{bmatrix}
362,78\\
517,35\\
602,97\\
\end{bmatrix} $.

11. Процесс исключения в методе исключения Гаусса также известен как _____________
a) Исключение в прямом направлении
b) Исключение в обратном направлении
c) Исключение в боковом направлении
d) Исключение в поперечном направлении
Просмотреть ответ

Ответ: a
Объяснение: Процесс исключения в методе исключения Гаусса, также известном как прямое исключение. В этом методе матрица сводится к верхней треугольной матрице.

12. Сокращенная форма Матричного метода исключения Гаусса также называется ____________
a) Эшелонная форма столбца
b) Эшелонная форма строки-столбца
c) Эшелонная форма столбца-строки
d) Эшелонная форма строки
Посмотреть ответ

Ответ: d
Объяснение: Сокращенная форма матрицы в методе исключения Гаусса называется формой эшелона строк. Это сказано потому, что в методе исключения Гаусса учитываются только операции со строками.

Sanfoundry Global Education & Learning Series – Численные методы.

Чтобы практиковать все области численных методов, здесь полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .

Категории Численные методы MCQ

Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия.

Метод Жордана-Гаусса

История возникновения метода

Практическое применение метода Жордана-Гаусса

Объяснение сущности метода Жордана-Гаусса

Получение обратной матрицы методом Жордана-Гаусса

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

+7-911-7987704

Метод Жордана-Гаусса для решения СЛАУ: основные понятия, примеры, определения

Основные понятия

Произвольный способ выбора разрешающих элементов

Выбор разрешающих элементов на главной диагонали матрицы системы

Метод Жордана-Гаусса — 📙 Математика

Решение систем линейных алгебраических уравнений в системе MATLAB

принцип, теорема и примеры решения задач

Историческая справка

Принцип метода Гаусса

Примеры решения систем уравнений

Калькулятор исключения Гаусса Джордана с шагами

Введение в Калькулятор исключения Гаусса Джордана

Формула, используемая калькулятором метода исключения Гаусса

Как пользоваться калькулятором метода Гаусса-Жордана?

Зачем использовать калькулятор исключения Гаусса?

Преимущества использования Калькулятора метода исключения Гаусса по Жордану

Другие связанные калькуляторы

Алан Уокер

Исключение Гаусса-Джордана | Меньше пробелов

Метод исключения Гаусса Вопросы и ответы

Добавить комментарий Отменить ответ