Логарифмические неравенства
1.Решить неравенство:
ОДЗ:
Решение:
Так как основание логарифма больше 1, то знак неравенства сохраняем:
Ответ:
2.Решить неравенство:
ОДЗ:
Решение:
Так как основание логарифма меньше 1, то знак неравенства меняем:
Пересекаем решение и ОДЗ, имеем:
3.Решить неравенство:
ОДЗ:
Решим методом интервалов. Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – тоже выколотая точка, так как знак строгий. Таким образом, .
Решение:
Переходим к сравнению подлогарифмических выражений, знак сохраняем: основание больше 1:
Корень числителя – , корень знаменателя – эта точка выколота всегда, корень числителя – точка закрашенная, она войдет в решение, так как знак неравенства не строгий. Таким образом, .
При наложении решения на ОДЗ получим:
Ответ: .
4.Решить неравенство:
ОДЗ:
Решение этой системы –
Решение:
Корни:
Поскольку знак неравенства нестрогий, то точки входят в решение: на рисунке их нужно изобразить закрашенными. Решение неравенства: .
Накладывая решение на область допустимых значений, получаем:
Ответ:
5.Решить неравенство:
ОДЗ:
Решение этой системы –
Решение:
Точка 1 является выколотой – это корень знаменателя, точка 2 – корень четной кратности, а мы помним, что в таких точках знак интервала не изменяется! Поэтому решение будет выглядеть так:
Решение неравенства
Решение неравенства:
Это полностью укладывается в ОДЗ, поэтому ответ таким и будет:
Ответ:
6.Решить неравенство:
ОДЗ:
Допустимые значения :
Решение неравенства проведем методом рационализации:
Упрощаем:
Раскладываем на множители:
Отмечаем полученные точки на координатной прямой:
Решение неравенства
Наложив это решение на ОДЗ, имеем:
Ответ:
easy-physic.ru
Логарифмические неравенства. Как решать логарифмические неравенства?
Если проще: это неравенства, в которых неизвестные (иксы) или выражения с ними находятся внутри логарифмов.
Примеры:
\(\log_3x≥\log_39\)
\(\log_3 {(x^2-3)}< \log_3{(2x)}\)
\(\log_{x+1}{(x^2+3x-7)}>2\)
\(\lg^2{(x+1)}+10≤11 \lg{(x+1)}\)
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.

|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)\({(x+1)}\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства. Напоминаю ОДЗ для логарифма \(\log_ab\):
\(b>0\), \(a>0\), \(a≠1\).
\(-\) число в основании логарифмов слева и справа одинаково;
\(-\) логарифмы слева и справа — «чистые», то есть нет никаких коэффициентов, умножений, делений и т.д. – только одинокие логарифмы и слева, и справа;
Кстати, в конце (после решения) не забудьте пересечь решения неравенства с ОДЗ.
Например:
|
1) \(\log_3{(x^2-3)}>\log_3{(2x)}\) |
Не написали ОДЗ и не пересекли с ним решение. Неравенство решено неверно. |
|
2) \(\log_5{(x-7)}≤\log_3{4} \) |
Основания логарифмов разные, переход к \(x-7≤4\) невозможен. |
|
3) \(\log_6{(x-2)}-\log_6{x}<\log_6{(2x)}\) |
Логарифмы не «чистые», так как слева есть разность логарифмов. Переход к \((x-2)-x<2x\) невозможен. |
|
4) \(\log_2{(x^2-24)}≥-\log_2x\) |
Логарифмы не «чистые» т.к. справа есть минус перед логарифмом. Переход к \(x^2-24≥-x\) невозможен. |
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\) |
Выпишем ОДЗ. |
|
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\) |
ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами. |
|
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\) |
Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) |
|
|
Запишем ОДЗ в виде интервалов. |
|
\(x∈(-∞;\)\(\frac{2}{3}\)\()∪(\)\(\frac{3}{2}\)\(;∞)\) |
С ОДЗ закончили, переходим к решению. |
|
Решение: |
Воспользовавшись свойствами логарифмов
и свойствами степени, преобразуем правую часть: |
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\) |
Мы привели неравенство к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем. |
|
\(\frac{3x-2}{2x-3}\)\(≥\) \(3\) |
Переносим \(3\) и приводим к общему знаменателю, пользуясь свойствами дробей. |
|
\(\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\) |
Раскрываем скобки, приводим подобные слагаемые. |
|
\(\frac{-3x+7}{2x-3}\)\(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
\(\frac{3x-7}{2x-3}\)\(≤\) \(0\) |
Далее выносим \(3\) из числителя и \(2\) из знаменателя. |
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\) |
Построим числовую ось и отметим на ней точки \(\frac{7}{3}\) и \(\frac{3}{2}\). Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль. |
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
Записываем окончательный ответ. |
Пример. Решить неравенство: \(\log^2_3x-\log_3x-2>0\)
Решение:
|
\(\log^2_3x-\log_3x-2>0\) |
Выпишем ОДЗ. |
|
ОДЗ: \(x>0\) |
Приступим к решению. |
|
Решение: \(\log^2_3x-\log_3x-2>0\) |
Перед нами типичное квадратно-логарифмическое неравенство. Делаем замену. |
|
\(t=\log_3x\) |
Раскладываем левую часть неравенства на множители. |
|
\(D=1+8=9\) |
Решаем неравенство методом интервалов. |
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену. |
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
Запишем ответ. |
Смотрите также:
Показательные неравенства
cos-cos.ru
Решение логарифмических неравенств
Решение логарифмических неравенств имеет много общего с решением показательных неравенств:
а) При переходе от логарифмов к выражениям, стоящим под знаком логарифма, мы также сравниваем основание логарифма с единицей;
б) Если мы решаем логарифмическое неравенство с помощью замены переменных, то нужно решать относительно замены до получения простейшего неравенства.
Однако, есть одно очень важное отличие: поскольку логарифмическая функция имеет ограниченную область определения, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, необходимо учитывать область допустимых значений.
Если при решении логарифмического уравнения можно найти корни уравнения, а потом сделать проверку, то при решении логарифмического неравенства этот номер не проходит: при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать ОДЗ неравенства.
Итак. Простейшее логарифмическое неравенство имеет вид:
V , где V — один из знаков неравенства: <,>, ≤ или ≥.
Если основание логарифма больше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
равносильно системе:
Если основание логарифма больше нуля и меньше единицы (), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
равносильно системе:
Рассмотрим примеры решения логарифмических неравенств.
1. Решим неравенство:
Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:
Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.
Решим систему неравенств:
Корни квадратного трехчлена: ,
Отсюда:
Ответ:
2. Решим неравенство:
Мы видим, что в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:
Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).
Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:
Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма. Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:
Отсюда:
Ответ:
3. Решим неравенство:
В нашем неравенстве логарифм стоит в квадрате, поэтому это логарифмическое неравенство мы будем решать с помощью замены переменных.
Сначала приведем логарифмы к одному основанию:
Введем замену переменных:
.
Получим квадратное неравенство:
Значит, .
Запишем это двойное неравенство в виде системы:
Вот только теперь, когда мы получили систему простейших неравенств относительно , мы можем вернуться к исходной переменной.
Перейдем к выражениям, стоящим под знаком логарифма:
Последнее неравенство системы — это ОДЗ неравенства. Заметим, что оно выполняется, если выполняется второе неравенство системы, поэтому нет необходимости его решать.
Решим систему.
Первое неравенство системы преобразуется к виду
Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значениях .
Второе неравенства преобразуется к виду , отсюда
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Логарифмические неравенства. Примеры и методы решения
Вам кажется, что до ЕГЭ еще есть время, и вы успеете подготовиться? Быть может, это и так. Но в любом случае, чем раньше школьник начинает подготовку, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одно из заданий, а значит, возможность получить дополнительный балл.

Вы уже знаете, что такое логарифм(log)? Мы очень надеемся, что да. Но даже если у вас нет ответа на этот вопрос, это не проблема. Понять, что такое логарифм очень просто.
Почему именно 4? В такую степень нужно возвести число 3, чтобы получилось 81. Когда вы поняли принцип, можно приступать и к более сложным вычислениям.
Неравенства вы проходили еще несколько лет назад. И с тех пор они постоянно встречаются вам в математике. Если у вас проблемы с решением неравенств, ознакомьтесь с соответствующим разделом.
Теперь, когда мы познакомились с понятиями по отдельности, перейдем к их рассмотрению в общем.
Логарифмические неравенства (определение)
Самое простое логарифмическое неравенство.
Простейшие логарифмические неравенства не ограничиваются этим примером, есть еще три, только с другими знаками. Зачем это нужно? Чтобы полнее понять, как решать неравенство с логарифмами. Теперь приведем более применимый пример, все еще достаточно простой, сложные логарифмические неравенства оставим на потом.
Как это решить? Все начинается с ОДЗ. О нем стоит знать больше, если хочется всегда легко решать любое неравенство.
Что такое ОДЗ? ОДЗ для логарифмических неравенств
Аббревиатура расшифровывается как область допустимых значений. В заданиях для ЕГЭ нередко всплывает данная формулировка. ОДЗ пригодится вам не только в случае логарифмических неравенств.
Посмотрите еще раз на вышеприведенный пример. Мы будем рассматривать ОДЗ, исходя из него, чтобы вы поняли принцип, и решение логарифмических неравенств не вызывало вопросов. Из определения логарифма следует что, 2х+4 должно быть больше нуля. В нашем случае это означает следующее.
Это число по определению должно быть положительным. Решите неравенство, представленное выше. Это можно сделать даже устно, здесь явно, что X не может быть меньше 2. Решение неравенства и будет определением области допустимых значений.
Теперь перейдем к решению простейшего логарифмического неравенства.
Отбрасываем из обеих частей неравенства сами логарифмы. Что в результате у нас остается? Простое неравенство.
Решить его несложно. X должен быть больше -0,5. Теперь совмещаем два полученных значения в систему. Таким образом,
Это и будет область допустимых значений для рассматриваемого логарифмического неравенства.
Зачем вообще нужно ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не входит в область допустимых значений, значит, ответ попросту не имеет смысла. Это стоит запомнить надолго, так как в ЕГЭ часто встречается необходимость поиска ОДЗ, и касается она не только логарифмических неравенств.
Алгоритм решения логарифмического неравенства
Решение состоит из нескольких этапов. Во-первых, необходимо найти область допустимых значений. В ОДЗ будет два значения, это мы рассмотрели выше. Далее нужно решить само неравенство. Методы решения бывают следующими:
- метод замены множителей;
- декомпозиции;
- метод рационализации.
В зависимости от ситуации стоит применять один из вышеперечисленных методов. Перейдем непосредственно к решению. Раскроем наиболее популярный метод, который подходит для решения заданий ЕГЭ практически во всех случаях. Далее мы рассмотрим метод декомпозиции. Он может помочь, если попалось особенно «заковыристое» неравенство. Итак, алгоритм решения логарифмического неравенства.
Примеры решения :
Мы не зря взяли именно такое неравенство! Обратите внимание на основание. Запомните: если оно больше единицы, знак остается прежним при нахождении области допустимых значений; в противном случае нужно изменить знак неравенства.
В результате мы получаем неравенство:
Теперь приводим левую часть к виду уравнения, равному нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Надеемся, что с решением такого простого уравнения у вас не будет проблем. Ответы -4 и -2. Это еще не все. Нужно отобразить эти точки на графике, расставить «+» и «-». Что нужно для этого сделать? Подставить в выражение числа из интервалов. Где значения положительны, там ставим «+».
Ответ: х не может быть больше -4 и меньше -2.
Мы нашли область допустимых значений только для левой части, теперь нужно найти область допустимых значений правой части. Это не в пример легче. Ответ: -2. Пересекаем обе полученные области.
И только теперь начинаем решать само неравенство.
Упростим его, насколько возможно, чтобы решать было легче.
Снова применяем метод интервалов в решении. Опустим выкладки, с ним уже и так все понятно по предыдущему примеру. Ответ.
Но этот метод подходит, если логарифмическое неравенство имеет одинаковые основания.
Решение логарифмических уравнений и неравенств с разными основаниями предполагает изначальное приведение к одному основанию. Далее применяйте вышеописанный метод. Но есть и более сложный случай. Рассмотрим один из самых сложных видов логарифмических неравенств.
Логарифмические неравенства с переменным основанием
Как решать неравенства с такими характеристиками? Да, и такие могут встретиться в ЕГЭ. Решение неравенств нижеследующим способом тоже полезно скажется на вашем образовательном процессе. Разберемся в вопросе подробным образом. Отбросим теорию, перейдем сразу к практике. Чтобы решать логарифмические неравенства, достаточно однажды ознакомиться с примером.
Чтобы решить логарифмическое неравенство представленного вида, необходимо привести правую часть к логарифму с тем же основанием. Принцип напоминает равносильные переходы. В итоге неравенство будет выглядеть следующим образом.
Собственно, остается создать систему неравенств без логарифмов. Используя метод рационализации, переходим к равносильной системе неравенств. Вы поймете и само правило, когда подставите соответствующие значения и проследите их изменения. В системе будут следующие неравенства.
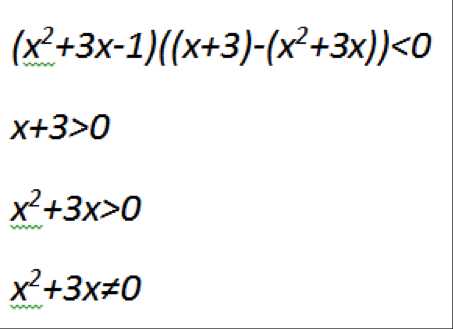
Воспользовавшись методом рационализации при решении неравенств нужно помнить следующее: из основания необходимо вычесть единицу, х по определению логарифма из обеих частей неравенства вычитается (правое из левого), два выражения перемножаются и выставляются под исходным знаком по отношению к нулю.
Дальнейшее решение осуществляется методом интервалов, здесь все просто. Вам важно понять отличия в методах решения, тогда все начнет легко получаться.
В логарифмических неравенствах много нюансов. Простейшие из них решать достаточно легко. Как сделать так, чтобы решать каждое из них без проблем? Все ответы вы уже получили в этой статье. Теперь впереди вас ждет длительная практика. Постоянно практикуйтесь в решении самых разных задач в рамках экзамена и сможете получить наивысший балл. Успехов вам в вашем непростом деле!
Похожие статьи
Рекомендуем почитать:
karate-ege.ru
Решение логарифмических неравенств
Разделы: Математика
Класс:
#}Цели урока:
Дидактические:
- 1 уровень – научить решать простейшие логарифмические неравенства, применяя определение логарифма, свойства логарифмов;
- 2 уровень – решать логарифмические неравенства, выбирая самостоятельно способ решения;
- 3 уровень – уметь применять знания и умения в нестандартных ситуациях.
Развивающие: развивать память, внимание, логическое мышление, навыки сравнения, уметь обобщать и делать выводы
Воспитательные: воспитывать аккуратность, ответственность за выполняемое задание, взаимопомощь.
Методы обучения: словесный, наглядный, практический, частично-поисковый, самоуправления, контроля.
Формы организации познавательной деятельности учащихся: фронтальный, индивидуальный, работа в парах.
Оборудование: набор тестовых заданий, опорный конспект, чистые листы для решений.
Тип урока: изучение нового материала.
Ход урока
1. Организационный момент. Объявляются тема и цели урока, схема проведения урока: каждому ученику выдается оценочный лист, который ученик заполняет в течении урока; для каждой пары учеников – печатные материалы с заданиями, выполнять задания нужно в парах; чистые листы для решений; опорные листы: определение логарифма; график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств.
Все решения после самооценки сдаются учителю.
Оценочный лист учащегося
| Учебный элемент 1 | Учебный элемент 2 | Учебный элемент 3 | Учебный элемент 4 | Учебный элемент 5 |
| 1. 2. 3. 4. 5. |
1. 2. 3. 4. |
1. 2. 3 |
1. 2. |
1. 2. |
| итог | итог | итог | итог | итог |
| Общий итог: | ||||
2. Актуализация знаний.
Указания учителя. Вспомните определение логарифма, график логарифмической функции и ее свойства. Для этого прочитайте текст на с.88–90, 98–101 учебника “Алгебра и начала анализа 10–11” под редакцией Ш.А Алимова, Ю.М Колягина и др.
Ученикам раздаются листы, на которых записаны: определение логарифма; изображен график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств, пример решения логарифмического неравенства, сводящегося к квадратному.
3. Изучение нового материала.
Решение логарифмических неравенств основано на монотонности логарифмической функции.
Алгоритм решения логарифмических неравенств:
А) Найти область определения неравенства (подлогарифмическое выражение больше
нуля).
Б) Представить (если возможно) левую и правую части неравенства в виде
логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция: если
t>1, то возрастающая; если 0<t>1, то убывающая.
Г) Перейти к более простому неравенству (подлогарифмических выражений),
учитывая, что знак неравенства сохранится, если функция возрастает, и изменится,
если она убывает.
Учебный элемент № 1.
Цель: закрепить решение простейших логарифмических неравенств
Форма организации познавательной деятельности учащихся: индивидуальная работа.
Задания для самостоятельной работы на 10 минут. Для каждого неравенства имеются несколько вариантов ответов, нужно выбрать верный и проверить по ключу.
КЛЮЧ: 13321, максимальное кол-во баллов – 6 б.
Указания учителя. Проверьте и оцените свою работу. Правильные ответы возьмите у учителя, проставьте количество набранных баллов себе в оценочный лист. Подписанные листы с решениями сдать учителю
Учебный элемент № 2.
Цель: закрепить решение логарифмических неравенств, применяя свойства логарифмов.
Указания учителя. Вспомните основные свойства логарифмов. Для этого прочитайте текст учебника на с.92, 103–104.
Задания для самостоятельной работы на 10 минут.
КЛЮЧ: 2113, максимальное кол-во баллов – 8 б.
Учебный элемент № 3.
Цель: изучить решение логарифмических неравенств методом сведения к квадратному.
Указания учителя: метод сведения неравенства к квадратному состоит в том, что нужно преобразовать неравенство к такому виду, чтобы некоторую логарифмическую функцию обозначить новой переменной, получив при этом квадратное неравенство относительно этой переменной.
Применим метод интервалов.
Указания учителя: Проверьте и оцените работу, правильные ответы возьмите у учителя. Поставьте количество баллов в оценочный лист.
Вы прошли первый уровень усвоения материала. Теперь вам придется самостоятельно выбрать метод решения логарифмических уравнений, используя все свои знания и возможности.
Учебный элемент № 4.
Цель: закрепить решение логарифмических неравенств, выбрав самостоятельно рациональный способ решения.
Задания для самостоятельной работы на 10 минут
Указания учителя. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Проставьте полученные баллы в оценочный лист.
Учебный элемент № 5.
Указания учителя. Молодцы! Вы освоили решение уравнений второго уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных и нестандартных ситуациях.
Задания для самостоятельного решения:
Указания учителя. Замечательно, если вы справились со всем заданием. Молодцы!
4. Итог урока. Проверьте и оцените свою работу. Подсчитайте количество баллов. Проставьте количество баллов в оценочный лист.
Оценка за весь урок зависит от числа набранных баллов по всем учебным элементам:
- если N ≥ 20, то вы получаете оценку “5”,
- при 16 ≤ N ≤ 19 – оценка “4”,
- при 8 ≤ N ≤ 15 – оценка “3”,
- при N < 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).
Оценочные лисы сдать учителю.
5. Домашнее задание: если вы набрали не более 15 б – выполните работу над ошибками (решения можно взять у учителя), если вы набрали более 15 б – выполните творческое задание по теме “Логарифмические неравенства”.
1.11.2011
urok.1sept.ru
Логарифмические неравенства. Видеоурок. Алгебра 11 Класс
На этом уроке мы изучим следующую тему: «Логарифмические неравенства». Для того чтобы научиться правильно решать простейшие логарифмические неравенства, необходимо повторить основные свойства логарифмических функций. На этом занятии мы вместе с преподавателем рассмотрим несколько примеров на указанную тему и научимся их правильно решать, применяя полученные ранее знания.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
Тема: Метод интервалов
Урок: Логарифмические неравенства
Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т. е. функции вида (). Здесь t – независимая переменная, а – конкретное число, у – зависимая переменная, функция.
Вспомним основные свойства логарифмической функции.
Рис. 1. График логарифмической функции при различных основаниях
1. Область определения: ;
2. Область значений: ;
3. Функция монотонна на всей своей области определения. При монотонно возрастает (когда аргумент возрастает от нуля до плюс бесконечности, функция возрастает от минус до плюс бесконечности, ). При монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности, ).
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
Рассмотрим решение логарифмического неравенства, когда основание логарифма .
Неравенство необходимо решать, применяя эквивалентные, равносильные преобразования. Рассмотрим схему. Поскольку мы рассматриваем логарифмическую функцию с основанием, большим единицы, помним, что функция монотонно возрастает. Отсюда:
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:
Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:
Например:
interneturok.ru
Урок 5. Логарифмические неравенства. Системы логарифмических неравенств. Теория.
На этом уроке мы рассмотрим метод решения логарифмических неравенств, основанный на свойствах логарифмической функции. Также мы поговорим о видах логарифмических неравенствах и систем логарифмических неравенств.
Данный урок поможет подготовиться к одному из типов задания С3.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 5. Логарифмические неравенства. Системы логарифмических неравенств
Теория
Конспект урока
На предыдущем уроке мы рассмотрели решение логарифмических уравнений и их систем. На этом уроке речь пойдет о логарифмических неравенствах и их системах.
Мы уже говорили о логарифмической функции и ее свойствах. Важным свойством, которым мы пользовались для решения логарифмических уравнений: монотонность.
Для график логарифмической функции выглядит следующим образом:
— возрастающая функция: чем больше , тем больше . Значит, . В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ: .
Объединяя, получаем: .
Для график логарифмической функции выглядит следующим образом:
— убывающая функция: чем больше , тем меньше . Значит, .
ОДЗ: .
Объединяя, получаем:
.
Лучше всего начинать решение неравенств с проверки ОДЗ. Поскольку даже на первом шаге решения можно получить выражение с измененной ОДЗ.
Например:
ОДЗ:
interneturok.ru
