РЕШЕНИЕ НЕРАВЕНСТВ С МОДУЛЕМ В СРЕДНЕЙ ШКОЛЕ
Введение
ГЛАВА I. ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ
ОРГАНИЗАЦИИ ОБУЧЕНИЯ РЕШЕНИЮ НЕРАВЕНСТВ С МОДУЛЕМ В СРЕДНЕЙ ШКОЛЕ
1.1 Некоторые сведения из истории появления неравенств с модулем 7
1.2. Психолого-педагогические основы обучения школьников при
решении неравенств с модулем 8
1.3. Различные подходы к определению понятия абсолютная величина.
Геометрический смысл модуля. Свойства 11
1.4. Виды неравенств с модулем и способы их решения 14
ГЛАВА II. МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ НЕРАВЕНСТВ С
МОДУЛЕМ В СРЕДНЕЙ ШКОЛЕ 24
2.1. Анализ обучения неравенств с модулем в УМК по программе
основной школы 24
2.2. Методические особенности изучения темы «неравенства с
модулем» на уроках алгебры в 9 классе на базовом и повышенном уровнях. .. 31
ЗАКЛЮЧЕНИЕ 49
СПИСОК ЛИТЕРАТУРЫ 52
ПРИЛОЖЕНИЕ
В различных разделах школьного курса математики, а также при изучении высшей математики и физики понятие модуль используется довольно часто.
В программе основного общего образования по математике [33, с. 35] в разделе арифметика в теме «Рациональные числа» коротко записано: «Модуль (абсолютная величина) числа». Больше это понятие не упоминается ни в указанной программе, ни в программе среднего (полного) образования. Вводится понятие «модуль» в курсе математики шестого класса через его геометрический смысл, но не как унитарная операция на множестве чисел.
Далее в 6 классе модуль используется при сравнении чисел, при умножении и делении положительных и отрицательных чисел, а также приводится несколько простейших уравнений и неравенств с использованием модуля.
В последующих классах только в некоторых учебниках вводится повторно понятие модуля числа и модуля выражения, и проскакивают эпизодические простейшие задания с модулем, например, линейные уравнения с модулем, но и они приводятся изредка и бессистемно.
Можно сказать, что ситуация с изучением неравенств с модулем в средней школе близка к катастрофической. После окончания как основной, так и средней школы обучающимся предстоит пройти ГИА по математике, а во множестве заданий части 2 ОГЭ и части С ЕГЭ встречаются задания с модулем самого разного вида, причем такого уровня сложности, который и не мыслился ранее.
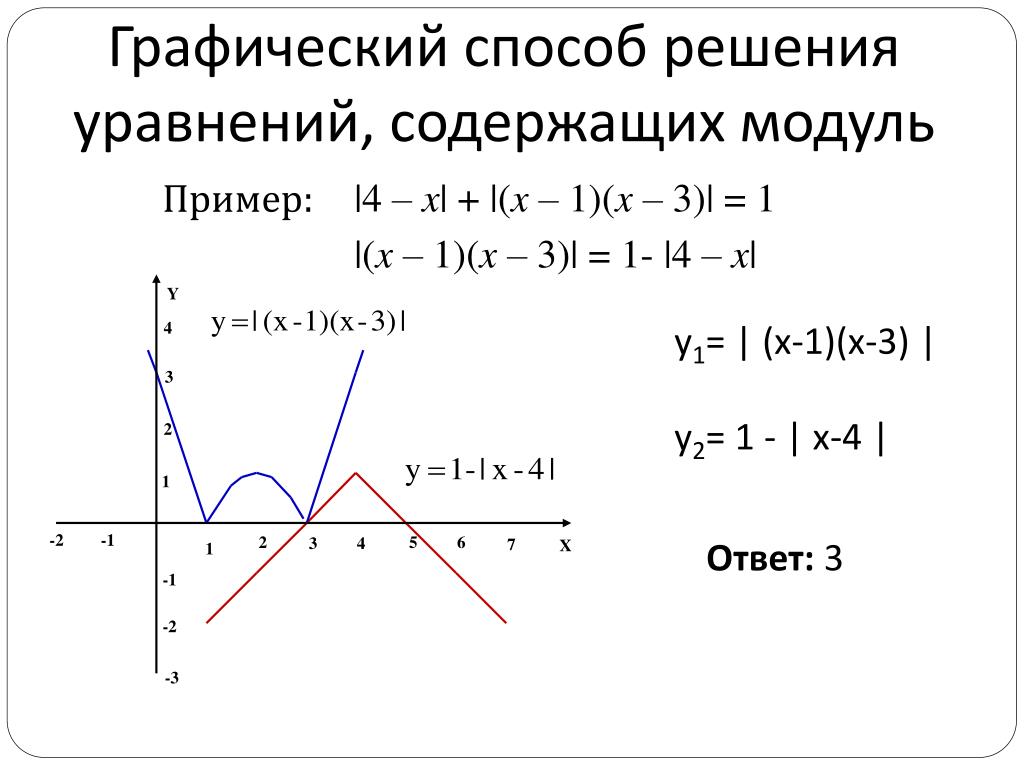
Кроме того, на вступительных экзаменах в высшие учебные заведения, а в последнее время и на Едином государственном экзамене, задания с модулем есть постоянно. Кто-то же должен научить школьников их решать, а это посильно осуществить и на школьных уроках математики, не прибегая к помощи репетиторов.
Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модуле и его свойствах, полученных обучающимися за весь период обучения. Актуальность, теоретическая и практическая значимость проблемы, ее недостаточная разработанность в литературе обусловили выбор темы дипломного проекта, определили его цель и задачи.
Проблема исследования: каковы особенности обучения решению неравенств с модулем.
Степень изученности проблемы. В настоящее время на страницах журнала «Математика в школе» и газеты «Математика» публикуется множество статей, посвященных теме «Модуль числа». Так Гуртова О.С. в своей статье «Решение неравенств с модулем в 9 классе делится опытом решения простейших неравенств на основании определения модуля числа, а Иванова Е.
Ю. предлагает еще один способ решения неравенств, основанный на понятии расстояния. Для обучающихся 7-9 классов В.Ф. Чаплыгин в статье «Сравнение и классификация в упражнениях с «модулями»» демонстрирует способ, основанный на сравнении выражений, стоящих под знаком модуля, а Смоляков А. О. публикует интересный подбор заданий на тему: «Решение уравнений и неравенств, содержащих знак модуля». Однако, проблему особенностей решения неравенств с модулем в средней школе эти авторы решали по отдельным аспектам, не соединив их в общую тему. Достаточно большой интересный опыт других педагогов, свои наработки мы попытались соединить в единую систему знаний по теме «Решение неравенств с модулем в средней школе».Объект исследования: неравенства с модулем.
Гипотеза: мы предполагаем, что систематическое использование различных способов для решения неравенств, содержащих абсолютную величину, приведет к повышению качества знаний по теме «Решение неравенств с модулем».
Целью дипломного проекта является разработка методики обучения решению неравенств, содержащих знак модуля в средней школе.
Для достижения цели в работе поставлены и решены следующие задачи:
1. Изучить определение понятия абсолютная величина, геометрический смысл и ее свойства.
2. Определить психолого-педагогические основы обучения школьников при решении неравенств с модулем.
3. Рассмотреть различные виды неравенств с модулем и способы их решения.
4. Изучить состояние и перспективы развития темы «Неравенства с модулем» по отношению к школе.
5. Обосновать и разработать методику обучения теме «Неравенства с модулем» для уроков алгебры в 9 классе.
Теоретическая и методическая база исследования. Теоретической базой исследования являются научные труды, результаты фундаментальных и прикладных исследований современных отечественных и зарубежных специалистов в области математики. Исследование основывается на методологии системного подхода, методов логического и сравнительного анализа.
Информационной базой исследования послужили отечественные и зарубежные публикации в переводе, различные справочные материалы, материалы конференций по исследуемой проблематике.
Практическая значимость работы. Результаты исследования могут быть использованы учителями математики при обучении детей решению неравенств с модулем в средней школе.
Структура работы. Работа состоит из введения, двух глав, заключения, списка литературы и приложения.
Конспект урока «Решение неравенств с модулем»
Урок по алгебре и началам математического анализа в 11 классе по теме «Решение неравенств с модулем». Урок проводится во время обобщающего повторения для систематизации знаний по данной теме и подготовке к ЕГЭ. Урок разработан с применением блочно-модульной технологии. Учащиеся оценивают каждый вид выполненной работы и заносят результаты в оценочный лист, выставляют себе отметку за работу на уроке.
Вы уже знаете о суперспособностях современного учителя?
youtube.com/embed/K0px2wo-Y7c?rel=0″> Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ
Просмотр содержимого документа
«Конспект урока «Решение неравенств с модулем»»
Тема: «Решение неравенств с модулем»
Тип урока: урок повторения и обобщения знаний, закрепления умений.
Цель: совершенствовать умения решать неравенства с модулем различными методами; умения самостоятельно применять знания в стандартных и нестандартных ситуациях;
развивать коммуникативные способности учащихся.
Учебный элемент | Учебный материал с указанием заданий. | Руководство по усвоению материала | ||||||||||||||
УЭ-0 (2 мин) | В процессе работы над учебными элементами вы должны: | Внимательно ознакомьтесь с интегрирующей целью модуля. УЭ1-УЭ4 соответствуют 1 уровню подготовки. УЭ5 обеспечивает 2 уровень. УЭ6 – 3 уровень подготовки. Вся работа над данным модулем сопровождается оценочным листом. | ||||||||||||||
УЭ-1 (10 мин) | Цель: выработка навыка решения неравенств с модулем методом замены совокупностью систем Решите неравенства:
| Вспомните алгоритм решения неравенств с модулем методом замены совокупностью систем. Для этого обратитесь к лекции и опорному конспекту. Выполните письменно самостоятельную работу. Правильные ответы получите от учителя. Исправьте ошибки и проставьте число набранных баллов в свой оценочный лист. Если набрано 6 баллов и больше, переходите к УЭ2. Если набрано меньше 6-ти баллов, следует прорешать задания другого варианта, аналогичные тем, в которых была допущена ошибка. | ||||||||||||||
УЭ-2 (10 мин) | Цель: закрепить умение решать неравенства с модулем методом введения новой переменной.
| Прочитайте внимательно решение примера № 1 из лекции. Выполните самостоятельную работу. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, проставьте количество набранных баллов в оценочный лист. Если набрано 5 баллов, то переходите к следующему этапу, если же меньше, то решайте задание другого варианта, аналогичные тому, в котором была ошибка. | ||||||||||||||
УЭ-3 (10 мин) | Цель: закрепить умение решать неравенства с модулем методом замены множителей.
. | Прочитайте внимательно решение примера №2 из лекции. Выполните самостоятельную работу. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, проставьте количество набранных баллов в оценочный лист. Если набрано 5 баллов, то переходите к следующему этапу, если же меньше, то решайте задание другого варианта, аналогичные тому, в котором была ошибка. | ||||||||||||||
УЭ-4 (13 мин) | Цель: закрепить умение решать неравенства с несколькими модулями. Самостоятельная работа.
| Прочитайте внимательно решение примера №3 из лекции. Выполните самостоятельную работу. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, проставьте количество набранных баллов в оценочный лист. Если набрано 5 баллов, то переходите к следующему этапу, если же меньше, то решайте задание другого варианта, аналогичные тому, в котором была ошибка. | ||||||||||||||
УЭ-5 (20 мин) | Вы прошли 1 уровень усвоения материала. Теперь вам самостоятельно придется выбрать метод решения неравенств. Выполните самостоятельную работу. 1 (3 балла) 2.+ (3 балла) 3. (2 балла) 4. (2 балла) | В случае затруднений воспользуйтесь подсказками. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Исправьте ошибки, проставьте количество набранных баллов в оценочный лист. | ||||||||||||||
УЭ-6 (20 мин) | Вы освоили решение неравенств 2 уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях. Самостоятельная работа. 1. (3 балла) 2. (3 балла) 3. (3 балла) 4. 5. (3 балла) | В случае затруднений воспользуйтесь подсказками. Проверьте и оцените свои работы. Исправьте ошибки, если они есть, подсчитайте количество баллов. Проставьте количество баллов в оценочный лист. Оцените свои работы. | ||||||||||||||
(5 мин) | Подведение итогов. Выставление отметок. Отметка за весь модуль зависит от суммы баллов по всем учебным элементам. Если сумма больше 36, то вы получаете «5», при получении от 27 до 36 баллов – отметка «4», при получении от 21 до 26 баллов – отметка «3», менее 21 балла вы получаете «2». Для тех, кто получил неудовлетворительную отметку проводится коррекционная работа. | Запись домашнего задания. |
(1 балл)
Проставьте набранные баллы в графу «Корректирующие задания».
(3 балла)Оценочный лист учащегося.
Фамилия | |||
Имя | |||
УЭ | Количество баллов за | Корректирующие задания | Общее количество баллов за этап |
№1 | |||
№2 | |||
№3 | |||
№4 | |||
№5 | |||
№6 | |||
Итоговое количество баллов | |||
Отметка | |||
Алгебра — абсолютные неравенства
Онлайн-заметки Пола
Главная
/
Алгебра
/
Решение уравнений и неравенств
/ Неравенства абсолютного значения
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.15: Неравенства абсолютного значения
В предыдущем разделе мы решали уравнения, содержащие абсолютные значения. В этом разделе мы хотим рассмотреть неравенства, содержащие абсолютные значения. Нам нужно будет рассмотреть два отдельных случая.
Неравенства с участием
< и \( \le \)Как и в случае с уравнениями, давайте начнем с довольно простого случая.
\[\слева| р \право| \ле 4\]
Это говорит о том, что каким бы ни было \(p\), оно должно находиться на расстоянии не более 4 от начала координат.
Это означает, что \(p\) должно быть где-то в диапазоне,
\[ — 4 \le p \le 4\]
Мы могли бы иметь подобное неравенство с < и получить аналогичный результат.
В общем, здесь можно использовать следующие формулы:
\[\require{bbox} \bbox[2pt,border:1px сплошной черный]{\begin{align*}{\mbox{If}}\left| р \право| \le b,\,\,\,b > 0\,\,\,\,\,\,\,\,\,\,\,{\mbox{тогда}} — b \le p \le b \\ {\mbox{Если}}\влево| р \право| Обратите внимание, что для этого требуется, чтобы \(b\) было положительным, как мы это делали с уравнениями. Давайте рассмотрим пару примеров. Пример 1 Решите каждую из следующих задач. Показать все решения Скрыть все решения a \(\left| {2x — 4} \right| < 10\) Показать решение На самом деле нечего делать, кроме как вставить формулу. \[- 10 < 2х - 4 < 10\] Теперь это не более чем довольно простое двойное неравенство, которое нужно решить, так что давайте сделаем это. \[\begin{массив}{c} — 6 < 2x < 14\\ - 3 < x < 7\end{массив}\] Обозначение интервала для этого решения: \(\left( { — 3,7} \right)\). b \(\left| {9m + 2} \right| \le 1\) Показать решение Здесь особо нечего делать. \[\begin{array}{c} — 1 \le 9m + 2 \le 1\\ — 3 \le 9m \le — 1\\ \displaystyle — \frac{1}{3} \le m \le — \frac{1}{9}\end{массив}\] Обозначение интервала: \(\left[ { — \frac{1}{3}, — \frac{1}{9}} \right]\). c \(\left| {3 — 2z} \right| \le 5\) Показать решение Нам нужно быть немного осторожными с решением двойного неравенства с этим, но в остальном он почти идентичен предыдущим двум частям. \[\begin{array}{c} -5 \le 3 — 2z \le 5\\ — 8 \le — 2z \le 2\\ 4 \ge z \ge — 1\end{array}\] В последнем шаге не забудьте поменять направление неравенств, так как мы поделили все на отрицательное число. Обозначение интервала для этого решения: \(\left[ { — 1,4} \right]\). Еще раз давайте начнем с простого числового примера. \[\слева| р \право| \ge 4\] Это говорит о том, что каким бы ни было \(p\), оно должно находиться на расстоянии не менее 4 от начала координат, поэтому \(p\) должно находиться в одном из следующих двух диапазонов: \[p \le — 4\hspace{0,25 дюйма}{\mbox{или}}\hspace{0,25 дюйма}p \ge 4\] Перед тем, как дать общее решение, мы должны рассмотреть распространенную ошибку, которую учащиеся совершают при решении подобных задач. \[ — 4 \ge p \ge 4\] Хотя это может показаться логичным, мы не можем не подчеркнуть, что ЭТО НЕ ПРАВИЛЬНО!! Вспомним, о чем говорит двойное неравенство. В двойном неравенстве мы требуем, чтобы оба неравенства выполнялись одновременно. Приведенное выше двойное неравенство будет означать, что \(p\) — это число, которое одновременно меньше -4 и больше 4. Это просто не имеет смысла. Нет числа, удовлетворяющего этому. Эти решения должны быть записаны в виде двух неравенств. Вот общая формула для них. \[\require{bbox} \bbox[2pt,border:1px сплошной черный]{\begin{align*}{\mbox{If}}\left| р \право| \ge b,\,\,\,b > 0\,\,\,\,\,\,\,\,\,\,\,{\mbox{тогда}}p \le — b{\mbox {или}}p \ge b\\ {\mbox{If}}\left| р \право| > b,\,\,\,b > 0\,\,\,\,\,\,\,\,\,\,\,{\mbox{тогда}}p < - b{\mbox{ или }}р > б\конец{выравнивание*}}\] Опять же, мы будем требовать, чтобы здесь \(b\) было положительным числом. Пример 2 Решите каждую из следующих задач. Показать все решения Скрыть все решения a \(\left| {2x — 3} \right| > 7\) Показать решение Опять же, \(p\) представляет количество внутри столбцов абсолютного значения, поэтому все, что нам нужно сделать здесь, это подставить формулу и затем решить два линейных неравенства. \[\begin{align*}2x — 3 & < - 7 & \hspace{0.25in} & {\mbox{or}} & \hspace{0.25in} 2x - 3 & > 7\\ 2x & < - 4 & \hspace{0,25 дюйма} & {\mbox{или}} & \hspace{0,25 дюйма} 2x & > 10\\ x & < - 2 & \hspace{0,25 дюйма} & {\mbox{или}} & \ hspace{0.25in} x & > 5\end{align*}\] Обозначение интервала для них: \(\left( { — \infty , — 2} \right)\) или \(\left( {5,\infty } \right)\). b \(\left| {6t + 10} \right| \ge 3\) Показать решение Давайте просто вставим формулы и перейдем сюда, \[\begin{align*}6t + 10 & \le — 3 &\hspace{0.25in} & {\mbox{or}} & \hspace{0.25in}6t + 10 &\ge 3\\ 6t & \ le — 13 & \hspace{0.25in} & {\mbox{or}} & \hspace{0.25in} 6t & \ge — 7\\ t & \le — \frac{{13}}{6} & \ hspace{0.25in} & {\mbox{or}} & \hspace{0.25in}t & \ge — \frac{7}{6}\end{align*}\] Обозначение интервала для них: \(\left( { — \infty , — \frac{{13}}{6}} \right]\) или \(\left[ { — \frac{7}{6 },\infty } \справа)\). c \(\left| {2 — 6y} \right| > 10\) Показать решение Опять же, здесь особо нечего делать. \[\begin{align*}2 — 6y & < - 10 & \hspace{0.25in} & {\mbox{or}} & \hspace{0.25in}2 - 6y & > 10\\ — 6y & < - 12 & \hspace{0. Обратите внимание, что нам пришлось изменить направление неравенства при делении на отрицательное число! Обозначение интервала для этих решений: \(\left( {2,\infty } \right)\) или \(\left( { — \infty , — \frac{4}{3}} \right)\). Хорошо, теперь нам нужно быстро взглянуть на то, что произойдет, если \(b\) равно нулю или отрицательно. Мы сделаем это с набором примеров и начнем с нуля. Пример 3 Решите каждую из следующих задач. Показать все решения Скрыть все решения Показать обсуждение Эти четыре примера, кажется, охватывают все наши основы. a \(\left| {3x + 2} \right| < 0\) Показать решение Теперь мы знаем, что \(\left| p \right| \ge 0\) не может быть меньше нуля. Следовательно, в данном случае решения нет, так как абсолютное значение не может быть строго меньше нуля ( т.е. отрицательный). b \(\left| {x — 9} \right| \le 0\) Показать решение Это почти то же самое, что и предыдущая часть. Мы по-прежнему не можем иметь абсолютное значение меньше нуля, однако оно может быть равно нулю. Таким образом, это будет иметь решение, только если \[\слева| {х — 9} \право| = 0\] и мы знаем как это решить из предыдущего раздела. \[х — 9= 0\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}x = 9\] c \(\left| {2x — 4} \right| \ge 0\) Показать решение В этом случае давайте снова вспомним, что независимо от того, что такое \(p\), мы гарантированно имеем \(\left| p \right| \ge 0\). Решением в этом случае являются все действительные числа или все возможные значения \(x\). В обозначении неравенства это будет \( — \infty < x <\infty \). d \(\left| {3x — 9} \right| > 0\) Показать решение Этот почти идентичен предыдущей части, за исключением того, что на этот раз обратите внимание, что мы не хотим, чтобы абсолютное значение когда-либо было равно нулю. Итак, нам все равно, какое значение принимает абсолютное значение, если оно не равно нулю. Это означает, что нам просто нужно избегать значений \(x\), для которых мы получаем \[\слева| {3x — 9} \право| = 0\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма} 3x — 9= 0\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма} x = 3\] Решением в этом случае являются все действительные числа, кроме \(x = 3\). Теперь давайте быстро рассмотрим примеры с отрицательными числами. Пример 4 Постановка задачи. Показать все решения Скрыть все решения Показать обсуждение Обратите внимание, что мы работаем с ними парами, потому что на этот раз, в отличие от предыдущего набора примеров, решения будут одинаковыми для всех. Оба (все четыре?) из них будут использовать тот факт, что независимо от того, что такое \(p\), мы гарантированно имеем \(\left| p \right| \ge 0\). Другими словами, абсолютные значения всегда положительны или равны нулю. a \(\left| {4x + 15} \right| < - 2\) и \(\left| {4x + 15} \right| \le - 2\) Показать решение Хорошо, если абсолютные значения всегда положительны или равны нулю, они никак не могут быть меньше или равны отрицательному числу. Следовательно, ни для одного из них нет решения. b \(\left| {2x — 9} \right| \ge — 8\) и \(\left| {2x — 9} \right| > — 8\) Показать решение В этом случае, если абсолютное значение положительно или равно нулю, оно всегда будет больше или равно отрицательному числу. Решением для каждого из них являются все действительные числа. Найти абсолютное значение числа очень просто, если вы используете числовую прямую! Помните, что абсолютное значение — это расстояние от нуля на числовой прямой. В этом уроке вы увидите, как вы можете думать об абсолютном значении очень интуитивным способом. Дайте нам знать, если у вас есть какие-либо вопросы по этому поводу! Задачи Word позволяют увидеть математику в действии! В этом руководстве показано, как преобразовать текстовую задачу в абсолютное неравенство. Затем посмотрите, как найти ответ, запишите его в нотации построителя наборов и изобразите на числовой прямой. Узнайте все об этом в этом уроке! Иногда самая трудная часть задачи со словами — выяснить, как превратить слова в математику. Этот учебник позволит вам увидеть шаги, которые нужно предпринять, чтобы сделать именно это! Вы увидите, как взять текстовую задачу и проанализировать ее, чтобы превратить в неравенство абсолютного значения.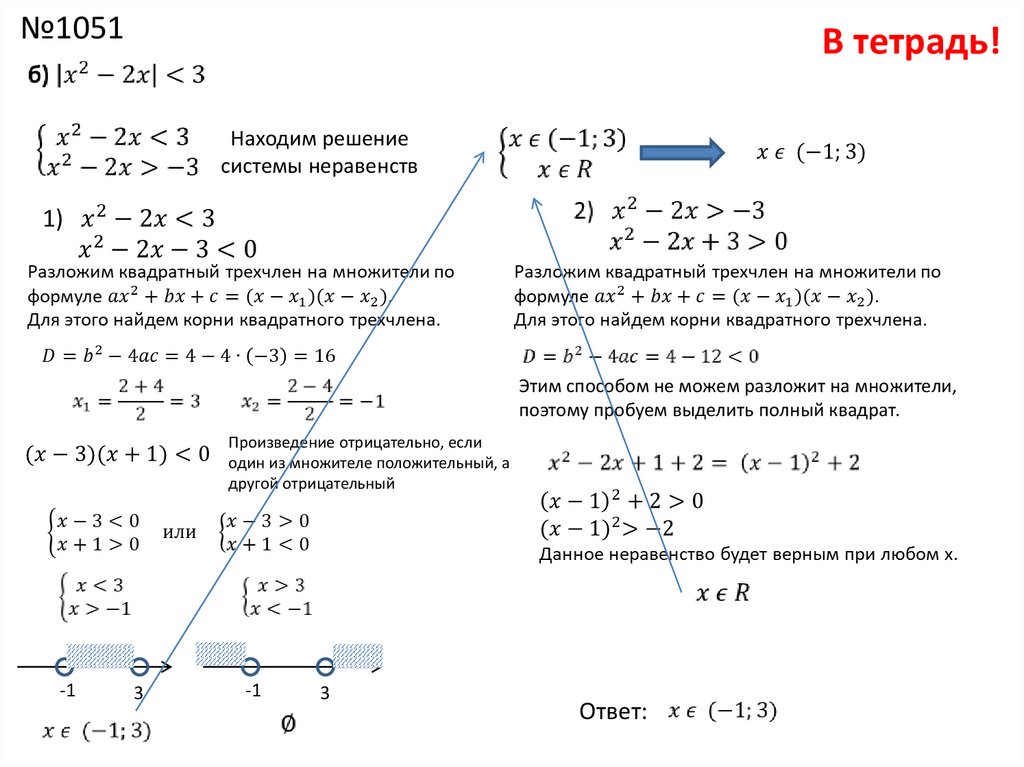
Как и в случае с уравнениями, \(p\) просто представляет все, что находится внутри полос абсолютного значения. Итак, с этим первым у нас есть
Неравенства с участием > и \( \ge \)
Многие студенты пытаются объединить их в одно двойное неравенство следующим образом: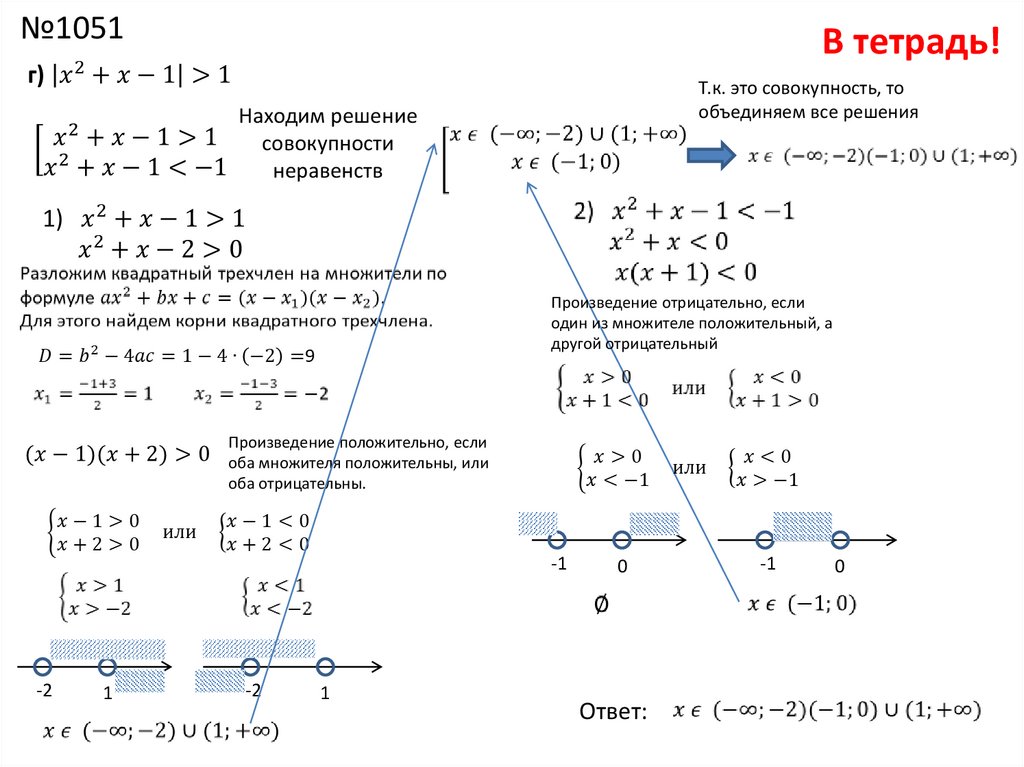
Давайте поработаем над парой примеров.
25in} & {\mbox{or}} & \hspace{0.25in} — 6y & > 8\\ y & > 2 & \hspace{0.25in} & {\mbox{or}} & \hspace{0.25in} y & < - \frac{4}{3}\end{align*}\]
Это означает, что независимо от того, что такое \(x\), мы можем быть уверены, что \(\left| {2x — 4} \right| \ge 0\) будет истинным, поскольку абсолютные значения всегда будут положительными или нулевыми.
Решение уравнений и неравенств с абсолютными значениями | Алгебра 2 | Уравнения и неравенства
Дополнительные темы
по решению уравнений и неравенств с абсолютной величиной Популярные учебные пособия
по решению уравнений и неравенств по абсолютной величине Как найти абсолютное значение положительных и отрицательных чисел?
В этом руководстве показано, как использовать числовую прямую для нахождения абсолютного значения. Что означает абсолютное значение?
Как решить задачу со словами, используя И абсолютное неравенство?
Как написать абсолютное неравенство из словесной задачи?
