Система уравнений: Калькулятор метода исключения
Инструкции: Используйте этот калькулятор, чтобы решить систему линейных уравнений, используя метод исключения, со всеми показанными шагами. Укажите два действительных линейных уравнения в соответствующих полях. ниже:
Подробнее о методе исключения для решения линейных систем
Вы можете решить систему линейных уравнений, используя различные варианты, каждый из которых имеет свои преимущества (и недостатки).
Когда у вас есть два уравнения и две переменные, вы обычно можете использовать график
метод решения системы, который по сути является методом поиска решений путем нахождения пересечения
между двумя линиями.
Или вы можете использовать метод подстановки для решения систем, который пытается решить сначала от одной переменной с точки зрения другой, чтобы затем используйте эту замену, чтобы заменить в другом уравнении и решить для одной переменной.
Как решить систему уравнений подстановкой?
Подход очень прост: 1) Выберите одно из двух уравнений, которое легко решить для любого \(x\) или \(y\), и решите для этой переменной, с точки зрения другой переменной.
Часто уравнения задаются как, например, «\(x = 2y + 3\)», где оно уже решено относительно \(x\), или, например, «\(y = 2x + 3\)», где оно уже решено решено для \(y\)
2) Теперь, когда вы решили для одной переменной в одном из уравнений, используйте эту переменную, для которой вы решили,
и подставьте его в другое уравнение.
3) Это уравнение будет с точки зрения другой переменной (не той, для которой вы изначально решили), и затем вы решите ее, и вы получите числовой результат.
4) С числовым результатом, найденным для другой переменной, вернитесь к исходной переменной, для которой вы решили, и подставьте значение, которое вы только что нашли. численно
Это калькулятор исключения Гаусса
Не совсем так, но идея та же: Исключите переменные, найдя эквивалентные уравнения (усилив) и добавив к этому к уменьшению количество переменных.
Для системы 2×2 метод исключения выбирает одну переменную для исключения с помощью соответствующего алгебраического преобразования и операции.
Технически, вы можете применить этот метод, чтобы решить 3 уравнения, используя вычисление исключения, но этот калькулятор
специально для систем 2×2.
Калькулятор метода исключения с шагами
Как решить систему уравнений методом исключения? Этот калькулятор покажет вам все шаги, необходимые для решения систему уравнений методом исключения.
Важнейшим шагом является определение того, какая переменная будет исключена, так как правильный выбор переменной может значительно упростить расчет.
Каковы шаги метода исключения?
1) Сначала решите, какую переменную вы будете исключать.
2) Во-вторых, решите, как вы будете устранять, чтобы усилить и использовать уравнения для проведения исключения.
3) В-третьих, как только вы исключите одну из переменных, найдите другую переменную.
4) Четвертое и последнее, как только вы нашли решение для одной из переменных, подставьте ее в любое уравнение (самое простое) так что вы решаете для оставшейся переменной.
Пример: Исключающая система уравнений с шагами
Предположим, что у вас есть следующая система уравнений:
\[\начать{матрицу} \displaystyle 2x+2y & = & 5\\\\\displaystyle x-y & = & 2 \end{матрица} \]
Используйте метод подстановки для решения приведенной выше системы линейных уравнений.
Решение:
Шаг 1: Выберите переменную для исключения
Умножая второе уравнение на \(2\), получаем:
\[\начать{матрицу} 2x+2y & = & 5\\\\2x-2y & = & 4 \end{матрица} \]
Теперь, когда мы усилили исходные уравнения, вычитание первого уравнения из второго уравнения дает
\[2x-2y-\влево(2x+2y\вправо)=4-5\] \[\Стрелка вправо -4y=-1\]
Из приведенного выше уравнения мы напрямую находим, что, разделив обе части уравнения на \(\displaystyle -4\), мы получим
\[y = \frac{-1}{-4} = \frac{1}{4}\] Шаг 2: Подставьте найденное значение в другое уравнение
Теперь снова подставим \(\displaystyle y = \frac{1}{4}\) в другое уравнение
\[2x+2\cdot \влево(\frac{1}{4}\вправо)=5\] \[\Стрелка вправо 2x+\frac{1}{2}=5\]
Подставив \(x\) в левую часть, а константы в правую, получим
\[\displaystyle 2 x = 5 — \frac{1}{2}\] \[\Стрелка вправо \displaystyle 2x = \frac{9}{2}\]
Теперь, найдя \(x\), разделив обе части уравнения на \(2\), получим следующее
\[\displaystyle x = \displaystyle \frac{ \frac{9}{2}}{ 2}\]
и упрощая окончательно получаем следующее
\[\displaystyle x=\frac{9}{4}\] Шаг 3: Проверка найденных решений путем обратного включения в исходные уравнения
Мы проверим, действительно ли найденные решения удовлетворяют уравнениям.
Подставляем \(\displaystyle x = \frac{9}{4}\) и \(\displaystyle y = \frac{1}{4}\) в предоставленные уравнения и получаем\[\begin{matrix } \displaystyle 2\cdot \left(\frac{9}{4}\right)+2\cdot \left(\frac{1}{4}\right) & = & 5\\\\\displaystyle \left( \фракция{9* = \displaystyle \frac{1}{4}\).
Решение систем с исключением Гаусса
Цели обучения
В этом разделе вы:
- Напишите расширенную матрицу системы уравнений.
- Напишите систему уравнений из расширенной матрицы.
- Выполнение операций со строками над матрицей.
- Решите систему линейных уравнений с помощью матриц.
Рис. 1. Немецкий математик Карл Фридрих Гаусс (1777–1855).
Карл Фридрих Гаусс жил в конце 18-го и начале 19-го веков, но до сих пор считается одним из самых плодовитых математиков в истории. Его вклад в математику и физику охватывает такие области, как алгебра, теория чисел, анализ, дифференциальная геометрия, астрономия и оптика, среди прочих. Его открытия, касающиеся теории матриц, изменили то, как математики работали последние два столетия.
Его открытия, касающиеся теории матриц, изменили то, как математики работали последние два столетия.
Впервые мы столкнулись с методом исключения Гаусса в книге «Системы линейных уравнений: две переменные». В этом разделе мы вернемся к этой технике решения систем, на этот раз с использованием матриц.
Написание расширенной матрицы системы уравнений
Матрица может служить средством для представления и решения системы уравнений. Чтобы выразить систему в матричной форме, мы извлекаем коэффициенты переменных и констант, и они становятся элементами матрицы. Мы используем вертикальную линию, чтобы отделить записи коэффициентов от констант, по существу заменяя знаки равенства. Когда система записывается в такой форме, мы называем ее расширенной матрицей.
Например, рассмотрим следующую[латекс]\,2\,×\,2\,[/латекс]систему уравнений.
[латекс]\begin{массив}{l}3x+4y=7\\ 4x-2y=5\end{массив}[/латекс]
Мы можем записать эту систему в виде расширенной матрицы:
[латекс ]\left[\begin{array}{rr}\hfill 3& \hfill 4\\ \hfill 4& \hfill -2\end{array}\text{ }|\text{ }\begin{array}{r}\ hfill 7\\ \hfill 5\end{array}\right][/latex]
Мы также можем написать матрицу, содержащую только коэффициенты. Это называется матрицей коэффициентов.
Это называется матрицей коэффициентов.
[латекс]\влево[\начало{массив}{cc}3& 4\\ 4& -2\end{массив}\право][/латекс]
Система уравнений три на три, такая как
[латекс]\begin{array}{l}3x-y-z=0\hfill \\ \text{ }x+y=5\hfill \\ \text{ }2x-3z=2\hfill \end{array}[ /latex]
имеет матрицу коэффициентов
[latex]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\\ \ hfill 2& \hfill 0& \hfill -3\end{array}\right][/latex]
и представлен расширенной матрицей
[латекс]\left[\begin{array}{rrr}\hfill 3& \hfill -1& \hfill -1\\ \hfill 1& \hfill 1& \hfill 0\\ \hfill 2& \hfill 0& \hfill -3 \end{array}\text{ }|\text{ }\begin{array}{r}\hfill 0\\ \hfill 5\\ \hfill 2\end{array}\right][/latex]
Уведомление что матрица написана так, что переменные выстраиваются в свои собственные столбцы: x -термы идут в первом столбце, y -термы во втором столбце и z -термы в третьем столбце. Очень важно, чтобы каждое уравнение было записано в стандартной форме[latex]\,ax+by+cz=d\,[/latex], чтобы переменные совпадали. Когда в уравнении отсутствует переменный член, коэффициент равен 0,9.0005
Когда в уравнении отсутствует переменный член, коэффициент равен 0,9.0005
Как
Учитывая систему уравнений, напишите расширенную матрицу.
- Запишите коэффициенты x -членов в виде чисел в первом столбце.
- Запишите коэффициенты y -членов в виде чисел во втором столбце.
- Если имеется z -членов, запишите коэффициенты в виде чисел в третьем столбце.
- Нарисуйте вертикальную линию и запишите константы справа от линии.
Запись расширенной матрицы для системы уравнений
Запись расширенной матрицы для заданной системы уравнений.
[латекс]\begin{array}{l}\text{ }x+2y-z=3\hfill \\ \text{ }2x-y+2z=6\hfill \\ \text{ }x-3y +3z=4\hfill \end{array}[/latex]
Показать решение
Попробуйте
Напишите расширенную матрицу данной системы уравнений.
[латекс]\begin{array}{l}4x-3y=11\\ 3x+2y=4\end{массив}[/latex]
Показать решение
Написание системы уравнений из расширенной матрицы
Мы можем использовать расширенные матрицы для решения систем уравнений, потому что они упрощают операции, когда системы не перегружены переменными. Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Однако важно понимать, как переключаться между форматами, чтобы сделать поиск решений более плавным и интуитивно понятным. Здесь мы будем использовать информацию в расширенной матрице, чтобы записать систему уравнений в стандартной форме.
Написание системы уравнений из расширенной матричной формы
Найдите систему уравнений из расширенной матрицы.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill -5\\ \hfill 2& \hfill -5& \hfill -4\\ \hfill -3& \hfill 5& \ hfill 4\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill -2\\ \hfill 5\\ \hfill 6\end{массив}\right][/latex]
Показать решение
Попробуйте
Напишите систему уравнений из расширенной матрицы.
[латекс]\left[\begin{array}{ccc}1& -1& \,\,1\\ 2& -1& \,\,3\\ 0& \,\,\,1& \,\,1\ конец {массив}\,\,\,|\,\,\begin{массив}{c}\,\,5\\ \,\,1\\ -9\end{array}\right][/latex]
Показать решение
Выполнение операций со строками над матрицей
Теперь, когда мы можем записывать системы уравнений в расширенной матричной форме, мы рассмотрим различные операции со строками, которые можно выполнять над матрицей, такие как сложение, умножение на константу и перестановка строк .
Выполнение операций со строками над матрицей — это метод, который мы используем для решения системы уравнений. Для того, чтобы решить систему уравнений, мы хотим преобразовать матрицу в строчно-ступенчатую форму, в которой единицы по главной диагонали от левого верхнего угла до нижнего правого угла, и нули в каждой позиции ниже главной диагонали как показано.
[латекс]\begin{array}{c}\text{Форма строки-эшелона}\\ \left[\begin{array}{ccc}1& a& b\\ 0& 1& d\\ 0& 0& 1\end{ array}\right]\end{array}[/latex]
Мы используем операции со строками, соответствующие операциям с уравнениями, чтобы получить новую матрицу, эквивалентную строкам в более простой форме. Вот рекомендации по получению формы ряд-эшелон.
- В любой ненулевой строке первое ненулевое число равно 1. Оно называется ведущим
- Все строки со всеми нулями размещаются внизу матрицы.
- Любой интерлиньяж 1 находится ниже и правее предыдущего интерлиньяжа 1.

- В любом столбце, содержащем ведущую единицу, во всех остальных позициях столбца есть нули.
Чтобы решить систему уравнений, мы можем выполнить следующие операции со строками, чтобы преобразовать матрицу коэффициентов в ступенчатую форму и выполнить обратную подстановку, чтобы найти решение.
- Поменять местами ряды. (Обозначение: [латекс]\,{R}_{i}\,↔\,\,{R}_{j}[/латекс])
- Умножить строку на константу. (Обозначение: [латекс]\,с{R}_{i}[/латекс])
- Добавить произведение строки, умноженной на константу, к другой строке. (Обозначение: [латекс]\,{R}_{i}+c{R}_{j})[/латекс]
Каждая из операций строки соответствует операциям, которые мы уже изучили для решения систем уравнений с тремя переменными. С этими операциями есть несколько ключевых ходов, которые быстро достигнут цели записи матрицы в форме строки-эшелона. Чтобы получить матрицу в форме строки-эшелона для поиска решений, мы используем метод исключения Гаусса, который использует операции со строками для получения 1 в качестве первой записи, чтобы строка 1 могла использоваться для преобразования оставшихся строк.
Исключение Гаусса
Метод исключения Гаусса относится к стратегии, используемой для получения формы строки-эшелона матрицы. Цель состоит в том, чтобы написать матрицу [латекс]\,А\,[/латекс] с номером 1 в качестве элемента вниз по главной диагонали и со всеми нулями ниже.
[латекс]A=\left[\begin{array}{rrr}\hfill {a}_{11}& \hfill {a}_{12}& \hfill {a}_{13}\\ \ hfill {a}_{21}& \hfill {a}_{22}& \hfill {a}_{23}\\ \hfill {a}_{31}& \hfill {a}_{32}& \hfill {a}_{33}\end{массив}\right]\stackrel{\text{После исключения Гаусса}}{\to}A=\left[\begin{array}{rrr}\hfill 1& \hfill \,\,{b}_{12}& \hfill \,\,{b}_{13}\\ \hfill 0& \hfill \,\,1& \hfill \,\,{b}_{23} \\ \hfill 0& \hfill \,\,0& \hfill \,\,1\end{массив}\right][/latex]
Первый шаг стратегии Гаусса включает в себя получение 1 в качестве первой записи, так что строка 1 может использоваться для изменения строк ниже.
Как сделать
При заданной расширенной матрице выполните операции над строками, чтобы получить форму строки-эшелона.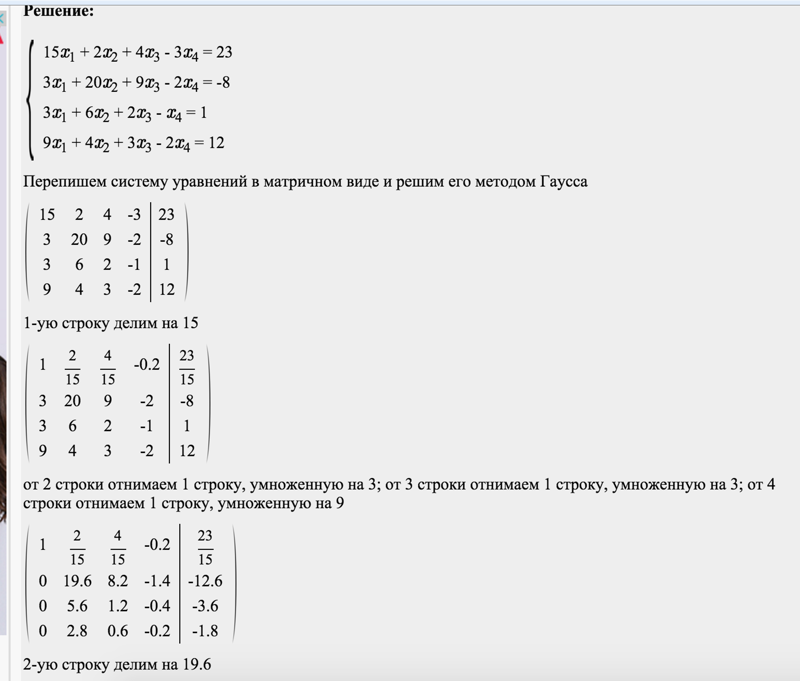
- В первом уравнении старший коэффициент должен быть равен 1. При необходимости поменяйте местами строки или умножьте на константу.
- Используйте операции со строками, чтобы получить нули в первом столбце после первой записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 2, столбце 2.
- Используйте операции со строками, чтобы получить нули вниз по столбцу 2, ниже записи 1.
- Используйте операции со строками, чтобы получить 1 в строке 3, столбце 3.
- Продолжайте этот процесс для всех строк, пока не будет 1 в каждом элементе вниз по главной диагонали, а ниже не останутся только нули.
- Если какие-либо строки содержат все нули, поместите их внизу.
Решение системы[latex]\,2×2\,[/latex] методом исключения Гаусса
Решите данную систему методом исключения Гаусса.
[латекс]\begin{array}{l}2x+3y=6\hfill \\ \text{ }x-y=\frac{1}{2}\hfill \end{array}[/latex]
Показать Решение
Попробуйте
Решите данную систему методом исключения Гаусса.
[латекс]\begin{array}{l}4x+3y=11\hfill \\ \text{ }\text{}\text{}x-3y=-1\hfill \end{array}[/latex ]
Показать решение
Использование исключения Гаусса для решения системы уравнений
Использование исключения Гаусса для решения заданного[latex]\,2\,×\,2\,[/latex]
система уравнений.
[латекс]\begin{array}{l}\text{ }2x+y=1\hfill \\ 4x+2y=6\hfill \end{array}[/latex]
Показать решение
Решение зависимой системы
Решение системы уравнений.
[латекс]\begin{array}{l}3x+4y=12\\ 6x+8y=24\end{массив}[/latex]
Показать решение
Выполнение операций над строками над расширенной матрицей 3×3 для получения формы строк-эшелонов
Выполнение операций над строками данной матрицы для получения формы строк-эшелонов.
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill -3& \hfill 4\\ \hfill 2& \hfill -5& \hfill 6\\ \hfill -3& \hfill 3& \hfill 4 \end{array}\text{ }|\text{ }\begin{array}{r}\hfill 3\\ \hfill 6\\ \hfill 6\end{array}\right][/latex]
Показать Решение
Попробуй
Запиши систему уравнений в ступенчато-строковой форме.
[латекс]\begin{array}{l}\text{ }x-2y+3z=9\hfill \\ \text{ }-x+3y=-4\hfill \\ 2x-5y+5z=17 \hfill \end{массив}[/latex]
Показать решение
Решение системы линейных уравнений с помощью матриц
Мы увидели, как написать систему уравнений с расширенной матрицей, а затем, как использовать операции со строками и обратную подстановку, чтобы получить ступенчатую форму. Теперь мы сделаем еще один шаг вперед, чтобы решить систему линейных уравнений 3 на 3. Общая идея состоит в том, чтобы исключить все переменные, кроме одной, с помощью операций со строками, а затем выполнить обратную замену для решения других переменных.
Решение системы линейных уравнений с помощью матриц
Решите систему линейных уравнений с помощью матриц.
[латекс]\begin{array}{c}\begin{array}{l}\hfill \\ \hfill \\ x\,\,\,\,-\,\,\,\,y\, \,\,+\,\,\,\,z=\,\,\,\,8\hfill \end{массив}\\ 2x\,\,+\,\,\,3y\,\, \,-\,\,\,z=-2\\ 3x\,\,\,-\,\,\,2y\,\,-9z=\,\,\,\,9\end{массив }[/latex]
Показать решение
Решение зависимой системы линейных уравнений с помощью матриц
Решите следующую систему линейных уравнений с помощью матриц.
[латекс]\begin{array}{r}\hfill -x-2y+z=-1\\ \hfill 2x+3y=2\,\,\,\,\\ \hfill y-2z=0 \,\,\,\,\end{массив}[/latex]
Показать решение
Попробуйте
Решите систему с помощью матриц.
[латекс]\begin{array}{c}x+4y-z=4\\ 2x+5y+8z=15\\ x+3y-3z=1\end{array}[/latex]
Показать Решение
Можно ли решить любую систему линейных уравнений методом исключения Гаусса?
Да, система линейных уравнений любого размера может быть решена методом исключения Гаусса.
Как
Дана система уравнений, решите ее с помощью матриц с помощью калькулятора.
- Сохранить расширенную матрицу как матричную переменную[латекс]\,\слева[А\справа],\,\слева[В\справа],\,\слева[С\справа]\текст{,} \ точки .[/латекс]
- Используйте функцию ref( в калькуляторе, вызывая каждую матричную переменную по мере необходимости.

Решение систем уравнений с матрицами с помощью калькулятора
Решите систему уравнений.
[латекс]\begin{array}{r}\hfill 5x+3y+9z=-1\\ \hfill -2x+3y-z=-2\\ \hfill -x-4y+5z=1\, \,\,\,\end{массив}[/latex]
Показать решение
Применение матриц 2 × 2 к финансам
Кэролин инвестирует в общей сложности 12 000 долларов США в две муниципальные облигации, по одной из которых выплачивается 10,5% годовых, а по другой — 12%. Годовой процент, полученный по двум инвестициям в прошлом году, составил 1335 долларов. Сколько было вложено по каждой ставке?
Показать решение
Применение матриц 3 × 3 к финансам
Ava инвестирует в общей сложности 10 000 долларов США в три счета, один из которых выплачивает 5% годовых, другой — 8% годовых, а третий — 9% годовых. Годовой процент, полученный по трем инвестициям в прошлом году, составил 770 долларов. Сумма, вложенная под 9%, вдвое превышала сумму, вложенную под 5%. Сколько было вложено по каждой ставке?
Сколько было вложено по каждой ставке?
Показать решение
Попробуй
Небольшая обувная компания взяла кредит в размере 1 500 000 долларов, чтобы расширить свой ассортимент. Часть денег была взята в долг под 7%, часть – под 8%, а часть – под 10%. Сумма займа под 10% в четыре раза превышала сумму займа под 7%, а годовой процент по всем трем кредитам составлял 130 500 долларов. Используйте матрицы, чтобы найти сумму займа по каждой ставке.
Показать решение
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем линейных уравнений с помощью исключения Гаусса.
- Решение системы двух уравнений с помощью расширенной матрицы
- Решение системы трех уравнений с помощью расширенной матрицы
- Расширенные матрицы на калькуляторе
Основные понятия
- Расширенная матрица — это матрица, содержащая коэффициенты и константы системы уравнений.
 См. (Рисунок).
См. (Рисунок). - Матрица, дополненная постоянным столбцом, может быть представлена в виде исходной системы уравнений. См. (Рисунок).
- Операции со строками включают умножение строки на константу, добавление одной строки к другой строке и перестановку строк.
- Мы можем использовать исключение Гаусса для решения системы уравнений. См. (Рисунок), (Рисунок) и (Рисунок).
- Операции со строками выполняются над матрицами для получения ступенчатой формы. См. (Рисунок).
- Чтобы решить систему уравнений, запишите ее в расширенной матричной форме. Выполните операции со строками, чтобы получить форму строки-эшелона. Обратно заменить, чтобы найти решения. См. (Рисунок) и (Рисунок).
- Калькулятор можно использовать для решения систем уравнений с использованием матриц. См. (Рисунок).
- Многие реальные проблемы можно решить с помощью расширенных матриц. См. (Рисунок) и (Рисунок).
Раздел Упражнения
Вербальные
Можно ли любую систему линейных уравнений записать в виде расширенной матрицы? Объясните, почему да или почему нет. Объясните, как записать эту расширенную матрицу.
Объясните, как записать эту расширенную матрицу.
Показать решение
Любую ли матрицу можно представить в виде системы линейных уравнений? Объясните, почему да или почему нет. Объясните, как записать эту систему уравнений.
Существует ли только один правильный метод использования строковых операций над матрицей? Попробуйте объяснить две разные операции со строками, которые можно использовать для решения расширенной матрицы [латекс]\left[\begin{array}{rr}\hfill 9& \hfill 3\\ \hfill 1& \hfill -2\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 0\\ \hfill 6\end{array}\right].[/latex]
Показать решение
Можно ли решить матрицу, запись которой равна 0 по диагонали? Объясните, почему да или почему нет. Что бы вы сделали, чтобы исправить ситуацию?
Может ли матрица, состоящая из 0 элементов для всей строки, иметь одно решение? Объясните, почему да или почему нет.
Показать решение
Алгебраический
Для следующих упражнений напишите расширенную матрицу для линейной системы.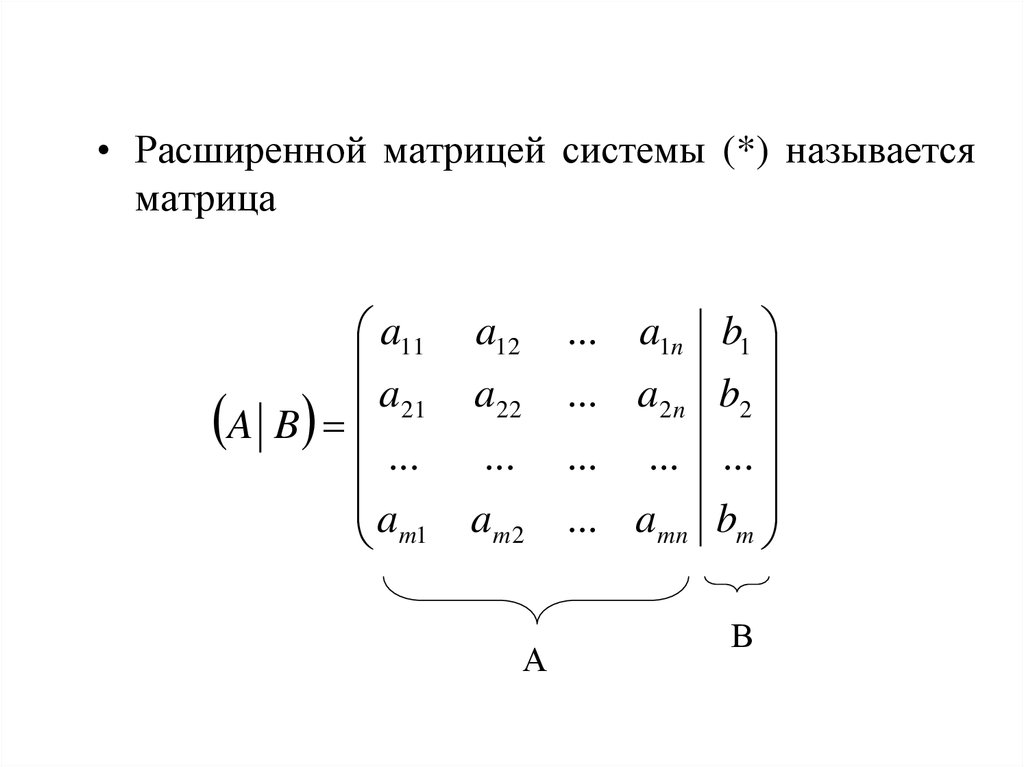
[латекс]\begin{array}{l}8x-37y=8\\ 2x+12y=3\end{массив}[/latex]
[латекс]\begin{массив}{l}\,\ text{ }16y=4\hfill \\ 9x-y=2\hfill \end{array}[/latex]
Показать решение
[латекс]\begin{array}{l}\text{ }3x+2y+10z=3\hfill \\ -6x+2y+5z=13\hfill \\ \text{ }4x+z=18\ hfill \end{массив}[/latex]
[латекс]\begin{array}{l}\hfill \\ \text{ }x+5y+8z=19\hfill \\ \text{ }12x+3y=4\hfill \\ 3x+4y+9z =-7\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}6x+12y+16z=4\hfill \\ \text{ }19x-5y+3z=-9\hfill \\ \text{ }x+2y=-8 \hfill \end{array}[/latex]
Для следующих упражнений напишите линейную систему из расширенной матрицы.
[латекс]\left[\begin{array}{rr}\hfill -2& \hfill 5\\ \hfill 6& \hfill -18\end{array}\text{ }|\text{ }\begin{array }{r}\hfill 5\\ \hfill 26\end{массив}\right][/latex]
Показать решение
[латекс]\left[\begin{array}{rr}\hfill 3& \hfill 4\\ \hfill 10& \hfill 17\end{array}\text{ }|\text{ }\begin{array}{ r}\hfill 10\\ \hfill 439\end{массив}\right][/latex]
[латекс]\left[\begin{array}{rrr}\hfill 3& \hfill 2& \hfill 0\\ \ hfill -1& \hfill -9& \hfill 4\\ \hfill 8& \hfill 5& \hfill 7\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 3\\ \hfill -1\\ \hfill 8\end{массив}\right][/latex]
Показать решение
[латекс]\left[\begin{array}{rrr}\hfill 8& \hfill 29& \hfill 1\\ \hfill -1& \hfill 7& \hfill 5\\ \hfill 0& \hfill 0& \hfill 3\end {array}\text{ }|\text{ }\begin{array}{r}\hfill 43\\ \hfill 38\\ \hfill 10\end{array}\right][/latex]
[латекс] \left[\begin{array}{rrr}\hfill 4& \hfill 5& \hfill -2\\ \hfill 0& \hfill 1& \hfill 58\\ \hfill 8& \hfill 7& \hfill -3\end{array}\ text{ }|\text{ }\begin{array}{r}\hfill 12\\ \hfill 2\\ \hfill -5\end{array}\right][/latex]
Показать решение
Для следующих упражнений решите систему методом исключения Гаусса.
[латекс]\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill 0\end{array}\text{ }|\text{ }\begin{array}{ r}\hfill 3\\ \hfill 0\end{array}\right][/latex]
[latex]\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 1& \ hfill 0\end{array}\text{ }|\text{ }\begin{array}{r}\hfill 1\\ \hfill 2\end{array}\right][/latex]
Показать решение
[латекс]\left[\begin{array}{rr}\hfill 1& \hfill 2\\ \hfill 4& \hfill 5\end{array}\text{ }|\text{ }\begin{array}{r }\hfill 3\\ \hfill 6\end{массив}\right][/latex]
[латекс]\left[\begin{array}{rr}\hfill -1& \hfill 2\\ \hfill 4& \ hfill -5\end{array}\text{ }|\text{ }\begin{array}{r}\hfill -3\\ \hfill 6\end{array}\right][/latex]
Показать решение
[латекс]\left[\begin{array}{rr}\hfill -2& \hfill 0\\ \hfill 0& \hfill 2\end{array}\text{ }|\text{ }\begin{array} {r}\hfill 1\\ \hfill -1\end{массив}\right][/latex]
[латекс]\begin{array}{l}\text{ }2x-3y=-9\hfill \\ 5x+4y=58\hfill \end{array}[/latex]
Показать решение
[латекс]\begin{массив}{l}6x+2y=-4\\ 3x+4y=-17\end{массив}[/latex]
[латекс]\begin{массив}{l}2x +3y=12\hfill \\ \text{ }4x+y=14\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}-4x-3y=-2\hfill \\ \,\text{ }3x-5y=-13\hfill \end{array}[/latex]
[ латекс]\begin{массив}{l}-5x+8y=3\hfill \\ \,10x+6y=5\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\,\text{ }3x+4y=12\hfill \\ -6x-8y=-24\hfill \end{массив}[/latex]
[латекс ]\begin{array}{l}-60x+45y=12\hfill \\ \text{ }20x-15y=-4\hfill \end{array}[/latex]
Показать решение
[латекс]\begin{array}{l}11x+10y=43\\ 15x+20y=65\end{массив}[/latex]
[латекс]\begin{array}{l}\text{ }2x-y=2\hfill \\ 3x+2y=17\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\begin{array}{l}\\ -1. 06x-2.25y=5.51\end{массив}\hfill \\ -5.03x-1.08y=5.40\hfill \end{массив}[/латекс]
06x-2.25y=5.51\end{массив}\hfill \\ -5.03x-1.08y=5.40\hfill \end{массив}[/латекс]
[латекс]\begin{array}{l}\frac{3}{4}x-\frac{3}{5}y=4\\ \frac{1}{4}x+\frac{2} {3}y=1\end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\frac{1}{4}x-\frac{2}{3}y=-1\\ \frac{1}{2}x+\frac{1 }{3}y=3\end{массив}[/latex]
[латекс]\left[\begin{массив}{rrr}\hfill 1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 1& \ hfill 1\\ \hfill 0& \hfill 0& \hfill 1\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 31\\ \hfill 45\\ \hfill 87\end {массив}\право][/латекс]
Показать решение
[латекс]\left[\begin{array}{rrr}\hfill 1& \hfill 0& \hfill 1\\ \hfill 1& \hfill 1& \hfill 0\\ \hfill 0& \hfill 1& \hfill 1\end{ array}\text{ }|\text{ }\begin{array}{r}\hfill 50\\ \hfill 20\\ \hfill -90\end{array}\right][/latex]
[латекс] \left[\begin{array}{rrr}\hfill 1& \hfill 2& \hfill 3\\ \hfill 0& \hfill 5& \hfill 6\\ \hfill 0& \hfill 0& \hfill 8\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 4\\ \hfill 7\\ \hfill 9\end{array}\right][/latex]
Показать решение
[латекс]\left[\begin{array}{rrr}\hfill -0. 1& \hfill 0.3& \hfill -0.1\\ \hfill -0.4& \hfill 0.2& \hfill 0.1\\ \hfill 0.6& \ hfill 0.1& \hfill 0.7\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 0.2\\ \hfill 0.8\\ \hfill -0.8\end{массив}\right] [/латекс]
1& \hfill 0.3& \hfill -0.1\\ \hfill -0.4& \hfill 0.2& \hfill 0.1\\ \hfill 0.6& \ hfill 0.1& \hfill 0.7\end{массив}\text{ }|\text{ }\begin{array}{r}\hfill 0.2\\ \hfill 0.8\\ \hfill -0.8\end{массив}\right] [/латекс]
[латекс]\begin{array}{l}\text{ }-2x+3y-2z=3\hfill \\ \text{ }4x+2y-z=9\hfill \\ \text { }4x-8y+2z=-6\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\text{ }x+y-4z=-4\hfill \\ \text{ }5x-3y-2z=0\hfill \\ \text{ }2x+ 6y+7z=30\hfill \end{массив}[/latex]
[латекс]\begin{array}{l}\text{ }2x+3y+2z=1\hfill \\ \text{ }-4x -6y-4z=-2\hfill \\ \text{ }10x+15y+10z=5\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\text{ }x+2y-z=1\hfill \\ -x-2y+2z=-2\hfill \\ 3x+6y-3z=5\hfill \end{array}[/latex]
[latex]\begin{array}{l}\,\text{ }x+2y-z=1\hfill \\ -x-2y+2z=-2\hfill \\ \text{ }3x+6y-3z=3\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\text{}\text{ }x+y=2\hfill \\ \text{ }x+z=1\hfill \\ -y-z=-3\ hfill \end{array}[/latex]
[latex]\begin{array}{l}x+y+z=100\hfill \\ \text{ }x+2z=125\hfill \\ -y+ 2z=25\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\frac{1}{4}x-\frac{2}{3}z=-\frac{1}{2}\\ \frac{1}{ 5}x+\frac{1}{3}y=\frac{4}{7}\\ \frac{1}{5}y-\frac{1}{3}z=\frac{2}{9 }\end{массив}[/latex]
[латекс]\begin{массив}{l}-\frac{1}{2}x+\frac{1}{2}y+\frac{1}{7} z=-\frac{53}{14}\hfill \\ \text{ }\frac{1}{2}x-\frac{1}{2}y+\frac{1}{4}z=3\ hfill \\ \text{ }\frac{1}{4}x+\frac{1}{5}y+\frac{1}{3}z=\frac{23}{15}\hfill \end{array} [/латекс]
Показать решение
[латекс]\begin{array}{l}-\frac{1}{2}x-\frac{1}{3}y+\frac{1}{4}z=-\frac{29}{ 6}\hfill \\ \text{ }\frac{1}{5}x+\frac{1}{6}y-\frac{1}{7}z=\frac{431}{210}\hfill \ \ -\frac{1}{8}x+\frac{1}{9}y+\frac{1}{10}z=-\frac{49}{45}\hfill \end{array}[/latex]
Extensions
В следующих упражнениях используйте метод исключения Гаусса для решения системы.
[латекс]\begin{array}{l}\frac{x-1}{7}+\frac{y-2}{8}+\frac{z-3}{4}=0\hfill \ \ \text{ }x+y+z=6\hfill \\ \text{ }\frac{x+2}{3}+2y+\frac{z-3}{3}=5\hfill \end{массив }[/латекс]
Показать решение
[латекс]\begin{array}{l}\frac{x-1}{4}-\frac{y+1}{4}+3z=-1\hfill \\ \text{ }\frac{ x+5}{2}+\frac{y+7}{4}-z=4\hfill \\ \text{ }x+y-\frac{z-2}{2}=1\hfill \end {массив}[/латекс]
[латекс]\begin{массив}{l}\текст{ }\frac{x-3}{4}-\frac{y-1}{3}+2z=-1 \hfill \\ \frac{x+5}{2}+\frac{y+5}{2}+\frac{z+5}{2}=8\hfill \\ \text{ }x+y+ z=1\hfill \end{массив}[/latex]
Показать решение
[латекс]\begin{array}{l}\frac{x-3}{10}+\frac{y+3}{2}-2z=3\hfill \\ \text{}\frac{x +5}{4}-\frac{y-1}{8}+z=\frac{3}{2}\hfill \\ \frac{x-1}{4}+\frac{y+4} {2}+3z=\frac{3}{2}\hfill \end{массив}[/latex]
[латекс]\begin{array}{l}\text{ }\frac{x-3}{4}-\frac{y-1}{3}+2z=-1\hfill \\ \frac{ x+5}{2}+\frac{y+5}{2}+\frac{z+5}{2}=7\hfill \\ \text{ }x+y+z=1\hfill \end {массив}[/latex]
Показать решение
Реальные приложения
Для следующих упражнений создайте расширенную матрицу, описывающую ситуацию, и найдите желаемое решение.
Каждый день в магазине кексов продается 5000 кексов с шоколадным и ванильным вкусом. Если шоколадный вкус в 3 раза популярнее ванильного, сколько каждого кекса продается в день?
В конкурирующем магазине кексов ежедневно продаются кексы на 4520 долларов. Шоколадные кексы стоят 2,25 доллара, а кексы «Красный бархат» — 1,75 доллара. Если общее количество кексов, продаваемых в день, равно 2200, сколько каждого вкуса продается каждый день?
Показать решение
Вы вложили 10 000 долларов США в два счета: один с простой процентной ставкой 3%, другой с процентной ставкой 2,5%. Если ваш общий процентный платеж через год составил 283,50 доллара, сколько было на каждом счете по прошествии года?
Вы вложили 2300 долларов на счет 1 и 2700 долларов на счет 2. Если общая сумма процентов через год составляет 254 доллара, а на счете 2 процентная ставка в 1,5 раза больше, чем на счете 1, каковы процентные ставки? Предположим, простые процентные ставки.
Показать решение
Bikes’R’Us производит велосипеды, которые продаются по цене 250 долларов. Это обходится производителю в 180 долларов за велосипед плюс первоначальный взнос в размере 3500 долларов. Через какое количество проданных велосипедов производитель станет безубыточным?
Крупный магазин бытовой техники рассматривает возможность покупки пылесосов у небольшого производителя. Магазин сможет приобрести пылесосы по 86 долларов за штуку, а стоимость доставки составит 9 долларов.200, независимо от того, сколько пылесосов продано. Если магазин должен начать получать прибыль после продажи 230 единиц, сколько он должен брать за пылесосы?
Показать решение
Три самых популярных вкуса мороженого — шоколадное, клубничное и ванильное, составляющие 83% вкусов, продаваемых в магазине мороженого. Если ванильное мороженое продается на 1% больше, чем клубничное, более чем в два раза, а шоколадное — на 11% больше, чем ванильное, то какую долю от общего потребления мороженого составляют ароматы ванили, шоколада и клубники?
В магазине мороженого растет спрос на три вкуса. В прошлом году банановое, тыквенное и каменистое мороженое составили 12% от общего объема продаж мороженого. В этом году те же три вида мороженого составили 16,9% продаж мороженого. Продажи каменистой дороги увеличились вдвое, продажи бананов выросли на 50%, а продажи тыквы выросли на 20%. Если мороженое «Каменная дорога» имеет на один процент меньше продаж, чем банановое мороженое, выясните процент продаж каждого отдельного мороженого в прошлом году.
В прошлом году банановое, тыквенное и каменистое мороженое составили 12% от общего объема продаж мороженого. В этом году те же три вида мороженого составили 16,9% продаж мороженого. Продажи каменистой дороги увеличились вдвое, продажи бананов выросли на 50%, а продажи тыквы выросли на 20%. Если мороженое «Каменная дорога» имеет на один процент меньше продаж, чем банановое мороженое, выясните процент продаж каждого отдельного мороженого в прошлом году.
Показать решение
Пакет ореховой смеси содержит кешью, фисташки и миндаль. Всего в пакете 1000 орехов, а миндаля на 100 меньше, чем фисташек. Орехи кешью весят 3 г, фисташки — 4 г, а миндаль — 5 г. Если мешок весит 3,7 кг, узнайте, сколько орехов каждого вида находится в мешке.
Пакет ореховой смеси содержит кешью, фисташки и миндаль. Изначально в мешке было 900 орехов. 30 % миндаля, 20 % кешью и 10 % фисташек были съедены, и теперь в мешке осталось 770 орехов. Изначально орехов кешью было на 100 штук больше, чем миндаля.

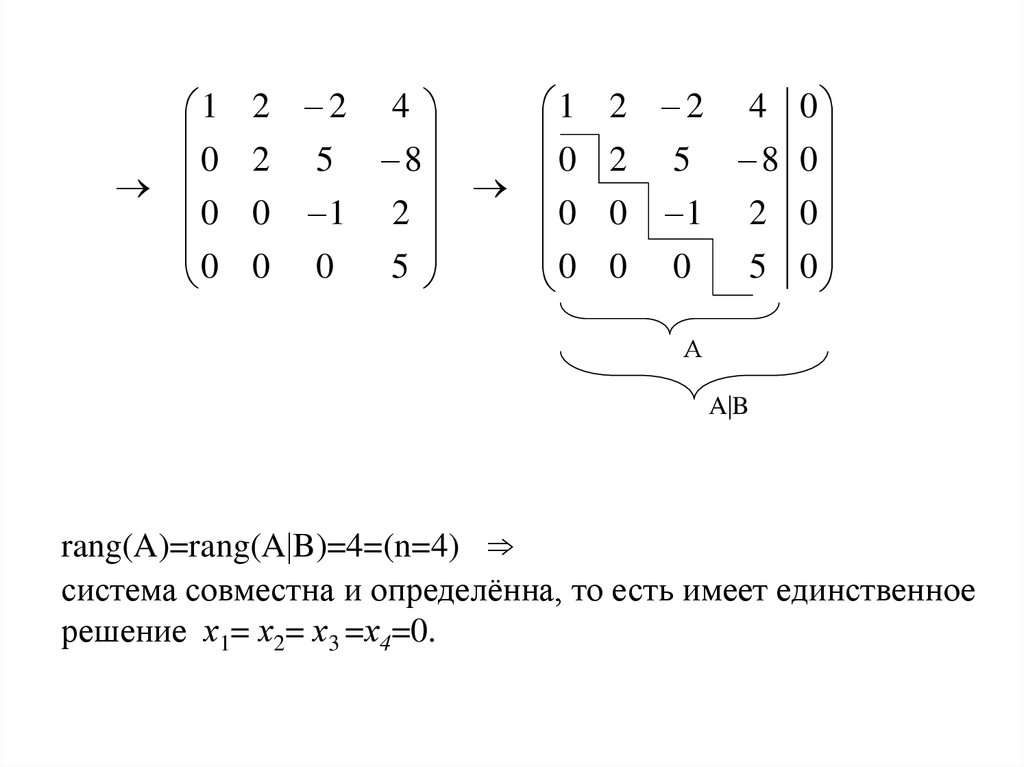

 См. (Рисунок).
См. (Рисунок).