§ Системы уравнений. Как решать системы уравнений
Прежде чем перейти к разбору как решать системы уравнений, давайте разберёмся, что называют системой уравнений с двумя неизвестными.
Запомните!
Системой уравнений называют два уравнения с двумя неизвестными (чаще всего неизвестные в них называют «x» и «y»), которые объединены в общую систему фигурной скобкой.
Например, система уравнений может быть задана следующим образом.
| x + 5y = 7 | |
| 3x − 2y = 4 |
Чтобы решить систему уравнений, нужно найти и «x», и «y».
Существуют два основных способа решения систем уравнений. Рассмотрим оба способа решения.
Способ подстановки
или
«железобетонный» метод
Первый способ решения системы уравнений называют способом подстановки или «железобетонным».
Название «железобетонный» метод получил из-за того, что с помощью этого метода практически всегда можно решить систему уравнений. Другими словами, если у вас не получается решить систему уравнений, всегда пробуйте решить её методом подстановки.
Разберем способ подстановки на примере.
| x + 5y = 7 | |
| 3x − 2y = 4 |
Выразим из первого уравнения «x + 5y = 7» неизвестное «x».
Важно!
Чтобы выразить неизвестное, нужно выполнить два условия:
- перенести неизвестное, которое хотим выразить, в левую часть уравнения;
- разделить и левую и правую часть уравнения на нужное число так, чтобы коэффициент при неизвестном стал равным единице.
Перенесём в первом уравнении «x + 5 y = 7» всё что содержит «x» в левую часть, а остальное в правую часть по правилу переносу.
При «x» стоит коэффициент равный единице, поэтому дополнительно делить уравнение
на число не требуется.
| x = 7 − 5y | |
| 3x − 2y = 4 |
Теперь, вместо «x» подставим во второе уравнение полученное выражение
«x = 7 − 5y» из первого уравнения.
| x = 7 − 5y | |
| 3(7 − 5y) − 2y = 4 |
Подставив вместо «x» выражение «(7 − 5y)» во второе уравнение, мы получили обычное линейное уравнение с одним неизвестным «y». Решим его по правилам решения линейных уравнений.
Чтобы каждый раз не писать всю систему уравнений заново, решим полученное уравнение «3(7 − 5y) − 2y = 4» отдельно. Вынесем его решение отдельно с помощью обозначения звездочка (*).
| 3(7 − 5y) − 2y = 4 (*) |
(*) 3(7 − 5y) − 2y = 4
21 − 15y − 2y = 4
− 17y = 4 − 21
− 17y = − 17 | :(−17)
y = 1
Мы нашли, что «y = 1». Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.
Вернемся к первому уравнению «x = 7 − 5y» и вместо «y» подставим в него полученное числовое значение.
Таким образом можно найти «x».
Запишем в ответ оба полученных значения.
| x = 7 − 5y | |
| y = 1 |
| x = 7 − 5 · 1 | |
| y = 1 |
| x = 2 | |
| y = 1 |
Способ сложения
Рассмотрим другой способ решения системы уравнений. Метод называется способ сложения. Вернемся к нашей системе уравнений еще раз.
| x + 5y = 7 | |
| 3x − 2y = 4 |
По правилам математики уравнения системы можно складывать. Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Наша задача в том, чтобы сложив исходные
уравнения, получить такое уравнение, в котором останется только одно неизвестное.
Давайте сейчас сложим уравнения системы и посмотрим, что из этого выйдет.
Запомните!
При сложения уравнений системы левая часть первого уравнения полностью складывается с левой частью второго уравнения, а правая часть полностью складывается с правой частью.
| x + 5y = 7 | (x + 5y) + (3x − 2y) = 7 + 4 | ||
| + => | x + 5y + 3x − 2y = 11 | ||
| 3x − 2y = 4 | 4x + 3y = 11 |
При сложении уравнений мы получили уравнение «4x + 3y = 11». По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
По сути, сложение уравнений в исходном виде нам ничего
не дало, так как в полученном уравнении мы по прежнему имеем оба неизвестных.
Вернемся снова к исходной системе уравнений.
| x + 5y = 7 | |
| 3x − 2y = 4 |
Чтобы при сложении неизвестное «x» взаимноуничтожилось, нужно сделать так, чтобы в первом уравнении при «x» стоял коэффициент «−3».
Для этого умножим первое уравнение на «−3».
Важно!
При умножении уравнения на число, на это число умножается каждый член уравнения.
| x + 5y = 7 | ·(−3) | |
| 3x − 2y = 4 |
| x ·(−3) + 5y · (−3) = 7 · (−3) | |
| 3x − 2y = 4 |
| −3x −15y = −21 | |
| 3x − 2y = 4 |
Теперь сложим уравнения.
| −3x −15y = −21 | (−3x −15y ) + (3x − 2y) = −21 + 4 | ||
| + => | −3x −15y + 3x − 2y = −21 + 4 | ||
| 3x − 2y = 4 | −17y = −17 |:(−17) | ||
| y = 1 |
Мы нашли «y = 1». Вернемся к первому уравнению и подставим вместо «y» полученное числовое значение и найдем «x».
| x = 7 − 5y | |
| y = 1 |
| x = 7 − 5 · 1 | |
| y = 1 |
| x = 2 | |
| y = 1 |
Ответ: x = 2; y = 1
Пример решения системы уравнения
способом подстановки
| x − 3y = 17 | |
| x − 2y = −13 |
Выразим из первого уравнения «x».
| x = 17 + 3y | |
| x − 2y = −13 |
Подставим вместо «x» во второе уравнение полученное выражение.
| x = 17 + 3y | |
| (17 + 3y) − 2y = −13 (*) |
(*) (17 + 3y) − 2y = −13
17 + 3y − 2y = −13
y = −13 − 17
y = −30
Подставим в первое уравнение полученное числовое значение «y = −30» и найдем «x».
| x = 17 + 3y | |
| y = −30 |
| x = 17 + 3 · (−30) | |
| y = −30 |
| x = 17 −90 | |
| y = −30 |
| x = −73 | |
| y = −30 |
Ответ: x = −73; y = −30
Пример решения системы уравнения
способом сложения
Рассмотрим систему уравнений.
| 3(x − y) + 5x = 2(3x − 2) | |
| 4x − 2(x + y) = 4 − 3y |
Раскроем скобки и упростим выражения в обоих уравнениях.
| 3x − 3y + 5x = 6x − 4 | |
| 4x − 2x − 2y = 4 − 3y |
| 8x − 3y = 6x − 4 | |
| 2x −2y = 4 − 3y |
| 8x − 3y − 6x = −4 | |
| 2x −2y + 3y = 4 |
| 2x − 3y = −4 | |
| 2x + y = 4 |
Мы видим, что в обоих уравнениях есть «2x».
Наша задача, чтобы при сложении уравнений «2x» взаимноуничтожились и в
полученном уравнении осталось только «y».
Для этого достаточно умножить первое уравнение на «−1».
| 2x − 3y = −4 |·(−1) | |
| 2x + y = 4 |
| 2x · (−1) − 3y · (−1) = −4 · (−1) | |
| 2x + y = 4 |
| −2x + 3y = 4 | |
| 2x + y = 4 |
Теперь при сложении уравнений у нас останется только «y» в уравнении.
| −2x + 3y = 4 | (−2x + 3y ) + (2x + y) = 4 + 4 | ||
| + => | −2x + 3y + 2x + y = 4 + 4 | ||
| 2x + y = 4 | 4y = 8 | :4 | ||
| y = 2 |
Подставим в первое уравнение полученное числовое значение «y = 2» и
найдем «x».
| −2x + 3y = 4 | |
| y = 2 |
| −2x + 3 · 2 = 4 | |
| y = 2 |
| −2x + 6 = 4 | |
| y = 2 |
| −2x = −2 | :(−2) | |
| y = 2 |
| x = 1 | |
| y = 2 |
Ответ: x = 1; y = 2
Решение системы линейных уравнений методом подстановки: алгоритм, правило, примеры
Алгоритм решения системы линейных уравнений методом подстановки
Например: ${\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.}$
Шаг 1
Из второго уравнения выражаем y:
y = x+1
Шаг 2
Подставляем выражение для y в первое уравнение:
3x+(x+1) = 5
Шаг 3 Решаем первое уравнение:
4x = 5-1
x = 1
Шаг 4
Подставляем значение x в выражение для y:
y = 1+1
Шаг 5
Находим y:
y = 2
Шаг 6
Записываем ответ:
(1;2)
В последовательной записи:
$$ {\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.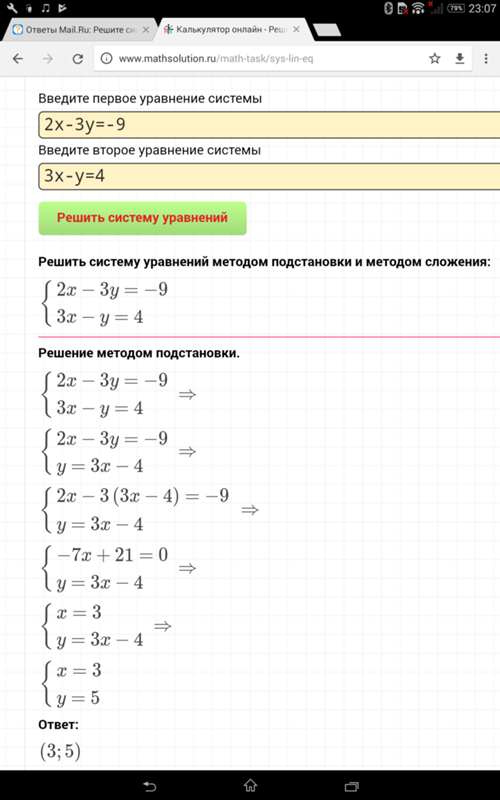 } \Rightarrow {\left\{ \begin{array}{c} 3x+y = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+(x+1) = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x = 5-1 \\ y = x+1 \end{array} \right.} \Rightarrow $$ $$ \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 2\end{array} \right.} $$
} \Rightarrow {\left\{ \begin{array}{c} 3x+y = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+(x+1) = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x = 5-1 \\ y = x+1 \end{array} \right.} \Rightarrow $$ $$ \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 2\end{array} \right.} $$
Ответ: (1;2)
Примеры
Пример 1. Решите систему уравнений методом подстановки:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = 3 \\ x = \frac{3y+4}{2} = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 7,5y+10-4y = 3 \\ x=1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3,5y = -7 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -2 \\ x = 1,5y+2 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} x = -1 \\ y = -2\end{array} \right.} $
} \Rightarrow {\left\{ \begin{array}{c} x = -1 \\ y = -2\end{array} \right.} $
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3y = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3\cdot \frac{3}{4} x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} (4- \frac{9}{4})x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow $
$\Rightarrow {\left\{ \begin{array}{c} x = 7 \cdot \frac{4}{7} = 4 \\ y = \frac{3}{4} x = \frac{3}{4} \cdot 4 = 3 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4 \\ y = 3 \end{array} \right.} $
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5a-4b = 9 \\ a = \frac{-3b-1}{2} = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end{array} \right. } \Rightarrow $
} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}-11,5b = 11,5 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
Ответ: (1;-1)
$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4b = 5 \\ b = \frac{-3a+1}{2} = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end{array} \right.} $
Ответ: (3;-4)
Пример 2. Найдите решение системы уравнений:
$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 | \times 4 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x-4y = 28 \\ 6x+y = 18 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end{array} \right.} \Rightarrow $
} \Rightarrow {\left\{ \begin{array}{c} x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end{array} \right.} \Rightarrow $
$\Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 24y+168+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 25y = -150 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4(-6+7) = 4 \\ y = -6 \end{array} \right.}$
Ответ: (4;-6)
$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 6 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 6 \end{array} \right.}\Rightarrow {\left\{ \begin{array}{c} 3x+2y = 1 \\ 2x+3y = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = \frac{-3x+1}{2} = -1,5x+0,5 \\ 2x+3(-1,5x+0,5) = -1\end{array} \right.} \Rightarrow$
$ \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ 2x-4,5x+1,5 = -1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ -2,5x = -2,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right. } $
} $
Ответ: (1;-1)
$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 10x-8y = -14 |:2 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-8y+25)-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} -40y+125-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -44y = -132 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.} $
Ответ: (1;3)
$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7(3y+2)+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 21y+14+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$
Ответ: (5;1)
Пример 3*. Найдите решение системы уравнений:
$ {\left\{ \begin{array}{c} \frac{3}{2x-5y} + \frac{8}{x+y} = 5 \\ \frac{12}{x+y} — \frac{1}{2x-5y} = 2 \end{array} \right.} $
Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{2x-5y} \\ b = \frac{1}{x+y} \end{array} \right.} $
Перепишем систему и найдём решение для новых переменных:
$$ {\left\{ \begin{array}{c} 3a+8b = 5 \\ 12b-a = 2 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 3(12b-2)+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 36b-6+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow $$
} \Rightarrow {\left\{ \begin{array}{c} 3(12b-2)+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 36b-6+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 44b = 11 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = \frac{1}{4} \end{array} \right.} $$
Получаем:
$$ {\left\{ \begin{array}{c} 2x-5y = \frac{1}{a} = 1 \\ x+y = \frac{1}{b} = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-5(4-x) = 1 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-20+5x = 1 \\ y = 4-x \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x = 21 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 3 \\ y = 1 \end{array} \right.} $$
Ответ: (3;1)
Решение систем уравнений с примерами решения
Содержание:
- Графический метод решения систем уравнений
- Начнём с графического метода
- Решение систем уравнений методом подстановки
- Симметричные системы уравнений с двумя неизвестными
Вспоминаем то, что знаем
Что такое график уравнения с двумя неизвестными?
Что представляет собой график линейного уравнения с двумя неизвестными?
Решите графическим методом систему линейных уравнений:
Открываем новые знания
Решите графическим методом систему уравнений:
Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту
В курсе алгебры 7-го класса вы изучали системы линейных уравнений.
Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Начнём с графического метода
Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.
Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.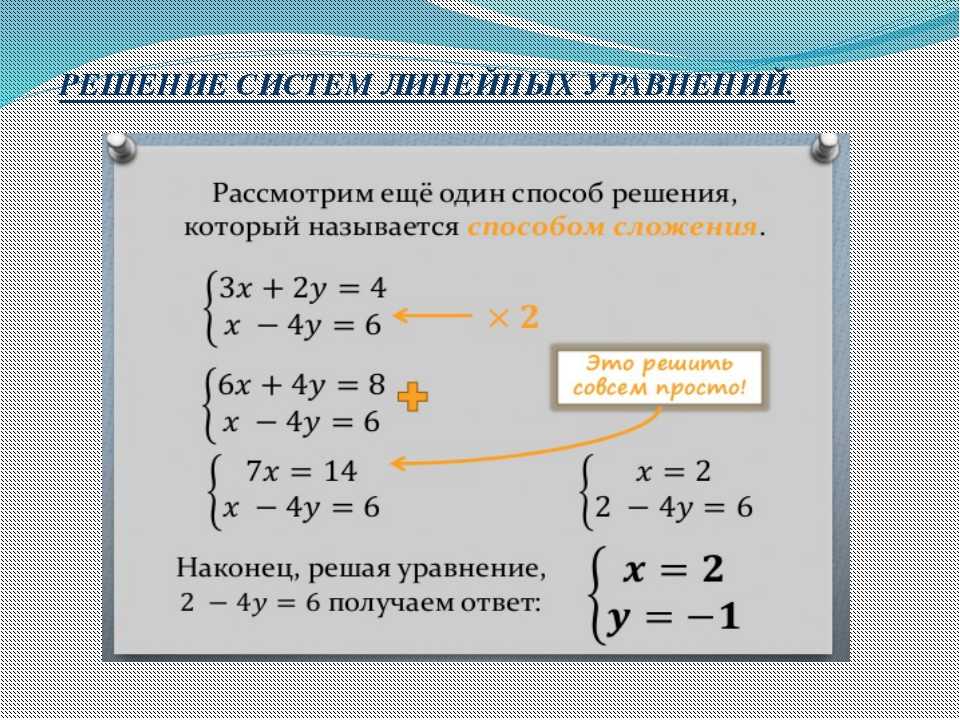
Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.
Возможно вам будут полезны данные страницы:
Общее решение уравнения |
Найти фундаментальную систему решений |
Исследовать ряд на абсолютную сходимость |
Исследовать ряд на условную сходимость |
Примеры с решением
Пример 1:
Решим систему уравнений:
Построим графики уравнений
Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).
Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).
Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.
Ответ: (2; 5) и (-1; 2).
Пример 2:
Выясним количество решений системы уравнений:
Построим графики уравнений
Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.
Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.
Ответ: Два решения.
Решение систем уравнений методом подстановки
Вспоминаем то, что знаем
Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.
Решите систему линейных уравнений методом подстановки:
Открываем новые знания
Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?
Решите систему уравнений методом подстановки:
Как решить систему двух уравнений с двумя неизвестными методом подстановки?
Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?
Ранее вы решали системы уравнений первой степени.
Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.
Пример 3:
Решим систему:
Пусть (х; у) — решение системы.
Выразим х из уравнения
Подставим найденное выражение в первое уравнение:
Решим полученное уравнение:
Найдём х:
Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.
Ответ: (5; 1), (-2;-2,5).
Чуть сложнее дело обстоит в следующем примере.
Пример 4:
Решим систему уравнений:
Пусть (х; у) — решение системы.
Выразим у из линейного уравнения:
Подставим найденное выражение в первое уравнение системы:
После преобразований получим:
Найдём у:
Ответ: (-0,5; 0,5), (4; 5).
Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».
Пример 5:
Решим систему:
Подставим во второе уравнение тогда его можно переписать в виде:
Теперь выразим х через у из первого уравнения системы:
Подставим в полученное ранее уравнение ху = 2:
Корни этого уравнения:
Найдём х:
.
Ответ: (2; 1), (-1;-2).
Иногда решить систему можно, используя метод алгебраического сложения.
Пример 6:
Решим систему:
Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:
.
Корни этого уравнения:
Подставим найденные значения в первое уравнение. Рассмотрим два случая:
1)
2) , получим уравнение корней нет.
Ответ: (0; 1), (1; 1).
Иногда упростить решение удаётся, используя различные варианты замены неизвестных.
Пример 7:
Решим систему уравнений:
Обозначим
Второе уравнение системы примет вид:
Решим полученное уравнение. Получим, умножая обе части на 2а:
Таким образом:
Осталось решить методом подстановки линейные системы:
Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями
Решение задач с помощью систем уравнений Знакомимся с новыми знаниями
Напомним, что при решении задач обычно действуют следующим образом:
1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;
2) решают полученную систему;
3) отвечают на вопрос задачи.
Пример 8:
Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.
Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.
Воспользуемся теоремой Пифагора:
Получим систему:
Решим систему. Выразим из первого уравнения у:
Подставим во второе уравнение:
Корни уравнения:
Найдём
С учётом условия получим ответ: длина — 12 см, ширина — 5 см.
Пример 9:
Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.
Найдите эти числа.
Введём обозначения.
Пусть х — первое число, у — второе число.
Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.
Получим систему:
Вычтем из второго уравнения первое. Получим:
Дальше будем решать методом подстановки:
Подставим в первое уравнение выражение для у:
Корни уравнения: (не подходит по смыслу задачи).
Найдём у из уравнения:
Получим ответ: 16 и 7.
Симметричные системы уравнений с двумя неизвестными
Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.
Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.
ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.
Например, если в системе уравнений
переставить местами неизвестные х и у, то получим систему:
Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.
Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:
Сначала научитесь выражать через неизвестные выражения:
Решение СЛАУ методами подстановки и сложения
- Понятие системы линейных уравнений
- Решение систем линейных уравнений методом подстановки
- Решение систем линейных уравнений методом сложения
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.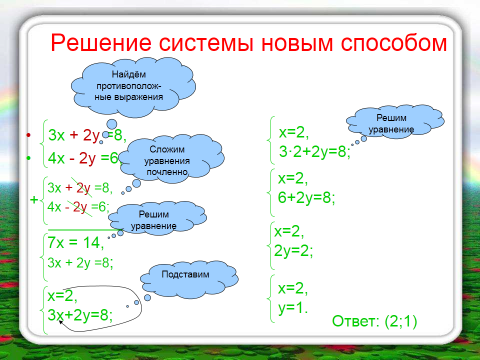
Например, уравнение
—
линейное, а уравнения и не являются линейными.
В общем виде система m линейных уравнений с n переменными записывается так:
. (1)
Числа
называются коэффициентами при переменных, а
—
свободными членами.
Совокупность чисел
называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.
Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений
с двумя переменными и два метода их решения — метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе
высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера —
основан на использовании определителей).
Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.
Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.
Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.
Пример 1. Решить систему линейных уравнений методом подстановки:
Выразим из первого уравнения данной системы y через x (можно и наоборот) и получим:
Подставив во второе уравнение данной системы вместо y выражение , получим систему
Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную.
Решим это уравнение:
В последней системе второе уравнение содержит только одну переменную.
Решим это уравнение:
Соответствующее значение y найдём, подставив вместо x число -5 в выражение , откуда
Пара (-5; 2) является решением системы линейных уравнений.
Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.
Пример 2. Решить систему линейных уравнений методом подстановки:
Из третьего уравнения системы выразим :
.
Подставим это выражение во второе уравнение данной системы:
.
Произведём преобразования и выразим из этого уравнения :
Полученные выражения для и подставим в первое уравнение системы и получим
.
Вместо можно вновь подставить его выражение, тогда получим уравнение с одним неизвестным:
откуда
.
Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:
Итак, решение данной системы линейных уравнений:
.
Пример 3. Решить систему линейных уравнений методом подстановки:
Из первого уравнения системы выразим :
.
Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:
Из третьего уравнения выразим :
Полученное выражение для подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:
.
Произведём преобразования и найдём :
Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:
Итак, решение данной системы линейных уравнений:
.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Системы линейных уравнений
При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной (равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.
Пример 4. Решить систему линейных уравнений методом сложения:
Решение. В уравнениях данной системы в этом примере системы коэффициенты при y — противоположные числа. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:
, или , .
Заменим одно из уравнений исходной системы, например, первое, уравнением . Получим систему
Решим полученную систему. Подставив значение
в уравнение , получим уравнение с одной переменной y:
Подставив значение
в уравнение , получим уравнение с одной переменной y:
Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением исходной системы, так как эти две системы линейных уравнений равносильны.
Пример 5. Решить систему линейных уравнений методом сложения
Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3, а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:
Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной: . Из этого уравнения находим, что . Получили
Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).
Пример 6. Решить систему линейных уравнений методом сложения:
Решение. Для упрощения решения произведём замену переменных:
, .
Приходим к системе линейных уравнений:
или
Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим , . Тогда .
Следовательно, имеем систему уравнений
или
Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим
.
Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования,
необходимые для решениях систем линейных уравнений в курсе высшей математики.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Системы линейных уравнений
Продолжение темы «Системы уравнений и неравенств»
Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений методом Гаусса
Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Решение систем линейных уравнений матричным методом (обратной матрицы)
Системы линейных неравенств и выпуклые множества точек
Начало темы «Линейная алгебра»
Определители
Матрицы
Поделиться с друзьями
Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Решения систем
линейных уравнений.
Метод подстановки и
метод сложения
7 класс.
Основными методами решения
систем уравнений считают:
Метод подстановки
Метод алгебраического сложения
Графический метод решения систем
уравнений
Повторим решение систем уравнений
методом подстановки.
Этапы решения
Пример
1. С помощью какого-либо
из уравнений выразить
одно неизвестное через
другое.
2. Подставить найденное
выражение в другое
уравнение системы: решить
получившееся уравнение с
одним неизвестным.
2 x y 4,
x 3 y 9;
Из первого уравнения
y = 2x − 4
x + 3(2x − 4) = 9;
x + 6x −12 = 9;
7x = 21;
x = 3.
Далее :
Этапы решения
3. Подставить найденное
значение одного
неизвестного в выражение
для другого неизвестного.
4. Записать ответ.
Пример
x = 3, тогда
y = 2x − 4 = 2∙3−4 = 2.
Ответ: (3; 2)
Решить систему уравнений способом подстановки
3x 2 y 27,
x 5 y 35.
Решение. 1) Из второго уравнения x = 35 − 5y
подставим в первое уравнение;
2) Решим его ,при этом второе уравнение пока
переписываем.
3) Теперь у подставим во второе уравнение .
Ответ: (5; 6)
Решить систему способом подстановки
Если же нужно решить систему у которой
Коэффициенты, например при х одинаковые.
2 x 3 y 10,
2 x 5 y 6;
1) Из первого уравнения
2) 2x = 10 + 3y подставим во второе уравнение:
10 + 3y + 5y = −6;
8y = −16; y = −2.
3) y = −2, 2x = 10 + 3∙(−2) =
= 4;
x = 2.
Ответ: (2; −2) Такие системы можно решить
другим способом –способом сложения.
Метод алгебраического сложения
Пример №1
Решить систему уравнений
7 x 2 y 27,
5 x 2 y 33.
Предположим, что x и y − это такие числа, при которых
оба равенства этой системы верны, т. е. (x ; y) − решение
данной системы.
Сложим эти равенства. Тогда снова получим верное
равенство, так как к равным числам прибавляются
равные числа:
7 x 2 y 27,
5 x 2 y 33.
12х = 60,
откуда х = 5.
Подставим х = 5 в одно из уравнений данной
системы, например в первое:
7∙5− 2y = 27,
35 − 2y = 27,
− 2y = − 8, y= 4.
Итак, если данная система имеет решение, то
этим решением может быть только пара чисел:
x = 5, y = 4.
Ответ: (5; 4)
5 x 3 y 29,
Решить систему уравнений
5 x 4 y 8.
Пример №2
Видим что коэффициенты при х одинаковые . Можно умножить
одно из них на (-1) , а можно вычесть из первого уравнения второе:
5 x 3 y 29,
5 x 4 y 8.
7 y 21,
откуда y = 3.
Подставим y = 3 в первое уравнение системы:
5x + 3∙3 = 29, 5х +9 = 29,
Ответ: (4; 3)
5х = 20, х = 4.
Рассмотренный способ решения систем
уравнений называется способом
алгебраического сложения.
Для исключения одного из неизвестных
нужно выполнить сложение или вычитание
левых и правых частей уравнений системы.
Способ алгебраического сложения оказывается
удобным для решения системы в том случае,
когда у обоих линейных уравнений
коэффициенты при каком-нибудь неизвестном
одинаковы или отличаются только знаком.
Метод алгебраического сложения
Этапы решения
1. Сложить почленно уравнения
системы, предварительно
умножив каждое из них на
подходящее число так, чтобы
после этого получилось одно
уравнение с одним неизвестным.
Пример
4 x 5 y 19 4
5
7
x
4
y
5
16 x 20 y 76
35x 20 y 25
51x = 51
2. Найти корень этого уравнения,
то есть найти значение одного из
неизвестных системы.
x=1
Метод алгебраического сложения
Этапы решения
3. Подставить найденное
значение одного из неизвестных
в любое из уравнений системы:
в результате снова получится
уравнение с одним неизвестным.
4. Решить это уравнение,
то есть найти значение второго
неизвестного.
5. Записать ответ
Пример
4 x 5 y 19
7 x 4 y 5
Подстановка в
первое уравнение даёт:
4∙1 + 5y = 19
5y = 15, y = 3
Ответ: ( 1; 3)
13. Пример №3. Если коэффициенты разные ,то можно их уравнять умножением всего уравнения на число .Первое умножаем на 3 ,второе на
(-2) ,чтобы получить противоположные коэффициенты .14. Задание на дом.
English Русский Правила
Решить систему линейных уравнений методом подстановки — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Метод подстановки в системе уравнений заключается в выражении одной переменной через другую.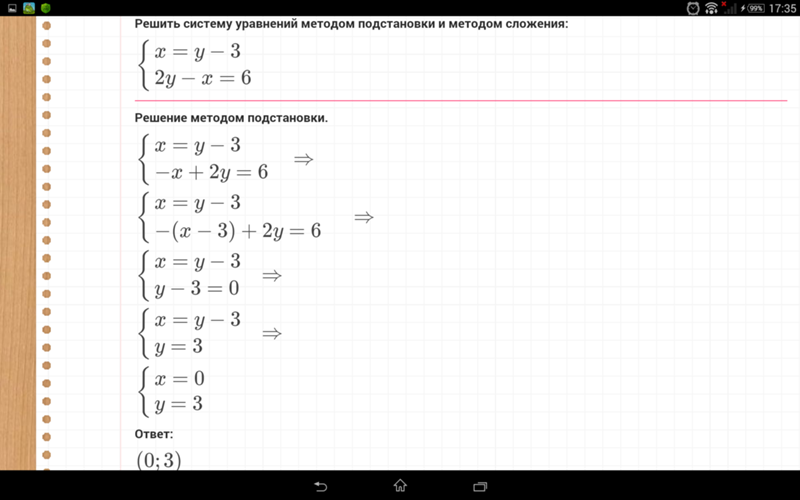 Результат подставляется в уравнение, которое теперь содержит одну переменную. После ее вычисления переходим к поиску второй неизвестной.
Результат подставляется в уравнение, которое теперь содержит одну переменную. После ее вычисления переходим к поиску второй неизвестной.
Решить систему уравнений методом подстановки онлайн – выбор студентов и учащихся школ. Заложенные в сервисе алгоритмы вычислений позволяют избежать ошибок, опечаток, неточностей, которые часто происходят при выполнении заданий самостоятельно.
- Настройте количество неизвестных в уравнении, кликая «-», «+».
- Введите данные в предназначенные для этого окна, после этого кликните кнопку «Рассчитать».
- Вам станет доступно пошаговое решение и ответ.
Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:
- Решение квадратных уравнений: формула корней, примеры
- Уравнение и его корни: определения, примеры
- Теорема Виета, формулы Виета
- Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
- Квадратные неравенства, примеры, решения
- Решение квадратных неравенств методом интервалов
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Решение квадратных уравнений
- Решение систем линейных уравнений методом Крамера
- Решение систем линейных уравнений методом Гаусса
- Решение систем линейных уравнений матричным методом
- Решение биквадратных уравнений
Решите систему уравнений методом подстановки
С помощью формулы, заложенной в калькулятор, вы решите систему методом подстановки быстро, бесплатно и без погрешностей. Результат выдается в виде поэтапных действий, а не только ответа. Поэтому вы легко сможете проверить себя и найти, где допустили ошибку. Наш сервис используют:
Результат выдается в виде поэтапных действий, а не только ответа. Поэтому вы легко сможете проверить себя и найти, где допустили ошибку. Наш сервис используют:
- Школьники. Не всегда новая тема, пройденная на уроке, хорошо усваивается. Каждый ученик может свериться с собственным решением.
- Родители. Чтобы удостовериться в достаточном уровне подготовки ребенка к занятиям и самому не углубляться в математические темы, достаточно сверить действия с полученными в сервисе.
- Студенты. В сложных заданиях попадаются промежуточные вычисления, на которых можно сэкономить время, получив готовый ответ.
- Преподаватели. При подготовке к урокам, семинарам, лекциям необходимо большое количество примеров. Также часто требуется быстрая проверка самостоятельных работ учащихся. В этом случае удобно не пересчитывать каждое задание, а упростить процесс и сделать его автоматизированным.
Не знаете, как решать систему уравнений методом подстановки? Узнайте ответ на задание с помощью кнопки «Рассчитать».
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
Метод замены | Решение системы уравнений подстановкой
Одним из методов алгебраического решения системы линейных уравнений с двумя переменными является метод подстановки. В этом методе мы находим значение любой из переменных, изолируя ее с одной стороны и беря все остальные члены с другой стороны уравнения. Затем подставляем это значение во второе уравнение. Он включает в себя простые шаги, чтобы найти значения переменных системы линейных уравнений методом подстановки. Давайте узнаем об этом подробно в этой статье.
В этом методе мы находим значение любой из переменных, изолируя ее с одной стороны и беря все остальные члены с другой стороны уравнения. Затем подставляем это значение во второе уравнение. Он включает в себя простые шаги, чтобы найти значения переменных системы линейных уравнений методом подстановки. Давайте узнаем об этом подробно в этой статье.
| 1. | Что такое метод замещения? |
| 2. | Решение систем уравнений методом подстановки |
| 3. | Разница между методом исключения и замены |
| 4. | Часто задаваемые вопросы о методе замены |
Что такое метод замены?
Метод подстановки — это простой способ алгебраического решения системы линейных уравнений и поиска решений переменных. Как следует из названия, он включает в себя нахождение значения переменной x через переменную y из первого уравнения, а затем подстановку или замену значения переменной x во втором уравнении. Таким образом, мы можем решить и найти значение переменной y. И, наконец, мы можем подставить значение y в любое из данных уравнений, чтобы найти x. Этот процесс также можно поменять местами, когда мы сначала находим x, а затем находим y.
Таким образом, мы можем решить и найти значение переменной y. И, наконец, мы можем подставить значение y в любое из данных уравнений, чтобы найти x. Этот процесс также можно поменять местами, когда мы сначала находим x, а затем находим y.
Определение метода подстановки
Метод подстановки — это один из алгебраических методов решения одновременных линейных уравнений. Он включает в себя подстановку значения любой из переменных из одного уравнения в другое уравнение. Двумя другими алгебраическими методами решения линейных уравнений являются метод исключения и метод перекрестного умножения. Помимо алгебраического метода, мы также можем решить систему линейных уравнений графически.
Рассмотрим пример решения двух уравнений x-2y=8 и x+y=5 методом подстановки.
Решение систем уравнений методом подстановки
Шаги по применению или использованию метода подстановки для решения системы уравнений приведены ниже:
- Шаг 1: Упростите данное уравнение, при необходимости расширив скобки.

- Шаг 2: Решите любое уравнение для любой из переменных. Вы можете использовать любую переменную, исходя из простоты расчета.
- Шаг 3: Подставьте полученное значение x или y в другое уравнение.
- Шаг 4: Теперь упростим новое уравнение, полученное с помощью арифметических операций, и решим уравнение для одной переменной.
- Шаг 5: Теперь подставьте значение переменной из Шаг 4 в любое из приведенных уравнений, чтобы найти другую переменную.
Вот пример решения системы уравнений методом подстановки: 2x+3(y+5)=0 и x+4y+2=0.
Решение:
Шаг 1: Итак, здесь мы можем упростить первое уравнение, чтобы получить 2x + 3y + 15 = 0. Теперь у нас есть два уравнения:
2x + 3y + 15 = 0 _____ ( 1)
x + 4y + 2 = 0 ______ (2)
Шаг 2: Решаем уравнение (2) относительно x. Итак, получаем x = -4y — 2.
Итак, получаем x = -4y — 2.
Шаг 3: Подставляем полученное значение x в уравнение (1). т. е. подставляя x = -4y-2 в уравнение 2x + 3y + 15 = 0, получаем 2(-4y-2) + 3y + 15 = 0,
Шаг 4: Теперь упростим новое уравнение. Получаем -8y-4+3y+15=0
-5y + 11 = 0
-5y = -11
y = 11/5
Шаг 5: Теперь подставим значение y в любое из приведенных уравнений. Подставим значение y в уравнение (2).
x + 4y + 2 = 0
x + 4 × (11/5) + 2 = 0
x + 44/5 + 2 = 0
x + 54/5 = 0
x = -54 /5
Следовательно, решив данную систему уравнений методом подстановки, получим x = -54/5 и y= 11/5.
Разница между методом исключения и замены
И метод исключения, и метод подстановки являются способами алгебраического решения линейных уравнений. Когда метод подстановки становится немного трудным для применения в уравнениях, содержащих большие числа или дроби, мы можем использовать метод исключения, чтобы облегчить наши вычисления. Давайте поймем разницу между этими двумя методами с помощью приведенной ниже таблицы:
Давайте поймем разницу между этими двумя методами с помощью приведенной ниже таблицы:
| Метод замены | Метод устранения |
|---|---|
| Здесь мы находим значение любой из переменных и подставляем его значение в другое уравнение. | В этом методе мы умножаем или делим одно или оба уравнения на число, чтобы сделать коэффициенты переменной x или переменной y одинаковыми в обоих уравнениях. Затем мы добавляем или вычитаем уравнения, чтобы исключить переменную с тем же коэффициентом. Таким образом, мы находим значение одной переменной, которое можно подставить в любое из уравнений, чтобы найти и другую переменную. |
| Метод подстановки лучше использовать, когда уравнения либо заданы в виде, либо могут быть приведены в виде x = ay + b и y = mx + n. | Лучше использовать метод исключения, когда коэффициент любого из слагаемых одинаков. Например, Ax+By+C=0 и Px+By+R=0. |
Важные примечания к методу подстановки:
- Чтобы начать с метода подстановки, сначала выберите уравнение с коэффициентом 1 хотя бы для одной из переменных и решите для той же переменной (с коэффициентом 1). Это упрощает процесс.
- Перед тем, как начать использовать метод подстановки, объедините все одинаковые термины (если они есть).
- После решения для одной переменной мы можем выбрать любое из заданных уравнений или любое уравнение во всем процессе, чтобы найти другую переменную.
- Если при решении методом подстановки мы получаем какое-либо верное утверждение, например, 3 = 3, 0 = 0 и т. д., то это означает, что система имеет бесконечно много решений.
- Если мы получим какое-либо ложное утверждение типа 3 = 2, 0 = 1 и т. д. при решении методом подстановки, то это означает, что система не имеет решения.
☛ Похожие темы:
Ознакомьтесь с этими статьями, посвященными методу замены.
- Калькулятор метода замены
- Калькулятор метода замены
- Решатель системы уравнений
Примеры методов замены
Пример 1: Шон получил два уравнения 5m−2n=17 и 3m+n=8. Можете ли вы помочь ему найти решение этих уравнений методом подстановки?
Решение: Даны два уравнения:
5m−2n=17 ____ (1)
3m+n=8 _____ (2)
Решение данных двух уравнений можно найти, выполнив следующие действия. :
- Из уравнения 2 мы можем найти значение n через m, где n = 8 — 3m
- Подставляем значение n в уравнение 1. Получаем, 5m — 2(8-3m)=17
5м — 2(8-3м)=17
5м — 16 + 6м =17
11м = 17 + 16
11m=33
m = 3
- Подставляем значение m в уравнение 2, получаем 3×3+n=8
9+n=8
n=8-9
n=-1
Ответ: Следовательно, методом подстановки мы выяснили, что m=3 и n=-1.

Пример 2: У Джеки есть два числа, сумма которых равна 20, а разница между ними равна 10. Найдите числа, используя метод подстановки решения линейных уравнений.
Решение: Пусть два числа будут x и y такими, что x>y. Дано, что x+y=20 ___ (1) и x−y=10 ___ (2). Из уравнения 1 получаем x = 20-y. Подставьте это значение в уравнение 2, чтобы найти значение y.
x−y=10
20-y-y=10
20-2y=10
20-10=2y
10=2y
y=10/2 = 5 9000 y в уравнении 1, мы получаем, x+5=20, что дает нам x=15.
Ответ: Следовательно, эти два числа — 15 и 5.
Пример 3: Решить данную систему линейных уравнений методом подстановки:
— 2x — 5 + 3x + y = 0 ___ (1)
3x + y = 11 ___ (2)
Решение: Как мы видим, первое уравнение можно еще больше упростить, комбинируя подобные члены. После упрощения получаем x+y-5=0.
 Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.
Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.15-3y+y=11
15-2y=11
15-11=2y
4=2y
y=4/2=2
Теперь подставим значение y в уравнение 1. Получаем x+2-5=0, что можно упростить до x = 3.
Ответ: Следовательно, методом подстановки имеем x=3 и y=2.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по методу замены
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о методе замены
Что такое метод подстановки в алгебре?
В алгебре метод подстановки является одним из способов решения линейных уравнений с двумя переменными. В этом методе мы подставляем значение переменной, найденное одним уравнением, во второе уравнение. Его очень легко использовать, когда у нас есть меньшие числа, но в случае больших чисел или дробных коэффициентов применять метод подстановки становится утомительно.
В этом методе мы подставляем значение переменной, найденное одним уравнением, во второе уравнение. Его очень легко использовать, когда у нас есть меньшие числа, но в случае больших чисел или дробных коэффициентов применять метод подстановки становится утомительно.
Когда следует использовать метод подстановки?
Метод подстановки можно применить к любой паре линейных уравнений с двумя переменными. Целесообразно использовать метод подстановки, когда мы имеем меньшие коэффициенты в терминах или когда уравнения заданы в виде x = ay+c и y=bx+p.
Что мы заменяем в методе замещения?
В методе подстановки мы подставляем значение одной переменной, найденное путем упрощения уравнения, в другое уравнение. Например, если в уравнениях m и n две переменные, то мы можем сначала найти значение m через n из любого из уравнений, а затем подставить это значение во второе уравнение, чтобы получить ответ n . Затем снова подставляем значение n в любое из данных уравнений.
Что общего между методом замены и методом исключения?
Оба метода включают процесс замены. В обоих методах мы сначала находим значение одной переменной, а затем подставляем его в любое из заданных уравнений. Таким образом, это характерно как для метода исключения, так и для метода замены.
Что такое первый шаг в методе замещения?
Первым шагом в методе подстановки является нахождение значения любой из переменных в одном уравнении через другую переменную. Например, если есть два уравнения x+y=7 и x-y=8, то из первого уравнения можно найти, что x=7-y. Это первый шаг применения метода замещения.
Каковы шаги метода замены?
Ниже приведены три простых шага метода подстановки :
- Найдите значение любой переменной из любого уравнения через другую переменную.
- Подставьте его в другое уравнение и решите.
- Снова подставьте значение второй переменной в любое из уравнений.
Как использовать метод подстановки с двумя переменными?
Имея две переменные, скажем, x и y, мы сначала находим значение x через y из любого из приведенных уравнений. Затем мы подставляем это значение в другое уравнение, чтобы найти значение y. Наконец, мы снова подставляем значение y в любое данное уравнение, чтобы найти x.
Затем мы подставляем это значение в другое уравнение, чтобы найти значение y. Наконец, мы снова подставляем значение y в любое данное уравнение, чтобы найти x.
Является ли метод замены только для линейных уравнений?
Нет, метод подстановки можно применять для любого типа уравнений. Например, уравнения y = x 2 и y = 3x + 4 можно решить методом подстановки.
Скачать БЕСПЛАТНЫЕ учебные материалы
ЛИСТКИ
Решение одновременных уравнений: метод подстановки и метод сложения | Справочник по алгебре
Что такое одновременные уравнения и системы уравнений?
Термины одновременные уравнения и системы уравнений относятся к условиям, когда две или более неизвестные переменные связаны друг с другом через равное количество уравнений.
Пример:
Для этого набора уравнений существует только одна комбинация значений x и y, которая удовлетворяет обоим.
Любое уравнение, рассматриваемое по отдельности, имеет бесконечное число правильных (x,y) решений, но вместе существует только одно. На графике это условие становится очевидным:
На графике это условие становится очевидным:
Каждая линия на самом деле является континуумом точек, представляющих возможные пары решений x и y для каждого уравнения.
Каждое уравнение в отдельности имеет бесконечное число упорядоченных пар (x,y) решений. Существует только одна точка, в которой две линейные функции x + y = 24 и 2x — y = -6 пересекаются (где одно из их многочисленных независимых решений работает для обоих уравнений), и именно в этой точке x равно значению 6, а y равно 18.
Однако обычно построение графика не является очень эффективным способом определения набора одновременных решений для двух или более уравнений. Это особенно нецелесообразно для систем с тремя и более переменными.
В системе с тремя переменными, например, решение будет найдено путем пересечения точек трех плоскостей в трехмерном координатном пространстве — сценарий, который нелегко визуализировать.
Решение одновременных уравнений методом подстановки
Для решения одновременных уравнений существует несколько алгебраических методов.
Пожалуй, проще всего понять метод подстановки .
Возьмем, к примеру, нашу задачу с двумя переменными:
В методе подстановки мы манипулируем одним из уравнений таким образом, что одна переменная определяется через другую:
переменной и замените ее на той же переменной в другом уравнении.
В этом случае мы берем определение y, которое равно 24 — x, и заменяем его на член y, найденный в другом уравнении:
Теперь, когда у нас есть уравнение только с одной переменной (x), мы можем решить его, используя «обычные» алгебраические методы:
подставьте это значение в любое из исходных уравнений и получите значение для y.
Или, чтобы избавить нас от работы, мы можем подставить это значение (6) в уравнение, которое мы только что создали, чтобы определить y через x, поскольку оно уже находится в форме для решения для y:
Применение метода подстановки к системам с тремя или более переменными включает аналогичную схему, только требует больше усилий.
В целом это верно для любого метода решения: количество шагов, необходимых для получения решения, быстро увеличивается с каждой дополнительной переменной в системе.
Чтобы решить для трех неизвестных переменных, нам нужно как минимум три уравнения. Рассмотрим этот пример:
Поскольку первое уравнение имеет простейшие коэффициенты (1, -1 и 1 для x, y и z соответственно), кажется логичным использовать его для разработки определения одной переменной в терминах два других.
Решайте для x с точки зрения Y и z:
Теперь мы можем заменить это определение x, где x появляется в двух других уравнениях:
. до их простейших форм:
До сих пор наши усилия сократили систему с трех переменных в трех уравнениях до двух переменных в двух уравнениях.
Теперь мы можем снова применить технику подстановки к двум уравнениям 4y — z = 4 и -3y + 4z = 36, чтобы найти либо y, либо z. Сначала я поработаю с первым уравнением, чтобы определить z через y:
Сначала я поработаю с первым уравнением, чтобы определить z через y:
Затем мы заменим это определение z через y там, где мы видим z в другом уравнении:
Теперь, когда значение y известно, мы можем подставить его в уравнение, определяющее z через y, и получить число для z: и z известны, мы можем подставить их в уравнение, в котором мы определили x через y и z, чтобы получить значение для x: и z из 2, 4 и 12 соответственно, которые удовлетворяют всем трем уравнениям.
Решение одновременных уравнений с использованием метода сложения
Хотя метод подстановки может быть самым простым для понимания на концептуальном уровне, нам доступны и другие методы решения.
Одним из таких методов является так называемый метод сложения , при котором уравнения добавляются друг к другу с целью сокращения переменных членов.
Возьмем нашу систему с двумя переменными, используемую для демонстрации метода подстановки:
Одно из наиболее часто используемых правил алгебры состоит в том, что вы можете выполнять любую арифметическую операцию над уравнением, если вы делаете это одинаково с обеими частями .
Что касается сложения, это означает, что мы можем добавлять любую величину, которую пожелаем, к обеим частям уравнения — при условии, что это одна и та же величина — без изменения истинности уравнения.
Таким образом, у нас есть возможность сложить соответствующие части уравнений вместе, чтобы сформировать новое уравнение.
Поскольку каждое уравнение является выражением равенства (одна и та же величина по обе стороны от знака =), добавление левой части одного уравнения к левой части другого уравнения справедливо до тех пор, пока мы добавляем правые части двух уравнений вместе.
В нашем примере набора уравнений, например, мы можем добавить x + y к 2x — y, а также добавить 24 и -6 вместе, чтобы сформировать новое уравнение.
Какая нам от этого польза? Изучите, что происходит, когда мы делаем это с нашим примером набора уравнений:
Поскольку верхнее уравнение содержало положительный член по оси y, а нижнее уравнение содержало отрицательный член по оси y, эти два члена сокращались в процессе сложения, не оставляя члена по оси y в сумме .
У нас осталось новое уравнение, но только с одной неизвестной переменной x! Это позволяет нам легко найти значение x:
Как только мы получим известное значение x, конечно, определение значения y будет простым вопросом замены (замена x числом 6 ) в одно из исходных уравнений.
В этом примере метод сложения уравнений хорошо сработал, чтобы получить уравнение с одной неизвестной переменной.
Как насчет примера, где все не так просто? Рассмотрим следующий набор уравнений:
Мы могли бы сложить эти два уравнения вместе — это вполне допустимая алгебраическая операция — но это не принесет нам пользы для получения значений x и y:
Полученное уравнение по-прежнему содержит две неизвестные переменные, как и исходные уравнения, поэтому мы не продвинулись дальше в получении решения.
Однако что, если бы мы могли манипулировать одним из уравнений так, чтобы иметь отрицательный член, который отменял бы соответствующий член в другом уравнении при добавлении?
Тогда система сведется к одному уравнению с одной неизвестной переменной, как и в последнем (случайном) примере.
Если бы мы могли только превратить член y в нижнем уравнении в член a — 2y, так что, когда два уравнения складываются вместе, оба члена y в уравнениях сокращаются, оставляя нам только член x, это принесло бы нам ближе к решению.
К счастью, сделать это несложно. Если мы умножим каждый член нижнего уравнения на -2, то получим искомый результат:
Теперь мы можем добавить это новое уравнение к исходному верхнему уравнению:0003
Решая для x, мы получаем значение 3:
Подставляя это вновь найденное значение для x в одно из исходных уравнений, значение
легко определяется:
3
Использование этого метода решения в системе с тремя переменными немного сложнее.
Как и в случае с подстановкой, вы должны использовать эту технику, чтобы сократить систему из трех уравнений с тремя переменными до двух уравнений с двумя переменными, а затем применить ее снова, чтобы получить одно уравнение с одной неизвестной переменной.
Чтобы продемонстрировать, я буду использовать систему уравнений с тремя переменными из раздела подстановки:
Поскольку коэффициенты верхнего уравнения равны 1 для каждой переменной, им будет легко манипулировать уравнением. и использовать в качестве инструмента отмены.
Например, если мы хотим исключить 3-кратный член из среднего уравнения, все, что нам нужно сделать, это взять верхнее уравнение, умножить каждый из его членов на -3, а затем добавить его к среднему уравнению следующим образом:
Мы можем избавить нижнее уравнение от пятикратного члена тем же способом: взять исходное верхнее уравнение, умножить каждый из его членов на 5, затем добавить это модифицированное уравнение к нижнему уравнению, оставив новое уравнение только с членами y и z:
На данный момент у нас есть два уравнения с теми же двумя неизвестными переменными, y и z:
3
очевидно, что член -z верхнего уравнения можно использовать для сокращения члена 4z в нижнем уравнении, если только мы умножим каждый член верхнего уравнения на 4 и сложим два уравнения вместе:
Взяв новое уравнение 13y = 52 и решив для y (путем деления обеих частей на 13), мы получим значение 4 для y.
Подстановка этого значения 4 вместо y в любое из уравнений с двумя переменными позволяет нам найти z.
Подстановка обоих значений y и z в любое из исходных уравнений с тремя переменными позволяет нам найти x.
Окончательный результат (я избавлю вас от алгебраических шагов, так как вы уже должны быть с ними знакомы!) состоит в том, что x = 2, y = 4 и z = 12,
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:
- Одновременные уравнения для анализа цепей Рабочий лист
Метод подстановки (системы линейных уравнений)
Когда два уравнения прямой пересекаются в одной точке, мы говорим, что они имеют единственное решение, которое можно описать как точку \color{red}\left( {x ,y} \right), в плоскости XY .
Метод подстановки используется для решения систем линейных уравнений путем нахождения точных значений x и y, соответствующих точке пересечения.
На диаграмме ниже показаны две произвольные линии, показывающие, где они пересекаются, как описано упорядоченной парой \left( {x,y} \right). В этом уроке мы заинтересованы в ручном решении этой общей точки.
В этом уроке мы заинтересованы в ручном решении этой общей точки.
Примеры решения системы уравнений методом подстановки
Пример 1: Используйте метод подстановки для решения приведенной ниже системы линейных уравнений.
Идея состоит в том, чтобы выбрать одно из двух заданных уравнений и решить любую из переменных, x или y. Результат нашего первого шага будет подставлен в другое уравнение. Результатом будет одно уравнение с одной переменной, которое можно решить как обычно.
Это полностью зависит от того, с каким уравнением, по вашему мнению, будет проще справиться. Выбор за вами.
Обратите внимание, что верхнее уравнение содержит переменную x, которая является «одной» — это означает, что ее коэффициент равен +1. Не забывайте всегда искать эту характеристику («единственную» переменную), потому что она сделает вашу жизнь намного проще.
Теперь я начну с решения верхнего уравнения для x.
Поскольку я знаю, чему равен x через y, я могу подставить это выражение в другое уравнение. Таким образом, я решу уравнение с одной переменной.
Таким образом, я решу уравнение с одной переменной.
Надеюсь, вы получите такое же значение y = — \,5. Теперь, когда я знаю точное значение y, я найду другую переменную (в данном случае x), вычислив ее значение в любом из двух исходных уравнений. Неважно, какое исходное уравнение вы выберете, поскольку в конечном итоге оно даст один и тот же ответ.
Тем не менее, я должен сказать, что «лучший» способ найти x — это использовать исправленное уравнение, которое я решил ранее, поскольку у меня есть «x = некоторое y». Верно?
Здесь я получаю x = 1. В точечной форме окончательный ответ можно записать как \left( {1, — \,5} \right). Помните, что это точка пересечения двух линий.
Всегда полезно проверять эти значения в исходных уравнениях, чтобы убедиться, что они действительно являются правильными ответами. Я предлагаю вам всегда проверять их.
Графически решение выглядит так.
Пример 2: Используйте метод подстановки для решения системы линейных уравнений.
Очевидным выбором здесь является выбор нижнего уравнения, потому что переменная y имеет положительный коэффициент, равный единице \left( { + 1} \right). Теперь я могу легко найти y через x. Для начала я вычту обе стороны в 3 раза.
Найдя y из нижнего уравнения, я теперь перехожу к верхнему уравнению и заменяю выражение для y через x. Результатом будет многоступенчатое уравнение с одной переменной.
Решите это уравнение, сначала упростив скобки. После этого объедините одинаковые термины с обеих сторон и изолируйте переменную слева. Ваше решение должно быть похоже на приведенное ниже.
Если вы правильно решили для x, вы также должны прийти к значению x = 3.
Поскольку исправленное уравнение дна уже записано в форме, которая мне нравится, я буду использовать его для решения для точного значения y.
С полученным значением y = 1 теперь я могу записать окончательный ответ в виде упорядоченной пары \left( {3,1} \right).
Как я упоминал ранее, всегда проверяйте окончательные ответы самостоятельно, чтобы увидеть, соответствуют ли они исходным уравнениям.
На графике решением является точка пересечения двух заданных линий.
Пример 3: Решить систему уравнений методом подстановки.
Это отличный пример, потому что у меня есть два подхода к решению проблемы. Переменные x и y имеют положительную единицу \left( { + 1} \right) в качестве коэффициентов. Это означает, что я могу пойти в любую сторону.
Для этого примера я найду у. Я могу легко сделать это, вычитая обе стороны на x, а затем переставляя.
Затем я запишу другое уравнение и заменю его y на y = — x + 3.
После решения приведенного выше многошагового уравнения я получаю x = 5. Теперь я перехожу к преобразованной версии уравнения первое уравнение, которое нужно решить для y.
Здесь я получаю y = — \,2. Тогда окончательный ответ: \left( {x,y} \right) = \left( {5, — \,2} \right).
Действительно, две прямые пересекаются в точке, которую мы вычислили!
Пример 4: Решить систему уравнений методом подстановки.
Я нахожу эту проблему интересной, потому что не могу найти ситуацию, когда переменная «одна». Опять же, наше определение «одиночества» — это коэффициент +1. Запомнить?
И верхнее, и нижнее уравнения здесь содержат переменную с отрицательным символом. Я предлагаю, чтобы всякий раз, когда вы видите что-то подобное, заменяли этот отрицательный символ на \textbf{- 1}. Я помещаю синюю стрелку прямо рядом с ним для акцента (см. ниже).
Отсюда я могу перейти к решению для y, используя верхнее уравнение, или для x, используя нижнее. В этом упражнении я буду работать над уравнением дна.
Обратите внимание, что для решения x я разделил все уравнение на — 1. Здесь вы можете видеть, что вид уравнения сильно изменился.
Надеюсь, у вас тоже есть y = — \,4. В противном случае проверьте и перепроверьте свои действия при решении многошагового уравнения.
Затем используйте это значение y и подставьте его в преобразованную версию нижнего уравнения, чтобы найти x.
Итак, я получаю x = — \,2. Окончательный ответ в упорядоченной паре: \left( {x,y} \right) = \left( { — \,2, — \,4} \right).
График соглашается с нами в том, где пересекаются две линии. Большой!
Пример 5: Используйте метод подстановки для решения системы линейных уравнений.
Первое, что я заметил здесь, это то, что не бывает случаев, когда коэффициент переменной равен +1 или -1. Некоторым это может показаться запутанным.
В этой задаче можно выделить y в верхнем уравнении и сделать то же самое для x в нижнем уравнении. Поработайте немного, и это должно иметь больше смысла.
Вы поймете, что либо x, либо y могут быть легко решены, потому что в процессе не генерируются дроби. В этом упражнении я решил решить первое уравнение для y.
Как и предполагалось, вычисление y прошло успешно. Теперь я буду использовать это значение для y и подставлю его в y нижнего уравнения. Затем я продолжу решать полученное уравнение, как обычно.
Если вы сделали это правильно, ваш ответ должен получиться как x = 2. Подставьте это значение x в исправленную версию верхнего уравнения, чтобы найти точное значение y.
Здесь я получил y = — \,5. Это делает наш окончательный ответ упорядоченной парой \left( {2, — \,5} \right).
График подтверждает наши расчетные значения x и y.
Вас также могут заинтересовать:
Метод подстановки Практические задачи с ответами
Метод исключения (системы уравнений)
Решение систем нелинейных уравнений
Метод подстановки | Магазин развивающей математики
Результаты обучения
- Использовать метод подстановки для решения систем уравнений
- Выразите решение несовместной системы уравнений, содержащей две переменные
- Выразите решение зависимой системы уравнений, содержащей две переменные
Решение системы уравнений методом подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики для классификации количества решений системы двух линейных уравнений. Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные числа или дроби, это не самый точный метод. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные числа или дроби, это не самый точный метод. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали замену по-разному. Например, когда мы использовали формулы для площади треугольника и простых процентов, мы подставляли значения, которые мы знали, в формулу, чтобы найти значения, которые мы не знали. Идея аналогична применительно к решению систем, в этом процессе всего несколько разных шагов. В методе подстановки мы решаем одно из уравнений для одной переменной, а затем подставляем результат в другое уравнение для решения второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен. Давайте начнем с примера, чтобы понять, что это значит.
Давайте начнем с примера, чтобы понять, что это значит.
Вы можете заменить значение переменной, даже если это выражение. Вот пример.
Помните, что решение системы уравнений должно быть решением каждого уравнения в системе. Упорядоченная пара [латекс](4,−1)[/латекс] работает для обоих уравнений, поэтому вы знаете, что она также является решением системы.
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной [latex]x[/latex] или [latex]y[/latex]. Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам может потребоваться переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете подставить ее в другое уравнение.
Пример
Решите следующую систему уравнений путем замены.
[латекс]\begin{array}{l}-x+y=-5\hfill \\ \text{ }2x — 5y=1\hfill \end{array}[/latex]
Показать решение
Вот краткое изложение шагов, которые мы используем для решения систем уравнений с использованием метода подстановки.
Как: Данную систему двух уравнений с двумя переменными решить методом подстановки
- Решить одно из двух уравнений для одной из переменных через другую.
- Подставьте выражение для этой переменной во второе уравнение, а затем найдите оставшуюся переменную.
- Подставьте это решение в любое из исходных уравнений, чтобы найти значение другой переменной. Если возможно, запишите решение в виде упорядоченной пары.
- Проверьте решение обоих уравнений.
Давайте рассмотрим несколько примеров, замена которых включает свойство распределения.
В следующем видео вам будет представлен пример решения системы двух уравнений методом подстановки.
Если бы вы выбрали другое уравнение для начала в предыдущих примерах, вы все равно смогли бы найти такое же решение. На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Попробуйте
Определите системы уравнений, которые не имеют решений или имеют бесконечное число решений
Вспомните, что несовместная система состоит из параллельных прямых, которые имеют одинаковый наклон, но разные y -пересечения. Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, такому как [латекс]12=0[/латекс].
Когда мы изучили методы решения линейных уравнений с одной переменной, то обнаружили, что одни уравнения не имеют решений, а другие имеют бесконечное множество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из Модуля 1 для решения линейных уравнений с одной переменной:
Решите для [латекс]х[/латекс]. [латекс]12+2x–8=7x+5–5x[/латекс]
[латекс]12+2x–8=7x+5–5x[/латекс]
[латекс] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\, \,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\конец{массив}[/латекс]
[латекс]\начало{массив} {l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\, \,\подчеркивание{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \, 5\конец{массив}[/латекс]
Это ложное утверждение означает, что нет решений этого уравнения. Точно так же вы можете увидеть подобный результат, когда используете метод подстановки для поиска решения системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Вы получаете ложное утверждение [латекс]−8=4[/латекс]. Что это значит? График этой системы проливает некоторый свет на происходящее.
Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [латекс]−8=4[/латекс] — это , а не решение. Это просто ложное утверждение, и оно указывает на то, что решения не существует.
Это просто ложное утверждение, и оно указывает на то, что решения не существует.
Давайте рассмотрим еще один пример, в котором нет решения.
Пример
Решите следующую систему уравнений.
[латекс]\begin{массив}{l}x=9 — 2y\hfill \\ x+2y=13\hfill \end{массив}[/latex]
Показать решение
В следующем видео мы покажем еще один пример использования подстановки для решения системы, которая не имеет решения.
Попробуйте
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное число решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
На этот раз вы получите истинное утверждение: [латекс]−4,5x=−4,5x[/латекс]. Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, представляющих одну и ту же прямую; две линии коллинеарны. Каждая точка на линии будет решением системы, поэтому метод подстановки дает истинное утверждение. В этом случае существует бесконечное множество решений.
Попробуйте
В следующем видео вы увидите пример решения системы, которая имеет бесконечное количество решений.
В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.
Резюме
Метод подстановки является одним из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).
Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).
Пожертвовать!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Решение систем уравнений тремя способами: замена, исключение и построение графика — Krista King Math
Всегда есть три способа решения системы уравнений
Есть три способа решения системы линейных уравнений: подстановка, исключение и построение графика. Давайте рассмотрим шаги для каждого метода.
Давайте рассмотрим шаги для каждого метода.
Подстановка Получить переменную саму по себе в одном из уравнений.
Возьмите выражение, которое вы получили для переменной на шаге 1, и подставьте его (замените скобками) в другое уравнение.
Решите уравнение шага 2 для оставшейся переменной.
Используйте результат шага 3 и подставьте его в уравнение из шага 1.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Исключение При необходимости переставьте оба уравнения так, чтобы сначала были члены ???x???, за которыми следовали члены ???y???, знак равенства и постоянный член (в этой последовательности). Если уравнение не имеет постоянного члена, это означает, что постоянный член равен ???0???.
Умножить одно (или оба) уравнения на константу, которая позволит сократить либо ???x???-члены, либо ???y???-члены при сложении или вычитании уравнений (когда их левая и правая части складываются отдельно или когда их левая и правая части вычитаются отдельно).
Сложите или вычтите уравнения.
Найдите оставшуюся переменную.
Подставьте результат шага 4 в одно из исходных уравнений и найдите другую переменную.
График Решить для ???y??? в каждом уравнении.
Постройте оба уравнения в одной декартовой системе координат.
Найти точку пересечения линий (точка пересечения линий).
Решение той же системы с подстановкой, затем с исключением, затем с построением графика
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого.
 🙂
🙂 Учить больше
Определение метода, который лучше всего подходит для решения системы: замена, исключение или построение графика
Теперь давайте рассмотрим несколько примеров, в которых нам нужно решить, какой из этих трех методов использовать.
Пример
Какой метод вы бы использовали для решения следующей задачи? Объясните, почему вы выбрали именно этот метод.
???х=у+2???
???3y-2x=15???
Самый простой способ решить эту систему — использовать подстановку, поскольку ???x??? уже изолирован в первом уравнении. Всякий раз, когда одно уравнение уже решено для переменной, подстановка будет самым быстрым и простым методом.
Несмотря на то, что вас не просят решить, вот шаги для решения системы:
Замените ???y+2??? за ???х??? во втором уравнении.
???3y-2(y+2)=15???
Раздать ???-2??? а затем объединить подобные термины.
???3y-2y-4=15???
???y-4=15???
Добавить ???4??? в обе стороны.
???y-4+4=15+4???
???y=19???
Вилка ???19??? для тебя??? в первое уравнение.
???х=у+2???
???х=19+2???
???х=21???
Единственное решение ???(21,19)???.
Существует три способа решения систем линейных уравнений: замена, исключение и построение графика.
Как решить систему с помощью метода исключения
Пример
Чтобы решить систему методом исключения, что было бы полезным первым шагом?
???x+3y=12???
???2x-y=5???
Когда мы используем исключение для решения системы, это означает, что мы собираемся избавиться (устранить) от одной из переменных. Таким образом, мы должны иметь возможность складывать уравнения или вычитать одно из другого, и при этом отменять либо ???x???-члены, либо ???y???-члены.
Любая из следующих опций была бы полезной в качестве первого шага:
Умножить первое уравнение на ???-2??? или???2???. Это даст нам ???2x??? или ???-2x??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Это даст нам ???2x??? или ???-2x??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Умножить второе уравнение на ???3??? или ???-3???. Это даст нам ???3г??? или ???-3г??? в обоих уравнениях, что приведет к сокращению членов ???y???, когда мы складываем или вычитаем.
Разделите второе уравнение на ???2???. Это даст нам ???x??? или ???-х??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Разделить первое уравнение на ???3???. Это даст нам ???y??? или ???-у??? в обоих уравнениях, что приведет к сокращению членов ???y???, когда мы складываем или вычитаем.
Повторим последний пример, но вместо метода исключения воспользуемся графом для поиска решения.
Решение системы путем построения графика обоих уравнений и поиска точек пересечения
Пример
Начертите оба уравнения, чтобы найти решение системы.
???х+3у=12???
???2x-y=5???
Чтобы изобразить эти уравнения в виде графика, давайте представим их обоим в форме пересечения наклона. Получаем
???x+3y=12???
???3y=-x+12???
???y=-\frac13x+4???
и
???2x-y=5???
???-y=-2x+5???
???y=2x-5???
Строка ???y=-(1/3)x+4??? пересекает ось ???y??? в точке ???4???, а затем имеет наклон ???-1/3???, поэтому ее график равен
Строка ???y=2x-5??? пересекает ось ???y??? в точке ???-5???, а затем имеет наклон ???2???, поэтому, если добавить его график к графику ???y= -(1/3)x+4???, получится
Глядя на точку пересечения, кажется, что решение приблизительно равно ???(3.75,2.75)???. На самом деле решение ???(27/7,19/7)\приблизительно(3,86,2,71)???, поэтому наша визуальная оценка ???(3,75,2,75)??? был не так далек.
Получить доступ к полному курсу Алгебра 1
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, алгебра 2, алгебра ii, решение систем, решение линейных систем, системы уравнений, системы линейных уравнений , подстановка, решение с подстановкой, исключение, решение с исключением, построение графика, решение с помощью графика, решение систем с подстановкой, решение систем с исключением, решение систем с помощью графика, метод подстановки, метод исключения
0 лайков Решение системы уравнений подстановкой
Решение системы уравнений методом подстановки полезно для решения системы уравнений. Это наиболее легко применимо к системам линейных уравнений. В этой статье мы рассмотрим метод замены. Мы обсудим, что такое метод подстановки и как решить систему уравнений подстановкой. Кроме того, мы решим несколько примеров. Это поможет лучшему пониманию. Итак, приступим к обсуждению.
Метод решения систем линейных уравнений подстановкой. Подстановка подразумевает подстановку одного уравнения в другое в качестве замены переменной. Подставляем одну переменную найденным значением для решения задачи.
Подставляем одну переменную найденным значением для решения задачи.
Метод подстановки очень полезен в таких темах, как линейная алгебра, компьютерное программирование и т. д. Примечательно, что решение систем уравнений методом подстановки очень несложно.
Прежде чем обсуждать, как решить систему уравнений подстановкой, давайте кратко рассмотрим систему уравнений.
Система линейных уравнений
Это набор из двух или более линейных уравнений.
Для двух переменных (x и y) график системы двух линейных уравнений представляет собой пару прямых на плоскости.
Здесь у нас есть три возможности:
- Прямые параллельны. Они будут пересекаться в нулевых точках.
- Линии пересекаются в одной точке.
- Линии пересекаются в бесконечных точках. Это означает, что два уравнения представляют аналогичную прямую.
Системы уравнений представляют собой математические задачи, включающие два или более уравнений.
Решения системы уравнений
В общем случае решение системы уравнений с двумя переменными представляет собой упорядоченную пару. Такое решение делает оба уравнения верными.
- Система, имеющая хотя бы одно решение, является согласованным решением
- Система, не имеющая решения, является несогласованным решением.
- Когда все решения одного уравнения являются решениями другого уравнения, уравнения являются зависимыми. (Это означает, что они оба представляют одну и ту же линию.)
- Иногда уравнения в системе не имеют общих решений. Такие уравнения системы независимы.
Решение системы уравнений методом подстановки даст один из следующих результатов:
(i) Только одно значение для каждой переменной в системе, т. е. одно решение
(ii) Неверное утверждение, т. нет решений
(iii) Верное утверждение, т. е. бесконечные решения
Как решить систему уравнений подстановкой Рассмотрим следующие уравнения:
y = 2x
x + y = 12
Здесь 1-е уравнение показывает, что y равно 2x. Это означает, что мы можем поставить это значение вместо y. Итак, давайте подставим значение y во 2-е уравнение.
Это означает, что мы можем поставить это значение вместо y. Итак, давайте подставим значение y во 2-е уравнение.
При таком значении y все уравнение будет включать одну переменную. Когда уравнение имеет одну переменную, мы можем легко найти его решение.
Подставляя значение y во второе уравнение,
x + 2x = 12
3x = 12
x = 12 / 3
x = 4
Итак, теперь у нас есть конкретное значение для x. Но не забывайте, вам нужно значение y. Нам нужно найти конкретное значение y. Для этого подставим значение x в 1-е уравнение.
y = 2x
y = 2(4) (подставив 4 вместо x)
y = 8
Итак, решив систему уравнений подстановкой, мы получили наше решение.
Решением данной системы уравнений является (4,8).
Лучше, если мы проверим эти решения. Для этого мы должны подставить решения обратно в систему уравнений.
1-е уравнение: y = 2x
Подстановка значений
8 = 2(4)
8 = 8
2-е уравнение: x + y = 12
Подстановка значений 1 + 2
3 9
12 = 12
Приведенная выше система уравнений является основным примером. Таким образом, вы можете легко понять концепцию.
Таким образом, вы можете легко понять концепцию.
Пойдем дальше.
Прежде чем использовать метод подстановки, сначала найдите переменную.
Обычно учащимся средней школы не удается получить уже приравненные значения x или y. Готового значения для замены не будет. Скорее, вы получите задачу в виде пары линейных уравнений для решения.
Рассмотрим систему уравнений:
3x + 4y = -5
2x – 3y = 8
Здесь мы можем заметить, что ни одно из приведенных выше уравнений еще не решено. Нет значения ни для x, ни для y, доступного для замены. Итак, мы должны сначала решить для x или y. Потом будем делать замену.
Как это сделать? Давайте обсудим.
Для решения систем линейных уравнений путем подстановки необходимо выполнить следующие шаги:
Шаг 1: Выберите одно уравнение из пары линейных уравнений.
Шаг 2: Теперь мы должны решить его для любой из его переменных (скажем, x или y).
Шаг 3: Подставьте значение переменной (решенное на шаге 2) в другое уравнение.
Шаг 4: Решите второе уравнение, чтобы найти значение другой переменной.
Шаг 5: Проверьте решения. Мы можем сделать это, подставив их в любое из исходных уравнений. Такое уравнение должно включать обе переменные.
Когда мы решаем системы линейных уравнений путем замены, как правило, одно уравнение и одна из переменных прокладывают путь к решению быстрее, чем другое. Чтобы хорошо это понять, давайте решим несколько примеров.
Решенные примеры Теперь попробуем решить систему уравнений подстановкой.
Здесь мы решим, выбрав переменную x и второе уравнение.
3x + 4y = -5
2x – 3y = 8
Сначала решим x для второго уравнения.
2x — 3y = 8
2x = 3y + 8
x = 3y / 2 + 4 (3 -е уравнение)
Далее мы заменим значение x, то есть 3Y / 2 + 4, в 1-е уравнение.
3x + 4y = -5
3(3y / 2 + 4) + 4y = -5
Теперь решим это уравнение.
9y / 2 + 12 + 4y = -5
17y / 2 = -5 – 12
17y / 2 = -17
y = -2
Здесь мы подставим значение y в любое уравнение у которого есть обе переменные x и y.
Подстановка значения y, т. е. y = -2, в 3-е уравнение.
x = 3y / 2 + 4
x = 3(-2) / 2 + 4
x = -6 / 2 + 4
x = -3 + 4
x = 1
Также студенты можно проверить их решения, подставив найденные значения в оба исходных уравнения.
Подстановка значений обеих переменных x и y в первое уравнение.
3x + 4y = -5
3(1) + 4(-2) = -5
3-8 = -5
-5 = -5
2x – 3y = 8
2(1 ) – 3(-2) = 8
2 + 6 = 8
8 = 8
Левая и правая стороны равны.
Следовательно, решения x = 1 и y = –2 верны.
Факт для рассмотрения: При решении систем линейных уравнений методом подстановки, если полученное решение правильное, то при проверке оно будет 0 = 0 (или LHS = RHS). Это показывает, что система зависима. Любое из исходных уравнений является решением. Однако, если метод подстановки приводит к неправильному решению, это не приведет к тому, что LHS = RHS (например, 0 = 4). Это показывает, что система несовместима. Для этой системы нет решения.
Это показывает, что система несовместима. Для этой системы нет решения.
Пример 2
-7x – 2y = -13
x – 2y = 11
Как и прежде, мы будем решать, выбирая переменную x и второе уравнение.
x = 11 + 2y
Теперь мы подставим это значение x в 1-е уравнение.
-7x – 2y = -13
-7(11 + 2y) – 2y = -13
-77 – 14y – 2y = -13
-77 – 16y = -13
-16y = -13 + 77
-16y = 64
y = -4 (при делении 64 на 12)
Теперь нам нужно найти x. Для этого подставьте значение y в 1-е уравнение.
x = 11 + 2y
x = 11+ 2(-4)
x = 11 – 8
x = 3
Следовательно, решением этой системы уравнений является (3, -4).
Проверка решений:
-7x – 2y = -13
-7(3) – 2(-4) = -13
-21 + 8 = -13
-13 = -13
х = 11 + 2y
3 = 11 + 2(-4)
3 = 11 – 8
3 = 3
Это доказывает, что значения или решения верны .
Прикладная задача - Периметр прямоугольника равен 60 м. Длина этого прямоугольника на 10 м больше его ширины. Вычислите размеры прямоугольника методом подстановки.
Пусть l — длина, а b — ширина.
Преобразование приведенной выше информации в систему уравнений: 2 (l + b) = 60
l = b + 10
(Здесь у нас есть переменные l и b вместо x и y)
On Подстановка значения l в 1-е уравнение,
2 [(B + 10) + B] = 60
2 [2b + 10] = 60
4b + 20 = 60
4b = 60 — 20
4b = 40
b = 10 (на деление 20 4)
Теперь, чтобы найти l:
Подставляем значение b во второе уравнение.
л = b + 10
л = 10 + 10
l = 20
Проверка обоих решений:
Подстановка значений в 1-е уравнение,
2 (l + b) = 60
2 (20 + 10) = 60
2 2 (30) 0 30 60 = 60
Подставляя значения во 2-е уравнение,
l = b + 10
20 = 10 + 10
20 = 20
Это доказывает правильность решения.

Взяв новое уравнение 13y = 52 и решив для y (путем деления обеих частей на 13), мы получим значение 4 для y.
Подстановка этого значения 4 вместо y в любое из уравнений с двумя переменными позволяет нам найти z.
Подстановка обоих значений y и z в любое из исходных уравнений с тремя переменными позволяет нам найти x.
Окончательный результат (я избавлю вас от алгебраических шагов, так как вы уже должны быть с ними знакомы!) состоит в том, что x = 2, y = 4 и z = 12,
СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:
- Одновременные уравнения для анализа цепей Рабочий лист
Метод подстановки (системы линейных уравнений)
Когда два уравнения прямой пересекаются в одной точке, мы говорим, что они имеют единственное решение, которое можно описать как точку \color{red}\left( {x ,y} \right), в плоскости XY .
Метод подстановки используется для решения систем линейных уравнений путем нахождения точных значений x и y, соответствующих точке пересечения.
На диаграмме ниже показаны две произвольные линии, показывающие, где они пересекаются, как описано упорядоченной парой \left( {x,y} \right).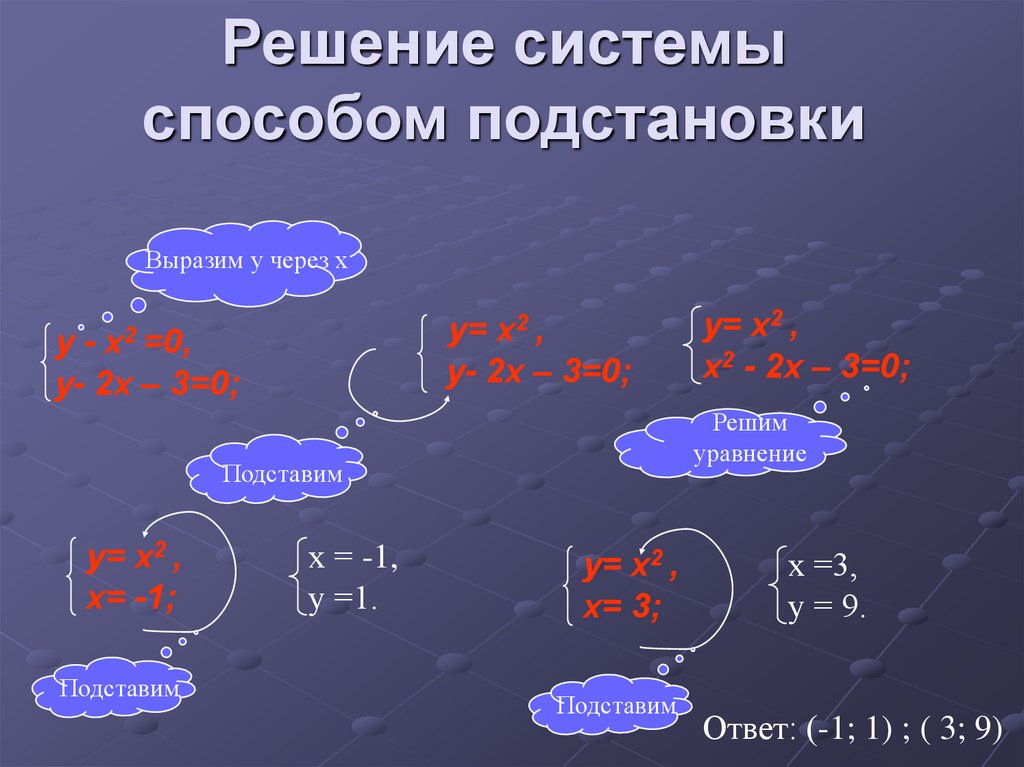 В этом уроке мы заинтересованы в ручном решении этой общей точки.
В этом уроке мы заинтересованы в ручном решении этой общей точки.
Примеры решения системы уравнений методом подстановки
Пример 1: Используйте метод подстановки для решения приведенной ниже системы линейных уравнений.
Идея состоит в том, чтобы выбрать одно из двух заданных уравнений и решить любую из переменных, x или y. Результат нашего первого шага будет подставлен в другое уравнение. Результатом будет одно уравнение с одной переменной, которое можно решить как обычно.
Это полностью зависит от того, с каким уравнением, по вашему мнению, будет проще справиться. Выбор за вами.
Обратите внимание, что верхнее уравнение содержит переменную x, которая является «одной» — это означает, что ее коэффициент равен +1. Не забывайте всегда искать эту характеристику («единственную» переменную), потому что она сделает вашу жизнь намного проще.
Теперь я начну с решения верхнего уравнения для x.
Поскольку я знаю, чему равен x через y, я могу подставить это выражение в другое уравнение. Таким образом, я решу уравнение с одной переменной.
Таким образом, я решу уравнение с одной переменной.
Надеюсь, вы получите такое же значение y = — \,5. Теперь, когда я знаю точное значение y, я найду другую переменную (в данном случае x), вычислив ее значение в любом из двух исходных уравнений. Неважно, какое исходное уравнение вы выберете, поскольку в конечном итоге оно даст один и тот же ответ.
Тем не менее, я должен сказать, что «лучший» способ найти x — это использовать исправленное уравнение, которое я решил ранее, поскольку у меня есть «x = некоторое y». Верно?
Здесь я получаю x = 1. В точечной форме окончательный ответ можно записать как \left( {1, — \,5} \right). Помните, что это точка пересечения двух линий.
Всегда полезно проверять эти значения в исходных уравнениях, чтобы убедиться, что они действительно являются правильными ответами. Я предлагаю вам всегда проверять их.
Графически решение выглядит так.
Пример 2: Используйте метод подстановки для решения системы линейных уравнений.
Очевидным выбором здесь является выбор нижнего уравнения, потому что переменная y имеет положительный коэффициент, равный единице \left( { + 1} \right). Теперь я могу легко найти y через x. Для начала я вычту обе стороны в 3 раза.
Найдя y из нижнего уравнения, я теперь перехожу к верхнему уравнению и заменяю выражение для y через x. Результатом будет многоступенчатое уравнение с одной переменной.
Решите это уравнение, сначала упростив скобки. После этого объедините одинаковые термины с обеих сторон и изолируйте переменную слева. Ваше решение должно быть похоже на приведенное ниже.
Если вы правильно решили для x, вы также должны прийти к значению x = 3.
Поскольку исправленное уравнение дна уже записано в форме, которая мне нравится, я буду использовать его для решения для точного значения y.
С полученным значением y = 1 теперь я могу записать окончательный ответ в виде упорядоченной пары \left( {3,1} \right).
Как я упоминал ранее, всегда проверяйте окончательные ответы самостоятельно, чтобы увидеть, соответствуют ли они исходным уравнениям.
На графике решением является точка пересечения двух заданных линий.
Пример 3: Решить систему уравнений методом подстановки.
Это отличный пример, потому что у меня есть два подхода к решению проблемы. Переменные x и y имеют положительную единицу \left( { + 1} \right) в качестве коэффициентов. Это означает, что я могу пойти в любую сторону.
Для этого примера я найду у. Я могу легко сделать это, вычитая обе стороны на x, а затем переставляя.
Затем я запишу другое уравнение и заменю его y на y = — x + 3.
После решения приведенного выше многошагового уравнения я получаю x = 5. Теперь я перехожу к преобразованной версии уравнения первое уравнение, которое нужно решить для y.
Здесь я получаю y = — \,2. Тогда окончательный ответ: \left( {x,y} \right) = \left( {5, — \,2} \right).
Действительно, две прямые пересекаются в точке, которую мы вычислили!
Пример 4: Решить систему уравнений методом подстановки.
Я нахожу эту проблему интересной, потому что не могу найти ситуацию, когда переменная «одна». Опять же, наше определение «одиночества» — это коэффициент +1. Запомнить?
И верхнее, и нижнее уравнения здесь содержат переменную с отрицательным символом. Я предлагаю, чтобы всякий раз, когда вы видите что-то подобное, заменяли этот отрицательный символ на \textbf{- 1}. Я помещаю синюю стрелку прямо рядом с ним для акцента (см. ниже).
Отсюда я могу перейти к решению для y, используя верхнее уравнение, или для x, используя нижнее. В этом упражнении я буду работать над уравнением дна.
Обратите внимание, что для решения x я разделил все уравнение на — 1. Здесь вы можете видеть, что вид уравнения сильно изменился.
Надеюсь, у вас тоже есть y = — \,4. В противном случае проверьте и перепроверьте свои действия при решении многошагового уравнения.
Затем используйте это значение y и подставьте его в преобразованную версию нижнего уравнения, чтобы найти x.
Итак, я получаю x = — \,2. Окончательный ответ в упорядоченной паре: \left( {x,y} \right) = \left( { — \,2, — \,4} \right).
График соглашается с нами в том, где пересекаются две линии. Большой!
Пример 5: Используйте метод подстановки для решения системы линейных уравнений.
Первое, что я заметил здесь, это то, что не бывает случаев, когда коэффициент переменной равен +1 или -1. Некоторым это может показаться запутанным.
В этой задаче можно выделить y в верхнем уравнении и сделать то же самое для x в нижнем уравнении. Поработайте немного, и это должно иметь больше смысла.
Вы поймете, что либо x, либо y могут быть легко решены, потому что в процессе не генерируются дроби. В этом упражнении я решил решить первое уравнение для y.
Как и предполагалось, вычисление y прошло успешно. Теперь я буду использовать это значение для y и подставлю его в y нижнего уравнения. Затем я продолжу решать полученное уравнение, как обычно.
Если вы сделали это правильно, ваш ответ должен получиться как x = 2. Подставьте это значение x в исправленную версию верхнего уравнения, чтобы найти точное значение y.
Здесь я получил y = — \,5. Это делает наш окончательный ответ упорядоченной парой \left( {2, — \,5} \right).
График подтверждает наши расчетные значения x и y.
Вас также могут заинтересовать:
Метод подстановки Практические задачи с ответами
Метод исключения (системы уравнений)
Решение систем нелинейных уравнений
Метод подстановки | Магазин развивающей математики
Результаты обучения
- Использовать метод подстановки для решения систем уравнений
- Выразите решение несовместной системы уравнений, содержащей две переменные
- Выразите решение зависимой системы уравнений, содержащей две переменные
Решение системы уравнений методом подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики для классификации количества решений системы двух линейных уравнений. Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные числа или дроби, это не самый точный метод. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные числа или дроби, это не самый точный метод. Что, если нам не задана точка пересечения или она не очевидна из графика? Можем ли мы все же найти решение системы? Конечно можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали замену по-разному. Например, когда мы использовали формулы для площади треугольника и простых процентов, мы подставляли значения, которые мы знали, в формулу, чтобы найти значения, которые мы не знали. Идея аналогична применительно к решению систем, в этом процессе всего несколько разных шагов. В методе подстановки мы решаем одно из уравнений для одной переменной, а затем подставляем результат в другое уравнение для решения второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен. Давайте начнем с примера, чтобы понять, что это значит.
Давайте начнем с примера, чтобы понять, что это значит.
Вы можете заменить значение переменной, даже если это выражение. Вот пример.
Помните, что решение системы уравнений должно быть решением каждого уравнения в системе. Упорядоченная пара [латекс](4,−1)[/латекс] работает для обоих уравнений, поэтому вы знаете, что она также является решением системы.
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной [latex]x[/latex] или [latex]y[/latex]. Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам может потребоваться переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете подставить ее в другое уравнение.
Пример
Решите следующую систему уравнений путем замены.
[латекс]\begin{array}{l}-x+y=-5\hfill \\ \text{ }2x — 5y=1\hfill \end{array}[/latex]
Показать решение
Вот краткое изложение шагов, которые мы используем для решения систем уравнений с использованием метода подстановки.
Как: Данную систему двух уравнений с двумя переменными решить методом подстановки
- Решить одно из двух уравнений для одной из переменных через другую.
- Подставьте выражение для этой переменной во второе уравнение, а затем найдите оставшуюся переменную.
- Подставьте это решение в любое из исходных уравнений, чтобы найти значение другой переменной. Если возможно, запишите решение в виде упорядоченной пары.
- Проверьте решение обоих уравнений.
Давайте рассмотрим несколько примеров, замена которых включает свойство распределения.
В следующем видео вам будет представлен пример решения системы двух уравнений методом подстановки.
Если бы вы выбрали другое уравнение для начала в предыдущих примерах, вы все равно смогли бы найти такое же решение. На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
На самом деле это вопрос предпочтений, потому что иногда нахождение переменной приводит к необходимости работать с дробями. Когда вы станете более опытными в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Попробуйте
Определите системы уравнений, которые не имеют решений или имеют бесконечное число решений
Вспомните, что несовместная система состоит из параллельных прямых, которые имеют одинаковый наклон, но разные y -пересечения. Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, такому как [латекс]12=0[/латекс].
Когда мы изучили методы решения линейных уравнений с одной переменной, то обнаружили, что одни уравнения не имеют решений, а другие имеют бесконечное множество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из Модуля 1 для решения линейных уравнений с одной переменной:
Решите для [латекс]х[/латекс].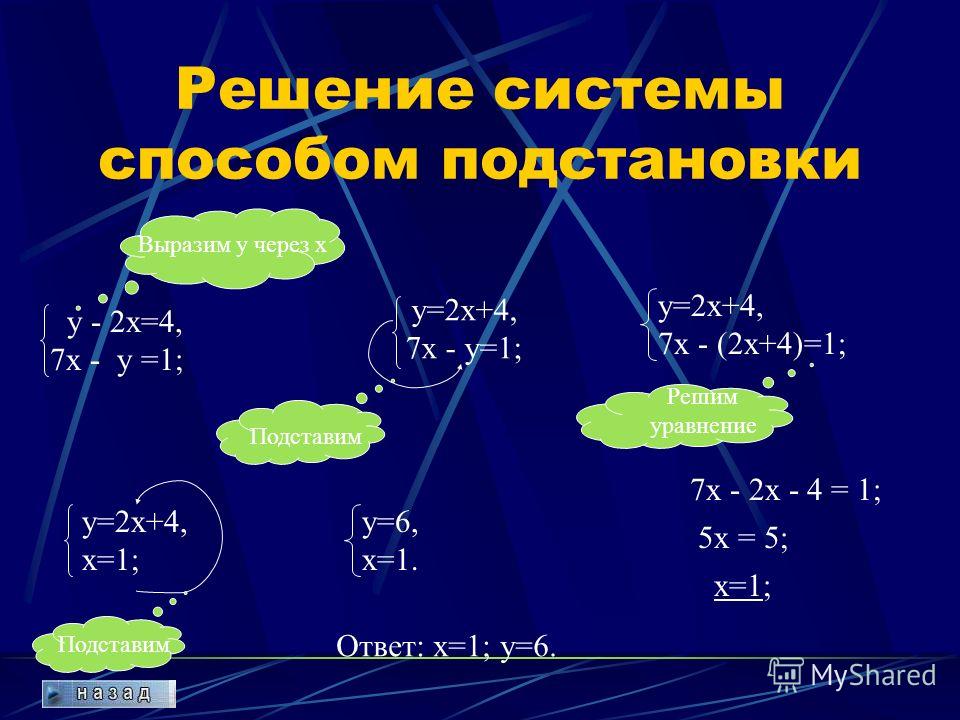 [латекс]12+2x–8=7x+5–5x[/латекс]
[латекс]12+2x–8=7x+5–5x[/латекс]
[латекс] \displaystyle \begin{array}{l}12+2x-8=7x+5-5x\\\,\, \,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\конец{массив}[/латекс]
[латекс]\начало{массив} {l}\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\, \,\подчеркивание{-2x\,\,\,\,\,\,\,\,\,\,-2x\,\,\,\,\,\,\,\,}\\\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \, 5\конец{массив}[/латекс]
Это ложное утверждение означает, что нет решений этого уравнения. Точно так же вы можете увидеть подобный результат, когда используете метод подстановки для поиска решения системы линейных уравнений с двумя переменными. В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Вы получаете ложное утверждение [латекс]−8=4[/латекс]. Что это значит? График этой системы проливает некоторый свет на происходящее.
Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [латекс]−8=4[/латекс] — это , а не решение. Это просто ложное утверждение, и оно указывает на то, что решения не существует.
Это просто ложное утверждение, и оно указывает на то, что решения не существует.
Давайте рассмотрим еще один пример, в котором нет решения.
Пример
Решите следующую систему уравнений.
[латекс]\begin{массив}{l}x=9 — 2y\hfill \\ x+2y=13\hfill \end{массив}[/latex]
Показать решение
В следующем видео мы покажем еще один пример использования подстановки для решения системы, которая не имеет решения.
Попробуйте
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное число решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
На этот раз вы получите истинное утверждение: [латекс]−4,5x=−4,5x[/латекс]. Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Но что означает этот тип ответа? Опять же, графики могут помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, представляющих одну и ту же прямую; две линии коллинеарны. Каждая точка на линии будет решением системы, поэтому метод подстановки дает истинное утверждение. В этом случае существует бесконечное множество решений.
Попробуйте
В следующем видео вы увидите пример решения системы, которая имеет бесконечное количество решений.
В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.
Резюме
Метод подстановки является одним из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).
Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных через другую переменную. Затем подставьте это выражение вместо этой переменной во второе уравнение. Затем вы можете решить это уравнение, так как теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (указывающее одно решение), неверное утверждение (указывающее отсутствие решений) или истинное утверждение (указывающее бесконечное количество решений).
Пожертвовать!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Решение систем уравнений тремя способами: замена, исключение и построение графика — Krista King Math
Всегда есть три способа решения системы уравнений
Есть три способа решения системы линейных уравнений: подстановка, исключение и построение графика.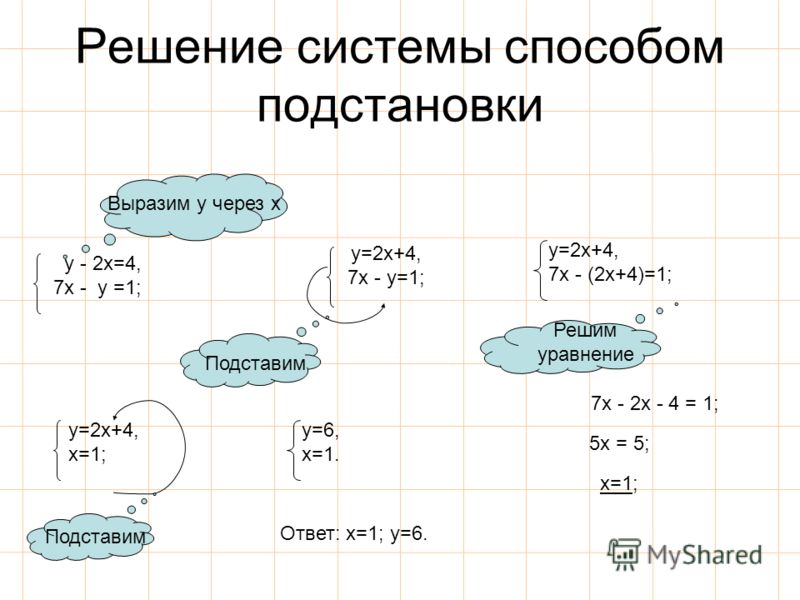 Давайте рассмотрим шаги для каждого метода.
Давайте рассмотрим шаги для каждого метода.
Получить переменную саму по себе в одном из уравнений.
Возьмите выражение, которое вы получили для переменной на шаге 1, и подставьте его (замените скобками) в другое уравнение.
Решите уравнение шага 2 для оставшейся переменной.
Используйте результат шага 3 и подставьте его в уравнение из шага 1.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
ИсключениеПри необходимости переставьте оба уравнения так, чтобы сначала были члены ???x???, за которыми следовали члены ???y???, знак равенства и постоянный член (в этой последовательности). Если уравнение не имеет постоянного члена, это означает, что постоянный член равен ???0???.

Умножить одно (или оба) уравнения на константу, которая позволит сократить либо ???x???-члены, либо ???y???-члены при сложении или вычитании уравнений (когда их левая и правая части складываются отдельно или когда их левая и правая части вычитаются отдельно).
Сложите или вычтите уравнения.
Найдите оставшуюся переменную.
Подставьте результат шага 4 в одно из исходных уравнений и найдите другую переменную.
Решить для ???y??? в каждом уравнении.
Постройте оба уравнения в одной декартовой системе координат.
Найти точку пересечения линий (точка пересечения линий).
Решение той же системы с подстановкой, затем с исключением, затем с построением графика
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого.
 🙂
🙂Учить больше
Определение метода, который лучше всего подходит для решения системы: замена, исключение или построение графика
Теперь давайте рассмотрим несколько примеров, в которых нам нужно решить, какой из этих трех методов использовать.
Пример
Какой метод вы бы использовали для решения следующей задачи? Объясните, почему вы выбрали именно этот метод.
???х=у+2???
???3y-2x=15???
Самый простой способ решить эту систему — использовать подстановку, поскольку ???x??? уже изолирован в первом уравнении. Всякий раз, когда одно уравнение уже решено для переменной, подстановка будет самым быстрым и простым методом.
Несмотря на то, что вас не просят решить, вот шаги для решения системы:
Замените ???y+2??? за ???х??? во втором уравнении.
???3y-2(y+2)=15???
Раздать ???-2??? а затем объединить подобные термины.
???3y-2y-4=15???
???y-4=15???
Добавить ???4??? в обе стороны.
???y-4+4=15+4???
???y=19???
Вилка ???19??? для тебя??? в первое уравнение.
???х=у+2???
???х=19+2???
???х=21???
Единственное решение ???(21,19)???.
Существует три способа решения систем линейных уравнений: замена, исключение и построение графика.
Как решить систему с помощью метода исключения
Пример
Чтобы решить систему методом исключения, что было бы полезным первым шагом?
???x+3y=12???
???2x-y=5???
Когда мы используем исключение для решения системы, это означает, что мы собираемся избавиться (устранить) от одной из переменных. Таким образом, мы должны иметь возможность складывать уравнения или вычитать одно из другого, и при этом отменять либо ???x???-члены, либо ???y???-члены.
Любая из следующих опций была бы полезной в качестве первого шага:
Умножить первое уравнение на ???-2??? или???2???. Это даст нам ???2x??? или ???-2x??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Это даст нам ???2x??? или ???-2x??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Умножить второе уравнение на ???3??? или ???-3???. Это даст нам ???3г??? или ???-3г??? в обоих уравнениях, что приведет к сокращению членов ???y???, когда мы складываем или вычитаем.
Разделите второе уравнение на ???2???. Это даст нам ???x??? или ???-х??? в обоих уравнениях, что приведет к тому, что ???x???-члены будут сокращаться, когда мы складываем или вычитаем.
Разделить первое уравнение на ???3???. Это даст нам ???y??? или ???-у??? в обоих уравнениях, что приведет к сокращению членов ???y???, когда мы складываем или вычитаем.
Повторим последний пример, но вместо метода исключения воспользуемся графом для поиска решения.
Решение системы путем построения графика обоих уравнений и поиска точек пересечения
Пример
Начертите оба уравнения, чтобы найти решение системы.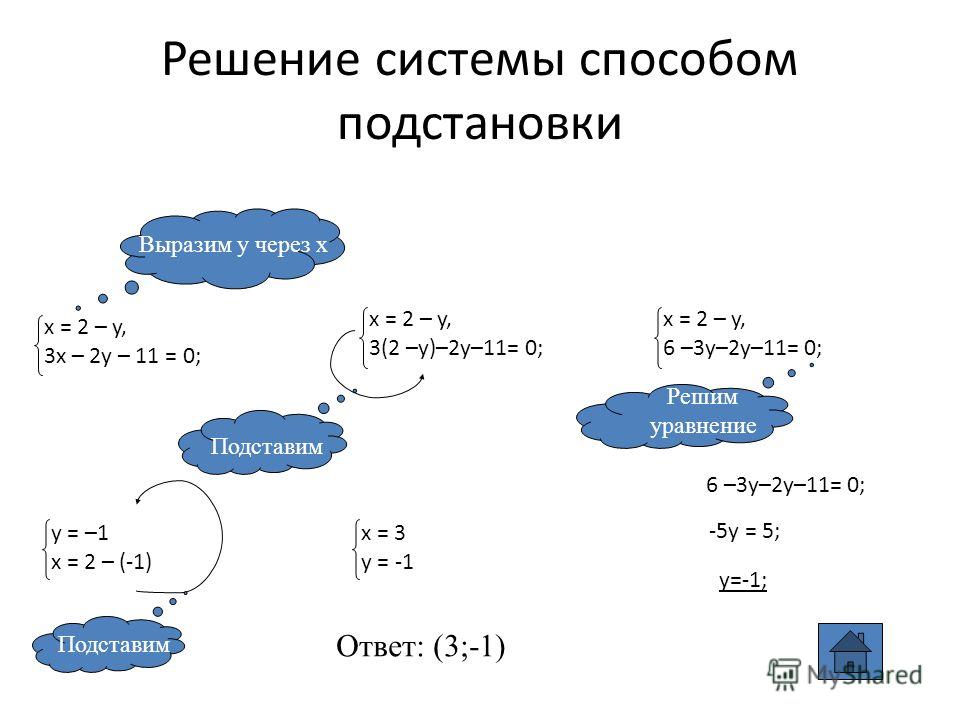
???х+3у=12???
???2x-y=5???
Чтобы изобразить эти уравнения в виде графика, давайте представим их обоим в форме пересечения наклона. Получаем
???x+3y=12???
???3y=-x+12???
???y=-\frac13x+4???
и
???2x-y=5???
???-y=-2x+5???
???y=2x-5???
Строка ???y=-(1/3)x+4??? пересекает ось ???y??? в точке ???4???, а затем имеет наклон ???-1/3???, поэтому ее график равен
Строка ???y=2x-5??? пересекает ось ???y??? в точке ???-5???, а затем имеет наклон ???2???, поэтому, если добавить его график к графику ???y= -(1/3)x+4???, получится
Глядя на точку пересечения, кажется, что решение приблизительно равно ???(3.75,2.75)???. На самом деле решение ???(27/7,19/7)\приблизительно(3,86,2,71)???, поэтому наша визуальная оценка ???(3,75,2,75)??? был не так далек.
Получить доступ к полному курсу Алгебра 1
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 1, алгебра i, алгебра 2, алгебра ii, решение систем, решение линейных систем, системы уравнений, системы линейных уравнений , подстановка, решение с подстановкой, исключение, решение с исключением, построение графика, решение с помощью графика, решение систем с подстановкой, решение систем с исключением, решение систем с помощью графика, метод подстановки, метод исключения
0 лайковРешение системы уравнений подстановкой
Решение системы уравнений методом подстановки полезно для решения системы уравнений. Это наиболее легко применимо к системам линейных уравнений. В этой статье мы рассмотрим метод замены. Мы обсудим, что такое метод подстановки и как решить систему уравнений подстановкой. Кроме того, мы решим несколько примеров. Это поможет лучшему пониманию. Итак, приступим к обсуждению.
Метод решения систем линейных уравнений подстановкой. Подстановка подразумевает подстановку одного уравнения в другое в качестве замены переменной. Подставляем одну переменную найденным значением для решения задачи.
Подставляем одну переменную найденным значением для решения задачи.
Метод подстановки очень полезен в таких темах, как линейная алгебра, компьютерное программирование и т. д. Примечательно, что решение систем уравнений методом подстановки очень несложно.
Прежде чем обсуждать, как решить систему уравнений подстановкой, давайте кратко рассмотрим систему уравнений.
Система линейных уравнений
Это набор из двух или более линейных уравнений.
Для двух переменных (x и y) график системы двух линейных уравнений представляет собой пару прямых на плоскости.
Здесь у нас есть три возможности:
- Прямые параллельны. Они будут пересекаться в нулевых точках.
- Линии пересекаются в одной точке.
- Линии пересекаются в бесконечных точках. Это означает, что два уравнения представляют аналогичную прямую.
Системы уравнений представляют собой математические задачи, включающие два или более уравнений.
Решения системы уравнений
В общем случае решение системы уравнений с двумя переменными представляет собой упорядоченную пару. Такое решение делает оба уравнения верными.
- Система, имеющая хотя бы одно решение, является согласованным решением
- Система, не имеющая решения, является несогласованным решением.
- Когда все решения одного уравнения являются решениями другого уравнения, уравнения являются зависимыми. (Это означает, что они оба представляют одну и ту же линию.)
- Иногда уравнения в системе не имеют общих решений. Такие уравнения системы независимы.
Решение системы уравнений методом подстановки даст один из следующих результатов:
(i) Только одно значение для каждой переменной в системе, т. е. одно решение
(ii) Неверное утверждение, т. нет решений
(iii) Верное утверждение, т. е. бесконечные решения
Как решить систему уравнений подстановкойРассмотрим следующие уравнения:
y = 2x
x + y = 12
Здесь 1-е уравнение показывает, что y равно 2x.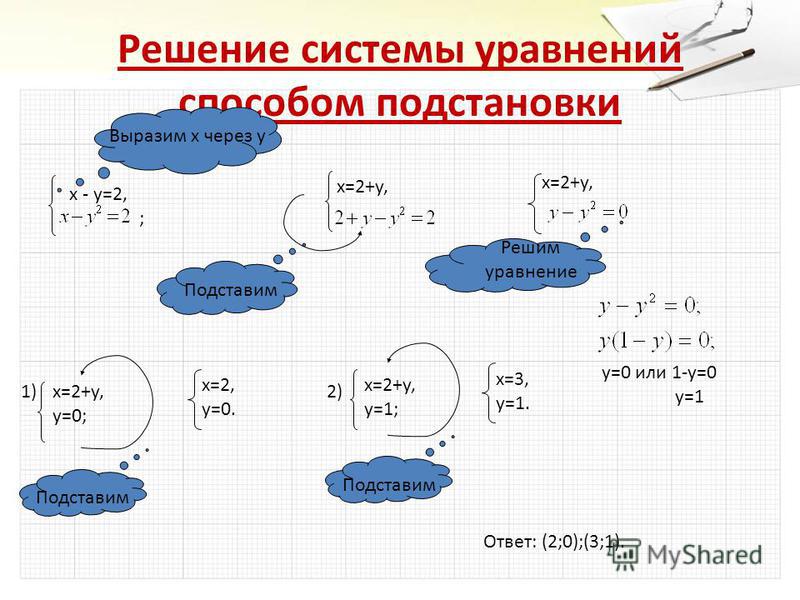 Это означает, что мы можем поставить это значение вместо y. Итак, давайте подставим значение y во 2-е уравнение.
Это означает, что мы можем поставить это значение вместо y. Итак, давайте подставим значение y во 2-е уравнение.
При таком значении y все уравнение будет включать одну переменную. Когда уравнение имеет одну переменную, мы можем легко найти его решение.
Подставляя значение y во второе уравнение,
x + 2x = 12
3x = 12
x = 12 / 3
x = 4
Итак, теперь у нас есть конкретное значение для x. Но не забывайте, вам нужно значение y. Нам нужно найти конкретное значение y. Для этого подставим значение x в 1-е уравнение.
y = 2x
y = 2(4) (подставив 4 вместо x)
y = 8
Итак, решив систему уравнений подстановкой, мы получили наше решение.
Решением данной системы уравнений является (4,8).
Лучше, если мы проверим эти решения. Для этого мы должны подставить решения обратно в систему уравнений.
1-е уравнение: y = 2x
Подстановка значений
8 = 2(4)
8 = 8
2-е уравнение: x + y = 12
Подстановка значений 1 + 2
3 9
12 = 12
Приведенная выше система уравнений является основным примером. Таким образом, вы можете легко понять концепцию.
Таким образом, вы можете легко понять концепцию.
Пойдем дальше.
Прежде чем использовать метод подстановки, сначала найдите переменную.
Обычно учащимся средней школы не удается получить уже приравненные значения x или y. Готового значения для замены не будет. Скорее, вы получите задачу в виде пары линейных уравнений для решения.
Рассмотрим систему уравнений:
3x + 4y = -5
2x – 3y = 8
Здесь мы можем заметить, что ни одно из приведенных выше уравнений еще не решено. Нет значения ни для x, ни для y, доступного для замены. Итак, мы должны сначала решить для x или y. Потом будем делать замену.
Как это сделать? Давайте обсудим.
Для решения систем линейных уравнений путем подстановки необходимо выполнить следующие шаги:
Шаг 1: Выберите одно уравнение из пары линейных уравнений.
Шаг 2: Теперь мы должны решить его для любой из его переменных (скажем, x или y).
Шаг 3: Подставьте значение переменной (решенное на шаге 2) в другое уравнение.
Шаг 4: Решите второе уравнение, чтобы найти значение другой переменной.
Шаг 5: Проверьте решения. Мы можем сделать это, подставив их в любое из исходных уравнений. Такое уравнение должно включать обе переменные.
Когда мы решаем системы линейных уравнений путем замены, как правило, одно уравнение и одна из переменных прокладывают путь к решению быстрее, чем другое. Чтобы хорошо это понять, давайте решим несколько примеров.
Решенные примерыТеперь попробуем решить систему уравнений подстановкой.
Здесь мы решим, выбрав переменную x и второе уравнение.
3x + 4y = -5
2x – 3y = 8
Сначала решим x для второго уравнения.
2x — 3y = 8
2x = 3y + 8
x = 3y / 2 + 4 (3 -е уравнение)
Далее мы заменим значение x, то есть 3Y / 2 + 4, в 1-е уравнение.
3x + 4y = -5
3(3y / 2 + 4) + 4y = -5
Теперь решим это уравнение.
9y / 2 + 12 + 4y = -5
17y / 2 = -5 – 12
17y / 2 = -17
y = -2
Здесь мы подставим значение y в любое уравнение у которого есть обе переменные x и y.
Подстановка значения y, т. е. y = -2, в 3-е уравнение.
x = 3y / 2 + 4
x = 3(-2) / 2 + 4
x = -6 / 2 + 4
x = -3 + 4
x = 1
Также студенты можно проверить их решения, подставив найденные значения в оба исходных уравнения.
Подстановка значений обеих переменных x и y в первое уравнение.
3x + 4y = -5
3(1) + 4(-2) = -5
3-8 = -5
-5 = -5
2x – 3y = 8
2(1 ) – 3(-2) = 8
2 + 6 = 8
8 = 8
Левая и правая стороны равны.
Следовательно, решения x = 1 и y = –2 верны.
Факт для рассмотрения: При решении систем линейных уравнений методом подстановки, если полученное решение правильное, то при проверке оно будет 0 = 0 (или LHS = RHS). Это показывает, что система зависима. Любое из исходных уравнений является решением. Однако, если метод подстановки приводит к неправильному решению, это не приведет к тому, что LHS = RHS (например, 0 = 4). Это показывает, что система несовместима. Для этой системы нет решения. Это показывает, что система несовместима. Для этой системы нет решения. |
Пример 2
-7x – 2y = -13
x – 2y = 11
Как и прежде, мы будем решать, выбирая переменную x и второе уравнение.
x = 11 + 2y
Теперь мы подставим это значение x в 1-е уравнение.
-7x – 2y = -13
-7(11 + 2y) – 2y = -13
-77 – 14y – 2y = -13
-77 – 16y = -13
-16y = -13 + 77
-16y = 64
y = -4 (при делении 64 на 12)
Теперь нам нужно найти x. Для этого подставьте значение y в 1-е уравнение.
x = 11 + 2y
x = 11+ 2(-4)
x = 11 – 8
x = 3
Следовательно, решением этой системы уравнений является (3, -4).
Проверка решений:
-7x – 2y = -13
-7(3) – 2(-4) = -13
-21 + 8 = -13
-13 = -13
х = 11 + 2y
3 = 11 + 2(-4)
3 = 11 – 8
3 = 3
Это доказывает, что значения или решения верны .
- Периметр прямоугольника равен 60 м. Длина этого прямоугольника на 10 м больше его ширины. Вычислите размеры прямоугольника методом подстановки.
Пусть l — длина, а b — ширина.
Преобразование приведенной выше информации в систему уравнений:2 (l + b) = 60
l = b + 10
(Здесь у нас есть переменные l и b вместо x и y)
On Подстановка значения l в 1-е уравнение,
2 [(B + 10) + B] = 60
2 [2b + 10] = 60
4b + 20 = 60
4b = 60 — 20
4b = 40
b = 10 (на деление 20 4)
Теперь, чтобы найти l:
Подставляем значение b во второе уравнение.
л = b + 10
л = 10 + 10
l = 20
Проверка обоих решений:
Подстановка значений в 1-е уравнение,
2 (l + b) = 60
2 (20 + 10) = 60
2 2 (30) 0 30 60 = 60
Подставляя значения во 2-е уравнение,
l = b + 10
20 = 10 + 10
20 = 20
Это доказывает правильность решения.




 Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.
Из этого уравнения найдем значение x через y, то есть x = 5-y. Теперь подставляем это значение в уравнение 2, получаем 3(5-y)+y=11.