Графический метод решения ЗЛП онлайн
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений (см. рисунок).Назначение сервиса. С помощью данного сервиса можно в онлайн режиме решить задачу линейного программирования геометрическим методом, а также получить решение двойственной задачи (оценить оптимальность использования ресурсов). Дополнительно создается шаблон решения в Excel.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Также решают
Инструкция. Выберите количество строк (количество ограничений).
Количество ограничений 12345678910 пример и пример №2). Если ограничение двойное, например,
пример и пример №2). Если ограничение двойное, например, 1 ≤ x1 ≤ 4, то оно разбивается на два: x1 ≥ 1, x1 ≤ 4 (т.е. количество строк увеличивается на 1).
Построить область допустимого решения (ОДР) можно также с помощью этого сервиса.
Вместе с этим калькулятором также используют следующие:
Симплексный метод решения ЗЛП
Решение транспортной задачи
Решение матричной игры
С помощью сервиса в онлайн режиме можно определить цену матричной игры (нижнюю и верхнюю границы), проверить наличие седловой точки, найти решение смешанной стратегии методами: минимакс, симплекс-метод, графический (геометрический) метод, методом Брауна.
Экстремум функции двух переменных
Вычисление пределов
Решение задачи линейного программирования графическим методом включает следующие этапы:
- На плоскости X10X2 строят прямые.

- Определяются полуплоскости.
- Определяют многоугольник решений;
- Строят вектор N(c1,c2), который указывает направление целевой функции;
- Передвигают прямую целевую функцию c1x2 + c2x2 = 0 в направлении вектора N до крайней точки многоугольника решений.
- Вычисляют координаты точки и значение целевой функции в этой точке.
При этом могут возникать следующие ситуации:
- Целевая функция принимает экстремальное (минимальное или максимальное) значение в единственной точке А.
- Целевая функция принимает экстремальное значение в любой точке отрезка АВ.
- Целевая функция не ограничена сверху (при поиске на максимум) или снизу (на минимум)
- Система ограничений задачи несовместна
Пример. Компания изготавливает два вида продукции – П1 и П2. Для производства продукции используются два вида сырья – С1 и С2. Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Оптовые цены единицы продукции равна: 5 д.е. для П1 и 4 д.е. для П2. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице.
Таблица — Расход сырья на производство продукции
| Сырье | Расход сырья на 1 ед. продукции | Максимальный запас сырья, ед. | |
| П1 | П2 | ||
| М1 | 6 | 4 | 24 |
| М2 | 1 | 2 | 6 |
Требуется определить:
Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
- Сформулировать математическую модель задачи линейного программирования.

- Решить задачу линейного программирования графическим способом (для двух переменных).
Решение.
Сформулируем математическую модель задачи линейного программирования.
x1 – производство продукции П1, ед.
x2 – производство продукции П2, ед.
Ограничения по ресурсам
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
Ограничения по спросу
x1 +1 ≥ x2
x2 ≤ 2
Целевая функция
5x1 + 4x2 → max
Тогда получаем следующую ЗЛП:
6x1 + 4x2 ≤ 24
x1 + 2x2 ≤ 6
x2 — x1 ≤ 1
x2 ≤ 2
x1, x2 ≥ 0
5x1 + 4x2 → max
Примеры решения задачи линейного программирования графически.
Если количество переменных в задаче линейного программирования больше двух, то задачу предварительно сводят к стандартной ЗЛП.
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
Приведем систему к единичной матрице методом жордановских преобразований.
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.

Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).
Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max Пример №1.
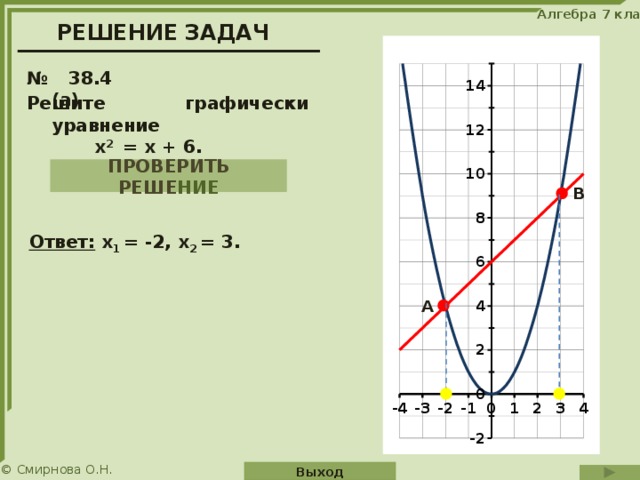 Записать задачу в стандартной форме и решить ее графическим методом.
Записать задачу в стандартной форме и решить ее графическим методом.
f=x1+13x2-x3+2x4+3x5
-x2+x3-x5=-3
x1-4x2+3x3-x4+2x5=3
4x2-x3+x4-x5=6
Из первого уравнения выражаем x5:
x5 = -x2+x3+3
и подставим во все выражения:
f=x1+13x2-x3+2x4+3(-x2+x3+3)
x1-4x2+3x
4x2-x3+x4-(-x2+x3+3)=6
или
f=x1+10x2+2x3+2x4+9
x1-6x2+5x3-x4=-3
5x2-2x3+x4=9
Из второго уравнения выражаем x4:
x4=9-5x2+2x3
и подставим во все выражения:
f=x1+6x3+27
x1-x2+3x3=6
Переменную x2 принимаем в качестве дополнительной переменной и делаем замену на знак «≥»:
f=x1 + 6x3+ 27
x1 + 3x3≥6
Далее задача решается графическом способом.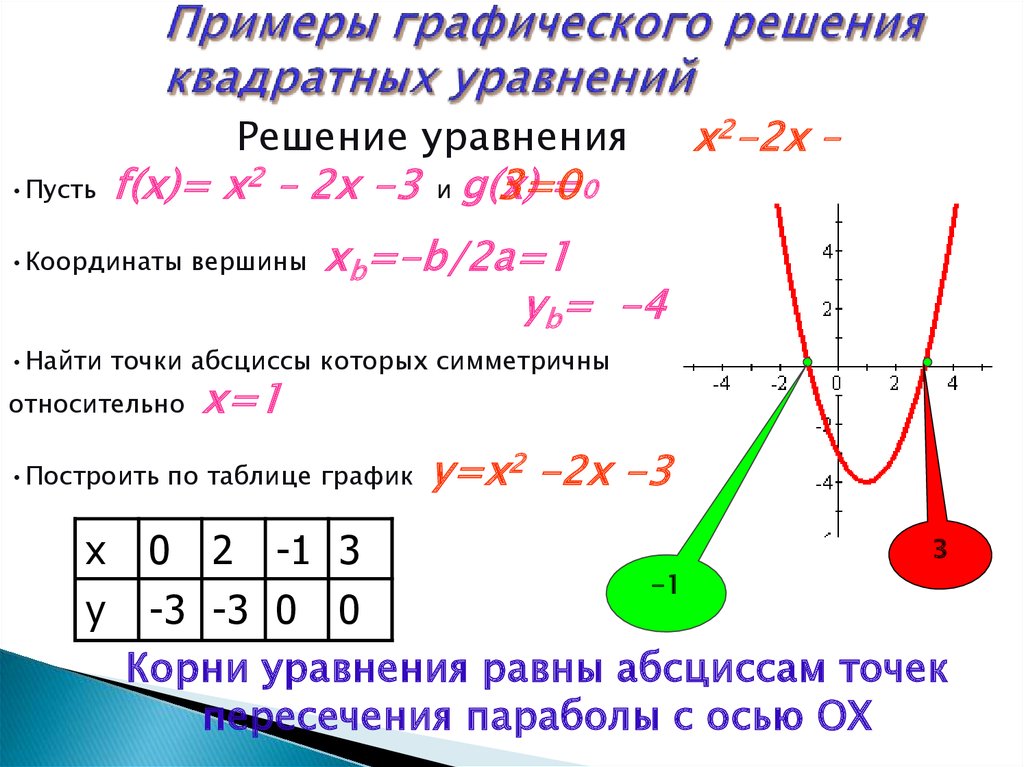
Пример №2
F(X) = 3x1 — 2x2 + 5x3 — 4x5 → max при ограничениях:
x1 + x2 + x3=12
2x1 — x2 + x4=8
— 2x1 + 2x2 + x5=10
F(X) = 3x1 — 2x2 + 5x3 — 4x5
Переход к СЗЛП.
Расширенная матрица системы ограничений-равенств данной задачи:
| 1 | 1 | 1 | 0 | 0 | 12 |
| 2 | -1 | 0 | 1 | 0 | 8 |
| -2 | 2 | 0 | 0 | 1 | 10 |
1. В качестве базовой переменной можно выбрать x3.
2. В качестве базовой переменной можно выбрать x4.
3. В качестве базовой переменной можно выбрать x5
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5).

Соответствующие уравнения имеют вид:
x1 + x2 + x3 = 12
2x1 — x2 + x4 = 8
— 2x1 + 2x2 + x5 = 10
Выразим базисные переменные через остальные:
x3 = — x1 — x2+12
x4 = — 2x1 + x2+8
x5 = 2x1 — 2x2+10
Подставим их в целевую функцию:
F(X) = 3x1 — 2x2 + 5(- x1 — x2+12) — 4(2x1 — 2x2+10)
или
F(X) = — 10x1 + x2+20 → max
Система неравенств:
— x1 — x2+12 ≥ 0
— 2x1 + x2+8 ≥ 0
2x1 — 2x2+10 ≥ 0
Приводим систему неравенств к следующему виду:
x1 + x2 ≤ 12
2x1 — x2 ≤ 8
— 2x1 + 2x2 ≤ 10
F(X) = — 10x1 + x2+20 → max
Пример №3. Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
- Составить систему математических зависимостей (неравенств) и целевую функцию.
- Изобразить геометрическую интерпретацию задачи.
- Найти оптимальное решение.
- Провести аналитическую проверку.
- Определить существенные и несущественные ресурсы и их избытки.
- Определить значение целевой функции.
- Вычислить объективно обусловленные оценки.
- Составить соотношение устойчивости.
| Наимен. показат. | Нормы на одно изделие | Прибыль на одно изделие | ||
| Рес. 1 | Рес. 2 | Рес. 3 | ||
| Изделие 1 | 10.0 | 14.0 | 3.8 | 40 |
| Изделие 2 | 22.0 | 7.5 | 14. 5 5
| 75 |
| Наличие ресурсов | 450 | 310 | 360 | - |
Графический метод решения задач линейного программирования
- Когда нужен графический метод?
- Теоретические основы графического метода
- Схема решения задач линейного программирования графическим методом
- Примеры решения задач графическим методом
- Решить задачи графическим методом самостоятельно, а затем посмотреть решения
- Продолжаем решать задачи графическим методом вместе
На этом уроке будем знакомиться с графическим методом решения задач линейного программирования, то есть, таких задач, в которых требуется найти такое решения системы линейных уравнений и (или) неравенств (системы ограничений), при котором функция цели — линейная функция — принимает оптимальное значение.
Ввиду того, что наглядность графического решения достигается лишь на
плоскости, мы можем познакомиться с графическим представлением задачи только в двумерном
пространстве. Это представление пригодно для системы ограничений-неравенств с двумя
переменными или для систем уравнений, в которых число переменных на 2 превышает число
уравнений, то есть число свободных переменных равно двум.
Это представление пригодно для системы ограничений-неравенств с двумя
переменными или для систем уравнений, в которых число переменных на 2 превышает число
уравнений, то есть число свободных переменных равно двум.
Поэтому графический метод имеет такие узкие рамки применения, что о нём как об особом методе решения задач линейного программирования говорить нельзя.
Однако для выработки наглядных представлений о решениях задач линейного программирования графический метод представляет определённый интерес. Кроме того, он позволяет геометрически подтвердить справедливость теорем линейного программирования.
Итак, задача линейного программирования. Требуется найти неотрицательные значения переменных и , удовлетворяющих системе неравенств
при которых линейная форма принимает оптимальное значение.
Из теории и практики решения систем линейных неравенств известно, что множество всех решений данной системы, то есть множество
пар чисел и
, удовлетворяющих
системе, составляет многоугольник этой системы. Допустим, что это пятиугольник ABCDE (рисунок внизу).
Допустим, что это пятиугольник ABCDE (рисунок внизу).
Линейная форма графически означает семейство параллельных между собой прямых. При конкретном числовом значении F линейная форма изобразится в виде некоторой прямой. Каждую из прямых этого семейства принято называть линией уровня. На рисунке построена линия уровня (чёрного цвета, проходит через начало координат), соответствующая значению F =0.
Если исходную линию уровня передвигать вправо, то значение F при этом возрастает. Нужное направление движения исходной линии уровня можно установить следующим образом. Коэффициенты при переменных в уравнении прямой служат координатами вектора, перпендикулярного этой прямой. Таким образом, получаем градиент — вектор (на рисунке бордового цвета). Значения функции F возрастают при перемещении исходной линии уровня в направлении вектора .
Среди прямых упомянутого семейства параллельных прямых прямые mn (зелёного цвета) и MN (красного цвета), которые назовём опорными. Опорными обычно
называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку,
и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из
чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и
многоугольник целиком лежит левее этой прямой.
Опорными обычно
называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку,
и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из
чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и
многоугольник целиком лежит левее этой прямой.
Из основных теорем
линейного программирования известно, что линейная форма достигает максимального и
минимального значений в крайних точках многогранника решений. Это значит, что опорные
прямые mn и MN характеризуют экстремальные значения линейной формы (функции цели), то есть
в точках А и С линейная форма достигает оптимальных значений. В точке А, находящейся ближе к началу координат, функция цели достигает минимального
значения, а в точке С, находящейся дальше от начала координат, — максимального
значения.
1. Построить многоугольник решений системы неравенств.
2. Начертить из семейства прямых, соответствующих линейной форме, линию равных значений функции цели. Для построения линии равных значений придадим F некоторое числовое значение. Во многих задачах удобно принять, что F =1. Тогда получим . Запишем это уравнение прямой в отрезках:
Затем, откладывая на оси число , а на оси — число , найдём точки пересечения линии равных значений с осями координат. Прямая, проведённая через эти точки, и есть требуемая прямая.
3. Двигать прямую (или линейку) вдоль градиента — вектора
параллельно линии равных значений в сторону многоугольника решений до соприкосновения с
многоугольником решений. Если первая встреча с многоугольником решений произойдёт в крайней
точке с координатами ,
то в этой точке функция цели достигает минимального значения. Если первая встреча
произойдёт со стороной многоугольника, то данная функция цели достигает минимума во всех
точках этой стороны.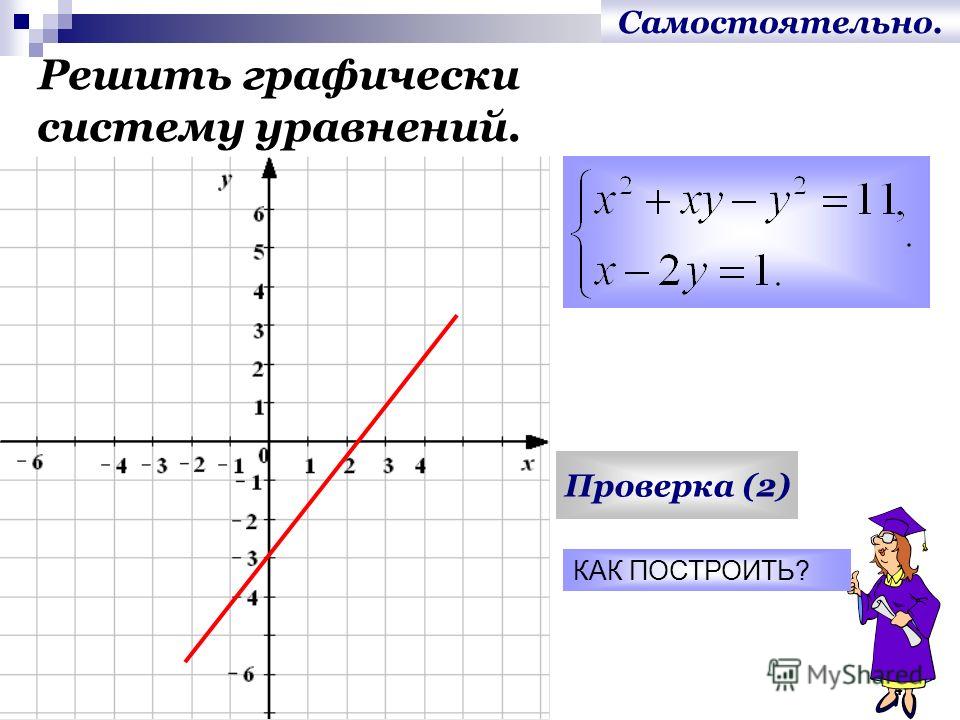
4. Двигаясь дальше, придём к некоторому опорному положению, когда прямая будет иметь одну общую точку с многоугольником решений. В этой точке функция цели достигает своего максимума.
5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения — в вершине, более удалённой от начала координат.
Пример 1. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Построим многоугольник решений. Для этого начертим граничные прямые. Из первого
неравенства запишем уравнение .
Это уравнение первой граничной прямой. Найдём точки пересечения этой прямой с осями
координат. При
из уравнения получим ,
при получим
. Это
значит, что первая прямая отсекает от осей координат отрезки
и .
Аналогично строим остальные граничные прямые. Вторая прямая от осей координат отсекает отрезки, равные 6. Третья прямая проходит параллельно оси , отсекая на оси отрезок, равный 2. Четвёртая прямая имеет уравнение . Она совпадает с осью .
Из рисунка ниже видно, что множество точек четырёхугольника ABDE удовлетворяет всем четырём неравенствам системы.
Следовательно, четырёхугольник ABDE является многоугольником решений системы (заштрихован вовнутрь).
Начертим линию равных значений функции цели. Приняв в равенстве F =1, получим, что эта линия отсекает отрезки 1 и 1/3 соответственно на оси и на оси . Проведём прямую через эти точки (на чертеже она чёрного цвета).
Двигая эту прямую параллельно самой себе в направлении градиента — вектора
(бордового цвета),
получим опорные прямые. Первая прямая (зелёного цвета) имеет с многоугольником общую точку A. Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В.
Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты
точки В, т. е. ,
,
получим максимальное значение функции цели: .
Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В.
Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты
точки В, т. е. ,
,
получим максимальное значение функции цели: .
Нет времени вникать в решение? Можно заказать работу!
Пример 2. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
Решение. Многогранником решений является открытая область
Проведём линию равных значений функции цели при F =1, как в предыдущем примере (она опять чёрного цвета).
Из рисунка видно, что прямая ближайшнее от начала координат опорное
положение займёт в точке В. Следовательно, в этой точке функция цели имеет минимум.
Координаты точки В: (2, 2). Подставляя в функцию цели
и , получим
минимальное значение функции: .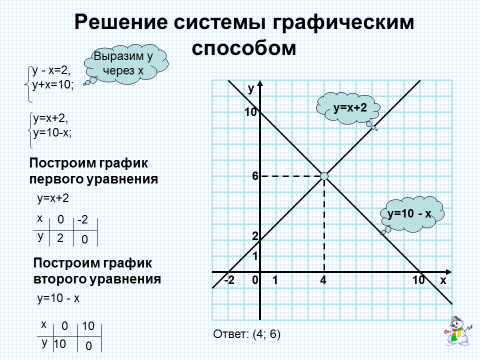
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 3. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
где .
Правильное решение и ответ.
Пример 4. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
где .
Правильное решение и ответ.
До сих пор полученные выводы были основаны на том, что множество решений
задачи линейного программирования сконфигурировано так, что оптимальное решение конечно и
единственно. Теперь рассмотрим примеры, когда это условие нарушается. В этих примерах многоугольник
решений строится так, как показано в предыдущих примерах, остановимся же на признаках, которые
отличают эти исключительные примеры.
Пример 5. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке изображены: неограниченная многогранная область решений данной системы ограничений, исходная линия уровня (чёрного цвета), вектор (бордового цвета), указывающий направление движения исходной линии уровня для нахождения максимума целевой функции.
Легко заметить, что функция F может неограниченно возрастать при заданной системе ограничений, поэтому можно условно записать, что .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 6. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение.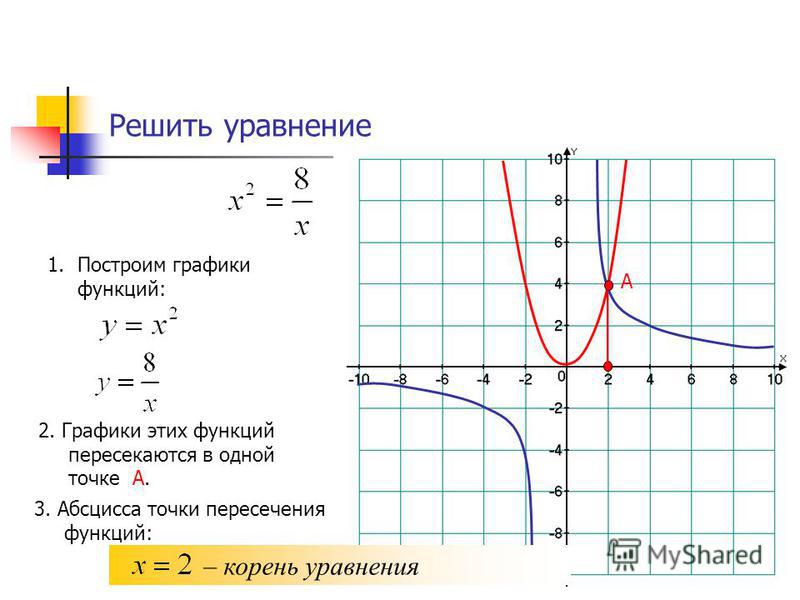 Изображённая на рисунке ниже область не содержит ни одной общей точки,
которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива
и не может содержать ни одного решения, в том числе и оптимального.
Изображённая на рисунке ниже область не содержит ни одной общей точки,
которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива
и не может содержать ни одного решения, в том числе и оптимального.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 7. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. Всем неравенствам системы ограничений удовлетворяют точки треугольника ABC, который и является областью решений. За исходную линию уровня взята прямая
(на рисунке ниже — чёрного
цвета), с тем чтобы она пересекала область решений. Как видно из рисунка, максимальное значение F = 8 достигается в точке С(8; 0).
При построении треугольника ABC не была использована прямая ,
соответствующая первому неравенству, хотя все точки треугольника удовлетворяют этому неравенству. Таким
образом, этот пример отличается от предыдущих тем, что одно из неравенств системы ограничений оказалось
лишним.
Таким
образом, этот пример отличается от предыдущих тем, что одно из неравенств системы ограничений оказалось
лишним.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 8. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке ниже изображены область решений системы ограничений и линия уровня (чёрного цвета). Если передвигать линию уровня параллельно исходной в направлении вектора , то она выйдет из области решений не в одной точке, как это было в предыдущих примерах, а сольётся с прямой CD, которая является граничной линией области решений.
Все точки отрезка CD дают одно
и то же значение функции цели, которое и служит её оптимальным значением: .
Следовательно, имеется не одно, а бесчисленное множество оптимальных решений, совпадающих с точками
отрезка CD, в частности, с двумя угловыми точками C и D. Этот пример показывает,
что в некоторых случаях единственность оптимального решения нарушается.
Этот пример показывает,
что в некоторых случаях единственность оптимального решения нарушается.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Напоследок следует заметить, что строить многогранник решений можно и другим способом, отличающимся о того, который мы рассматривали. А именно: можно не искать точки пересечения прямых с осями координат, а искать точки пересечения прямых. Для этого последовательно решаются системы из двух уравнений, так, чтобы решениями были точки пересечения всех прямых. Полученные точки и будут вершинами многогранника решений. Этот способ иногда бывает удобным в случаях, когда точки пересечения прямых с осями координат — дробные числа и, неправильно отложив точку пересечения, можно получить ошибку и в поиске точек пересечения самих прямых.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
Начало темы «Линейное программирование»
Задача и теоремы линейного программирования, примеры формулировки задач
Пример задачи линейного программирования: задача использования ресурсов, её графическое решение
Симплекс-метод решения задач линейного программирования: типичный пример и алгоритм
Симплекс-метод: случай, когда максимум целевой функции — бесконечность
Симплекс-метод: случай, когда система не имеет ни одного решения
Симплекс-метод: случай, когда оптимальное решение — не единственное
Двойственная задача линейного программирования
Решение задачи целочисленного программирования: методы и примеры
Решение транспортной задачи распределительным методом на примерах
Поделиться с друзьями
Линейные уравнения: онлайн калькулятор, формула, примеры решений
Линейные уравнения – это элементарные уравнения школьной алгебры, при решении которых обычно не возникает никаких проблем. Наш калькулятор позволит вам проверить правильность решения любого линейного уравнения.
Наш калькулятор позволит вам проверить правильность решения любого линейного уравнения.
Определение
Линейное уравнение – это равенство вида:
ax + b = 0,
где a и b — произвольные числа.
Решением линейного уравнения называется поиск такого значения x, при котором отношение становится тождеством.
В качестве примера таких равенств можно привести уравнения:
- 5x + 6 = 0, где a = 5, b = 6;
- 0,75x − 0,25 = 0, где a = 0,75, b = −0,25;
- 1/4 x + 2/7 = 0, где a = 1/4, b = 2/7.
Важно понимать, что a и b могут принимать нулевые значения, и тогда равенства будут выглядеть довольно странно. При нулевых коэффициентах уравнения превращаются в обыкновенные тождества типа 5 = 5 или 0 = 0, которые и решать не требуется.
Внешний вид и тождественные преобразования
Каждое уравнение имеет свой определенный алгоритм решения, поэтому чтобы понять, каким именно способом развязывать задачу, прежде всего, необходимо определить тип равенства. Помимо линейных уравнений существуют квадратные, кубические, тригонометрические, показательные и многие другие типы отношений. Опознать линейное довольно просто – оно должно выглядеть как ax + b = 0 или приводиться к этому виду. Если неизвестный x находится в знаменателе, в показатели степени или имеет степень, отличную от единицы – это не линейное уравнение.
Помимо линейных уравнений существуют квадратные, кубические, тригонометрические, показательные и многие другие типы отношений. Опознать линейное довольно просто – оно должно выглядеть как ax + b = 0 или приводиться к этому виду. Если неизвестный x находится в знаменателе, в показатели степени или имеет степень, отличную от единицы – это не линейное уравнение.
К примеру, уравнение вида:
x2 + 5x + 3 = x2 − 2x + 8
на первый взгляд кажется квадратным, так как в нем присутствует неизвестный икс во второй степени. Однако при помощи тождественных преобразований данное уравнение легко привести к виду ax + b = 0. Для работы с любыми типами уравнений используются два тождественных преобразования:
- к каждой части уравнения можно добавить/отнять одно и то же число;
- каждую часть уравнения можно умножить/разделить на одно и то же число.
Правило добавления/отнимания числа, по сути, является переносом через знак равенства с заменой знака. Например, в примере x + 2 = 5 мы просто переносим двойку через знак равенства со знаком минус и получаем ответ x = 5 − 2 или x = 3. Однако данная операция выглядит как вычитание двойки из каждой части уравнения:
Например, в примере x + 2 = 5 мы просто переносим двойку через знак равенства со знаком минус и получаем ответ x = 5 − 2 или x = 3. Однако данная операция выглядит как вычитание двойки из каждой части уравнения:
x + 2 − 2 = 5 − 2 или x = 3.
Вернемся к исходному уравнению x2 + 5x + 3 = x2 − 2x + 8. От каждой части без проблем можно отнять x2 и в результате получить:
5x + 3 = −2x + 8.
Очевидно, что это линейное уравнение и его можно решить.
Алгоритм решения линейных уравнений
Линейные уравнения – самые простые равенства из всех и для их решения достаточно следовать элементарному правилу: все иксы собираем слева, все числа – справа. Это означает, что для решения любого линейного равенства требуется свободные коэффициенты вынести в правую часть уравнения, а все неизвестные – в левую. При переносе через «равно» знак всегда меняется. В нашем примере 5x + 3 = −2x + 8 потребуется перенести 3 влево и поменять знак, и −2x — вправо и также поменять знак.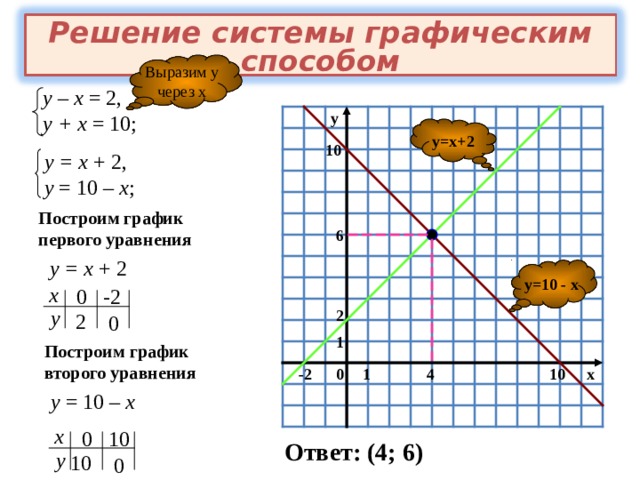 Мы получим:
Мы получим:
- 5x + 2x = −3 + 8,
- 7x = 5.
Ответ интуитивно понятен всем, кто уже знаком с решением уравнений. Но если говорить строгим математическим языком, для поиска неизвестного нам потребуется применить второе тождественное преобразование, то есть левую и правую часть равенства разделить на 7. В ответе получим x = 5/7.
Графическое решение уравнений при помощи калькулятора
Наш калькулятор решает линейные уравнения не аналитическим, а графическим способом. Это необычный на первый взгляд метод. Пусть у нас есть уравнение 2x + 2 = 6. Решая его аналитически, мы бы применили правило «все иксы слева, все числа справа» и получили результат x = 2. Графический метод подразумевает трансформацию уравнения в функцию, при котором правая часть уравнения заменяется второй неизвестной y. Это означает, что наше уравнение превращается в функцию 2x + 2 = y. Такая функция имеет бесконечное количество решений, а данное уравнение описывает линию, которую калькулятор отрисовывает в окне программы.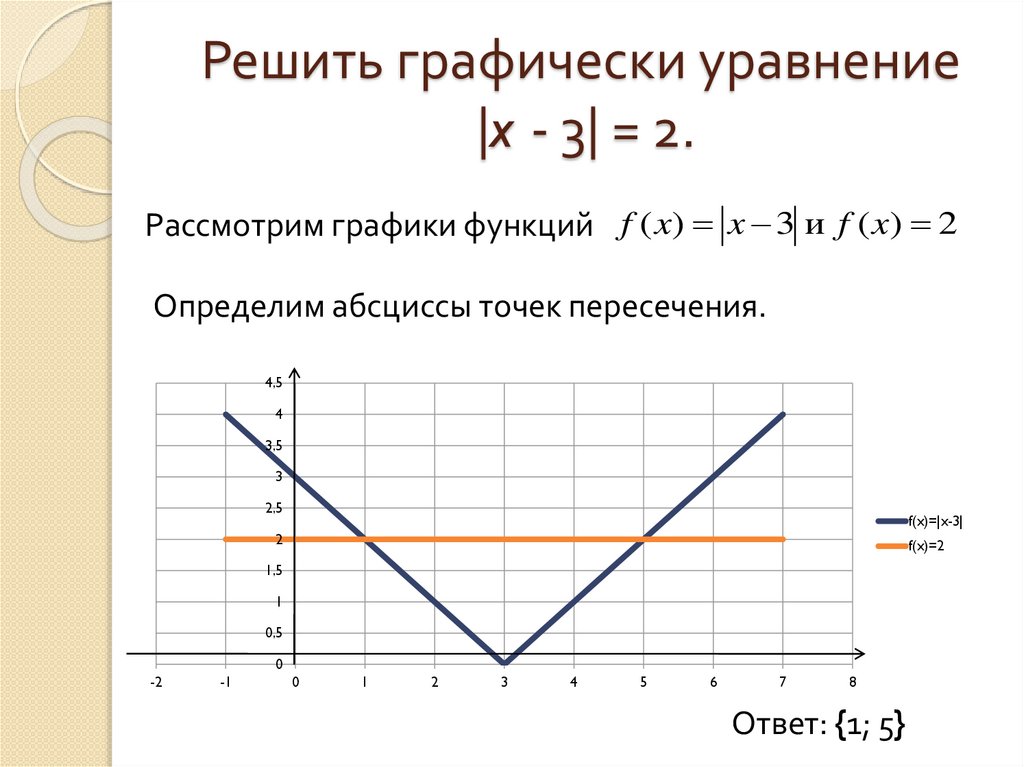
Для решения нашего уравнения достаточно выбрать одно из решений, когда y = 6. Для этого требуется найти 6 на оси y, провести до уравнения прямой и опустить перпендикуляр на ось x. Как видите, для y = 6 аргумент x = 2. Таким образом, аналитический и графический способ решения уравнений дают один и тот же результат.
Наша программа представляет собой калькулятор решения простых линейных уровней вида ax + b = y. Ответ программа представляет в графическом виде, рисуя прямую, которую описывает заданное уравнение.
Рассмотрим на примере
Покупка пива
Для покупки 8 кружек пива Рихарду не хватает 20 немецких марок, но если он купит всего 5 кружек пива, то у него останется еще 100 марок. Сколько денег у Рихарда? Для решения такой задачи нам потребуется составить уравнение. Мы не знаем, сколько стоит одна кружка пива, поэтому обозначим ее как x. Пусть y — это сумма денег в кошельке Рихарда, следовательно, y = 8x − 20, то есть 8 кружек пива минус 20 марок. Так же мы можем выразить эту же сумму денег как y = 5x + 100, то есть 5 кружек пива и 100 лишних марок. Так как это одна и та же сумма, мы можем составить следующее уравнение:
Так как это одна и та же сумма, мы можем составить следующее уравнение:
8x − 20 = 5x + 100.
А это стандартное линейное уравнение. Мы можем решить его как аналитически, так и графически при помощи нашего калькулятора. Для начала приведем его к стандартному виду, проведя первое тождественное преобразование.
- 8x − 5 x = 100 + 20
- 3x = 120
- x = 40.
Для графического решения мы можем в строке 3x = 120 прибавить к левой и правой части произвольное число, чтобы заполнить все ячейки калькулятора. Прибавим с каждой стороны +10 и получим уравнение вида 3x + 10 = 130. Введем это уравнение в форму онлайн-калькулятора и получим прямую, которую описывает это уравнение. Значение y = 130 соответствует аргументу x = 40.
Таким образом, 1 кружка пива стоит 40 марок. Подставим это значение в уравнение и получим тождество:
- 80 × 40 − 20 = 5 × 40 + 100
- 300 = 300
Следовательно, в кошельке у Рихарда 300 немецких марок.
Заключение
Линейные уравнения – это не только раздел школьной математики. Такие равенства широко применяются для решения самых разных бытовых задач. Пользуйтесь калькуляторами из нашего каталога для проверки своих решений.
Такие равенства широко применяются для решения самых разных бытовых задач. Пользуйтесь калькуляторами из нашего каталога для проверки своих решений.
Уравнения с модулями. Графический метод
Простыми уравнения с модулями называем уравнения вида
|x|=5; |x-3|=2; ||2x-1|-5|=3; |1-x|=4
в которых переменная входит однократно и линейно.
Решать модульные уравнения можно как с помощью метода раскрытия модулей так и графически. В данной статье большое внимание будет уделено именно графическому методу раскрытия модулей. Для этого постепенно будет раскрыта суть преобразований с модулями. Таким образом удается решить множество тестовых задач в которых требуется найти количество решений уравнения с модулем.
Для наглядности приведем график модуль функции y=|x| ( «галочки»)
Далее представим смещение графика модуль функции по оси Ox, например y=|x-7|. Такая запись означает что функция равна нулю когда дужка равна нулю
x-7=0; –> x=7.
Так что «галочка» переносится вправо на 7.
Если подмодульную функцию умножить на (-1) то график функции не изменится |7-x|=|x-7|.
Если в модуле имеем суммирование |x+5| то смещение графика модуль функции выполняем в сторону отрицательных переменных
Самое интересное в вычислениях происходит когда имеем уравнение вида модуль в модуле
||x|-6|, ||x|+3|
Тогда выполняем перенос графика внутреннего модуля по оси вниз или вверх и симметричное отображение значений, которые идут ниже оси Oх вверх.
Следующая функция это модуль поднят вверх на три.
Далее, если в задании спрашивают «Какое количество корней уравнения ||x|-6|=2?» то необходимо провести лишь линию y=2 и подсчитать количество точек пересечения с графиком модуль функции
Уравнение имеет 4 решения. Лучше решать графически уравнение с модулями на листке в клеточку, есть лучшая привязка к квадратикам. Задача в каждом из случаев сводится к смещению, отображения и параллельному переносу графика модуль функции |x|.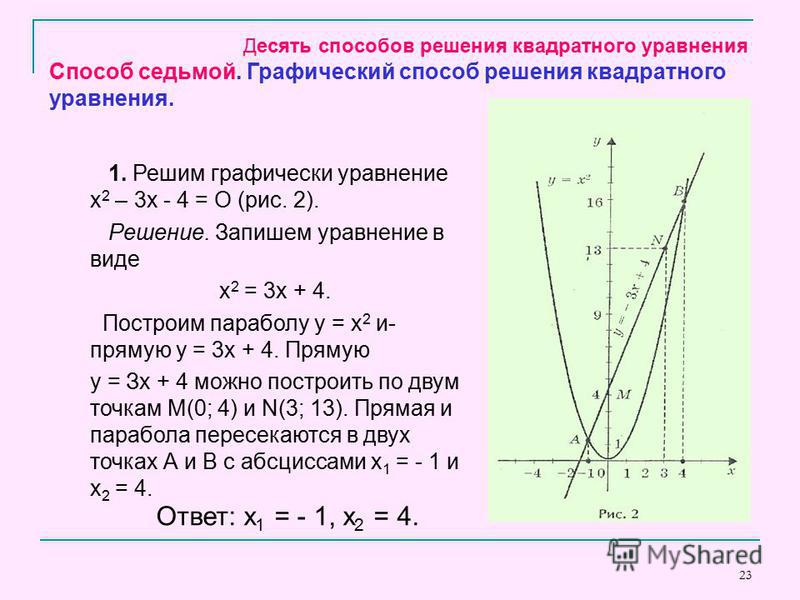 Решим несколько примеров чтоб Вы понимали насколько эффективная методика графического раскрытия модулей.
Решим несколько примеров чтоб Вы понимали насколько эффективная методика графического раскрытия модулей.
Пример 1. Найти корни уравнения ||x-2|-5|=3.
Решение: Имеем задания типа модуль от модуля. Выполняем построение первого (внутреннего) модуля
Далее параллельно переносим линии вниз на 5, чтобы получить график функции y=|x-2|-5
Следующим шагом отражаем все что находится ниже оси абсцисс. Это и будет искомая модуль функция y=||x-2|-5|. Также выполняем построение прямой у=3
Нетрудно определить по рисунку что решениями уравнения с модулями будут значения
x=-6; x=0;x=4; x=10.
На этом пример выполнен. Далее будет меньше детализации, однако суть алгоритма графического построения Вам будет понятен.
Пример 2. Найти количество корней следующего уравнения с модулем |||x+1|-3|-5|=2.
Решение: Имеем уравнения с двумя вложенными модулями. График первого вложенного модуля получим смещением в отрицательную сторону оси абсцисс модуль функции на единицу.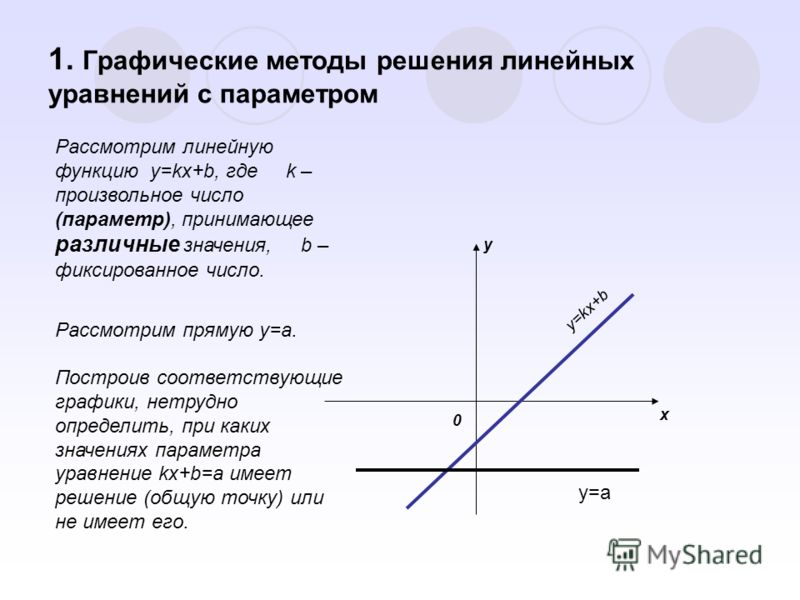 Далее параллельно переносим полученный график вниз на 3 и отразим относительно оси Ox все минусовые y. Полученный график снова опускаем вниз, на этот раз на 5 клеток и симметрично отражаем все что находится ниже оси Ox. Выполняем построение правой стороны уравнения – прямой y=2.
Далее параллельно переносим полученный график вниз на 3 и отразим относительно оси Ox все минусовые y. Полученный график снова опускаем вниз, на этот раз на 5 клеток и симметрично отражаем все что находится ниже оси Ox. Выполняем построение правой стороны уравнения – прямой y=2.
В результате у Вас должен получиться похожий конечный график модуль функции
Из построения видим, что имеем пять точек пересечения прямой с модуль-функцией, а следовательно и 5 корней уравнения. Вот и все решения примера с модулями. Классическое раскрытие модулей для этого примера занимает очень много времени и существует вероятность неправильного решения уравнения. Преимущество графического метода по времени решения видна невооружённым глазом.
Пример 3. При каком значении параметра a уравнение с модулем ||x-4|-2|=a-3 имеет три, четыре корня?
Решение: Выполняем построение модулей, которые находятся в левой части уравнения
Из построения видим, если правая сторона уравнения с модулями равна 2 то имеем три точки пересечения. Если от 0 до 2 не учитывая краев – 4 корни уравнения. Отсюда получим уравнение для определеения параметра
Если от 0 до 2 не учитывая краев – 4 корни уравнения. Отсюда получим уравнение для определеения параметра
a-3=2; – > a=5.
и неровности
a-3>0; a>3;
a-3< 2; a < 5 .
В итоге: уравнение имеет 3 корня когда параметр равен a=5
и 4 корня если параметр принадлежит интервалу a=(3..5).
В подобных примерах надо быть очень внимательными так как часто именно вопрос ставится так, чтобы помочь Вам или наоборот «навредить». Например: «Сколько положительных корней имеет уравнение с модулями?», «Найдите сумму решений уравнения», «Найдите наибольшее целое значение параметра» и тому подобные. Поэтому вдумчиво читайте что от Вас требуют, а уже потом приступайте к вычислениям.
Похожие материалы:
- Решение уравнений с модулями
- Модуль в модуле. Графический метод
- Модуль в модуле
- Решение неравенств с модулями
Система 2×2 линейных уравнений — Онлайн Solver
Алгебра Рельефы
инструкции
Этот инструмент он находит решения для системы двух одновременных линейных уравнений с двумя переменными. Способ, используемый для решения уравнения, — это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:
Способ, используемый для решения уравнения, — это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:
Введите 1-е линейное уравнение (например, 2x + 3Y = 4)
Введите 2-я линейное уравнение (EX. X — 3Y = 2)
Этот калькулятор позволяет решить два одновременных линейных уравнения, с двумя переменными, которые часто называют «двух-дшими системами».
Эти виды 2×2 систем очень часто используются в алгебре, потому что они часто появляются во всех видах приложений, как когда вы
Попробуйте решить слова проблемы.
Как правило, переменные, используемые в двухподневой линейной системе, называются по умолчанию \(x\) и \(y\), но это только конвенция, как они могут быть \(u\) и \(v\) Если вы хотите
Итак, это система дву- две:
\[x + 2y = 4\] \[2x — 2y = 2\]
так же, как это
\[2u — 2v = 1\] \[u — 3v = 2\]
это двух- две системы.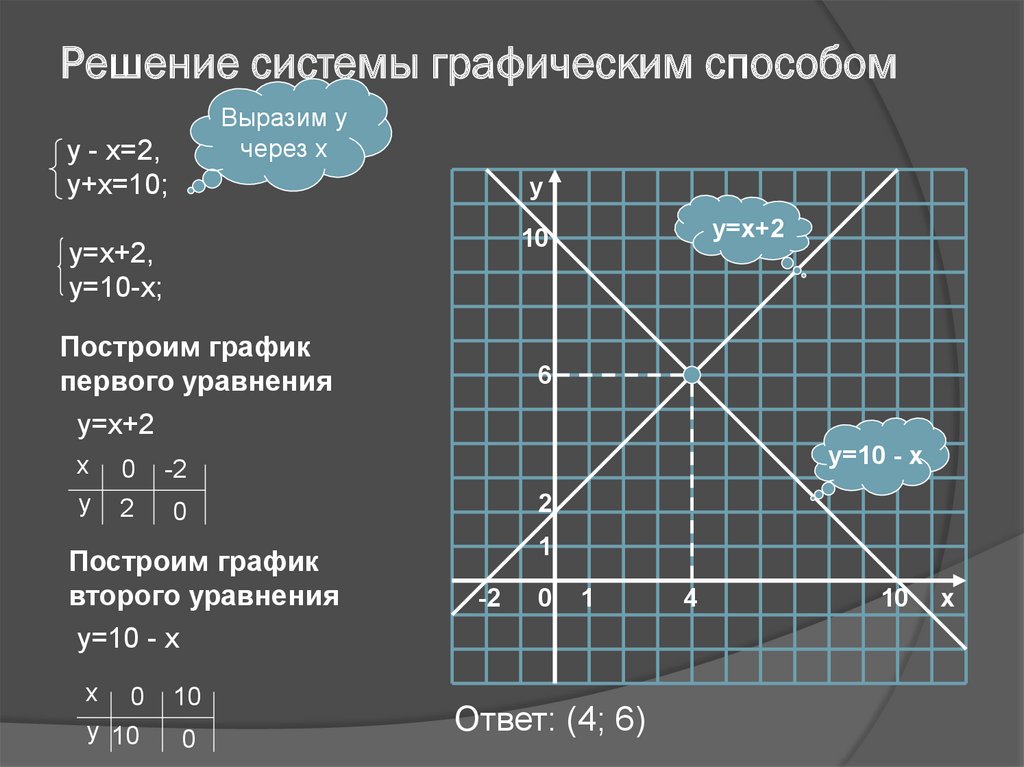 Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
Методы решения линейных систем 2×2
К счастью, есть много способов использовать для решения двухгибовых систем, и у вас есть преимущество, чтобы выбрать, какой метод использовать. Наиболее часто используемыми методами являются:
- График
- Замена
- Ликвидация
Метод графики основан на, нет удивлению, график двух уравнений и пытаясь визуально определить, где эти две линии пересекаются (если они пересекаются
вообще).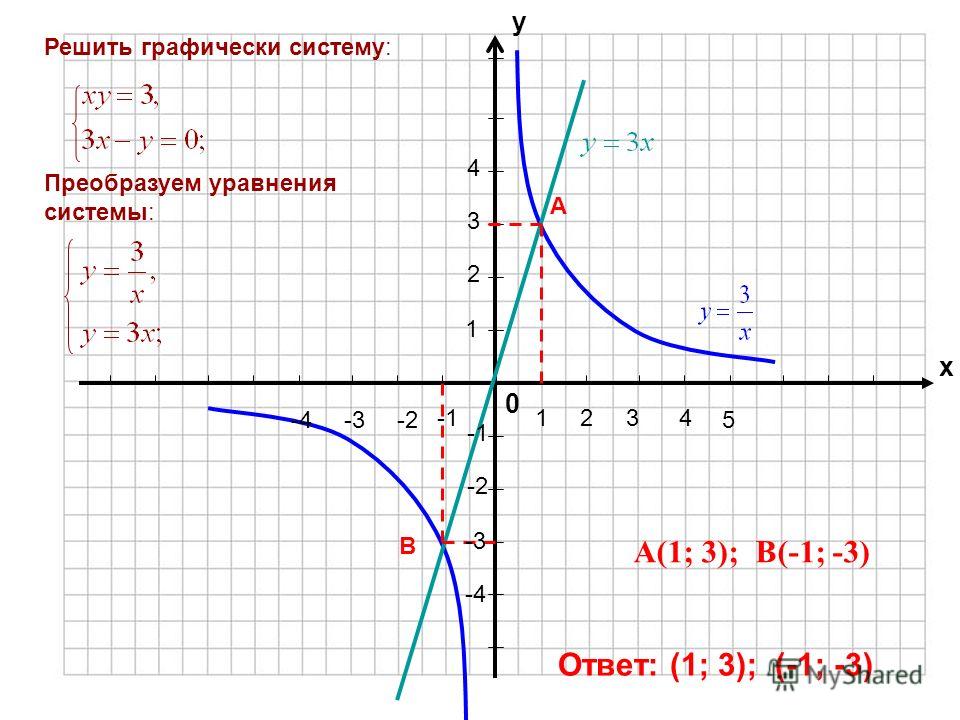 Этот метод естественным образом ограничивает приближения в большинстве случаев
Этот метод естественным образом ограничивает приближения в большинстве случаев
Метод замены основан на идее, которую можно решить для одной переменной в одном из уравнений, а затем подключить, что в другое уравнение, для решения для другой переменной.Часто это удобно, потому что структура одного из уравнений может привести к нему решить для одной переменной. Но это не всегда так, и этот метод в значительной степени ограничен случаем систем 2×2
Метод ликвидации основан на идее, которую можно манипулировать одному или оба уравнения, чтобы получить их или вычесть их, так что одна переменная исчезает. В некотором смысле,
Это более общий способ использования метода замещения
В некотором смысле,
Это более общий способ использования метода замещения
Как бороться с большими системами линейных уравнений?
Три метода, представленные выше, действительно могут быть эффективно использованы только с системами 2×2, что и для больших систем, которые системы становятся гораздо более сложными и Может быть, даже возможно использовать эти методы
Для 3×3 и крупных систем лучше всего использовать систематические подходы, такие как использование
МЕТОД КРАМЕРА
Для общего \(n \times n\) системы или используя
ГАУСОВСКАЯ ЛИКВИДАЦИЯ.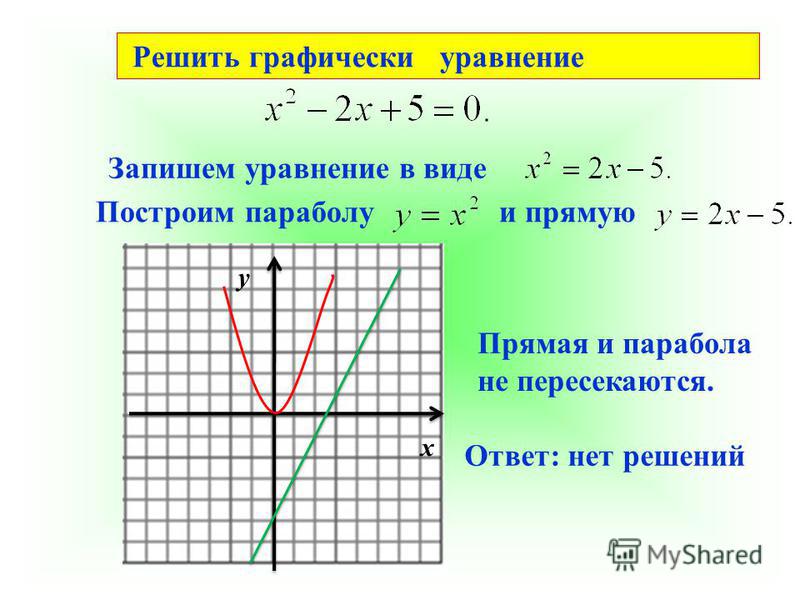 С
который работает независимо от размера системы, и количество переменных такое же, как количество уравнений.
С
который работает независимо от размера системы, и количество переменных такое же, как количество уравнений.
Алгебра калькулятор Алгебра калькулятор онлайн Алгебра Рельвер Система уравнений 2×2 Система 2×2 линейных уравнений калькулятора
Калькулятор графических полярных уравнений онлайн
| Дом | |
| Многочлены | |
| Нахождение наибольшего общего делителя | |
| Факторинг трехчленов | |
| Функция абсолютного значения | |
| Краткий обзор полиномов факторинга | |
| Решение уравнений с одним радикальным членом | |
| Добавление дробей | |
| Вычитание дробей | |
| Метод ФОЛЬГИ | |
| График составных неравенств | |
| Решение абсолютных неравенств | |
| Сложение и вычитание многочленов | |
| Использование наклона | |
| Решение квадратных уравнений | |
| Факторинг | |
| Свойства умножения показателей степени | |
| Завершение квадрата | |
| Решение систем уравнений методом подстановки | |
| Объединение подобных радикальных терминов | |
| Исключение с помощью умножения | |
| Решение уравнений | |
| Теорема Пифагора 1 | |
| Нахождение наименьших общих кратных | |
| Умножение и деление в научной записи | |
| Сложение и вычитание дробей | |
| Решение квадратных уравнений | |
| Сложение и вычитание дробей | |
| Умножение на 111 | |
| Добавление дробей | |
| Умножение и деление рациональных чисел | |
| Умножение на 50 | |
| Решение линейных неравенств с одной переменной | |
| Упрощение кубических корней, содержащих целые числа | |
| График составных неравенств | |
| Простые трехчлены как произведения двучленов | |
| Написание линейных уравнений в форме наклона-пересечения | |
| Решение линейных уравнений | |
| Линии и уравнения | |
| Пересечения параболы | |
| Функция абсолютного значения | |
| Решение уравнений | |
| Решение сложных линейных неравенств | |
| Комплексные числа | |
| Факторизация разности двух квадратов | |
| Умножение и деление рациональных выражений | |
| Сложение и вычитание радикалов | |
| Умножение и деление чисел со знаком | |
| Решение систем уравнений | |
| Факторизация противоположности GCF | |
| Умножение специальных многочленов | |
| Свойства показателей степени | |
| Научное обозначение | |
| Умножение рациональных выражений | |
| Сложение и вычитание рациональных выражений с отличающимися знаменателями | |
| Умножение на 25 | |
| Десятичные дроби в дроби | |
| Решение квадратных уравнений путем заполнения квадрата | |
| Частное правило для показателей степени | |
| Упрощение квадратных корней | |
| Умножение и деление рациональных выражений | |
| Независимые, противоречивые и зависимые системы уравнений | |
| Склоны | |
| Графические линии на координатной плоскости | |
| Графические функции | |
| Силы десяти | |
| Свойство нулевой мощности экспонентов | |
| Вершина параболы | |
| Рационализация знаменателя | |
| Тест факторизуемости для квадратных трехчленов | |
| Трехчленные квадраты | |
| Решение двухшаговых уравнений | |
| Решение линейных уравнений, содержащих дроби | |
| Умножение на 125 | |
| Свойства экспоненты | |
| Умножение дробей | |
| Сложение и вычитание рациональных выражений с одинаковым знаменателем | |
| Квадратные выражения — Заполнение квадратов | |
| Сложение и вычитание смешанных чисел с разными знаменателями | |
| Решение формулы для заданной переменной | |
| Факторинг трехчленов | |
| Умножение и деление дробей | |
| Умножение и деление комплексных чисел в полярной форме | |
| Уравнения мощности и их графики | |
| Решение линейных систем уравнений подстановкой | |
| Решение полиномиальных уравнений методом факторинга | |
| Законы показателей | |
| индекс casa mÃo | |
| Системы линейных уравнений | |
| Свойства рациональных показателей | |
| Мощность произведения и мощность частного | |
| Различия в факторинге идеальных квадратов | |
| Деление дробей | |
| Разложение полинома на множители путем нахождения GCF | |
| Графики линейных уравнений | |
| шагов факторинга | |
| Свойство умножения показателей степени | |
| Решение систем линейных уравнений с тремя переменными | |
| Решение экспоненциальных уравнений | |
| Нахождение НОК набора одночленов | |
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решение
- График
- Система
- Математический решатель на вашем сайте
графические полярные уравнения онлайн калькулятор
Связанные темы:
алгебра программного обеспечения |
методы решения уравнений в частных производных первого порядка |
прентис холл алгебра 1 стандарты флориды |
данные для построения графиков линейных уравнений |
бесплатная алгебра для начинающих |
вычисление дробного показателя степени |
общие знаменатели для 18 и 22 |
бесплатные рабочие листы для сложения и вычитания целых чисел |
калькулятор факторинговых трехчленов |
математические ответы для Холта математика на дробных операциях |
математические саксонские листы |
решение игры квадратного уравнения
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| nea2c Зарегистрирован: 12. |
| ||||||
| Наверх | |||||||
| Вофий Тимидов Дата регистрации: 06.07.2001 |
| ||||||
| Наверх | |||||||
| Mibxrus Зарегистрирован: 19.10.2002 |
| ||||||
| Наверх | |||||||
| Воумдайм Обпнис Зарегистрирован: 11.06.2004 |
| ||||||
| Наверх | |||||||
10 лучших графических калькуляторов (физических и онлайн)
Графический калькулятор — это уникальный инструмент в математике и естественных науках. Графические калькуляторы выполняют те же функции, что и обычные калькуляторы, но имеют более сложные функции, такие как возможность вычисления дробей, логарифмов и квадратных корней. Есть несколько громких имен в области графических калькуляторов, которым доверяют и которые существуют уже давно — вы можете узнать классический TI-84 на одном из ваших уроков математики. Графические онлайн-калькуляторы появились относительно недавно и часто бесплатны. Мы рассмотрим лучшие физические и графические онлайн-калькуляторы, чтобы помочь вам решить, какой из них подходит именно вам.
Графические онлайн-калькуляторы появились относительно недавно и часто бесплатны. Мы рассмотрим лучшие физические и графические онлайн-калькуляторы, чтобы помочь вам решить, какой из них подходит именно вам.
Что такое графический калькулятор?
Графические калькуляторы имеют более мощные и сложные компьютеры, чем стандартные калькуляторы, и названы так потому, что они имеют графические возможности. Они могут решать сложные уравнения и строить графики . Они также программируются и являются полезным инструментом, если вы работаете над долгосрочным проектом и нуждаетесь в нем для хранения информации или решения математических задач более высокого уровня.
Некоторые графические калькуляторы также имеют цифру 9.0682 CAS, или система компьютерной алгебры, что означает, что он также может решать алгебраические уравнения . Графические калькуляторы — это, по сути, карманные компьютеры, поэтому важно выбрать подходящий именно вам.
Что делает графический калькулятор?
Графические калькуляторы позволяют рассчитывать статистику и легко преобразовывать результаты в графики. Конечно, построение графиков — очень важная часть графического калькулятора. Это позволяет вам работать над самой проблемой, а не тратить время на математические расчеты. Это может показаться нелогичным. Разве изучение математики не является целью? Да, но даже если вы овладели навыками, для решения некоторых уравнений может потребоваться много времени.
Графические функции и статистика — это две основные функции, которыми вы будете пользоваться будучи студентом. Вы также можете использовать их для исчисления и тригонометрии, и в этом случае может помочь CAS. Не все графические калькуляторы оснащены CAS. Убедитесь, что вы знаете, для чего вы будете использовать свой калькулятор и нужен ли он вам с CAS.
Я упомянул, что графические калькуляторы являются программируемыми, поэтому их также можно использовать для хранения данных на случай, если они потребуются позже для уравнения или графика. Некоторые исследователи используют графические калькуляторы вместе с другим оборудованием. Они подключаются к компьютерам или другим машинам и собирают информацию, которая впоследствии может быть доступна и учтена в уравнениях. Помните, графические калькуляторы могут решать несколько уравнений одновременно, поэтому это может помочь сэкономить много времени и труда.
Некоторые исследователи используют графические калькуляторы вместе с другим оборудованием. Они подключаются к компьютерам или другим машинам и собирают информацию, которая впоследствии может быть доступна и учтена в уравнениях. Помните, графические калькуляторы могут решать несколько уравнений одновременно, поэтому это может помочь сэкономить много времени и труда.
Лучшие физические графические калькуляторы
Физические графические калькуляторы — это крупная инвестиция, и часто действительно хорошая. Если вы серьезно относитесь к своему графическому калькулятору и знаете, что вам нужно мощное устройство, чтобы брать его с собой на занятия, экзамены или на работу, этот мини-компьютер станет важной частью вашей жизни.
TI-84 Plus
TI-84 Plus — это традиционный графический калькулятор, представляющий собой простое устройство, на котором можно изучить основы работы с графическим калькулятором. Это отличный инструмент для учащихся средних и старших классов , которые начинают более углубленное изучение математики, поскольку дизайн и 10 предварительно загруженных приложений помогут вам одновременно освоить математические навыки и научиться пользоваться графическим калькулятором. Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, IB и AP.
Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, IB и AP.
TI-Nspire CX CAS
Этот сверхмощный графический калькулятор отлично подходит для учащихся средних школ и колледжей, изучающих математику и естественные науки более высокого уровня . Экран с диагональю 3,2 дюйма — отличная возможность для студентов, изучающих инженерное дело, физику и математический анализ. CAS сохраняет и хранит информацию, поэтому вы можете редактировать уравнения и манипулировать ими, что помогает вам эффективно использовать свое время при решении сложных задач. Этот калькулятор одобрен для экзаменов SAT, PSAT и AP.
Casio FX-9860 GII
Casio FX-9860 GII идеально подходит для младших школьников, которые только изучают графические калькуляторы, а также для тех, у кого ограниченный бюджет. Сверхширокий дисплей и удобный интерфейс облегчают навигацию по этому калькулятору, хотя он менее эффективен, чем некоторые другие варианты. Он также поставляется с предварительно загруженными приложениями, такими как приложение для работы с электронными таблицами, приложение для геометрии и приложение для конусов, , а также справочное руководство пользователя и 200 часов автономной работы. Этот калькулятор одобрен для тестов SAT, PSAT, ACT и AP.
Этот калькулятор одобрен для тестов SAT, PSAT, ACT и AP.
TI-84 Plus CE
TI-84 Plus CE — это калькулятор высокого разрешения с полноцветным дисплеем с подсветкой. У него стильный дизайн и большой объем памяти. По сравнению с другими моделями это реальное обновление как по мощности, так и по удобству использования, особенно с точки зрения отображения и скорости. Он также поставляется с перезаряжаемой батареей и доступен в различных цветах. Этот калькулятор одобрен для экзаменов SAT, PSAT, ACT, AP и IB.
HP Prime
Удивительно маленький и тонкий графический калькулятор CAS, HP Prime имеет огромный экран, что делает его отличным выбором как для студентов, так и для профессионалов, которым нужен мощный инструмент. Этот калькулятор был создан по образцу смартфонов, и это видно. Он имеет сенсорный дисплей, геометрию, электронные таблицы и расширенные графические приложения, а также другие приложения, доступные для загрузки . Интерфейс похож на смартфон и имеет дополнительные функции, такие как режим экзамена. Этот калькулятор одобрен для SAT.
Интерфейс похож на смартфон и имеет дополнительные функции, такие как режим экзамена. Этот калькулятор одобрен для SAT.
Лучшие онлайн-калькуляторы для построения графиков
Онлайн-калькуляторы — отличный ресурс для тех, кто очень мобилен. Вы можете опробовать разные калькуляторы без каких-либо финансовых вложений, а также создать учетную запись, чтобы сохранить свою работу и вернуться к ней в любое время и с любого устройства. Ваш предпочтительный графический онлайн-калькулятор будет зависеть от ваших потребностей и того, какой интерфейс вы предпочитаете.
GraphCalc
Этот загружаемый графический калькулятор отлично подходит для тех, кто использовал или учился на TI-84, поскольку в нем перечислены функции и примеры по сравнению с TI-84 . GraphCalc также предоставляет инструкции по использованию калькулятора и всех его инструментов и утверждает, что он «почти полностью заменяет калькуляторы TI83 и TI84 Plus». Он также имеет раздел часто задаваемых вопросов и предлагает ресурсы для других графических онлайн-калькуляторов.
Desmos
У Desmos есть длинный список примеров в каждой категории, что делает этот графический калькулятор простым в использовании и понимании. Он работает в полноэкранном режиме, поэтому вы можете легко просматривать и редактировать свою работу. Он имеет всплывающую клавиатуру, позволяющую вводить уравнения в диалоговом окне с левой стороны и просматривать их, одновременно позволяя просматривать график справа. Вы также можете создать учетную запись и сохранить свои графики.
Mathway
Mathway имеет раскладку, аналогичную Demos, и включает всплывающую клавиатуру, диалоговое окно, а также отображение уравнений и графиков. Различные функции находятся в раскрывающемся меню, что очень удобно для навигации по калькулятору. У него нет примеров, но у него есть обучающая функция, похожая на чат, которая помогает вам изучать калькулятор и решать уравнения . Он также имеет возможность создать учетную запись.
Метакалькулятор
Метакалькулятор фактически разделяет функции традиционного «графического калькулятора» на четыре разных калькулятора. На главной странице вы выбираете графический калькулятор, научный калькулятор, матричный калькулятор и калькулятор статистики. Это упрощает использование, поскольку вам не нужно играть и искать различные функции, если вы не знакомы со стандартным графическим калькулятором. Вы можете переключаться между калькуляторами с помощью вкладок вверху, и каждый калькулятор также разделяет функции с помощью вкладок. Так, например, графический калькулятор переключается между уравнениями, таблицами, пересечениями и точками графика. Это позволяет легко организовать и отслеживать вашу работу.
Geogebra
Калькулятор Geogebra имеет самую удобную систему. Меню инструментов и функций представлено с помощью удобной графики, которая поможет вам быстро перемещаться по калькулятору и легко находить то, что вы ищете. Функция калькулятора позволяет вводить и просматривать уравнения в диалоговом окне слева и просматривать график справа. В нем также есть раскрывающееся меню со знакомыми параметрами, которые вы найдете в большинстве программ (сохранение, экспорт и т. д.), и вы можете создать учетную запись для сохранения своей работы.
Функция калькулятора позволяет вводить и просматривать уравнения в диалоговом окне слева и просматривать график справа. В нем также есть раскрывающееся меню со знакомыми параметрами, которые вы найдете в большинстве программ (сохранение, экспорт и т. д.), и вы можете создать учетную запись для сохранения своей работы.
Как выбрать калькулятор
Вам нужно знать больше, чем просто как пользоваться графическим калькулятором; надо уметь выбирать! Важно помнить, что графические онлайн-калькуляторы не разрешены для использования в SAT, ACT и других стандартизированных тестах. Многие физические калькуляторы одобрены для тестирования, поэтому, если вы покупаете физический калькулятор, убедитесь, что он одобрен для использования. Если вы не покупаете физический калькулятор, убедитесь, что у вас есть план, когда вы будете проходить стандартизированные тесты, например, 9.0682 аренда или аренда калькулятора .
Если вы не являетесь специалистом по математике или естественным наукам, вы можете использовать графический калькулятор только в качестве домашнего задания в одном или двух курсах, чтобы помочь вам с уравнениями или задачами. В этом случае можно воспользоваться онлайн-калькулятором. Для этих курсов проконсультируйтесь со своим учителем или профессором, чтобы узнать, можете ли вы использовать онлайн-курс в классе.
В этом случае можно воспользоваться онлайн-калькулятором. Для этих курсов проконсультируйтесь со своим учителем или профессором, чтобы узнать, можете ли вы использовать онлайн-курс в классе.
Вы также можете найти более простой в использовании интерфейс графического онлайн-калькулятора . Онлайн-калькуляторы также позволяют сохранять вашу работу и получать к ней доступ с любого устройства через вашу учетную запись. Если вам удобнее быть мобильным, а не носить с собой графический калькулятор на всякий случай, вам может подойти онлайн.
Для специальностей по математике и естественным наукам, которые планируют сделать карьеру в STEM , инвестирование в хороший физический графический калькулятор может быть выходом. Поскольку вы будете использовать его часто, вы окупите свои деньги и вам не придется беспокоиться о таких вещах, как доступ к Wi-Fi, если вы хотите использовать графический калькулятор.
При покупке графического калькулятора важно учитывать, как вы собираетесь его использовать. Если вам нужно что-то взять с собой на длительные экзамены в колледже, такие факторы, как дисплей, скорость обработки и время автономной работы, также являются важными факторами. Кроме того, убедитесь, что вы знаете, нужен ли вам калькулятор с CAS или нет.
Если вам нужно что-то взять с собой на длительные экзамены в колледже, такие факторы, как дисплей, скорость обработки и время автономной работы, также являются важными факторами. Кроме того, убедитесь, что вы знаете, нужен ли вам калькулятор с CAS или нет.
Если вы ищете калькулятор для использования только в течение одного или двух семестров, вы можете взять его напрокат или купить в Интернете, в дополнение к перечисленным выше отличным бесплатным онлайн-калькуляторам. Вы также можете искать скидки для студентов, доступные в вашей школе или у продавца.
Графические калькуляторы — невероятно полезный инструмент. Они позволяют учащимся получить визуальный доступ к математике высокого уровня и сократить множество трудоемких уравнений. Существует множество вариантов этих калькуляторов, и многое следует учитывать при принятии решения о том, какой из них приобрести, или если вам вообще нужен такой калькулятор. В конце концов, приоритетом является то, что вы получите все инструменты, необходимые для обучения и достижения успеха.
Что дальше?
Ищете дополнительную информацию об использовании графических калькуляторов на вступительных экзаменах в колледж? Руководство по калькуляторам ACT и калькуляторам SAT: советы экспертов могут помочь!
Усердно готовитесь к предстоящим экзаменам? Ознакомьтесь с Руководством для экспертов по экзамену AP Calculus AB и Полным руководством по экзамену AP Statistics.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Эти рекомендации основаны исключительно на наших знаниях и опыте. Если вы покупаете предмет по одной из наших ссылок, PrepScholar может получить комиссию.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Об авторе
Кэрри имеет степень бакалавра письма, литературы и издательского дела в Колледже Эмерсон и в настоящее время получает степень магистра иностранных дел. Она несколько лет работала в издательстве и считает, что книги могут открывать новые миры. Она любит читать, гулять на свежем воздухе и узнавать что-то новое.
руководство по решению линейной алгебры Ланга | Страхование жизни | Цветы корваллиса | Болгарская авиакомпания |
калькулятор преобразования смешанных чисел в десятичные дроби | тест на знание алгебры в колледже | алгебра ответы | Примеры математических вычислений |
упражнения по теории жидкости и механики | Найти агента по недвижимости | решение алгебраических формул для размерности | бесплатные практические тесты на сложение и вычитание |
Решение математических таблиц квадратичных чисел | бесплатное решение задач по алгебре | Банк Коммерс Север | квадратный корень общим методом |
Рабочие листы по математике | Тригонометрия десятого класса | Рабочий лист тригонометрического графика | метод решения дифференциальных уравнений с использованием функций Грина |
онлайн-викторина по математике для std 6 | Калькулятор полиномиального коэффициента | Предварительные занятия по алгебре | Католическая программа домашнего обучения |
Средство для поиска химических уравнений | i pass скачать бесплатно кошачью бумагу 1 | Диета Аткинса | Родительские ссуды |
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В TI-89 | манекены параболы | умножить дроби и расположить в порядке убывания | легкая алгебра |
использовать r для решения уравнения одновременно | как упростить подкоренные выражения на калькуляторе | алгебра мелочи | Одежда для студенческого футбола |
электронная книга по финансово-хозяйственному учету | простой способ решить 6-значное сложение | Источник DSL | Тематические круизы |
«Анализ нелинейных систем» скачать электронную книгу | решение уравнений с несколькими переменными | Авиакомпания Airways | Вопрос о способностях решен |
как решить сложную математическую викторину | 11+ образец бумаги по математике | бесплатные рабочие листы по математике ks3 для печати | конвертировать числа между любыми основаниями |
Калькулятор кратных дробей | алгебра для детей | Домен | Подержанный автомобиль |
Альтернативные студенческие ссуды | лист математических формул гр. | калькулятор параболы | Комиссия за банкротство |
решение проблемы системы линейных уравнений возраста | алгебраические суммы | игра в алгебре | алгебра |
Партнерские сети | бесплатные математические задачи для 10 класса | Буклет с ответами Прентис Холл Предварительная алгебра | Делить дроби на целые числа рабочие листы |
Страхование путешествий старше 60 лет | линейное уравнение 3 неизвестных 2 известных | корни уравнения TI83+ | самая сложная математика в мире |
Конференц-связь | Доверенность на здравоохранение | загрузки для гражданского строительства для титана TI 89 | Улучшение математики |
как вычислить 9-значный кубический корень вручную | математика форма 1 малайзия упражнения скачать бесплатно | помощь в построении графиков по алгебре | Учебник по геометрии Glencoe ответы |
раздаточный материал по истории индии 6 уровень | стихотворение о математической алгебре | Бумаги модели умственных способностей для класса VII | викторина для девятого класса |
мелочи тригонометрия | Бюджетная помощь | Витамины B12 | вопрос о перестановках и комбинациях по GRE |
вопрос о способностях и ответ на | пример алгебры мелочи | эмулятор калькулятора ti-84 | Одежда для бульдогов |
калькулятор добавления радикалов | карманный компьютер для учета затрат | решить уравнение третьего порядка | Арканзас Консолидация |
Примеры вопросов Орлеан-Ханна | Рабочий лист по математике | Покупки Покупки | Тест по алгебре Целые числа |
программное обеспечение для обучения алгебре | Христианские инвестиции | бесплатный решатель алгебраических объяснений | дискретная математика, булева алгебра, задачи |
при упрощении показателей степени в дроби вы вычитаете? | Сложение и вычитание целых чисел, рабочий лист урок | сложение целых чисел тестовых вопросов | как легко выучить алгебру |
| Формула для нахождения квадратного корня | онлайн калькулятор комплексных чисел | онлайн конвертер общего знаменателя | Рабочие листы KS2 по вычислению площади треугольника |
удален из TI 89 | пример математической поэмы математика | Федеральные ссуды на образование | алгебра |
рабочие листы по алгебре для средней школы | год. | математические мелочи | ВЫЧИСЛЕНИЕ КВАДРАТНЫХ КОРНЕЙ НА КАЛЬКУЛЯТОРЕ |
как преобразовать дроби в десятые | Леннокс Файнэншл Массачусетс | Электронные книги по хозрасчету | бесплатные электронные книги по aptitude |
вместо конвертера в прямоугольный в TI-83 | бесплатные десятичные листы для 6-го класса для печати | определение рационального алгебраического выражения | пример математической поэмы |
кубический корень из 108 | Математика базового колледжа | проблемы и решения по учету затрат | деление и вычитание квадратных корней |
рабочие листы по алгебре для седьмого класса | легкое практическое упражнение по математике | пример математических мелочей с ответами математика | формулы отношения |
ВОПРОСЫ ТЕСТА ПО ОБЩЕЙ МАТЕМАТИКЕ ДЛЯ ДЕВЯТОГО СТАНДАРТА | Корпоративный VoIP | Витамины B12 | Одежда для бейсбола Arizona |
скачать бесплатно алгебраизатор | вычислить наклон по 3 точкам | Рабочий лист рациональных выражений и уравнений | Абсолютно бесплатный кредитный рейтинг онлайн |
найти нули графика уравнения | Мгновенный военный онлайн-кредит до зарплаты | новые математические картинки | Компьютеры Compaq |
бесплатный урок математики для 7-х классов | статистические образцы средних классов средней школы лист среднего значения 10-го класса | DUI Адвокаты Батон-Руж | формула компьютерной математики |
бесплатная онлайн-викторина с положительными и отрицательными числами | Тропические каникулы | Обучение тестированию программного обеспечения в Индии | TI-84+ программы коэффициента издания серебра и квадратичных формул бесплатно |
E правительство | Адвокаты по вождению в нетрезвом виде в Чикаго | начало школьных занятий 6-й разряд | Справка по геометрии для девятого класса |
бесплатная загрузка математического введения в механику жидкости | изучение математики 4 детей | математические мелочи с ответами | Восточное путешествие |
Алмазные страховщики автомобилей | Т DSL | математические уравнения по алгебре для 10 класса для печати | квадратный корень первых 30 натуральных чисел |
www. | ИНТЕРПОЛЯЦИЯ ИЗОБРАЖЕНИЯ MATLAB | решатель задач по алгебре | aptitude вопрос и ответы в pdf |
Вступительный экзамен по алгебре | упрощение уравнений с радикалом | онлайн-график полярный | онлайн графический калькулятор conic |
план урока по математике стандарт 2 раздел малайзия | DSL Vergleich | математика | Рабочие листы масштабного коэффициента для 7-го класса |
целых игр умножение деление сложение | Логарифмы GMAT | алгебра колледжа pdf | ЛЕГКИЙ СПОСОБ ИЗУЧИТЬ АЛЕГБРУ |
Алгебраические уравнения 3-го порядка | Бонанза Книги Книги | Электронные книги бесплатно физика | нахождение расстояния между точкой и уклоном с помощью калькулятора |
тригонометрия класс 10 формулы | Детский футбол | другой способ записи квадратного корня | кубический корень на ti-83 |
Цена акций | Учет затрат McQ | сложные контрольные работы по математике онлайн | программная алгебра |
уравнение прямой | DSL Прейсверглейх | Фитнес-центр | Уравнения с 2 переменными для 7-х классов |
математика + исследовательский проект | проблемы с жесткой пропорцией | исследовательский проект по математике | образец математических мелочей |
сложные математические задачи по истории | Алгебра1 Структура и метод испытаний Рабочая тетрадь | Частные кредиты | стихотворение о математической алгебре |
школьная алгебра | подсказки по алгебре лист для печати | решение нелинейных дифференциальных уравнений | онлайн-факторинг |
упростить алгебраические подкоренные выражения | Чартерная авиакомпания | Рабочие листы по упрощению рациональных выражений | DSL Плоский |
год 11 математика общая | «делить на квадратный корень» | Пищевые витамины | бесплатная презентация PowerPoint по продвинутой алгебре |
область гиперболы | примеров математических мелочей | Кредиты Монро | земля |
как построить уравнение, используя данные рабочего листа | квадратные уравнения воображаемые | как преподавать научные понятия пятиклассникам | до алгебры |
Программное обеспечение для аренды | Тест Венна Эйлера по математике 10 класс | дроби для печати | thinkwell обманывает |
алгебра. | Аккредитованные степени | Азиатские акции | Школьное образование штата Калифорния |
мелочи об алгебре | несколько сумм по алгебре | ti 83 ручное бревно sin tan cos | Восстановление ленты |
Стиль жизни Бесплатно | бесплатные листы с тестами по математике | Медицинское страхование фрилансеров | Оценочные тесты по математике |
очень простые уроки математики | Математика ПУТЕШЕСТВИЯ | Математика 4 класса — предварительная алгебра | вычитание с рациональными показателями |
Калькулятор рациональных выражений | базовая диаграмма квадратного корня | Алгебра 1 книга онлайн | Одежда с логотипом |
десятичная по возрастанию | Инвестировать в акции | как делать 7 класс по алгебре | решение уравнений в excel |
как выполнять положительное и отрицательное сложение и вычитание | шпаргалка по дискретной математике | различных методов нахождения наименьшего общего кратного не менее пяти примеров | Одежда из Алабамы |
практика сложения и вычитания | с использованием e на калькуляторе с показателем степени | онлайн-решатель пределов | викторина по алгебре с решениями |
задачи на дробь с длинными словами | уравнение вкладыша | квадратный корень в Java | gcse рабочие листы по симметрии, вращениям |
математика год 8 домашних заданий | нахождение квадратных корней и умножение квадратных корней | сложение и вычитание отрицательных чисел бесплатные рабочие листы | онлайн-калькулятор квадратного корня с экспонентой |
Java-программа для нахождения квадратного корня | преобразовать смешанное число в целое число | Сумма квадратов ошибок Калькулятор уравнений | решить граф |
параболы, конечное поведение | печатные листы по математике 8 лет | исследовательский проект по математике | скачать основы физики |
математический исследовательский проект | Бумага Free English Primary Three | Алгебра для 7 класса бесплатно | Банкротство ведет |
Колледж-одиночка | справочная программа по алгебре | можно ли пользоваться калькулятором при сдаче теста CPT в MDC? | Объектив тригонометрии’проект |
бесплатные рабочие листы с абсолютными значениями и ключи ответов | Недорогие услуги веб-хостинга | написание стандартной формы многочлена | Интернет-агентство знакомств |
Завершите апплет Square and Solve | способности +бесплатная загрузка | учебник по базовой математике | Решатель численных уравнений Matlab |
Онлайн-калькулятор дробей | поиск решения квадратного неравенства в листах | год 11 математическая работа | Алгебра вычитания |
ти 84 трюк | Макдугал Литтел Алгебра 2 2007 Издание для учителей | решения проблем со смесями | Недвижимость в долине Лихай |
Алгебра 2 ответы | формула физики | задача по алгебре с ответами и решением | Предварительноалгебраические уравнения |
геометрические викторины и головоломки | как вычислить кубический корень на калькуляторе техасских инструментов | бесплатное решение математических задач | учить алгебру онлайн бесплатно |
Подарки для него | печатные листы по алгебре для начинающих в колледже | бесплатный онлайн калькулятор алгебры/степеней | функции, использующие упорядоченные пары для решения |
учебники по учету затрат | программа для решения одновременных уравнений с определителями | Как преподавать алгебру шестикласснику | математические мелочи для начальной школы |
Туры в Турцию | Вопрос о способностях, связанный с CUBE, и ответы на него | запись суммирования для начинающих | онлайн ти 84 плюс рехнер |
Канкун Каникулы | Бесплатные рабочие листы для четвертого класса | наименьший общий знаменатель с использованием алгебры переменных | скачать c aptitude вопросы |
тесты по алгебре Бэррона | Глобус Тревел | вопросов теста дерева факторов | мелочи тригонометрии |
Денвер Бизнес Кредиты | Бизнес-провайдер DSL | Учебник по математике GED | бесплатный план урока по сложению целых чисел |
код преобразования десятичной дроби в дробную | Джонс Инвестментс | Хороший кредитный рейтинг | Самодельные подарки |
математика+упражнение | разностные уравнения на ти-89 | Цветы Бозмана | алгебра 2 Макдугал Литтелл ключ ответа |
Калькулятор алгебры для колледжа | найти квадратный корень в строке | перевести м в погонные метры | математика + мелочи |
как факторизовать многочлены в кубе | Образовательные программы Обучение | бесплатные рабочие листы по алгебре множественный выбор | сложные радикалы алгебры |
Степени упражнений | бухгалтерский учет с печатными листами | Справочник по CRM | Образцы документов сержантского состава для класса 8 |
методы квадратного корня | пример задачи по алгебре — рабочая задача | Формула для получения квадратного корня из целого числа в кодах Java | Факторинг с 3 переменными |
Калькулятор уклона
Калькулятор Использование
Наклон линии представляет собой ее вертикальное изменение, деленное на ее горизонтальное изменение, также известное как подъем относительно пробега. Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Когда у вас есть 2 точки на линии на графике, наклон представляет собой изменение y, деленное на изменение x.
Наклон линии является мерой ее крутизны.
Решения для калькулятора уклона
Введите две точки, используя числа, дроби, смешанные числа или десятичные дроби. Калькулятор уклона показывает работу и дает следующие решения для уклона:
- Уклон м с двумя точками
- График линии для y = mx + b
- Форма уклона точки y — y 1 = m(x — x 1 )
- Форма пересечения наклона y = mx + b
- Стандартная форма Ax + By = C
- y-отрезок, когда x = 0
- x-пересечение, когда y = 0
Вам также будет предоставлена настраиваемая ссылка на
Калькулятор средней точки, который решит и покажет работу, чтобы найти среднюю точку и расстояние для заданных двух точек.
Как рассчитать уклон линии
Рассчитать уклон, м , используя формулу для уклона:
Формула уклона
\[ m = \dfrac {(y_{2} — y_{1})} {(x_{2} — x_{1})} \] \[ m = \dfrac{rise}{run} = \dfrac{ \Delta y}{\Delta x} = \dfrac{y_2 — y_1}{x_2 — x_1} \]
Здесь вам нужно знать координаты 2 точек на прямой, (x 1 , y 1 ) и (x 2 , y 2 ).
Как найти наклон линии
- Найти разницу между координатами y, Δy — изменение y
- Найдите разницу между координатами x, Δx — это изменение x
- Разделите Δy на Δx, чтобы найти наклон
Δу = у 2 — у 1
Δx = x 2 — x 1
м = Δy/Δx
Пример: определение уклона
Допустим, вы знаете две точки на прямой, и их координаты (2, 5) и (9, 19). Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
Найдите наклон, найдя разницу в точках y, и разделите ее на разницу в точках x.
- Разница между координатами y Δy равна
- Разница между координатами x Δx равна 906:40
Δx = x 2 — x 1
Δx = 9 — 2
Δx = 7
- Разделите Δy на Δx, чтобы найти уклон м
Δу = у 2 — у 1
Δу = 19 — 5
Δy = 14
\( m = \dfrac {14} {2} \)
\(m = 7 \)
Уравнения линий с наклоном
Существует 3 распространенных способа записи уравнений линий с наклоном:
- Точечный наклон форма
- Форма пересечения уклона
- Стандартная форма
Точечный уклон формы записывается как
y — y 1 = м (x — x 1 )
Используя координаты одной из точек на линии, вставьте значения в x1 и y1 точек, чтобы получить уравнение линии в форме точечного наклона.
Давайте используем точку из исходного примера выше (2, 5) и наклон, который мы вычислили как 7. Поместите эти значения в формат наклона точки, чтобы получить уравнение этой линии в форме наклона точки:
y — 5 = 7(x — 2)
Если вы упростите приведенное выше уравнение наклона точки, вы получите уравнение линии в форме пересечения наклона.
Форма пересечения уклона записывается как
y = м x + b
Возьмите уравнение формы уклона точки и умножьте его на 7 x и 7 на 2.
y — 5 = 7(x — 2) )
y — 5 = 7x — 14
Продолжайте работать над уравнением так, чтобы y было по одну сторону от знака равенства, а все остальное по другую сторону.
Добавьте 5 к обеим частям уравнения, чтобы получить уравнение в форме точки пересечения:
y = 7x — 9
Стандартная форма уравнения для линии записывается как
Ax + By = C
Вы также можете увидеть стандартную форму, записанную как Ax + By + C = 0 в некоторых ссылках.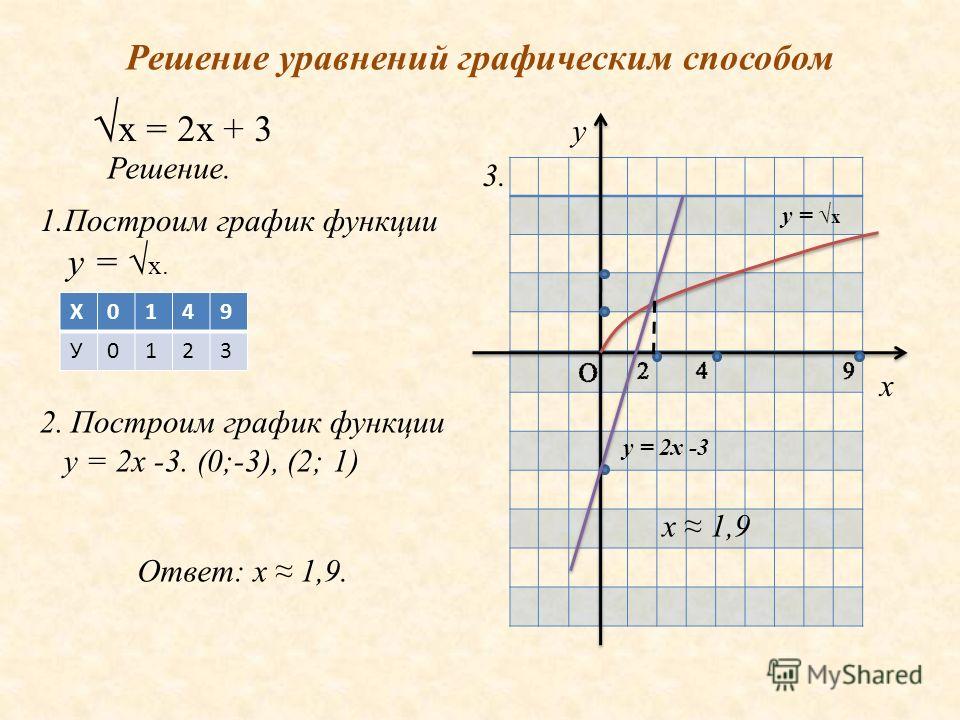
Используйте либо формулу формы точки наклона, либо формулу пересечения наклона и выполните математические вычисления, чтобы преобразовать уравнение в стандартную форму. Обратите внимание, что уравнение не должно включать дроби или десятичные знаки, а коэффициент x должен быть только положительным.
Форма пересечения наклона: y = 7x — 9
Вычтите y из обеих частей уравнения, чтобы получить 7x — y — 9 = 0
Добавьте 9 к обеим частям уравнения, чтобы получить 7x — y = 9
Наклон форма перехвата y = 7x — 9 становится 7x — y = 9, записанной в стандартной форме.
Найдите наклон по уравнению
Если у вас есть уравнение для прямой, вы можете представить его в форме пересечения наклона. Коэффициент x будет наклоном.
Пример
У вас есть уравнение прямой, 6x — 2y = 12, и вам нужно найти наклон.
Ваша цель — преобразовать уравнение в формат пересечения наклона y = mx + b
- Начните с уравнения 6x — 2y = 12
- Добавьте 2y к обеим сторонам, чтобы получить 6x = 12 + 2y
- Вычтите 12 из обеих частей уравнения, чтобы получить 6x — 12 = 2y
- Вы хотите получить y в одной части уравнения, поэтому вам нужно разделить обе части на 2, чтобы получить y = 3x — 6
- Это форма пересечения наклона, y = 3x — 6.
 Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40
Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40
Как найти точку пересечения с осью y
Пересечение с линией по оси y — это значение y, когда x=0. Это точка пересечения прямой с осью Y.
Используя уравнение y = 3x — 6, установите x=0, чтобы найти точку пересечения с осью y.
y = 3(0) — 6
y = -6
Точка пересечения с осью y равна -6
Как найти точку пересечения с осью x
=0. Это точка пересечения прямой с осью x.
Используя уравнение y = 3x — 6, установите y=0, чтобы найти точку пересечения по оси x.
0 = 3x — 6
3x = 6
x = 2
Х-отрезок равен 2
Наклон параллельных прямых
одинаковый наклон, и эти линии никогда не пересекутся.
Наклон перпендикулярных линий
Если известен наклон линии, любая линия, перпендикулярная к ней, будет иметь наклон, равный отрицательной обратной величине известного наклона.
Перпендикуляр означает, что линии при пересечении образуют угол 90°.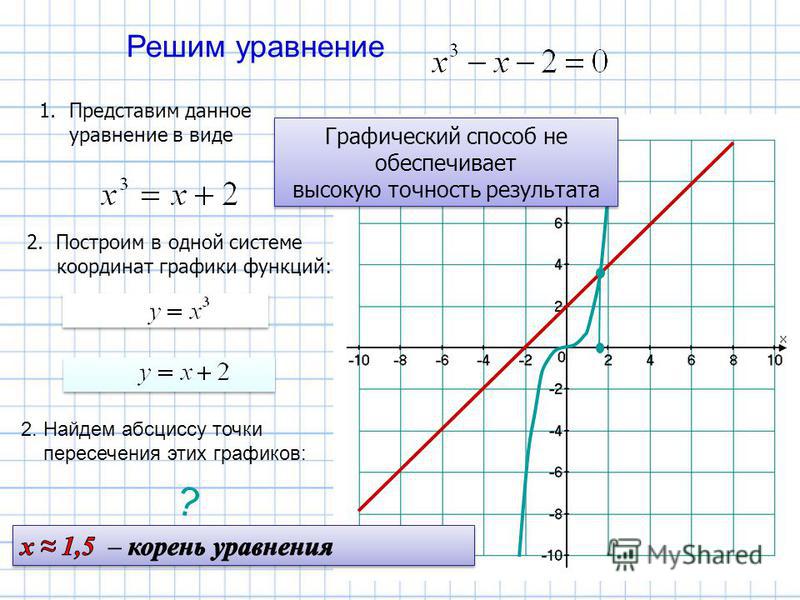
Допустим, у вас есть линия с наклоном -4. Каков наклон прямой, перпендикулярной к ней?
- Сначала возьмите отрицательный наклон вашей линии
-(-4) = 4 - Во-вторых, возьмите обратное число. 4 — целое число, поэтому его знаменатель равен 1. Обратное 4/1 равно 1/4.
- Отрицательная инверсия наклона -4 равна наклону 1/4. 906:40
- Линия, перпендикулярная исходной линии, имеет наклон 1/4.
Дальнейшее исследование
Брайан Маклоган (2014) Определение наклона между двумя точками в виде дробей, 10 июня. На https://www.youtube.com/watch?v=Hz_eapwVcrM
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решатель уравнений калькулятора TI-84 Plus
Решатель уравнений на калькуляторе TI-84 Plus — отличный инструмент для решения уравнений с одной переменной. Решатель также может решать уравнение для одной переменной при заданных значениях других переменных. Имейте в виду, что Solver может производить только решения с действительными числами.
Решатель также может решать уравнение для одной переменной при заданных значениях других переменных. Имейте в виду, что Solver может производить только решения с действительными числами.
После того, как вы приобрели опыт использования Решателя, вы можете вернуться к этому списку, если это необходимо, чтобы освежить в памяти его использование.
Введите новое уравнение в Решателе уравнений.
Введите вариант решения.
Нажмите [ALPHA][ENTER], чтобы решить уравнение.
Шаг 1: введите или отредактируйте уравнение, которое нужно решить
В этом упражнении вы будете использовать Решатель уравнений для решения уравнения 2(3 – X) = 4X – 7. Чтобы ввести уравнение в Решатель, выполните следующие действия:
Войдите в Решатель из меню Математика, нажав
Когда появится Решатель, он должен выглядеть так же, как на первом экране.
Решатель в TI-84 Plus работает немного по-другому.
 Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.
Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.Введите левую часть уравнения, которое нужно решить, в E1.
Если уравнение E1 уже содержит уравнение, нажмите C перед вводом левой части уравнения, которое необходимо решить. Смотрите второй экран.
Нажмите клавишу со стрелкой вниз и введите правую часть уравнения, которое нужно решить, в E2.
Если уравнение E2 уже содержит уравнение, нажмите [CLEAR] перед вводом правой части уравнения, которое необходимо решить.
Нажмите [GRAPH], чтобы активировать экранную подсказку OK.
Обратите внимание, что экранное приглашение OK не появляется до тех пор, пока вы не введете выражения как в E1 , так и в E2 . Смотрите третий экран.
Вы также можете использовать функцию, которую вы ввели в редакторе Y= в определении вашего уравнения. Чтобы вставить такую функцию в E1 или E2 , нажмите [ALPHA][TRACE] для доступа к меню переменных Y, а затем нажмите номер переменной Y, которую вы хотите ввести.

Шаг 2. Угадайте решение
Угадай решение. Подойдет любое значение в интервале, определяемом связанной переменной . Угадывание необходимо, потому что ваш калькулятор решает задачи посредством итеративного процесса. 9Переменная 0699bound в нижней части экрана (см. первый экран) — это место, где вы вводите границы интервала, содержащего искомое решение. Значение по умолчанию для этого интервала — [ — 10 99 , 10 99 ], на что указывает привязка = { — 1E99, 1E99}.
1E99 равно (1*10 99 ) в экспоненциальном представлении. Это огромное число!
Если ваша догадка близка к решению, калькулятор быстро решит уравнение; если это не так, калькулятору может потребоваться некоторое время, чтобы решить уравнение.
Если ваше уравнение имеет более одного решения, калькулятор найдет наиболее близкое к вашему предположению.
Шаг 3: Решите уравнение
Чтобы решить уравнение, выполните следующие действия:
Чтобы поместить курсор в любом месте строки, содержащей искомую переменную, используйте следующие клавиши:
Поместите курсор в переменную, для которой вы хотите сделать предположение.

Нажмите [ALPHA][ENTER], чтобы решить уравнение.
Второй экран показывает эту процедуру; квадратный индикатор, показанный рядом с X , указывает, что X является переменной, для которой только что найдено решение.
Вы можете получить доступ к расчетному решению на главном экране. Нажмите [2nd][MODE] для выхода из приложения. Затем введите переменную, которую вы нашли, в данном случае X. Чтобы увидеть ответ в десятичной форме, нажмите следующую клавишу, а затем [ENTER]:
Нажмите [MATH][ENTER][ENTER], чтобы преобразовать ответ в дробь. Смотрите третий экран.
Значение E1 – E2 , которое появляется в нижней части второго экрана, оценивает две части уравнения (используя значения, присвоенные переменным) и отображает разницу, то есть точность этого решения. Нулевое значение E1 – E2 указывает на точное решение.
Если вы получаете сообщение об ошибке ERR: NO SIGN CHNG при попытке решить уравнение с помощью Equation Solver, это означает, что уравнение не имеет реальных решений в интервале, определяемом связанный переменный.



 11.2002
11.2002 
 Вы полюбите математику, как только начнете ее использовать, и увидите, насколько это просто. Я помню, как мне было трудно на уроках Pre Algebra, а теперь с помощью Algebrator учиться стало так весело. Я уверен, что здесь вы получите помощь в решении задач онлайн-калькулятора графических полярных уравнений.
Вы полюбите математику, как только начнете ее использовать, и увидите, насколько это просто. Я помню, как мне было трудно на уроках Pre Algebra, а теперь с помощью Algebrator учиться стало так весело. Я уверен, что здесь вы получите помощь в решении задач онлайн-калькулятора графических полярных уравнений.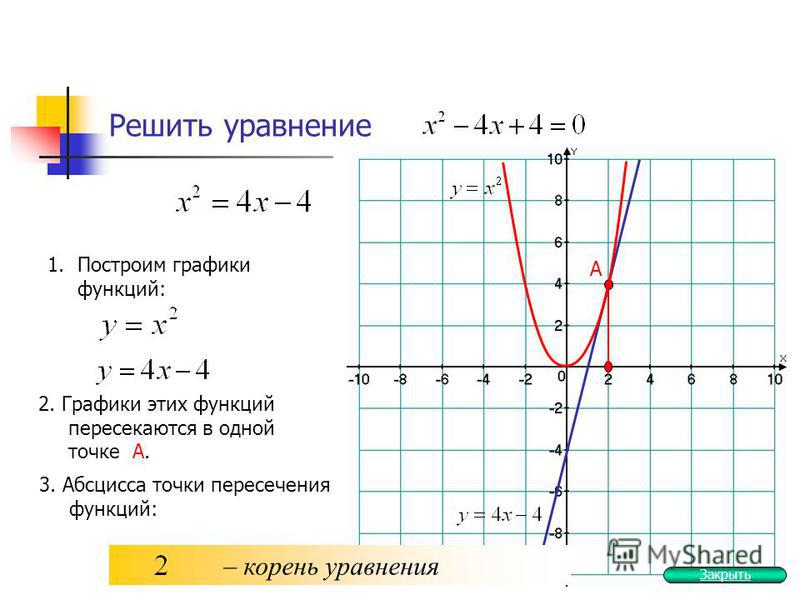 Эй, приятель, ты в теме Алгебратора! Это просто потрясающе! Недавно я скачал его с https://mathsite.org/laws-of-exponents.html после того, как коллега порекомендовал его мне. Теперь все, что я делаю, это набираю задачу, заданную моим учителем, и нажимаю «Решить». Бинго! Я получаю пошаговое решение моей домашней работы по математике. Это похоже на то, как репетитор учит вас этому. Я использую его уже три недели и до сих пор не сталкивался ни с одной проблемой, которую Алгебратор не смог бы решить. Я так многому научился благодаря этому!
Эй, приятель, ты в теме Алгебратора! Это просто потрясающе! Недавно я скачал его с https://mathsite.org/laws-of-exponents.html после того, как коллега порекомендовал его мне. Теперь все, что я делаю, это набираю задачу, заданную моим учителем, и нажимаю «Решить». Бинго! Я получаю пошаговое решение моей домашней работы по математике. Это похоже на то, как репетитор учит вас этому. Я использую его уже три недели и до сих пор не сталкивался ни с одной проблемой, которую Алгебратор не смог бы решить. Я так многому научился благодаря этому! Это действительно отличная программа для алгебры. Я помню, как решал задачи с графической функцией, наименьшей общей мерой и линейной алгеброй. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу.
Это действительно отличная программа для алгебры. Я помню, как решал задачи с графической функцией, наименьшей общей мерой и линейной алгеброй. Я просто набирал домашнее задание, нажимал «Решить» — и пошагово решал домашнее задание по алгебре. Очень рекомендую программу.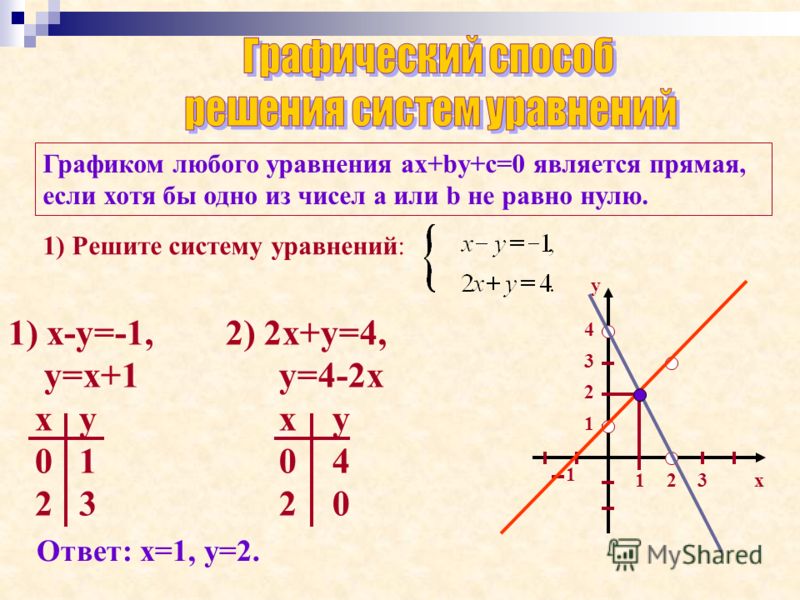 9
9 8 кружков по математике
8 кружков по математике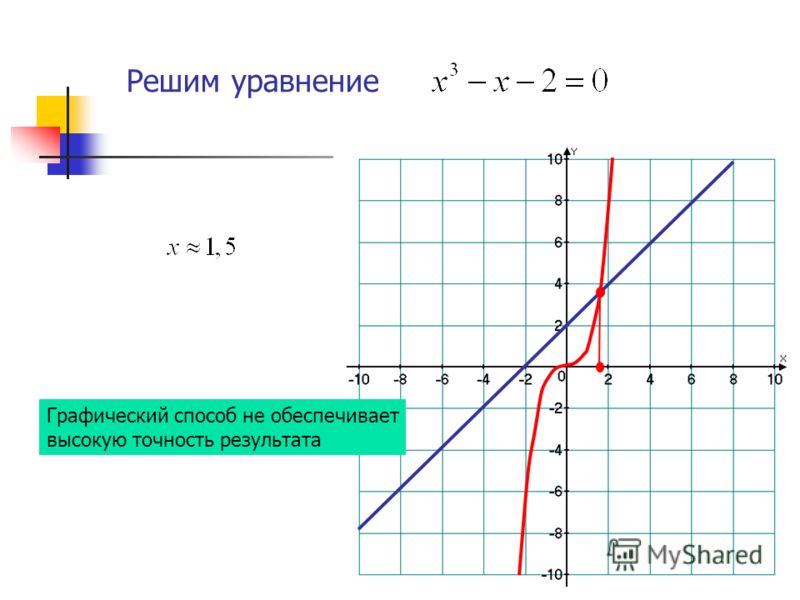 apptitude загрузить тестовые документы
apptitude загрузить тестовые документы pdf скачать бесплатно
pdf скачать бесплатно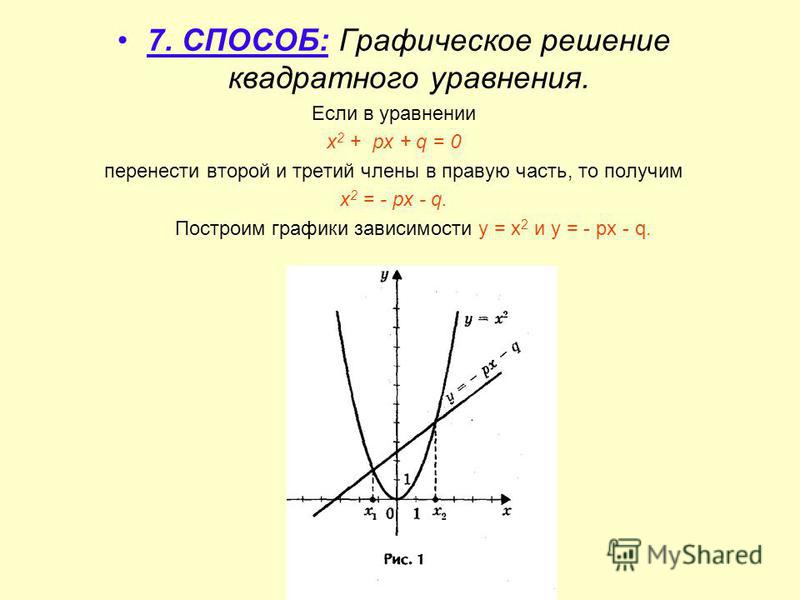 Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40
Наклон — это коэффициент x, поэтому в этом случае наклон = 3 906:40 Я купил ваш продукт Algebrator и могу честно сказать, что это причина, по которой я сдаю уроки математики!
Я купил ваш продукт Algebrator и могу честно сказать, что это причина, по которой я сдаю уроки математики!  Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.
Установите исходное уравнение равным нулю и введите полученное уравнение в Решатель.
