Решение уравнений всех видов: Виды уравнений и способы их решения

Виды уравнений в таблице (математика, 5 класс)

4.5

Средняя оценка: 4.5

Всего получено оценок: 848.

Обновлено 11 Января, 2021

4.5

Средняя оценка: 4.5

Всего получено оценок: 848.

Обновлено 11 Января, 2021

Перед решением любого уравнения, необходимо задаться вопросом, а что за уравнение перед нами на данный момент? Ведь видов уравнений достаточно много и каждый из них характеризуется своим подходом для решения, ОДЗ и многими другими факторами, без которых решить уравнение просто невозможно.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Линейное уравнение

Линейное уравнение это классическое уравнение вида:

$$ах+в=0$$

Решается простым перенесением слагаемых из одной части уравнения в другую с противоположным знаком и делением всего выражения на коэффициент при х. Встречаются интересные варианты, где нужно привести подобные слагаемые тем или иным образом, но в общем и целом решаются такие уравнения достаточно легко.

2+bx+c=0$$

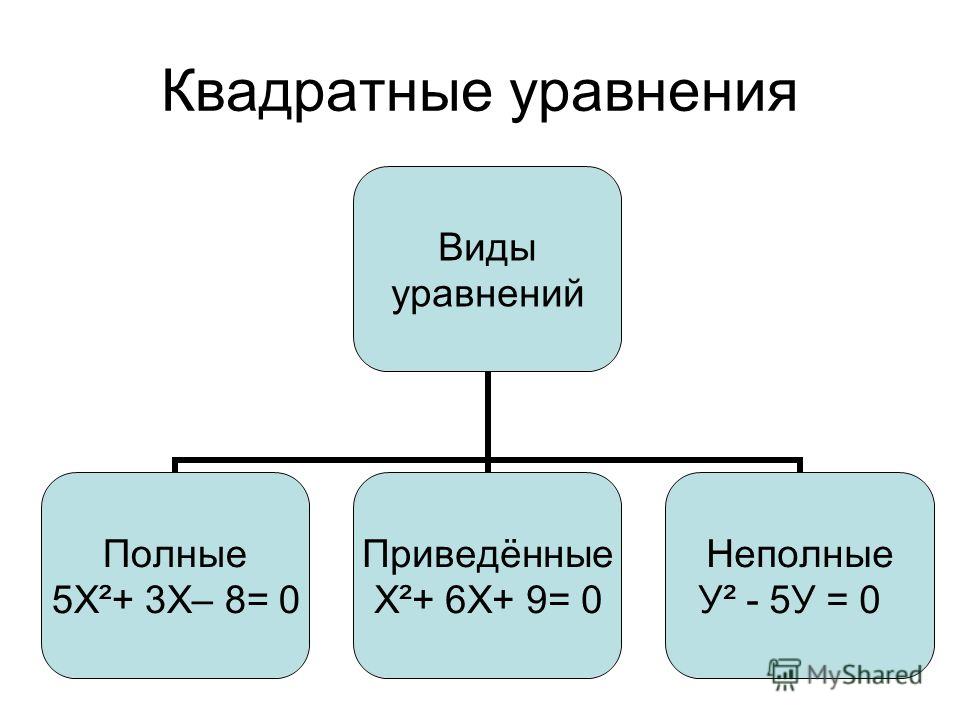
Решается такое уравнение с помощью дискриминанта или теоремы Виета.

Существуют неполные квадратные уравнения, у которых один из коэффициентов b или с равен 0. Неполные уравнения решаются с помощью вынесения общего множителя за скобку или разложением на множители с помощью формулы разности квадратов.

Степенные уравнения со степенью от 3 и выше проще решить графическим способом или разложением на множители.

Дело в том, что любое уравнение можно решить как графически, то есть построить график функции, так и алгебраически,то есть с помощью преобразований.

Графический способ предполагает построение графика функции, а после нахождение значения х, которому соответствует значение y, равное 0 (т.е. точку пересечения с осью Ох). Это значение и будет корнем уравнения, которое записывается в ответ.

Дробные уравнения

Дробные уравнения, это уравнения, содержащие дробь, в знаменателе которых есть переменная. В таких уравнениях знаменатели дробей не могут принимать значений, равных нулю.

Это отражается в ОДЗ и учитывается при выборе действительных корней.

При решении любого уравнения могут появиться посторонние корни. Для того, чтобы их отсеять приходится вводить ОДЗ, т.е. интервал, значения которого может принимать х. Если корень не входит в этот интервал, то выражение теряет смысл, а значит такие корни не могут являться ответом примера.

Иррациональные уравнения

Иррациональные уравнения это уравнения, содержащие знак радикала. Для радикалов четных степеней особенно важно правильно записать ОДЗ. Подкоренное значение таких радикалов не может являться отрицательным числом, и значение радикала не может равняться отрицательному выражению.

Тригонометрические уравнения

Тригонометрические уравнения, это уравнения, в которых неизвестное является аргументом тригонометрической функции.

Неизвестное может находиться не в аргументе тригонометрической функции, а складываться, например, с косинусом 30 градусов. В этом случае уравнение нельзя назвать тригонометрическим, поскольку косинус 30 градусов это определенное число.

Другие виды уравнений

Существуют так же дифференциальные уравнения, содержащие производные различного рода, предельные, показательные и логарифмические уравнения. Все эти уравнения изучаются в началах высшей математики. Для того, чтобы приступить к этим видам уравнений придется пройти долгий путь и научится решать уже перечисленные виды. Специально для быстрого изучения этой темы в учебниках приводят таблицы видов уравнений.

Что мы узнали?

Мы узнали, какие виды уравнений существуют в математике. Наметили пути решения, а также возможное наличие посторонних корней. Поговорили о том, что такое ОДЗ и для чего оно необходимо. Выделили уравнения высшей школы математики.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Валерия Ильичёва

  5/5

• Артём Сладков

  4/5

• Александр Котков

  5/5

• Галина Коноплёва

  5/5

• Роман Малеваный

  4/5

• Kostya Malxasyan

  5/5

• Андрей Маслин

  5/5

• Андрей Волков

  4/5

• Андрей Ефимов

  5/5

• Константин Никитич

  5/5

Оценка статьи

4. 5

Средняя оценка: 4.5

Всего получено оценок: 848.

---

А какая ваша оценка?

Виды уравнений, формулы и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Определение и основные виды уравнений

Например.

Некоторые классы уравнений решаются аналитически (среди алгебраических это линейные, квадратные, кубические уравнения и уравнения четвертой степени), то есть решение записывается в виде формулы. Алгебраические уравнения высших степеней (более, чем четвертая) в общем случае аналитического решения не имеют, хотя некоторые сводятся к уравнениям низших степеней.

В общем случае, если аналитическое решение не существует, применяют численные методы.

Алгебраические уравнения

Алгебраическим уравнением называется уравнение вида

   

где — многочлен переменных , которые называются переменными или неизвестными.

Например.

Степенью алгебраического уравнения называется степень многочлена .

Линейным уравнением от неизвестных называется уравнение вида

   

Например. — линейное уравнение с одной переменной.

Квадратным уравнением (уравнением второй степени) называется уравнение

   

Здесь — переменная, — старший или первый коэффициент, — второй коэффициент, — свободный коэффициент.

Например.

Квадратное уравнение называется приведенным, если старший коэффициент равен единице.

Например.

Уравнением с параметрами называется математическое равенство, внешний вид и решение которого зависит от значений одного или нескольких параметров.

Например.

Уравнение, содержащее трансцендентные функции, называется трансцендентным.

Например.

Трансцендентная функция — это аналитическая функция, не являющаяся алгебраической. Алгебраической называется элементарная функция, которая в окрестности каждой точки области определения может быть неявно задана с помощью алгебраического уравнения.

Функциональным называется уравнение, которое определяет связь между значением функции (или функций) в одной точке с её значениями в других точках.

Например.

Уравнение, в котором неизвестная функция стоит под знаком производной, называется

дифференциальным.

Например.

Интегральным уравнением называется уравнение, в котором неизвестная функция находится под знаком интеграл.

Например.

Понравился сайт? Расскажи друзьям!

Решение линейных уравнений: все типы

Горячая математика

Ан уравнение должен иметь знак равенства, как в 3 Икс + 5 знак равно 11 .

А линейное уравнение это тот, в котором переменная (переменные) умножается на числа или добавляется к числам, ничего более сложного, чем это (без показателей степени, квадратных корней, 1 Икс , или любое другое веселое дело).

А решение к уравнению это число который можно подключить к переменной, чтобы сделать истинное числовое выражение.

Например, заменив 2 за Икс в 3 Икс + 5 знак равно 11 дает

3 ( 2 ) + 5 знак равно 11 , что говорит 6 + 5 знак равно 11 ; это правда! Так 2 является решением.

Но как нам начать с уравнения и получить (не угадать) решение?

Одношаговые линейные уравнения

Некоторые линейные уравнения можно решить с помощью одной операции. Для этого типа уравнения используйте обратный операция решать.

Пример 1:

Решить для н .

н + 8 знак равно 10

Обратной операцией сложения является вычитание. Итак, вычтите 8 с обеих сторон.

н + 8 − 8 знак равно 10 − 8 н знак равно 2

Пример 2:

Решить для у .

3 4 у знак равно 15

Обратной операцией умножения является деление. Итак, делим обе части на 3 4 ( что равносильно умножению на 4 3 ) .

4 3 ⋅ 3 4 у знак равно 4 3 ⋅ 15

у знак равно 20

Двухшаговые линейные уравнения

Чаще всего нам нужны две операции для решения линейной задачи. уравнение.

Пример 3:

Решить для Икс .

3 Икс + 5 знак равно 11

3 Икс + 5 знак равно 11	данный уравнение.
3 Икс + 5 − 5 знак равно 11 − 5	Чтобы изолировать переменную, мы следуем порядку операций в обратном порядке. Мы отменяем сложение до того, как отменяем умножение. Вычесть 5 с обеих сторон.
3 Икс знак равно 6	Мы отменили одну операцию. Еще один, чтобы пойти.
3 Икс 3 знак равно 6 3	Разделите обе части на 3 .
Икс знак равно 2	Мы решили уравнение!

То, что делает эти уравнения линейный является что высшая сила Икс является Икс 1 (нет Икс 2 или другой полномочия; для тех, см. квадратные уравнения а также многочлены ).

Другие линейные уравнения имеют более одной переменной: например, у знак равно 3 Икс + 2 . Это уравнение имеет не одно, а бесконечно много решений; решения могут быть графически как линия на плоскости.

Формы линейных уравнений – объяснение и примеры

Существуют три основные формы линейных уравнений. Это три наиболее распространенных способа записи уравнения линии, чтобы информацию о линии было легко найти.

В частности, существуют три основные формы линейных уравнений: наклон-пересечение, точка-наклон и стандартная форма. Каждая из них подчеркивает различные качества линии, но преобразовать одну из этих форм в другую несложно.

В этой статье мы обсудим эти три формы линейных уравнений. Однако перед чтением обязательно просмотрите статьи о наклоне линии и уравнении линии.

Этот раздел включает следующие подтемы:

• Какие существуют формы линейных уравнений?
• Наклон точки
• Наклон Точка пересечения
• Стандартная форма

Какие существуют формы линейных уравнений?

Напомним, что линейное уравнение — это математическое уравнение, определяющее линию.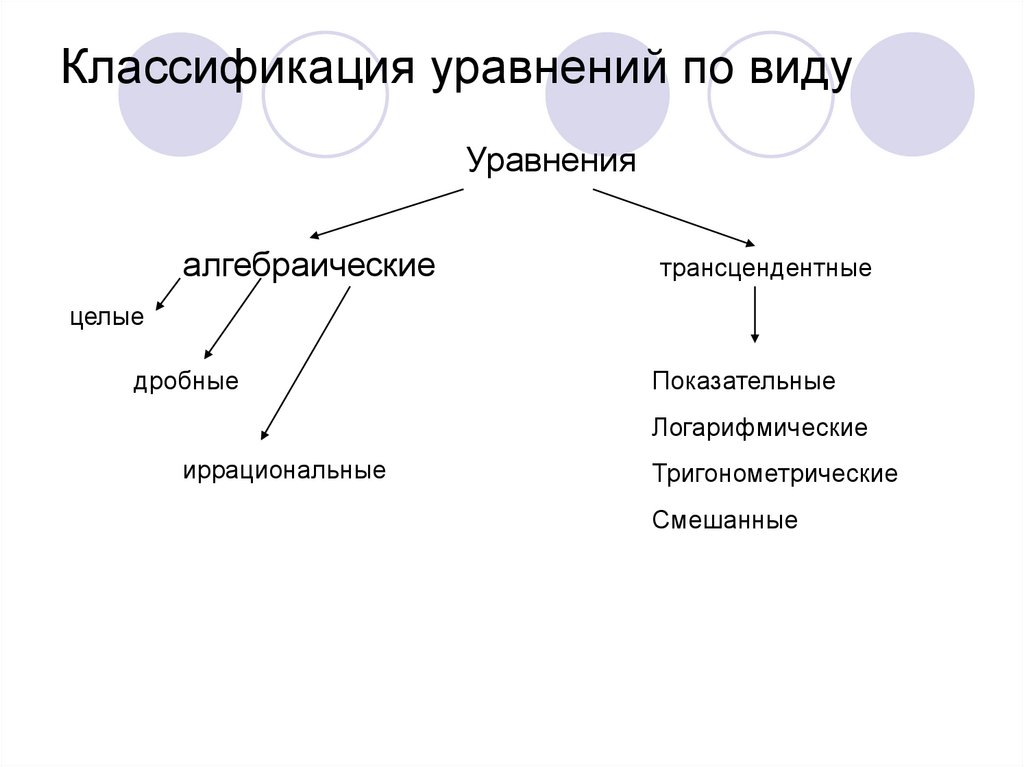 Хотя каждое линейное уравнение соответствует ровно одной строке, каждая строка соответствует бесконечному количеству уравнений. Эти уравнения будут иметь переменную, наибольшая степень которой равна 1.

Три основные формы уравнения: форма пересечения наклона, форма точка-наклон и стандартная форма. Эти уравнения дают достаточно информации о линии, чтобы мы могли легко их изобразить.

Что нам нужно для определения линии?

Нам нужны две точки, чтобы однозначно определить линию. Однако если у нас есть наклон и точка, мы можем легко использовать наклон, чтобы найти вторую точку и построить линию.

Форма точки-наклона (или наклона точки) и форма пересечения наклона (или пересечения наклона) говорят нам об одной точке и наклоне линии. Стандартная форма дает нам две определенные точки, а именно точки пересечения x и y, хотя по предоставленной информации нетрудно найти наклон.

Наклон точки

Как следует из названия, форма точка-наклон дает одну точку на линии и ее наклон. Эта форма обычно не используется для построения графика. Однако чаще он используется для перехода от словесного описания или графического изображения линии к линии с пересечением наклона или к стандартной форме.

Если заданная точка (x _{1 ​​} , y _{1 ​​} ), a наклон равен m, уравнение прямой в форме точки-наклона:

y-y _{1 ​​} = m(x-x _{1 ​​} ).

Поскольку на каждой линии бесконечно много точек, существует бесконечно много способов записать форму точка-наклон.

Обратите внимание, что эту форму также можно использовать, если заданы две точки, и ни одна из них не является точкой пересечения с осью y. (Напомним, что точка пересечения по оси y имеет вид (0, y _{1 ​​} ).) Это потому, что мы можем использовать две точки для нахождения наклона. Однако, если у нас есть точка пересечения по оси y, мы можем пропустить форму точки-наклона и вместо этого использовать форму точки-наклона.

Пересечение наклона

Форма пересечения наклона передает наклон и пересечение оси Y линии. На самом деле технически это частный случай формы точка-наклон.

Если линия имеет наклон m и точку пересечения с осью y (0, b), форма точки пересечения с наклоном будет следующей:

y=mx+b.

Если бы эта точка была записана в форме точка-наклон, мы бы имели:

y-b=m(x-0).

Упрощение выходов:

y=mx-0+b

y=mx+b.

Если дан график линии, нам все равно придется вычислять наклон. Если линия пересекает ось Y в четкой точке, лучше всего использовать ее в качестве одной из точек, используемых для расчета наклона. Затем мы можем просто подставить значения прямо в уравнение пересечения наклона. Однако, если точка пересечения с осью Y неясна, то форма точки пересечения может быть получена из уравнения точка-наклон.

Стандартная форма

Стандартная форма уравнения:

Ax+By=C

Где A, B и C — целые числа, а A неотрицательно.

Эта форма полезна двумя способами. А именно, это помогает нам решить систему уравнений и помогает нам найти точки пересечения уравнения.

Решение уравнений

Во-первых, стандартная форма позволяет нам легко решать системы уравнений. Поскольку он имеет только целые числовые коэффициенты, можно просто выстроить переменные, а затем сложить и вычесть уравнения.

Существуют определенные стратегии, которые мы можем использовать, чтобы найти, где эти уравнения пересекаются. В частности, мы можем перемножить уравнения так, чтобы, например, коэффициенты x были одинаковыми. Затем, если мы вычтем уравнения, у нас останется уравнение с одной переменной с y. Решение для y дает значение y для точки, где пересекаются два уравнения.

Поскольку не имеет значения, найдем ли мы сначала значение x или y точки пересечения, обычно люди решают, для какой из переменных проще выполнять вычисления.

Поиск пересечений

Стандартная форма также позволяет легко находить пересечения линии по осям x и y. Помните, что точка пересечения y — это значение y, когда x = 0, а точка пересечения x — это значение x, когда y = 0. По сути, это точки, в которых линия пересекает две оси.

Чтобы найти точку пересечения с осью y, установите x=0. Тогда имеем:

A(0)+By=C

By=C

y=C/B.

Аналогично, чтобы найти точку пересечения по оси x, установите y=0. Тогда имеем:

Ax+B(0)=C

Ax=C

x=C/A.

Примеры

В этом разделе будут рассмотрены распространенные примеры, включающие формы линейных уравнений.

Пример 1

Каковы наклон и точка пересечения по оси Y прямой, проходящей через точки (1, 2) и (3, 5)?

Пример 1 Решение

Мы знаем, что можем найти наклон линии, разделив разницу между значениями y двух точек на разницу между значениями x тех же двух точек. В этом случае наклон равен:

м = ^(2-5) ⁄ _(1-3) = ^-3 / _-2 = ³ / _2.

Теперь, так как у нас есть точка a и наклон , мы можем использовать формулу точка-наклон. Любая точка будет работать, но мы можем использовать меньшие значения и пусть (1, 2) будет (x _{1 ​​}, y _{1 ​​}).

Y-2 = ³ / ₂ (x-1)

Y-2 = ³ / ₂ X- ³ / ₂

y = / ₂

y = / ₂

Y = / ₂

^/ / ₂

³ /_. x+ ¹ / ₂

Следовательно, наклон равен ³ / ₂ , а точка пересечения с осью Y равна ¹ / ₂ .

Пример 2

Каковы наклон и точка пересечения линии, показанной ниже?

Пример 2 Решение

Пересечение по оси Y, т. е. точка, в которой линия пересекает ось Y, легко увидеть. Это (0, 1). Нам также нужно найти вторую точку, чтобы мы могли найти наклон. Хотя есть много вариантов, мы можем выбрать (3, 3) для иллюстрации.

Таким образом, наклон равен:

м= ^(1-3) / _(0-3) = ^-2 / _-3 = ² / _3.

6 зная точку пересечения, мы можем просто подставить значения в уравнение наклона и точки пересечения, чтобы получить:

y= ² / ₃ x+1.

Пример 3

Каковы точки пересечения по осям x и y линии 4x+2y=-7?

Пример 3 Решение

Поскольку это уравнение уже имеет стандартную форму, мы можем легко найти точки пересечения. В этом случае A=4, B=2 и C=-7.

Напомним, что точка пересечения с осью y равна:

y= ^C / _B .

Следовательно, точка пересечения с осью y:

y= ^-7 / ₂ .

Аналогично, напомним, что точка пересечения с осью x равна:

x= ^C / _A.

Следовательно, точка пересечения с x равна:

x= ^-7

/ 50 4.

Пример 4

Линия k равна y=7/2x-4 в форме пересечения наклона. Найдите стандартную форму k.

Пример 4 Решение

Преобразование из формы пересечения наклона в стандартную форму требует некоторых алгебраических операций.

Сначала поместите обе переменные x и y на одну сторону:

y= ⁷ / ₂ x-4

^-7 / ₂ x+y=-4

25 Теперь, нам нужно умножить обе части уравнения на одно и то же число, чтобы коэффициенты x и y были целыми числами.

Так как коэффициент при х делится на 2, то надо все умножить на 2:

-7x+2y=-4.

Поскольку A должно быть положительным, мы также должны умножить все уравнение на -1:

7x-2y=4.

Следовательно, A=7, B=-2 и C=4.

Пример 5

Напишите уравнение линии, показанной ниже, во всех трех формах. Затем перечислите наклон и оба пересечения.

Пример 5 Решение

Поскольку у нас есть график, нам нужно будет найти две точки, чтобы найти наклон. К сожалению, точка пересечения с осью Y находится не на линиях сетки, поэтому нам придется выбрать две другие точки. Точки (1, 2) и (-1, -3). Следовательно, наклон равен:

m= ⁽²⁺³⁾ / ₍₁₊₁₎ = ⁵ / ₂ = ⁵ / _2.

Форма пересечения склона. Пусть (1, 2) будет точкой (x _{1 ​​} , y _{1 ​​} ). Тогда имеем:

y-2= ⁵ / ₂ (x-1).

y-2= ⁵ / ₂ x- ⁵ / ₂

y= ⁵ / ₂ x- ¹ / _2.

Теперь нам нужно преобразовать это в стандартную форму. Как и раньше, мы поместим переменные с одной стороны:

^-5 / ₂ x+y= ^-1 / _2.

Теперь нам нужно алгебраически манипулировать уравнением так, чтобы не являются дробями. Мы можем сделать это, умножив обе части на 2, чтобы получить:

-5x+2y=-1.

Наконец, мы можем умножить обе части уравнения на -1, чтобы коэффициент при x был положительным:

5x-2y=1.

Следовательно, три формы уравнения:

Точка-наклон: y-2= ⁵ / ₂ (x-1).

Наклон-пересечение: y= ⁵ / ₂ x- ¹ / _2.

Стандарт: 5x-2y=1.

Мы можем использовать эти уравнения для получения точек пересечения. Форма точки пересечения наклона дает понять, что точка пересечения по оси y равна ^-1 / ₂ . Для x-перехвата мы можем использовать стандартную форму, потому что ^C / _A — это х-перехват.