Решение уравнения с 3 степенью: Как решить уравнения 3 степени онлайн

Решение кубических уравнений методом разложения на множители

Уравнение 3 степени a(x) = a₃*x³ + a₂*x² + a₁*x + a₀, a₃ ≠ 0, может иметь самое большее 3 корня. Кубическое уравнение всегда имеет по крайней мере один действительный корень, так как если корнем является комплексное число, то и комплексно сопряженное тоже будет его корнем.

Таким образом, кубический многочлен a(x) всегда можно разложить на два множителя, один из которых линейный, а второй квадратичный

В свою очередь многочлен второй степени a₃x² + bx + c может иметь 2 различных действительных корня, 1 действительный корень или 2 комплексно сопряженных корня.

Соответственно, получаем такие случаи разложения на множители a(x):

Таким образом, приравнивая каждый множитель в разложении к нулю, найдем все корни кубического уравнения в каждом случае. Рассмотрим решение кубических уравнений методом разложения на множители на примерах.

Пример 1. Решить уравнение x³ — 3x² — 4x + 6 = 0.

Решение.

Делителями свободного члена являются числа: ±1, ±2, ±3, ±6. Значит, корни уравнения нужно искать среди них. Простой подстановкой убеждаемся, что корнем уравнения является число 1. Следовательно, исходное уравнение эквивалентно (x — 1)*(a₃x² + bx + c) = 0.

Чтобы найти многочлен a₃x² + bx + c, нужно левую часть исходного уравнения разделить на x — 1. Для деления многочлена на двучлен будем использовать схему Горнера.

Таким образом, x³ — 3x² — 4x + 6 = (x — 1)(x² — 2x — 6). Следовательно, исходное уравнение эквивалентно (x — 1) (x² — 2x — 6) = 0.

Осталось решить квадратное уравнение x² — 2x — 6 = 0.

Ответ: -1- √7, 1 ,-1+√7.

Лучшие математические приложения для школьников и их родителей, студентов и учителей.

Подробнее …

Пример 2. Решить уравнение -2x³ + 3x² — 4x — 9 = 0.

Решение.

Делителями свободного члена являются числа: ±1, ±3, ±9. Делителями старшего коэффициента являются числа: ±1, ±2.

Значит, корни исходного уравнения могут быть среди чисел: ±1, ±3, ±9,

±

1/2

, ±

3/2

, ±

9/2

.

Снова простой подстановкой убеждаемся, что -1 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x + 1.

Таким образом, -2x³ + 3x² — 4x — 9 = (x + 1)(-2x²

 + 5x — 9). Следовательно, исходное уравнение эквивалентно (x + 1) (-2x² + 5x — 9)=0. Решая квадратное уравнение -2x² + 5x — 9 = 0, получаем, что его дискриминант

Ответ: -1.

Пример 3. Решить уравнение 2x³ — x² — 8x + 4 = 0.

Решение.

Делителями свободного члена являются числа: ±1, ±2, ±4. Делителями старшего коэффициента являются числа: ±1, ±2.

Значит, корни исходного уравнения могут быть среди чисел: ±1, ±2, ±4.

Простой подстановкой убеждаемся, что 2 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x — 2.

Таким образом, 2x³ — x² — 8x + 4 = (x — 2)(2x² + 3x — 2). Следовательно, исходное уравнение эквивалентно (x — 2) (2x² + 3x — 2) = 0. Решая квадратное уравнение 2x² + 3x — 2 = 0, получаем,

Ответ: -2,

, 2.

Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он довольно громоздкий, но иногда бывает очень полезным при решении разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x₀)*(a₃x² + bx + c).

Раскрывая скобки, получим a(x) = a₃x³ + x²(b — a₃x₀) + x*(c — bx₀) — cx₀.

Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a₃,b,c и x₀. Рассмотрим применение метода неопределенных коэффициентов на примерах.

Пример 4. Решить уравнение x³ + 2x² — 5x — 6 = 0.

Решение.

Так как любой многочлен 3 степени можно представить в виде a₃x³ + x²(b — a₃x₀) + x*(c — bx₀) — cx₀, то приравнивая коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:

Выразим из первого уравнения x₀ = b — 2 и подставим в два оставшихся. Получим

Теперь выразим переменную c из первого уравнения и подставим во второе.

Раскрывая скобки во втором уравнении и решая его, находим b:

Если b=4, то c=3, x₀ = 2. Следовательно, x³ + 2x² — 5x — 6 = (x — 2)(x² — 4x + 3)=(x — 2)(x + 1)(x + 3).

Если b = 1, то c = -6, x₀ = -1. Следовательно, x³ + 2x

2 — 5x — 6 = (x + 1)(x² + x — 6)=(x + 1)(x + 3)(x — 2).

Если b = -1, то c = -2, x₀ = -3. Следовательно, x³ + 2x² — 5x — 6=(x + 3)(x² — x — 2) = (x + 3)(x — 2)(x + 1).

Таким образом, исходное уравнение эквивалентно уравнению (x + 3)(x — 2)(x + 1) = 0.

Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -3, x = 2, x = -1.

Ответ: -3, -1, 2.

Пример 5. Решить уравнение 2x³ + x² — 5x + 2 = 0.

Решение.

Приравнивая соответствующие коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:

Выразим из первого уравнения x₀ = 

(b — 1)/2

и подставим в два оставшихся. Получим

Теперь из первого уравнения выразим переменную c и подставим во второе.

Умножая левую и правую части второго уравнения на 4 и раскрывая скобки, находим b:

Если b=2, то c=-4, x₀ = 

. Следовательно, 2x³ + x² — 5x + 2 = (x — 

)(2x² + 2x — 4) = 2(x — 

)(x — 1)(x + 2).

Если b = 3, то c = -2, x₀ = 1. Следовательно, 2x³ + x² — 5x + 2 = (x — 1)(2x² + 3x — 2)=2(x — 1)(x — 

)(x + 2).

Если b = -3, то c = 1, x₀ = -2. Следовательно, 2x³ + x² — 5x + 2 = (x + 2)(2x² — 3x + 1) = 2(x + 2)(x — 

)(x — 1).

Следовательно, исходное уравнение эквивалентно уравнению 2(x + 2)(x — 

)(x — 1) = 0.

Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -2, x = 

, x = 1.

Ответ: -2,

, 1.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Справочник по математике

Алгебра

Кубические уравнения

Схема метода Кардано

Приведение кубических уравнений к трехчленному виду

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи

Формула Кардано

Пример решения кубического уравнения

Схема метода Кардано

      Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени (кубических уравнений)

a0x3 + a1x2 + + a2x + a3= 0,

(1)

где a₀, a₁, a₂, a₃ – произвольные вещественные числа,

      Вывод формулы Кардано состоит из двух этапов.

      На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями.

      На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.

Приведение кубических уравнений к трехчленному виду

      Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

x3 + ax2 + bx + c = 0,

(2)

где a, b, c – произвольные вещественные числа.

      Заменим в уравнении (2) переменную x на новую переменную y по формуле:

(3)

      Тогда, поскольку

то уравнение (2) примет вид

В результате уравнение (2) примет вид

(4)

      Если ввести обозначения

то уравнение (4) примет вид

y3 + py + q= 0,

(5)

где p, q – вещественные числа.

      Уравнения вида (5) и являются трёхчленными кубическими уравнениями, у которых отсутствует член со второй степенью неизвестного.

      Первый этап вывода формулы Кардано завершён.

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи

      Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде

(6)

где   t   – новая переменная.

      Поскольку

то выполнено равенство:

      Следовательно, уравнение (5) переписывается в виде

(7)

      Если теперь уравнение (7) умножить на   t,   то мы получим квадратное уравнение относительно   t :

(8)

Формула Кардано

      Решение уравнения (8) имеет вид:

      В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:

(9)

      В развернутой форме эти решения записываются так:

	(10)
	(11)

      Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.

      Действительно,

      С другой стороны,

      Таким образом,

и для решения уравнения (5) мы получили формулу

которая и называется «Формула Кардано».

      Замечание. Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).

Пример решения кубического уравнения

      Пример. Решить уравнение

x3 – 6x2 – 6x – 2 = 0.

(13)

      Решение. Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену

x = y + 2.

(14)

      Тогда получим

x³ – 6x² – 6x – 2 =
= (y + 2)³– 6(y + 2)² –
– 6(y + 2) – 2 =
= y³ + 6y² + 12y + 8 – 6y² –
– 24y – 24 – 6y – 12 – 2 =
= y³ – 18y – 30.

      Следовательно, уравнение (13) принимает вид

y3 – 18y – 30 = 0.

(15)

      Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену

(16)

      Тогда поскольку

то уравнение (15) примет вид

(17)

      Далее из (17) получаем:

      Отсюда по формуле (16) получаем:

      Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу

или использовали формулу

      Далее из равенства (18) в соответствии с (14) получаем:

      Таким образом, мы нашли у уравнения (13) вещественный корень

      Замечание 1. У уравнения (13) других вещественных корней нет.

      Замечание 2. Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Решение уравнений третьей степени — HintFox

Кубическое уравнение – алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ах3 + bх2 + сх + d = 0, а ≠ 0

Заменяя в этом уравнении х новым неизвестным у, связанным с х равенством х = у – (b/3а), кубическое уравнение можно привести к более простому (каноническому) виду: у3 + pу + q = 0, где p = — b2 + с, q = 2b – bс + d

3а2 а 27а3 3а2 а решение этого уравнения можно получить с помощью формулы Кардано .

1. 1 История кубических уравнений

Термин «кубическое уравнение» ввели Р. Декарт (1619 г. ) и У. Оутред (1631г. ).

Первые попытки найти решения задач, сводящихся к кубическим уравнениям, были сделаны математиками древности (например, задачи об удвоении куба и трисекции угла).

Математики средневековья Востока создали довольно развитую теорию (в геометрической форме) кубических уравнений; наиболее обстоятельно она изложена в трактате доказательств задач алгебры и алмукабалы «Омара Хайя» (около 1070 года), где рассмотрен вопрос о нахождении положительных корней 14 видов кубических уравнений, содержащих в обеих частях только члены с положительными коэффициентами.

В Европе впервые в тригонометрической форме решение одного случая кубического уравнения дал Виет (1953 г. ).

Первое решение в радикалах одного из видов кубических уравнений удалось найти С. Ферро (около 1515 г. ), однако оно не было опубликовано. Открытие независимо повторили Тарталья (1535 г. ), указав правило решения еще двух других видов кубических уравнений. Опубликованы эти открытия в 1545 году Дж. Кардано, который упомянул об авторстве Н. Тартальи.

В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.

Начнём с упрощения

Если кубическое уравнение общего вида ах3 + bх2 + сх + d = 0, где а ≠ 0, разделить на а, то коэффициент при х3 станет равен 1. Поэтому в дальнейшем будем исходить из уравнения х3 + Pх2 + Qх + R = 0. (1)

Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:

(а + b)3 = а3 + 3а2b + 3аb2 + b3.

Чтобы не путаться в коэффициентах, заменим здесь а на х и перегруппируем слагаемые:

(х + b)3 = х3 + 3bх2 + 3b2х + b3. (2)

Мы видим, что надлежащим образом b, а именно взяв b = P/3, можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения х3 + Pх2 + Qх + R = 0 только коэффициентом при х и свободным членом. Сложим уравнение х3 + Pх2 + Qх + R = 0 и (х + b)3 = х3 + 3bх2 + 3b2х + b3 и приведём подобные:

(х + b)3 + (Q – 3b2)х + R – b3 = 0.

Если здесь сделать замену y = х + b, получим кубическое уравнение относительно у без члена с у2: у3 + ру + q = 0.

Итак, мы показали, что в кубическом уравнении х3 + Pх2 + Qх + R = 0 с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида х3 + рх + q = 0. (3)

1. 2 История формулы Кардано

Формула Кардано названа по имени Дж. Кардано, впервые опубликовавшего её в 1545 году.

Автор этой формулы Никколо Тарталья. Он создал это решение в 1535 г. специально для участия в математическом состязании, в котором, естественно, победил. Тарталья, сообщая формулу (в стихотворной форме) Кардано, представил только ту часть решения кубического уравнения, в которой корень имеет одно (действительное) значение.

Результаты Кардано в этой формуле относятся к рассмотрению так называемого неприводимого случая, в котором уравнение имеет три значения (действительных значений, в те времена не было ни мнимых, ни даже отрицательных чисел, хотя попытки в этом направлении были). Однако, вопреки тому, что Кардано указал в своей публикации на авторство Тартальи, формулу называют именем Кардано.

1. 3 Формула Кардано

Теперь давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:

(а + b)3 = а3 + b3 + 3аb(а + b).

Сравните эту запись с уравнением х3 + рх + q = 0 и попробуйте установить связь между ними. Подставим в нашу формулу х = а + b: х3 = а3 + b3 + 3аbх, или х3 – 3аbх – (а3 + b3) = 0

Теперь уже ясно: для того, чтобы найти корень уравнения х3 + рх + q = 0, достаточно решить систему уравнений а3 + b3 = — q, а3 + b3 = — q, или

3аb = — p,а3b3 = — p 3,

3 и взять в качестве х сумму а и b. Заменой и = а3, v = b3 эта система приводится к совсем простому виду: и + v = — q, иv = — p 3.

Дальше можно действовать по-разному, но все «дороги» приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при х со знаком минус, а произведение – свободному члену. Отсюда следует, что и и v – корни уравнения t2 + qt – (p/3)3 = 0.

Выпишем эти корни: t1,2 = — q ± q 2 + p 3.

Переменные а и b равны кубическим корням из t1 и t2, а искомое решение кубического уравнения х3 + рх + q = 0 – сумме этих корней: х = 3 – q + q 2 + p 3+ 3 – q – q 2 + p 3.

2 2 3 2 2 3

Эта формула известна как формула Кардано.

Решаем уравнения

Прежде, чем посмотреть на формулу Кардано в работе, поясним, как по одному корню кубического уравнения х3 + рх + q = 0 найти другие его корни, если они есть.

Пусть известно, что наше уравнение имеет корень h. Тогда его левую часть можно разложить на линейный и квадратный множители. Делается это очень просто. Подставляем в уравнение выражение свободного члена через корень q = — h4 – ph и пользуемся формулой разности кубов:

0 = х3 – h4 + px – ph = (x – h)(x2 + hx + h3) + p(x — h) = (x – h)(x2 + hx + h3 + p).

Теперь можно решить квадратное уравнение х2 + hx + h3 + p = 0 и найти остальные корни данного кубического уравнения.

Итак, мы во всеоружии и, казалось бы, можем справиться с любым кубическим уравнением. Давайте попробуем свои силы.

1. Начнем с уравнения х3 + 6х – 2 = 0

Подставляем в формулу Кардано p = 6 и q = -2 и после несложных сокращений получаем ответ: х = 3√4 – 3√2. Что ж, формула вполне симпатичная. Только перспектива выносить множитель х – (3√4 – 3√2) из левой части уравнения и решать остающееся квадратное уравнение со «страшными» коэффициентами для вычисления других корней не очень-то вдохновляет. Однако, присмотревшись к уравнению внимательнее, можно успокоиться: функция в левой части строго возрастает и поэтому может обращаться в нуль только один раз . Значит, найденное число – единственный действительный корень уравнения.

у у = х3 + 6х – 2

3√4 – 3√2 х

Рис. 1 График функции у = х3 + 6х – 2 пересекает ось абсцисс в одной точке — 3√4 – 3√2.

2. Следующий пример – уравнение х3 + 3х – 4 = 0.

Формула Кардано дает х = 3 2 + √5 + 3 2 — √5.

Как и в предыдущем примере, мы видим, что этот корень единственный. Но не нужно обладать сверхпроницательностью, чтобы, глядя на уравнение, угадать его корень: х = 1. Приходится признать, что формула выдала обычную единицу в таком причудливом виде. Между прочим, упростить это громоздкое, но не лишенное изящества выражение алгебраическими преобразованиями не удается – кубические иррациональности в нем неустранимы.

3. Ну а теперь возьмем уравнение, заведомо имеющее три действительных корня. Составить его легко – просто перемножим три скобки вида х – b. Нужно только позаботиться, чтобы сумма корней равнялась нулю, ведь, по общей теореме Виета, она отличается от коэффициента при х2 только знаком. Самый простой набор таких корней – это 0, 1 и – 1.

Применим формулу Кардано к уравнению х (х – 1)(х + 1) = 0, или х3 – х = 0.

Полагая в ней p = -1 и q = 0, получаем х = 3 √ — 1/27 + 3 — √ — 1/27.

у у = х (х — 1)(х + 1)

Рис. 2 Уравнение х (х – 1)(х + 1) = 0 имеет три действительных корня: -1, 0 и 1. Соответственно график функции у = х (х – 1)(х + 1) пересекает ось абсцисс в трех точках.

Под знаком квадратного корня появилось отрицательное число. Такое бывает и при решении квадратных уравнений. Но квадратное уравнение в этом случае не имеет действительных корней, а у кубического их целых три!

Более тщательный анализ показывает, что мы попали в эту ловушку не случайно. Уравнение х3 + px + q = 0 имеет три действительных корня тогда и только тогда, когда выражение Δ = (q/2)2 + (p/3)3 под квадратным корнем в формуле Кардано отрицательно . Если Δ > 0, то действительный корень один (рис. 3, б), а если Δ = 0, то их два (один из них – двукратный), за исключением случая p = q = 0, когда все три корня сливаются.

у Δ 0 у = -pх — q у = х3

0 х 0 х у = -pх — q у = х3 а) б)

Рис. 3 Кубическое уравнение х3 + px + q = 0 можно представить в виде х3 = -px – q. Отсюда видно, что корням уравнения будут соответствовать абсциссы точек пересечения двух графиков: у = х3 и у = -px – q. Если Δ 0 – один.

1. 4 Теорема Виета

Теорема Виета. Если целое рациональное уравнение степени n, приведенное к стандартному виду, имеет n различных действительных корней х1, х2,. хn, то они удовлетворяют равенствам: х1 + х2 + + хn = — а1 , а0 х1х2 + х1х3 + + хn-1хn = а2 а0 х1 · х2 · · хn = (-1)nаn.

Для корней уравнения третьей степени а0х3 + а1х2 + а2х + а3 = 0, где а0 ≠ 0 справедливы равенства х1 + х2 + х3 = — а1, а0 х1х2 + х1х3 + х2х3 = а2, а0 х1х2х3 = — а3.

1. 5 Теорема Безу. Схема Горнера

Решение уравнений тесно связано с разложением многочленов на множители. Поэтому при решении уравнений важно все, что связано с выделением в многочлене линейных множителей, т. е. с делением многочлена А(х) на двучлен х – α. Основой многих знаний о делении многочлена А(х) на двучлен х – α, является теорема, принадлежащая французскому математику Этьену Безу (1730-1783 гг. ) и носящая его имя.

Теорема Безу. Остаток от деления многочлена А(х) на двучлен х – α равен А(α) (т. е. значению многочлена А(х) при х = α).

Пример 1.

Найдем остаток от деления многочлена А(х) = х4 – 6х3 + 8 на х + 2.

Решение. По теореме Безу остаток от деления на х + 2 равен А(-2) = (-2)4 – 6(-2)3 + 8 = 72.

Удобный способ нахождения значений многочлена при заданном значении переменной х ввел английский математик Вильямс Джордж Горнер (1786-1837 гг. ). Этот способ впоследствии получил название схемы Горнера. Он состоит в заполнении некоторой таблицы из двух строк. Например, чтобы вычислить А(-2) в предыдущем примере, в верхней строке таблицы перечисляем коэффициенты данного многочлена, записанного в стандартной форме х4 – 6х3 + 8 = х4 + (-6)х3 + 0 · х2 + 0 · х + 8.

Коэффициент при старшей степени дублируем в нижней строке, а перед ним записываем значение переменной х = -2, при котором вычисляется значение многочлена. Получается следующая таблица:

1 -6 0 0 8

Пустые клетки таблицы заполняем по следующему правилу: крайнее справа число нижней строки умножается на -2 и складывается с числом, стоящим над пустой клеткой. По этому правилу в первой пустой клетке стоит число (-2) · 1 + (-6) = -8, во второй клетке ставится число (-2) · (-8) + 0 = 16, в третьей клетке – число (-2) · 16 + 0 = — 32, в последней клетке – число (-2) · (-32) + 8 = 72. Полностью заполненная по схеме Горнера таблица выглядит так:

1 -6 0 0 8

-2 1 -8 16 -32 72

Число в последней клетке и есть остаток от деления многочлена на х + 2, А(-2) = 72.

На самом деле из полученной таблицы, заполненной по схеме Горнера, можно записать не только остаток, но и неполное частное

Q(x) = x3 – 8×2 + 16x – 32, так как число, стоящее на второй строке (не считая с последнего), — это коэффициенты многочлена Q(x) – неполного частного от деления на х + 2.

Пример 2.

Решим уравнение х3 – 2х2 – 5х + 6 = 0

Выпишем все делители свободного члена уравнения: ± 1, ± 2, ± 3, ± 6.

х = 1, х = -2, х = 3

Ответ: х = 1, х = -2, х = 3

2. ЗАКЛЮЧЕНИЕ

Сформулирую основные выводы о проделанной работе.

В процессе работы я познакомился с историей развития проблемы решения уравнения третьей степени. Теоретическая значимость полученных результатов заключается в том, что осознанно занимает место формулы Кардано в решении некоторых уравнений третьей степени. Я убедился в том, что формула решения уравнения третьей степени существует, но из-за её громоздкости она не популярна и не очень надежна, так как не всегда достигает конечного результата.

В дальнейшем можно рассматривать такие вопросы: как узнать заранее, какие корни имеет уравнение третьей степени; можно ли кубическое уравнение решить графическим способом, если можно, то как; как оценить приближенно корни кубического уравнения?

“Методы решения уравнений четвертой степени”

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области

Педагогический проект по теме:

“Методы решения уравнений четвертой степени”

Выполнила Чурина

Елена Вениаминовна,

учитель математики первой

квалификационной категории

Г. Южа

2021 год

Содержание

Актуальность

Цель и задачи работы:………………………………

1. Исторические сведения об уравнениях четвёртой степени……стр.

2. Определение уравнения 4 степени………………………….стр.

3. Способы решения уравнений 4 степени……………………………стр.

3.1. Схема метода Феррари……………………….стр.

3.2. Разложение на множители. Кубическая резольвента……………стр.

3.3. Теорема Виета для уравнения 4 степени……………………..стр.

3.4. Решение уравнений 4 степени по схеме Горнера……………………стр.

4.Решение некоторых уравнений 4 степени……………………………стр.

4.1. Решение биквадратного уравнения………………………………стр.

4.2. Решение уравнения способом группировки………………….стр.

4.3. Решение уравнения по свободному члену……………………стр.

4.4. Графический метод………………………………………..стр.

4.5. Применение формул сокращенного умножения. Выделение полного квадрата………………………………………………..стр.

5. Исследование………………………………………………стр.

6. Выводы

7. Заключение

8. Тренировочные задания для отработки различных способов решения уравнений высших степеней……………………………………………стр.

Список литературы

Актуальность

Как все знают, в математике одна из важнейших вещей — это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый учащийся 9 класса. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен.

Задания с уравнениями высших степеней есть в контрольных измерительных материалах  при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый.

Цель работы: узнать и разобрать методы решения уравнений высших степеней.

Задачи:

Изучить литературу по истории приемов решения уравнений 4-й стпени

Обобщить накопленные знания об уравнениях4-й степени и способах их решения.

Сделать выводы.

Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать уравнения 4-й степени?

Гипотеза: существует универсальный способ для решения всех видов уравнений 4-степеней.

Объект исследования: уравнения 4-й степени

Предмет изучения: методы и приемы решениях уравнений 4-й степени, в том числе

1. Исторические сведения об уравнениях четвёртой степени

Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.

Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.

Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие.

Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г.). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.

В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не  существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу.

2. Определение уравнения 4 степени

Уравнение четвёртой степени —алгебраическое уравнение вида:

,

при этом a≠0 и где a,b,c,d,e- любые числа.

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).

3. Способы решения уравнений 4 степени.

3.1 Схема метода Феррари

     

a0x4 + a1x3 + a2x2 + a3x + a4 = 0,

(1)

где a0, a1, a2, a3, a4 –  произвольные вещественные числа, причем 

      Метод Феррари состоит из двух этапов.

      На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.

      На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.

Приведение уравнений 4-ой степени

      Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид

x4 + ax3 + bx2 + cx + d = 0,

(2)

где a, b, c, d –  произвольные вещественные числа.

      Сделаем в уравнении (2) замену

(3)

где y –  новая переменная.

      Тогда, поскольку

то уравнение (2) принимает вид

(4)

      Если ввести обозначения

то уравнение (4) примет вид

y4 + py2 + qy + r = 0,

(5)

где p, q, r –  вещественные числа.

      Первый этап метода Феррари  завершён.

3.2.Разложение на множители. Кубическая резольвента

      Добавив и вычитая в левой части уравнения (5) выражение

2sy2 + s2,

где s –  некоторое число, которое мы определим чуть позже, из (5) получим

      Следовательно, уравнение (5) принимает вид

(6)

      Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения

(7)

то уравнение (6) примет вид

(8)

      Избавляясь от знаменателя, уравнение (7) можно переписать в виде

или, раскрыв скобки, — в виде

(9)

      Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).

      Если какое-нибудь решение  кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».

      Действительно,

      Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение

(10)

а также квадратное уравнение

(11)

      Вывод метода Феррари завершен.

Пример решения уравнения 4-ой степени

      Пример. Решить уравнение

x4 + 4×3 – 4×2 – 20x – 5 = 0.

(12)

      Решение. В соответствии с (3) сделаем в уравнении (12) замену

x = y – 1.

(13)

      Поскольку

x4 + 4×3 – 4×2 – 20x – 5 = (y – 1)4 + 4(y – 1)3 – 4(y – 1)2 – 20(y – 1)– 5 = 
= y4 – 4y3 + 6y2 – 4y + 1 + 4y3 – 12y2 + 12y – 4 – 4y2 + 8y – 4 – 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8,

то в результате замены (13) уравнение (12) принимает вид

y4 – 10y2 – 4y + 8 = 0.

(14)

      В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства

p = – 10,      q = – 4,       r = 8.

(15)

      В силу (9)  и (15) кубической резольвентой для уравнения (14) служит уравнение

2s3 + 10s2 – 16s – 84 = 0,

которое при сокращении на 2 принимает вид:

s3 + 5s2 – 8s – 42 = 0.

(16)

      Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число

s = – 3.

(17)

      Подставляя значения (15) и (17) в формулу (10), получаем уравнение

y2 – 2y – 4 = 0,

корни которого имеют вид:

(18)

      Подставляя значения (15) и (17) в формулу (11), получаем уравнение

y2 + 2y – 2 = 0,

корни которого имеют вид:

(19)

      В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):

      Ответ.  

Но эти способы очень сложны. Рассмотрю более простые способы, с помощью которых можно решить некоторые уравнения 4-й четверти.

3.3Теорема Виета для уравнения четвёртой степени

Корни уравнения четвёртой степени {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами {\displaystyle a,\,b,\,c,\,d,\,e}следующим образом:

{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}

3.4.Решение уравнений четвертой степени по схеме Горнера

2x4 + 5x3 — 11x2 — 20x + 12 = 0

Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:

1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена

-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена

2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена

Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:

	2	5	-11	-20	12
2

В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления.

Они считаются так:

2 5 -11 -20 12 2	Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки.
2 5 -11 -20 12 2 9	2 ∙ 2 + 5 = 9
	2 ∙ 9 — 11 = 7
	2 ∙ 7 — 20 = -6
	2 ∙ (-6) + 12 = 0

	2	5	-11	-20	12
2	2	9	7	-6	0

Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.

Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.

(х-2)(2х3+9х2+7х-6)=0

Многочлен, являющийся вторым множителем попробуем разложить на множители подобным образом.

Отыщем опять делители свободного члена. В данном случае делителями числа -6: ±1, ±2, ±3, ±4, ±6.

Число -2 является корнем многочлена. Напишем найденный корень в схему Горнера и начнем заполнять ячейки:

	2	5	-11	-20	12
2	2	9	7	-6	0
-2

Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки.

-2 ∙ 2 + 9 = 5

-2 ∙ 5 + 7 = -3

-2 ∙ (-3) — 6 = 0

	2	5	-11	-20	12
2	2	9	7	-6	0
-2	2	5	-3	0

Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению. {2}-4ac}}}{2a}}}.}

Пример.

Решить уравнение

Замена

из этого следует, что уравнение имеет два корня.

Обратная замена

т.е. невозможно

Ответ: .

4.2. Решение уравнения способом группировки

Способом группировки можно решить уравнение 4 степени.

Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель.

Решим на примере.

2х4-5х3+2х2-5х=0

(2х4-5х3)+( 2х2-5х)=0

х3(2х-5)+х(2х-5)=0

(2х-5)(х3-х)=0

х(2х-5)(х2-1)=0

х(2х-5)(х-1)(х+1)=0

х=0 или 2х-5=0 или х-1=0 или х+1=0

х1=0 х2=2,5 х3=1 х4=-1

4.3. Решение уравнения по свободному члену

Любое уравнение вида   можно свести к приведенному уравнению той же степени, домножив обе его части на  и выполнив замену переменной вида :

Полученные коэффициенты   тоже будут целыми.

Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида  .

Алгоритм решения.

Находим целые корни уравнения.

Целые корни уравнения  , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде  , где  — корень уравнения, а  — частное от деления  на .

Продолжаем подставлять выписанные ранее делители в уравнение , начиная с  (так как корни могут повторяться). Как только получаем тождество, то корень  найден и уравнение предстает в виде , где  — частное от деления  на .

И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где  — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.

Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.

Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения  любым способом.

Решить уравнение .

Во-первых, найдем все целые корни данного уравнения.

Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.

Будем подставлять их по очереди в исходное равенство до получения тождества.

При х=1 имеем . То есть х=1 является корнем уравнения.

Разделим многочлен  на (х-1) столбиком:

Следовательно, .

Продолжим перебор делителей, но уже для равенства :

При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.

Разделим  на (х+1) столбиком:

Таким образом,

Продолжаем перебор делителей для равенства , начиная с х = -1:

Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.

Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена .

, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных.

4.4.Графический метод.

Иногда полезно рассмотреть эскизы графиков функций у=ƒ(x) и у=g(x), входящих в уравнение ƒ(x) = g(x). Это может помочь выяснить:

1) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения;

2) наличие или отсутствие корней, их количество.

Пример: (материал взят из ОГЭ 2016г.)

x4=(3x-10)2

Решение №3: x4=(3x-10)2

1) Рассмотрим две функции: у = х4 и у =(3х-10)2.

2) Построим график функции у = х4 — график парабола ветви направлены вверх.

3) Построим график линейной функции у = (3х-10)2. Это парабола ветви, которой направлены вверх.

4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение).

Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения.

Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества.

4.5. Применение формул сокращенного умножения. Выделение полного квадрата.

Этот метод основан на использовании формул: 

а2-b2=(а-b)(а+b)a2+2ab+b2=(a+b)2a2−2ab+b2=(a−b)2

а3+b3=(а+b)(а2-аb+b2)а3-b3=(а-b)(а2+аb+b2)(а+b)3=а3+3а2b+3аb2+b3

(а-b)3= а3-3а2b+3аb2-b3,

Пример: х4=(3х-10)2

Способ 1: Используем формулу сокращенного умножения х4-(3х-10)2=0

(х2-3х+10)(х2+3х-10)=0

х2-3х+10=0 или х2+3х-10=0

D=9-40=-31 D=9+40=49

корней нет х1=-5, х2=2.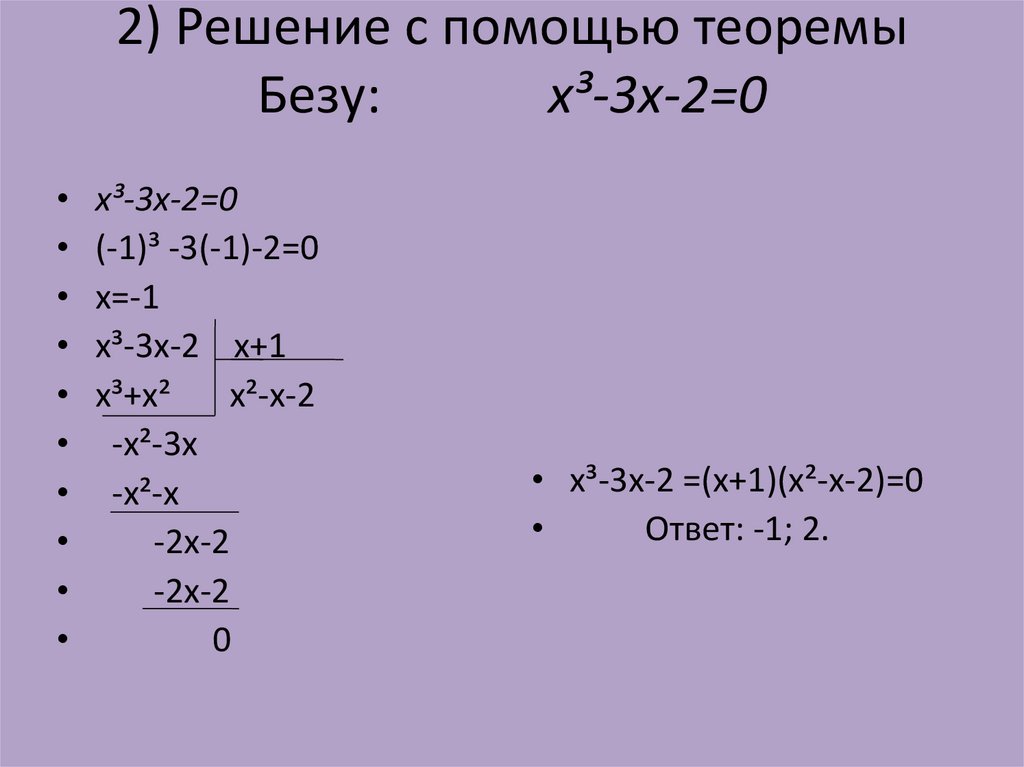

Ответ: х1=-2, х2=5.

6. Выводы:

1. Уравнения высших степеней решали еще более 500 тыс. лет назад.

2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ.

3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников.

7. Заключение

В данной работе рассмотрены способы решения уравнений 4-й степени.

А также рассмотрены приёмы решения уравнений 4-й степени, которые позволяют быстрее и проще решить такие уравнения.

Данные приёмы решения заслуживают внимания, поскольку каждые из них интересны и уникальны. Овладение данными приёмами поможет экономить время и эффективно решать уравнения. Потребность в быстром и упрощенном решении обусловлена применением этих навыком на экзаменах.

Таким образом, цель работы — узнать и разобрать методы решения уравнений высших степеней- достигнуты. Гипотеза доказана, существует универсальный способ решения уравнений 4-й степени. Это способ Феррари.

Источники:

Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6.

. М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999.

 В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин,
А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998.

 Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003.

 М. А.Еремин «Уравнения высших степеней» — Арзамас, 2003.

А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975.

Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995.

 И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954.

10.https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/

11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html

12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени

Приложение 1

Тренировочные задания для отработки различных способов решения уравнений 4-й степени.

№1 Решите уравнения способом замены: , б) X4-2×2-8=0,

в) x4-8×2-9=0, г) x4-7×2+12=0, д) 3×4-13×2+4=0, е) 2×4-19×2+9=0,

ж) 3×4-13×2+4=0, з) (x2+4x)(x2+4x-17)=60=0, и) (x2-5x)(x2-5x+10)+24=0,

к)(x2-3x)2-2(x2-3x)=8, л) (x2+x)2-11(x2+x)=12, 1

м) ()+10=0, н) ()=3; о)

№2 Решите уравнения, раскладывая левую часть на множители способом группировки:

а) 2×4-5×3+2×2-5x=0,

б) 6×4-3×3+12×2-6x=0,

в) 2×4+3×3-8×2-12x=0,

г) 2×4-5×3-18×2+45x=0. 3

Получим подробное решение:

Дано уравнение:

               3
8 = (1/2 + 3*x) 

преобразуем:

Вынесем общий множитель за скобки

              /               2\    
-9*(-1 + 2*x)*\7 + 12*x + 12*x /    
-------------------------------- = 0
               8                    

Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.

Получим ур-ния

9   9*x    
- - --- = 0
8    4     

               2    
7 + 12*x + 12*x  = 0

решаем получившиеся ур-ния:

1.

9   9*x    
- - --- = 0
8    4     

Переносим свободные слагаемые (без x)

из левой части в правую, получим:

-9*x       
---- = -9/8
 4         

Разделим обе части ур-ния на -9/4

x = -9/8 / (-9/4)

Получим ответ: x1 = 1/2

2. 2 — 8*x + 5 = 0

Чтобы решить такое возвратное кубическое уравнение, то введите данное уравнение в калькулятор:

Дано уравнение:

             2      3    
5 - 8*x - 8*x  + 5*x  = 0

преобразуем

   3          2                  
5*x  + 5 - 8*x  + 8 - 8*x - 8 = 0

или

   3         3      2          2              
5*x  - 5*(-1)  - 8*x  - -8*(-1)  - 8*x - 8 = 0

  / 3       3\     / 2       2\                
5*\x  - (-1) / - 8*\x  - (-1) / - 8*(x + 1) = 0

          / 2           2\                                     
5*(x + 1)*\x  - x + (-1) / + -8*(x + 1)*(x - 1) - 8*(x + 1) = 0

Вынесем общий множитель 1 + x за скобки

получим:

        /  / 2           2\                \    
(x + 1)*\5*\x  - x + (-1) / - 8*(x - 1) - 8/ = 0

или

        /              2\    
(1 + x)*\5 - 13*x + 5*x / = 0

тогда:

x1 = -1

и также

получаем ур-ние

              2    
5 - 13*x + 5*x  = 0

Это уравнение вида

a*x^2 + b*x + c = 0

Квадратное уравнение можно решить

с помощью дискриминанта. 3 = 0:

x1 = -1

            ____
     13   \/ 69 
x2 = -- + ------
     10     10  

            ____
     13   \/ 69 
x3 = -- - ------
     10     10  

3.1.2. Разложение выражений на множители

Глава 3. Решение уравнений и неравенств

3.1.

3.1.2.

Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде

F1 (x) · F2 (x) · …  · Fn (x) = 0,

(5)

где выражения F_k (x), k = 1, …, n «проще» функций f (x) и g (x), представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители F_k (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель).

Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.

1. Вынесение общего множителя за скобку

В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.

Пример 1

Разложить на множители многочлен x⁵ – 2x³ + x².

Показать решение

2. Применение формул сокращённого умножения

Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы:

Пример 2

Разложить на множители многочлен (x – 2)⁴ – (3x + 1)⁴.

Показать решение

3. Применение выделения полного квадрата

Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.

Пример 3

Разложить на множители многочлен x⁴ + 4x² – 1.

Показать решение

4. Группировка

Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.

5. Метод неопределённых коэффициентов

Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.

Теоретической основой метода являются следующие утверждения.

• Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
• Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
• Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞. Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox.

Пример 4

Разложить на множители многочлен 3x³ – x² – 3x + 1.

Показать решение

6. Теорема о корнях многочлена

Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2. 1.4. После того, как корень x = α угадан, многочлен P_n (x) представим в виде P_n (x) = (x – α) · P_n – 1 (x), где P_n – 1 (x) − многочлен степени на 1 меньше, чем P_n (x).

Пример 5

Разложить на множители многочлен x³ – 5x² – 2x + 16.

Показать решение

7. Разложение относительно параметра

Суть этого метода легче всего понять на примере.

Пример 6

Разложить на множители многочлен x⁴ – 10x² – x + 20.

Показать решение



Главная   Онлайн учебники   База репетиторов России   Тренажеры по математике   Подготовка к ЕГЭ 2017 онлайн
Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия. А также: online подготовка к ЕГЭ на College.ru, библиотека ЭОРов и обучающие программы на Multiring.ru.

Кубический многочлен — определение, формула, график, примеры

Кубический многочлен — это тип многочлена, основанный на степени, т. е. наибольшем показателе переменной. Следовательно, кубический многочлен — это многочлен с наивысшей степенью переменной или степени, равной 3. Многочлен — это алгебраическое выражение с переменными и константами с показателями в виде целых чисел. Давайте узнаем больше о кубических полиномах, определении, формулах и решим несколько примеров.

1.	Определение кубического многочлена
2.	Решение кубического многочлена
3.	График кубического многочлена
4.	Корни кубического многочлена
5.	Часто задаваемые вопросы о кубическом многочлене

Определение кубического многочлена

Кубический многочлен — это многочлен со старшим показателем степени переменной, т. е. степенью переменной, равной 3. В зависимости от степени многочлен делится на 4 типа, а именно нулевой многочлен, линейный многочлен, квадратичный многочлен и кубический многочлен. Общая форма кубического многочлена имеет вид p(x): ax ³ + bx ² + cx + d, a ≠ 0, где a, b и c — коэффициенты, а d — константа, причем все они равны вещественные числа. Уравнение, включающее кубический многочлен, называется кубическим уравнением. Некоторыми примерами кубического многочлена являются p(x): x ³ — 5x ² + 15x — 6, r(z): πz ³ + (√2) ¹⁰ .

Формула кубического полинома

Формула кубического полинома имеет общий вид: + сх + d = 0,

Решение кубического многочлена

Общая форма кубического полинома: ax ³ + bx ² + cx + d, a ≠ 0. Решая кубический многочлен, мы всегда должны преобразовать уравнение в кубическое уравнение, разбив его на квадратное уравнение, а затем решить его двумя различными способами — факторная теорема и метод синтетического деления. Давайте посмотрим, как решать уравнения в обоих методах.

Кубический многочлен с синтетическим делением

Синтетическое деление — это метод, используемый для выполнения операции деления многочленов, когда делитель является линейным множителем. Мы можем представить деление двух многочленов в виде: p(x)/q(x) = Q + R/(q(x))

где

• p(x) — делимое
• q(x) — линейный делитель
• Q — частное
• R — остаток

При решении кубического многочлена мы используем метод синтетического деления, и шаги следующие:

• Шаг 1: Проверяем, имеет ли кубический многочлен стандартную форму.
• Шаг 2: Запишите коэффициенты вместо делимого и ноль линейного множителя вместо делителя.
• Шаг 3: Уменьшите первый коэффициент, умножьте его и запишите под следующим коэффициентом.
• Шаг 4: Добавьте их и запишите значение ниже.
• Шаг 5: Повторяйте предыдущие 2 шага, пока не дойдете до последнего члена.
• Шаг 6: Отделите последний полученный член, который является остатком.
• Шаг 7: Теперь сгруппируйте коэффициенты с переменными, чтобы получить частное.

Теорема о кубическом многочлене с множителями

Теорема о множителях — разновидность теоремы о полиномиальных остатках, которая связывает множители многочлена и его нули. Согласно факторной теореме (x – a) можно рассматривать как фактор многочлена p(x) степени n ≥ 1 тогда и только тогда, когда p(a) = 0. Здесь a – любое действительное число. Формула факторной теоремы такова: p(x) = (x – a) q(x). Важно отметить, что все следующие утверждения справедливы для любого многочлена p(x):

• (x – a) является коэффициентом p(x).
• р(а) = 0,
• Остаток равен нулю, когда p(x) делится на (x – a).
• Решение p(x) = 0 есть a, а нуль функции p(x) есть a.

Факторная теорема в основном применима для многочленов нулевой, единичной и второй степени. Для таких степеней, как 3 и 4, таких как кубический многочлен, теорема о факторах используется вместе с синтетическим делением, и шаги следующие:

• Шаг 1: Используйте метод синтетического деления, чтобы разделить заданный многочлен p(x) на заданный двучлен (x−a)
• Шаг 2: После завершения деления остаток должен быть равен 0. Если остаток не равен нулю, это означает, что (x-a) не является множителем p(x).
• Шаг 3: Используя алгоритм деления, запишите заданный полином как произведение (x-a) и квадратного частного q(x)
• Шаг 4: Если возможно, умножьте квадратное частное дальше.
• Шаг 5: Выразите заданный полином как произведение его множителей.

Например: Рассмотрим такое деление: (x ³ — 2x ³ — 8x — 35)/(x — 5). Многочлен имеет порядок 3. Делитель является линейным множителем. Давайте воспользуемся синтетическим делением, чтобы найти частное. Таким образом, частное на порядок меньше заданного полинома. Это x ² + 3x + 7, а остаток равен 0. (x ³ — 2x ³ — 8x — 35)/(x — 5) = x ² + 3x + 7.

График кубического многочлена

Кубическая полиномиальная функция третьей степени имеет форму, показанную справа, и может быть представлена ​​как y = ax ³ + bx ² + cx + d, где a, b, c и d действительные чисел и a ≠ 0. Когда кубический многочлен не может быть решен с помощью вышеупомянутых методов, мы можем решить его графически. Точки, в которых график пересекает ось x, считаются решением и называются корнями кубического многочлена. При построении графика кубического многочлена нам необходимо помнить о двух важных аспектах:

• Если знак a положительный, то график будет идти снизу вверх.
• Если знак a отрицательный, то график будет направлен сверху вниз.

График кубического полинома выглядит следующим образом:

Функция кубического полинома

Кубические полиномы можно решать так же, как и квадратные уравнения. Но чтобы сделать его намного проще, мы можем использовать некоторые из этих специальных продуктов:

• Совершенный куб (2 формы): ³ ± 3а ² б + 3аб ² ± б ³ = (а ± б) ³
• Разность кубов: a ³ − b ³ = (a − b)(a ² + ab +b ² )
• Сумма кубов: a ³ + b ³ = (a + b)(a ² − ab + b ² )

Решим эту кубическую полиномиальную функцию y ³ – 2y ² – y + 2. Начнем с факторизации уравнения:

у ³ – 2у ² – у + 2 = у ² (у – 2) – (у – 2)

= (у ² – 1) (у – 2)

3 = (y + 1) (y – 1) (y – 2)

y = 1, -1 и 2.

Корни кубических многочленов

Решение кубического уравнения называется корнями кубического уравнения. В большинстве случаев у кубического многочлена есть 3 корня, но иногда мы получаем два или только один. Когда кубический многочлен решается графически, мы получаем точные корни или когда мы решаем уравнение с формулой, мы получаем корни. Предположим, что p,q и r являются тремя корнями уравнения ax ³ + бх ² + сх + д. Формулы таковы:

• p + q + r = — b/a
• pq + qr + rp = c/a
• pqr = — д/д

Например: Решите следующее кубическое уравнение, x ³ — 12x ² + 39x — 28 = 0.

Решение: Рассмотрим 3 корня a — b, a и a + b.

p = a — b, q = a, r = a + b

Из уравнения, x ³ — 12x ² + 39x — 28 = 0 знаем,

a = 1, b = — 12, c = 39, d = — 28

Сумма корней = — b/a

a — b + a + a + b = — (-12)/1

3a = 12

a = 4.

Мы можем найти два корня, разложив уравнение на множители и превратив его в квадратное уравнение. Посмотрите на изображение ниже.

x ² — 8x + 7 = 0

x ² — 7x — x + 7 = 0

x(x — 7) — 1 (x — 7) = 0

3 (x — 9 1) (х — 7) = 0

х -1 = 0 и х — 7 = 0

x = 1 и x = 7

Таким образом, корни равны 1, 4 и 7.

Связанные темы

Ниже перечислены некоторые темы, связанные с кубическим полиномом.

• Нули кубического многочлена
• Полиномиальная функция
• Линейные, квадратичные и кубические многочлены

Часто задаваемые вопросы о кубических полиномах

Что такое кубический многочлен с примером?

Кубический многочлен — это тип многочлена со степенью 3, т. е. старший показатель переменной равен 3. Общая форма кубического многочлена записывается как p(x): ax ³ + bx ² + cx + d, a ≠ 0, где a, b и c — коэффициенты, а d — константа, причем все они являются действительными числами.

Как найти кубические многочлены?

Кубические многочлены могут быть решены путем преобразования кубического уравнения в квадратное уравнение. Решение кубического многочлена выполняется двумя способами — теоремой о факторах и синтетическим делением.

Как использовать теорему о факторах для кубических многочленов?

Для решения кубических многочленов по теореме о факторах используются следующие шаги:

• Используйте метод синтетического деления, чтобы разделить заданный многочлен p(x) на заданный двучлен (x−a)
• После завершения деления остаток должен быть равен 0. Если остаток не равен нулю, это означает, что (x-a) не является множителем p(x).
• Используя алгоритм деления, запишите данный полином как произведение (x-a) и квадратного частного q(x)
• Если возможно, разложите квадратное частное дальше.
• Выразите заданный полином как произведение его множителей.

Как использовать метод синтетического деления для кубических многочленов?

Кубические полиномы решаются синтетическим методом с использованием общих шагов, таких как взятие одних коэффициентов, уменьшение первого, умножение на ноль линейного множителя и добавление со следующим коэффициентом, и так повторяется до конца.

По какой формуле можно построить кубический многочлен?

Формула для построения кубического полинома: ax ³ + bx ² + cx + d = 0.

Формула кубического уравнения — выучить формулу кубического уравнения

Формула кубического уравнения используется для представления кубического уравнения . Многочлен третьей степени известен как кубический многочлен, или мы можем назвать его кубическим уравнением. Кубические уравнения имеют по крайней мере один действительный корень, и они могут иметь до 3 действительных корней. Корни кубического уравнения также могут быть мнимыми, но по крайней мере 1 должен быть действительным. Формула кубического уравнения вместе с несколькими решенными примерами объясняется ниже. Давайте исследуем их.

Что такое формула кубического уравнения?

Формулу кубического уравнения также можно использовать для получения кривой кубического уравнения. Представление кубического уравнения с помощью формулы кубического уравнения очень полезно для нахождения корней кубического уравнения. Многочлен степени n будет иметь n нулей или корней. Кубическое уравнение имеет следующий вид:

ax ³ +bx ² +cx+d=0

Кубическое уравнение можно решить двумя способами

i)    Trial — Ошибка и синтетическое разделение
ii)    Факторизация.

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами

Закажите бесплатный пробный урок

Давайте посмотрим на применение формулы кубического уравнения в следующих решенных примерах.

 

Примеры использования формулы кубического уравнения

Пример 1: Выберите кубические многочлены из следующих:

• p(x): 5x ² + 6x + 1
• р(х): 2х + 3
• q(z): z ² − 1
• г(г): г ² + (√2) ⁹
• г(г): √5z ²
• с(х): 10х
• р(у): у ³ − 6 лет ² + 11 лет − 6
• q(y): 81y ³ − 1
• г(г): г + 3

Решение:  Кубические многочлены среди приведенных выше многочленов:

Кубические многочлены

р(у): у 3 − 6 лет 2 + 11 лет − 6 q(y): 81 год 3 − 1 г(г): г 2 + (√2) 9

Пример 2: Найдите корни следующего кубического уравнения 2x ³ + 3x ² – 11x – 6 = 0

Решение:

Найти: Корни данного уравнения.

Это уравнение не может быть решено с помощью метода факторизации, мы будем использовать метод проб и ошибок, чтобы найти один корень.

Обычно мы начинаем со значения «1».

f (1) = 2 + 3 – 11 – 6 ≠ 0
f (–1) = –2 + 3 + 11 – 6 ≠ 0
f (2) = 16 + 12 – 22 – 6 = 0

Значение «2» делает L.H.S равным «0». Следовательно, два — это один из трех корней.

Теперь мы воспользуемся методом синтетического деления, чтобы найти два других корня.

Мы разделим наше уравнение на (x-2) и частное даст нам два других корня. Мы разделим наше уравнение на (x-2), и частное даст нам два других корня.
Частное: (2x ² + 7x + 3)
Факторизация этого частного,
(2x+1) (x+3)
Отсюда мы получаем значения x as,
x = -1/2 и x = -3
Ответ: Итак, три корня кубического уравнения: x = 2, x = -1/2 и x = -3

Пример 3: Используя формулу кубического уравнения, решите кубическое уравнение x ³ – 2x ² – x + 2.

Решение:

Сначала мы проверим, можем ли мы разложить кубическое уравнение на множители или нет, если его нельзя разложить на множители, мы должны использовать метод синтетического деления. Но в этом случае, посмотрев, мы можем сказать, что это уравнение можно решить с помощью факторизации. Посмотрим, как.
х ³ – 2х ² – х + 2.
= х ² (х – 2) – (х – 2)
= (х ² – 1) (х – 2)
= (х + 1) (х – 1) (х – 2)
Мы можем заключить, что
x = -1, x = 1 и x = 2. 

Ответ: Итак, три корня кубического уравнения: x = -1, x = 1 и x = 2.

Часто задаваемые вопросы по формуле кубического уравнения

Что такое формула кубического уравнения?

Формулу кубического уравнения также можно использовать для получения кривой кубического уравнения. Представление кубического уравнения с помощью формулы кубического уравнения очень полезно для нахождения корней кубического уравнения. Многочлен степени n будет иметь n нулей или корней. Кубическое уравнение имеет следующий вид: ax ³ +bx ² +cx+d=0

Как решать кубические полиномы, используя формулу кубического полинома?

Наиболее часто используемая стратегия решения кубического уравнения:

• Шаг 1: Приведение кубического многочлена к квадратному уравнению.
• Шаг 2: Решите квадратное уравнение, используя квадратную формулу.

Что такое уравнение для формулы кубических многочленов?

Кубическое уравнение представляет собой алгебраическое уравнение третьей степени и имеет вид ось ³ + bx ² + cx + d = 0, где a, b и c — коэффициенты, а d — константа.

Рабочие листы по математике и
наглядный учебный план

Как решать кубические уравнения

Решение полиномиальных функций является ключевым навыком для всех, кто изучает математику или физику, но понимание процесса, особенно когда речь идет о функциях более высокого порядка, может быть довольно сложным. Кубическая функция — один из самых сложных типов полиномиальных уравнений, которые вам, возможно, придется решать вручную. Хотя это может быть не так просто, как решение квадратного уравнения, есть несколько методов, которые вы можете использовать, чтобы найти решение кубического уравнения, не прибегая к страницам и страницам подробной алгебры. 91+d = 0

Каждое решение для x называется «корнем» уравнения. Кубические уравнения имеют либо один действительный корень, либо три, хотя они могут повторяться, но всегда есть хотя бы одно решение.

Тип уравнения определяется наибольшей степенью, поэтому в приведенном выше примере это не было бы кубическим уравнением, если a = 0 , потому что член наибольшей степени был бы равен bx ² и было бы быть квадратным уравнением. Это означает, что следующие уравнения являются кубическими: 92 = 0

Решение с использованием теоремы о факторах и синтетического деления

Самый простой способ решить кубическое уравнение включает в себя немного догадок и алгоритмический тип процесса, называемый синтетическим делением. Начало, тем не менее, в основном такое же, как метод проб и ошибок для решения кубического уравнения. Попробуйте угадать, какой из корней. Если у вас есть уравнение, в котором первый коэффициент a равен 1, то немного легче угадать один из корней, потому что они всегда являются множителями постоянного члена, который представлен выше как 92 − 2x + 24 = 0

Вы должны угадать одно из значений x , но поскольку a = 1, в этом случае вы знаете, что каким бы ни было значение, оно должно быть в 24 раза больше. первый такой множитель равен 1, но это оставит:

1 – 5 – 2 + 24 = 18

Что не равно нулю, и −1 даст:

−1 – 5 + 2 + 24 = 20

Что опять же не ноль. Далее, x = 2 даст:

8 – 20 – 4 + 24 = 8

Еще один провал. Попытка x = -2 дает:

-8 — 20 + 4 + 24 = 0

Это означает, что x = -2 является корнем кубического уравнения. Это показывает преимущества и недостатки метода проб и ошибок: вы можете получить ответ без долгих размышлений, но это отнимает много времени (особенно если вам нужно перейти к более высоким факторам, прежде чем найти корень). К счастью, когда вы нашли один корень, вы можете легко решить остальную часть уравнения.

Ключом является включение теоремы о факторах. Это говорит о том, что если 92 + ax + b) = 0

Слагаемые во второй группе скобок имеют форму квадратного уравнения, поэтому, если найти соответствующие значения для a и b , уравнение можно решить.

Этого можно добиться с помощью синтетического деления. Сначала запишите коэффициенты исходного уравнения в верхней строке таблицы с разделительной чертой, а затем известный корень справа:

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x=-2 \\ & & & & & \\ \hline & & & & & \end{массив}

Оставьте один запасной ряд и добавьте под ним горизонтальную линию. Сначала возьмите первое число (в данном случае 1) вниз до строки под горизонтальной линией

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x =-2 \\ & & & & \\ \hline 1 & & & & \end{array}

Теперь умножьте полученное число на известный корень. В этом случае 1 × −2 = −2, и это записывается под следующим числом в списке следующим образом:

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x=-2 \\ & -2 & & & \\ \hline 1 & & & & \end{array}

Затем добавьте числа во второй столбец и поместите результат под горизонтальной чертой:

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x=-2 \\ & -2 & & & \\ \hline 1 & -7 & & & \end{array}

Теперь повторите только что пройденный процесс с новым числом под горизонталью строка: Умножьте на корень, поместите ответ в пустое место в следующем столбце, а затем добавьте столбец, чтобы получить новое число в нижней строке. Остается:

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x=-2 \\ & -2 & 14 & & \\ \hline 1 & -7 & 12 & & \end{array}

И затем повторите процесс в последний раз.

\def\arraystretch{1.5} \begin{array}{cccc:c} 1 & -5 & -2 & 24 & x=-2 \\ & -2 & 14 & -24 & \\ \hline 1 & -7 & 12 & 0 & \end{array}

Тот факт, что последний ответ равен нулю, говорит вам, что у вас правильный корень, так что если это не ноль, то вы где-то ошиблись. 92 − 7x + 12) = (x – 3) (x – 4)

Вы можете умножить это, чтобы проверить, если хотите. Не расстраивайтесь, если вы не можете сразу увидеть факторизацию; это требует немного практики. Это оставляет исходное уравнение как:

(x + 2) (x — 3) (x — 4) = 0

Которое, как вы сразу видите, имеет решения в x = -2, 3 и 4 (все из которых множители 24, исходная постоянная). Теоретически также можно увидеть всю факторизацию, начиная с исходной версии уравнения, но это намного сложнее, поэтому лучше найти одно решение путем проб и ошибок и использовать подход, описанный выше, прежде чем пытаться обнаружить ошибку. факторизация. 92}

и

r = {c \над{1pt}3a}

Использование этой формулы требует много времени, но если вы не хотите использовать метод проб и ошибок для решения кубического уравнения, а затем квадратного формула, это работает, когда вы проходите через все это.

Как решать уравнения 1-й, 2-й и 3-й степени

Содержание

При изучении математики мы можем столкнуться с задачей решения различных типов уравнений, поэтому в этом посте мы увидим, как решать первые, вторые, и уравнения третьей степени.

Возможные варианты решений

Во-первых, нам нужно понять, каковы возможные решения для решения уравнений, вот они:

Мы определяем как множество возможных решений уравнения.

1-Нет решения: некоторые уравнения не имеют решения, т. е. нет значения переменной, которое могло бы сделать уравнение проверенным или истинным. Вот пример:

Упрощаем уравнение умножая через скобки получаем

и, вычитая из обеих частей, мы получаем 6 = 10, что неверно, и поэтому мы делаем вывод, что для этого уравнения нет решения, т. Е. Пусто или .

2- Уникальное решение: уравнения могут иметь единственное решение, которое их подтверждает, а это означает, что существует одно и только одно значение переменной, которое делает уравнение верным. Вот несколько примеров:

Пример 1:

вычитая 5 с обеих сторон, мы получаем

и разделив на 3 обе части, получим

Вот оно, решение, которое мы ищем, и оно единственное. является единственным значением для того, чтобы уравнение было верным, .

Пример 2:

Вычитая из обеих частей, чтобы исключить в правой части уравнения, мы получаем

и, добавляя 14 к обеим частям, мы получаем, разделив на 4, мы получаем, мы получить одно и только одно значение для i.e.

3- Несколько решений: уравнения могут иметь несколько решений, где есть несколько значений для проверки уравнения, вот пример этого:

мы можем сделать умножение скобок и получить

Используя факторизованную запись уравнения, чтобы правая часть была равна 0, одна из двух скобок должна быть равна 0, и для этого мы имеют два случая:

Либо вычитая 5, мы получаем и деля на 2, мы получаем ,

, либо и добавляя 3 для обеих сторон, мы получаем .

Итак, у этого уравнения есть два возможных решения.

4- Бесконечные решения: Уравнение с бесконечными решениями — это уравнение, всегда проверяемое независимо от значения , давайте посмотрим на следующий пример:

упрощая обе части, получаем

и затем

вычитая из обеих сторон получаем .

Путем упрощения уравнения мы получили, что оно всегда истинно, оно не зависит от значения , поэтому независимо от значения уравнения всегда истинно, и, поскольку имеет бесконечные возможные значения, у нас есть бесконечные решения для этого уравнение.

Теперь, увидев различные варианты числа возможных решений, давайте посмотрим, как решать уравнения первой, второй и третьей степени.

Решение уравнений первой степени

Определение

Мы называем уравнением первой степени любое уравнение, записанное следующим образом: степень не находится в этой форме, но после упрощения она всегда заканчивается формой выше.

Мы называем это уравнением первой степени из-за того, что переменная начинается до степени 1, и это самая высокая степень переменной в уравнении, что означает .

Алгебраический метод

Чтобы решить уравнение первой степени, мы сначала упрощаем его, если оно не упрощается, чтобы получить вид, а затем все, что нам нужно, это передать b в другую сторону и разделить на a, т. е.

и вот оно решение уравнения

Пример:

Упростим уравнение

тогда получим вид

т.е.

Геометрический метод

Мы можем решить уравнение геометрически, рассматривая обе части уравнения как уравнение прямой линии, что означает, что левая часть является уравнением прямой, а правая часть — уравнением прямой.

Затем мы можем провести обе линии в ортометрической плоскости, и мы нарисуем линию и линию, эквивалентную оси x (поскольку ось x — это линия с )

(т.е. ) означает точку, где две линии пересекаются, поэтому, рисуя линию и беря место ее пересечения с осью x, мы получаем наше решение, и оно совпадает с алгебраическим методом.

Пример:

Давайте решим уравнение

Мы нарисуем линию с помощью уравнения

Мы выберем 2 значения и получим соответствующее значение, а затем нарисуем две точки на плоскости и нарисуем новую линию проходящей через две точки, а координата точки пересечения прямой и оси абсцисс является решением уравнения.

Решение уравнений второй степени

Определение

Уравнением второй степени мы называем каждое уравнение стандартной формы с , действительные числа и отличные от нуля. Оно называется уравнением второй степени, потому что наибольшая степень в этом уравнении равна 2 (т.е. ).

Разложение на умножение двух уравнений первой степени

Метод решения уравнения второй степени состоит в том, чтобы записать его в виде умножения двух уравнений первой степени и решить путем нахождения решения двух уравнений первой степени.

Как разложить уравнение второй степени на множители?

Если мы рассмотрим уравнение второй степени, подобное следующему:

Итак, чтобы перейти от правосторонней формы к левосторонней факторизованной форме, нам нужно выяснить значения и знать значение и из правосторонней формы . Давайте попробуем пример:

Нам нужно разделить на 2, чтобы удалить множитель и получить форму

, поэтому мы получаем:

Теперь с этой формой мы знаем, что и .

Итак, нам нужно найти два числа и что их сумма равна 10 и их произведение равно 21.

У нас и 21 можно записать как произведение как или , а так как должно быть равно 10 у нас , значит значения и те, которые делают и .

После этого все, что нам нужно сделать, это записать уравнение в виде .

итак, получаем:

Теперь решение простое, так как произведение двух первой степени равно нулю, то мы точно знаем, что либо первый член произведения равен нулю, либо второй равен к нулю, что означает либо или , мы решаем каждый член первой степени левой части, мы получаем:

и, следовательно, мы имеем два решения уравнения второй степени , .

Мы можем проверить, задав значение или , как показано ниже:

Решение уравнения второй степени с использованием дискриминанта

Дискриминантом уравнения назовем выражение , обычно оно обозначается буквой , т.е.

В зависимости от знака дискриминанта мы можем определить количество и значение, если оно есть, из решений, и возможные случаи следующие:

1- Если дискриминант строго положителен (), то уравнение имеет два различных решения, и решения таковы:

.

Пример:

Определим решения уравнения:

Вычислим:

поэтому имеем

Мы заключаем, что уравнение имеет два различных решения, и они следующие:

3

2- Если дискриминант равен нулю, то уравнение имеет один двойной корень, а это означает, что уравнение имеет два одинаковых решения, то есть одно повторяющееся (или удвоенное) решение. Решение дается следующим образом:

Пример:

Определим решения уравнения:

вычисляя получаем:

   

Делаем вывод, что уравнение имеет одно решение: ; .

Причина, по которой мы называем это решение двойным корнем или повторным решением, состоит в том, что уравнение на самом деле может быть записано как произведение одного и того же полинома первой степени и, следовательно, одного и того же решения для двух полиномов первой степени.

Если взять предыдущий пример, то имеем:

3-Если дискриминант строго отрицательный (), то уравнение не имеет решений.

Пример:

Давайте решим уравнение

вычислив, что получим: он отрицательный).

Решение уравнения второй степени с использованием алгебраических тождеств

В этом методе мы используем алгебраическое тождество

,

, где переменная и действительное число.

Чтобы решить уравнение, мы делаем следующие шаги:

1- Делим обе части на , получаем: .

2- Вычитаем с каждой стороны, получаем: .

3- Добавляем значение (т.е. квадрат одной половины ) к обеим сторонам и получаем:

.

4- Теперь у нас левая часть записывается как Расширение алгебраического тождества, поэтому мы можем записать левую часть следующим образом:

.

5- Извлекаем корень из обеих частей и решаем полученное уравнение.

Для лучшего объяснения воспользуемся этим методом на примере:

Сначала делим на 3, получаем: .

Во-вторых, вычитаем по 4 с обеих сторон, получаем: .

В-третьих, прибавляем к обеим сторонам, получаем: .

Упрощаем правую часть:

,

,

.

Далее, запишем левую часть как алгебраическое тождество, получим: .

В-пятых, извлекаем квадратный корень из обеих частей, получаем: .

В-шестых, вычитаем с обеих сторон, получаем: .

Итак, у нас есть два решения уравнения второй степени, решения:

.

Решая геометрически

мы можем построить график функции и найти какие значения с помощью графического программного обеспечения или графического калькулятора.

Построив график функции , мы получим график, представляющий собой параболу, решение уравнения эквивалентно определению значения для точек пересечения графика с осью x. Есть три случая:

• Во-первых, график пересекается с осью x в двух точках, что означает, что уравнения имеют два различных решения (соответствует случаю, когда ).
• Во-вторых, график пересекается с осью x только в одной точке, а это означает, что уравнение имеет одно двойное решение (соответствует случаю, когда ).
• В-третьих, график не пересекается с осью x, то есть уравнение не имеет решений (соответствует случаю, когда ).

На следующем рисунке показаны три возможных случая:

Решение уравнений третьей степени

Определение

Мы называем уравнением третьей степени или кубическим уравнением каждое уравнение в упрощенном виде имеет следующую стандартную форму:

где , и — действительные числа, отличные от 0.

Это уравнение называется уравнением третьей степени, потому что наибольшая степень в этом уравнении равна 3 (т.е. ).

Решение уравнения третьей степени

По числу возможных решений, в отличие от уравнений первой и второй степени, уравнение третьей степени имеет хотя бы одно решение. Алгебраически причина в том, что член с наибольшей степенью , т. е. зарастает остальными членами и стремится к бесконечности в обе стороны в зависимости от знака, а это означает, что при очень малых отрицательных значениях для () стремятся к , а при очень больших положительных значения для () стремятся (или наоборот, в зависимости от знака коэффициента при члене ), то есть при переходе от одной бесконечности к другой она хотя бы один раз проходила нулем. Возможны три случая: одно, два или три решения.

Чтобы решить уравнение третьей степени, было бы полезно, если бы мы знали одно решение (или корень) для начала. Зная одно решение (помните, что каждое кубическое уравнение имеет по крайней мере одно решение), мы продолжаем разлагать уравнение третьей степени на множители в виде произведения полинома первой степени (используя известное нам решение) на полином второй степени. На данный момент мы не знаем коэффициентов многочлена второй степени, поэтому мы узнаем их значение, а затем решаем уравнение второй степени, и, следовательно, получаем решения уравнения третьей степени.

Для лучшего понимания давайте попробуем решить это уравнение:

зная, что это решение.

Поскольку это решение, то левая часть уравнения третьей степени может быть представлена ​​как произведение полинома первой степени на полином второй степени , что означает, что мы можем записать уравнение в виде:

Теперь нам нужно найти значения и , для этого воспользуемся первой развернутой формой полинома третьей степени, т. е.

расширяя левую часть, мы получаем:

Так как обе стороны теперь в стандартной форме, чтобы выяснить значения , и . Все, что нам нужно сделать, это приравнять каждый коэффициент слева к соответствующему коэффициенту справа, другими словами:

• Во-первых, коэффициенты члена равны, т.е.
• Во-вторых, коэффициенты при члене равны, т.е.
• В-третьих, коэффициенты при члене равны, т.е.
• В-четвертых, константы (коэффициенты члена , означающего действительное число без ) равны, т.е.

Теперь определим значения и :

Итак, у нас есть

и поэтому

у нас есть , заменив a на 1, мы найдем так

Следовательно, мы имеем значения , , .

, поэтому факторизованная форма теперь выглядит следующим образом:

Теперь осталось решить уравнение второй степени

, используя любой из методов, которые мы видели ранее, мы получаем два решения

Следовательно, уравнение третьей степени имеет три различных решения, и уравнение может быть записано в факторизованной форме

.

Как мы упоминали ранее, есть три возможных случая количества решений: одно, два или три решения, и, поскольку мы начинаем с известного решения, для определения количества решений используется полином второй степени, и оно выглядит следующим образом:

• Если многочлен второй степени не имеет решения, то у нас есть только одно решение, с которого мы начали.
• В случае, если многочлен второй степени имеет одно решение (удвоенный корень), то для уравнения третьей степени мы имеем всего два решения, то, с которого начали, и то, что из многочлена второй степени.
• Если многочлен второй степени имеет два различных решения, то всего у нас есть три решения: то, с которого мы начали, и два решения из многочлена второй степени.

Обратите внимание, что в случае, если константа в стандартной форме третьего уравнения равна нулю, это означает, что уравнение имеет форму

мы знаем, что это решение, поскольку каждый член имеет

, поэтому нам не нужно проходить весь процесс для определения коэффициентов второй степени, мы просто берем в качестве множителя и получаем нашу факторизованную форму следующим образом.

с , а уже известны и определять их нет необходимости, поэтому приступаем непосредственно к решению уравнения второй степени.

Пример:

решим уравнение

так как константы нет то возьмем множитель

Мы знаем, что это решение, поэтому мы приступаем к решению уравнения второй степени

, используя один из показанных методов, прежде чем получим два решения или .

Мы заключаем, что уравнение имеет три решения, и факторизованная форма .

решая геометрически

Геометрически, причина, по которой уравнение третьей степени имеет хотя бы одно решение, состоит в том, что график проходит от к или наоборот (от к ), и поэтому мы уверены, что график пересекается с осью x по крайней мере один раз.

Чтобы решить уравнение третьей степени, мы можем построить график функции и найти ее значения с помощью графического программного обеспечения или графического калькулятора.

Решение уравнения эквивалентно определению значения для точки пересечения графика и оси x. Возможны три случая:

1. График пересекается только в одной точке с осью x, поэтому уравнение имеет только одно решение.
2. График имеет две точки пересечения с осью абсцисс, поэтому уравнение имеет два различных решения (одно из них дублируется).
3. График пересекается с осью x в трех точках, поэтому уравнение имеет три различных решения.

На следующем рисунке показаны различные возможные случаи.

Заключение

В заключение знание этих методов решения может сделать процесс решения уравнений первой, второй и третьей степени простым, легким и простым с четкими шагами.

Вы хотите получить больше удовольствия! Проверьте график ниже и посмотрите, как графики меняются в зависимости от значений коэффициентов. Отметьте тип уравнения, которое вы хотите отобразить (одно или несколько), затем проведите пальцем, чтобы изменить значения , и и посмотрите, как динамически меняются графики. Наслаждаться!

Решение кубических уравнений.

Методы и примеры

В математике многочленом называется алгебраическое выражение, состоящее из переменных, коэффициентов и арифметических операций, таких как сложение, вычитание, умножение или деление. Общая форма многочлена: ax ⁿ + bx ^n-1 + cx ^n-2 +… + 1. Уравнение — это математическое выражение, выражающее отношение между двумя значениями. Алгебраическое уравнение — это уравнение, имеющее вид ax ⁿ + bx ^n-1 + cx ^n-2 +… + 1 = 0. Например, 2x-5 = 0 является примером алгебраического уравнения, где (2x-5) является полиномом. Существуют различные типы алгебраических уравнений в зависимости от высшей степени переменной, такие как линейное уравнение, квадратное уравнение, кубическое уравнение, уравнение и т. д.

Кубическое уравнение — это алгебраическое уравнение, в котором полином высшей степени равен 3. Некоторые примеры кубических уравнений:

x ³ — 4x ² + 15x — 9 = 0, 2x ³ — 4x ² + 5 = 0, и т. Д.

Общая форма кубического уравнения —

. ³ + bx ² + cx + d = 0, a ≠ 0

где,

a, b, и c — коэффициенты, а d 90 — константа.

Как решать кубические уравнения?

Кубическое уравнение можно решить традиционным способом, сведя его к квадратному уравнению, а затем решив либо с помощью факторизации, либо по квадратной формуле. Подобно тому, как квадратное уравнение имеет два корня, кубическое уравнение имеет три корня. Кубическое уравнение может иметь три действительных корня или действительный корень и два мнимых корня. Любое уравнение, в том числе и кубическое, всегда должно быть сначала приведено в стандартную форму.

Например, если задано уравнение 2x ² -5 = x + 4/x, то мы должны привести его к стандартной форме, т. е. 2x ³ -x ² -5x- 4 = 0. Теперь мы можем решить уравнение любым подходящим способом.

Кубическое уравнение можно решить следующими способами:

• Нахождение целочисленных решений с помощью списков множителей
• Использование графического метода

Решение кубического уравнения с использованием множителей полинома

Пример: Найдите корни уравнения f(x) = 3x ³ −16x ² + 23x − 6 = 0.

Решение:

= 3x

: 900 ³ −16x ² + 23x − 6 = 0.

Сначала разложите многочлен на множители, чтобы получить корни.

Поскольку константа равна +6, возможные множители равны 1, 2, 3, 6.

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69– 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Мы знаем, что если f(a) = 0, то (x-a) является множителем f(x).

Итак, (x – 2) и (x – 3) являются множителями f(x). Теперь, чтобы найти остальные факторы, используйте метод синтетического деления.

(x – 2)(x – 3) = (x ² – 5x + 6)

 

Итак, (3x-1) – это еще один множитель f(x).

Итак,

корни данного уравнения равны 1/3, 2 и 3.

Решение уравнения графическим методом

Кубическое уравнение решается графически, если вы не можете решить данное уравнение другими способами. Итак, нам нужен точный рисунок данного кубического уравнения. Корни уравнения — это точки, в которых график пересекает ось X. Число действительных решений кубического уравнения равно количеству пересечений графика кубического уравнения с осью x.

Пример: Найдите корни уравнения f(x) = x ³ − 4x ² − 9x + 36 = 0, используя графический метод.

Решение:

Полученное выражение: f(x) = x ³ − 4x ² − 9x + 36 = 0.

Теперь просто подставим случайные значения x на график для заданного function:

x	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56‬	0	19‬	40	36	24	10	0	0	16

Мы видим, что график срезает X-Axis на 3 пункта 3. , следовательно, существует 3 действительных решения.

Судя по графику, решения: x = -3, x = 3 и x = 4.

Следовательно, корни данного уравнения равны -3, 3 и 4.

Задачи, основанные на решении кубическое уравнение

Задача 1. Найдите корни f(x) = x ³ – 4x ² -3x + 6 = 0,

Решение:

x 900 = x ³ – 4x ² -3x + 6 = 0.

Сначала разложите многочлен на множители, чтобы получить корни.

Поскольку константа равна +6, возможные коэффициенты равны 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Итак, (x – 1) является фактором данного уравнения. Теперь, чтобы найти остальные факторы, используйте метод синтетического деления.

 

Итак, f(x) = x ³ – 4x ² -3x + 6 = (x – 1) (x ² – 3x – 6) = 0

Мы знаем, что корнями квадратного уравнения ax ² + bx + c = 0 являются √(3 ² – 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Следовательно, корни данного кубического уравнения равны 1, (3+ √33)/2 и (3–√33)/2. Решение:

Заданное выражение: f(x) = 4x ³ – 10x ² + 4x = 0

⇒ x (4x ² – 10x + 4) = 0

⇒ 904 – 9 0 x (43×2 90 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 или 4x – 2 = 0, x – 2 = 0

⇒ x = 0 или x = 1/2 или x = 2

Следовательно, корни данного уравнения равны 0, 1/2 и 2.

Задача 3: найти корни уравнения f(x) = x ³ + 3x ² + x + 3 = 0.

Решение:

Данное выражение: f(x) = x ³ + 3 x 2.

⇒ х ² (х + 3) + 1(х + 3) = 0

⇒ (х + 3) (х ² + 1) = 0

⇒ х + 3 = 0 или х ² + 1 = 0

⇒ x = -3, ±i

Итак, данное уравнение имеет действительный корень, т.е. -3, и два мнимых корня, т.е. ±i.

Задача 4: найти корни уравнения f(x) = x ³ — 3x ² — 5x + 7 = 0.

Решение:

Указано.

Сначала разложите многочлен на множители, чтобы получить корни.

Поскольку константа равна +7, возможные множители равны 1 и 7.

f(1) = 1 – 3 – 5 + 7 = 0

f(7) = 343 – 147 – 35 + 7 ≠ 0

Итак, (x – 1) является множителем данного уравнения. Теперь для нахождения остальных коэффициентов используем синтетический метод деления.

 

Итак, f(x) = x ³ – 3x ² – 5x + 7  = (x – 1) (x ² – 2x – 7) = 0

Мы знаем, что корни квадратное уравнение ax ² + bx + c = 0 are,

x = [-b ± √(b ² -4ac)]/2a

x = [2 ± √(2 ² –4) (1)(-7)]/2(1)

  = (2 ± √30)/2

Следовательно, корни данного кубического уравнения равны 1, (2+√30)/2 и (2 –√30)/2.

Задача 5: найти корни уравнения f(x) = x ³ − 6x ² + 11x − 6 = 0, используя графический метод.

Решение:

Заданное выражение: f(x) = x ³ − 6x ² + 11x − 6 = 0.

Теперь просто заменим x на график случайными значениями Функция:

4

4

5

0008

70008

x	1	2	3	5
F (x)	0	0	0		240003
240003
240003
		ось абсцисс в 3 точках, следовательно, существует 3 действительных решения. Судя по графику, решения: x = 1, x = 2 и x = 3. Следовательно, корни данного уравнения равны 1, 2 и 3. Решение кубических уравнений Решение кубических уравнений Эта страница предназначена для чтения после двух других: одна на что значит решить уравнение а другой по алгебраическим числам, расширения поля и связанные с ними идеи. Представим себя перед кубом. уравнение x 3 + ax 2 +bx +c = 0. Решить это уравнение означает записать формулу его корней, где формула должна быть выражением, построенным из коэффициенты a, b и c и фиксированные действительные числа (т. е. числа, не зависящие от а, б и в) с помощью только сложения, вычитание, умножение, деление и извлечение корнеплоды. Как и на других страницах, я попытаюсь показать, что можно вывести такую ​​формулу, следуя стандарту математические инстинкты, без потребности в таинственных вспышки вдохновения. Я конечно не утверждаю, что любой здравомыслящий человек должен уметь вывести формулу за час-два — нахождение нужного стандартного математического инстинкт» обычно включает в себя несколько попыток, которые не работают. Тем не менее, список подходящих для пробы в том или ином случае ситуация обычно не слишком длинная. Если вы молоды и амбициозны и еще не умеете решать кубики, я бы порекомендовал иметь или, возможно, прочитав эту страницу, а затем попробуй. Ваши шансы на успех за несколько часов вероятно, выше, чем вы думаете. Начнем с одного из самых полезных (и очевидных) общие принципы решения задач по математике. Если вы пытаетесь решить проблему, посмотрите, может адаптировать известное вам решение к аналогичной проблеме. Используя этот принцип, можно не начинать с чесаться с каждой новой проблемой. Важно не то трудность самой проблемы, но сложность разница между проблемой и другими задачи, решения которых известны. Решение квадратичных уравнений В данном случае совершенно очевидно, что аналогичный проблема, которую мы должны решить, состоит в том, чтобы найти решение квадратное уравнение x 2 + 2ax + b = 0. (У меня есть ставлю множитель 2 просто для удобства — конечно не имеет никакого значения математически.) Как мы это делаем? Итак, мы «наблюдаем», что x 2 + 2ax +b = (x+a) 2 + b-a 2 , который быстро приводит к решению х = -а +/- (а 2 -b) 1/2 Это наблюдение было умным? Будет полезно остановиться на этот более элементарный вопрос, прежде чем продолжить кубический. Итак, давайте представим, что мы даже не знаем, как решать квадратные уравнения. Одно из направлений мысли, которое может привести нас к решению, заключается в следующем. После изучения общего уравнения x 2 + 2ax +b = 0 и, не имея никаких идей, мы возвращаемся к следующему вопросу. Есть ли особые случаи, которые я знаю, как решить? Потом с некоторым смущением отмечаем про себя, что мы можно решить уравнение при a = 0. То есть мы можем решить уравнение x 2 + b = 0 (поскольку мы можем взять квадратные корни). Далее мы, возможно, заметим, что если b=a 2 , то имеем уравнение x 2 + 2ax + a 2 = 0, которое можно переписать (x+a) 2 = 0. Как только мы заметили это, мы поймем, что помогает не то, что правая часть равна нулю, а левая часть идеальный квадрат. Следовательно, мы можем решить (x+a) 2 =б для любого б. Это дает нам целое семейство квадратичных уравнений, которые мы можем решить, поэтому мы были бы безумны, если бы не задали следующий вопрос. Существуют ли квадратные уравнения, которые нельзя записывается в виде (x+a) 2 =b? Чтобы ответить на этот вопрос, нам нужно вернуть его в исходное состояние. форму, умножив скобку и принимая b на левую сторону. Это дает нам уравнение x 2 + 2ax + a 2 -b = 0. Тогда ясно что мы можем сделать 2а любым числом, которое захотим, и что, сделав Итак, мы можем сделать 2 -b любой другой номер, который мы хотим. Так квадратное решается. Если вы думаете, что это слишком много, чтобы заметить, что уравнение x 2 + 2ax + a 2 = 0 может решить, то вот еще один маршрут. Это не займет много времени любопытство узнать, является ли 1+2 1/2 алгебраическим число или большой талант, чтобы заметить, что если x=1+2 1/2 тогда (x-1) 2 = 2. Обобщение этого примера приводит быстро к наблюдению, что уравнения вида (х+а) 2 =b можно решить. Предварительное упрощение кубика. Каким было бы естественное обобщение на кубики процесс заполнения квадрата? Чтобы ответить на вопрос такого рода часто бывает полезной следующая тактика. Дайте общее описание того, что это такое хотелось бы обобщить. Я попытаюсь проиллюстрировать, что я имею в виду, просто сделав это. Для завершения квадрата заметим, что (х+а/2) 2 = х 2 + топор +а 2 /4, так что мы можем записать любое квадратное число, начинающееся с x 2 + ax как (x+a/2) 2 плюс константа. Чтобы положить это другое образом, если мы допустим y=x+a/2, то y удовлетворяет квадратному уравнению особо простой формы y 2 +C=0. Из конечно, как только мы решили уравнение для y, это легко получить решение для x, так как x очень простое линейная функция y. Что было проще в уравнении для y? Есть два разумные ответы на этот вопрос, и стоит глядя на них обоих. Во-первых, следует отметить, что уравнение для y включает только y 2 и константа член — таким образом, замена x на y позволяет нам предположить, что коэффициент линейного члена равен нулю. Второй очевиднее — проще потому, что позволив себе извлечения квадратных корней, мы заявили, что уравнения форма y 2 +C=0 решается одним махом. Это направление мысли приводит к двум вопросам. 1. Есть ли аналогичный способ упростить кубик чтобы некоторые из коэффициентов стали равны нулю? 2. Есть ли аналогичный способ упростить кубик так что он принимает форму y 3 +К=0? Ответ на вопрос 1 найти несложно. Если y=x+t, затем y 3 =x 3 +3tx 2 +3t 2 х+t 3 . Следовательно, если t=a/3, то куб х 3 + топор 2 +bx +c может переписать как y 3 + py +q, где (для чего стоит) p=b-3t 2 и q=c-bt+2t 3 . Написание этого с точки зрения a имеем p=b-a 2 /3 и q=c-ab/3+2a 3 /27. Что касается второго вопроса, мы можем начать думать о это, задав себе следующее прямое обобщение вопрос, который мы задали о квадратичных. Существуют ли кубические уравнения, которые нельзя записывается в виде (x+a) 3 =b, и если да, то какие могут? Расширяя и вычитая, мы обнаруживаем, что можем легко решить уравнения вида x 3 + 3ax 2 + 3a 2 x + а 3 — б = 0 Когда уравнение x 3 + топор 2 + bx +c = 0 этого типа? Сравнивая с предыдущим мы видим, что он имеет требуемый вид, если пара (a,b) форма (3с,3с 2 ) для некоторых s, что является тогда и только тогда если a 2 = 3b. Поэтому естественно возникает следующий вопрос. Можем ли мы заменить x некоторым y=x+t так, чтобы y удовлетворяет кубу с a’ 2 = 3b’ (где a’ и b’ коэффициенты y 2 и y соответственно). Этот подход выглядит многообещающе, потому что t дает нам одну степень свободы и все, что мы хотим, это одно условие — что а’ 2 -3b’ должно быть равно нулю. Очевидно, как ответить на вопрос, поэтому пусть нам идти вперед и сделать это. Записав x=y-t и подставив, получим уравнение (у-т) 3 + а(у-т) 2 + б(у-т) +с = 0 , который преобразуется в у 3 + (а-3т)у 2 + (b-2at+3t 2 у) + c-bt+at 2 +t 3 Это дает нам a’=a-3t и b’=b-2at+3t 2 . Следовательно, а’ 2 -3b’=а 2 -6at+9t 2 -3b+6at-9t 2 =а 2 -3b. Мы показали, что мы не можем изменить количество a 2 -3b путем замены вида y=x+t. В других словами, ответ на вопрос 2 выше — нет, по крайней мере, когда «подобным образом» означает, что мы должны использовать такую ​​замену. немного более причудливый способ сказать, что 2 -3b не меняется, это позвонить это инвариант . Является ли несчастным случаем, что 2 -3b является инвариантом? Дальнейшее размышление дает нам причину этого явления и показывает, что мы были глупы, когда ожидали, что кубик можно решить так просто. Вы, наверное, уже заметили, что 2 -3b=-3p, где p было коэффициент линейного члена, который мы получили, когда мы преобразовали кубический x 3 + ax 2 + bx +c в более простой кубический у 3 + ру + кв. Мы выбрали y равным x+a/3, и это легко увидеть. что никакой другой выбор не привел бы к коэффициенту у 2 быть нулем. Следовательно, обнаруженный нами инвариант имеет интерпретацию (как всегда следует ожидать): это коэффициент линейного член, когда квадратичный член был удален заменой форма y=x+t. Но теперь очевидно, что эта величина является инвариантом. После все, если я подставлю y=x+s (для любые s) и потом спрошу, что дальнейшая замена z=y+r удалит квадратичный член, ответ заключается в том, что z=x+r+s и r+s должны быть равны /3. Следовательно, p, который я получаю для y такое же, как p, которое я получаю для x. Тупик и как из него выйти. На самом деле было заранее очевидно, что второй подход решение кубика было обречено на провал, так как, если бы это было возможно чтобы «завершить куб», тогда каждый кубик будет иметь вид (х+а) 3 +б. Но если бы это было правдой, то почему бы нам удосужились преобразовать куб в такую ​​форму? Итак, собрать куб не только невозможно, это невозможно по простым и веским причинам. С другой стороны, не завершение куба естественное обобщение завершения квадрат? Теперь, когда мы попытались и потерпели неудачу, хотя мы упустили наш главный шанс решить кубик (который был чтобы увидеть, как мы решили квадратное и адаптировать наш метод). Однако такое пораженческое отношение часто является ошибкой. Возможно, можно даже выразить это мнение с помощью другого общего принцип. Может быть много способов адаптировать или обобщить доказательство. Но как же, спрашивается, искать разные обобщения? Позвольте мне изменить более раннее предложение. Дайте описание аргумента, который хотелось бы обобщить. Объясните, почему это сработало. Делать объяснение более расплывчатое и более общее, а затем попытаться найти разные аргументы, которые работают по одним и тем же (расплывчатым) причинам. Чтобы мы могли применить это на практике, позвольте мне еще раз подскажите как решать квадратное. Пусть у=х+а/2. Тогда y удовлетворяет квадратному уравнению особо простой формы y 2 +C=0. Как только мы решили это уравнение для y, это легко получить решение исходного уравнения относительно x, так как x является очень простой линейной функцией y. Почему, в общих чертах, это сработало? Нам нужно было два свойства у. Во-первых, y должен удовлетворять уравнению, которое мы умели решать, а во-вторых х должен зависеть от у простым способом — так что, как только мы узнали y, мы могли бы работать Икс. Если мы хотим перенести этот подход на кубический, то у нас должны быть четкие ответы на следующие два вопроса. (i) Какие уравнения мы можем решить? (ii) Как мы готовы позволить у зависеть от х? Ответ на первый вопрос мы более-менее знаем уже. Мы можем решать линейные и квадратные уравнения, и также кубические уравнения, если они имеют красивую форму х 3 +С=0. Что касается второго, то до сих пор мы рассматривали замены вида y=x+t. Какие еще замены может быть есть? Я отвечу на этот вопрос еще одним проверенным временем метод, который встречается во всей математике. Сделайте самое общее, что только можно себе представить. Затем, когда вы обнаружите, что вам нужны определенные свойства, сделайте что вы сделали более конкретно, введя эти свойства. Предположим, что мы сделали замену y=f(x). (Это трудно понять, как мы могли бы быть более общими, чем это.) Давайте предположим, что это приводит к уравнению для y, которое мы можем решить. Когда знание y будет полезным? Ответ очевиден — когда мы можем решить уравнение y=f(x) относительно x через y. Но мы знать, какие уравнения мы можем решить — линейные, квадратные и простые кубические уравнения. Мы уже пробовали линейные замены и увидели их ограничения, поэтому у нас осталось два разумных возможности для f(x). Один х 2 +ax+b (это не трудно увидеть, что дающий x 2 другой коэффициент не будет иметь существенного значения) и другой х 3 +с. Следуя некоторым очень общим методам решения проблем, мы к идее, которая определенно нова. Немного отойдя, мы понял, что важная вещь в замене y=x+t в решение квадратного уравнения не было магическим или была линейной, но обратимой в том смысле, что мы могли дать формула для x через y. Теперь тупик вышел из тупика что у нас есть подход, чтобы попробовать с кубическим. Это может не сработать, но иметь подход, который может работать, а может и не работать, гораздо лучше, чем вообще никакого подхода. Подстановка, решающая кубики. Если бы линейная замена работала для квадратных уравнений, то что звучит более вероятно для кубических уравнений — квадратичная замена или особый вид кубического замена? Как-то квадратичный более перспективен, поскольку это соответствует общему описанию степени один меньше, чем в уравнении, которое пытаются решить. Это не особенно убедительный аргумент, но худшее, что может случиться, это то, что мы попробуем это, и это не Работа. Итак, давайте посмотрим, что мы можем получить с заменой у=х 2 +ux+v. Теперь мы столкнулись с проблемой. Мы надеемся, что вы будете удовлетворяют кубике особенно простого вида. Но это Очевидно, что удовлетворяет любому куб.? Если вы сделаете не находите это очевидным, то это тот момент, когда он будет помогите прочитать мою страницу на алгебраические числа, потому что там я неоднократно использовал трюк, который работает и здесь (и который, я подчеркиваю, возникло естественным образом в этом контексте). Мы знаем, что x удовлетворяет уравнению x 3 + топор 2 + bx +c = 0 Но это значит, что каждый раз, когда мы записываем многочлен в x мы можем заменить x 3 на -ax 2 -bx-c, x 4 by -ax 3 -bx 2 -cx и так далее. То есть каждое полиномиальное выражение от x равно некоторому квадратичная функция x. Но у 2 и у 3 являются полиномиальными функциями от x и, следовательно, равны квадратичным те. Это тривиально верно и для 1, и для y. Следовательно числа 1, у, у 2 и у 3 все форма rx 2 +sx+t. Чтобы y удовлетворяло кубике, мы нужна нетривиальная линейная комбинация 1, y, y 2 и y 3 равно нулю. Для его получения нужно решить три однородных линейных уравнения с четырьмя неизвестными, которые мы всегда можно сделать. Итак, теперь мы можем более точно описать возможный метод: пусть y=x 2 +ux+v, вычислить y 2 и y 3 через x, привести их к квадратичным используя тот факт, что х 3 =-ax 2 -bx-c, найти нетривиальную линейную зависимость между 1, у, у 2 и у 3 , выпишите соответствующий кубический y 3 +dy 2 +ey+f в y и, наконец, (самая важная часть) умно выберите вас и v таким образом, что d 2 =3e. У нас нет гарантии, что это сработает, потому что может быть, как это случилось с линейными заменами, просто — это без выбора u и v, что делает д 2 равно 3е, а может быть и так, хотя такой выбор существует, зависимость u и v от a, b и c настолько сложны, что мы не знаем, как решить полученные уравнения. Разумно не слишком сильно беспокоиться о первой потенциальной трудности, потому что теперь у нас есть дополнительная степень свободы, и кажется, нет аргумента, говорящего нам, что это никак не может помочь. Однако, если ты сейчас уйдешь и попытаться проработать детали изложенного аргумента выше вы увидите, что усложнение есть что-то одно точно стоит побеспокоиться. Действительно, может показаться, что после какое-то время, что для того, чтобы вычислить u и v, у вас будет решить квинтикс . Позвольте мне считать, что просто погрузиться в плохая идея. В любом случае, это еще одно хорошее решение проблемы стратегия попробовать более простые (но менее общие) подходы во-первых, на всякий случай, если они работают. Итак, как мы можем сделать приведенные выше расчеты выполнимы? Одной из очевидных идей является использование упрощения, которое мы получили ранее: мы могли бы также предположить, что a = 0. Это позволит нам заменить x 3 от -px-q. На самом деле, немного приятнее сказать, что х 3 =px+q, что мы можем сделать, изменив определения p и кв. А как насчет замены y=x 2 +ux+v? Что ж, вспоминая инвариант, который мы открыли ранее, мы должны реализовать что y удовлетворяет кубике, которую мы можем легко решить тогда и только тогда, когда y-v делает. Так что мы могли бы также сэкономить на алгебре, установив v=0. В других словами, мы не только упростим расчеты, установив y=x 2 +ux, мы даже не будем терять общности. Вот некоторые расчеты, которые возникают, когда начинают с уравнение х 3 =px+q, устанавливает y=x 2 +ux и пытается найти кубику, удовлетворяющую y. Делая это напрямую (что вычислив y 2 и y 3 и решив некоторые одновременные уравнения) все еще становится неприятно, но расчеты могут быть управляемыми за счет упрощения по мере продвижения вдоль, как это сделано ниже. Я также сэкономлю время, написав C в означают константу (зависящую от p,q и u), которая может варьироваться от линия к строке. x 3 =px+q у=х 2 +ux y 2 =x 4 +2ux 3 +u 2 x 2 =(u 2 +p)x 2 +(2up+q)x+2uq =(u 2 +p)y+(up+q-u 3 )x+2uq у 3 =(и 2 +р)у 2 +(up+q-u 3 )xy+2uqy =(и 2 +р)у 2 +(up+q-u 3 )(x 3 +ux 2 )+2uqy =(и 2 +р)у 2 +(up+q-u 3 )(ux 2 +px)+2uqy+C =(и 2 +р)у 2 +(up+q-u 3 )(uy+(p-u 2 )x)+2uqy+C Из более ранней строки у нас есть (вверх+к-у 3 )х =у 2 -(у 2 +р)у+С так что это равно (у 2 +р)у 2 +(up+q-u 3 )uy+(p-u 2 )(y 2 -(u 2 +p)y) +2уки+С =2py 2 +(u 2 p+3uq-p 2 )y+C Таким образом, y удовлетворяет кубическому уравнению г 3 -2py 2 -(u 2 p+3uq-p 2 )y-C=0 и все, что осталось решить, можно ли выбрать тебя таким образом, что (-2p) 2 =-3(u 2 p+3uq-p 2 ) то есть такой что 3pu 2 +9qu+p 2 =0 Это, будучи квадратичным по u, может быть решено. Используя это значения u получается кубика по y, которая может быть «завершена». Это дает решение y. Тогда х можно вычислить из y путем решения еще одного квадратного уравнения. Конечно, получившаяся формула, если ее доработать, было бы довольно неприятно, и теперь я должен сказать, что лучше были обнаружены методы (включая различные замены) что приводит к более легким расчетам и более аккуратным ответам. Они легко найти в Интернете, но все, как правило, имеют «волшебное» качество в них. Я также должен сказать, что я не обсудили раздражающую проблему, что не все «решения» которые возникают вышеописанным способом, обязательно будут растворами, поскольку знание y не определяет однозначно x. Просто посмотреть, какие могут быть другие разумные замены, вернемся к вопросу о том, какие из них позволяют вычислить Икс. Мы заметили, что могли бы сделать это, если бы у была квадратичной функцией х. Но в этом не было абсолютной необходимости, даже если бы мы могли решать только квадратные уравнения. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт