Ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Маша сложила нить пополам, получившуюся двойную нить снова сложила пополам, а затем еще раз пополам.
В треугольнике ABC известно, что AC=6, BC=8, угол C равен 90°. Найдите радиус описанной около этого треугольника окружность. На пишите пожалуйста решение
Назовем наибольшим делителем составного натурального числа его самый большой, не равный ему, делитель. Наименьшим делителем назовем его самый маленький, не равный единице, делитель. Например, у числа
—+—+—=30 Заполните пустые места используя данные числа (1,3,5,7,9,11,13,15) Одно и тоже число можно использовать несколько раз.
«Если строитель построил человеку дом и свою работу сделал непрочно, а дом, который он построил, рухнул и убил хозяина, то этот строитель должен быть казнен. Если он убил сына хозяина, то должны
Пользуйтесь нашим приложениемАлгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.§ 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ.  РАЦИОНАЛЬНЫЕ ЧИСЛА. РАЦИОНАЛЬНЫЕ ЧИСЛА.§ 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов.  § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители.  § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76.  § 130. Примеры графического решения уравнений и систем уравнений. |
Системы линейных и квадратных уравнений
| Линейное уравнение — это уравнение линии . | |
| Квадратное уравнение представляет собой уравнение параболы и имеет по крайней мере одну переменную в квадрате (например, х 2 ) | |
| И вместе они образуют Систему линейного и квадратного уравнения |
Система из этих двух уравнений может быть решена (найти место их пересечения) либо:
- Графически (путем их построения на графике функций и увеличения)
- или используя Алгебра
Как решить с помощью алгебры
- Преобразование обоих уравнений в формат «y =»
- Установить их равными друг другу
- Упростить до формата «= 0» (как стандартное квадратное уравнение)
- Решите квадратное уравнение!
- Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x,y) баллов в качестве ответов
Пример поможет:
Пример: Решите эти два уравнения:
- y = x 2 — 5x + 7
- у = 2х + 1
Превратите оба уравнения в формат «y=»:
Они оба в формате «y=», так что переходите сразу к следующему шагу
Установите их равными друг другу
x 2 — 5x + 7 = 2x + 1
Упростить в «= 0 (аналогично стандартному квадратному уравнению)
Вычесть 2x с обеих сторон: x 2 — 7x + 7 = 1
Вычесть 1 с обеих сторон: x 2 — 7x + 6 = 0
900 03
Решить квадратное уравнение!
(самая сложная часть для меня)
Вы можете прочитать, как решать квадратные уравнения, но здесь мы будем учитывать квадратное уравнение:
Начните с: x 2 — 7x + 6 = 0
Перепишите -7x как -x-6x: x 2 — x — 6x + 6 = 0
Тогда: x(x-1) — 6(x-1) = 0
Тогда: (x-1)(x-6) = 0
Что дает нам решения x=1 и x=6
Используйте линейное уравнение для вычисления соответствующих значений «y», поэтому мы получаем ( x,y) баллы как ответы
Соответствующие значения y (см. также график):
также график):
- для x= 1 : y = 2x+1 = 3
- для х= 6 : у = 2х+1 = 13
Наше решение: две точки (1,3) и (6,13)
Я думаю об этом как о трех стадиях:
Объединить в квадратное уравнение ⇒ Решить квадратное уравнение ⇒ Подсчитать точки
Решения
Возможны три случая:
- Нет реального решения (происходит, когда они никогда не пересекаются)
- Одно действительное решение (когда прямая только касается квадрата)
- Два реальных решения (как в примере выше)
Время для другого примера!
Пример: Решите эти два уравнения:
- y — x 2 = 7 — 5x
- 4г — 8х = -21
Превратите оба уравнения в формат «y=»:
Первое уравнение: y — x 2 = 7 — 5x
Добавьте x 2 к обеим сторонам: y = x 2 + 7 — 5x 900 11
Второе уравнение: 4y — 8x = -21
Добавьте 8x к обеим частям: 4y = 8x — 21
Разделите все на 4: y = 2x — 5,25
Установить их равными друг другу
x 2 — 5x + 7 = 2x — 5,25
Упростить до формата «= 0» (как стандартное квадратное уравнение)
Вычесть 2x с обеих сторон: x 2 — 7x + 7 = -5,25
Прибавить 5,25 к обеим сторонам: x 2 — 7x + 12,25 = 0
90 002 Решите квадратное уравнение!
Использование квадратной формулы из квадратных уравнений:
- x = [-b ± √(b 2 -4ac)] / 2a
- х = [7 ± √((-7) 2 -4×1×12,25)] / 2×1
- х = [7 ± √(49-49)] / 2
- х = [7 ± √0] / 2
- х = 3,5
Только одно решение! («Дискриминант» равен 0)
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы мы получили (x,y) баллов в качестве ответов
Соответствующее значение y:
- для x = 3,5 : у = 2x-5,25 = 1,75
Наше решение: (3. 5,1.75)
5,1.75)
Пример из реальной жизни
Бум!
Пушечное ядро летит по воздуху по параболе:
y = 2 + 0,12x — 0,002x 2
Земля наклонена вверх: y = 0,15x
Куда приземляется пушечное ядро?
Оба уравнения уже имеют формат «y =», поэтому приравняем их друг к другу:
0,15x = 2 + 0,12x — 0,002x преобразовать в формат «= 0» :
Перенести все члены влево: 0,002x 2 + 0,15x — 0,12x — 2 = 0
Упростить: 0,002x 2 + 0,03x — 2 = 0
Умножить на 500: x 2 + 15x — 1000 = 0
Решить квадратное уравнение:
Разделить 15x на -25x+40x: x 2 -25x + 40x — 1000 = 0
Тогда: х (x-25) + 40(x-25) = 0
Тогда: (x+40)(x-25) = 0
x = -40 или 25
Отрицательный ответ можно игнорировать, поэтому x = 25
Используйте линейное уравнение, чтобы вычислить соответствующее значение «y»:
y = 0,15 x 25 = 3,75
Таким образом, пушечное ядро ударяется о склон в точке (25, 3. 75)
75)
Вы также можете найти ответ графически с помощью графического редактора функций:
Обе переменные в квадрате
Иногда ОБА члена квадратного числа можно возвести в квадрат:
Пример: Найдите точки пересечения
Окружности x 2 + y 2 = 25
И прямой линии 3y — 2x = 6
9 0002Сначала поместите строку в «y =» формат:
Переместить 2x вправо: 3y = 2x + 6
Разделить на 3: y = 2x/3 + 2
СЕЙЧАС. Вместо того, чтобы делать круг в формате «y=», мы можем использовать замену ( замените «y» в квадратном выражении линейным выражением):
Поместите y = 2x/3 + 2 в уравнение окружности: x 2 + (2x/3 + 2) 2 = 25
Расширьте: x 2 + 4x 2 /9 + 2(2x/3)(2) + 2 2 = 25
Умножить все на 9: 9x 2 + 4x 2 + 2(2x)(2)(3) + (9)(2 2 ) = (9)(25)
Упростить: 13x 2 + 24x + 36 = 225
Вычесть 225 от обе стороны: 13x 2 + 24x — 189 = 0
Теперь это в стандартной квадратичной форме, давайте решим это:
13x 2 + 24x — 189 = 0
Разделить 24x в 63x-39x: 13x 2 + 63x — 39x — 189 = 0
Тогда: x(13x + 63) — 3(13x + 63) = 0
Тогда: (x — 3)(13x + 63) = 0
Итак: x = 3 или -63/13
Теперь вычислите значения y:
Подставьте x = 3 в линейное уравнение:
- 3 года — 6 = 6
- 3 года = 12
- г = 4
- Итак, одна точка равна (3, 4)
Подставьте x = -63/13 в линейное уравнение:
- 3 года + 126/13 = 6
- г + 42/13 = 2
- г = 2 — 42/13 = 26/13 — 42/13 = -16/13
- Значит другая точка (-63/13, -16/13)
8184, 8185, 8186, 8187, 8188, 8189, 8190, 8191, 8192, 8193, 8194, 8195, 8196, 8197, 8198
Решение линейно-квадратичных систем
Горячая математика Вероятно, вы уже решали системы линейных уравнений. А как насчет системы двух уравнений, где одно уравнение линейное, а другое квадратичное?
А как насчет системы двух уравнений, где одно уравнение линейное, а другое квадратичное?
Мы можем использовать вариант метода подстановки для решения систем этого типа.
Помните, что форма уравнения наклона и точки пересечения для прямой имеет вид y=mx+b, а стандартная форма уравнения для параболы с вертикальной осью симметрии имеет вид y=ax2+bx+c, a≠0 .
Во избежание путаницы с переменными запишем линейное уравнение в виде y=mx+d, где m наклон и d является y-пересечением линии.
Подставить выражение для y из линейного уравнения, в квадратное уравнение. То есть подставьте mx+d для тебя в y=ax2+bx+c .
mx+d=ax2+bx+c
Теперь перепишите новое квадратное уравнение в стандартной форме.
Вычесть мх+д с обеих сторон.
(mx+d)−(mx+d)=(ax2+bx+c)−(mx+d)0=ax2+(b−m)x+(c−d)
Теперь у нас есть квадратное уравнение с одной переменной, решение которого можно найти по квадратной формуле.
Решения уравнения ax2+(b−m)x+(c−d)=0
даст x-координаты точек пересечения графиков прямой и параболы. Соответствующие координаты y можно найти с помощью линейного уравнения.
Соответствующие координаты y можно найти с помощью линейного уравнения.
Другой способ решения системы — построить график двух функций на одной координатной плоскости и определить точки пересечения.
Пример 1:
Найдите точки пересечения прямой y=2x+1 и парабола y=x2−2.
Замена 2x+1 для y в y=x2−2.
2x+1=x2−2
Запишите квадратное уравнение в стандартной форме.
2x+1-2x-1=x2-2-2x-10=x2-2x-3
Используйте квадратную формулу, чтобы найти корни квадратного уравнения.
Здесь a=1, b=−2, и c=−3.
x=−(−2) ± (−2)2 − 4(1)(−3)2(1)=2 ± 4 + 122=2 ± 42=3, −1
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
х=3⇒у=2(3)+1 =7x=−1⇒y=2(−1)+1 =−1
Следовательно, точками пересечения являются (3,7)
и (−1,−1).
Начертите параболу и прямую на координатной плоскости.
Аналогичный метод можно использовать для нахождения точек пересечения прямой и окружности.
Пример 2:
Найдите точки пересечения линии y=−3x и окружность x2+y2=3.
Замена −3x для тебя в х2+у2=3 .
x2+(−3x)2=3
Упрощение.
x2+9×2=310×2=3×2=310
Извлечение квадратного корня, x=±310.
Подставьте значения x в линейное уравнение, чтобы найти соответствующие значения y.
х=310⇒у=-3(310) =-3310x=- 310⇒y=-3(-310) =3310
Таким образом, точками пересечения являются (310, −3310) и (−310, 3310).
Нарисуйте окружность и прямую линию на координатной плоскости.
…или линия и эллипс.
Пример 3:
Решить систему уравнений y=−5 и х29+у24=1.
Замена −5 для тебя в −5.
x29+(−5)24=1
Упрощение.
x29+(-5)24=14×236+9(25)36=14×2+225=364×2=-189×2=-1894
Здесь мы имеем отрицательное число как квадрат числа. Итак, два уравнения не имеют действительных решений.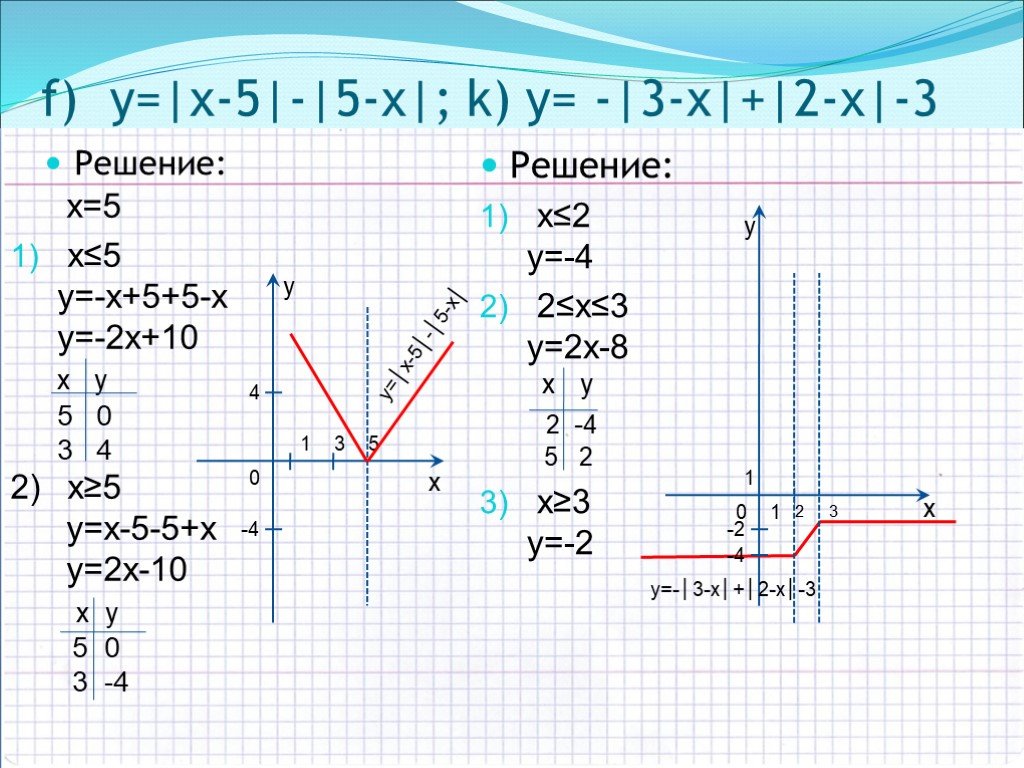

 03.16
03.16 Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с.
Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с.