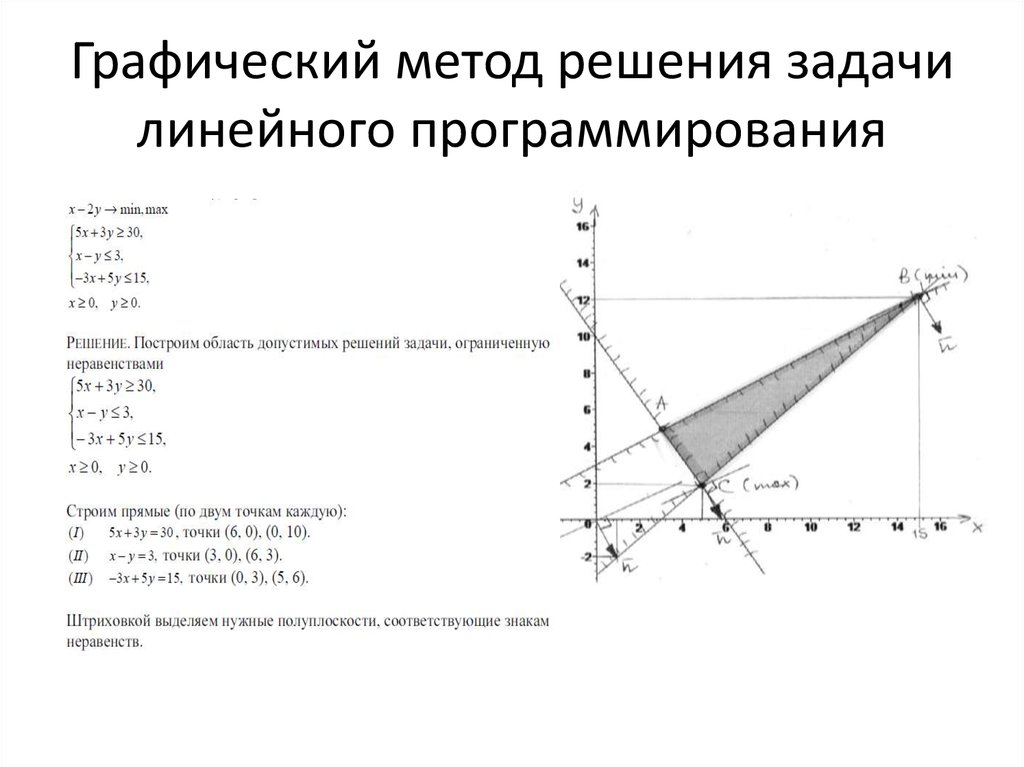
Решение задачи линейного программирования графически в трехмерном пространстве
Если в задаче три переменные, то она тоже допускает графическое решение в трехмерном пространстве. При этом рисунок делается условный, не строго выдерживая масштаб. Однако взаимное расположение точек на осях должно быть верным и соответствующим их числовым значениям.Решить задачу линейного программирования двумя методами: графически в трехмерном пространстве и симплекс-методом.
f = 2x + 5y + 2z → max
при условиях x+4y+4z ≤ 16, 3x+2y+4z ≤ 20, x,y,z ≥ 0
Находится линия пересечения этих треугольников. Точнее, находятся координаты двух точек, являющихся концами части этой линии пересечения, лежащей в первом октанте. Множество допустимых планов (как правило) является симплексом с конечным числом угловых точек. Все эти угловые точки указывают на рисунке и точно вычисляют их координаты.
x+4y+4z = 16
3x+2y+4z = 20
1) при z = 0
x+4y = 16
3x+2y = 20
-5x = -24, откуда x = 4,8; y = 2,8; z = 0
x+4z = 16
3x+4z = 20
2x = 4, откуда x = 2, y = 0, z = 3
Потом вычисляют значение целевой функции во всех угловых точках и выбирают из них оптимальное.

F(4,8; 2,8; 0) = 2*4,8 + 5*2,8 + 2*0 = 23,6
F(2; 0; 3) = 2*2+ 5*0 + 2*3 = 10
Ответ: x = 4,8; y = 2,8; z = 0, fmax = 23,6
Пример №1. Решить задачу линейного программирования графически в трехмерном пространстве.
f(x) = 3x1 + 5x2 – x3
при ограничениях
x1 + x2 + 2x3 = 6
x2 + x3 – x4 = 4
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
Решение. Проведем анализ задачи. В задаче 4 переменные и 2 основных ограничения в виде равенств (не считая условия неотрицательности). Так как ограничения даны в виде равенств, то задача в канонической форме. В данном виде геометрически задачу не решить, так как много переменных.
 Эти переменные можно исключить из задачи, тем самым упростив её формулировку. Исключаемыми переменными объявим первую и последнюю.
Эти переменные можно исключить из задачи, тем самым упростив её формулировку. Исключаемыми переменными объявим первую и последнюю.
Для этого из первого условия системы ограничений выразим x1 = 6- x2 — 2x3 , а из второго уравнения x4 = x2 + x3 — 4.
Подставим x1 = 6- x2 — 2x3 в целевую функцию и получим новую целевую функцию
F = 18 + 2x2 – 7x3 и новую систему ограничений без переменных x1, x4:
x2 + x3 ≥ 4
x2 ≥ 0, x3 ≥ 0
За счет неотрицательности исключаемых переменных получили неравенства в разные стороны.
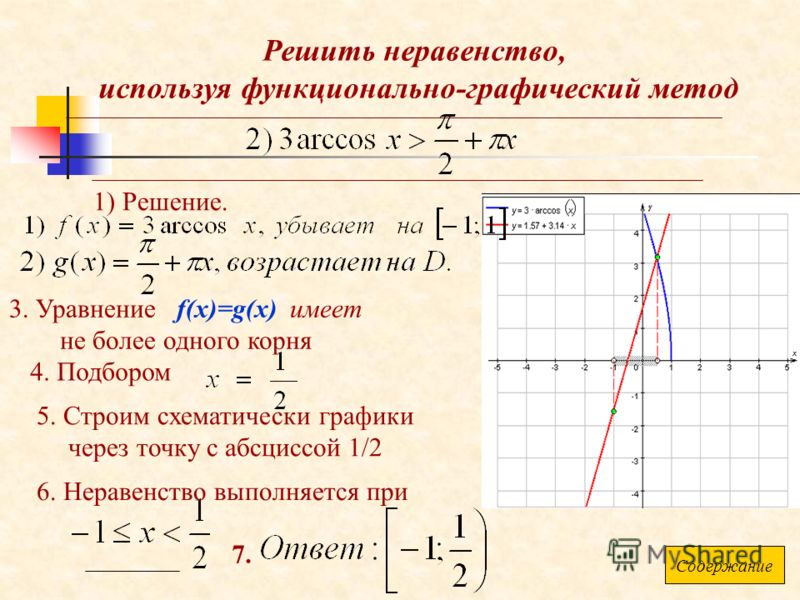
Полученную задачу линейного программирования стандартного вида на плоскости решим графически. На плоскости x2Ox3 изобразим множество допустимых планов, которое удовлетворяет системе ограничений.
 Получим треугольник с вершинами в точках B(4,0), C(6,0), A(2,2).
Получим треугольник с вершинами в точках B(4,0), C(6,0), A(2,2).
Вычислим значение новой целевой функции в этих угловых точках:
F(B) = F(4,0) = 18 + 8 = 26
F(C) = F(6,0) = 18 + 12 = 30
F(A)= F(2,2) = 18 + 4 – 14 = 8
Получили решение вспомогательной (новой) задачи: x2 = 6, x3 = 0, F = 30.
Отсюда вычисляем оптимальный план и максимум исходной задачи:
x1 = 6 – 6 — 0 = 0, x4 = 6 + 0 – 4 = 2, f = F = 30
Ответ. x1 = 0, x2 = 6, x3 = 0, x4 = 2, fmax = 30.
Для решения этой задачи также можно использовать калькулятор.
Пример №2. Найти графическим методом или симплекс-методом какое-нибудь решение системы.
x + y + z = 10
5x +2y +z ≥ 26
6x + 5y + 3z ≤ 57
Решение.
Здесь не задана целевая функция. Однако графическим методом можно найти область допустимых значений (ОДР). Для этого выразить
Для этого выразить z=10-x-y и подставить в другие уравнения:
5x+2y+10-x-y ≥ 26
6x+5y+30-3x-3y ≤ 57
или
4x+y ≥ 16
3x+2y ≤ 27
Таким образом, осталось две переменные.
Решение задачи графическим методом. Методы решения задач линейного программирования с n-переменными
Методы решения задач линейного программирования с n-переменными
курсовая работа
Задача решается графическим методом, если разность между количеством переменных и количеством ограничений равна двум.
n=4 (количество переменных)
m=2 (количество ограничений)
n-m=4-2=2
Выразим две переменные:
Подставим значения переменных в целевую функцию.
Найдем координаты прямых.
I. 1266,239-1,191x2-0,203x4=0
1,191x2+0,203x4=1266,239
x2=1063,172-0,17x4
x2 | 1063,172 | 893,172 | |
x4 | 0 | 1000 |
II. 278,525-0,16x2-0,431x4=0
278,525-0,16x2-0,431x4=0
0,16x2+0,431x4=278,525
x4=646,229-0,371x2
x2 | 0 | 1000 | |
x4 | 646,229 | 275,229 |
III. 55255,72+4,35x2+7,188x4=0
-4,35x2-7,188x4=55255,72
x2= -12702,464-1,652x4
x2 | -11050,464 | -3817,536 | |
x4 | -1000 | -10000 |
Построим область допустимых решений задачи, ограниченную прямыми:
x2=1063,172-0,17x4(I)
x4=646,229-0,371x2 (II)
x2= -12702,464-1,652x4 (III)
Найдем max:
Рис. 1 График функции
1 График функции
Построим линию уровня 55255,72+4,35x
Ответ: Чтобы достичь максимальной прибыли предприятие должно выпустить 1061 изделий товара B и 257 изделий товара D.
Делись добром 😉
Анализ решения задачи линейного программирования на чувствительность к параметрам модели
3.Решение задачи симплекс-методом
От неравенств ограничений переходим к ограничениям равенствам. Переменные х3,х4,х5 — базисные, а x1, x2 -свободные…
Графический метод решения задачи линейного программирования
2.2 Решение задачи симплекс-методом
1) Математическая модель задачи
Пусть х1, х2, х3, х4 — число единиц изделий А, Б, В и неокрашенные В. Тогда целевая функция задачи:
W = 25×1+20×2+50×3+30×4 max. Ограничения по трудовым ресурсам…
Ограничения по трудовым ресурсам…
Методы решения задач линейного программирования с n-переменными
Решение задачи графическим методом
Задача решается графическим методом, если разность между количеством переменных и количеством ограничений равна двум…
Методы решения задач линейного программирования с n-переменными
Решение задачи симплекс-методом
Решим прямую задачу линейного программирования симплекс-методом…
Моделирование и оптимизация автомобильных дорог
2.3. Решение задачи симплекс-методом
Математическая модель задачи имеет вид: Для упрощения расчетов заменяем ограничения (1.1.) условием неотрицательности: Перейдем к минимизации целевой функции…
Оптимизация потоков в сети связи
4. Решение задачи симплекс — методом
Для решения задачи симплекс-методом составляется исходная симплекс-таблица, содержащая М строк и N столбцов. В нее заносятся коэффициенты системы ограничений и целевой функции с соответствующими знаками. Переменные…
Переменные…
Постановка и решение транспортной параметрической задачи
4.3 Решение задачи аналитическим методом
Полагая k=0, по известному алгоритму составим опорное решение методом Фогеля. Полученный опорный план перевозок и алгоритм выполнения с нахождением минимальных разностей стоимостей перевозок (Cij) в каждом столбце и строке изображен на рисунке 4…
Применение линейного программирования для решения оптимизационных задач
2.1 Решение ЗЛП графическим методом
Для сохранения здоровья и работоспособности человек должен в сутки потреблять не менее 63 усл.ед. белков, не менее 147 усл.ед. жиров и не менее 126 усл.ед. углеводов. Для простоты допустим…
Программная реализация методов решения системы линейных уравнений
1.4 Решение задачи математическим методом
Метод Крамера.
При решении систем линейных уравнений по методу Крамера последовательно выполняется следующий алгоритм:
1. Записывают систему в матричном виде (если это еще не сделано).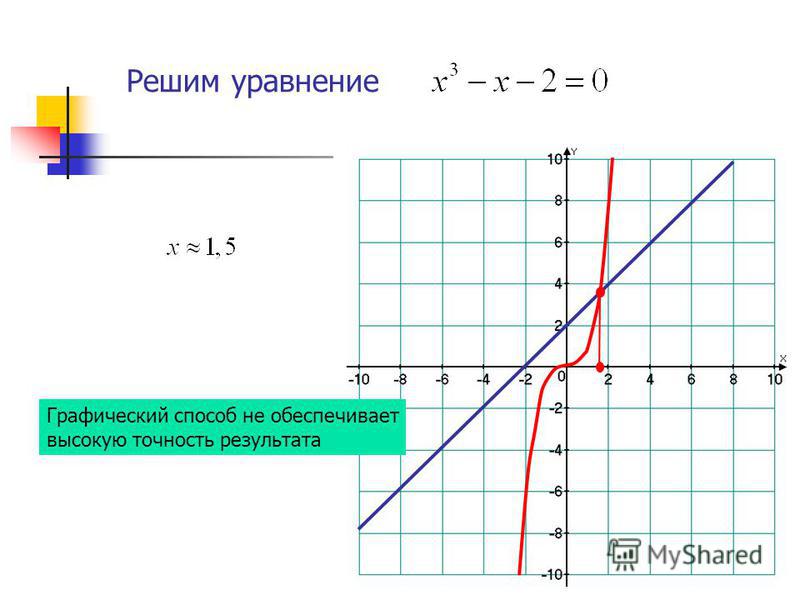 2. Вычисляют главный определитель системы:
3…
2. Вычисляют главный определитель системы:
3…
Решение дифференциального уравнения методами Эйлера и Эйлера-Коши
2.2 Решение задачи методом Эйлера
Решить дифференциальное уравнение на отрезке [0;4] с точностью =0.01 Найдем первую точку(M1) с шагом h=1. h=1 x1=x0+1=1 M1=(1;1) Найдем вторую точку(M2). x2=x1+1=2 = M2=(2;1) Найдем третью точку(M3). h=1 x3=x2+1=3 M3=(3;) Найдем четвертую точку(M4)…
Решение задачи линейного программирования
4. Решение задачи симплекс-методом
…
Решение задачи линейного программирования графическим методом
2.2. Методика решения задач ЛП графическим методом.
I. В ограничениях задачи (1.2) заменить знаки неравенств знаками точных равенств и построить соответствующие прямые. II. Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.2)…
Составление оптимального плана производства тракторных и автомобильных глушителей математическими методами
4. Решение задачи симплекс-методом
Приведение задачи к каноническому виду:
Каноническая задача линейного программирования отличается от других задач тем, что ее системой (ограничений является система уравнений, а не неравенств, и все переменные не отрицательные. ..
..
Составление оптимального плана производства тракторных и автомобильных глушителей математическими методами
5. Решение задачи графическим методом
Графическим методом решаются задачи линейного программирования, записанные в каноническом виде и удовлетворяющие условию X< 2, где n — число неизвестных системы ограничений; r — ранг системы векторов условий…
Транспортная задача
3. Решение задачи аналитическим методом
Шаг 1 (Проверка на сбалансированность). Общее число запасов на складах 95, общая потребность 95. Следовательно, задача является сбалансированной. Шаг 2 (Отыскание начального решения методом минимального элемента)…
Линейные уравнения с двумя переменными
Линейное уравнение с двумя переменными — это уравнение, в котором две переменные имеют показатель степени 1. Система уравнений с двумя переменными имеет единственное решение, не имеет решений или имеет бесконечно много решений. Линейная система уравнений может иметь n переменных.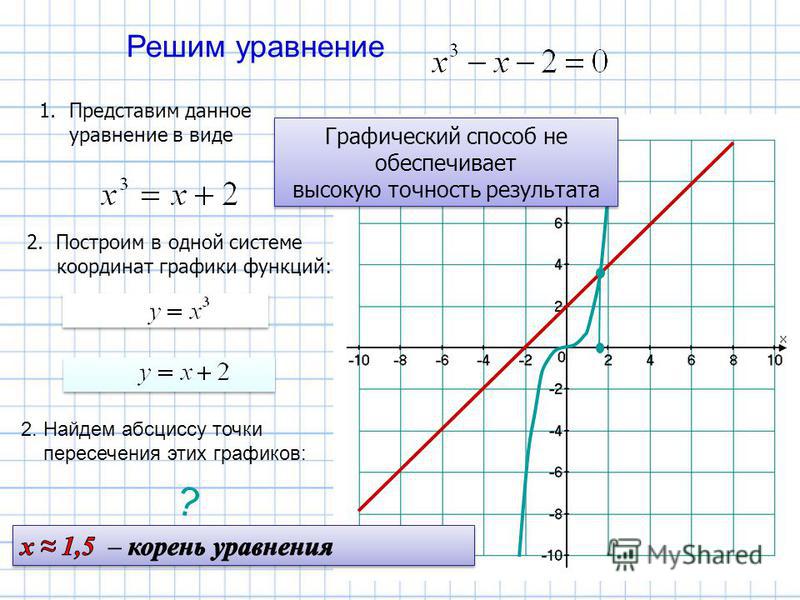 Важно помнить, что при решении линейных уравнений с n числом переменных необходимо иметь n уравнений для решения и определения значения переменных. Множество решений, полученных в результате решения этих линейных уравнений, представляет собой прямую линию. Линейные уравнения с двумя переменными — это алгебраические уравнения, которые имеют форму (или могут быть преобразованы в форму) y = mx + b, где m — наклон, а b — точка пересечения с осью y. Это уравнения первого порядка. Например, у = 2х + 3 и 2у = 4х + 9.являются линейными уравнениями с двумя переменными.
Важно помнить, что при решении линейных уравнений с n числом переменных необходимо иметь n уравнений для решения и определения значения переменных. Множество решений, полученных в результате решения этих линейных уравнений, представляет собой прямую линию. Линейные уравнения с двумя переменными — это алгебраические уравнения, которые имеют форму (или могут быть преобразованы в форму) y = mx + b, где m — наклон, а b — точка пересечения с осью y. Это уравнения первого порядка. Например, у = 2х + 3 и 2у = 4х + 9.являются линейными уравнениями с двумя переменными.
| 1. | Что такое линейные уравнения с двумя переменными? |
| 2. | Формы линейных уравнений с двумя переменными |
| 3. | Методы решения линейных уравнений с двумя переменными |
| 4. | Часто задаваемые вопросы о линейных уравнениях с двумя переменными |
Что такое линейные уравнения с двумя переменными?
Линейные уравнения с двумя переменными — это уравнения, в которых каждая из двух переменных имеет наивысший показатель степени 1 и имеет одно, ни одного или бесконечно много решений. Стандартная форма линейного уравнения с двумя переменными: ax + by + c = 0, где x и y — две переменные. Решения также можно записать упорядоченными парами, например (x, y). Графическое представление системы линейных уравнений с двумя переменными включает две прямые линии, которые могут быть пересекающимися, параллельными или совпадающими.
Стандартная форма линейного уравнения с двумя переменными: ax + by + c = 0, где x и y — две переменные. Решения также можно записать упорядоченными парами, например (x, y). Графическое представление системы линейных уравнений с двумя переменными включает две прямые линии, которые могут быть пересекающимися, параллельными или совпадающими.
Формы линейных уравнений с двумя переменными
Линейное уравнение с двумя переменными может быть представлено в различных формах, таких как стандартная форма, форма пересечения и форма точка-наклон. Например, одно и то же уравнение 2x+3y=9 может быть представлено в каждой из форм, таких как 2x+3y-9=0 (стандартная форма), y = (-2/3)x + 3 (форма пересечения наклона), и y — 5/3 = -2/3 (x + (-2)) (форма точка-наклон). Посмотрите на приведенное ниже изображение, показывающее все эти три формы представления линейных уравнений с двумя переменными с примерами.
Система уравнений означает набор уравнений, и они называются одновременными линейными уравнениями. Мы научимся решать линейные уравнения с двумя переменными разными методами.
Мы научимся решать линейные уравнения с двумя переменными разными методами.
Методы решения линейных уравнений с двумя переменными
Существует пять методов решения системы линейных уравнений с двумя переменными. Эти методы описаны ниже:
- Графический метод
- Метод замены
- Метод перекрестного умножения
- Метод устранения
- Метод определения
Графический метод решения линейных уравнений с двумя переменными
Шаги графического решения линейных уравнений с двумя переменными приведены ниже:
- Шаг 1 уравнение.
- Шаг 2 : Чтобы построить уравнение вручную, сначала преобразуйте его в форму y=mx+b, решив уравнение относительно y.
- Шаг 3 : Начните задавать значения x как 0, 1, 2 и т. д. и найдите соответствующие значения y или наоборот.
- Шаг 4 : Определите точку, где пересекаются обе линии.

- Шаг 5 : Точка пересечения является решением данной системы.
Пример: Найдите решение следующей системы уравнений графически.
-х+2у-3 =0
3x+4y-11=0
Решение: Мы изобразим их на графике и посмотрим, пересекаются ли они в какой-либо точке. Как вы можете видеть ниже, обе линии встречаются в (1, 2). Таким образом, решение данной системы линейных уравнений есть x=1 и y=2.
Но обе линии не всегда могут пересекаться. Иногда они могут быть параллельны. В этом случае система линейных уравнений с двумя переменными решения не имеет. В некоторых других случаях обе линии совпадают друг с другом. В этом случае каждая точка на этой прямой является решением данной системы и, следовательно, данная система имеет бесконечное число решений.
Непротиворечивая и непротиворечивая система линейных уравнений:
- Если система имеет решение, то говорят, что она непротиворечива;
- , в противном случае говорят, что он несовместим.

Независимая и зависимая система линейных уравнений:
- Если система имеет единственное решение, то она независима.
- Если оно имеет бесконечное число решений, то оно зависимо. Это означает, что одна переменная зависит от другой.
Рассмотрим систему двух линейных уравнений: a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 Здесь мы может понять, когда линейная система с двумя переменными непротиворечива/непротиворечива и независима/зависима.
Метод подстановки
Чтобы решить систему двух линейных уравнений с двумя переменными с использованием метода подстановки, мы должны использовать шаги, указанные ниже:
- Шаг 1: Решите одно из уравнений для одной переменной.
- Шаг 2: Подставьте это в другое уравнение, чтобы получить уравнение с одной переменной.
- Шаг 3: Решите для переменной.

- Шаг 4: Подставьте его в любое из уравнений, чтобы получить значение другой переменной.
Пример: Решите следующую систему уравнений методом подстановки.
х+2у-7=0
2x-5y+13=0
Решение: Решим уравнение x+2y-7=0 для y:
х+2у-7=0
⇒ 2y=7-x
⇒ y=(7-x)/2
Подставим это в уравнение 2x-5y+13=0:
2x-5y+13=0
⇒ 2x-5((7-x)/2)+13=0
⇒ 2x-(35/2)+(5x/2)+13=0
⇒ 2х + (5х/2) = 35/2 — 13
⇒ 9x/2 = 9/2
⇒ x=1
Подставим x=1 в уравнение y=(7-x)/2:
y=(7-1)/2 = 3
Следовательно, решение данной системы равно x=1 и y=3.
Метод перекрестного умножения
Рассмотрим систему линейных уравнений: а 1 х + b 1 у + с 1 = 0 и 0.
Чтобы решить это с помощью метода перекрестного умножения, мы сначала запишем коэффициенты каждого из x и y и констант следующим образом:
Здесь стрелки указывают, что эти коэффициенты необходимо умножить. Теперь мы напишем следующее уравнение путем перекрестного умножения и вычитания произведений.
Теперь мы напишем следующее уравнение путем перекрестного умножения и вычитания произведений.
\(\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}=\dfrac{y}{c_{1} a_{2}-c_{2} a_{1} }=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}}\)
Из этого уравнения мы получаем два уравнения:
\(\begin{align}
\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \\[0,2 см] \dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2 } б_{1}}
\end{align}\)
Решая каждое из них относительно x и y, решение данной системы:
\(\begin{align}
x&=\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\\[0,2 см] y&= \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}
\end{align}\)
Метод исключения
Чтобы решить систему линейных уравнений с двумя переменными методом исключения, мы будем использовать шаги, указанные ниже:
- Шаг 1: Расположите уравнения в стандартная форма: ax+by+c=0 или ax+by=c.
- Шаг 2: Проверьте, не приведет ли добавление или вычитание уравнений к отмене переменной.

- Шаг 3: Если нет, умножьте одно или оба уравнения либо на коэффициент x, либо на y так, чтобы их сложение или вычитание привело к исключению любой из переменных.
- Шаг 4: Решите полученное уравнение с одной переменной.
- Шаг 5: Подставьте его в любое из уравнений, чтобы получить значение другой переменной.
Пример: Решите следующую систему уравнений методом исключения.
2x+3y-11=0
3x+2y-9=0
Сложение или вычитание этих двух уравнений не приведет к отмене какой-либо переменной. Нацелимся на отмену x. Коэффициенты при x в обоих уравнениях равны 2 и 3. Их НОК равен 6. Мы сделаем коэффициенты при x в обоих уравнениях 6 и -6 такими, чтобы члены x сокращались при сложении уравнений.
3 × (2x+3y-11=0)
⇒ 6х+9у-33=0
-2 × (3x+2y-9=0)
⇒ -6x-4y+18=0
Теперь добавим эти два уравнения:
6x+9y-33=0
-6x-4y+18=0
Сложив оба приведенных выше уравнения, мы получим
⇒ 5г-15=0
⇒ 5г=15
⇒ y=3
Подставьте это в одно из двух данных уравнений и решите полученную переменную относительно x.
2x+3y-11=0
⇒ 2х+3(3)-11=0
⇒ 2x+9-11=0
⇒ 2x=2
⇒ x=1
Следовательно, решением данной системы уравнений является x=1 и y=3.
Метод определителя
Определитель матрицы 2 × 2 получается путем перекрестного умножения элементов, начиная с верхнего левого угла, и вычитания произведений.
Рассмотрим систему линейных уравнений с двумя переменными: a 1 x + b 1 y = c 1 и a 2 x + b 2 y = c . Чтобы решить их с помощью метода определителей (известного также как правило Краммера), выполните следующие шаги:
- Шаг 1: Сначала находим определитель, образованный коэффициентами при x и y, и обозначаем его Δ.
Δ = \(\left|\begin{array}{ll}a_1 & b_1 \\a_2 & b_2\end{array}\right| = a_1 b_2 — a_2b_1\) - Шаг 2: Затем находим определитель Δ x , который получается путем замены первого столбца Δ константами.

Δ x = \(\left|\begin{array}{ll}c_1 & b_1 \\c_2 & b_2\end{массив}\right| = c_1 b_2 — c_2b_1\) - Шаг 3: Затем мы находим определитель Δ y , который получается путем замены второго столбца Δ константами.
Δ y = \(\left|\begin{array}{ll}a_1 & c_1 \\a_2 & c_2\end{массив}\right| = a_1 c_2 — a_2c_1\)
Теперь решение данной системы линейных уравнений получается по формулам:
х = Δ х / Δ
y = Δ y / Δ
Приемы и советы по линейным уравнениям с двумя переменными:
При решении уравнений методом подстановки или методом исключения:
- Если мы получим истинное уравнение (например, что-то вроде 0 = 0, -1 = -1 и т. д.), то это означает, что система имеет бесконечное число решений.
- Если мы получим неверное уравнение (например, 0 = 2, 3 = -1 и т. д.), то это означает, что система не имеет решения.
☛Связанные темы:
Проверьте эти статьи, связанные с концепцией линейных уравнений с двумя переменными в математике.
- Калькулятор решения линейных уравнений
- Калькулятор формул
- Калькулятор системы уравнений
- Калькулятор линейного графика
Примеры линейных уравнений с двумя переменными
Пример 1: Сумма цифр двузначного числа равна 8. При перестановке цифр число увеличивается на 18. Найдите число.
Решение: Предположим, что x и y — это разряд десятков и разряд единиц искомого числа. Тогда число равно 10x+y.
И число, когда цифры перевернуты, будет 10y+x.
Вопрос гласит: «Сумма цифр двузначного числа равна 8».
Таким образом, мы получаем линейное уравнение с двумя переменными: x+y=8.
⇒ у=8-х
Кроме того, при перестановке цифр число увеличивается на 18.
Итак, уравнение 10y+x =10x+y+18
⇒ 10(8-x)+x=10x+(8-x)+18 (путем подстановки значения y)
⇒ 80-10х+х=10х+8-х+18
⇒ 80-9х=9х+26
⇒ 18х = 54
⇒ x=3Подставляя x=3 в y=8-x, получаем
⇒ у = 8-3 = 5
⇒ 10x+y=10(3)+5 =35
Ответ: Нужно число 35.
Пример 2: В копилке Джейка 11 монет (только четвертак или десятицентовик) общей стоимостью 1,85 доллара. Сколько десятицентовиков и четвертаков в копилке?
Решение: Предположим, что количество десятицентовиков равно x, а количество четвертаков равно y в копилке. Составим линейные уравнения с двумя переменными на основе заданной информации.
Поскольку монет всего 11, x+y=11 ⇒ y=11-x.
Мы знаем, что 1 цент = 10 центам, а 1 квартер = 25 центам.
Общая стоимость денег в копилке составляет 1,85 доллара (185 центов).Таким образом, мы получаем уравнение 10x + 25y = 185
⇒ 10х + 25(11-х) = 185 (так как у = 11-х)
⇒ 10х + 275 — 25х = 185
⇒ -15х +275 =185
⇒ -15x=-90
⇒ x = 6Подставьте это значение x в x+y=11.
⇒ у=11-6=5Ответ: Следовательно, количество десятицентовиков равно 6, а количество четвертаков равно 5.
Пример 3: По реке лодка может пройти 30 миль вверх по течению за 2 часа.
 Та же лодка может пройти 51 милю вниз по течению за 3 часа. Найти,
Та же лодка может пройти 51 милю вниз по течению за 3 часа. Найти,- Какова скорость лодки в стоячей воде?
- Какова скорость течения?
Решение: Предположим, что:
- скорость лодки в стоячей воде = х миль в час
- скорость течения = y миль в час.
При движении вверх по течению течение уменьшает скорость лодки и скорость лодки против течения = (x-y). По течению скорость течения добавляется к скорости лодки, а скорость лодки по течению = (x+y).
Таким образом,
Расстояние (d)
Время (т) Скорость Скорость = (д/т) Восходящий поток 30 2 (х-у) 30/2=15 Вниз по течению 51 3 (х+у) 51/3=17 Используя последние два столбца таблицы, мы можем составить линейные уравнения с двумя переменными:
х-у=15
x+y=17Складывая оба уравнения, мы получаем:
2х = 32
⇒ x=16Подставить x=16 в x+y=17
16+у= 17
y=1Ответ: Следовательно, скорость лодки 16 миль в час, а скорость течения 1 миля в час.

перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по линейным уравнениям с двумя переменными
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о линейных уравнениях с двумя переменными
Что понимают под линейными уравнениями с двумя переменными?
Линейное уравнение — это уравнение со степенью 1. Линейное уравнение с двумя переменными — это тип линейного уравнения, в котором присутствуют 2 переменные. Например, 2x — y = 45, x+y = 35, a-b = 45 и т. д.
Как определить линейное уравнение с двумя переменными?
Мы можем идентифицировать линейное уравнение с двумя переменными, если оно представлено в виде ax+by+c = 0, состоит из двух переменных x и y и высшая степень данного уравнения равна 1.
Можете ли вы решить линейное уравнение с двумя переменными?
Да, мы можем решить уравнение с двумя переменными, используя разные методы и убедившись, что в данной системе уравнений присутствуют два уравнения, чтобы получить значения переменных. Если существует одно решение, это означает, что данные прямые пересекаются, если нет решения, то это означает, что данные уравнения являются параллельными прямыми. Если возможных решений бесконечно много, это означает, что данные уравнения образуют совпадающие прямые.
Как графически представить линейные уравнения с двумя переменными?
Мы можем представить линейные уравнения с двумя переменными графически, используя шаги, указанные ниже:
- Шаг 1: Система двух уравнений с двумя переменными может быть решена графически путем графического отображения каждого уравнения путем преобразования его к форме y=mx+b путем решения уравнения для y.
- Шаг 2: Определяются точки пересечения обеих линий.

- Шаг 3: Точка пересечения является решением данной системы линейных уравнений с двумя переменными.
Как решить систему линейных уравнений с двумя переменными?
У нас есть разные методы решения системы линейных уравнений:
- Графический метод
- Метод замены
- Метод перекрестного умножения
- Метод устранения
- Детерминантный или матричный метод
Сколько решений имеет линейное уравнение с двумя переменными?
Предположим, у нас есть 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0. Решения линейного уравнения с двумя переменными:





 Та же лодка может пройти 51 милю вниз по течению за 3 часа. Найти,
Та же лодка может пройти 51 милю вниз по течению за 3 часа. Найти,
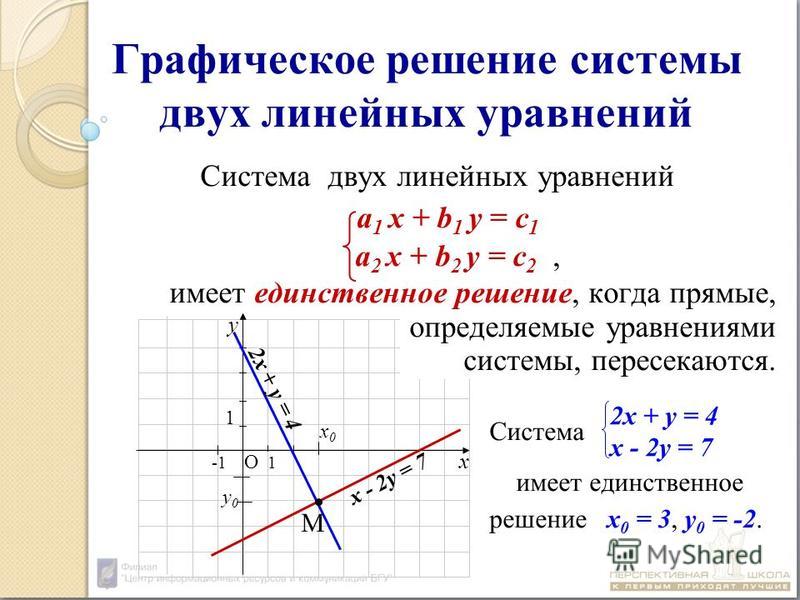

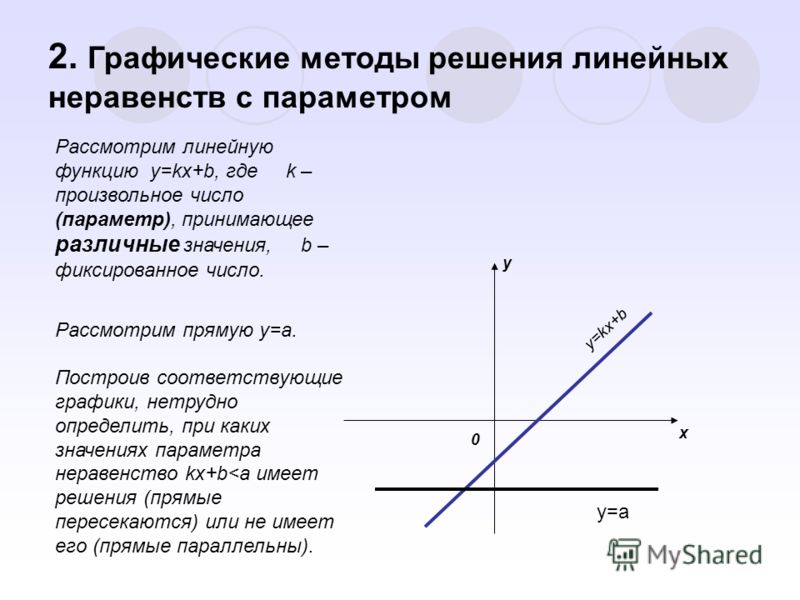
 Графическое представление линейных уравнений с двумя переменными состоит из двух прямых линий, которые могут быть пересекающимися, параллельными или совпадающими.
Графическое представление линейных уравнений с двумя переменными состоит из двух прямых линий, которые могут быть пересекающимися, параллельными или совпадающими.
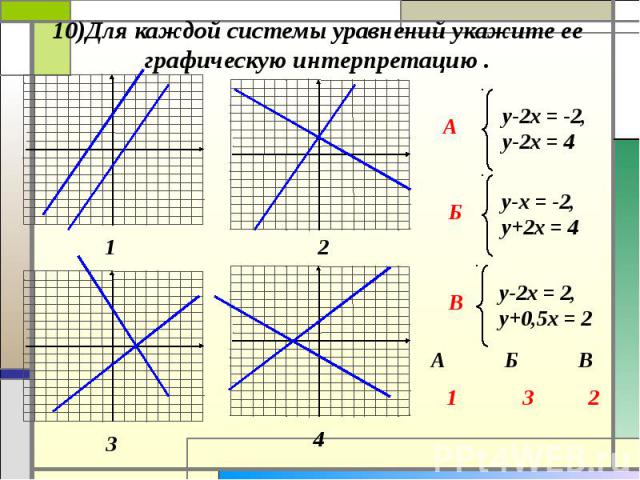
 Если система имеет решение, то говорят, что она непротиворечива; в противном случае говорят, что он несовместим.
Если система имеет решение, то говорят, что она непротиворечива; в противном случае говорят, что он несовместим. Теперь запишем следующее уравнение путем умножения и вычитания.
Теперь запишем следующее уравнение путем умножения и вычитания.