Уравнения и неравенства с модулем
В курсе разбираются различные идеи для решения уравнений и неравенств с модулем.
Преподаватели: Михаил Владимирович Штильман
Записаться
Этот курс включает:
- Доступ на разных устройствах
- Неограниченный доступ к материалам
О курсе
В этом курсе мы вспомним понятие модуля числа и разберем основные способы решения уравнений и неравенств с модулем. В курсе встретится не только универсальный метод для решения таких задач, но и более простые способы для некоторых популярных случаев.
В этом курсе вы можете получить электронный сертификат, правильно решив 80% тестовых заданий. После выполнения всех задач, перейдите во вкладку «Прогресс».
Для кого курс
Курс рассчитан на школьников 8 класса. Хотя для прохождения курса не требуется даже умение решать квадратные уравнения, посмотреть его может быть интересно и более старшим школьникам – некоторые идеи курса было бы полезно освежить и им.
Как проходит обучение
-
Регистрируйтесь
Регистрируйтесь и выбирайте курс — он сразу появится в вашем личном кабинете
-
Смотрите видеолекции
Проходите уроки курса, смотрите видео и дополнительные материалы
-
Выполняйте задания
В курсе нет дедлайнов: можно начать учиться в любое время и выбрать удобный темп
Программа курса
Блок 1.
Введение. Простейшие уравнения с модулемВ этом блоке мы дадим определение модуля числа и раскроем его геометрический смысл. Также здесь мы решим простейшие уравнения, содержащие модуль.
Блок 2. Метод интервалов для уравнений с модулями
Здесь мы разберем универсальный метод для решения уравнений с модулями – метод интервалов. Также найдем одну возможность делать решение попроще и покороче.
Блок 3. Решение уравнений вида |f(x)|=g(x)
Здесь мы научимся решать уравнения, содержащие одно выражение с модулем, более простым способом.
Блок 4. Применение геометрического смысла модуля для решения задач
В этом блоке мы научимся решать разные задания с помощью геометрического смысла модуля. При этом решения будут получаться практически устными!
Блок 5. Метод интервалов для неравенств с модулями
А здесь мы научимся решать с помощью метода интервалов неравенства с модулями. И заодно обсудим, как иногда можно сократить решение.
Блок 6.
Решение неравенств вида |f(x)|⩾ g(x) и |f(x)|⩽ g(x).В этом блоке мы научимся решать неравенства с модулем не методом интервалов, а более простым способом.
Введение в курс
Преподаватели
Штильман Михаил Владимирович
Преподаватель математики ГФМЛ №30
Неравенства с модулем. Новый взгляд на решение
Наиболее сложно решаемыми задачами школьной математики являются неравенства, содержащие переменные под знаком модуля. Для успешного решения таких неравенств необходимо хорошо знать свойства модуля и иметь навыки их использования.
Основные понятия и свойства
Модуль (абсолютная величина) действительного числа обозначается и определяется следующим образом:
К простым свойствам модуля относятся следующие соотношения:
, , и .
Отметим, что последние два свойства справедливы для любой четной степени.
Кроме того, если , где , то и
Более сложные свойства модуля, которые можно эффективно использовать при решении уравнений и неравенств с модулями, формулируются посредством следующих теорем:
Теорема 1. Для любых аналитических функций и справедливо неравенство .
Теорема 2. Равенство равносильно неравенству .
Теорема 3. Равенство равносильно неравенству .
Наиболее распространенными в школьной математике неравенствами, содержащие неизвестные переменные под знаком модуля, являются неравенства вида и , где некоторая положительная константа.
Теорема 4. Неравенство равносильно двойному неравенству , а решение неравенства сводится к решению совокупности неравенств и .
Данная теорема является частным случаем теорем 6 и 7.
Более сложными неравенствами, содержащие модуль, являются неравенства вида , и .
Методы решения таких неравенств можно сформулировать посредством следующих трех теорем.
Теорема 5. Неравенство равносильно совокупности двух систем неравенств
и (1)
Доказательство. Так как , то
, или .
Отсюда вытекает справедливость (1).
Теорема 6. Неравенство равносильно системе неравенств
(2)
Доказательство. Так как , то из неравенства следует, что .
При таком условии неравенство будет равносильно неравенству и при этом вторая система неравенств (1) окажется несовместной.
Теорема доказана.
Теорема 7. Неравенство равносильно совокупности одного неравенства и двух систем неравенств
, и (3)
Доказательство. Поскольку , то неравенство всегда выполняется, если .
Пусть , тогда неравенство будет равносильно неравенству , из которого вытекает совокупность двух неравенств и .
Теорема доказана.
Рассмотрим типовые примеры решения задач на тему «Неравенства, содержащие переменные под знаком модуля».
Решение неравенств с модулем
Наиболее простым методом решения неравенств с модулем является метод, основанный на раскрытии модулей. Этот метод является универсальным, однако в общем случае его применение может привести к весьма громоздким вычислениям.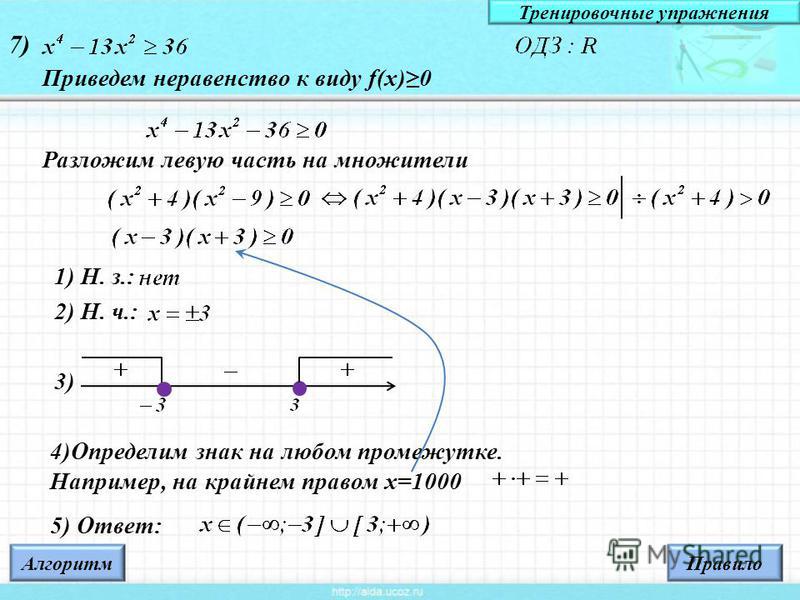
Поэтому учащиеся должны знать и другие (более эффективные) методы и приемы решения таких неравенств. В частности, необходимо иметь навыки применения теорем, приведенных в настоящей статье.
Пример 1. Решить неравенство
. (4)
Решение. Неравенство (4) будем решать «классическим» методом – методом раскрытия модулей. С этой целью разобьем числовую ось точками и на интервалы и рассмотрим три случая.
1. Если , то , , , и неравенство (4) принимает вид или .
Так как здесь рассматривается случай , то является решением неравенства (4).
2. Если , то из неравенства (4) получаем или . Так как пересечение интервалов и является пустым, то на рассматриваемом интервале решений неравенства (4) нет.
3. Если , то неравенство (4) принимает вид или . Очевидно, что также является решением неравенства (4).
Ответ: , .
Пример 2. Решить неравенство .
Решение. Положим, что . Так как , то заданное неравенство принимает вид или . Поскольку , то и отсюда следует или .
Однако , поэтому или .
Ответ: .
Пример 3.
Решить неравенство. (5)
Решение. Так как , то неравенство (5) равносильно неравенствам или . Отсюда, согласно теореме 4, имеем совокупность неравенств и .
Ответ: , .
Пример 4. Решить неравенство
. (6)
Решение. Обозначим . Тогда из неравенства (6) получаем неравенства , , или .
Отсюда, используя метод интервалов, получаем . Так как , то здесь имеем систему неравенств
(7)
Решением первого неравенства системы (7) является объединение двух интервалов и , а решением второго неравенства – двойное неравенство .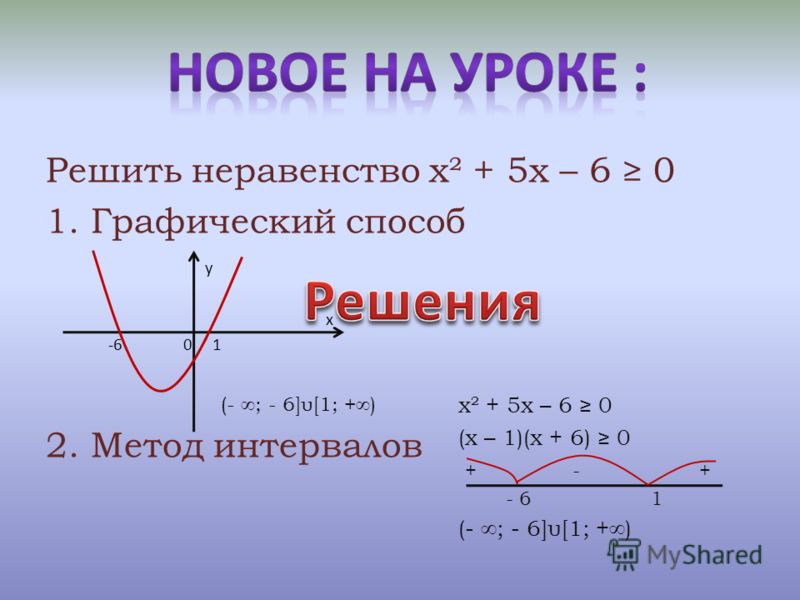
Отсюда следует, что решение системы неравенств (7) представляет собой объединение двух интервалов и .
Ответ: ,
Пример 5. Решить неравенство
. (8)
Решение. Преобразуем неравенство (8) следующим образом:
, ,
или .
Применяя метод интервалов, получаем решение неравенства (8).
Ответ: .
Примечание. Если в условии теоремы 5 положить и , то получим .
Пример 6. Решить неравенство
. (9)
Решение. Из неравенства (9) следует . Преобразуем неравенство (9) следующим образом:
, ,
, или
.
Так как , то или .
Ответ: .
Пример 7. Решить неравенство
. (10)
Решение.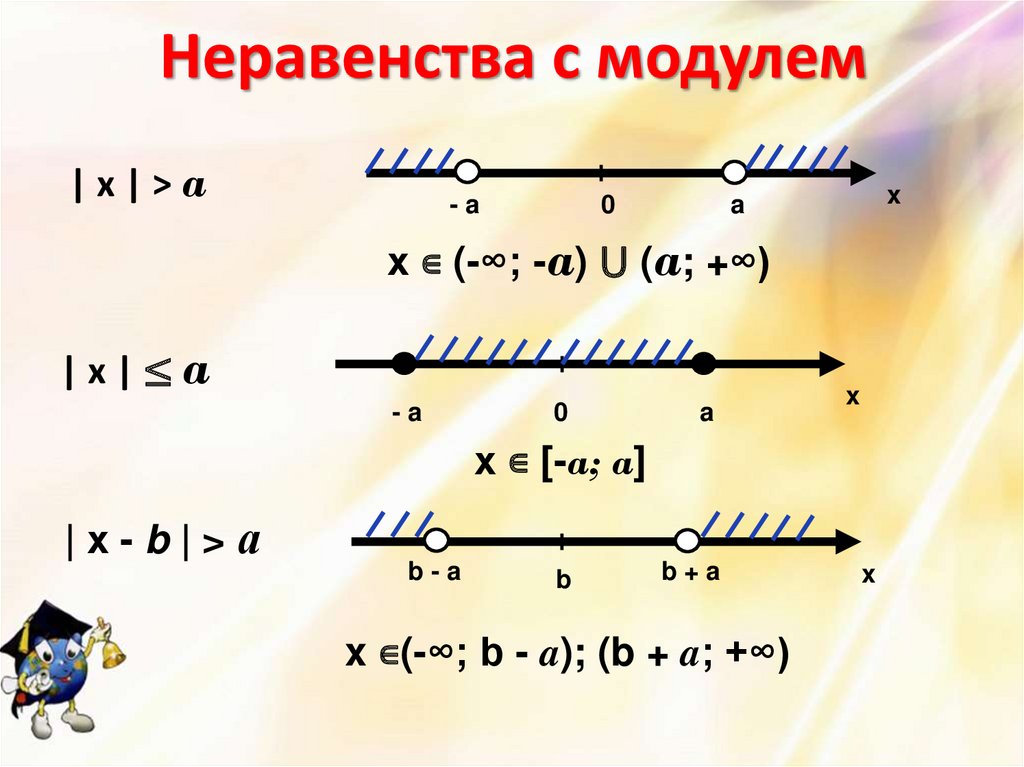
Так как и , то или .
В этой связи и неравенство (10) принимает вид
или
. (11)
Отсюда следует, что или . Так как , то и из неравенства (11) вытекает или .
Ответ: .
Примечание. Если к левой части неравенства (10) применить теорему 1, то получим . Отсюда и из неравенства (10) следует, что или . Так как , то неравенство (10) принимает вид или .
Пример 8. Решить неравенство
. (12)
Решение. Так как , то и из неравенства (12) следует или . Однако , поэтому или . Отсюда получаем или .
Ответ: .
Пример 9. Решить неравенство
. (13)
Решение.
Согласно теореме 7 решением неравенства (13) являются или .
Пусть теперь . В таком случае и неравенство (13) принимает вид или .
Если объединить интервалы и , то получим решение неравенства (13) вида .
Ответ: .
Пример 10. Решить неравенство
. (14)
Решение. Перепишем неравенство (14) в равносильном виде: . Если к левой части данного неравенства применить теорему 1, то получим неравенство .
Отсюда и из теоремы 1 следует, что неравенство (14) выполняется для любых значений .
Ответ: любое число.
Пример 11. Решить неравенство
. (15)
Решение. Применяя теорему 1 к левой части неравенства (15), получаем . Отсюда и из неравенства (15) вытекает уравнение , которое имеет вид .
Согласно теореме 3, уравнение равносильно неравенству . Отсюда получаем .
Ответ: .
Пример 12. Решить неравенство
. (16)
Решение. Из неравенства (16), согласно теореме 4, получаем систему неравенств
или
При решении неравенства воспользуемся теоремой 6 и получим систему неравенств из которой следует .
Рассмотрим неравенство . Согласно теореме 7, получаем совокупность неравенств и . Второе неравенство совокупности справедливо для любого действительного .
Следовательно, решением неравенства (16) являются .
Ответ: .
Пример 13. Решить неравенство
. (17)
Решение. Согласно теореме 1 можно записать
(18)
Принимая во внимание неравенство (17), делаем вывод о том, что оба неравенства (18) обращаются в равенства, т.
е. имеет место система уравнений
По теореме 3 данная система уравнений равносильна системе неравенств
или
Ответ: .
Пример 14. Решить неравенство
. (19)
Решение. Так как , то . Умножим обе части неравенства (19) на выражение , которое для любых значений принимает только положительные значения. Тогда получим неравенство, которое равносильно неравенству (19), вида
.
Отсюда получаем или , где . Так как и , то решением неравенства (19) являются и .
Ответ: , .
Для более глубокого изучения методов решения неравенств с модулем можно посоветовать обратиться к учебным пособиям, приведенных в списке рекомендованной литературы.
Рекомендуемая литература
1. Сборник задач по математике для поступающих во втузы / Под ред.
М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.
2. Супрун В.П. Математика для старшеклассников: методы решения и доказательства неравенств. – М.: Ленанд / URSS, 2018. – 264 с.
3. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS, 2017. – 296 с.
Остались вопросы?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Решение неравенств с использованием калькулятора абсолютного значения
| Дом | |
| Полиномы | |
| Нахождение наибольшего общего делителя | |
| Факторинг трехчленов | |
| Функция абсолютного значения | |
| Краткий обзор полиномов факторинга | |
| Решение уравнений с одним радикальным членом | |
| Добавление дробей | |
| Вычитание дробей | |
| Метод ФОЛЬГИ | |
| Графики составных неравенств | |
| Решение абсолютных неравенств | |
| Сложение и вычитание многочленов | |
| Использование наклона | |
| Решение квадратных уравнений | |
| Факторинг | |
| Свойства умножения показателей степени | |
| Завершение квадрата | |
| Решение систем уравнений методом подстановки | |
| Объединение подобных радикальных терминов | |
| Исключение с помощью умножения | |
| Решение уравнений | |
| Теорема Пифагора 1 | |
| Нахождение наименьших общих кратных | |
| Умножение и деление в научной записи | |
| Сложение и вычитание дробей | |
| Решение квадратных уравнений | |
| Сложение и вычитание дробей | |
| Умножение на 111 | |
| Добавление дробей | |
| Умножение и деление рациональных чисел | |
| Умножение на 50 | |
| Решение линейных неравенств с одной переменной | |
| Упрощение кубических корней, содержащих целые числа | |
| График составных неравенств | |
| Простые трехчлены как произведения двучленов | |
| Написание линейных уравнений в форме наклона-пересечения | |
| Решение линейных уравнений | |
| Линии и уравнения | |
| Пересечения параболы | |
| Функция абсолютного значения | |
| Решение уравнений | |
| Решение сложных линейных неравенств | |
| Комплексные числа | |
| Факторизация разности двух квадратов | |
| Умножение и деление рациональных выражений | |
| Сложение и вычитание радикалов | |
| Умножение и деление чисел со знаком | |
| Решение систем уравнений | |
| Факторизация противоположности GCF | |
| Умножение специальных многочленов | |
| Свойства показателей степени | |
| Научное обозначение | |
| Умножение рациональных выражений | |
| Сложение и вычитание рациональных выражений с отличающимися знаменателями | |
| Умножение на 25 | |
| Десятичные дроби в дроби | |
| Решение квадратных уравнений путем заполнения квадрата | |
| Частное правило для показателей степени | |
| Упрощение квадратных корней | |
| Умножение и деление рациональных выражений | |
| Независимые, противоречивые и зависимые системы уравнений | |
| Склоны | |
| Графические линии на координатной плоскости | |
| Графические функции | |
| Силы десяти | |
| Свойство нулевой мощности экспонентов | |
| Вершина параболы | |
| Рационализация знаменателя | |
| Тест факторизуемости для квадратных трехчленов | |
| Трехчленные квадраты | |
| Решение двухшаговых уравнений | |
| Решение линейных уравнений, содержащих дроби | |
| Умножение на 125 | |
| Свойства экспоненты | |
| Умножение дробей | |
| Сложение и вычитание рациональных выражений с одинаковым знаменателем | |
| Квадратные выражения — Заполнение квадратов | |
| Сложение и вычитание смешанных чисел с разными знаменателями | |
| Решение формулы для заданной переменной | |
| Факторинг трехчленов | |
| Умножение и деление дробей | |
| Умножение и деление комплексных чисел в полярной форме | |
| Уравнения мощности и их графики | |
| Решение линейных систем уравнений подстановкой | |
| Решение полиномиальных уравнений методом факторинга | |
| Законы экспонентов | |
| индекс casa mÃo | |
| Системы линейных уравнений | |
| Свойства рациональных показателей | |
| Мощность произведения и мощность частного | |
| Различия в факторинге идеальных квадратов | |
| Деление дробей | |
| Разложение полинома на множители путем нахождения GCF | |
| Графики линейных уравнений | |
| шагов факторинга | |
| Свойство умножения показателей степени | |
| Решение систем линейных уравнений с тремя переменными | |
| Решение экспоненциальных уравнений | |
| Нахождение НОК набора одночленов | |
- Выражение
- Уравнение
- Неравенство
- Свяжитесь с нами
- Упрощение
- Фактор
- Расширение 9CM
- GCF0647
- Решить
- График
- Система
- Решить
- График
- Система
- ваш сайт 90 6 на сайте Математический решатель 6 на сайте
решение неравенств с использованием калькулятора абсолютного значения
Связанные темы:
восьмеричный калькулятор с дробями |
алгебра веселые рабочие листы неравенство |
математическая вероятность и комбинация gre |
рассчитать мои факторные деревья |
проверьте мой ответ, упрощая радикалы |
ответь на мою математическую задачу бесплатно |
решатель сложных неравенств |
онлайн-курсы английского языка |
переписывание рациональных выражений |
Меррилл ответы по предварительной алгебре |
нахождение площадей квадрата по его показателям на графике
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| 7 из 12 Дата регистрации: 25. |
| ||||||
| Наверх | |||||||
| амеич Зарегистрирован: 21. |
| ||||||
| Наверх | |||||||
| такси Дата регистрации: 05.12.2002 |
| ||||||
| Наверх | |||||||
| ninemad Дата регистрации: 15.08.2003 |
| ||||||
| Наверх | |||||||
| Коэм Зарегистрирован: 22.10.2001 |
| ||||||
| Наверх | |||||||
| Воумдайм Обпнис Зарегистрирован: 11.06.2004 |
| ||||||
| Наверх | |||||||
07.2003 
03.2005 
..
Я думаю, именно благодаря подробному объяснению решения проблем весь процесс кажется таким простым. Это действительно очень хорошая программа, и я могу за нее поручиться.
Где я могу получить это программное обеспечение?
Просто введите задачу из домашней работы и нажмите «Решить» — и пошаговое решение моей домашней работы по математике будет готово. Я использовал его на нескольких занятиях по алгебре — алгебре колледжа, алгебре среднего уровня и алгебре колледжа. Очень рекомендую программу.Решение абсолютных неравенств — MathCracker.com
Алгебра Учебники
Абсолютное неравенство – это неравенство, в котором присутствует одно или несколько
абсолютная величина
.
Напомним, что неравенство почти как уравнение, только вместо знака «=» у нас стоит «≤» или «≥».
Это различие приводит к тому, что набор решений обычно является областью, как и для большинства неравенств. А тот факт, что здесь задействованы абсолютные значения, указывает на некоторый особый подход к их разрешению.
В этом уроке мы сосредоточимся на конкретных навыках, необходимых для решения этого типа неравенства, которое содержит одно или более абсолютных значений. Кроме того, мы будем предполагать, что одна или две переменные \(x\) и/или \(y\) участвуют в неравенстве.
Что такое абсолютное неравенство?
Для целей этого анализа мы будем рассматривать неравенство абсолютного значения как неравенство, включающее одну или две переменные, по крайней мере, с одним абсолютным значением.
Например, ниже у нас есть абсолютное неравенство с двумя переменными \(x\) и \(y\):
\[|3x+2y-1| \ge 1\]Или также мы могли бы иметь следующее неравенство абсолютного значения только с одной переменной:
\[|3x-1| \ле 2\]Для наших целей и для целей методов, используемых для их разрешения, мы будем иметь дело с неравенствами обоих типов (с одной и двумя переменными)
Как решать абсолютные неравенства?
При решении уравнений или неравенств на самом деле не существует серебряной пули, которая решает все.
Каждая проблема индивидуальна и может иметь свои особенности.
Лучшее, что мы можем сделать, это предоставить ряд шагов, которые помогут вам в процессе решения неравенства.
Шаг 1: Для каждого абсолютного значения определите области, в которых аргумент абсолютного значения отрицательный и где он неотрицательный.
Шаг 2: Если в неравенстве есть только одно абсолютное значение, решите его в обеих областях (где аргумент абсолютного значения отрицательный, а где неотрицательный).
Шаг 3: Если в неравенстве более одного абсолютного значения, вам нужно пересечь все области, чтобы получить набор меньших разделов. В каждом разделе вам нужно ТОЧНО знать знак каждого аргумента. Затем решите неравенство во всех областях.
Шаг 4: Как только вы получите частичное решение, которое находится в каждой из областей, окончательное решение будет просто объединением этих частичных решений.
Простыми словами: вам нужно найти области, где вы точно знаете знак аргумента абсолютных значений (чтобы вы могли избавиться от них).
Несколько примеров должны прояснить эти шаги.
ПРИМЕР 1Решите следующее неравенство
\[| 2x + 4y — 1 | \ge 2\]ОТВЕЧАТЬ:
Чтобы решить неравенство, нам нужно использовать шаги, которые были указаны выше.
Шаг 1: Существует только одно абсолютное значение, поэтому нам нужно определить, является ли аргумент отрицательным или неотрицательным. Поэтому сначала нужно решить:
\[2x + 4y — 1 \ge 0\]Есть несколько стратегий для решения вышеизложенного, но самый простой из них — сначала решить уравнение
\[2x + 4y — 1 = 0\] что означает, что \(4y = -2x + 1\) или то же самое, что \(y = -\frac{1}{2}x + \frac{1}{4}\), что соответствует линии с наклоном \(m = -\frac{1}{2}\) и y-отрезок \(n = \frac{1}{4}\).
Теперь, чтобы позаботиться о \(2x + 4y — 1 \ge 0\), мы проверяем, удовлетворяет ли точка \((0,0)\) неравенству:
\[2(0) + 4(0) — 1 = -1 <0\]Итак, \((0,0)\) удовлетворяет или не удовлетворяет неравенству. Вывод состоит в том, что линия с наклоном \(m = -\frac{1}{2}\) и точкой пересечения с осью y \(n = \frac{1}{4}\) делит плоскость на две области:
Для точек ниже линии (мы называем эту область 1, \(R_1\)) мы получаем, что \(2x + 4y — 1 < 0\)
Для точек над линией , включая саму линию (мы называем эту область 2, \(R_2\)) получаем, что \(2x + 4y — 1 \ge 0\)
Почему это важно? Почему мы берем на себя все эти проблемы? Потому что на \(R_1\) мы получаем это, поскольку \(2x + 4y — 1 < 0\), тогда \(| 2x + 4y - 1 | = -(2x + 4y - 1) \).
Точно так же на \(R_2\) мы получаем, что поскольку \(2x + 4y — 1 \ge 0\), то \(| 2x + 4y — 1 | = 2x + 4y — 1 \).
Шаг 2: Теперь нам нужно решить неравенство в области 1, \(R_1\) :
\[| 2x + 4y — 1 | \ge 2\] \[\Стрелка вправо -(2x + 4y — 1) \ge 2\] \[\Rightarrow 2x + 4y — 1 \le -2 \text{ (умножение на (-1) меняет направление неравенства)}\] \[\Стрелка вправо 2x + 4y \le -1\] \[\Стрелка вправо 4y \le -2x — 1\] \[\Стрелка вправо y \le -\frac{1}{2}x — \frac{1}{4} \] Это соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и точкой пересечения по оси y \(n = -\frac{1}{4}\). Но не забывайте, что вы находитесь на \(R_1\), а найденная нами линия находится НИЖЕ границы \(R_1\) (см. график ниже).
Чтобы уточнить, поскольку мы исходим из предположения, что находимся в \(R_1\), нам нужно, чтобы мы находились НИЖЕ линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси y \ (n = \frac{1}{4}\). В этом предположении мы решили исходное неравенство, и нам также нужно оказаться ниже линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси y \(n = -\frac{1}{4 }\). Эти два условия должны выполняться одновременно, поэтому мы получаем пересечение двух областей.
Таким образом, частичное решение в этом случае соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси y \(n = -\frac{1} {4}\).
Теперь нам нужно решить неравенство на области 2, \(R_2\) :
\[| 2x + 4y — 1 | \ge 2\] \[\Стрелка вправо 2x + 4y — 1 \ge 2\] \[\Стрелка вправо 2x + 4y \ge 3\] \[\Стрелка вправо 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \] Это соответствует всем точкам выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\). Но не забывайте, что вы находитесь на \(R_2\), и эта линия находится ВЫШЕ границы \(R_2\) (см. график ниже).
Найдя пересечение между \(R_2\) и областью выше, мы получаем, что решением части в этом случае являются все точки выше или на линии с наклоном \(m = -\frac{1}{2}\) и y-перехват \(n = \frac{3}{4}\).
Шаг 4: Теперь окончательное решение представляет собой объединение всех решений частей из предыдущих частей: Окончательное решение — это все точки НИЖЕ или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси y \(n = -\frac{1}{4}\), ПЛЮС все точки ВЫШЕ или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси y \(n = \фракция{3}{4}\).
Графически получаем
что завершает разрешение неравенства.
ПРИМЕР 2Решите следующее двойное абсолютное неравенство
\[| 2x — 1 | \ge |х + 3|\]ОТВЕЧАТЬ:
Это двойное абсолютное неравенство, потому что есть 2 абсолютных значения. Это означает, что поиск регионов потребует немного больше работы (относительно).
Шаг 1: Для первого абсолютного значения решаем:
\[2x- 1 \ge 0\] \[\Стрелка вправо \,\, 2x \ge 1\] \[\Стрелка вправо \,\, х \ge \frac{1}{2}\]Итак, мы получаем, что \(2x- 1 \ge 0\) на \([\frac{1}{2}, +\infty)\) и \(2x- 1 < 0\) на \((-\ infty, \frac{1}{2})\).
Для второго абсолютного значения решаем:
\[х+3\ге 0\] \[\Стрелка вправо \,\, х \ge -3\] Итак, мы получаем, что \(x+3 \ge 0\) на \([-3, +\infty)\) и \(x+3 < 0\) на \((-\infty, -3)\ ).
Итак, мы определяем 4 области:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). На этой области мы получаем: \(2x- 1 \ge 0\) И \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). На этой области получаем: \(2x- 1 \ge 0\) И \(x+3 < 0\), хотя эта область пуста.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). В этой области мы получаем: \(2x- 1 < 0\) И \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). В этой области мы получаем: \(2x-1 <0\) И \(x+3 <0\).
Шаг 2: Теперь нам нужно решить двойное абсолютное неравенство для каждой из четырех областей:
• На \(R_1\):
Здесь мы получаем \(2x- 1 \ge 0\) И \(x+3 \ge 0\), так что тогда
\[| 2x — 1 | \ge |х + 3|\] \[\Стрелка вправо \,\, 2x — 1 \ge x + 3\] \[\Стрелка вправо \,\, 2x — x \ge 3 — (-1)\] \[\Стрелка вправо \,\, х \ge 4\] Итак, чтобы получить часть решения, нам нужно пересечь \(x \ge 4\) или \([4, +\infty)\) с \(R_1\).
Таким образом, соответствующее частичное решение: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• На \(R_2\):
Эта часть решения пуста (\(\varnothing\)).
• На \(R_3\):
Здесь мы получаем \(2x- 1 < 0\) И \(x+3 \ge 0\), так что тогда
\[| 2x — 1 | \ge |х + 3|\] \[\Стрелка вправо \,\, -(2x — 1) \ge x + 3\] \[\Стрелка вправо \,\, 2x — 1 \le -x — 3\] \[\Стрелка вправо \,\, 2x — (-x) \le -3 — (-1)\] \[\Стрелка вправо \,\, 3x \le -2\] \[\Стрелка вправо \,\, х \le -\frac{2}{3}\] Итак, чтобы получить решение этой части, нам нужно пересечь \( x \le -\frac{2}{3}\) или \( (-\infty, -\frac{2}{3}]\) с \(R_3\).
Таким образом, соответствующее частичное решение: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2} {3}] \)
• На \(R_4\):
Здесь мы получаем \(2x- 1 <0\) И \(x+3 <0\), так что тогда
\[| 2x — 1 | \ge |х + 3|\] \[\Стрелка вправо \,\, -(2x — 1) \ge -(x + 3)\] \[\Стрелка вправо \,\, 2x — 1 \le x + 3\] \[\Стрелка вправо \,\, 2x — x \le 3 — (-1)\] \[\Стрелка вправо \,\, х \le 4\]Итак, чтобы получить решение этой части, нам нужно пересечь \( x \le 4 \) или \((-\infty, 4]\) с \(R_4\).
Таким образом, соответствующее частичное решение: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Шаг 4: Наконец, мы получаем объединение решений частей, чтобы получить решение исходного заданного неравенства
\[(-\infty, -3) \cup [-3, -\frac{2}{3}] \cup [4, +\infty) = (-\infty, -\frac{2}{3} ] \cup [4, +\infty) \] Никто не говорил, что это будет коротким, верно? Что ж. Это не очень сложно, просто нужно быть систематичным и придерживаться плана.
Подробнее о неравенствах с абсолютным значением
Почему мы вообще беспокоимся о такого рода неравенстве? Мы заботимся, потому что у них действительно есть приложения на практике.
Например, в геометрии расстояния в реальной линии должны быть представлены как абсолютное значение, потому что это должен быть неотрицательным.
Может возникнуть некоторая геометрическая ситуация, в которой нужно найти все точки реальной прямой, находящиеся на минимум на расстоянии 2 от точки 3. Такая ситуация может быть описана следующим неравенством:
\[| х-3 |\ge 2\]
Разберемся в приведенном выше неравенстве. Точка \(x\) — это точка, в которой мы хотим удовлетворить неравенству. Расстояние от \(x\) до точки 3 представлено как \(|x — 3|\).
Затем мы пытаемся найти точки, которые находятся на расстоянии не менее 2 от точки 3, поэтому тогда расстояние \(|x — 3|\) должно быть не менее 2, что объясняет \(|x — 3| \ge 2.\)
Это всего лишь один из видов задач с абсолютным неравенством, который вы можете встретить на практике.
Можно ли найти абсолютное неравенство, не имеющее решения?
Вы держите пари. Здесь у вас есть один \(|2x| < |x|\). Неравенство может быть просто невыполнимым, как в случае с этим, которое я только что вам привел.
Как насчет графического отображения абсолютных значений неравенства?
Процесс их графического отображения, по существу, идет рука об руку с процессом их решения: вам нужно найти
области, где вы точно знаете, являются ли аргументы абсолютных значений положительными или отрицательными.