Графическое неравенство! Алгебра Алимов 10-11 класс Упр 172 параграф 10 – Рамблер/класс
Графическое неравенство! Алгебра Алимов 10-11 класс Упр 172 параграф 10 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Привет! Поможете: решить графически неравенство.
1) √х ≥ х; 2) √х < х; 3) √х > х-2; 4) √х ≤ х — 2.
ответы
Привееет! Конечно)
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Решение линейных неравенств и систем линейных неравенств с двумя переменными графическим методом.
 | План-конспект занятия:
| План-конспект занятия:Графическое решение неравенств, системы совокупностей неравенств с двумя переменными
Пусть f(x,y) и g(x, y) – два выражения с переменными х и у и областью определения Х. Тогда неравенства вида f(x, y) > g(x, y) или f(x, y)
Значение переменных х, у из множества Х, при которых неравенство обращается в истинное числовое неравенство, называется его решением и обозначается (x, y). Решить неравенство – это значит найти множество таких пар.
Если каждой паре чисел (x, y) из множества решений неравенства поставить в соответствие точку М(x, y), получим множество точек на плоскости, задаваемое этим неравенством. Его называют графиком данного неравенства. График неравенства обычно является областью на плоскости.
Чтобы изобразить множество решений неравенства f(x, y) > g(x, y), поступают следующим образом. Сначала заменяют знак неравенства знаком равенства и находят линию, имеющую уравнение f(x,y) = g(x,y). Эта линия делит плоскость на несколько частей. После этого достаточно взять в каждой части по одной точке и проверить, выполняется ли в этой точке неравенство f(x, y) > g(x, y). Если оно выполняется в этой точке, то оно будет выполняться и во всей части, где лежит эта точка. Объединяя такие части, получаем множество решений.
После этого достаточно взять в каждой части по одной точке и проверить, выполняется ли в этой точке неравенство f(x, y) > g(x, y). Если оно выполняется в этой точке, то оно будет выполняться и во всей части, где лежит эта точка. Объединяя такие части, получаем множество решений.
Задача. Решить графически неравенство y > x.
Решение. Сначала заменим знак неравенства знаком равенства и построим в прямоугольной системе координат линию, имеющую уравнение y = x.
Эта линия делит плоскость на две части. После этого возьмем в каждой части по одной точке и проверим, выполняется ли в этой точке неравенство y > x.
Задача. Решить графически неравенство
х2 + у2 £ 25.
Решение. Сначала заменим знак неравенства знаком равенства и проведем линию х2 + у2 = 25. Это окружность с центром в начале координат и радиусом 5. Полученная окружность делит плоскость на две части. Проверяя выполнимость неравенства х2 + у2 £ 25 в каждой части, получаем, что графиком является множество точек окружности и части плоскости внутри окружности.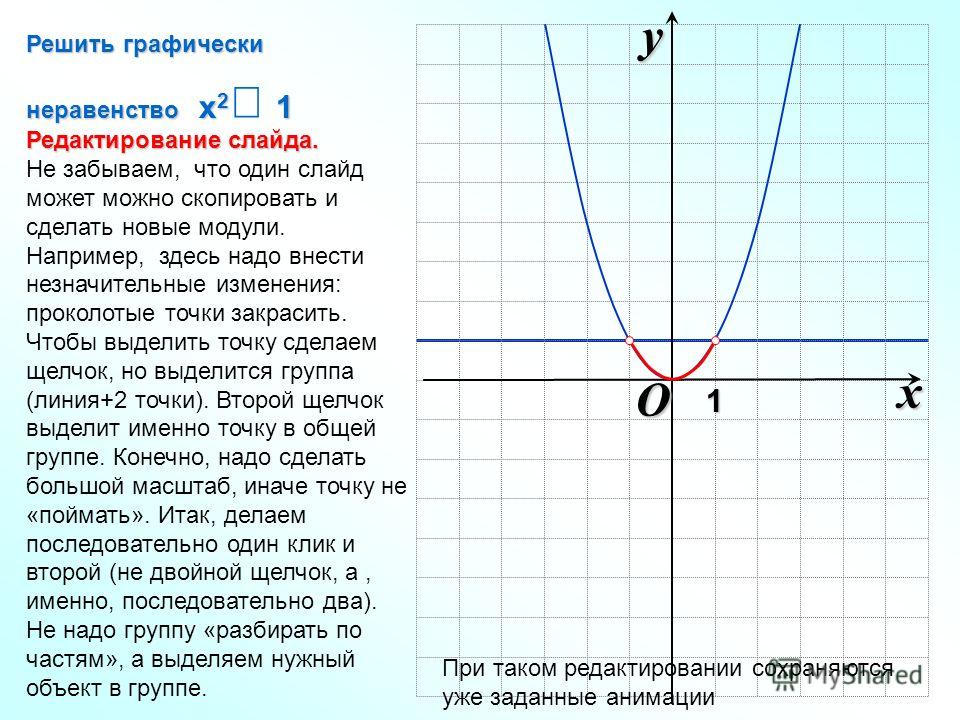
Пусть даны два неравенства f1(x, y) > g1(x, y) и f2(x, y) > g2(x, y).
Системы совокупностей неравенств с двумя переменными
Система неравенств представляет собой конъюнкцию этих неравенств. Решением системы является всякое значение (x, y), которое обращает каждое из неравенств в истинное числовое неравенство. Множество решений системы неравенств есть пересечение множеств решений неравенств, образующих данную систему.
Совокупность неравенств представляет собой дизъюнкцию этих неравенств. Решением совокупности является всякое значение (x, y), которое обращает в истинное числовое неравенство хотя бы одно из неравенств совокупности. Множество решений совокупности есть объединение множеств решений неравенств, образующих совокупность.
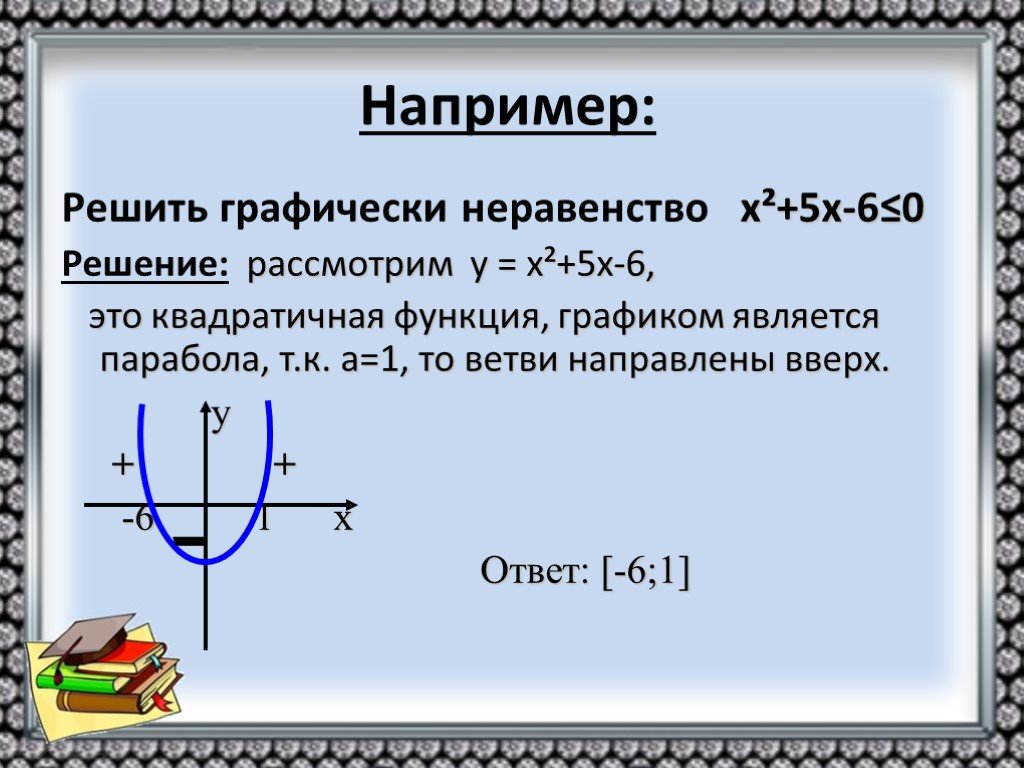
Задача. Решить графически систему неравенств
Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х и х2 + у2 = 25. Решаем каждое неравенство системы.
Графиком системы будет множество точек плоскости, являющихся пересечением (двойная штриховка) множеств решений первого и второго неравенств.
Задача. Решить графически совокупность неравенств
Решение. Сначала заменяем знак неравенства знаком равенства и проводим в одной системе координат линии у = х + 4 и х2 + у2 = 16. Решаем каждое неравенство совокупности. Графиком совокупности будет множество точек плоскости, являющихся объединением множеств решений первого и второго неравенств.
Упражнения для самостоятельной работы
1. Решите графически неравенства: а) у > 2x; б) у
в) x2 + y2 > 9; г) x2 + y2 £ 4.
2. Решите графически системы неравенств:
а) в)
б) г)
3. Решите графически совокупности неравенств:
а) в)
б) г)
ORCCA Графическое решение уравнений и неравенств
¶Цели: Содержание курса PCC и руководство по результатам
- MTH 65 CCOG 6
Уравнения и неравенства можно решать, просто хорошо читая график. В этом разделе мы используем этот подход к решению уравнений. 2-3,6x+32\text{,}\) мы начнем с перестановки членов, чтобы мы могли применить квадратную формулу. Это потребовало бы много работы карандашом и бумагой и много возможностей для человеческих ошибок. Альтернатива 92-3,6x+32\) дают тот же результат. Этот результат примерно равен \(28,677\text{,}\), но сейчас это не имеет значения. Имеет значение значение \(x\), примерно \(22,46\text{,}\). Это одно из решений уравнения.
2-3,6x+32\text{,}\) мы начнем с перестановки членов, чтобы мы могли применить квадратную формулу. Это потребовало бы много работы карандашом и бумагой и много возможностей для человеческих ошибок. Альтернатива 92-3,6x+32\) дают тот же результат. Этот результат примерно равен \(28,677\text{,}\), но сейчас это не имеет значения. Имеет значение значение \(x\), примерно \(22,46\text{,}\). Это одно из решений уравнения.
Вторая точка пересечения также показывает нам, что \(74,207\) является еще одним приближенным решением. Мы можем заключить, что набор решений уравнения приблизительно равен \(\{22,46,74,207\}\text{.}\)
Пример 9.4.4.
Графически решить уравнение \(-0,01(x-90)(х+20)=25\текст{.}\)
Объяснение
Начните с построения двух кривых на одном графике: \(y=\text{left}\) и \(y=\text{right}\text{.}\) Специально для этого примера \(y =-0,01(x-90)(x+20)\) и \(y=25\text{.}\)
epspdfpngsvgtex
Рисунок 9.4.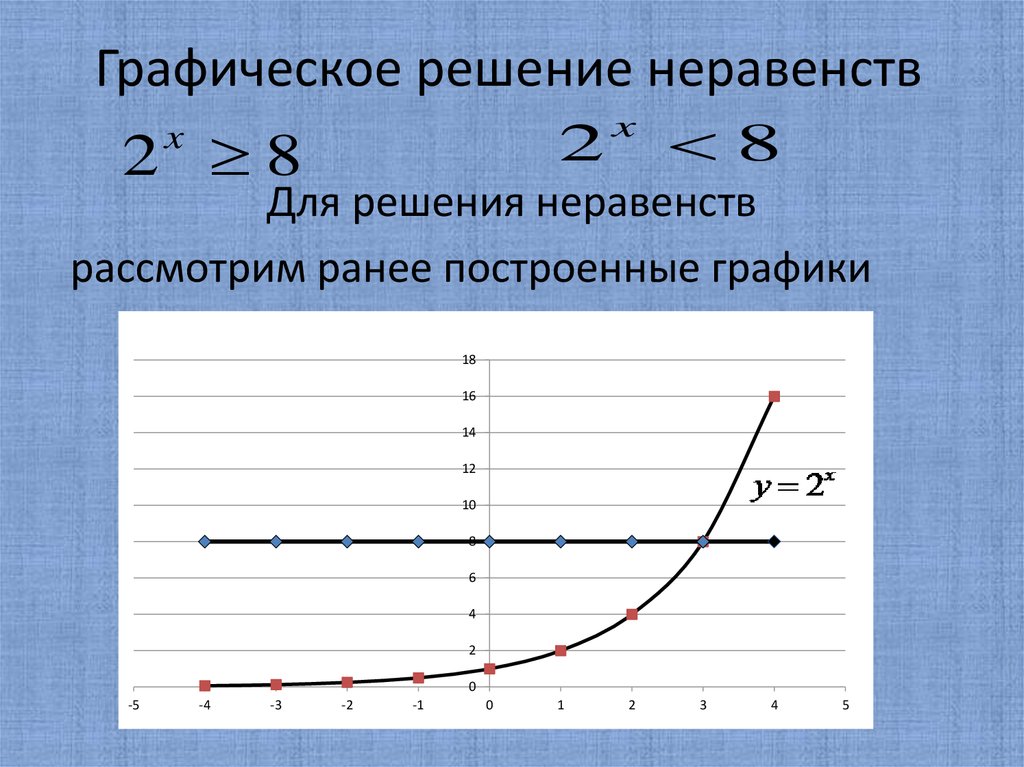 5. \(y=-0.01(x-90)(x+20)\) и \(y=25\)
5. \(y=-0.01(x-90)(x+20)\) и \(y=25\)Точками пересечения являются \((12.807,25)\) и \((57.913,25)\ text{,}\), что говорит нам о том, что решения приблизительно равны \(12,807\) и \(57,913\text{.}\). Набор решений приблизительно равен \(\{12,807, 57,913\}\text{.}\)
Одна замечательная особенность графического решения уравнений заключается в том, что на самом деле не имеет значения, какого рода это уравнение. В уравнении может быть математика, которую вы специально не изучали, но пока что-то (например, компьютер или ваш учитель) предоставляет вам графики, вы все равно можете решить уравнение.
Пример 9.4.6.
Графически решить уравнение \(\lvert x+5\rvert=\frac{1}{x+1}\text{.}\)
Пояснение
Если вы изучали алгебру только по этому учебнику, в этом уравнении есть некоторые незнакомые фрагменты. Вертикальные полосы в \(\lvert x+5\rvert\) представляют базовое математическое понятие абсолютного значения, которое вы можете освежить в Приложении A.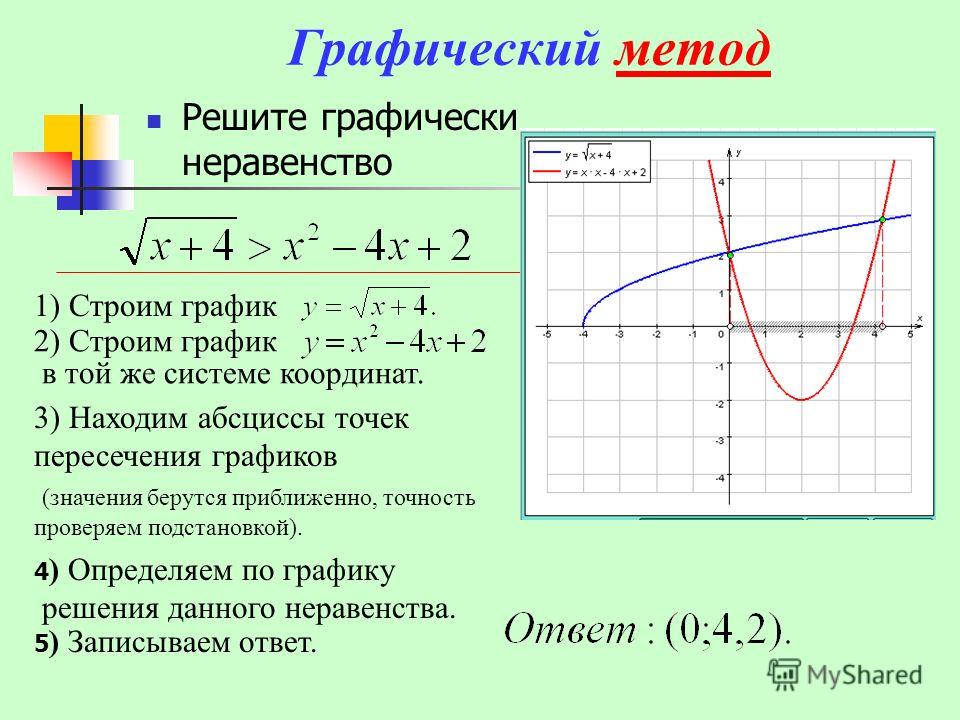 3. С другой стороны уравнения стоит выражение \(\frac{1}{x+1}\text{,}\) с переменной в знаменателе. В этом учебнике такие вещи еще не обсуждались.
3. С другой стороны уравнения стоит выражение \(\frac{1}{x+1}\text{,}\) с переменной в знаменателе. В этом учебнике такие вещи еще не обсуждались.
Несмотря на то, что у нас еще нет общих знаний об этих видах математических выражений и их графиков, мы все же можем доверять какому-то источнику, который предоставит нам графики.
epspdfpngsvgtex
Рисунок 9.4.7. \(y=\lvert x+5\rvert\) и \(y=\frac{1}{x+1}\)Похоже, что есть только одна точка пересечения около \((-0,7639,4,236) \text{.}\) Таким образом, набор решений примерно равен \(\{-0,7639\}\text{.}\)
Если мы решаем графически и что-то уже предоставляет вам график, то даже не нужно имеют математические выражения для двух кривых.
Пример 9.4.8.
На рисунке 9.4.9 изображены две кривые. Горизонтальная ось представляет годы, одна кривая представляет население Калифорнии, а другая кривая представляет население Нью-Йорка. В каком году население Калифорнии сравнялось с населением Нью-Йорка?
Похоже, что есть только одна точка пересечения примерно в \((1963,17. 5)\text{.}\) Таким образом, набор решений приблизительно равен \(\{1963\}\text{.}\) Но в контексте , это говорит о том, что в 1963 году население Калифорнии сравнялось с населением Нью-Йорка.
5)\text{.}\) Таким образом, набор решений приблизительно равен \(\{1963\}\text{.}\) Но в контексте , это говорит о том, что в 1963 году население Калифорнии сравнялось с населением Нью-Йорка.
epspdfpngsvgtex
Рисунок 9.4.9. Население Калифорнии и Нью-ЙоркаПодраздел 9.4.2 Решение неравенств с помощью графика
В первой части этой книги мы узнаем, как решать линейные неравенства, такие как \(2x+1\lt5\), используя алгебру. Используя графы вместо символической алгебры, мы можем решать неравенства с более сложными математическими выражениями, а также неравенства в контексте, которые могут даже не иметь математических выражений.
Пример 9.4.10.
На рисунке 9.4.11 изображены две кривые. Горизонтальная ось представляет годы, одна кривая представляет процент женщин США в возрасте 25–34 лет, участвующих в рабочей силе, а другая кривая представляет процент женщин США в возрасте 45–54 лет, участвующих в рабочей силе. Когда процент в группе 25–34 лет был больше, чем процент в группе 45–54 лет?
Кривая для женщин 25–34 лет поднимается над другой кривой между 19 годами75 и 1997.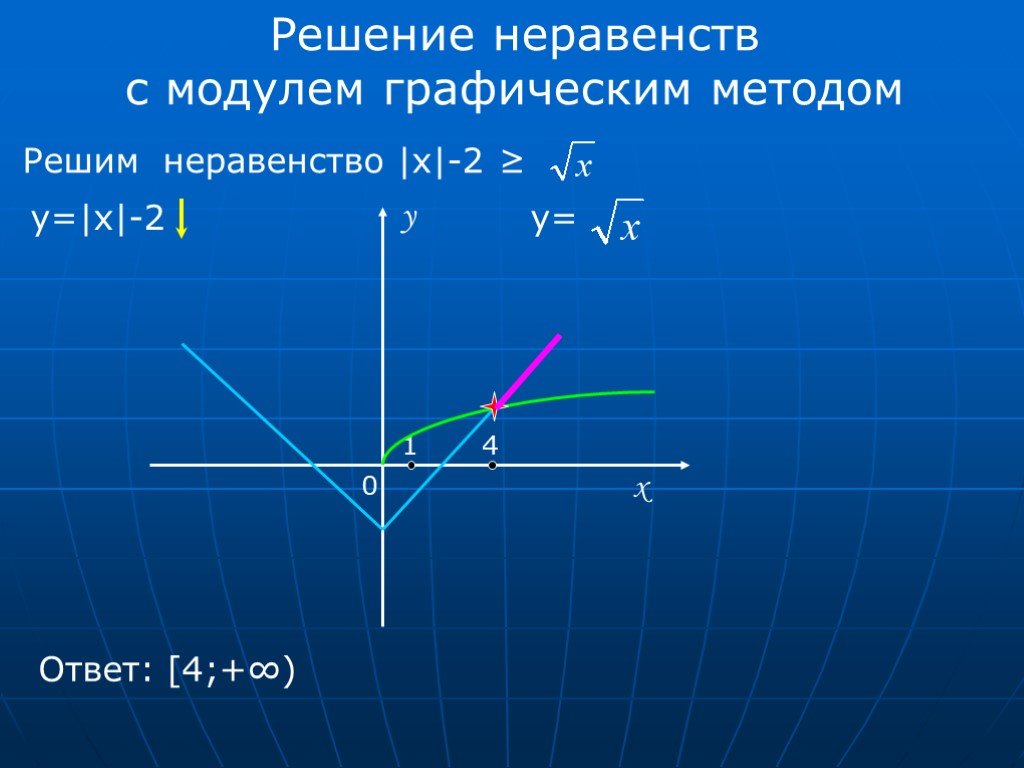
epspdfpngsvgtex
Рисунок 9.4.11. Женщины в рабочей силеПолезно еще раз взглянуть на этот график с некоторыми комментариями. Мы хотели, чтобы кривая 25–34 была больше, чем кривая 45–54. Визуально фиксируем прицел на указанную область. Набор решений, который мы ищем, это 92-70t+300 \geq -5t+300\text{,}\) нам нужно определить, где \(y\)-значения параболы выше (или равны) значениям прямой. Эта область выделена на рисунке 9.4.15.
Мы видим, что эта область включает все значения \(t\) между, включая, \(t=-3,25\) и \(t=0\text{.}\). Таким образом, решения этого неравенства включают все значения \(t\), для которых \(-3.25\le t \le 0\text{.}\) Мы можем записать этот набор решений в интервальной записи как \([-3.25,0]\) или в наборе нотация -builder как \(\{t \mid -3.
epspdfpngsvgtex
Рисунок 9.4.16.Иногда кривая резко «останавливается», и нам нужно распознать это при решении неравенства.
Пример 9.4.17.
Решите неравенство \(1-x\gt\sqrt{x+5}\) с помощью графика. 9{\text{полупарабола}}\text{,}\) мы хотим определить область, где линия выше полупараболы. В то время как линия простирается все выше и выше влево, полупарабола резко останавливается в \((-5,0)\text{.}\) Таким образом, набор решений должен остановиться в соответствующем месте. Как показано, набор решений — это интервал \([-5,-1)\text{.}\)
epspdfpngsvgtex
Рисунок 9.4.19. \(y=1-x\) и \(y=\sqrt{x+5}\)Вопросы для чтения 9.
 4.3 Вопросы для чтения
4.3 Вопросы для чтения1. 92+x=1-\sqrt{x-1}\text{?}\)
3.
Набор решений неравенства, как правило, не является одним числом или небольшим набором чисел. В общем случае набор решений неравенства представляет собой .
Упражнения 9.4.4 Упражнения
Точки пересечения
1.
Используйте технологию, чтобы построить несколько графиков и определить, сколько раз графики следующих кривых пересекаются друг с другом.
\(y={\left(441-17x\right)\!\left(-67-16x\right)}\) и \(y={-8000}\) пересекаются
ноль раз
однократно
два раза
три раза
2.
Используйте технологию, чтобы построить несколько графиков и определить, сколько раз графики следующих кривых пересекаются друг с другом.
\(y={\left(-143-12x\right)\!\left(-344+11x\right)}\) и \(y={-9000}\) пересекаются
ноль раз
однократно
9{2}}+\frac{23}{50}x-\frac{52}{25}}\text{.Каковы точки пересечения?
Решить \({x-2}={\left|x+\left|x-3\right|-4\right|}\text{.}\)
Решить \({x-2}\gt{\left|x+\left|x-3\right|-4\right|}\text{.}\)
- 1.
- Нарисуйте линию левой части неравенства, y=2x+4, в системе координат.

- 2.
- Проведите линию правой части неравенства y=0 в системе координат.
- 3.
- Отметьте точку пересечения графиков. Графики выглядят следующим образом:
- 4.
- Считайте значение x в точке пересечения. Из рисунка видно, что графики пересекаются при x=−2. Вы также видите, что функция y=2x+4 находится над y=0 справа от −2. Следовательно, ответ x>−2.
- 1.
- Нарисуйте график левой части неравенства в системе координат.
- 2.
- Нарисуйте график правой части неравенства в той же системе координат.
- 3.
- Отметьте точки пересечения графиков.
- 4.
- Прочитайте значение x точек, где пересекаются графики.
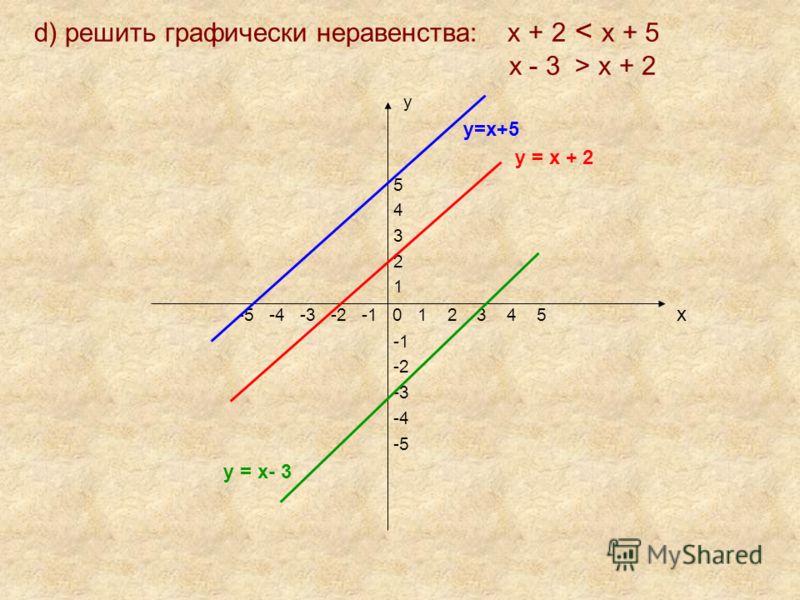
- 1.
- Нарисуйте график левой части неравенства в системе координат, y=x2.
- 2.
- Нарисуйте график правой части неравенства в той же системе координат, y=4.

 }\)
}\)20.
Уравнения \(y={x-2}\) и \(y={\left|x+\left|x-3\right|-4\right|}\) построены.
epspdfpngsvgtex
Как решать неравенства графически
Энциклопедия>Алгебра>Уравнения и неравенства>Неравенства>Интервалы и таблицы со знаками>Как решать неравенства графически
Здесь вы научитесь решать неравенства графически. Когда у вас есть неравенство, вы можете думать о нем как о двух функциях, связанных вместе знаком неравенства. То есть можно нарисовать график левой части неравенства и нарисовать график правой части неравенства, поставив перед выражениями «y=».
Пример 1
Решите неравенство 2x+4>0 графически
Правило
Графические решения неравенств
Пример 2
Решить неравенство x2≥4 графически