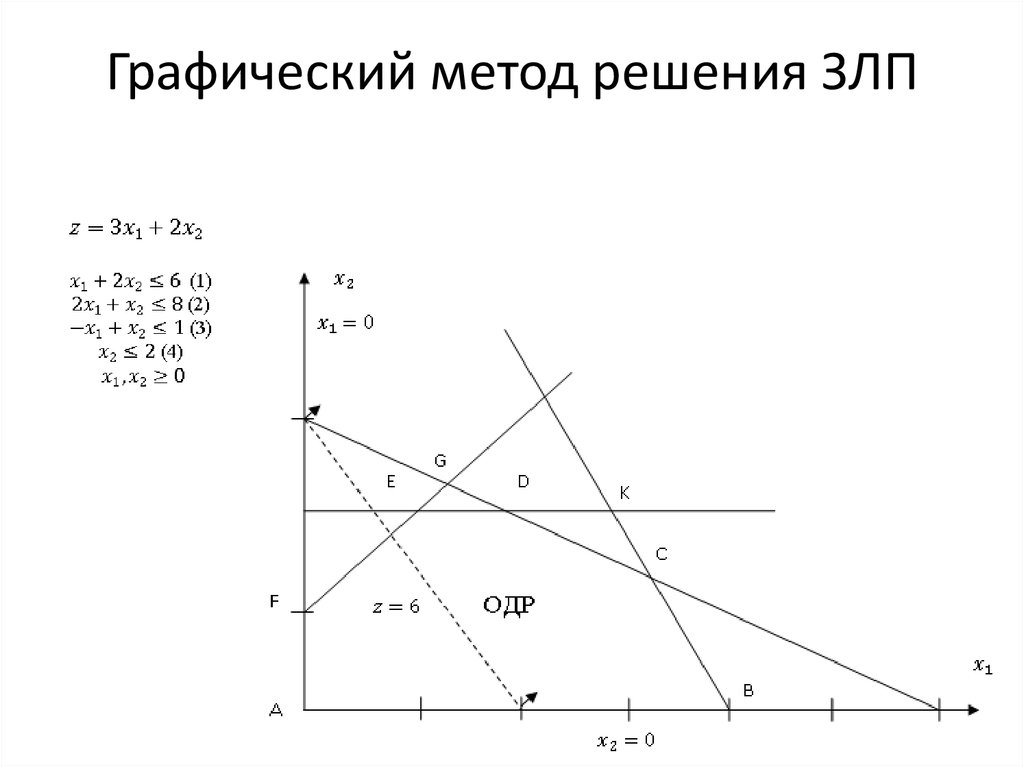
Пример решения задачи линейного программирования графическим методом
В данной работе описывается решение задачи линейного программирования при помощи графического метода.
Общественные науки в целом
Рефераты
Вуз: Независимое исследование (нет вуза)
ID: 5ed3f9a81db9460001532376
UUID: da784dd0-859b-0138-b663-0242ac180003
Язык: Русский
Опубликовано: больше 2 лет назад
Просмотры: 45
Find:
Highlight allMatch case
Current View
Current View
Automatic ZoomActual SizeFit PageFull Width50%75%100%125%150%200%300%400%
Enter the password to open this PDF file:
—
File size:
—
Title:
—
Author:
—
Subject:
—
Keywords:
—
Creation Date:
—
Modification Date:
—
Creator:
—
PDF Producer:
—
PDF Version:
—
Page Count:
—
Ваулина В.
А.,
УрГЭУ
Пример решения задачи линейного программирования
графическим методом
Линейное программирование — это раздел математики, в котором
рассматриваются методы решения экстремальных задач с линейным
функционалом и линейными ограничениями.
Существуют два наиболее распространенных способа решения задач
линейного
программирования: графический
метод и симплекс-метод.
Графический метод существенно нагляднее и обычно проще для понимания
решения. Также этот метод позволяет практически одновременно найти
решение на минимум и максимум.
Основные шаги по решению ЗПЛ графическим методом следующие:
построить область допустимых решений задачи (выпуклый многоугольник),
который определяется как пересечение полуплоскостей, соответствующих
неравенствам задачи, построить линию уровня целевой функции, и, наконец,
двигать линию уровня в нужном направлении, пока не достигнем крайней
точки области — оптимальной точки (или множества).
В отличие от графического метода, симплексный метод практически не
имеет ограничений на задачу, может быть любое количество переменных и
т.
{
x 1+ x2 ≤150,
2 x 1+5 x 2 ≤600,
5 x 1 +2 x 2 ≤600,
x1,2 ≥ 0.
}
F ( x )=200 x 1+100 x 2 → max
Применим описанные выше шаги решения.
Рецензии:
Авторизуйтесь, чтобы добавить рецензию
— у работы пока нет рецензий —
1 Найти решение задачи линейного программирования графическим методом
Высшая математика, Решение задач
1.
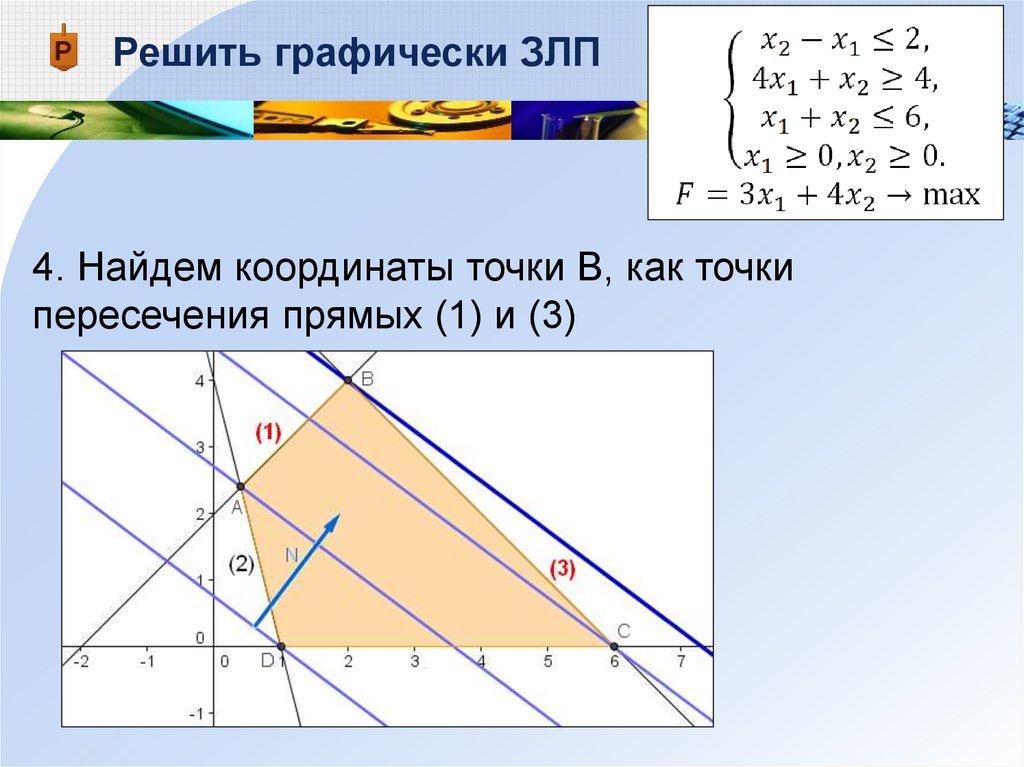Найти решение задачи линейного программирования графическим методом.
2. Провести анализ чувствительности оптимального решения задачи.
.
(1)
1. Определим область допустимых решений задачи, то есть решим графически систему неравенств (1). Штриховкой обозначены полуплоскости, являющиеся решением каждого из неравенств.
Область допустимых значений – это пересечение множеств решений, то есть выпуклый четырехугольник .
Построим линию уровня целевой функции .
Вектор-градиент, составленный из коэффициентов целевой функции , указывает направление возрастания. Двигаем линию уровня параллельно себе до выхода из области допустимых решений.
Из графика видно, что целевая функция достигает максимума, когда линия уровня проходит через точку .
Решая систему
находим ее координаты: .
При этом целевая функция достигает максимума .
при .
352425000
Анализ чувствительности оптимального решения к изменению параметров.
1. Изменение коэффициентов целевой функции.
В общем виде целевую функцию задачи ЛП можно записать следующим образом:
Максимизировать или минимизировать .
Изменение значений коэффициентов и приводит к изменению угла наклона прямой . Существует интервалы изменения коэффициентов и , когда текущее оптимальное решение сохраняется. Необходимо определить интервал оптимальности для отношения (или и ).
В данной задаче оптимальное решение соответствует точке – пересечение прямых и . При изменении коэффициентов и точка останется точкой оптимального решения до тех пор, пока угол наклона линии будет лежать между углами наклона этих двух прямых.
(при условии ).
Угловой коэффициент прямой .
Угловой коэффициент прямой .
Угловой коэффициент меняет знак, нужно рассмотреть 2 случая.
При получаем интервал оптимальности
или
при .
При получаем интервал оптимальности
или
при .
При целевая функция принимает вид – вертикальная прямая.
Условие сохранения оптимальности решения , откуда .При целевая функция принимает вид – горизонтальная прямая, не является оптимальным решением в точке .
Практический смысл имеет нахождение интервала оптимальности одного из коэффициентов при фиксированном другом.
Зафиксируем значение (исходное значение). Тогда границы интервала оптимальности определим из условия равенства углам наклона прямым и .
и ; ;
и ; ; .
То есть, при оптимальное решение не изменится при .
Аналогично, при фиксированном допустимые значения .
2. Анализ чувствительности решения к изменению правой части ограничений.
Перепишем условие задачи:
.
Точка оптимального решения – пересечение прямых и , поэтому ограничения (I) и (II) являются связывающими, (III) и (IV) – несвязывающие.
Выясним, насколько можно увеличить запас ресурса М1, чтобы улучшить полученное оптимальное решение.
0-127000
Из рисунка видно, что прямую можно перемещать параллельно себе до точки Е.
Треугольник становится областью допустимых решений. При дальнейшем перемещении это ограничение становится избыточным, то есть не влияющим на оптимальное решение.
Точка Е – пересечение прямых и . Найдем ее координаты, решая систему
.
Значение М1 в точке Е: .
При этом значение целевой функции .
Перемещая прямую в другую сторону, находим, что ОДР (область допустимых решений) стягивается в точку D, которая определяет нижнюю границу интервала осуществимости для ресурса М1.
.
Значение М1 в точке В: .
При этом значение целевой функции .
В условии задачи нет требования неотрицательности целевой функции, поэтому такое решение является допустимым.
Определим влияние ограничения М2 на оптимальное решение.
Из рисунка видно, что прямую можно перемещать в направлении градиента целевой функции до точки F, при этом ОДР – четырехугольник .
F – это точка пересечения прямой с осью , ее координаты .
При этом .
Значение целевой функции .
Найдем значение М2, при котором еще существует
Решение:
.
Для М2: .
И последнее. Определим влияние несвязывающих ограничений (III) и (IV) на оптимальное решение.
Из рисунка находим, что прямую (ограничение (III)) можно перемещать вниз до точки , при этом оптимальное решение не изменится.
Перемещение прямой в другую сторону не влияет на оптимальное решение.
Аналогично, прямую (ограничение (IV)) можно переместить параллельным переносом до точки .
Тогда значение (правая часть неравенства IV).
3. Выводы.
1. Решение ЗЛП
при ограничениях
существует.
при .
2. Существуют интервалы оптимальности коэффициентов целевой функции (не изменяющие полученного оптимального решения)
При оптимальное решение не изменится при .
При фиксированном допустимые значения .
3. При увеличении значения ограничения (I) до М1=12,2 максимальное значение целевой функции увеличится до .
Ценность ресурса М1 выше ценности ресурса М2, то есть изменение количества ресурсов на одну единицу приводит к большему увеличению целевой функции в первом случае.
x+y le 50 «…(2)» 3x+y le 90″ …(3)» x ge 0, y ge 0″ …(4)»
КУМАР ПРАКАШАН-ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ-УЧЕБНИК ИЛЛЮСТРАЦИИ ДЛЯ ПРАКТИК РАБОТА
11 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Войти, если уже куплено
Обновлено: 27-06-2022
Текст Решение
Ответ
Правильный ответ Следовательно, максимальное значение Z равно 120 в точке (30, 0)
Ответить
Пошаговое решение от экспертов, которое поможет вам в разрешении сомнений и получении отличных оценок на экзаменах.
Похожие видео
Графически решите следующую задачу линейного программирования: Максимизируйте Z=4x+y .
. . (1) , с учетом ограничений: x+y≤50 . . .(2), 3x+y≤90 . . .(3) , х≥0,y≥0 . . .(4)
Графически решите следующую LPP:
Максимизируйте : Z = 4x + y
С учетом следующих ограничений:
x+y≤50
3x+y≤90
x≥10
и y≥0.
412655416
Графически решить следующую задачу линейного программирования:
Решите следующую задачу линейного программирования графически: Максимизируйте Z = 4x +y . . . (1) с учетом ограничений: х+у≤50 . . .(2) 3x+y≤90 . . .(3) х≥0,у≥0 . . .(4)
642566679
Решите графически следующую задачу линейного программирования: Максимизируйте: z=4x+y С учетом ограничений: x+y≤503x+y≤90x≥0,y≥0
642761030
Решите графически следующую задачу линейного программирования: Максимизируйте: z=3x+5y с учетом ограничений: x+4y≤80,x+y≤50x≥0,y≥0.
642761032
Графически решите следующую задачу линейного программирования: Минимизируйте Z=3x+5y с учетом ограничений x+3y≤3,x+y≤2,x≥0,y≥0.
642761042
Графически решите следующую задачу LLp:
Максимизируйте Z = 4x + y
с учетом ограничений: x + y ≤ 50, 3x + y ≤ 90, x ≥ 10, y ≥ 0,
642809425
Графически решить следующие задачи линейного программирования: задачи программирования графически:
Максимизируйте Z = 50x + 15y с учетом ограничений 5x+y≤100,x+y≤60,x,y≥0.
642810735
Решите графически следующие задачи линейного программирования:
Максимизируйте: Z = 5x +7y с учетом ограничений x+y≤4,3x+8y≤24,10x+7y≤35,x,y≥0.
642810736
Графически решить следующие задачи линейного программирования:
Минимизировать: Z = 3x + 5y с учетом ограничений −2x+y≤4,x+y≥3,x−2y≤2,x,y≥0.
642810737
Графически решите следующую задачу линейного программирования: Максимизируйте: z=4x+y С учетом ограничений: x+y≤503x+y≤90x≥0,y≥0
646540860
Решите следующую задачу линейного программирования задача графически
Максимизировать z = 4x + y с учетом ограничений x+y≤50,3x+y≤90,x,y≥0
646540878
Графически решить следующую задачу линейного программирования: 0
646935323
Раздел 4.
2 Вопрос 2 – Часто задаваемые вопросы по математикеТеперь, когда у нас есть несколько задач линейного программирования, давайте посмотрим, как мы можем решить их, используя граф системы неравенств. Задача линейного программирования для крафтовой пивоварни оказалась следующей:
Рисунок 2. Допустимая область для задачи о крафтовой пивоварне.
Заштрихованная область соответствует всем возможным комбинациям пейл-эля и портера, удовлетворяющим ограничениям. Поскольку решение по максимизации прибыли должно исходить из этой области, она называется допустимой областью. Это означает, что упорядоченные пары в заштрихованной области являются возможными решениями задачи линейного программирования.
Чтобы решить задачу линейного программирования, нам нужно найти, какая комбинация х 1 и х 2 приводят к наибольшей прибыли. Мы могли бы выбрать возможную комбинацию из графика и рассчитать прибыль в каждом месте на графике, но это заняло бы очень много времени.
Вместо этого мы выберем значение прибыли и найдем все упорядоченные пары на графике, которые соответствуют этой прибыли.
Предположим, мы начинаем с прибыли в размере 3 000 000 долларов. Подставьте это значение в целевую функцию, чтобы получить уравнение
3 000 000 = 100 x 1 + 80 x 2
Если изобразить эту линию на том же графике, что и систему неравенств, мы получим пунктирную линию, обозначенную как P = 3 000 000. Линия, на которой прибыль постоянна, называется линией изопрофита. Префикс iso- означает, что линия изопрофита имеет одинаковую прибыль. Вдоль линии изоприбыли P = 3 000 000 каждая комбинация светлого эля и портера приводит к прибыли в размере 3 000 000 долларов.
Рисунок 3. Несколько уровней прибыли: 3 000 000, 4 000 000 и 5 000 000 долларов.
Линии изопрофита P = 4 000 000 и P = 5 000 000 могут быть построены таким же образом и изображены на рисунке 3.
По мере увеличения прибыли линии изопрофита смещаются все дальше вправо. Более высокие уровни прибыли приводят к аналогичным линиям, которые все дальше и дальше от начала координат. В конце концов линия изопрофита выходит за пределы допустимой области. Для равноотстоящих уровней прибыли мы получаем на графике равноотстоящие параллельные линии. Обратите внимание, что P = 5 000 000 полностью находится за пределами заштрихованной области. Это означает, что никакая комбинация бледного эля и портера не удовлетворит неравенство и не принесет прибыли в размере 5 000 000 долларов. Существует линия изопрофита, P ≈ 4 706 564, которая просто заденет достижимую область. Эта изопрофитная линия будет касаться места пересечения границы ограничения пропускной способности и границы ограничения количества прыжков. Точки, в которых пересекаются границы ограничений, называются угловыми точками допустимой области.
Рис. 4. Оптимальный уровень производства крафтовой пивоварни, округленный до одного десятичного знака.
Изопрофит для этого уровня также изображен на графике.
Если прибыль превышает этот уровень, линия изопрофита больше не содержит упорядоченных пар из допустимой области. Это означает, что этот уровень прибыли является максимальным, и он достигается в точке угла, где производится 35 328,2 барреля пейл-эля и 14 671,8 барреля портера.
Две границы ограничений пересекаются в угловой точке, соответствующей оптимальному решению. Эти ограничения, ограничения пропускной способности и переходов, называются обязательными ограничениями. Ограничение солода не пересекает угловую точку, которая максимизирует прибыль, поэтому это необязательное ограничение.
Для ресурсов, соответствующих ограничениям привязки, используются все ресурсы. В этом случае все мощности и хмель используются для производства оптимального количества пива. Однако не весь солод используется, поэтому ограничение по солоду не является обязательным при оптимальном решении.
Тот факт, что оптимальное решение находится в угловой точке допустимой области, позволяет сделать следующий вывод.
Оптимальное решение задачи линейного программирования находится в угловой точке допустимой области или вдоль линии, соединяющей две соседние угловые точки допустимой области.
Если допустимая область ограничена, всегда будет оптимальное решение. Неограниченные допустимые области могут иметь или не иметь оптимального решения.
Мы можем использовать это понимание для разработки следующей стратегии решения задач линейного программирования с двумя переменными решения.
1. Построить график допустимой области с помощью системы неравенств в задаче линейного программирования.
2. Найдите угловые точки допустимой области.
3. В каждой угловой точке найти значение целевой функции.
Исследуя значение целевой функции, мы можем найти максимальное или минимальное значение. Если допустимая область ограничена, максимальное и минимальное значения целевой функции будут иметь место в одной или нескольких угловых точках. Если две соседние угловые точки приводят к одному и тому же максимальному (или минимальному) значению, то максимальное (или минимальное) значение также имеет место во всех точках на линии, соединяющей соседние угловые точки.
Неограниченные допустимые области могут иметь или не иметь оптимальные значения. Однако, если допустимая область находится в первом квадранте и коэффициенты целевой функции положительны, то минимальное значение имеется в одной или нескольких угловых точках. Максимального значения в этой ситуации нет. Как и в случае с ограниченной областью, если минимум возникает в двух соседних угловых точках, он также возникает на линии, соединяющей соседние угловые точки.
Рисунок 5. Допустимая область на графике (a) может быть заключена в круг, поэтому это ограниченная допустимая область. Допустимая область на графике (b) простирается бесконечно далеко в правый верхний угол, поэтому ее нельзя заключить в круг. Эта допустимая область неограничена.
Пример 2 Решение задачи линейного программирования графически
Решите задачу линейного программирования графически:
Решение Допустимая область находится в первом квадранте после ограничений неотрицательности и включена в систему неравенств.
Два других неравенства преобразуются в уравнения и изображаются в виде графика с использованием горизонтальной и вертикальной точек пересечения.
Мы можем изобразить эти пересечения в первом квадранте и соединить их сплошными линиями, чтобы получить следующий график.
Рисунок 6 – Границы допустимой области в Примере 2. Поскольку неравенства не являются строгими неравенствами, границы проведены сплошными линиями.
Чтобы определить, какая часть этого графика соответствует допустимой области, нам нужно проверить исходные неравенства с точкой из графика. Хотя мы могли бы выбрать любую упорядоченную пару, которая не находится ни на одной из строк, в этом примере мы проверим с (1, 1).
Контрольная точка находится в наборе решений каждого неравенства. Нарисуйте стрелки на каждой линии, указывающие в направлении контрольной точки.
Рисунок 7. Поскольку оба неравенства верны, стрелки на каждой линии должны указывать в направлении контрольной точки.
Наборы решений для неравенств перекрываются в нижнем левом углу графика.
Рисунок 8 – Допустимая область для задачи линейного программирования в примере 2.
Оптимальное решение задачи линейного программирования должно исходить из этой области. Поскольку это ограниченная допустимая область, максимум будет иметь место в одной из угловых точек. Из графика и точек пересечения границ мы можем легко определить три угловые точки: (0, 0), (2, 0) и (0, 2). Еще одна угловая точка находится на пересечении прямых 2 x + y = 4 и x + 2 y = 4. Мы можем найти эту угловую точку методами подстановки, исключения или с помощью матриц , В этом примере мы будем использовать метод подстановки, поскольку его легко найти для переменной в одном из уравнений.
Чтобы применить метод подстановки к системе уравнений
, решите первое уравнение для y . Если мы вычтем 2 x из обеих частей первого уравнения, мы получим y = -2 x + 4.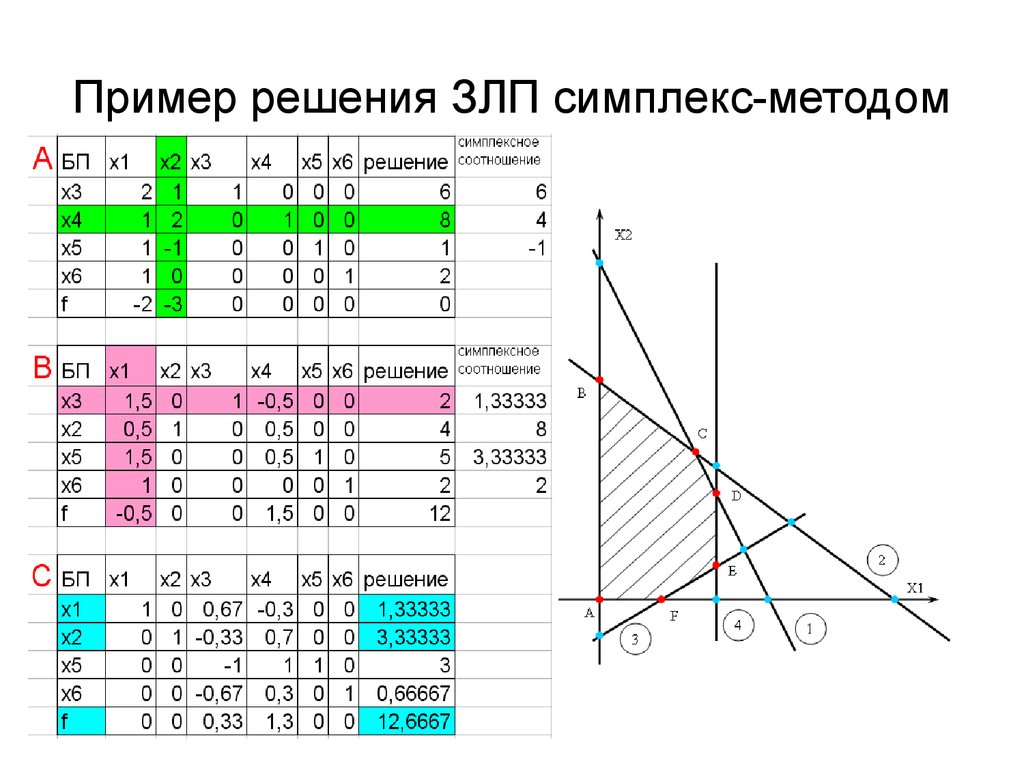
Замените y на -2 x + 4 во втором уравнении и найдите . x ,
Чтобы найти y , подставьте значение x в y = -2 x + 4, чтобы получить
Решение системы: x = 4 / 3 и y = 4 / 3.
Обозначим угловые точки на графике и вычислим значение целевой функции в каждой из них.
Рисунок 9 – Возможная область с помеченными угловыми точками.
Так как 44 / 3 составляет приблизительно 14,67, угловая точка в ( 4 / 3 , 4 / 3 ) дает максимальное значение целевой функции.
Пример 3 Решение задачи линейного программирования графически
Решите задачу линейного программирования графически:
Решение Чтобы построить график системы неравенств, нам нужно выбрать независимую переменную для построения графика на горизонтальной оси.
Хотя выбор произвольный, в этом примере мы построим график y 1 по горизонтальной оси и y 2 по вертикальной оси.
Эта задача линейного программирования включает ограничения неотрицательности, y 1 ≥ 0 и y 2 ≥ 0. На графике мы учтем эти ограничения, изобразив систему неравенств в первом только квадрант.
Границы для двух других ограничений графически изображаются с использованием формы пересечения наклона линии и пересечений.
Рисунок 10 – Границы первых двух ограничений в задаче линейного программирования в примере 3. График показан в первом квадранте из-за неотрицательности ограничений.
Обратите внимание, что границы нарисованы сплошными линиями, поскольку неравенства не являются строгими неравенствами. Чтобы заштриховать решение на графике, подставьте контрольную точку (0, 0) в каждое неравенство.
Поскольку каждое неравенство неверно, на каждой линии нарисуйте стрелки, указывающие в сторону от контрольной точки.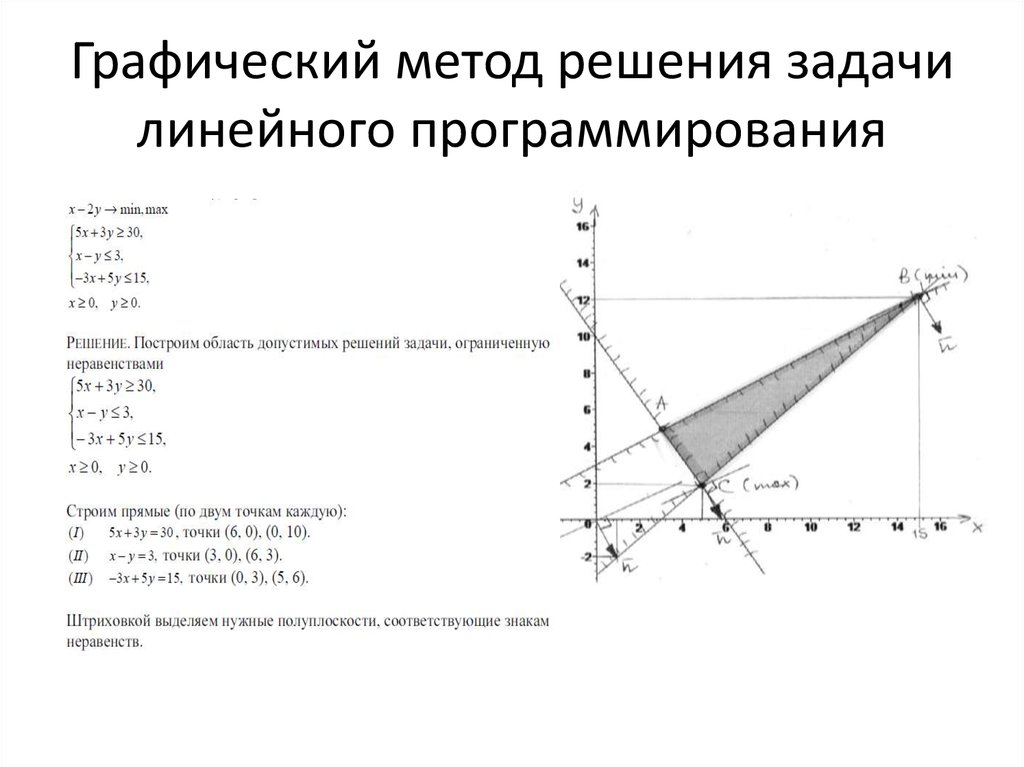
Рисунок 11. Поскольку каждое неравенство неверно в точке (0, 0), сторона, противоположная каждой контрольной точке, должна быть заштрихована.
Затенение каждого неравенства совпадает в правой верхней части графика.
Рисунок 12 – Допустимая область для системы неравенств для Примера 3.
Допустимая область простирается бесконечно далеко вправо вверх. Эта допустимая область неограничена, так как ее нельзя заключить в круг. Минимальное значение может существовать, а может и не существовать.
В допустимой области видны три угловые точки. Две угловые точки (0, 8) и (8, 0) находятся на линиях, нарисованных ранее. Третья угловая точка возникает, где линия Y 2 = — 1 / 4 Y 1 + 2 и линия 7 Y 1 + 4
1
1 1 + 4 1 + 4 1 + 4 1 + 4 1 + 2 и линия 7 Y 1 + 4 + 4 1 + 2. Рисунок 13 – Угловые точки допустимой области. Начиная с первого уравнения, y 2 = – 1 / 4 y 1 + 2, решается для y 2 , это метод замены для решения точки пересечения. Заменитель y 2 = — 1 / 4 Y 1 + 2 до 7 Y 1 + 2 до 7 Y 1 + 2 до 7 Y 1 + 2 до 7 Y 2 1 + 2 до 7 Y 1 + 2 до 7 Y 1 + 2 до 7 Y 1 + 2 до 7 Y 1 + 2 до 7 Y Решите это уравнение, выделив y 1 : Поместите это значение в первое уравнение, чтобы получить y 2 = – 1 / 4 (4) + 2 = 1. Таким образом, третья угловая точка расположена в (4) + 2 = 1. Чтобы найти минимальное значение целевой функции w = 4 y 1 + y 2 , подставьте угловые точки. Рисунок 14 – Возможная область с помеченными угловыми точками. Оказывается, что минимум находится в упорядоченной паре ( y 1 , y 2 ) = (0, 8). Чтобы убедиться, что минимум расположен в точке (0, 8), посмотрите на три изоуровня w = 4, w = 8 и w = 12. Уровень должен проходить через угловую точку, но где лежат остальные уровни? Если мы установим w равным каждому из этих уровней в целевой функции и добавим их к графикам, мы увидим, как изоуровни ведут себя вблизи допустимой области. Как и ожидалось, уровень w = 8 проходит через угловую точку в точке (0, 8). Более высокие уровни w , такие как w = 12, проходят через допустимую область. Нас интересует минимальное значение целевой функции. Наименьшее значение w , которое включает любые точки в допустимой области, равно 9.0121 w В каждом из предыдущих примеров было одно оптимальное решение. В следующем примере есть много возможных решений задачи линейного программирования. Каждое решение дает одно и то же значение целевой функции. Решите задачу линейного программирования графически: Решение Как и в предыдущих примерах, ограничения неотрицательности позволяют построить график системы неравенств только в первом квадранте . Линия x = 8 — это вертикальная линия, проходящая через горизонтальную ось в точке (8, 0). Мы можем разместить эти три линии на графике, как показано на рисунке 15. Рисунок 15 – График границы каждого неравенства в примере 4. Чтобы заштриховать решение на графике, подставьте контрольную точку в каждое неравенство. Рисунок 16. Поскольку каждое неравенство верно, заштрихуйте полуплоскость, образованную каждым неравенством, где лежит контрольная точка. Отдельные наборы решений перекрываются в допустимой области, показанной ниже. Рисунок 17 – Допустимая область для системы неравенств в примере 4. Поскольку эта допустимая область ограничена, максимальное значение целевой функции расположено в одной из угловых точек или на линии, соединяющей соседние угловые точки. Несколько угловых точек легко идентифицируются по точкам пересечения. Красная граница, заданная линией х + 3 у = 24, и зеленая линия, заданная х = 8, пересекаются в одной из этих угловых точек. Если мы подставим x = 8 в x + 3 y = 24, мы можем вычислить y и получить первую угловую точку: / 3 ). Рисунок 18 – Возможная область с показанной угловой точкой. Другая угловая точка находится там, где красная линия, x + 3 y = 24, пересекает синюю линию, – x + 6 y = 30. Используя метод подстановки, мы можем найти x в первом уравнении, чтобы получить x = -3 y + 24. Подставьте выражение -3 y + 24 вместо x во втором уравнении и найдите y :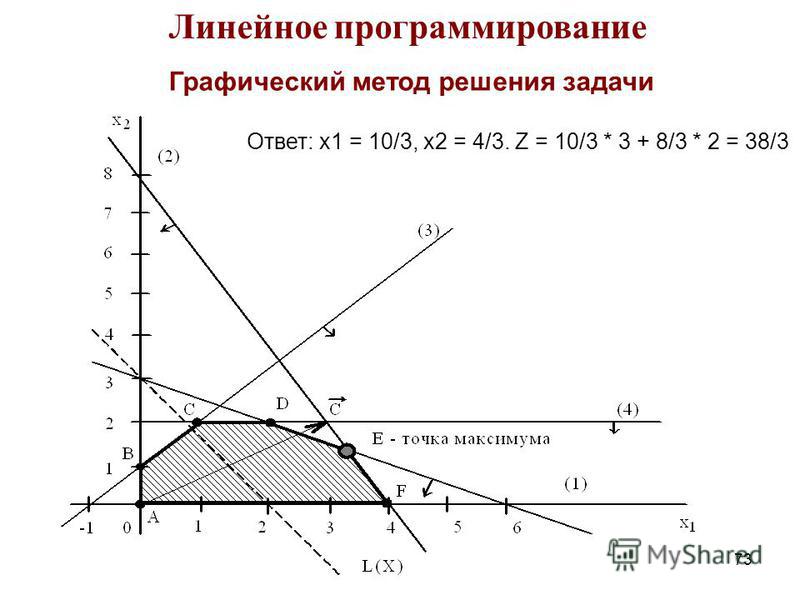
32 крест.
у 1 , у 2 ) = (4, 1).
По мере увеличения w линии изоуровня перемещаются все дальше и дальше в допустимую область, что означает, что допустимая область не имеет максимального значения. Пример 4 Решение задачи линейного программирования графически
Чтобы начертить границы трех других ограничений, преобразуйте каждое из неравенств в уравнения: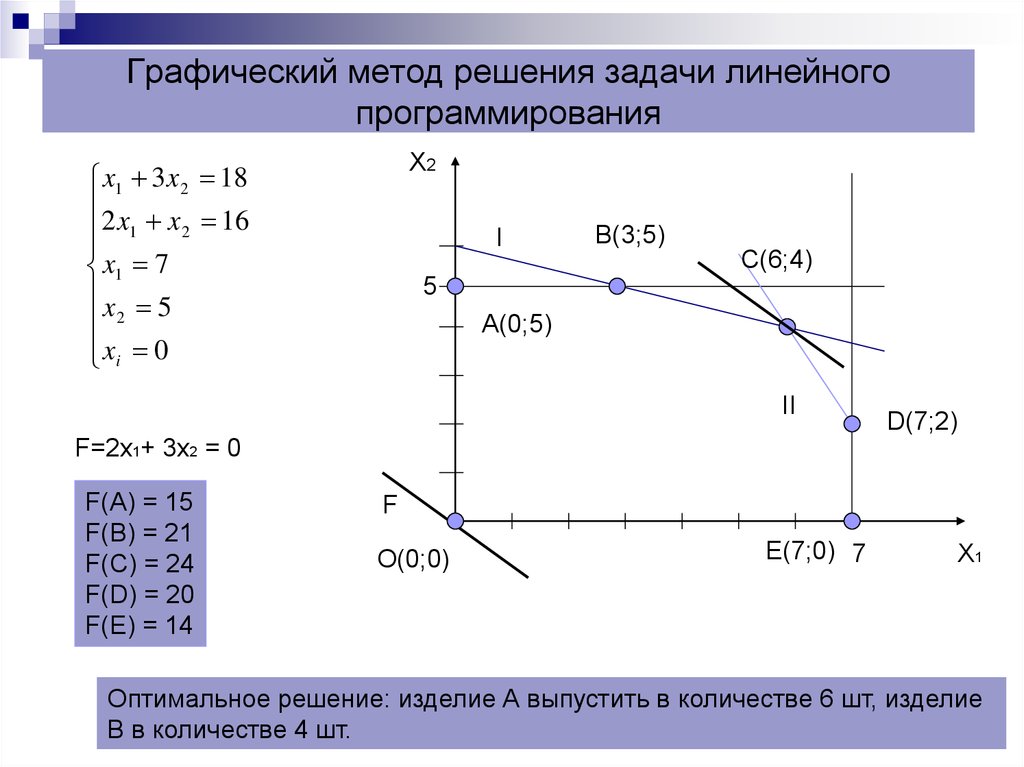
Однако две угловые точки в правом верхнем углу допустимой области не столь очевидны.
Рисунок 19 – Допустимая область с угловыми точками на (6, 6) и показано (8, 16 / 3 ).
Теперь, когда у нас есть угловые точки, мы можем подставить координаты в целевую функцию, чтобы найти максимальное значение.
Рисунок 20 – Угловые точки и соответствующие им значения целевой функции.
Две соседние угловые точки дают одно и то же значение, z = 120. Это означает, что целевая функция максимальна в любой точке линии, соединяющей (6, 6) и (8, 16 / 3 ).
Рисунок 21 – Изоуровень z = 120 проходит через две соседние угловые точки, указывая на то, что целевая функция оптимизируется в любом месте на линии, соединяющей точки.
Если изобразить изоуровень 5 x + 15 y = 120 на допустимой области, мы увидим, что он проходит через эти точки.
Для любого более высокого изоуровня линия будет находиться за пределами допустимой области.