Решить систему уравнений методом сложения онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Системой уравнений называют два и более уравнения, содержащих несколько неизвестных, объединенных фигурной скобкой. Существует несколько способов решения системы уравнений, одним из которых является метод сложения. Его суть заключается в том, чтобы после выполнения операции сложения исходная система уравнений приобрела такой вид, в котором будет только одна неизвестная. При сложении уравнений левая и правая часть первого и второго уравнения складываются в полном объеме.
Так же читайте нашу статью «Решить алгебраическое уравнение онлайн решатель»
Для наглядности решим систему уравнений следующего вида:
\[\left\{\begin{matrix} 3(x — y) + 5x = 2(3x — 2)\\ 4x — 2(x + y) = 4 — 3y \end{matrix}\right.
Выполним упрощение уравнения с помощью раскрытия скобок:
\[\left\{\begin{matrix} 3x — 3y + 5x = 6x — 4\\ 4x — 2x — 2y = 4 — 3y\\ \end{matrix}\right.\]
\[\left\{\begin{matrix} 8x — 3y = 6x — 4\\ 2x -2y = 4 — 3y\\ \end{matrix}\right.\]
\[\left\{\begin{matrix} 8x-3y — 6x = -4\\ 2x-2y + 3y = 4\\ \end{matrix}\right.\]
\[\left\{\begin{matrix} 2x — 3y = -4\\ 2x + y = 4 \end{matrix}\right.\]
Из полученного результата видно, что в 1 и 2 уравнении есть \[2x.\] Теперь нам необходимо сделать все, чтобы остался только \[y.\] Выполним умножение 1го уравнения на -1:
\[\left\{\begin{matrix} 2x — 3y = -4 & |\cdot(-1)\\ 2x + y = 4 \\ \end{matrix}\right.\]
\[\left\{\begin{matrix} 2x (-1)- 3y (-1)= -4\cdot(-1)\\ 2x + y = 4\\ \end{matrix}\right.\]
\[\left\{\begin{matrix} -2x + 3y = 4\\ 2x + y = 4 \end{matrix}\right.\]
Далее произведем сложение уравнений:
\[\left\{\begin{matrix} -2x + 3y = 4\\ 2x + y = 4 \end{matrix}\right. \Rightarrow \left\{\begin{matrix} (-2x
+ 3y ) + (2x + y) = 4 + 4 \\ -2x+ 3y+ 2x+ y= 4 + 4\ \end{matrix}\right. \]
\]
\[y = 2\]
После сложения и выполнения простых операций мы получили значение \[y=2.\] Подставим его в 1е уравнение:
\[\left\{\begin{matrix} -2x + 3y = 4\\ y = 2 \end{matrix}\right.\]
\[\left\{\begin{matrix} -2x + 3 \cdot 2 = 4\\ -2x + 6 = 4 \end{matrix}\right.\]
\[\left\{\begin{matrix} -2x — 2 |\div (-2)\\ y = 2 \end{matrix}\right.\]
\[\left\{\begin{matrix} x = 1\\ y = 2 \end{matrix}\right.\]
Ответ: \[x = 1, y= 2.\]
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.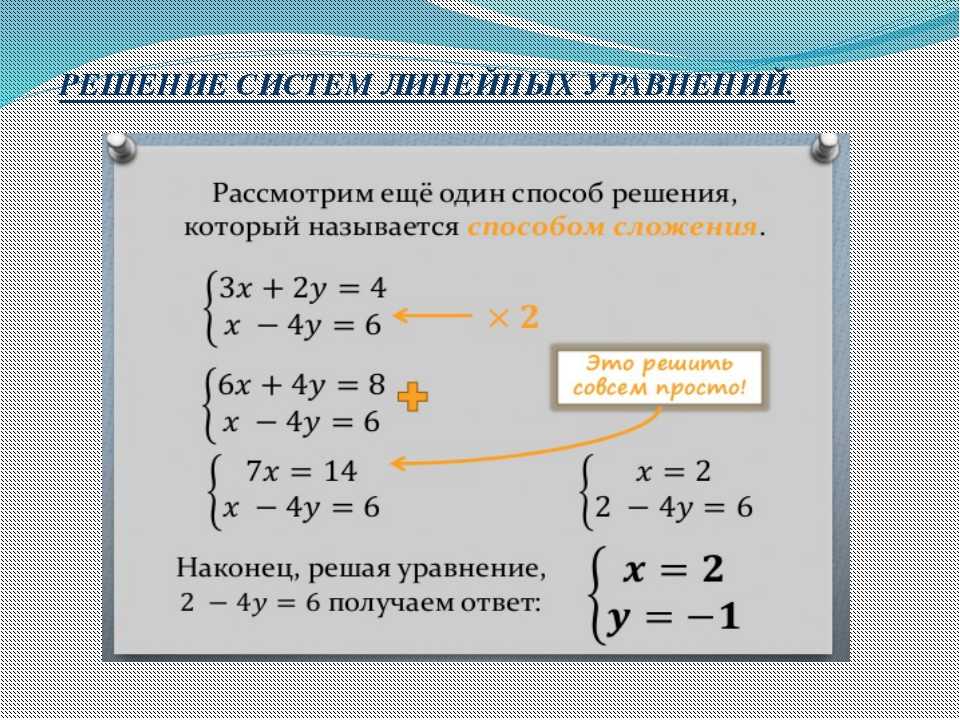
Как решить систему уравнений x- y = 7 и — 2x + 5y = — 8?
Манипулируя первым уравнением и комбинируя его со вторым, мы можем, в конце концов, прийти к ответу: x = 9, y = 2.
Ваша цель — удалить из задачи одну из переменных. Вы можете видеть, что первое уравнение имеет x, а второе уравнение имеет -2x. Если мы удвоим первое уравнение, мы получим:
#2x — 2y = 14#
Затем мы просто добавим это ко второму уравнению:
#2x — 2y = 14#
+#-2x + 5y = -8#
#3y=6#
Положительное 2x и отрицательное 2x сокращаются, остается только 3y = 6.
Разделить с обеих сторон на 3, и мы получаем y=2.
Наконец, просто подставьте 2 вместо y в любом из уравнений (я выберу первое, так как оно проще):
#x-2=7#
Добавьте 2 к обеим сторонам, чтобы получить x=9.
Таким образом, наш окончательный ответ: x = 9, y = 2.
Ссылка на ответ
Вам нужно будет решить одну из переменных, используя метод подстановки.
Начните с решения переменной #x# или #y#, сначала исключив или сократив одну из переменных. Затем мы можем подставить эту переменную в первое уравнение и решить второе уравнение , начните с умножения первого уравнения на #2# и прибавьте результат ко второму, чтобы отменить переменную #x#
#2 * ( x — y = 7) = 2x — 2y = 14 -># Добавьте это к второе уравнение
#- 2x + 5y = -8#
#+2x — 2y = 14#
#………………….#
# 3y = 6 #
# y = 2#
Теперь подставьте #2# вместо #y# в первое уравнение для решения #x#
# x — 2 +2 = 7 +2 #
# x = 9 #
Теперь мы решили обе переменные. Убедитесь, что оба уравнения равны.
Ссылка для ответа
Точка пересечения двух линий #(9,2)#.
См. объяснение процесса.
Решить систему уравнений:
Это линейные уравнения. Поскольку они представляют собой систему, оба уравнения решаются одновременно подстановкой. Полученные значения x и y являются точкой пересечения двух линий на графике.
Два уравнения:
#x-y=7##color(white)(…)andcolor(white)(…)##-2x+5y=-8#
Первое уравнение : #x-y=7#
#x-y=7#
Добавьте #y# к обеим сторонам.
#x=7+y#
Второе уравнение: #-2x+5y=-8#
Подставьте #7+y# вместо #x# в уравнении.
#-2(7+y)+5y=-8#
Упрощение.
#-14-2y+5y=-8#
Добавьте #14# с обеих сторон.
#-2y+5y=-8+14#
Упрощение.
#3y=6#
Разделите обе части на #3#.
#y=2#
Теперь подставьте значение #y# обратно в первое уравнение и найдите #x#.
#x-2=7#
Добавьте #2# к обеим сторонам.
#x=9#
Точка пересечения #(9,2)#.
Ссылка для ответа
Влияние этого вопроса
11454 просмотров по всему миру
Вы можете повторно использовать этот ответ
Лицензия Creative Commons
Как понять, как определить наилучший метод решения системы уравнений, а затем решить систему?
Система уравнений
Сара Б.
Не могу понять? Не знаю, что я делаю неправильно. ПОМОЩЬ!!!!!!!!!!!!!!!!
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Джон Р. ответил 18/12/12
Репетитор
4.6 (55)
Джон Р.: учитель математики, естественных наук и истории
Смотрите таких репетиторов
Смотрите таких репетиторов
Есть три метода, которые обычно используются для решения системы уравнений. Это графическое изображение, замена и исключение. Все три метода дадут один и тот же ответ, но каждый из них имеет свои преимущества и недостатки.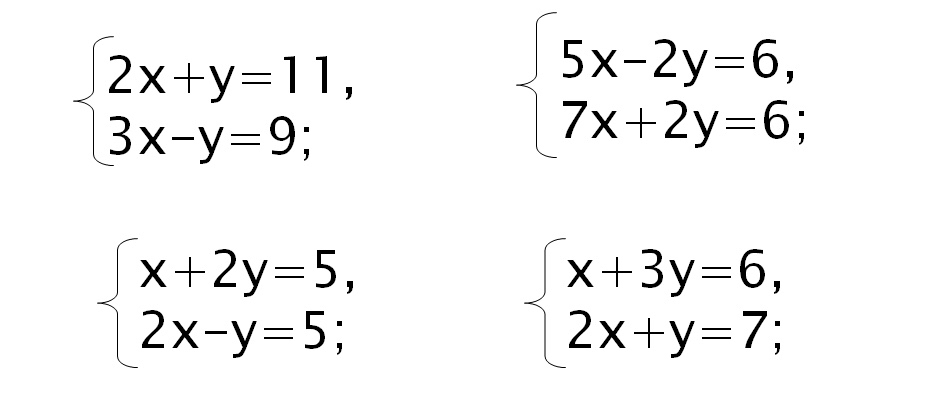
Графика: Лучше всего знакомить новичков с решением систем двух уравнений с двумя переменными, используя графики, поскольку они дают им визуальное представление о том, что они ищут. Графики менее точны и часто требуют больше времени, чем другие методы. Я рекомендую использовать график для поиска решения только в том случае, если проблема связана с уже нарисованным графиком, а пересечение находится в точной координате.
Подстановка: Подстановка дает то преимущество, что уравнение уже записано для второй переменной, когда вы найдете первую. Подстановку лучше всего использовать, когда одно (или оба) уравнения уже решены для одной из переменных. Он также хорошо работает, если одна из переменных имеет коэффициент 1,9.0003
Устранение: Устранение — это метод, который я использую почти каждый раз. Если вы не уверены, какой метод использовать, я рекомендую вам использовать исключение. Исключение лучше всего использовать, когда оба уравнения имеют стандартную форму (Ax + By = C).
Я надеюсь, что это дало вам некоторое представление о том, какой метод следует использовать. Все три метода дадут одно и то же решение. Кроме того, вы всегда должны проверять свой ответ в обоих уравнениях, чтобы убедиться, что он правильный.
Голосовать за 3 Понизить
Подробнее
Отчет
Морис С. ответил 17.12.12
Репетитор
4.9 (899)
Квалифицированное и эффективное обучение так, как ВЫ учитесь!
Об этом репетиторе ›
Об этом репетиторе ›
Если у вас есть система уравнений, есть три основных метода ее решения:
Исключение, замена и построение графика.
Выбор используемого метода основан на уравнениях.
Если вы можете легко умножить одно из уравнений на выбранный вами множитель, а затем вычесть полученное новое уравнение из другого уравнения в системе и тем самым исключить одну из переменных, оставив вам одно уравнение с одной переменной, тогда устранение является хорошим выбором.
Если одно из уравнений может быть решено для одной из переменных, а затем вы можете подставить эту переменную в другое уравнение, создав таким образом уравнение с одной переменной, подстановка будет хорошим выбором.
И если вы можете преобразовать уравнения либо в форму наклон-пересечение, либо в форму точка-наклон, вы можете просто нанести обе линии на график и найти решение на пересечении линий.
Если вам нужна дополнительная информация о любом из этих методов, пожалуйста, прокомментируйте этот ответ для получения дополнительной помощи.
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.

