Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выразите вектор ЕА – ЕС через вектор MN.2.4: Решение уравнений и неравенств с помощью графиков
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19688
- Дэвид Арнольд
- College of the Redwoods
В этой главе основное внимание уделялось функциям и интерпретации их графиков. В этом разделе мы продолжаем в том же духе и обратимся к решению уравнений и неравенств с помощью графиков.
Уравнения будут иметь вид \(f(x) = g(x)\), а неравенства будут иметь вид \(f(x) < g(x)\) и/или \(f(x) > g (Икс)\).
Вы можете удивиться, почему мы не упомянули неравенства вида \(f(x) \leq g(x)\) и \(f(x) \geq g(x)\). Причиной этого упущения является тот факт, что решение неравенства \(f(x) \leq g(x)\) есть просто объединение решений \(f(x) = g(x)\) и \(f(x) Мы начнем со сравнения значений двух функций f и g при различных значениях x в их областях определения. Предположим, что мы оцениваем две функции f и g при определенном значении x. Возможен один из трех исходов. Либо \[f(x)=g(x), \quad \text { или } \quad f(x)>g(x), \quad \text { или } \quad f(x) Довольно просто сравнить два значения функции по конкретному значению, если для каждой функции заданы правила. 9{2}=9 \quad \text { и } \quad g(3)=2(3)+3=9\] так что ясно, \(f(3) = g(3)\). Мы также можем сравнивать значения функций при определенном значении x, изучая графики функций. Например, рассмотрим графики двух функций f и g на рисунке \(\PageIndex{1}\). Рисунок \(\PageIndex{1}\) Далее предположим, что мы проводим пунктирную вертикальную линию через точку пересечения графиков f и g, затем выбираем значение x, лежащее слева пунктирной вертикальной линии, как показано на рисунке \(\PageIndex{2}\)(a). Поскольку график f лежит над графиком g для всех значений x, лежащих слева от пунктирной вертикальной линии, будет иметь место, что \(f(x) > g(x)\) для всех таких x (см. рисунок \(\PageIndex{2}\)(a)). С другой стороны, график f лежит ниже графика g для всех значений x, лежащих справа от пунктирной вертикальной линии. Следовательно, для всех таких x будет иметь место \(f(x) < g(x)\) (см. рисунок \(\PageIndex{2}\)(b)). Рисунок \(\PageIndex{2}\). Сравнивая f и g. Наконец, если мы выберем значение x точки пересечения графиков f и g, то для этого значения x будет так, что f(x) и g(x) равны; то есть \(f(x) = g(x)\) (см. Рисунок \(\PageIndex{3}\). Значения функций f(x) и g(x) равны там, где графики функций f и g пересекаются. Подведем итоги. Резюме Давайте рассмотрим пример. Пример \(\PageIndex{2}\) Имея графики f и g на рисунке \(\PageIndex{4}\)(a), используйте построитель множеств и нотацию интервала для описания решения неравенство f(x) < g(x). Затем аналогичным образом найдите решения неравенства f(x) > g(x) и уравнения f(x) = g(x). Решение Чтобы найти решение f(x) < g(x), мы должны найти, где график f лежит ниже графика g. Сравнение функций
Рисунок \(\PageIndex{4}\). Сравнивая f и g.
Обратите внимание, что заштрихованные точки на оси x имеют значения x меньше 2. Следовательно, решение f(x) < g(x) есть \[(-\infty, 2)=\{x : x <2\}\]
Аналогичным образом, решение f(x) > g(x) находится путем определения того, где график f лежит над графиком g, и заштриховывания соответствующих значений x на x- оси (см. рисунок \(\PageIndex{5}\)(a)). Решением f(x) >
g(x) является \((2, \infty)\) или, альтернативно, \(\{x : x>2\}\). Чтобы найти решение f(x) = g(x), отметьте, где график f пересекает график g, затем заштрихуйте значение x этой точки пересечения на оси x (см.
рисунок \( \PageIndex{5}\)(б)). Следовательно, решение f(x) = g(x) есть \(\{x : x = 2\}\). Это не интервал, поэтому нецелесообразно описывать это решение интервальной нотацией.
Рисунок \(\PageIndex{5}\). Дальнейшие сравнения.
Давайте посмотрим на другой пример.
Пример \(\PageIndex{3}\)
Имея графики f и g на рисунке \(\PageIndex{6}\)(a), используйте как построитель множеств, так и нотацию интервала для описания решения неравенства f(x) > g(x). Затем аналогичным образом найдите решения неравенства f(x) < g(x) и уравнения f(x) = g(x).
Рисунок \(\PageIndex{6}\). Сравнивая f и g.
Чтобы найти решение f(x) > g(x), мы должны найти, где график f находится над графиком g. Проведите пунктирные вертикальные линии через точки пересечения графиков f и g (см. рисунок \(\PageIndex{6}\)(b)), затем обратите внимание, что график f лежит над графиком g между пунктирной вертикалью только что нарисованные линии.
Следовательно, решением неравенства f(x) > g(x) является совокупность всех x, лежащих между пунктирными вертикальными линиями. Мы заштриховали эту коллекцию по оси X красным цветом (или более толстыми линиями для тех, кто просматривает черно-белые изображения) на рисунке \(\PageIndex{6}\)(b).
Обратите внимание, что точки, заштрихованные на оси x на рисунке \(\PageIndex{6}\)(b), имеют значения x от −2 до 3. Следовательно, решение f(x) > g(x) равно
\[(-2,3)=\{x :-2 Аналогичным образом решение f(x) < g(x) находится, отмечая, где график f лежит ниже графика g и заштриховывает соответствующие значения x на оси x (см. рис. 7(a)). Таким образом, решение f(x) < g(x) равно \[(-\infty,-2) \cup(3, \infty)=\{x : x<-2 \text { или } x >3\}\] Чтобы найти решение f(x) = g(x), обратите внимание, где график f пересекает график g, и заштрихуйте значение x каждой точки пересечения на оси x (см. рисунок \( \PageIndex{7}\)(б)). Таким образом, решение f(x) = g(x) равно \(\{x : x=-2\) или \(x=3\}\). Рисунок \(\PageIndex{7}\). Дальнейшие сравнения. Теперь мы знаем, что решением f(x) = g(x) является множество всех x, для которых пересекаются графики f и g. Поэтому графический калькулятор становится незаменимым помощником при решении уравнений. Пример \(\PageIndex{4}\) Используйте графический калькулятор для решения уравнения что уравнение (6) имеет вид f(x) = g(x), где \[f(x)=1,23 x-4,56 \quad \text { и } \quad g(x)=5,28-2,35 x \] Таким образом, наш подход будет состоять в том, чтобы нарисовать графики f и g, а затем найти значение x точки пересечения. Сначала загрузите f(x) = 1,23x − 4,56 в Y1 и g(x) = 5,28 − 2,35x в Y2 в меню Y= графического калькулятора (см. рисунок \(\PageIndex{8}\)( а)). Выберите 6:ZStandard в меню ZOOM, чтобы создать графики на рисунке \(\PageIndex{8}\)(b). Рисунок \(\PageIndex{8}\). Рисуем графики f(x) = 1,23x−4,56 и g(x) = 5,28−2,35x. Решением уравнения (6) является значение x точки пересечения графиков f и g на рисунке (\PageIndex{8}\)(b). Мы воспользуемся утилитой intersect в меню CALC графического калькулятора, чтобы определить координаты точки пересечения. Действуем следующим образом: Рисунок \(\PageIndex{9}\). Использование утилиты пересечения. Результат этой последовательности шагов показан на рисунке \(\PageIndex{10}\). Координаты точки пересечения приблизительно равны (2,7486034, −1,179218). Значение x этой точки пересечения является решением уравнения (6). То есть решение \(1,23x — 4,56 = 5,28 — 2,35x\) примерно равно \(x \приблизительно 2,7486034\). Рисунок \(\PageIndex{10}\). Координаты точки пересечения. Резюме Рекомендации. Вам нужно будет обсудить ожидания со своим учителем, но мы ожидаем, что наши ученики резюмируют свои результаты следующим образом. 1. Настройте систему координат.6 Пометьте и масштабируйте каждую ось с помощью xmin, xmax, ymin и ymax. 2. Скопируйте изображение в окне просмотра в свою систему координат. Подпишите каждый график его уравнением. 3. 4. Заштрихуйте и обозначьте решение уравнения на оси x. 9{2}-3\) и \(g(x)=1,23 x+1,25\) в Y1 и Y2 в меню Y= соответственно, как показано на рисунке \(\PageIndex{12}\)(a). Выберите 6:ZStandard в меню ZOOM, чтобы создать графики, показанные на рисунке \(\PageIndex{12}\)(b). Чтобы найти точки пересечения графиков f и g, мы выполняем ту же последовательность шагов, что и в примере \(\PageIndex{4}\), до точки, где калькулятор просит вас сделать предположение (т. е. 2nd CALC, 5: пересечение, ввод первой кривой, ввод второй кривой). Поскольку есть две точки пересечения, когда калькулятор попросит вас 9{2}-3\) и \(g(x) = 1,23x + 1,25\). сделать предположение, вы должны переместить курсор (с помощью клавиш со стрелками) так, чтобы он был ближе к точке пересечения, которую вы хотите найти, чем к другой точке пересечения. С помощью этой техники получаются две точки пересечения, изображенные на рисунках \(\PageIndex{13}\)(a) и (b). Рисунок \(\PageIndex{13}\). Точки пересечения графиков функций f и g. Приблизительные координаты первой точки пересечения (−1,626682, −0,7508192). Вторая точка пересечения имеет приблизительные координаты (3.0737411, 5.0307015). Важно помнить, что каждый раз, когда вы берете в руки калькулятор, вы получаете только приблизительное значение. Возможно, вы получите несколько иной результат для точек пересечения. Например, вы можете получить (-1,626685, -0,7508187) для точки пересечения. Основываясь на положении курсора, когда вы отмечали кривые и делали предположения, вы можете получить немного разные приближения. Обратите внимание, что это второе решение очень близко к тому, которое мы нашли, отличаясь только несколькими последними десятичными знаками, и вполне приемлемо в качестве ответа. 9{2} − 3 > 1,23x + 1,25\) приблизительно равно \[(-\infty,-1,626682] \cup[3,0737411, \infty)=\{x : x \leq-1,626682 \text { или } x \geq 3.0737411\}\] Когда мы оцениваем функцию f при определенном значении x, возможен только один из трех результатов. \[f(x)=0, \quad \text { или } \quad f(x)>0, \quad \text { или } \quad f(x)<0\] То есть, либо f(x) равно нулю, либо f(x) положительно, либо f(x) отрицательно. Других возможностей нет. Мы могли бы начать заново, используя совершенно новый подход, или мы можем опираться на то, что уже знаем. Мы выбираем последний подход. Предположим, нас попросили сравнить f(x) с нулем? Равно ли оно нулю, больше нуля или меньше нуля? Положим g(x) = 0. Теперь, если мы хотим сравнить функцию f с нулем, нам нужно только сравнить f с g, что мы уже умеем делать. Чтобы найти, где f(x) = g(x), отметим, где пересекаются графики f и g, чтобы найти, где f(x) > g(x), отметим, где график f лежит над графиком g , и, наконец, чтобы найти, где f(x) < g(x), мы просто отмечаем, где график f лежит ниже графика g. Однако график g(x) = 0 представляет собой горизонтальную линию, совпадающую с осью x. Действительно, g(x) = 0 — это уравнение оси x. Это рассуждение приводит к следующим ключевым результатам. резюме Например: Рисунок \(\PageIndex{15}\). Сравнение функции f с нулем. Далее мы определим некоторые важные термины. Определение Если f(a) = 0, то a называется нулем функции f. График f пересекает ось x в точке \((a, 0)\), точке, называемой точкой пересечения x графика f. 9{2}-1,24 х-3,84\). Наша стратегия будет состоять в том, чтобы нарисовать график f, а затем определить, где график f лежит ниже или на оси x. Действуем следующим образом: Рисунок (\PageIndex{16}\). Нахождение точки пересечения с нулем или х с помощью калькулятора. Последним шагом является интерпретация результатов и запись нашего решения на нашем домашнем листе. Ссылаясь на рекомендации Summary 7, мы приходим к графику, показанному на рисунке (\PageIndex{18}\). 9{2}-1,24 х-3,84\), заметим: \[[-2. спросил Изменено
7 лет, 2 месяца назад Просмотрено
162 раза $\begingroup$
92-1=0$ на $x$ ($x=0$ не является решением), но это не помогает мне решить уравнение. Я начал задаваться вопросом, действительно ли уравнения, которые могут быть решены (или, по крайней мере, упрощены) путем деления обеих частей на некоторое $f(x)$, были именно теми, где $f(x)=0$ является решением: путем удаления решение, деление приводит уравнение к более простому виду. Это особенно очевидно в этом примере, приведенном в принятом ответе на этот вопрос: $$(x-1)(x-2)(x-3)(x-4)(x-5)(x-6)=0 . При последовательном делении на $x-1$, $x-2$ и т. д. уравнение становится проще по мере удаления решений до тех пор, пока решений не останется ($1=0$). Однако и принятый ответ, и цитата в самом вопросе говорят, что $f(x)=0$ может быть решением, что я также понимаю, поскольку не может быть решением. Итак, существуют ли уравнения, в которых деление на некоторый $f(x)$ значительно улучшает разрешение уравнения, при этом $f(x)=0$ не является решением? 92+1=0$ не имеет решений в вещественных числах (легко видеть, потому что $f(x)\ge1$ для каждого $x$). Это то, что вы ищете? В качестве более сложного примера можно взять уравнение $$\sin(2x)=0$$
решать на отрезке $(0,\pi)$. Поскольку $\sin(2x)=2\sin(x)\cos(x)$, мы можем разделить обе части на $2\sin(x)$ (поскольку $\sin(x)$ положительно на рассматриваемом интервале ), чтобы найти решения именно там, где $\cos(x)=0$. Это дало бы нам ровно одно решение при $x=\frac{\pi}{2}$. $\endgroup$ 2 $\begingroup$ Ну, это зависит.
Поскольку этот набор решений не является интервалом, было бы неуместно описывать его интервальной нотацией. Решение уравнений и неравенств с помощью графического калькулятора
4 Просто нажмите клавишу ENTER, чтобы использовать текущую позицию курсора в качестве догадки.
Проведите пунктирную вертикальную линию через точку пересечения.
Сравнение функций с нулем
Либо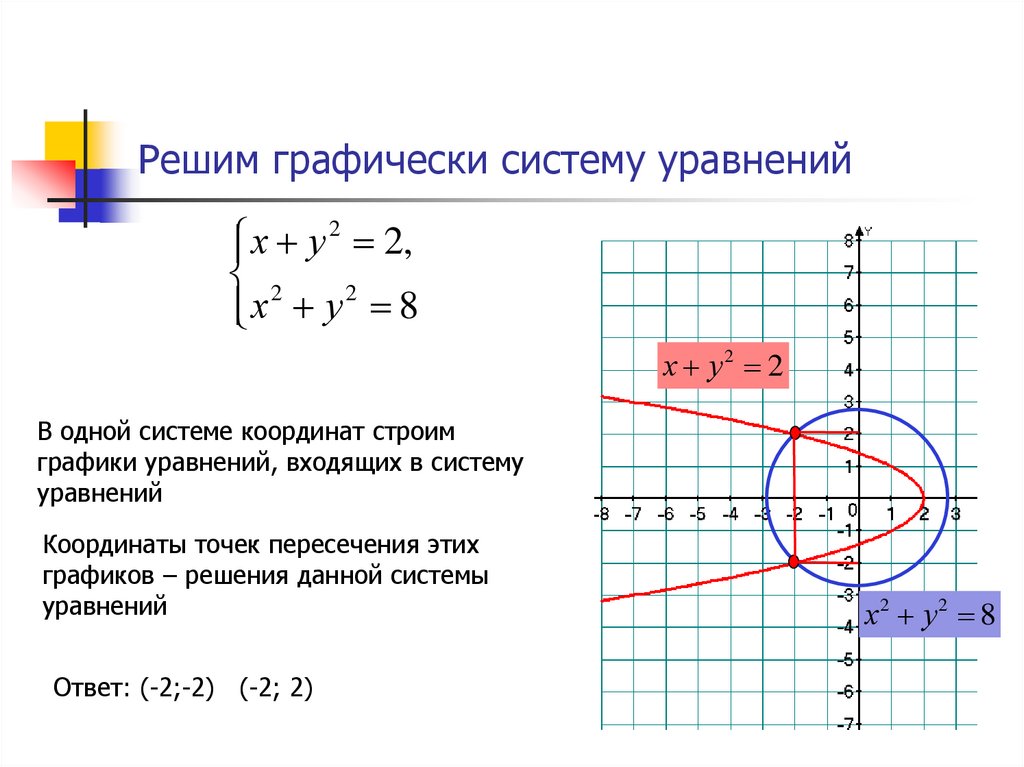
Таким образом, решением f(x) < 0 является \((-\infty, 1)=\{x : x<1 \}\).
Нажмите ENTER, чтобы записать этот «левый предел».
Обратите внимание, что координата x точки пересечения приблизительно равна −2,157931.
157931,7.1179306]=\{x :-2.157931 \leq x \leq 7.1179306\}\] На этой странице нет тегов.
Предварительное вычисление алгебры — Уравнение, решенное делением на $f(x)$, где $f(x)=0$ не является решением
$$