ОГЭ по математике, базовый уровень. Квадратные уравнения
Задание №7 из ОГЭ прошлых лет, рекомендованные как тренировочные.
Задача № 1
Уравнение
x2 + px + q = 0
имеет корни: −5; 7. Найдите q.
Решение
Из условия задачи известно, что данное уравнение имеет два корня:
х1 = -5
х2 = 7
Составим систему уравнений, в которую подставим имеющиеся корни:
Из первого уравнения выразим q:
q = 5p — 25 (1)
Полученное выражение подставим во второе уравнение:
49 + 7p + (5p — 25) = 0
49 + 7p + 5p — 25 = 0
7p + 5p = 25 — 49
12p = — 24
p = -2
Полученное значение «p» подставим в (1):
q = 5· (- 2) — 25 = — 10 — 25 = — 35
Ответ: −35.
Задача № 2
Найдите корни уравнения
x2 + 7x — 18 = 0
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение
Перед нами классическое квадратное уравнение. Решим его через нахождение дискриминанта:
D = b2 – 4ac = 72 – 4 · 1 · (-18) = 49 + 72 = 121
Значение дискриминанта больше нуля, следовательно, уравнение имеет два корня.
Тогда корни можем найти по формуле:
Запишем получившиеся корни в порядке возрастания: -92
Ответ: −92
Задача № 3
Найдите корни уравнения
х2 + 4 = 5х
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
Решение
Преобразуем уравнение и запишем в виде:
х2 — 5х + 4 = 0
Решим его через нахождение дискриминанта:
D = b2 – 4ac = 52 – 4 · 1 · 4 = 25 — 16 = 9
Значение дискриминанта больше нуля, следовательно, уравнение имеет два корня.
Тогда, корни можем найти по формуле:
Запишем получившиеся корни в порядке возрастания: 14
Ответ: 14
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Брестский государственный университет им.
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-10 классов. Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях!
Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях!
Мордовский государственный университет им. В.П. Огарева
В.П. Огарева
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-5 классов. Я считаю, что математика отлично тренирует память, логику и мышление, а также несомненно развивает творчески, поэтому я с удовольствием помогаю детям подружиться с ней. Процесс изучения математики приносит моим ученикам много положительных эмоций, они с большим интересом начинают решать ,казалось бы, до этого трудные задачи. Давайте вместе с вами отправимся в увлекательное путешествие в страну Математика, чтобы навсегда полюбить ее! Оставить заявку
Я считаю, что математика отлично тренирует память, логику и мышление, а также несомненно развивает творчески, поэтому я с удовольствием помогаю детям подружиться с ней. Процесс изучения математики приносит моим ученикам много положительных эмоций, они с большим интересом начинают решать ,казалось бы, до этого трудные задачи. Давайте вместе с вами отправимся в увлекательное путешествие в страну Математика, чтобы навсегда полюбить ее! Оставить заявкуКриворожский педагогический университет
Проведенных занятий:
Форма обучения:Дистанционно (Скайп)
Репетитор 5-9 классов.
Математика 11 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
50 Индивидуальных вариантов ( карточек ) «Квадратные уравнения» (теорема Виета + частные случаи)
Работа №1 Решите уравнения
1) x²–9x+14=0 2) x²–10x+24=0 3) x²–5x+4=0 4) x²–6x+8=0 5) x²–12x+27=0 6) x²–3x+2=0
7) x²+13x+40=0 8) x²+11x+24=0 9) x²+5x+6=0 10) x²+10x+24=0 11) x²+15x+56=0 12) x²+7x+10=0
13) x²–22x+117=0 14) x²+16x+39=0 15) x²+15x+36=0 16) x²–24x+135=0 17) x²+14x+24=0 18) x²+19x+70=0
19) x²–6x–7=0 20) x²+x–6=0 21) x²+3x–28=0 22) x²–x–30=0 23) x²–2x–3=0 24) x²–3x–10=0
25) x²+16x+39=0 26) x²–18x+65=0 27) x²+24x+108=0 28) x²–16x+63=0 29) x²–14x+49=0 30) x²–8x+16=0
31) x²+17x+52=0 32) x²+33x+162=0 33) x²+15x+50=0 34) x²+27x+92=0 35) x²+15x+44=0 36) x²+20x+36=0
37) x²+403x+402=0 38) x²+324x+963=0 39) x²–113x+112=0 40) x²–333x+990=0 41) x²–428x+2947=0 42) x²+202x+201=0
43) x²+10x–8075=0 44) x²+4x–6396=0 45) x²–10x–8075=0 46) x²+12x–6364=0 47) x²+12x–364=0 48) x²+8x–8084=0
49) 2x²+3x+1=0 50) 7x²+11x–18=0 51) 7x²+3x–10=0 52) 2x²+13x–15=0 53) 19x²–20x+1=0 54) 19x²–13x–6=0
Работа №2 Решите уравнения
1) x²–10x+21=0 2) x²–14x+48=0 3) x²–15x+56=0 4) x²–17x+72=0 5) x²–10x+16=0 6) x²–13x+40=0
7) x²+14x+40=0 8) x²+7x+10=0 9) x²+13x+40=0 10) x²+13x+30=0 11) x²+9x+18=0 12) x²+16x+60=0
13) x²+21x+98=0 14) x²+23x+120=0 15) x²–15x+26=0 16) x²–15x+50=0 17) x²+17x+70=0 18) x²–17x+52=0
19) x²–5x–24=0 20) x²+x–12=0 21) x²+x–72=0 22) x²+7x–18=0 23) x²–3x–40=0 24) x²–5x–14=0
25) x²–3x–54=0 26) x²–4x–96=0 27) x²–10x+16=0 28) x²–22x+105=0 29) x²+5x+6=0 30) x²–26x+133=0
31) x²+24x+63=0 32) x²+23x+22=0 33) x²+23x+102=0 34) x²+19x+18=0 35) x²+30x+161=0 36) x²+32x+175=0
37) x²+226x+1320=0 38) x²+339x+2324=0 39) x²+426x+1688=0 40) x²+407x+2800=0 41) x²+403x+802=0 42) x²+126x+720=0
43) x²–14x–4851=0 44) x²–8x–884=0 45) x²+14x–4851=0 46) x²+8x–6384=0 47) x²–2x–3599=0 48) x²+6x–8091=0
49) 4x²–5x+1=0 50) 11x²–6x–17=0 51) 9x²–8x–17=0 52) 2x²–9x+7=0 53) 14x²–13x–1=0 54) 24x²+7x–17=0
Работа №3 Решите уравнения
1) x²–10x+24=0 2) x²–13x+42=0 3) x²–12x+36=0 4) x²–14x+45=0 5) x²–14x+40=0 6) x²–10x+16=0
7) x²+5x+6=0 8) x²+6x+5=0 9) x²+3x+2=0 10) x²+6x+8=0 11) x²+15x+54=0 12) x²+13x+40=0
13) x²–20x+91=0 14) x²–21x+98=0 15) x²+19x+88=0 16) x²+21x+98=0 17) x²+21x+104=0 18) x²–17x+70=0
19) x²–5x–24=0 20) x²–3x–40=0 21) x²–3x–28=0 22) x²–2x–48=0 23) x²–4x–12=0 24) x²+5x–14=0
25) x²–3x–18=0 26) x²–2x–8=0 27) x²–21x+98=0 28) x²–14x+40=0 29) x²–12x+32=0 30) x²–22x+96=0
31) x²+16x+60=0 32) x²+26x+133=0 33) x²+34x+145=0 34) x²+14x+13=0 35) x²+21x+54=0 36) x²+25x+66=0
37) x²+423x+422=0 38) x²–426x+1688=0 39) x²+326x+1605=0 40) x²+214x+424=0 41) x²–318x+1872=0 42) x²–345x+1364=0
43) x²+12x–6364=0 44) x²+4x–9996=0 45) x²–6x–8091=0 46) x²+8x–384=0 47) x²–4x–9996=0 48) x²+14x–351=0
49) 2x²–5x–7=0 50) 7x²–8x+1=0 51) 15x²–2x–17=0 52) 19x²–18x–1=0 53) 13x²+7x–20=0 54) 29x²+5x–34=0
Работа №4 Решите уравнения
1) x²–15x+50=0 2) x²–6x+9=0 3) x²–19x+88=0 4) x²–6x+5=0 5) x²–8x+7=0 6) x²–16x+60=0
7) x²+16x+64=0 8) x²+8x+12=0 9) x²+18x+81=0 10) x²+9x+20=0 11) x²+10x+21=0 12) x²+7x+12=0
13) x²+18x+65=0 14) x²+22x+117=0 15) x²+21x+90=0 16) x²+18x+77=0 17) x²+16x+60=0 18) x²–23x+120=0
19) x²+3x–40=0 20) x²+2x–35=0 21) x²–5x–24=0 22) x²–3x–54=0 23) x²–x–56=0 24) x²+x–12=0
25) x²–7x+12=0 26) x²+15x–54=0 27) x²+16x+48=0 28) x²+12x+27=0 29) x²+10x–56=0 30) x²–12x–108=0
31) x²+23x+22=0 32) x²+11x+10=0 33) x²+17x+60=0 34) x²+24x+108=0 35) x²+31x+84=0 36) x²+25x+114=0
37) x²+138x+792=0 38) x²–446x+2640=0 39) x²+235x+924=0 40) x²–408x+2807=0 41) x²+403x+402=0 42) x²+126x+605=0
43) x²+14x–8051=0 44) x²+12x–8064=0 45) x²+6x–391=0 46) x²–4x–6396=0 47) x²+14x–9951=0 48) x²+2x–4899=0
49) 5x²+4x–9=0 50) 10x²+9x–1=0 51) 8x²+11x–19=0 52) 5x²–21x–26=0 53) 25x²–4x–29=0 54) 21x²+8x–13=0
Работа №5 Решите уравнения
1) x²–18x+80=0 2) x²–5x+6=0 3) x²–3x+2=0 4) x²–16x+60=0 5) x²–10x+9=0 6) x²–13x+22=0
7) x²+13x+36=0 8) x²+11x+30=0 9) x²+7x+12=0 10) x²+8x+12=0 11) x²+14x+45=0 12) x²+17x+70=0
13) x²–23x+120=0 14) x²–19x+60=0 15) x²+20x+99=0 16) x²–22x+117=0 17) x²+16x+39=0 18) x²+21x+98=0
19) x²+5x–24=0 20) x²+3x–10=0 21) x²–2x–48=0 22) x²+4x–45=0 23) x²+x–6=0 24) x²–3x–28=0
25) x²+4x–32=0 26) x²–4x–21=0 27) x²–14x+24=0 28) x²+x–30=0 29) x²+16x–36=0 30) x²–17x–38=0
31) x²+32x+156=0 32) x²+16x+55=0 33) x²+23x+42=0 34) x²+22x+85=0 35) x²+19x+48=0 36) x²+30x+81=0
37) x²+329x+2254=0 38) x²–314x+624=0 39) x²–417x+2060=0 40) x²–134x+264=0 41) x²–248x+1452=0 42) x²+126x+720=0
43) x²+12x–1564=0 44) x²–12x–6364=0 45) x²+10x–8075=0 46) x²+4x–896=0 47) x²–10x–8075=0 48) x²+14x–1551=0
49) 5x²–4x–1=0 50) 7x²+9x–16=0 51) 8x²+3x–5=0 52) 10x²–21x+11=0 53) 17x²–7x–10=0 54) 29x²+18x–47=0
Работа №6 Решите уравнения
1) x²–15x+50=0 2) x²–17x+70=0 3) x²–13x+30=0 4) x²–11x+28=0 5) x²–17x+72=0 6) x²–12x+32=0
7) x²+12x+35=0 8) x²+6x+5=0 9) x²+21x+110=0 10) x²+12x+27=0 11) x²+8x+16=0 12) x²+18x+80=0
13) x²+21x+98=0 14) x²+19x+60=0 15) x²–19x+78=0 16) x²–18x+72=0 17) x²–15x+36=0 18) x²+22x+112=0
19) x²–5x–24=0 20) x²–4x–21=0 21) x²–3x–28=0 22) x²+2x–24=0 23) x²+x–20=0 24) x²+x–42=0
25) x²–x–6=0 26) x²–7x–18=0 27) x²–12x+27=0 28) x²+4x–32=0 29) x²–24x+135=0 30) x²+18x+56=0
31) x²+32x+156=0 32) x²+31x+130=0 33) x²+25x+114=0 34) x²+19x+48=0 35) x²+28x+147=0 36) x²+16x+60=0
37) x²–316x+1555=0 38) x²+205x+606=0 39) x²–314x+624=0 40) x²–434x+1293=0 41) x²+226x+1320=0 42) x²–412x+820=0
43) x²–12x–6364=0 44) x²+12x–864=0 45) x²–12x–2464=0 46) x²–8x–6384=0 47) x²+8x–8084=0 48) x²–8x–384=0
49) 4x²+3x–1=0 50) 3x²+7x+4=0 51) 15x²–13x–2=0 52) 17x²–4x–13=0 53) 24x²+13x–11=0 54) 31x²–21x–52=0
Работа №7 Решите уравнения
1) x²–11x+18=0 2) x²–14x+33=0 3) x²–13x+36=0 4) x²–16x+63=0 5) x²–12x+35=0 6) x²–6x+8=0
7) x²+17x+72=0 8) x²+10x+25=0 9) x²+11x+18=0 10) x²+20x+100=0 11) x²+8x+15=0 12) x²+19x+88=0
13) x²–17x+52=0 14) x²–18x+77=0 15) x²+24x+135=0 16) x²–16x+39=0 17) x²–23x+120=0 18) x²+19x+78=0
19) x²+5x–14=0 20) x²–2x–24=0 21) x²+7x–8=0 22) x²–5x–36=0 23) x²+3x–54=0 24) x²+7x–18=0
25) x²+4x–45=0 26) x²–15x+56=0 27) x²–3x–88=0 28) x²+13x+22=0 29) x²–20x+64=0 30) x²–10x–144=0
31) x²+25x+126=0 32) x²+35x+174=0 33) x²+32x+87=0 34) x²+27x+92=0 35) x²+23x+90=0 36) x²+24x+108=0
37) x²–318x+1872=0 38) x²–137x+786=0 39) x²+402x+800=0 40) x²–305x+1204=0 41) x²+426x+2105=0 42) x²–327x+1926=0
43) x²+6x–1591=0 44) x²+6x–6391=0 45) x²–12x–3564=0 46) x²+14x–3551=0 47) x²–10x–2475=0 48) x²+4x–396=0
49) 5x²+2x–3=0 50) 7x²–6x–13=0 51) 13x²+2x–11=0 52) 3x²+2x–5=0 53) 26x²+5x–21=0 54) 17x²–31x+14=0
Работа №8 Решите уравнения
1) x²–11x+24=0 2) x²–12x+11=0 3) x²–7x+6=0 4) x²–9x+20=0 5) x²–10x+21=0 6) x²–13x+36=0
7) x²+10x+21=0 8) x²+12x+11=0 9) x²+19x+90=0 10) x²+13x+22=0 11) x²+5x+6=0 12) x²+8x+15=0
13) x²–16x+60=0 14) x²–19x+60=0 15) x²–13x+22=0 16) x²–19x+70=0 17) x²+16x+48=0 18) x²+18x+65=0
19) x²–x–42=0 20) x²–3x–18=0 21) x²–7x–18=0 22) x²+6x–16=0 23) x²+2x–24=0 24) x²+4x–5=0
25) x²–11x+30=0 26) x²+x–56=0 27) x²–9x+18=0 28) x²+2x–8=0 29) x²–21x+38=0 30) x²+11x+28=0
31) x²+17x+60=0 32) x²+23x+90=0 33) x²+26x+69=0 34) x²+24x+119=0 35) x²+27x+126=0 36) x²+18x+65=0
37) x²+205x+804=0 38) x²+407x+2406=0 39) x²–118x+672=0 40) x²–111x+110=0 41) x²+327x+1610=0 42) x²+345x+1364=0
43) x²+8x–8084=0 44) x²–14x–351=0 45) x²+4x–2496=0 46) x²–12x–6364=0 47) x²+2x–9999=0 48) x²+2x–2499=0
49) 4x²+3x–7=0 50) 8x²+5x–3=0 51) 13x²+5x–18=0 52) 2x²–3x+1=0 53) 7x²+8x–15=0 54) 26x²–21x–5=0
Работа №9 Решите уравнения
1) x²–11x+10=0 2) x²–6x+5=0 3) x²–17x+66=0 4) x²–7x+6=0 5) x²–12x+35=0 6) x²–13x+36=0
7) x²+12x+20=0 8) x²+14x+48=0 9) x²+18x+81=0 10) x²+12x+11=0 11) x²+10x+21=0 12) x²+16x+63=0
13) x²+12x+20=0 14) x²+18x+72=0 15) x²+17x+42=0 16) x²+19x+88=0 17) x²–15x+44=0 18) x²–20x+99=0
19) x²+3x–18=0 20) x²–4x–32=0 21) x²+2x–3=0 22) x²+7x–8=0 23) x²–7x–8=0 24) x²–6x–27=0
25) x²+2x–48=0 26) x²+13x+42=0 27) x²–25x+114=0 28) x²–9x–70=0 29) x²–3x–54=0 30) x²+13x+36=0
31) x²+29x+54=0 32) x²+30x+125=0 33) x²+16x+39=0 34) x²+21x+54=0 35) x²+23x+60=0 36) x²+28x+52=0
37) x²–214x+633=0 38) x²–217x+1266=0 39) x²–233x+232=0 40) x²+223x+660=0 41) x²+117x+666=0 42) x²+237x+1160=0
43) x²+10x–875=0 44) x²–4x–9996=0 45) x²+4x–8096=0 46) x²+6x–891=0 47) x²–12x–4864=0 48) x²+10x–1575=0
49) 4x²+3x–1=0 50) 9x²–5x–14=0 51) 7x²+3x–10=0 52) 7x²+17x–24=0 53) 4x²–23x+19=0 54) 15x²+29x+14=0
Работа №10 Решите уравнения
1) x²–19x+90=0 2) x²–15x+50=0 3) x²–13x+36=0 4) x²–8x+7=0 5) x²–16x+63=0 6) x²–12x+20=0
7) x²+15x+50=0 8) x²+13x+42=0 9) x²+13x+30=0 10) x²+5x+4=0 11) x²+13x+36=0 12) x²+7x+6=0
13) x²–14x+40=0 14) x²+19x+78=0 15) x²+14x+24=0 16) x²–20x+99=0 17) x²+20x+91=0 18) x²–17x+66=0
19) x²–x–20=0 20) x²–2x–3=0 21) x²+x–30=0 22) x²+2x–48=0 23) x²+3x–10=0 24) x²+3x–54=0
25) x²+17x+72=0 26) x²–7x–18=0 27) x²–9x–162=0 28) x²+6x–72=0 29) x²+x–56=0 30) x²–15x–76=0
31) x²+26x+69=0 32) x²+19x+18=0 33) x²+14x+13=0 34) x²+16x+60=0 35) x²+27x+126=0 36) x²+12x+20=0
37) x²+227x+1540=0 38) x²+437x+2160=0 39) x²+107x+606=0 40) x²–111x+110=0 41) x²+227x+1110=0 42) x²–216x+1260=0
43) x²–4x–396=0 44) x²+12x–4864=0 45) x²+12x–864=0 46) x²+4x–1596=0 47) x²–10x–3575=0 48) x²–14x–851=0
49) 3x²–2x–5=0 50) 7x²–11x+4=0 51) 10x²+11x–21=0 52) 11x²+18x+7=0 53) 14x²+23x–37=0 54) 28x²+15x–43=0
Работа №11 Решите уравнения
1) x²–6x+8=0 2) x²–12x+36=0 3) x²–13x+30=0 4) x²–20x+100=0 5) x²–17x+72=0 6) x²–9x+14=0
7) x²+7x+12=0 8) x²+13x+30=0 9) x²+6x+5=0 10) x²+10x+24=0 11) x²+8x+7=0 12) x²+8x+16=0
13) x²–12x+20=0 14) x²+18x+65=0 15) x²–19x+60=0 16) x²–13x+30=0 17) x²–21x+104=0 18) x²+19x+90=0
19) x²+x–42=0 20) x²–2x–8=0 21) x²+x–2=0 22) x²+4x–21=0 23) x²+3x–4=0 24) x²–7x–18=0
25) x²+10x+21=0 26) x²–8x–65=0 27) x²+10x+24=0 28) x²–x–42=0 29) x²–22x+57=0 30) x²–8x+16=0
31) x²+13x+22=0 32) x²+26x+25=0 33) x²+31x+58=0 34) x²+26x+48=0 35) x²+24x+23=0 36) x²+33x+162=0
37) x²–348x+2387=0 38) x²–211x+210=0 39) x²+224x+444=0 40) x²+104x+400=0 41) x²–202x+400=0 42) x²+418x+2472=0
43) x²+14x–3551=0 44) x²+12x–6364=0 45) x²+2x–1599=0 46) x²+2x–2499=0 47) x²–2x–9999=0 48) x²+10x–1575=0
49) 5x²–2x–3=0 50) 7x²+9x–16=0 51) 11x²–10x–1=0 52) 12x²+11x–1=0 53) 23x²–3x–26=0 54) 25x²+22x–47=0
Работа №12 Решите уравнения
1) x²–15x+50=0 2) x²–13x+36=0 3) x²–18x+77=0 4) x²–15x+56=0 5) x²–5x+4=0 6) x²–13x+40=0
7) x²+15x+56=0 8) x²+8x+12=0 9) x²+12x+20=0 10) x²+13x+40=0 11) x²+16x+63=0 12) x²+19x+88=0
13) x²–12x+20=0 14) x²–16x+48=0 15) x²+21x+90=0 16) x²+16x+28=0 17) x²–18x+77=0 18) x²–16x+60=0
19) x²+6x–27=0 20) x²–2x–35=0 21) x²+6x–7=0 22) x²–5x–24=0 23) x²–6x–7=0 24) x²+x–12=0
25) x²+20x+99=0 26) x²+11x+24=0 27) x²–15x–76=0 28) x²–7x+10=0 29) x²–2x–8=0 30) x²+14x–95=0
31) x²+17x+42=0 32) x²+31x+84=0 33) x²+26x+25=0 34) x²+25x+114=0 35) x²+33x+116=0 36) x²+16x+48=0
37) x²+313x+622=0 38) x²+326x+1920=0 39) x²–334x+993=0 40) x²+235x+1150=0 41) x²–224x+444=0 42) x²+413x+822=0
43) x²+6x–4891=0 44) x²–12x–1564=0 45) x²–10x–375=0 46) x²+8x–3584=0 47) x²+14x–2451=0 48) x²+6x–891=0
49) 5x²+6x+1=0 50) 4x²+11x+7=0 51) 9x²+14x+5=0 52) 8x²–9x+1=0 53) 16x²+23x–39=0 54) 22x²–17x–39=0
Работа №13 Решите уравнения
1) x²–9x+8=0 2) x²–14x+45=0 3) x²–19x+90=0 4) x²–7x+10=0 5) x²–15x+50=0 6) x²–11x+18=0
7) x²+14x+48=0 8) x²+12x+35=0 9) x²+12x+27=0 10) x²+7x+10=0 11) x²+21x+110=0 12) x²+17x+66=0
13) x²+14x+40=0 14) x²–17x+66=0 15) x²+20x+91=0 16) x²–21x+98=0 17) x²–18x+80=0 18) x²–19x+60=0
19) x²+5x–24=0 20) x²–4x–32=0 21) x²+4x–32=0 22) x²–7x–8=0 23) x²+4x–5=0 24) x²+x–30=0
25) x²+4x–96=0 26) x²–4x–32=0 27) x²–15x+36=0 28) x²–15x+50=0 29) x²+20x+51=0 30) x²+x–12=0
31) x²+20x+84=0 32) x²+16x+60=0 33) x²+29x+154=0 34) x²+31x+150=0 35) x²+30x+81=0 36) x²+24x+108=0
37) x²+401x+400=0 38) x²–407x+2406=0 39) x²–242x+480=0 40) x²–318x+1872=0 41) x²+423x+842=0 42) x²–126x+488=0
43) x²–6x–9991=0 44) x²–2x–1599=0 45) x²–14x–351=0 46) x²+12x–8064=0 47) x²–14x–851=0 48) x²+2x–6399=0
49) 4x²–3x–7=0 50) 4x²–9x+5=0 51) 3x²+16x–19=0 52) 14x²+3x–17=0 53) 11x²+14x+3=0 54) 11x²–26x+15=0
Работа №14 Решите уравнения
1) x²–16x+64=0 2) x²–13x+42=0 3) x²–10x+25=0 4) x²–14x+40=0 5) x²–19x+88=0 6) x²–8x+15=0
7) x²+14x+48=0 8) x²+16x+60=0 9) x²+14x+45=0 10) x²+11x+30=0 11) x²+13x+30=0 12) x²+12x+20=0
13) x²–21x+90=0 14) x²–14x+40=0 15) x²+18x+56=0 16) x²+17x+60=0 17) x²+13x+22=0 18) x²–15x+44=0
19) x²+2x–24=0 20) x²–x–2=0 21) x²+x–12=0 22) x²–7x–18=0 23) x²–x–42=0 24) x²+5x–24=0
25) x²+3x–40=0 26) x²+2x–24=0 27) x²–22x+96=0 28) x²+24x+95=0 29) x²+10x+25=0 30) x²+11x+24=0
31) x²+32x+112=0 32) x²+33x+116=0 33) x²+27x+110=0 34) x²+27x+140=0 35) x²+31x+58=0 36) x²+11x+10=0
37) x²–337x+2310=0 38) x²+144x+423=0 39) x²–446x+1768=0 40) x²+139x+924=0 41) x²–112x+111=0 42) x²–115x+336=0
43) x²+2x–399=0 44) x²–6x–391=0 45) x²+8x–2484=0 46) x²+12x–364=0 47) x²+12x–9964=0 48) x²+10x–1575=0
49) 3x²–2x–1=0 50) 9x²+7x–2=0 51) 2x²–15x–17=0 52) 9x²–17x+8=0 53) 23x²–24x+1=0 54) 14x²–13x–27=0
Работа №15 Решите уравнения
1) x²–11x+28=0 2) x²–6x+8=0 3) x²–16x+63=0 4) x²–19x+88=0 5) x²–13x+36=0 6) x²–18x+80=0
7) x²+10x+21=0 8) x²+11x+18=0 9) x²+13x+22=0 10) x²+15x+54=0 11) x²+17x+70=0 12) x²+10x+16=0
13) x²+14x+24=0 14) x²+14x+33=0 15) x²+24x+135=0 16) x²–17x+30=0 17) x²+18x+77=0 18) x²–18x+65=0
19) x²–6x–16=0 20) x²–x–6=0 21) x²–2x–35=0 22) x²+7x–8=0 23) x²+2x–48=0 24) x²+x–72=0
25) x²+19x+34=0 26) x²–9x–36=0 27) x²+14x+40=0 28) x²–22x+105=0 29) x²–16x+63=0 30) x²+x–20=0
31) x²+29x+54=0 32) x²+20x+84=0 33) x²+23x+22=0 34) x²+31x+168=0 35) x²+14x+13=0 36) x²+20x+51=0
37) x²+409x+2814=0 38) x²+307x+1510=0 39) x²+107x+606=0 40) x²–436x+1728=0 41) x²–149x+994=0 42) x²+238x+1617=0
43) x²+6x–4891=0 44) x²+4x–9996=0 45) x²–4x–1596=0 46) x²+14x–9951=0 47) x²–14x–351=0 48) x²–2x–6399=0
49) 4x²–5x+1=0 50) 10x²–11x–21=0 51) 11x²+7x–4=0 52) 9x²+4x–5=0 53) 22x²+15x–37=0 54) 2x²+3x–5=0
Работа №16 Решите уравнения
1) x²–9x+20=0 2) x²–19x+88=0 3) x²–15x+44=0 4) x²–7x+12=0 5) x²–17x+70=0 6) x²–16x+60=0
7) x²+20x+100=0 8) x²+15x+56=0 9) x²+12x+20=0 10) x²+16x+63=0 11) x²+14x+49=0 12) x²+13x+36=0
13) x²+13x+30=0 14) x²–16x+28=0 15) x²–13x+22=0 16) x²–16x+39=0 17) x²–21x+98=0 18) x²+14x+33=0
19) x²+3x–54=0 20) x²–3x–18=0 21) x²+2x–35=0 22) x²+x–12=0 23) x²–5x–6=0 24) x²+x–30=0
25) x²–16x+64=0 26) x²+3x–18=0 27) x²–3x–54=0 28) x²+5x–104=0 29) x²–20x+96=0 30) x²–x–30=0
31) x²+21x+90=0 32) x²+26x+105=0 33) x²+27x+110=0 34) x²+15x+26=0 35) x²+29x+28=0 36) x²+21x+80=0
37) x²+247x+1446=0 38) x²+322x+640=0 39) x²+449x+3094=0 40) x²–141x+140=0 41) x²+326x+1605=0 42) x²–447x+3080=0
43) x²+8x–2484=0 44) x²–8x–884=0 45) x²–8x–9984=0 46) x²–12x–9964=0 47) x²–6x–2491=0 48) x²+12x–8064=0
49) 3x²+2x–5=0 50) 3x²+11x+8=0 51) 9x²+10x–19=0 52) 13x²–2x–11=0 53) 7x²–22x–29=0 54) 5x²+9x–14=0
Работа №17 Решите уравнения
1) x²–18x+80=0 2) x²–16x+60=0 3) x²–5x+4=0 4) x²–11x+30=0 5) x²–12x+27=0 6) x²–13x+40=0
7) x²+10x+16=0 8) x²+17x+70=0 9) x²+6x+8=0 10) x²+6x+9=0 11) x²+7x+12=0 12) x²+14x+40=0
13) x²+22x+112=0 14) x²–21x+98=0 15) x²+22x+117=0 16) x²+15x+36=0 17) x²–16x+60=0 18) x²–15x+36=0
19) x²–3x–40=0 20) x²–5x–36=0 21) x²–6x–16=0 22) x²–x–20=0 23) x²+6x–27=0 24) x²–2x–35=0
25) x²–9x–22=0 26) x²–4x–45=0 27) x²+17x+42=0 28) x²+17x+66=0 29) x²–5x+6=0 30) x²+22x+105=0
31) x²+25x+100=0 32) x²+26x+133=0 33) x²+30x+161=0 34) x²+12x+20=0 35) x²+17x+16=0 36) x²+19x+18=0
37) x²+433x+1290=0 38) x²–306x+1505=0 39) x²–206x+808=0 40) x²–239x+1624=0 41) x²–316x+1860=0 42) x²–339x+2324=0
43) x²+8x–9984=0 44) x²+10x–375=0 45) x²–4x–6396=0 46) x²+4x–396=0 47) x²–10x–375=0 48) x²+2x–8099=0
49) 5x²+2x–7=0 50) 9x²+7x–16=0 51) 5x²–11x–16=0 52) 2x²+11x+9=0 53) 11x²+8x–19=0 54) 11x²–28x+17=0
Работа №18 Решите уравнения
1) x²–12x+27=0 2) x²–6x+8=0 3) x²–15x+56=0 4) x²–12x+36=0 5) x²–15x+54=0 6) x²–10x+21=0
7) x²+6x+8=0 8) x²+4x+3=0 9) x²+19x+88=0 10) x²+15x+44=0 11) x²+8x+12=0 12) x²+12x+27=0
13) x²+15x+50=0 14) x²+18x+77=0 15) x²+16x+39=0 16) x²+22x+117=0 17) x²+20x+75=0 18) x²–16x+28=0
19) x²–x–42=0 20) x²+6x–7=0 21) x²+5x–36=0 22) x²–6x–16=0 23) x²+4x–45=0 24) x²+5x–14=0
25) x²–15x–34=0 26) x²–25x+144=0 27) x²–26x+144=0 28) x²+x–72=0 29) x²+14x+40=0 30) x²–19x+70=0
31) x²+15x+50=0 32) x²+28x+147=0 33) x²+27x+72=0 34) x²+20x+19=0 35) x²+33x+162=0 36) x²+26x+69=0
37) x²–417x+2466=0 38) x²+423x+1260=0 39) x²–427x+2940=0 40) x²+217x+1060=0 41) x²+328x+2247=0 42) x²–333x+990=0
43) x²+10x–375=0 44) x²+14x–9951=0 45) x²+2x–2499=0 46) x²+10x–9975=0 47) x²–2x–6399=0 48) x²+10x–8075=0
49) 2x²–3x–5=0 50) 11x²+4x–15=0 51) 8x²+7x–1=0 52) 8x²+11x+3=0 53) 8x²–7x–1=0 54) 9x²+17x–26=0
Работа №19 Решите уравнения
1) x²–8x+12=0 2) x²–15x+56=0 3) x²–11x+24=0 4) x²–16x+60=0 5) x²–5x+4=0 6) x²–19x+90=0
7) x²+14x+45=0 8) x²+11x+18=0 9) x²+7x+10=0 10) x²+8x+7=0 11) x²+12x+35=0 12) x²+10x+25=0
13) x²–18x+45=0 14) x²–17x+30=0 15) x²+18x+65=0 16) x²–22x+117=0 17) x²–18x+65=0 18) x²–21x+90=0
19) x²+x–2=0 20) x²+4x–5=0 21) x²+3x–4=0 22) x²–2x–35=0 23) x²–8x–9=0 24) x²+x–12=0
25) x²+11x+18=0 26) x²+3x–70=0 27) x²+9x–112=0 28) x²+4x–45=0 29) x²+20x+51=0 30) x²+9x+20=0
31) x²+31x+84=0 32) x²+16x+60=0 33) x²+14x+24=0 34) x²+15x+14=0 35) x²+25x+66=0 36) x²+24x+44=0
37) x²+221x+220=0 38) x²+213x+422=0 39) x²+314x+933=0 40) x²–246x+968=0 41) x²–127x+726=0 42) x²+313x+930=0
43) x²+10x–9975=0 44) x²–14x–851=0 45) x²+2x–899=0 46) x²+2x–2499=0 47) x²+4x–9996=0 48) x²–2x–2499=0
49) 5x²–4x–9=0 50) 3x²–8x+5=0 51) 16x²–15x–1=0 52) 13x²+2x–15=0 53) 10x²+11x–21=0 54) 10x²–3x–7=0
Работа №20 Решите уравнения
1) x²–14x+40=0 2) x²–13x+42=0 3) x²–12x+27=0 4) x²–12x+20=0 5) x²–10x+9=0 6) x²–14x+33=0
7) x²+18x+81=0 8) x²+17x+70=0 9) x²+14x+48=0 10) x²+19x+90=0 11) x²+5x+6=0 12) x²+10x+25=0
13) x²+24x+135=0 14) x²+21x+104=0 15) x²–17x+60=0 16) x²+20x+96=0 17) x²–18x+72=0 18) x²+15x+26=0
19) x²+2x–35=0 20) x²+x–6=0 21) x²–3x–18=0 22) x²+4x–21=0 23) x²+3x–28=0 24) x²–x–72=0
25) x²+14x–95=0 26) x²+17x+70=0 27) x²–16x+63=0 28) x²+20x+36=0 29) x²–14x+49=0 30) x²–22x+105=0
31) x²+18x+32=0 32) x²+25x+66=0 33) x²+30x+144=0 34) x²+16x+55=0 35) x²+29x+154=0 36) x²+11x+10=0
37) x²–343x+682=0 38) x²+433x+862=0 39) x²+204x+800=0 40) x²+143x+420=0 41) x²–135x+396=0 42) x²+245x+726=0
43) x²–2x–2499=0 44) x²+2x–6399=0 45) x²+4x–9996=0 46) x²–12x–4864=0 47) x²+12x–864=0 48) x²+10x–9975=0
49) 5x²+2x–7=0 50) 3x²–10x–13=0 51) 11x²+10x–1=0 52) 7x²+16x+9=0 53) 21x²–8x–29=0 54) 11x²+15x+4=0
Работа №21 Решите уравнения
1) x²–14x+48=0 2) x²–12x+36=0 3) x²–17x+72=0 4) x²–14x+45=0 5) x²–15x+50=0 6) x²–10x+16=0
7) x²+18x+81=0 8) x²+11x+30=0 9) x²+12x+32=0 10) x²+19x+88=0 11) x²+10x+25=0 12) x²+14x+40=0
13) x²–21x+108=0 14) x²+22x+105=0 15) x²–19x+78=0 16) x²–15x+36=0 17) x²+18x+45=0 18) x²–20x+96=0
19) x²+2x–35=0 20) x²+3x–4=0 21) x²+x–6=0 22) x²–3x–4=0 23) x²+2x–15=0 24) x²+x–12=0
25) x²–18x+32=0 26) x²–14x+24=0 27) x²+15x+56=0 28) x²+25x+126=0 29) x²–28x+171=0 30) x²–3x–88=0
31) x²+26x+120=0 32) x²+31x+58=0 33) x²+19x+34=0 34) x²+29x+54=0 35) x²+34x+145=0 36) x²+17x+16=0
37) x²+402x+401=0 38) x²–105x+306=0 39) x²–114x+440=0 40) x²+416x+2460=0 41) x²–144x+423=0 42) x²–222x+440=0
43) x²+14x–6351=0 44) x²–6x–6391=0 45) x²+8x–8084=0 46) x²+2x–6399=0 47) x²+6x–9991=0 48) x²+14x–9951=0
49) 4x²–3x–1=0 50) 7x²+10x–17=0 51) 6x²+5x–11=0 52) 21x²–5x–26=0 53) 8x²–9x+1=0 54) 8x²–5x–3=0
Работа №22 Решите уравнения
1) x²–7x+10=0 2) x²–20x+99=0 3) x²–13x+22=0 4) x²–9x+18=0 5) x²–11x+28=0 6) x²–11x+30=0
7) x²+10x+21=0 8) x²+11x+10=0 9) x²+13x+42=0 10) x²+11x+24=0 11) x²+15x+56=0 12) x²+8x+7=0
13) x²–17x+66=0 14) x²+12x+20=0 15) x²+21x+108=0 16) x²–17x+70=0 17) x²+17x+70=0 18) x²–21x+104=0
19) x²+3x–10=0 20) x²–2x–35=0 21) x²+6x–16=0 22) x²+4x–21=0 23) x²–4x–21=0 24) x²+3x–18=0
25) x²–9x+20=0 26) x²–2x–35=0 27) x²–5x–126=0 28) x²+19x+60=0 29) x²+11x+24=0 30) x²–18x+81=0
31) x²+35x+174=0 32) x²+29x+138=0 33) x²+29x+54=0 34) x²+17x+30=0 35) x²+17x+60=0 36) x²+23x+90=0
37) x²–112x+111=0 38) x²+217x+1470=0 39) x²+315x+936=0 40) x²–314x+1240=0 41) x²–124x+363=0 42) x²+335x+1324=0
43) x²+6x–9991=0 44) x²–10x–875=0 45) x²–2x–4899=0 46) x²+12x–364=0 47) x²+14x–3551=0 48) x²–14x–351=0
49) 5x²–6x–11=0 50) 11x²–2x–9=0 51) 8x²+5x–13=0 52) 13x²+18x–31=0 53) 5x²–2x–7=0 54) 21x²–22x+1=0
Работа №23 Решите уравнения
1) x²–4x+3=0 2) x²–11x+18=0 3) x²–12x+11=0 4) x²–5x+6=0 5) x²–13x+42=0 6) x²–19x+90=0
7) x²+17x+66=0 8) x²+5x+6=0 9) x²+9x+18=0 10) x²+10x+24=0 11) x²+18x+80=0 12) x²+21x+110=0
13) x²+23x+120=0 14) x²–21x+104=0 15) x²–14x+24=0 16) x²+17x+60=0 17) x²+18x+72=0 18) x²+18x+45=0
19) x²+x–30=0 20) x²–5x–24=0 21) x²+3x–10=0 22) x²+3x–54=0 23) x²+4x–32=0 24) x²+3x–18=0
25) x²+18x+81=0 26) x²+12x+32=0 27) x²–3x–108=0 28) x²–11x–152=0 29) x²–15x+26=0 30) x²+7x–98=0
31) x²+31x+150=0 32) x²+31x+58=0 33) x²+28x+115=0 34) x²+21x+54=0 35) x²+25x+46=0 36) x²+15x+14=0
37) x²+113x+222=0 38) x²+203x+402=0 39) x²–244x+723=0 40) x²–231x+230=0 41) x²–102x+200=0 42) x²+204x+603=0
43) x²+12x–9964=0 44) x²+14x–9951=0 45) x²+8x–6384=0 46) x²–8x–884=0 47) x²+4x–896=0 48) x²+12x–3564=0
49) 2x²–3x+1=0 50) 2x²–11x–13=0 51) 2x²–5x+3=0 52) 19x²+13x–32=0 53) 10x²–21x+11=0 54) 26x²–7x–33=0
Работа №24 Решите уравнения
1) x²–10x+21=0 2) x²–12x+20=0 3) x²–10x+9=0 4) x²–18x+80=0 5) x²–15x+54=0 6) x²–15x+50=0
7) x²+15x+56=0 8) x²+8x+15=0 9) x²+7x+12=0 10) x²+14x+45=0 11) x²+17x+72=0 12) x²+4x+4=0
13) x²–13x+30=0 14) x²–14x+33=0 15) x²–23x+120=0 16) x²+18x+45=0 17) x²–20x+84=0 18) x²+20x+84=0
19) x²–3x–40=0 20) x²+2x–24=0 21) x²–x–30=0 22) x²+3x–10=0 23) x²+x–30=0 24) x²–8x–9=0
25) x²+3x–10=0 26) x²–19x+60=0 27) x²–3x–18=0 28) x²+24x+108=0 29) x²+3x–108=0 30) x²–14x+33=0
31) x²+28x+27=0 32) x²+22x+72=0 33) x²+26x+25=0 34) x²+26x+105=0 35) x²+31x+108=0 36) x²+20x+19=0
37) x²+137x+786=0 38) x²–241x+240=0 39) x²+123x+122=0 40) x²–326x+1288=0 41) x²+318x+2177=0 42) x²+436x+1728=0
43) x²–4x–1596=0 44) x²–2x–4899=0 45) x²+14x–851=0 46) x²+14x–9951=0 47) x²–6x–9991=0 48) x²–8x–1584=0
49) 4x²+3x–7=0 50) 11x²+8x–3=0 51) 4x²–3x–7=0 52) 3x²+20x–23=0 53) 8x²–17x+9=0 54) 23x²+15x–38=0
Работа №25 Решите уравнения
1) x²–5x+6=0 2) x²–15x+50=0 3) x²–14x+40=0 4) x²–9x+14=0 5) x²–19x+90=0 6) x²–12x+20=0
7) x²+13x+30=0 8) x²+10x+16=0 9) x²+7x+12=0 10) x²+11x+10=0 11) x²+12x+32=0 12) x²+21x+110=0
13) x²–20x+91=0 14) x²–15x+36=0 15) x²+21x+104=0 16) x²+16x+55=0 17) x²+22x+117=0 18) x²+23x+120=0
19) x²–5x–14=0 20) x²–5x–6=0 21) x²+x–6=0 22) x²–2x–63=0 23) x²+6x–16=0 24) x²+5x–6=0
25) x²–4x–21=0 26) x²+8x–20=0 27) x²+14x+33=0 28) x²+15x+54=0 29) x²–x–6=0 30) x²+7x–18=0
31) x²+17x+70=0 32) x²+21x+20=0 33) x²+27x+72=0 34) x²+31x+58=0 35) x²+29x+54=0 36) x²+21x+38=0
37) x²+346x+1705=0 38) x²+338x+1992=0 39) x²+443x+882=0 40) x²+344x+684=0 41) x²+425x+1266=0 42) x²+326x+1288=0
43) x²–6x–9991=0 44) x²+2x–9999=0 45) x²–2x–2499=0 46) x²+12x–4864=0 47) x²–4x–9996=0 48) x²+8x–3584=0
49) 4x²–5x+1=0 50) 3x²–10x+7=0 51) 7x²+8x–15=0 52) 7x²–2x–9=0 53) 26x²+25x–51=0 54) 15x²–11x–26=0
Работа №26 Решите уравнения
1) x²–8x+15=0 2) x²–12x+35=0 3) x²–9x+18=0 4) x²–14x+40=0 5) x²–9x+14=0 6) x²–12x+11=0
7) x²+21x+110=0 8) x²+9x+14=0 9) x²+10x+16=0 10) x²+15x+56=0 11) x²+5x+6=0 12) x²+15x+50=0
13) x²–18x+80=0 14) x²+22x+117=0 15) x²–19x+90=0 16) x²–13x+30=0 17) x²+18x+65=0 18) x²+13x+30=0
19) x²–5x–24=0 20) x²+3x–10=0 21) x²–2x–8=0 22) x²+7x–18=0 23) x²+x–2=0 24) x²–6x–16=0
25) x²–11x+30=0 26) x²+4x–117=0 27) x²–3x–18=0 28) x²–16x+63=0 29) x²+9x–162=0 30) x²+16x+63=0
31) x²+32x+175=0 32) x²+20x+84=0 33) x²+23x+22=0 34) x²+34x+189=0 35) x²+13x+30=0 36) x²+30x+29=0
37) x²–243x+242=0 38) x²–338x+1992=0 39) x²–127x+840=0 40) x²+414x+1233=0 41) x²–105x+500=0 42) x²–123x+122=0
43) x²+6x–891=0 44) x²–4x–1596=0 45) x²+12x–864=0 46) x²+4x–896=0 47) x²–6x–391=0 48) x²+10x–1575=0
49) 3x²–4x+1=0 50) 11x²+5x–16=0 51) 5x²+12x+7=0 52) 4x²–5x+1=0 53) 7x²–24x–31=0 54) 29x²+15x–14=0
Работа №27 Решите уравнения
1) x²–12x+32=0 2) x²–9x+20=0 3) x²–11x+24=0 4) x²–6x+9=0 5) x²–14x+48=0 6) x²–10x+25=0
7) x²+12x+36=0 8) x²+5x+6=0 9) x²+14x+33=0 10) x²+8x+16=0 11) x²+11x+30=0 12) x²+7x+12=0
13) x²–15x+36=0 14) x²+17x+30=0 15) x²+15x+50=0 16) x²+16x+28=0 17) x²+23x+126=0 18) x²+20x+91=0
19) x²–x–20=0 20) x²–x–72=0 21) x²+2x–24=0 22) x²+2x–3=0 23) x²+x–6=0 24) x²+2x–15=0
25) x²+20x+51=0 26) x²–5x–66=0 27) x²+4x–45=0 28) x²–14x+48=0 29) x²+13x+42=0 30) x²+18x+80=0
31) x²+21x+20=0 32) x²+23x+90=0 33) x²+19x+84=0 34) x²+29x+28=0 35) x²+23x+42=0 36) x²+18x+32=0
37) x²+441x+440=0 38) x²–222x+440=0 39) x²–147x+710=0 40) x²–146x+705=0 41) x²+445x+1326=0 42) x²–428x+2947=0
43) x²–8x–2484=0 44) x²+10x–8075=0 45) x²–14x–3551=0 46) x²–4x–6396=0 47) x²–4x–396=0 48) x²+2x–2499=0
49) 5x²+3x–2=0 50) 7x²+8x–15=0 51) 16x²+3x–13=0 52) 9x²+2x–7=0 53) 23x²–24x–47=0 54) 5x²+13x–18=0
Работа №28 Решите уравнения
1) x²–13x+30=0 2) x²–9x+20=0 3) x²–12x+11=0 4) x²–8x+15=0 5) x²–11x+24=0 6) x²–5x+6=0
7) x²+10x+24=0 8) x²+12x+27=0 9) x²+9x+14=0 10) x²+9x+20=0 11) x²+8x+12=0 12) x²+6x+8=0
13) x²–20x+99=0 14) x²–14x+33=0 15) x²–22x+117=0 16) x²+21x+98=0 17) x²–19x+78=0 18) x²–21x+108=0
19) x²–5x–24=0 20) x²–x–30=0 21) x²+3x–54=0 22) x²–2x–35=0 23) x²+3x–40=0 24) x²+3x–18=0
25) x²–23x+112=0 26) x²–13x+36=0 27) x²+x–6=0 28) x²+21x+98=0 29) x²–15x–34=0 30) x²+19x+34=0
31) x²+27x+126=0 32) x²+27x+110=0 33) x²+21x+98=0 34) x²+29x+28=0 35) x²+25x+24=0 36) x²+24x+108=0
37) x²–235x+1150=0 38) x²–423x+422=0 39) x²+248x+1687=0 40) x²–317x+2170=0 41) x²–319x+2184=0 42) x²+405x+1604=0
43) x²+8x–8084=0 44) x²–4x–3596=0 45) x²–8x–2484=0 46) x²–2x–399=0 47) x²–14x–8051=0 48) x²+14x–1551=0
49) 3x²+4x+1=0 50) 10x²–3x–7=0 51) 13x²–4x–9=0 52) 21x²–19x–2=0 53) 13x²–8x–5=0 54) 17x²+15x–2=0
Работа №29 Решите уравнения
1) x²–20x+99=0 2) x²–9x+20=0 3) x²–8x+15=0 4) x²–13x+30=0 5) x²–3x+2=0 6) x²–8x+12=0
7) x²+7x+6=0 8) x²+8x+15=0 9) x²+7x+12=0 10) x²+14x+40=0 11) x²+11x+18=0 12) x²+18x+80=0
13) x²–22x+117=0 14) x²+18x+72=0 15) x²+16x+55=0 16) x²+16x+60=0 17) x²–18x+77=0 18) x²+23x+120=0
19) x²–x–42=0 20) x²–3x–10=0 21) x²–2x–63=0 22) x²–2x–3=0 23) x²+3x–40=0 24) x²+x–6=0
25) x²–3x–10=0 26) x²–x–6=0 27) x²–6x–16=0 28) x²–2x–15=0 29) x²–9x–112=0 30) x²–15x+54=0
31) x²+21x+38=0 32) x²+20x+64=0 33) x²+13x+22=0 34) x²+20x+51=0 35) x²+16x+48=0 36) x²+28x+96=0
37) x²–224x+663=0 38) x²+434x+1720=0 39) x²+138x+917=0 40) x²–245x+726=0 41) x²–403x+402=0 42) x²–215x+636=0
43) x²–10x–3575=0 44) x²–12x–364=0 45) x²+8x–384=0 46) x²+6x–1591=0 47) x²–14x–9951=0 48) x²+8x–1584=0
49) 3x²–2x–5=0 50) 7x²–3x–4=0 51) 7x²+4x–11=0 52) 3x²–4x–7=0 53) 17x²+19x–36=0 54) 25x²+3x–22=0
Работа №30 Решите уравнения
1) x²–14x+48=0 2) x²–13x+30=0 3) x²–13x+40=0 4) x²–19x+90=0 5) x²–20x+99=0 6) x²–14x+33=0
7) x²+19x+90=0 8) x²+12x+27=0 9) x²+11x+30=0 10) x²+7x+10=0 11) x²+11x+24=0 12) x²+17x+72=0
13) x²+19x+70=0 14) x²+23x+126=0 15) x²+15x+44=0 16) x²+18x+80=0 17) x²+17x+60=0 18) x²+19x+90=0
19) x²+5x–24=0 20) x²–3x–10=0 21) x²+8x–9=0 22) x²–x–72=0 23) x²–7x–18=0 24) x²+3x–28=0
25) x²–17x+72=0 26) x²+15x+44=0 27) x²+8x–128=0 28) x²+27x+162=0 29) x²–16x–36=0 30) x²–13x–114=0
31) x²+22x+85=0 32) x²+25x+46=0 33) x²+22x+57=0 34) x²+29x+100=0 35) x²+31x+108=0 36) x²+29x+28=0
37) x²+317x+1866=0 38) x²+404x+1600=0 39) x²+108x+707=0 40) x²+421x+420=0 41) x²+401x+400=0 42) x²+227x+1110=0
43) x²–2x–399=0 44) x²–10x–375=0 45) x²+2x–4899=0 46) x²–2x–6399=0 47) x²+12x–2464=0 48) x²–6x–4891=0
49) 5x²–6x+1=0 50) 10x²+11x+1=0 51) 4x²–3x–1=0 52) 2x²+21x–23=0 53) 12x²–23x–35=0 54) 21x²+10x–11=0
Работа №31 Решите уравнения
1) x²–6x+8=0 2) x²–15x+56=0 3) x²–10x+21=0 4) x²–9x+20=0 5) x²–12x+35=0 6) x²–11x+24=0
7) x²+11x+28=0 8) x²+11x+24=0 9) x²+8x+16=0 10) x²+9x+18=0 11) x²+15x+54=0 12) x²+18x+80=0
13) x²–22x+117=0 14) x²–19x+90=0 15) x²+16x+39=0 16) x²+17x+66=0 17) x²+17x+30=0 18) x²–13x+22=0
19) x²+6x–7=0 20) x²–5x–36=0 21) x²+5x–36=0 22) x²+4x–12=0 23) x²+x–42=0 24) x²–x–6=0
25) x²–15x–34=0 26) x²+11x–102=0 27) x²+4x–45=0 28) x²+4x–32=0 29) x²+x–20=0 30) x²+18x+81=0
31) x²+14x+13=0 32) x²+25x+46=0 33) x²+25x+114=0 34) x²+20x+36=0 35) x²+31x+130=0 36) x²+34x+168=0
37) x²–307x+1510=0 38) x²–405x+2000=0 39) x²+244x+960=0 40) x²+145x+564=0 41) x²–433x+1290=0 42) x²–128x+732=0
43) x²–12x–1564=0 44) x²+2x–899=0 45) x²+8x–4884=0 46) x²–12x–864=0 47) x²+4x–9996=0 48) x²+14x–1551=0
49) 5x²+6x–11=0 50) 7x²+4x–3=0 51) 12x²+7x–19=0 52) 5x²–21x+16=0 53) 9x²+16x–25=0 54) 28x²+29x–57=0
Работа №32 Решите уравнения
1) x²–8x+12=0 2) x²–9x+20=0 3) x²–12x+36=0 4) x²–10x+21=0 5) x²–7x+6=0 6) x²–17x+72=0
7) x²+11x+28=0 8) x²+16x+63=0 9) x²+21x+110=0 10) x²+5x+6=0 11) x²+13x+36=0 12) x²+13x+22=0
13) x²–17x+30=0 14) x²–19x+70=0 15) x²+19x+78=0 16) x²+16x+39=0 17) x²–19x+60=0 18) x²–21x+108=0
19) x²–x–42=0 20) x²–3x–18=0 21) x²–5x–14=0 22) x²–5x–6=0 23) x²–x–20=0 24) x²–4x–5=0
25) x²–9x–52=0 26) x²–6x–16=0 27) x²+27x+162=0 28) x²–6x–72=0 29) x²–9x+14=0 30) x²+18x+81=0
31) x²+29x+154=0 32) x²+23x+60=0 33) x²+30x+144=0 34) x²+35x+196=0 35) x²+15x+14=0 36) x²+22x+21=0
37) x²+148x+852=0 38) x²+323x+960=0 39) x²+137x+786=0 40) x²+149x+994=0 41) x²+235x+1150=0 42) x²–245x+964=0
43) x²–8x–384=0 44) x²–8x–2484=0 45) x²+8x–3584=0 46) x²+4x–396=0 47) x²–2x–8099=0 48) x²+2x–2499=0
49) 6x²+5x–1=0 50) 7x²–6x–13=0 51) 9x²+4x–13=0 52) 9x²–17x+8=0 53) 21x²+16x–5=0 54) 24x²–13x–11=0
Работа №33 Решите уравнения
1) x²–13x+22=0 2) x²–14x+40=0 3) x²–18x+80=0 4) x²–16x+60=0 5) x²–4x+4=0 6) x²–5x+6=0
7) x²+10x+25=0 8) x²+13x+30=0 9) x²+8x+7=0 10) x²+17x+72=0 11) x²+14x+40=0 12) x²+19x+90=0
13) x²–17x+42=0 14) x²+18x+72=0 15) x²–15x+50=0 16) x²+13x+22=0 17) x²+17x+52=0 18) x²+24x+135=0
19) x²–x–12=0 20) x²+3x–54=0 21) x²–2x–24=0 22) x²–6x–7=0 23) x²+5x–24=0 24) x²+7x–18=0
25) x²–8x–65=0 26) x²+3x–18=0 27) x²+24x+135=0 28) x²–5x–126=0 29) x²+14x+48=0 30) x²+15x+50=0
31) x²+16x+60=0 32) x²+17x+66=0 33) x²+13x+12=0 34) x²+19x+48=0 35) x²+21x+68=0 36) x²+16x+55=0
37) x²+432x+431=0 38) x²–204x+404=0 39) x²–219x+1484=0 40) x²+224x+663=0 41) x²+442x+441=0 42) x²–216x+1260=0
43) x²–14x–1551=0 44) x²+2x–399=0 45) x²–2x–8099=0 46) x²+8x–4884=0 47) x²+12x–364=0 48) x²+10x–8075=0
49) 5x²+6x–11=0 50) 5x²–9x+4=0 51) 8x²–15x+7=0 52) 9x²+16x+7=0 53) 8x²–5x–13=0 54) 25x²+12x–13=0
Работа №34 Решите уравнения
1) x²–10x+9=0 2) x²–15x+54=0 3) x²–10x+16=0 4) x²–15x+56=0 5) x²–16x+60=0 6) x²–14x+40=0
7) x²+11x+30=0 8) x²+15x+56=0 9) x²+8x+7=0 10) x²+7x+12=0 11) x²+12x+36=0 12) x²+14x+40=0
13) x²–19x+60=0 14) x²–20x+96=0 15) x²+13x+30=0 16) x²–23x+126=0 17) x²+24x+135=0 18) x²–20x+91=0
19) x²+5x–6=0 20) x²–3x–10=0 21) x²+x–30=0 22) x²+x–12=0 23) x²–x–12=0 24) x²+5x–14=0
25) x²+11x–42=0 26) x²+16x+63=0 27) x²–5x–50=0 28) x²–4x–12=0 29) x²–17x+70=0 30) x²+4x–32=0
31) x²+21x+90=0 32) x²+24x+80=0 33) x²+21x+98=0 34) x²+32x+112=0 35) x²+19x+18=0 36) x²+28x+147=0
37) x²+128x+847=0 38) x²+142x+141=0 39) x²–226x+1320=0 40) x²–207x+1400=0 41) x²+403x+802=0 42) x²+416x+2460=0
43) x²–12x–1564=0 44) x²+10x–2475=0 45) x²–8x–8084=0 46) x²–12x–864=0 47) x²–8x–884=0 48) x²–14x–8051=0
49) 5x²–6x+1=0 50) 2x²–9x–11=0 51) 16x²+15x–31=0 52) 12x²+17x–29=0 53) 25x²–12x–37=0 54) 4x²–19x–23=0
Работа №35 Решите уравнения
1) x²–10x+9=0 2) x²–13x+40=0 3) x²–14x+40=0 4) x²–7x+6=0 5) x²–19x+90=0 6) x²–14x+49=0
7) x²+8x+15=0 8) x²+13x+22=0 9) x²+16x+60=0 10) x²+8x+12=0 11) x²+6x+9=0 12) x²+10x+16=0
13) x²–16x+39=0 14) x²+24x+135=0 15) x²–18x+56=0 16) x²+15x+50=0 17) x²+15x+44=0 18) x²–22x+112=0
19) x²+x–6=0 20) x²+3x–40=0 21) x²–5x–14=0 22) x²+2x–15=0 23) x²+x–56=0 24) x²–4x–5=0
25) x²+18x+72=0 26) x²+22x+96=0 27) x²–14x+48=0 28) x²+14x+45=0 29) x²–9x+20=0 30) x²+7x–144=0
31) x²+31x+58=0 32) x²+22x+72=0 33) x²+13x+12=0 34) x²+25x+46=0 35) x²+18x+45=0 36) x²+20x+75=0
37) x²–347x+1710=0 38) x²+206x+1005=0 39) x²–137x+786=0 40) x²+402x+401=0 41) x²–443x+442=0 42) x²–134x+264=0
43) x²+4x–3596=0 44) x²+12x–6364=0 45) x²+2x–4899=0 46) x²+8x–6384=0 47) x²+8x–4884=0 48) x²+6x–891=0
49) 5x²–6x+1=0 50) 11x²–8x–19=0 51) 13x²–3x–16=0 52) 4x²–19x+15=0 53) 3x²–7x+4=0 54) 6x²–23x–29=0
Работа №36 Решите уравнения
1) x²–7x+12=0 2) x²–10x+16=0 3) x²–17x+72=0 4) x²–10x+9=0 5) x²–12x+32=0 6) x²–17x+66=0
7) x²+10x+24=0 8) x²+9x+8=0 9) x²+15x+50=0 10) x²+9x+18=0 11) x²+12x+20=0 12) x²+11x+24=0
13) x²+13x+22=0 14) x²–15x+50=0 15) x²–18x+72=0 16) x²+16x+60=0 17) x²+14x+24=0 18) x²–17x+60=0
19) x²–4x–45=0 20) x²–x–12=0 21) x²–5x–6=0 22) x²+4x–32=0 23) x²–8x–9=0 24) x²–5x–36=0
25) x²–2x–99=0 26) x²–21x+104=0 27) x²–11x–26=0 28) x²–3x–70=0 29) x²–12x–28=0 30) x²–23x+126=0
31) x²+34x+168=0 32) x²+19x+34=0 33) x²+19x+70=0 34) x²+22x+105=0 35) x²+16x+55=0 36) x²+31x+58=0
37) x²+204x+603=0 38) x²+444x+1323=0 39) x²+237x+1160=0 40) x²+331x+330=0 41) x²–335x+996=0 42) x²+409x+2814=0
43) x²–6x–391=0 44) x²–2x–399=0 45) x²–4x–9996=0 46) x²+6x–391=0 47) x²–6x–891=0 48) x²+2x–9999=0
49) 4x²+5x–9=0 50) 9x²+8x–1=0 51) 16x²–5x–21=0 52) 19x²–2x–17=0 53) 16x²+9x–7=0 54) 30x²–19x–49=0
Работа №37 Решите уравнения
1) x²–12x+32=0 2) x²–10x+25=0 3) x²–9x+20=0 4) x²–13x+42=0 5) x²–9x+14=0 6) x²–10x+16=0
7) x²+21x+110=0 8) x²+13x+36=0 9) x²+11x+30=0 10) x²+4x+3=0 11) x²+13x+42=0 12) x²+6x+9=0
13) x²–14x+24=0 14) x²–16x+28=0 15) x²+17x+66=0 16) x²+23x+120=0 17) x²+15x+36=0 18) x²–21x+90=0
19) x²+4x–12=0 20) x²–6x–27=0 21) x²–3x–54=0 22) x²+6x–16=0 23) x²–3x–40=0 24) x²–x–56=0
25) x²–17x+42=0 26) x²+13x–114=0 27) x²–10x–56=0 28) x²+14x+40=0 29) x²–15x+36=0 30) x²–11x+28=0
31) x²+15x+26=0 32) x²+28x+27=0 33) x²+26x+88=0 34) x²+26x+25=0 35) x²+31x+150=0 36) x²+12x+11=0
37) x²+223x+442=0 38) x²–303x+602=0 39) x²+413x+1230=0 40) x²–245x+726=0 41) x²+116x+660=0 42) x²+105x+404=0
43) x²+2x–899=0 44) x²–6x–891=0 45) x²–2x–2499=0 46) x²–12x–864=0 47) x²+6x–3591=0 48) x²+4x–396=0
49) 5x²+6x+1=0 50) 9x²–7x–2=0 51) 13x²+2x–15=0 52) 17x²–4x–13=0 53) 25x²+11x–36=0 54) 5x²+27x–32=0
Работа №38 Решите уравнения
1) x²–18x+77=0 2) x²–13x+30=0 3) x²–10x+9=0 4) x²–14x+33=0 5) x²–14x+45=0 6) x²–17x+66=0
7) x²+6x+5=0 8) x²+8x+16=0 9) x²+11x+24=0 10) x²+6x+8=0 11) x²+13x+42=0 12) x²+9x+18=0
13) x²–16x+60=0 14) x²+20x+99=0 15) x²+17x+30=0 16) x²–15x+36=0 17) x²+15x+44=0 18) x²+22x+112=0
19) x²+6x–7=0 20) x²–5x–24=0 21) x²–3x–10=0 22) x²+3x–40=0 23) x²–3x–18=0 24) x²–4x–45=0
25) x²–3x–28=0 26) x²+x–72=0 27) x²–20x+91=0 28) x²+21x+90=0 29) x²–21x+90=0 30) x²–20x+84=0
31) x²+28x+27=0 32) x²+17x+30=0 33) x²+12x+20=0 34) x²+23x+76=0 35) x²+16x+39=0 36) x²+30x+56=0
37) x²+144x+423=0 38) x²+114x+333=0 39) x²–124x+244=0 40) x²+304x+1200=0 41) x²+145x+564=0 42) x²–114x+224=0
43) x²–12x–864=0 44) x²–14x–4851=0 45) x²–4x–396=0 46) x²–2x–8099=0 47) x²+12x–4864=0 48) x²–10x–375=0
49) 3x²+4x+1=0 50) 10x²+7x–3=0 51) 9x²+13x–22=0 52) 17x²+11x–6=0 53) 7x²+20x–27=0 54) 5x²–17x–22=0
Работа №39 Решите уравнения
1) x²–17x+70=0 2) x²–18x+81=0 3) x²–7x+6=0 4) x²–11x+28=0 5) x²–11x+24=0 6) x²–10x+16=0
7) x²+18x+80=0 8) x²+9x+18=0 9) x²+9x+20=0 10) x²+17x+66=0 11) x²+11x+28=0 12) x²+19x+88=0
13) x²–17x+60=0 14) x²+19x+70=0 15) x²+23x+126=0 16) x²–21x+108=0 17) x²–20x+91=0 18) x²+21x+108=0
19) x²+2x–15=0 20) x²+7x–18=0 21) x²+7x–8=0 22) x²+3x–40=0 23) x²–5x–14=0 24) x²–2x–35=0
25) x²+11x+28=0 26) x²+18x+32=0 27) x²–13x–68=0 28) x²+17x+60=0 29) x²–3x–70=0 30) x²+18x+72=0
31) x²+15x+50=0 32) x²+16x+48=0 33) x²+25x+46=0 34) x²+18x+32=0 35) x²+21x+68=0 36) x²+24x+44=0
37) x²+335x+1324=0 38) x²+115x+336=0 39) x²+433x+1290=0 40) x²+104x+303=0 41) x²–302x+301=0 42) x²–143x+420=0
43) x²–6x–3591=0 44) x²–6x–8091=0 45) x²–8x–3584=0 46) x²–12x–864=0 47) x²–2x–6399=0 48) x²–8x–884=0
49) 3x²–4x–7=0 50) 5x²+6x+1=0 51) 3x²+11x+8=0 52) 11x²+20x–31=0 53) 22x²+15x–37=0 54) 17x²+23x–40=0
Работа №40 Решите уравнения
1) x²–16x+55=0 2) x²–18x+81=0 3) x²–12x+32=0 4) x²–13x+40=0 5) x²–14x+45=0 6) x²–4x+3=0
7) x²+11x+30=0 8) x²+7x+6=0 9) x²+12x+20=0 10) x²+12x+32=0 11) x²+9x+18=0 12) x²+15x+56=0
13) x²+12x+20=0 14) x²+16x+28=0 15) x²–22x+117=0 16) x²+19x+78=0 17) x²+22x+112=0 18) x²–20x+96=0
19) x²+3x–10=0 20) x²–5x–24=0 21) x²+6x–27=0 22) x²+3x–4=0 23) x²–8x–9=0 24) x²–3x–18=0
25) x²–3x–10=0 26) x²–7x+10=0 27) x²–12x–133=0 28) x²+15x+54=0 29) x²+13x–114=0 30) x²–11x–102=0
31) x²+32x+112=0 32) x²+25x+46=0 33) x²+30x+104=0 34) x²+22x+40=0 35) x²+26x+48=0 36) x²+21x+38=0
37) x²–315x+936=0 38) x²–307x+2100=0 39) x²–246x+1205=0 40) x²+302x+301=0 41) x²+316x+1860=0 42) x²+347x+1710=0
43) x²+2x–4899=0 44) x²+8x–4884=0 45) x²+2x–2499=0 46) x²+6x–891=0 47) x²+12x–1564=0 48) x²–10x–1575=0
49) 3x²–4x+1=0 50) 11x²–8x–19=0 51) 5x²–2x–7=0 52) 7x²–19x–26=0 53) 13x²–16x+3=0 54) 28x²–29x+1=0
Работа №41 Решите уравнения
1) x²–12x+35=0 2) x²–8x+15=0 3) x²–7x+10=0 4) x²–15x+54=0 5) x²–18x+80=0 6) x²–10x+24=0
7) x²+9x+18=0 8) x²+13x+22=0 9) x²+11x+10=0 10) x²+18x+80=0 11) x²+15x+50=0 12) x²+21x+110=0
13) x²–21x+90=0 14) x²–20x+96=0 15) x²–18x+72=0 16) x²+13x+22=0 17) x²+15x+36=0 18) x²–18x+77=0
19) x²+3x–4=0 20) x²–3x–18=0 21) x²+4x–45=0 22) x²–5x–14=0 23) x²–2x–24=0 24) x²–2x–35=0
25) x²–x–12=0 26) x²+11x+28=0 27) x²–24x+119=0 28) x²–3x–10=0 29) x²+8x–105=0 30) x²+19x+48=0
31) x²+26x+133=0 32) x²+16x+39=0 33) x²+18x+56=0 34) x²+22x+57=0 35) x²+27x+110=0 36) x²+30x+56=0
37) x²+115x+550=0 38) x²–403x+402=0 39) x²–313x+930=0 40) x²–213x+212=0 41) x²+129x+854=0 42) x²–413x+822=0
43) x²–8x–6384=0 44) x²+8x–384=0 45) x²+2x–2499=0 46) x²+14x–351=0 47) x²+8x–884=0 48) x²–4x–4896=0
49) 5x²–3x–2=0 50) 8x²+3x–5=0 51) 7x²–11x–18=0 52) 18x²+5x–23=0 53) 19x²–7x–12=0 54) 21x²–11x–32=0
Работа №42 Решите уравнения
1) x²–10x+16=0 2) x²–11x+10=0 3) x²–11x+18=0 4) x²–12x+32=0 5) x²–8x+12=0 6) x²–11x+30=0
7) x²+6x+8=0 8) x²+16x+55=0 9) x²+15x+54=0 10) x²+7x+12=0 11) x²+11x+24=0 12) x²+12x+32=0
13) x²–21x+90=0 14) x²+16x+39=0 15) x²–19x+84=0 16) x²–19x+78=0 17) x²+14x+24=0 18) x²+18x+45=0
19) x²+3x–10=0 20) x²+6x–27=0 21) x²+5x–14=0 22) x²+4x–45=0 23) x²–5x–36=0 24) x²+x–20=0
25) x²+x–12=0 26) x²–15x–76=0 27) x²–9x+20=0 28) x²–13x–114=0 29) x²–21x+38=0 30) x²–12x+35=0
31) x²+30x+161=0 32) x²+28x+52=0 33) x²+14x+13=0 34) x²+26x+48=0 35) x²+29x+78=0 36) x²+31x+168=0
37) x²+126x+720=0 38) x²+306x+1208=0 39) x²–336x+1980=0 40) x²+134x+520=0 41) x²–406x+2400=0 42) x²+122x+240=0
43) x²–10x–4875=0 44) x²+4x–3596=0 45) x²+4x–4896=0 46) x²–10x–9975=0 47) x²–4x–896=0 48) x²–6x–891=0
49) 5x²–3x–8=0 50) 9x²–5x–4=0 51) 4x²+7x+3=0 52) 9x²–17x–26=0 53) 7x²+20x–27=0 54) 25x²+22x–47=0
Работа №43 Решите уравнения
1) x²–13x+30=0 2) x²–11x+10=0 3) x²–8x+12=0 4) x²–14x+40=0 5) x²–10x+21=0 6) x²–9x+18=0
7) x²+15x+50=0 8) x²+14x+48=0 9) x²+14x+45=0 10) x²+10x+21=0 11) x²+5x+4=0 12) x²+19x+88=0
13) x²–17x+52=0 14) x²+18x+72=0 15) x²–18x+65=0 16) x²+19x+90=0 17) x²–18x+77=0 18) x²+20x+96=0
19) x²–5x–24=0 20) x²–7x–8=0 21) x²+x–20=0 22) x²+2x–24=0 23) x²–3x–28=0 24) x²–x–30=0
25) x²+x–12=0 26) x²+x–72=0 27) x²+3x–18=0 28) x²–17x+52=0 29) x²+4x–32=0 30) x²–7x–18=0
31) x²+15x+36=0 32) x²+17x+60=0 33) x²+19x+34=0 34) x²+25x+24=0 35) x²+11x+10=0 36) x²+21x+80=0
37) x²+307x+1806=0 38) x²–343x+342=0 39) x²+424x+844=0 40) x²–402x+401=0 41) x²–202x+400=0 42) x²+325x+966=0
43) x²–14x–6351=0 44) x²+14x–9951=0 45) x²+12x–864=0 46) x²+2x–1599=0 47) x²–10x–4875=0 48) x²–12x–864=0
49) 5x²–4x–9=0 50) 3x²+11x–14=0 51) 9x²–16x+7=0 52) 21x²–11x–10=0 53) 21x²–13x–8=0 54) 20x²+31x–51=0
Работа №44 Решите уравнения
1) x²–14x+40=0 2) x²–16x+64=0 3) x²–5x+6=0 4) x²–9x+18=0 5) x²–6x+9=0 6) x²–19x+90=0
7) x²+21x+110=0 8) x²+19x+88=0 9) x²+6x+8=0 10) x²+12x+32=0 11) x²+16x+60=0 12) x²+10x+24=0
13) x²+19x+78=0 14) x²+14x+24=0 15) x²–22x+112=0 16) x²–20x+75=0 17) x²–17x+60=0 18) x²+21x+104=0
19) x²+2x–8=0 20) x²+3x–54=0 21) x²–2x–48=0 22) x²+x–20=0 23) x²+4x–5=0 24) x²–2x–24=0
25) x²–8x–20=0 26) x²+4x–32=0 27) x²–21x+54=0 28) x²+2x–15=0 29) x²–x–42=0 30) x²+x–72=0
31) x²+26x+48=0 32) x²+17x+30=0 33) x²+11x+10=0 34) x²+24x+23=0 35) x²+23x+60=0 36) x²+18x+65=0
37) x²+345x+1026=0 38) x²–135x+650=0 39) x²–346x+2040=0 40) x²–214x+424=0 41) x²+207x+1400=0 42) x²–121x+120=0
43) x²+10x–3575=0 44) x²–4x–6396=0 45) x²–8x–6384=0 46) x²–4x–1596=0 47) x²–6x–8091=0 48) x²+8x–384=0
49) 2x²+5x+3=0 50) 4x²–11x–15=0 51) 11x²+8x–19=0 52) 7x²+4x–3=0 53) 11x²–24x–35=0 54) 26x²–19x–45=0
Работа №45 Решите уравнения
1) x²–18x+81=0 2) x²–11x+30=0 3) x²–16x+63=0 4) x²–15x+50=0 5) x²–9x+14=0 6) x²–10x+21=0
7) x²+5x+6=0 8) x²+14x+45=0 9) x²+14x+49=0 10) x²+12x+36=0 11) x²+9x+20=0 12) x²+10x+16=0
13) x²–12x+20=0 14) x²–21x+108=0 15) x²+21x+90=0 16) x²+16x+60=0 17) x²+13x+30=0 18) x²+15x+50=0
19) x²–2x–63=0 20) x²+5x–36=0 21) x²+3x–54=0 22) x²–3x–4=0 23) x²–6x–27=0 24) x²–7x–8=0
25) x²+3x–28=0 26) x²–x–20=0 27) x²+16x–57=0 28) x²–24x+119=0 29) x²+12x–45=0 30) x²–9x+18=0
31) x²+22x+21=0 32) x²+31x+130=0 33) x²+17x+30=0 34) x²+17x+42=0 35) x²+24x+23=0 36) x²+21x+98=0
37) x²–215x+844=0 38) x²+243x+242=0 39) x²–121x+120=0 40) x²–436x+2580=0 41) x²+328x+1932=0 42) x²–446x+2640=0
43) x²+10x–875=0 44) x²+6x–8091=0 45) x²+4x–1596=0 46) x²–10x–3575=0 47) x²+2x–899=0 48) x²–2x–1599=0
49) 6x²–5x–1=0 50) 2x²–3x+1=0 51) 16x²+15x–31=0 52) 9x²+10x+1=0 53) 4x²+21x+17=0 54) 25x²+12x–37=0
Работа №46 Решите уравнения
1) x²–16x+63=0 2) x²–7x+12=0 3) x²–17x+70=0 4) x²–12x+35=0 5) x²–10x+24=0 6) x²–11x+30=0
7) x²+10x+9=0 8) x²+10x+24=0 9) x²+12x+35=0 10) x²+14x+48=0 11) x²+13x+42=0 12) x²+14x+33=0
13) x²+21x+98=0 14) x²+22x+105=0 15) x²+23x+120=0 16) x²–20x+96=0 17) x²–19x+60=0 18) x²+16x+28=0
19) x²+3x–18=0 20) x²–6x–27=0 21) x²+3x–54=0 22) x²+6x–7=0 23) x²–3x–4=0 24) x²+4x–21=0
25) x²–11x–80=0 26) x²–15x+36=0 27) x²–9x–52=0 28) x²+11x+18=0 29) x²–14x–51=0 30) x²+5x–104=0
31) x²+20x+36=0 32) x²+13x+12=0 33) x²+19x+34=0 34) x²+19x+70=0 35) x²+23x+112=0 36) x²+26x+133=0
37) x²+232x+231=0 38) x²+335x+1650=0 39) x²–421x+420=0 40) x²+132x+260=0 41) x²+325x+1284=0 42) x²+303x+302=0
43) x²–12x–8064=0 44) x²–2x–9999=0 45) x²–2x–2499=0 46) x²–4x–896=0 47) x²–14x–8051=0 48) x²+12x–864=0
49) 4x²+5x–9=0 50) 7x²+10x+3=0 51) 8x²+15x–23=0 52) 19x²–14x–33=0 53) 13x²–6x–19=0 54) 28x²–25x–53=0
Работа №47 Решите уравнения
1) x²–7x+6=0 2) x²–14x+48=0 3) x²–14x+49=0 4) x²–10x+24=0 5) x²–4x+3=0 6) x²–10x+21=0
7) x²+6x+8=0 8) x²+17x+66=0 9) x²+9x+18=0 10) x²+13x+42=0 11) x²+11x+28=0 12) x²+19x+90=0
13) x²–19x+84=0 14) x²–22x+117=0 15) x²–16x+28=0 16) x²–15x+50=0 17) x²+17x+52=0 18) x²+15x+36=0
19) x²+2x–3=0 20) x²–x–12=0 21) x²+3x–40=0 22) x²+x–42=0 23) x²+5x–6=0 24) x²–3x–18=0
25) x²–19x+84=0 26) x²+13x+36=0 27) x²–12x+32=0 28) x²+9x–52=0 29) x²+7x+10=0 30) x²+3x–54=0
31) x²+23x+22=0 32) x²+23x+102=0 33) x²+33x+162=0 34) x²+34x+168=0 35) x²+30x+161=0 36) x²+26x+69=0
37) x²+448x+2652=0 38) x²–105x+500=0 39) x²+113x+112=0 40) x²–407x+2406=0 41) x²–106x+408=0 42) x²+214x+424=0
43) x²–10x–6375=0 44) x²–14x–1551=0 45) x²+10x–9975=0 46) x²–8x–9984=0 47) x²–2x–6399=0 48) x²+6x–2491=0
49) 2x²+5x+3=0 50) 11x²–2x–13=0 51) 6x²+11x–17=0 52) 10x²+11x–21=0 53) 16x²+21x+5=0 54) 17x²–6x–23=0
Работа №48 Решите уравнения
1) x²–16x+63=0 2) x²–14x+40=0 3) x²–20x+99=0 4) x²–15x+54=0 5) x²–14x+49=0 6) x²–14x+48=0
7) x²+7x+10=0 8) x²+11x+28=0 9) x²+11x+10=0 10) x²+12x+35=0 11) x²+16x+55=0 12) x²+11x+18=0
13) x²+14x+40=0 14) x²+18x+45=0 15) x²–21x+98=0 16) x²–17x+42=0 17) x²+15x+26=0 18) x²–24x+135=0
19) x²–4x–5=0 20) x²+6x–16=0 21) x²+5x–6=0 22) x²–3x–4=0 23) x²–2x–63=0 24) x²+x–20=0
25) x²–x–6=0 26) x²–7x+12=0 27) x²–4x+4=0 28) x²–21x+90=0 29) x²+5x–24=0 30) x²+6x–16=0
31) x²+27x+92=0 32) x²+18x+17=0 33) x²+29x+28=0 34) x²+20x+64=0 35) x²+32x+156=0 36) x²+17x+52=0
37) x²+137x+910=0 38) x²+114x+224=0 39) x²+307x+2100=0 40) x²+123x+242=0 41) x²+333x+662=0 42) x²–304x+1200=0
43) x²+12x–3564=0 44) x²–4x–3596=0 45) x²–2x–399=0 46) x²+8x–6384=0 47) x²+10x–3575=0 48) x²–14x–6351=0
49) 5x²+2x–7=0 50) 3x²–7x+4=0 51) 9x²+2x–7=0 52) 11x²+3x–8=0 53) 2x²–21x+19=0 54) 2x²+13x–15=0
Работа №49 Решите уравнения
1) x²–4x+4=0 2) x²–17x+72=0 3) x²–19x+90=0 4) x²–9x+8=0 5) x²–15x+44=0 6) x²–10x+25=0
7) x²+9x+14=0 8) x²+6x+8=0 9) x²+8x+15=0 10) x²+20x+100=0 11) x²+13x+40=0 12) x²+7x+10=0
13) x²–19x+78=0 14) x²+19x+84=0 15) x²+14x+33=0 16) x²–17x+52=0 17) x²+19x+90=0 18) x²–14x+24=0
19) x²–x–72=0 20) x²+x–12=0 21) x²+6x–27=0 22) x²+6x–7=0 23) x²–4x–32=0 24) x²+3x–18=0
25) x²+23x+120=0 26) x²+13x+30=0 27) x²–x–42=0 28) x²+3x–108=0 29) x²–5x–14=0 30) x²–18x+56=0
31) x²+20x+84=0 32) x²+24x+119=0 33) x²+15x+26=0 34) x²+29x+78=0 35) x²+18x+72=0 36) x²+18x+32=0
37) x²–343x+342=0 38) x²–309x+2114=0 39) x²+113x+222=0 40) x²+249x+1694=0 41) x²–114x+440=0 42) x²–306x+1800=0
43) x²–8x–4884=0 44) x²+12x–3564=0 45) x²–4x–4896=0 46) x²–10x–375=0 47) x²+12x–2464=0 48) x²+14x–4851=0
49) 2x²–3x+1=0 50) 9x²+5x–14=0 51) 10x²–9x–1=0 52) 4x²+11x+7=0 53) 19x²+2x–17=0 54) 23x²+26x+3=0
Работа №50 Решите уравнения
1) x²–18x+77=0 2) x²–11x+28=0 3) x²–7x+10=0 4) x²–13x+30=0 5) x²–13x+42=0 6) x²–13x+36=0
7) x²+15x+44=0 8) x²+6x+8=0 9) x²+12x+11=0 10) x²+13x+40=0 11) x²+13x+22=0 12) x²+12x+20=0
13) x²+19x+84=0 14) x²+12x+20=0 15) x²+22x+112=0 16) x²–14x+24=0 17) x²–17x+60=0 18) x²–19x+90=0
19) x²–4x–5=0 20) x²–4x–32=0 21) x²+4x–12=0 22) x²–2x–35=0 23) x²–4x–21=0 24) x²–x–30=0
25) x²+14x+48=0 26) x²–3x–28=0 27) x²–x–72=0 28) x²+19x+78=0 29) x²–21x+38=0 30) x²–3x–40=0
31) x²+14x+13=0 32) x²+23x+112=0 33) x²+28x+147=0 34) x²+27x+92=0 35) x²+16x+15=0 36) x²+16x+55=0
37) x²–335x+1650=0 38) x²+346x+2040=0 39) x²+334x+993=0 40) x²–333x+662=0 41) x²+332x+331=0 42) x²+117x+560=0
43) x²–2x–399=0 44) x²+2x–1599=0 45) x²–10x–375=0 46) x²–2x–4899=0 47) x²–4x–9996=0 48) x²–4x–4896=0
49) 3x²–4x–7=0 50) 4x²+7x+3=0 51) 15x²–11x–26=0 52) 16x²–19x–35=0 53) 17x²+11x–28=0 54) 15x²–29x+14=0
Теорема Виета
youtube.com/embed/a0XWFZvrlwg» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>В математике существуют специальные приемы, с которыми многие квадратные уравнения решаются очень быстро и без всяких дискриминантов. Более того, при надлежащей тренировке многие начинают решать квадратные уравнения устно, буквально «с первого взгляда».
К сожалению, в современном курсе школьной математики подобные технологии почти не изучаются. А знать надо! И сегодня мы рассмотрим один из таких приемов — теорему Виета. Для начала введем новое определение.
Квадратное уравнение вида x2 + bx + c = 0 называется приведенным. Обратите внимание: коэффициент при x2 равен 1. Никаких других ограничений на коэффициенты не накладывается.
Примеры:
- x2 + 7x + 12 = 0 — это приведенное квадратное уравнение;
- x2 − 5x + 6 = 0 — тоже приведенное;
- 2x2 − 6x + 8 = 0 — а вот это нифига не приведенное, поскольку коэффициент при x2 равен 2.

Разумеется, любое квадратное уравнение вида ax2 + bx + c = 0 можно сделать приведенным — достаточно разделить все коэффициенты на число a. Мы всегда можем так поступить, поскольку из определения квадратного уравнения следует, что a ≠ 0.
Правда, далеко не всегда эти преобразования будут полезны для отыскания корней. Чуть ниже мы убедимся, что делать это надо лишь тогда, когда в итоговом приведенном квадратом уравнении все коэффициенты будут целочисленными. А пока рассмотрим простейшие примеры:
Задача. Преобразовать квадратное уравнение в приведенное:
- 3x2 − 12x + 18 = 0;
- −4x2 + 32x + 16 = 0;
- 1,5x2 + 7,5x + 3 = 0;
- 2x2 + 7x − 11 = 0.
Разделим каждое уравнение на коэффициент при переменной x2. Получим:
- 3x2 − 12x + 18 = 0 ⇒ x2 − 4x + 6 = 0 — разделили все на 3;
- −4x2 + 32x + 16 = 0 ⇒ x2 − 8x − 4 = 0 — разделили на −4;
- 1,5x2 + 7,5x + 3 = 0 ⇒ x2 + 5x + 2 = 0 — разделили на 1,5, все коэффициенты стали целочисленными;
- 2x2 + 7x − 11 = 0 ⇒ x2 + 3,5x − 5,5 = 0 — разделили на 2.
 При этом возникли дробные коэффициенты.
При этом возникли дробные коэффициенты.
Как видите, приведенные квадратные уравнения могут иметь целые коэффициенты даже в том случае, когда исходное уравнение содержало дроби.
Теперь сформулируем основную теорему, для которой, собственно, и вводилось понятие приведенного квадратного уравнения:
Теорема Виета. Рассмотрим приведенное квадратное уравнение вида x2 + bx + c = 0. Предположим, что это уравнение имеет действительные корни x1 и x2. В этом случае верны следующие утверждения:
- x1 + x2 = −b. Другими словами, сумма корней приведенного квадратного уравнения равна коэффициенту при переменной x, взятому с противоположным знаком;
- x1 · x2 = c. Произведение корней квадратного уравнения равно свободному коэффициенту.
Примеры. Для простоты будем рассматривать только приведенные квадратные уравнения, не требующие дополнительных преобразований:
- x2 − 9x + 20 = 0 ⇒ x1 + x2 = − (−9) = 9; x1 · x2 = 20; корни: x1 = 4; x2 = 5;
- x2 + 2x − 15 = 0 ⇒ x1 + x2 = −2; x1 · x2 = −15; корни: x1 = 3; x2 = −5;
- x2 + 5x + 4 = 0 ⇒ x1 + x2 = −5; x1 · x2 = 4; корни: x1 = −1; x2 = −4.

Теорема Виета дает нам дополнительную информацию о корнях квадратного уравнения. На первый взгляд это может показаться сложным, но даже при минимальной тренировке вы научитесь «видеть» корни и буквально угадывать их за считанные секунды.
Задача. Решите квадратное уравнение:
- x2 − 9x + 14 = 0;
- x2 − 12x + 27 = 0;
- 3x2 + 33x + 30 = 0;
- −7x2 + 77x − 210 = 0.
Попробуем выписать коэффициенты по теореме Виета и «угадать» корни:
- x2 − 9x + 14 = 0 — это приведенное квадратное уравнение.
По теореме Виета имеем: x1 + x2 = −(−9) = 9; x1 · x2 = 14. Несложно заметить, что корни — числа 2 и 7; - x2 − 12x + 27 = 0 — тоже приведенное.
По теореме Виета: x1 + x2 = −(−12) = 12; x1 · x2 = 27. Отсюда корни: 3 и 9; - 3x2 + 33x + 30 = 0 — это уравнение не является приведенным.
 Но мы это сейчас исправим, разделив обе стороны уравнения на коэффициент a = 3. Получим: x2 + 11x + 10 = 0.
Но мы это сейчас исправим, разделив обе стороны уравнения на коэффициент a = 3. Получим: x2 + 11x + 10 = 0.
Решаем по теореме Виета: x1 + x2 = −11; x1 · x2 = 10 ⇒ корни: −10 и −1; - −7x2 + 77x − 210 = 0 — снова коэффициент при x2 не равен 1, т.е. уравнение не приведенное. Делим все на число a = −7. Получим: x2 − 11x + 30 = 0.
По теореме Виета: x1 + x2 = −(−11) = 11; x1 · x2 = 30; из этих уравнений легко угадать корни: 5 и 6.
Из приведенных рассуждений видно, как теорема Виета упрощает решение квадратных уравнений. Никаких сложных вычислений, никаких арифметических корней и дробей. И даже дискриминант (см. урок «Решение квадратных уравнений») нам не потребовался.
Разумеется, во всех размышлениях мы исходили из двух важных предположений, которые, вообще говоря, не всегда выполняются в реальных задачах:
- Квадратное уравнение является приведенным, т.
 е. коэффициент при x2 равен 1;
е. коэффициент при x2 равен 1; - Уравнение имеет два различных корня. С точки зрения алгебры, в этом случае дискриминант D > 0 — по сути, мы изначально предполагаем, что это неравенство верно.
Однако в типичных математических задачах эти условия выполняются. Если же в результате вычислений получилось «плохое» квадратное уравнение (коэффициент при x2 отличен от 1), это легко исправить — взгляните на примеры в самом начале урока. Про корни вообще молчу: что это за задача, в которой нет ответа? Конечно, корни будут.
Таким образом, общая схема решения квадратных уравнений по теореме Виета выглядит следующим образом:
- Свести квадратное уравнение к приведенному, если это еще не сделано в условии задачи;
- Если коэффициенты в приведенном квадратном уравнении получились дробными, решаем через дискриминант. Можно даже вернуться к исходному уравнению, чтобы работать с более «удобными» числами;
- В случае с целочисленными коэффициентами решаем уравнение по теореме Виета;
- Если в течение нескольких секунд не получилось угадать корни, забиваем на теорему Виета и решаем через дискриминант.

Задача. Решите уравнение: 5x2 − 35x + 50 = 0.
Итак, перед нами уравнение, которое не является приведенным, т.к. коэффициент a = 5. Разделим все на 5, получим: x2 − 7x + 10 = 0.
Все коэффициенты квадратного уравнения целочисленные — попробуем решить по теореме Виета. Имеем: x1 + x2 = −(−7) = 7; x1 · x2 = 10. В данном случае корни угадываются легко — это 2 и 5. Считать через дискриминант не надо.
Задача. Решите уравнение: −5x2 + 8x − 2,4 = 0.
Смотрим: −5x2 + 8x − 2,4 = 0 — это уравнение не является приведенным, разделим обе стороны на коэффициент a = −5. Получим: x2 − 1,6x + 0,48 = 0 — уравнение с дробными коэффициентами.
Лучше вернуться к исходному уравнению и считать через дискриминант: −5x2 + 8x − 2,4 = 0 ⇒ D = 82 − 4 · (−5) · (−2,4) = 16 ⇒ … ⇒ x1 = 1,2; x2 = 0,4.
Задача. Решите уравнение: 2x2 + 10x − 600 = 0.
Для начала разделим все на коэффициент a = 2. Получится уравнение x2 + 5x − 300 = 0.
Это приведенное уравнение, по теореме Виета имеем: x1 + x2 = −5; x1 · x2 = −300. Угадать корни квадратного уравнения в данном случае затруднительно — лично я серьезно «завис», когда решал эту задачу.
Придется искать корни через дискриминант: D = 52 − 4 · 1 · (−300) = 1225 = 352. Если вы не помните корень из дискриминанта, просто отмечу, что 1225 : 25 = 49. Следовательно, 1225 = 25 · 49 = 52 · 72 = 352.
Теперь, когда корень из дискриминанта известен, решить уравнение не составит труда. Получим: x1 = 15; x2 = −20.
Смотрите также:
- Следствия из теоремы Виета
- Как решать квадратные уравнения
- Стандартный вид числа
- Задача B3 — работа с графиками
- Пробный ЕГЭ 2012 от 7 декабря.
 Вариант 6 (без производной)
Вариант 6 (без производной) - Опасные ошибки в задачах на площади
1) 3×2 − 18 = 0; 3) x2 − x − 20 = 0; 5) x2 + 6x − 2 = 0; 2) 8×2 − 3x = 0; 4) 3×2 − 2x − 8 = 0; 6) x2 − 4x + 6 = 0. 2. составьте приведённое квадратное уравнение, сумма корней которого равна числу −6, а произведение — числу 3. 3. одна из сторон прямоугольника на 6 см меньше другой. найдите стороны прямоугольника, если его площадь равна 72 см2. 4. число 5 является корнем уравнения 4×2 + 6x + k = 0. найдите второй корень уравнения и значение k. 5. при каком значении a уравнение 4×2 + 8x + a = 0 имеет единственный корень? 6. известно, что x1 и x2 — корни уравнения x2 + 10x + 4 = 0. не решая уравнения, найдите значение выражения . — Знания.org
1) 4×2 − 12 = 0; 3) x2 − 6x − 16 = 0; 5) x2 − 7x + 4 = 0;
2) 7×2 + 5x = 0; 4) 15×2 − 4x − 3 = 0; 6) x2 + 5x + 9 = 0.
2. Составьте приведённое квадратное уравнение, сумма корней которого равна числу 4, а произведение — числу −3.
3. Одна из сторон прямоугольника на 3 см больше другой. Найдите стороны прямоугольника, если его площадь равна 88 см2.
Найдите стороны прямоугольника, если его площадь равна 88 см2.
4. Число −3 является корнем уравнения 5×2 + mx − 12 = 0. Найдите второй корень уравнения и значение m.
5. При каком значении a уравнение 3×2 − 6x + a = 0 имеет единственный корень?
6. Известно, что x1 и x2 — корни уравнения x2 + 6x − 13 = 0. Не решая уравнения, найдите значение выражения .
Вариант 4
1. Решите уравнение:
1) 3×2 − 18 = 0; 3) x2 − x − 20 = 0; 5) x2 + 6x − 2 = 0;
2) 8×2 − 3x = 0; 4) 3×2 − 2x − 8 = 0; 6) x2 − 4x + 6 = 0.
2. Составьте приведённое квадратное уравнение, сумма корней которого равна числу −6, а произведение — числу 3.
3. Одна из сторон прямоугольника на 6 см меньше другой. Найдите стороны прямоугольника, если его площадь равна 72 см2.
4. Число 5 является корнем уравнения 4×2 + 6x + k = 0. Найдите второй корень уравнения и значение k.
5. При каком значении a уравнение 4×2 + 8x + a = 0 имеет единственный корень?
6. Известно, что x1 и x2 — корни уравнения x2 + 10x + 4 = 0. Не решая уравнения, найдите значение выражения .
Не решая уравнения, найдите значение выражения .
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
1.1 Факторинг x 2 + 7x-18
Первый член равен x 2 его коэффициент равно 1.
Средний член + 7x, его коэффициент равен 7.
Последний член, «константа», равен -18
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -18 = -18
Шаг-2: Найдите два множителя -18, сумма которых равен коэффициенту среднего члена, равному 7.
| -18 | + | 1 | = | -17 | ||
| -9 | + | 2 | = | -7 | ||
| -6 | + | 3 | = | -3 | ||
| -3 | + | 6 | = | 3 | ||
| -2 | + | 9 | = | 7 | Вот и все |
Шаг 3: Перепишите полином, разделяя средний член, используя два фактора, найденные на шаге 2 выше, -2 и 9
x 2 — 2x + 9x — 18
Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • ( x-2)
Сложите последние 2 члена и вычтите общие множители:
9 • (x-2)
Шаг 5: сложите четыре члена шага 4:
(x + 9) • (x-2 )
Требуемая факторизация
Уравнение в конце шага 1:
(x + 9) • (x - 2) = 0
Шаг 2:
Теория — Корни продукта:
2. 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов содержится в произведении
Любое решение для члена = 0 также решает продукт = 0.
Решение уравнения с одной переменной:
2.2 Решите: x + 9 = 0
Вычтите 9 из обеих частей уравнения:
x = -9
Решение уравнения с одной переменной:
2.3 Решите: x-2 = 0
Добавьте 2 к обеим сторонам уравнения:
x = 2
Дополнение: Решение квадратного уравнения напрямую
Решение x 2 + 7x-18 = 0 напрямую
Ранее мы разложили этот многочлен на множители, разделив средний член. Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
3. 1 Найдите вершину y = x 2 + 7x-18
1 Найдите вершину y = x 2 + 7x-18
Параболы имеют наибольшее значение или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна -3.5000
Подставляя в формулу параболы -3,5000 для x, мы можем вычислить координату y:
y = 1,0 * -3,50 * -3,50 + 7,0 * -3,50 — 18,0
или y = -30,250
Parabola, Graphing Vertex и X-Intercepts:
Корневой график для: y = x 2 + 7x-18
Ось симметрии (пунктирная линия) {x} = {- 3,50}
Вершина в точке {x, y} = {-3,50, -30,25 }
x -Перехват (корни):
Корень 1 при {x, y} = {-9.00, 0.00}
Корень 2 при {x, y} = {2.00, 0.00}
Решите квадратное уравнение, заполнив квадрат
3.2 Решение x 2 + 7x-18 = 0, заполнив квадрат.
Добавьте 18 к обеим сторонам уравнения:
x 2 + 7x = 18
Теперь умный бит: возьмите коэффициент при x, равный 7, разделите его на два, получив 7/2, и возведите его в квадрат. давая 49/4
Добавьте 49/4 к обеим частям уравнения:
В правой части мы имеем:
18 + 49/4 или, (18/1) + (49/4)
Общий знаменатель две дроби равны 4. Сложение (72/4) + (49/4) дает 121/4
Сложение (72/4) + (49/4) дает 121/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 + 7x + (49/4) = 121/4
Сложение 49/4 завершает левую часть в виде полного квадрата:
x 2 + 7x + (49/4) =
(x + (7/2)) • (x + (7/2)) =
(x + ( 7/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x 2 + 7x + (49/4) = 121/4 и
x 2 + 7x + (49/4) = (x + (7/2)) 2
, то по закону транзитивность,
(x + (7/2)) 2 = 121/4
Мы будем называть это уравнение уравнением. # 3.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x + (7/2)) 2 равен
(x + (7/2)) 2/2 =
(x + (7/2)) 1 =
x + (7/2)
Теперь, применяя принцип квадратного корня к уравнению.# 3.2.1 получаем:
x + (7/2) = √ 121/4
Вычтем 7/2 с обеих сторон, чтобы получить:
x = -7/2 + √ 121/4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 + 7x — 18 = 0
имеет два решения:
x = -7/2 + √ 121/4
или
x = -7/2 — √ 121 / 4
Обратите внимание, что √ 121/4 можно записать как
√ 121 / √ 4, что равно 11/2
Решите квадратное уравнение с помощью квадратичной формулы
3. 3 Решение x 2 + 7x-18 = 0 по квадратичной формуле.
3 Решение x 2 + 7x-18 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = 7
C = -18
Соответственно B 2 — 4AC =
49 — (-72) =
121
Применение квадратичной формулы:
-7 ± √ 121
x = ——————
2
Можно ли упростить √ 121?
Да! Разложение на простые множители 121 равно
11 • 11
Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
√ 121 = √ 11 • 11 =
± 11 • √ 1 =
± 11
Итак, теперь мы смотрим на:
x = (-7 ± 11) / 2
Два реальных решения:
x = (-7 + √121) / 2 = (- 7 + 11) / 2 = 2.000
или:
x = (- 7-√121) / 2 = (- 7-11) / 2 = -9. 000
000
Было найдено два решения:
- x = 2
- x = -9
Для данного квадратного уравнения X2 7X 18 0 проверьте математику класса 10 CBSE
Подсказка: При решении квадратного уравненияПервое из Всего мы находим два фактора, сумма которых равна коэффициенту среднего члена.{\ text {2}}} \] его коэффициент равен \ [{\ text {1}} \]
Кроме того, средний член равен \ [{\ text {- 7X}} \], его коэффициент равен \ [{\ text {- 7}} \]
Кроме того, последний член «константа» равен \ [{\ text {- 18}} \]
Здесь мы должны умножить коэффициент первого члена на константу \ [{\ text {1 \ times — 18 = — 18}} \]
Теперь нам нужно найти произведение двух множителей: \ [{\ text {- 18}} \], сумма которого равна коэффициенту среднего члена, который равен \ [{\ text {- 7}} \]
Теперь нам нужно построить это следующим образом:
\ [{\ text {- 18 + 1 = — 17}} \]
\ [{\ text {- 2 + 9 = 7}} \]
\ [{\ text {- 6 + 3 = — 3}} \]
\ [{\ text {- 9 + 2 = — 7}} \]
Здесь мы получаем \ [{ \ text {- 9 + 2 = — 7}} \]
Перепишите данное квадратное уравнение как разделение среднего члена, используя два фактора, найденные выше, а именно \ [{\ text {- 9}} \] и \ [ {\ text {2}} \]
\ [\ Rightarrow {{\ text {x}} ^ {\ text {2}}} {\ text {- 9x + 2x — 18 = 0}}.
 … \ left (1 \ right) \]
… \ left (1 \ right) \] Теперь мы должны сложить первые два члена в \ [\ left (1 \ right) \] и вытащить такие же множители: \ [{\ text {x (x — 9)}} \]
Кроме того, мы можем сложить последние два члена, извлекая аналогичные множители: \ [{\ text {+ 2 (x — 9)}} \]
Итак, мы получаем
\ [\ Rightarrow {\ text {(x + 2) (x — 9)}} {\ kern 1pt} {\ text {= 0}} \]
Это желаемая факторизация.
Также мы можем записать это как \ [{\ text {(x + 2) = 0}} \] и \ [{\ text {(x — 9)}} {\ kern 1pt} {\ text {= 0 }} \]
Теперь мы получаем корни данного квадратного уравнения.
\ [{\ text {x = — 2, x = 9}} \]
Следовательно, \ [\ sqrt {\ text {3}} \] и \ [{\ text {4}} \] являются а не корни данного уравнения.
Примечание: Квадратное уравнение с действительным или комплексным коэффициентом имеет два решения, называемых корнями.
Действительные константы — это многочлены нулевой степени.
Эти два решения могут отличаться, а могут и не быть; любые они могут быть или не быть настоящими.
Метод факторизации может использоваться, когда квадратное уравнение может быть разложено на линейные множители.
Для данного продукта, если весь продукт должен быть равен нулю, то любой коэффициент будет равен нулю.
И наоборот, если продукт равен нулю, то некоторый коэффициент этого продукта должен быть равен нулю.
Факторинг квадратных уравнений — методы и примеры
Есть ли у вас представление о факторизации многочленов ? Поскольку теперь у вас есть основная информация о многочленах, мы узнаем, как решать квадратичные многочлены с помощью факторизации.
Прежде всего, давайте быстро рассмотрим квадратное уравнение .Квадратное уравнение — это многочлен второй степени, обычно в форме f (x) = ax 2 + bx + c, где a, b, c, ∈ R, и a ≠ 0. Термин «a» означает называется старшим коэффициентом, а «c» — абсолютным членом f (x).
Каждое квадратное уравнение имеет двух значений неизвестной переменной, обычно называемых корнями уравнения (α, β). Мы можем получить корни квадратного уравнения, разложив уравнение на множители.
Мы можем получить корни квадратного уравнения, разложив уравнение на множители.
По этой причине факторизация является фундаментальным шагом на пути к решению любого уравнения в математике.Давай выясним.
Как разложить квадратное уравнение на множители?
Факторинг квадратного уравнения можно определить как процесс разбиения уравнения на произведение его факторов. Другими словами, мы также можем сказать, что факторизация — это обратное умножению.
Для решения квадратного уравнения ax 2 + bx + c = 0 путем факторизации используются следующие шаги :
- Разверните выражение и при необходимости очистите все дроби.
- Переместите все члены в левую часть знака равенства.
- Факторизуйте уравнение, разбив средний член.
- Приравняйте каждый коэффициент к нулю и решите линейные уравнения
Пример 1
Решите: 2 (x 2 + 1) = 5x
Решение
Разверните уравнение и переместите все члены слева от знака равенства.
⟹ 2x 2 — 5x + 2 = 0
⟹ 2x 2 — 4x — x + 2 = 0
⟹ 2x (x — 2) — 1 (x — 2) = 0
⟹ ( x — 2) (2x — 1) = 0
Приравняем каждый множитель к нулю и решим
⟹ x — 2 = 0 или 2x — 1 = 0
⟹ x = 2 или x = 1212
Следовательно, решения x = 2, 1/2.
Пример 2
Решить 3x 2 — 8x — 3 = 0
Решение
3x 2 — 9x + x — 3 = 0
⟹ 3x (x — 3) + 1 (x — 3) = 0
⟹ (x — 3) (3x + 1) = 0
⟹ x = 3 или x = -13
Пример 3
Решите следующее квадратное уравнение ( 2x — 3) 2 = 25
Решение
Разверните уравнение (2x — 3) 2 = 25, чтобы получить;
⟹ 4x 2 — 12x + 9-25 = 0
⟹ 4x 2 — 12x — 16 = 0
Разделите каждый член на 4, чтобы получить;
⟹ x 2 — 3x — 4 = 0
⟹ (x — 4) (x + 1) = 0
⟹ x = 4 or x = -1
Существует множество методов факторизации квадратных уравнений. В этой статье мы сделаем акцент на том, как разложить квадратные уравнения на множители, в которых коэффициент при x 2 равен 1 или больше 1.
В этой статье мы сделаем акцент на том, как разложить квадратные уравнения на множители, в которых коэффициент при x 2 равен 1 или больше 1.
Поэтому мы будем использовать метод проб и ошибок, чтобы получить правильные множители для данного квадратного уравнения.
Факторинг, когда коэффициент x
2 равен 1Чтобы разложить квадратное уравнение вида x 2 + bx + c, старший коэффициент равен 1. Вам необходимо определить два числа, произведение и сумма которых равны c и b соответственно.
СЛУЧАЙ 1: Когда b и c положительны
Пример 4
Решите квадратное уравнение: x 2 + 7x + 10 = 0
Перечислите множители 10:
1 × 10, 2 × 5
Определите два множителя с произведением 10 и суммой 7:
1 + 10 ≠ 7
2 + 5 = 7.
Проверьте множители, используя свойство распределения умножения.
(x + 2) (x + 5) = x 2 + 5x + 2x + 10 = x 2 + 7x + 10
Факторы квадратного уравнения: (x + 2) (x + 5)
Приравнивание каждого множителя к нулю дает;
x + 2 = 0 ⟹x = -2
x + 5 = 0 ⟹ x = -5
Следовательно, решением будет x = — 2, x = — 5
Пример 5
х 2 + 10х + 25.
Решение
Определите два фактора с произведением 25 и суммой 10.
5 × 5 = 25 и 5 + 5 = 10
Проверьте факторы.
x 2 + 10x + 25 = x 2 + 5x + 5x + 25
= x (x + 5) + 5x + 25
= x (x + 5) + 5 (x + 5)
= (x + 5) (x + 5)
Следовательно, x = -5 — это ответ.
СЛУЧАЙ 2: Когда b положительно, а c отрицательно
Пример 6
Решите x 2 + 4x — 5 = 0
Решение
Запишите множители -5.
1 × –5, –1 × 5
Определите факторы, произведение которых равно — 5, а сумма равна 4.
1 — 5 ≠ 4
–1 + 5 = 4
Проверьте факторы, используя свойство распределения.
(x — 1) (x + 5) = x 2 + 5x — x — 5 = x 2 + 4x — 5
(x — 1) (x + 5) = 0
x — 1 = 0 ⇒ x = 1 или
x + 5 = 0 ⇒ x = -5
Следовательно, x = 1, x = -5 — решения.
СЛУЧАЙ 3: Когда оба значения b и c отрицательны
Пример 7
x 2 — 5x — 6
Решение
Запишите множители — 6:
1 × –6, –1 × 6, 2 × –3, –2 × 3
Теперь определите факторы, произведение которых равно -6, а сумма равна –5:
1 + (–6) = –5
Проверьте коэффициенты используя распределительное свойство.
(x + 1) (x — 6) = x 2 -6 x + x — 6 = x 2 — 5x — 6
Приравняйте каждый множитель к нулю и решите, чтобы получить;
(x + 1) (x — 6) = 0
x + 1 = 0 ⇒ x = -1, или
x — 6 = 0 ⇒ x = 6
Следовательно, решение x = 6, x = -1
СЛУЧАЙ 4: Когда b отрицательно, а c положительно
Пример 8
x 2 — 6x + 8 = 0
Решение
Запишите все множители 8 .
–1 × — 8, –2 × –4
Определите факторы, произведение которых равно 8, а сумма равна -6
–1 + (–8) ≠ –6
–2 + (–4) = –6
Проверьте коэффициенты с помощью распределительного свойства.
(x — 2) (x — 4) = x 2 — 4 x — 2x + 8 = x 2 — 6x + 8
Теперь приравняйте каждый множитель к нулю и решите выражение, чтобы получить;
(x — 2) (x — 4) = 0
x — 2 = 0 ⇒ x = 2 или
x — 4 = 0 ⇒ x = 4
Пример 9
Разложить на множители x 2 + 8x + 12.
Решение
Запишите множители 12;
12 = 2 × 6 или = 4 × 3
Найдите множители, сумма которых равна 8:
2 + 6 = 8
2 × 6 ≠ 8
Используйте свойство распределения для проверки множителей;
= x 2 + 6x + 2x + 12 = (x 2 + 6x) + (2x + 12) = x (x + 6) +2 (x + 6)
= x (x + 6 ) +2 (x + 6) = (x + 6) (x + 2)
Приравняем каждый множитель к нулю, чтобы получить;
(x + 6) (x + 2)
x = -6, -2
Факторинг, когда коэффициент x
2 больше 1Иногда старший коэффициент квадратного уравнения может быть больше чем 1.В этом случае мы не можем решить квадратное уравнение, используя общие множители.
Следовательно, нам нужно рассмотреть коэффициент при x 2 и множители при c, чтобы найти числа, сумма которых равна b.
Пример 10
Решите 2x 2 — 14x + 20 = 0
Решение
Определите общие множители уравнения.
2x 2 — 14x + 20 ⇒ 2 (x 2 — 7x + 10)
Теперь мы можем найти множители (x 2 — 7x + 10).Поэтому запишите множители 10:
–1 × –10, –2 × –5
Определите факторы, сумма которых равна — 7:
1 + (–10) ≠ –7
–2 + (–5) = –7
Проверьте коэффициенты, применив распределительное свойство.
2 (x — 2) (x — 5) = 2 (x 2 — 5 x — 2x + 10)
= 2 (x 2 — 7x + 10) = 2x 2 — 14x + 20
Приравняйте каждый множитель к нулю и решите;
2 (x — 2) (x — 5) = 0
x — 2 = 0 ⇒ x = 2 или
x — 5 = 0 ⇒ x = 5
Пример 11
Решить 7x 2 + 18x + 11 = 0
Решение
Запишите множители 7 и 11.
7 = 1 × 7
11 = 1 × 11
Примените свойство распределения, чтобы проверить коэффициенты, как показано ниже:
(7x + 1) (x + 11) ≠ 7x 2 + 18x + 11
(7x + 11) (x + 1) = 7x 2 + 7x + 11x + 11 = 7x 2 + 18x + 11
Теперь приравняйте каждый множитель к нулю и решите, чтобы получить;
7x 2 + 18x + 11 = 0
(7x + 11) (x + 1) = 0
x = -1, -11/7
Пример 12
Решить 2x 2 — 7x + 6 = 3
Решение
2x 2 — 7x + 3 = 0
(2x — 1) (x — 3) = 0
x = 1/2 или x = 3
Пример 13
Решить 9x 2 + 6x + 1 = 0
Решение
Разложите на множители, чтобы получить:
(3x + 1) (3x + 1) = 0
(3x + 1) = 0,
Следовательно, x = −1 / 3
Пример 14
Разложить на множители 6x 2 — 7x + 2 = 0
Решение
6x 2 — 4x — 3x + 2 = 0
Разложите выражение на множители;
⟹ 2x (3x — 2) — 1 (3x — 2) = 0
⟹ (3x — 2) (2x — 1) = 0
⟹ 3x — 2 = 0 или 2x — 1 = 0
⟹ 3x = 2 или 2x = 1
⟹ x = 2/3 или x = ½
Пример 15
Разложить на множители x 2 + (4 — 3y) x — 12y = 0
Решение
Разверните уравнение;
x 2 + 4x — 3xy — 12y = 0
Разложить на множители;
⟹ x (x + 4) — 3y (x + 4) = 0
x + 4) (x — 3y) = 0
⟹ x + 4 = 0 или x — 3y = 0
⟹ x = -4 или x = 3y
Таким образом, x = -4 или x = 3y
Практические вопросыРешите следующие квадратные уравнения путем факторизации:
- 3x 2 -20 = 160 — 2x 2
- (2x — 3) 2 = 49
- 16x 2 = 25
- (2x + 1) 2 + (x + 1) 2 = 6x + 47
- 2x 2 + x — 6 = 0
- 3x 2 = x + 4
- (x — 7) (x — 9) = 195
- x 2 — (a + b) x + ab = 0
- x 2 + 5 x + 6 = 0
- x 2 -2 x — 15 = 0
Ответы
- 6, -6
- -2, 5
- — 5/4, 5/4
- -3, 3
- -2, 3/2
- -1 , 4/3
- -6, 22
- a, b
- –3, –2
- 5, — 3
Решите квадратные уравнения по квадратичной формуле — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите квадратные уравнения, используя формулу корней квадратного уравнения
- Используйте дискриминант, чтобы предсказать количество решений квадратного уравнения
- Определите наиболее подходящий метод для решения квадратного уравнения
Прежде чем начать, пройдите тест на готовность.
- Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
Когда мы решали квадратные уравнения в последнем разделе, завершая квадрат, мы каждый раз предпринимали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ — «да». В этом разделе мы выведем и воспользуемся формулой, чтобы найти решение проблемы. квадратное уровненеие.
Мы уже видели, как решить формулу для конкретной переменной «в целом», чтобы мы выполняли алгебраические действия только один раз, а затем использовали новую формулу для нахождения значения конкретной переменной. Теперь мы рассмотрим этапы завершения квадрата в целом, чтобы решить квадратное уравнение для x . Возможно, будет полезно взглянуть на один из примеров в конце последнего раздела, где мы решали уравнение формы, когда вы читаете алгебраические шаги ниже, поэтому вы видите их как с числами, так и со словом «в целом». ’
’
Последнее уравнение — квадратичная формула.
Квадратичная формула
Решения квадратного уравнения вида даются формулой:
Чтобы использовать квадратичную формулу, мы подставляем значения в выражение в правой части формулы. Затем мы делаем все математические вычисления, чтобы упростить выражение. Результат дает решение (я) квадратного уравнения.
Как решить квадратное уравнение с помощью квадратной формулы
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Если вы произносите формулу во время написания каждой задачи, вы быстро запомните ее. И помните, квадратная формула — это уравнение. Обязательно начинайте с «».
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Когда мы решали квадратные уравнения с помощью свойства квадратного корня, мы иногда получали ответы с радикалами. То же самое может случиться и при использовании квадратичной формулы. Если в качестве решения мы получаем радикал, окончательный ответ должен иметь радикал в его упрощенной форме.
То же самое может случиться и при использовании квадратичной формулы. Если в качестве решения мы получаем радикал, окончательный ответ должен иметь радикал в его упрощенной форме.
Решите, используя дискриминант.
Решение
Мы можем использовать квадратичную формулу, чтобы найти переменную в квадратном уравнении, независимо от того, называется ли оно « x ».
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Мы не можем извлечь квадратный корень из отрицательного числа. Итак, когда мы подставляем, и в квадратную формулу, если величина внутри радикала отрицательна, квадратное уравнение не имеет реального решения.Мы увидим это в следующем примере.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Все квадратные уравнения, которые мы решили до сих пор в этом разделе, были записаны в стандартной форме,. Иногда нам нужно сделать некоторую алгебру, чтобы привести уравнение в стандартную форму, прежде чем мы сможем использовать квадратичную формулу.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы «очищали дроби», умножая обе части уравнения на ЖК-дисплей. Это дало нам возможность решить эквивалентное уравнение — без дробей. Мы можем использовать ту же стратегию с квадратными уравнениями.
Решите, используя дискриминант.
Решите, используя дискриминант.
Решите, используя дискриминант.
Подумайте об уравнении. Мы знаем из принципа нулевого произведения, что это уравнение имеет только одно решение:.
Мы знаем из принципа нулевого произведения, что это уравнение имеет только одно решение:.
В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения с полным квадратом также дает только одно решение.
Решите, используя дискриминант.
Решение
Вы узнали, что это идеальный квадрат?
Решите, используя дискриминант.
Решите, используя дискриминант.
Использование дискриминанта для предсказания числа решений квадратного уравнения
Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два решения, иногда одно решение, иногда нет реальных решений. Есть ли способ предсказать количество решений квадратного уравнения, не решая его на самом деле?
Да, количество внутри корня квадратной формулы позволяет нам легко определить количество решений.Эта величина называется дискриминантом.
Дискриминант
В квадратичной формуле величина называется дискриминантом.
Давайте посмотрим на дискриминант уравнений на (Рисунок), (Рисунок) и (Рисунок), а также на количество решений этих квадратных уравнений.
Когда дискриминант положительный , квадратное уравнение имеет два решения .
Когда дискриминант ноль , квадратное уравнение имеет одно решение .
Когда дискриминант отрицательный , квадратное уравнение не имеет реальных решений .
Определите количество решений каждого квадратного уравнения:
ⓐⓑⓒⓓ
ⓐ нет реальных решений ⓑ 2 ⓒ 1 ⓓ нет реальных решений
Определите количество решений каждого квадратного уравнения:
ⓐⓑⓒⓓ
ⓐ 2 ⓑ нет реальных решений ⓒ 1 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения
Мы использовали четыре метода для решения квадратных уравнений:
- Факторинг
- Свойство квадратного корня
- Завершение квадрата
- Квадратичная формула
Вы можете решить любое квадратное уравнение, используя квадратичную формулу, но это не всегда самый простой метод.
Определите наиболее подходящий метод решения квадратного уравнения.
- Сначала попробуйте Факторинг . Если квадратичные множители легко, этот метод очень быстрый.
- Далее попробуйте применить свойство квадратного корня . Если уравнение соответствует форме или, его можно легко решить с помощью свойства квадратного корня.
- Используйте квадратичную формулу . Любое квадратное уравнение можно решить с помощью квадратной формулы.
А как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают не использовать его.Нам нужно было включить его в эту главу, потому что мы завершили квадрат в целом, чтобы получить квадратную формулу. Вы также будете использовать процесс завершения квадрата в других областях алгебры.
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
Решение
ⓐ
Так как уравнение находится в, наиболее подходящим методом является использование свойства квадратного корня.
ⓑ
Мы понимаем, что левая часть уравнения представляет собой трехчлен полного квадрата, и поэтому факторинг будет наиболее подходящим методом.
ⓒ
Приведите уравнение в стандартную форму.
В то время как наша первая мысль может заключаться в том, чтобы попробовать факторинг, размышления обо всех возможностях проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода.
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
коэффициент ⓑ Свойство квадратного корня ⓒ Квадратичная формула
Определите наиболее подходящий метод для решения каждого квадратного уравнения:
ⓐⓑⓒ
ⓐ Квадратичная формула ⓑ факторинг ⓒ Свойство квадратного корня
Практика ведет к совершенству
Решите квадратные уравнения с помощью квадратичной формулы
В следующих упражнениях решите, используя квадратичную формулу.
Использование дискриминанта для прогнозирования числа решений квадратного уравнения
В следующих упражнениях определите количество решений каждого квадратного уравнения.
ⓐ нет реальных решений ⓑ 1
ⓒ 2 ⓓ нет реальных решений
ⓐ 1 ⓑ нет реальных решений
ⓒ 1 ⓓ 2
Определите наиболее подходящий метод для решения квадратного уравнения
В следующих упражнениях определите наиболее подходящий метод (разложение на множители, квадратный корень или квадратная формула) для решения каждого квадратного уравнения. Не решай.
Не решай.
коэффициент ⓑ квадратный корень
ⓒ Квадратичная формула
коэффициент ⓑ квадратный корень
коэффициент
Повседневная математика
Ракета запускается прямо с корабля в море.Решите уравнение для количества секунд, в течение которых ракета будет находиться на высоте 640 футов.
Архитектор проектирует холл гостиницы. Она хочет иметь треугольное окно, выходящее в атриум, с шириной окна на 6 футов больше высоты. Из-за ограничений по энергопотреблению площадь окна должна составлять 140 квадратных футов. Решите уравнение для высоты окна.
Письменные упражнения
Решите уравнение
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
ⓐⓑ
ⓒ ответы будут отличаться
Решите уравнение
ⓐ, заполнив квадрат
ⓑ с помощью квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глоссарий
- дискриминант
- В квадратной формуле величина называется дискриминантом.
Решение уравнений по факторингу
Решение квадратных уравнений с помощью факторинга
Научиться решать уравнения — одна из наших основных целей в алгебре. До сих пор мы решали линейные уравнения степени 1.В этом разделе мы изучим технику, которую можно использовать для решения некоторых уравнений степени 2. Квадратичное уравнение Полиномиальное уравнение с одной переменной степени 2. — это любое уравнение, которое может быть записано в стандартной форме Квадратичное уравнение, записанное в форме ах2 + Ьх + с = 0.
, где a , b и c — действительные числа и a 0. Ниже приведены некоторые примеры квадратных уравнений, все из которых будут решены в этом разделе:
Решение квадратного уравнения в стандартной форме называется корневым решением квадратного уравнения в стандартной форме. . Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Квадратное уравнение x2 + x − 6 = 0 имеет два решения, а именно x = −3 и x = 2.
. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Квадратное уравнение x2 + x − 6 = 0 имеет два решения, а именно x = −3 и x = 2.
Пример 1: Убедитесь, что x = −3 и x = 2 являются решениями x2 + x − 6 = 0.
Решение: Чтобы проверить решения, подставьте значения для x , а затем упростите, чтобы увидеть, является ли результат истинным.
Ответ: Оба значения дают верные утверждения.Следовательно, они оба являются решениями уравнения.
Наша цель — разработать алгебраические методы нахождения решений квадратных уравнений. Первый метод требует свойства нулевого продукта: любой продукт равен нулю тогда и только тогда, когда хотя бы один из факторов равен нулю .:
Другими словами, если какой-либо продукт равен нулю, то один или оба переменных фактора должны быть равны нулю.
Пример 2: Решить: (x − 8) (x + 7) = 0.
Решение: Это уравнение состоит из произведения двух величин, равных нулю; следовательно, применяется свойство нулевого продукта. Одно или оба количества должны быть равны нулю.
Чтобы убедиться, что это решения, подставьте их вместо переменной x .
Обратите внимание, что каждое решение дает коэффициент, равный нулю.
Ответ: Решения 8 и −7.
Квадратное уравнение не может быть дано в его факторизованной форме.
Пример 3: Решить: x2 + 3x − 10 = 0.
Решение: Цель состоит в том, чтобы произвести продукт, равный нулю. Мы можем сделать это, факторируя трехчлен в левой части уравнения.
Затем примените свойство нулевого произведения и установите каждый коэффициент равным нулю.
Это оставляет нам два линейных уравнения, каждое из которых может быть решено относительно x.
Проверьте решения, подставив их в исходное уравнение, чтобы убедиться, что мы получаем истинные утверждения.
Ответ: Решения — 5 и 2.
Использование свойства нулевого произведения после факторизации квадратного уравнения в стандартной форме является ключом к этой технике. Однако квадратное уравнение не может быть дано в стандартной форме, и поэтому перед факторизацией могут быть предприняты некоторые предварительные шаги.Шаги, необходимые для решения путем факторизации Процесс решения уравнения, равного нулю, путем факторизации и последующего установления каждого переменного множителя равным нулю. описаны в следующем примере.
Пример 4: Решить: 2×2 + 10x + 20 = −3x + 5.
Решение:
Шаг 1: Выразите квадратное уравнение в стандартной форме. Для применения свойства нулевого продукта квадратное выражение должно быть равно нулю.Используйте свойства сложения и вычитания равенства, чтобы объединить противоположные стороны, похожие на члены, и получить ноль на одной стороне уравнения.
Для применения свойства нулевого продукта квадратное выражение должно быть равно нулю.Используйте свойства сложения и вычитания равенства, чтобы объединить противоположные стороны, похожие на члены, и получить ноль на одной стороне уравнения.
В этом примере прибавьте 3x и вычтите 5 с обеих сторон.
Шаг 2: Разложите квадратное выражение на множители.
Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным нулю.
Шаг 4: Решите полученные линейные уравнения.
Ответ: Решения: −5 и −3/2. Проверка не обязательна.
Пример 5: Решить: 9×2 + 1 = 6x.
Решение: Запишите это в стандартной форме, вычтя 6x с обеих сторон.
После того, как уравнение имеет стандартную форму, коэффициент равен нулю.
Это трехчлен в виде полного квадрата. Следовательно, установка каждого коэффициента равным нулю приводит к повторному решению.
Повторяющееся решение называется двойным корнем Корень, который повторяется дважды. и не нужно писать дважды.
Ответ: Решение 1/3.
Попробуй! Решите: x2−3x = 28.
Ответ: x = −4 или x = 7
Не все квадратные уравнения в стандартной форме являются трехчленами. Мы часто сталкиваемся с двучленами.
Пример 6: Решить: x2−9 = 0.
Решение: Это квадратное уравнение дается в стандартной форме, где бином в левой части представляет собой разность квадратов. Фактор:
Затем установите каждый коэффициент равным нулю и решите.
Ответ: Решениями являются 3 и −3, которые также можно записать как ± 3.
Пример 7: Решить: 5×2 = 15x.
Решение: При осмотре мы видим, что x = 0 является решением этого квадратного уравнения.Поскольку деление на ноль не определено, мы не хотим делить обе части этого уравнения на x . В общем, мы не хотим делить обе части любого уравнения на переменную или выражение, содержащее переменную. Мы обсудим это более подробно позже. Первый шаг — переписать это уравнение в стандартной форме с нулем на одной стороне.
Затем разложите выражение на множители. Обратите внимание, что бином слева имеет GCF 5x.
Установите каждый коэффициент равным нулю.
Ответ: Решения 0 и 3.
Пример 8: Решите: (2x + 1) (x + 5) = 11.
Решение: Это квадратное уравнение, по-видимому, учитывается; следовательно, может возникнуть соблазн установить каждый коэффициент равным 11. Однако это приведет к неверным результатам. Мы должны переписать уравнение в стандартной форме, равной нулю, чтобы мы могли применить свойство нулевого произведения.
Однако это приведет к неверным результатам. Мы должны переписать уравнение в стандартной форме, равной нулю, чтобы мы могли применить свойство нулевого произведения.
Когда он будет в стандартной форме, мы можем разложить на множители, а затем установить каждый множитель равным нулю.
Ответ: Решения: 1/2 и −6.
Пример 9: Решить: 15×2−25x + 10 = 0.
Решение: Начнем с факторинга GCF 5. Затем разложим полученный трехчлен на множители.
Затем мы устанавливаем каждый переменный коэффициент равным нулю и решаем для x .
Обратите внимание, что коэффициент 5 не является переменным фактором и, следовательно, не вносит вклад в набор решений.
Ответ: Решения 2/3 и 1.
Пример 10: Фактор: 52×2 + 76x − 13 = 0.
Решение: Очистите дроби, умножив обе части уравнения на ЖК-дисплей, который равен 6.
На данный момент у нас есть эквивалентное уравнение с целочисленными коэффициентами, которое, как обычно, можно разложить на множители. Начнем с множителей 15 и 2.
Коэффициент при среднем члене равен 7 = 3 (−1) +5 (2).Фактор:
Установите каждый коэффициент равным нулю и решите.
Ответ: Решения — 2/3 и 1/5.
Попробуй! Решить: 4×2−9 = 0.
Ответ: −3/2 и 3/2
Поиск уравнений с заданными решениями
Состояние нулевого продукта,
Верно и обратное:
В этом случае мы можем написать следующее:
Мы используем это свойство, чтобы находить уравнения по решениям.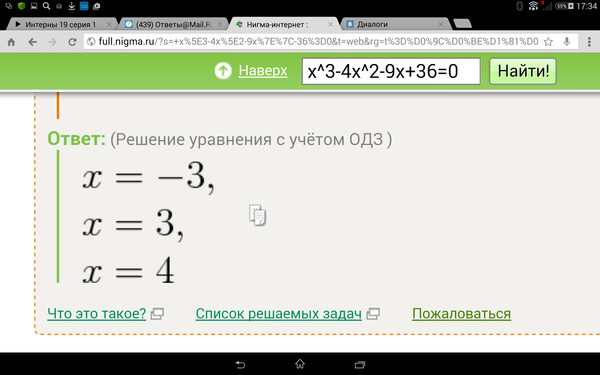 Для этого шаги решения путем факторинга выполняются в обратном порядке.
Для этого шаги решения путем факторинга выполняются в обратном порядке.
Пример 11: Найдите квадратное уравнение с решениями −7 и 2.
Решение: Имея решения, мы можем определить два линейных фактора.
Произведение этих линейных множителей равно нулю, когда x = −7 или x = 2:
Умножьте биномы и представьте уравнение в стандартной форме.
Ответ: x2 + 5x − 14 = 0. Мы можем проверить наше уравнение, подставив данные ответы, чтобы увидеть, получим ли мы истинное утверждение. Кроме того, приведенное выше уравнение не является уникальным, поэтому проверка становится важной, когда наше уравнение отличается от чужого. Это оставлено как упражнение.
Пример 12: Найдите квадратное уравнение с целыми коэффициентами, учитывая решения 1/2 и −3/4.
Решение: Чтобы избежать дробных коэффициентов, мы сначала очищаем дроби, умножая обе части на знаменатель.
Примените свойство нулевого произведения и умножьте.
Ответ: 8×2 + 2x − 3 = 0
Попробуй! Найдите квадратное уравнение с целыми коэффициентами при решениях −1 и 2/3.
Ответ: 3×2 + x − 2 = 0
Решение полиномиальных уравнений с помощью факторинга
Свойство нулевого произведения верно для любого числа факторов, составляющих уравнение.Если выражение равно нулю и может быть разложено на линейные коэффициенты, тогда мы сможем установить каждый коэффициент равным нулю и решить для каждого уравнения.
Пример 13: Решить: 3x (x − 5) (3x − 2) = 0.
Решение: Установите каждый переменный коэффициент равным нулю и решите.
Ответ: Решения: 0, 5 и 2/3.
Конечно, нельзя ожидать, что уравнение будет дано в факторизованной форме.
Пример 14: Решите: x3 + 2×2−9x − 18 = 0.
Решение: Начните с полного факторизации левой стороны.
Установите каждый коэффициент равным нулю и решите.
Ответ: Решения: −2, −3 и 3.
Обратите внимание, что степень многочлена равна 3, и мы получили три решения. В общем, для любого полиномиального уравнения с одной переменной степени n основная теорема алгебры гарантирует, что будет столько же (или меньше) действительных решений многочлена с одной переменной, сколько его степени.гарантирует n реальных решений или меньше. Мы видели, что многие многочлены не множатся. Это не означает, что уравнения, включающие эти неактивируемые многочлены, не имеют реальных решений. Фактически, многие полиномиальные уравнения, не учитывающие множители, действительно имеют реальные решения. Мы узнаем, как решать эти типы уравнений, продолжая изучать алгебру.
Мы узнаем, как решать эти типы уравнений, продолжая изучать алгебру.
Попробуй! Решите: −10×3−18×2 + 4x = 0.
Ответ: −2, 0, 1/5
Основные выводы
- Многочлен может иметь самое большее количество решений, равных его степени.Следовательно, квадратные уравнения могут иметь до двух вещественных решений.
- Чтобы решить квадратное уравнение, сначала запишите его в стандартной форме. Как только квадратное выражение станет равным нулю, разложите его на множители, а затем установите каждый переменный множитель равным нулю. Решения полученных линейных уравнений являются решениями квадратного уравнения.
- Не все квадратные уравнения можно решить с помощью факторизации. Мы узнаем, как решать квадратные уравнения, которые не учитываются позже в ходе курса.
- Чтобы найти квадратное уравнение с заданными решениями, выполните процесс решения путем факторизации в обратном порядке.

- Если какой-либо многочлен разложен на линейные множители и установлен на ноль, то мы можем определить решения, установив каждый переменный множитель равным нулю и решив каждый отдельно.
Тематические упражнения
Часть A: Решения квадратных уравнений
Определите, является ли данный набор значений решениями квадратного уравнения.
1. {−3, 5}; x2−2x − 15 = 0
2. {7, −1}; x2−6x − 7 = 0
3. {−1/2, 1/2}; х2−14 = 0
4. {−3/4, 3/4}; х2−916 = 0
5. {−3, 2}; х2-х-6 = 0
6. {−5, 1}; x2−4x − 5 = 0
Решить.
7. (x − 3) (x + 2) = 0
8. (x + 5) (x + 1) = 0
9. (2x − 1) (x − 4) = 0
10.(3x + 1) (3x − 1) = 0
11. (x − 2) 2 = 0
12. (5x + 3) 2 = 0
13. 7x (x − 5) = 0
14. −2x (2x − 3) = 0
15. (x − 12) (x + 34) = 0
16. (x + 58) (x − 38) = 0
17. (14x + 12) (16x − 23) = 0
18. (15x − 3) 2 = 0
19. −5 (x + 1) (x − 2) = 0
20. 12 (x − 7) (x − 6) = 0
21. (x + 5) (x − 1) = 0
22.(х + 5) (х + 1) = 0
23. −2 (3x − 2) (2x + 5) = 0
24. 5 (7x − 8) 2 = 0
Часть B: Решить факторингом
Решить.
25. x2 − x − 6 = 0
26. x2 + 3x − 10 = 0
27. y2−10y + 24 = 0
28. y2 + 6y − 27 = 0
29. x2−14x + 40 = 0
30. x2 + 14x + 49 = 0
31. x2−10x + 25 = 0
32.3×2 + 2x − 1 = 0
33. 5×2−9x − 2 = 0
34. 7y2 + 20y − 3 = 0
35. 9×2−42x + 49 = 0
36. 25×2 + 30x + 9 = 0
37. 2y2 + y − 3 = 0
38. 7×2−11x − 6 = 0
39. 2×2 = −15x + 8
40. 8x − 5 = 3×2
41. x2−36 = 0
42. x2−100 = 0
43. 4×2-81 = 0
44. 49×2−4 = 0
45.х2 = 4
46. 9y2 = 1
47. 16y2 = 25
48. 36×2 = 25
49. 4×2−36 = 0
50. 2×2−18 = 0
51. 10×2 + 20x = 0
52. −3×2 + 6x = 0
53. 25×2 = 50x
54. x2 = 0
55. (x + 1) 2−25 = 0
56. (x − 2) 2−36 = 0
57. 5x (x − 4) = — 4 + x
58.(x − 1) (x − 10) = 22
59. (x − 3) (x − 5) = 24
60. −2x (x − 9) = x + 21
61. (x + 1) (6x + 1) = 2x
62. (x − 2) (x + 12) = 15x
63. (х + 1) (х + 2) = 2 (х + 16)
64. (x − 9) (2x + 3) = 2 (x − 9)
Очистите дроби, сначала умножив обе части на ЖК-дисплей, а затем решив.
65. 115×2 + 13x + 25 = 0
66. 114×2−12x + 37 = 0
67.32×2−23 = 0
68. 52×2−110 = 0
69. 314×2−212 = 0
70. 13×2−15x = 0
71. 132×2−12x + 2 = 0
72. 13×2 + 56x − 12 = 0
73. Стороны квадрата имеют размер x + 3 единицы. Если площадь составляет 25 квадратных единиц, найдите x .
74. Высота треугольника на 2 единицы больше его основания. Если площадь 40 квадратных единиц, то найдите длину основания.
75. Стороны прямоугольного треугольника имеют меры, являющиеся последовательными целыми числами. Найдите длину гипотенузы. (Подсказка: гипотенуза — самая длинная сторона. Примените теорему Пифагора.)
76. Прибыль в долларах от производства и продажи нестандартных ламп размером x определяется функцией P (x) = — 10×2 + 800x − 12000. Сколько ламп нужно продать и произвести, чтобы они окупились? (Подсказка: мы выходим на уровень безубыточности, когда прибыль равна нулю.)
Предполагая сухие дорожные условия и среднее время реакции, безопасный тормозной путь, d футов среднего автомобиля, определяется по формуле d = 120v2 + v , где v представляет собой скорость движения автомобиля. машина в милях в час.Для каждой приведенной ниже проблемы, учитывая тормозной путь, определите безопасную скорость.
77. 15 футов
78. 40 футов
79. 75 футов
80. 120 футов
Часть C: Нахождение уравнений с заданными решениями
Найдите квадратное уравнение с целыми коэффициентами, имея следующие решения.
81. −3, 1
82.−5, 3
83. −10, −3
84. −7, −4
85. −1, 0
86,0, 3/5
87. −2, 2
88. −1/2, 1/2
89. −4, 1/3
90. 2/3, 2/5
91. −1/5, −2/3
92. −3/2, 3/4
93,3, двойной корень
94. −5, двойной корень
Часть D. Решение полиномиальных уравнений
Решить.
95. 7x (x + 5) (x − 9) = 0
96. (x − 1) (x − 2) (x − 3) = 0
97. −2x (x − 10) (x − 1) = 0
98. 8x (x − 4) 2 = 0
99. 4 (x + 3) (x − 2) (x + 1) = 0
100. −2 (3x + 1) (3x − 1) (x − 1) (x + 1) = 0
101. x3 − x2−2x = 0
102. 2×3 + 5×2−3x = 0
103. 5×3−15×2 + 10x = 0
104. −2×3 + 2×2 + 12x = 0
105.3×3−27x = 0
106. −2×3 + 8x = 0
107. x3 + x2 − x − 1 = 0
108. x3 + 2×2−16x − 32 = 0
109. 8×3−4×2−18x + 9 = 0
110. 12×3 = 27x
Часть E: Темы дискуссионной доски
111. Объясните, почему 2 (x + 5) (x − 5) = 0 имеет два решения, а 2x (x + 5) (x − 5) = 0 имеет три решения.
112. Составьте собственное квадратное уравнение и разместите его вместе с решениями на доске обсуждений.
113. Объясните своими словами, как решить квадратное уравнение в стандартной форме.
ответов
1: Есть
3: Есть
5: №
7: −2, 3
9: 1/2, 4
11: 2
13: 0, 5
15: −3/4, 1/2
17: -2, 4
19: -1, 2
21: −5, 1
23: −5/2, 2/3
25: −2, 3
27: 4, 6
29: 4, 10
31: 5
33: -1/5, 2
35: 7/3
37: −3/2, 1
39: −8, ½
41: −6, 6
43: −9/2, 9/2
45: -2, 2
47: −5/4, 5/4
49: −3, 3
51: −2, 0
53: 0, 2
55: −6, 4
57: 1/5, 4
59: -1, 9
61: -1/2, -1/3
63: −6, 5
65: −3, −2
67: −2/3, 2/3
69: ± 7
71: 8
73: 2 шт.
75: 5 шт.
77: 10 миль в час
79:30 миль в час
81: x2 + 2x − 3 = 0
83: x2 + 13x + 30 = 0
85: х2 + х = 0
87: x2−4 = 0
89: 3×2 + 11x − 4 = 0
91: 15×2 + 13x + 2 = 0
93: x2−6x + 9 = 0
95: −5, 0, 9
97: 0, 1, 10
99: −3, −1, 2
101: -1, 0, 2
103: 0, 1, 2
105: −3, 0, 3
107: -1, 1
109: −3/2, 1/2, 3/2
6.{2} = 9 \).
Член с квадратным фактором изолирован, поэтому мы начинаем с применения свойства квадратного корня.
На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.
Решения: \ (- 2 \) и \ (- 8 \).
В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, которые не учитывают множители. {2} + b x + c = 0 \)
как уравнение вида
Этот процесс называется , завершение квадрата 4 .{2} = \ color {Cerulean} {1} \)
Чтобы завершить квадрат, добавьте \ (1 \) к обеим сторонам, завершите квадрат и затем решите, извлекая корни.
На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.
Ответ :
Решения: \ (- 8 \) и \ (6 \).
Примечание
В предыдущем примере решения — целые числа. Если это так, то будет учитываться исходное уравнение.
Если уравнение множится, мы можем решить его путем факторизации.{2} — 10 х + 26 = 0 \).
Решение
Начните с вычитания \ (26 \) из обеих частей уравнения.
Здесь \ (b = -10 \), и мы определяем значение, завершающее квадрат, следующим образом:
Чтобы получить квадрат, добавьте \ (25 \) к обеим сторонам уравнения. {2} + 18 \), где \ (t \) представляет время через секунды после падения объекта.{2} + 50 \), где \ (t \) представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю? (Округлите до ближайшей сотой доли секунды.)
- Ответ
1. \ (\ pm 9 \)
3. \ (\ pm \ frac {1} {3} \)
5. \ (\ pm 2 \ sqrt {3} \)
7. \ (\ pm \ frac {3} {4} \)
9. \ (\ pm \ frac {\ sqrt {2}} {2} \)
11. \ (\ pm 2 \ sqrt {10} \)
13. \ (\ pm i \)
15. \ (\ pm \ frac {\ sqrt {5}} {5} \)
17. \ (\ pm \ frac {\ sqrt {2}} {4} i \)
19.\ (\ pm 2 i \)
21. \ (\ pm \ frac {2} {3} \)
23. \ (\ pm 2 \ sqrt {2} \)
25. \ (\ pm 2 i \ sqrt {2} \)
27. \ (\ pm \ frac {\ sqrt {10}} {5} \)
29. \ (- 9, -5 \)
31. \ (5 \ pm 2 \ sqrt {5} \)
33. \ (- \ frac {2} {3} \ pm \ frac {\ sqrt {6}} {3} i \)
35. \ (\ frac {- 2 \ pm 3 \ sqrt {3}} {6} \)
37. \ (\ frac {1} {3} \ pm \ frac {\ sqrt {6}} {6} i \)
39.{2} = 3 (3 т + 1) \)
- \ ((3 t + 2) (t-4) — (t-8) = 1-10 t \)
- Ответ
1. \ (- 15 \ pm \ sqrt {10} \)
3. 1 \ (\ pm 2 \ sqrt {2} \)
5. 1 \ (\ pm i \ sqrt {3} \)
7. \ (- 15,5 \)
9. \ (- \ frac {1} {3}, 1 \)
11. \ (\ frac {-1 \ pm \ sqrt {5}} {2} \)
13. \ (\ frac {-3 \ pm \ sqrt {17}} {2} \)
15. \ (- \ frac {3} {2} \ pm \ frac {\ sqrt {11}} {2} i \)
17.\ (\ frac {7 \ pm 3 \ sqrt {3}} {2} \)
19. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)
21. \ (\ frac {2 \ pm \ sqrt {5}} {2} \)
23. \ (\ frac {-3 \ pm \ sqrt {6}} {3} \)
25. \ (\ frac {-1 \ pm \ sqrt {10}} {3} \)
27. \ (\ frac {3 \ pm 2 \ sqrt {6}} {2} \)
29. 1 \ (\ pm 2 i \)
31. \ (\ frac {1 \ pm \ sqrt {17}} {4} \)
33. \ (\ frac {-1 \ pm \ sqrt {7}} {3} \)
35. 2 \ (\ pm 2 \ sqrt {5} \)
37.{2} -6 (6 x + 1) = 0 \)
- Ответ
1. \ (0.19,1.31 \)
3. \ (- 0,45,1,12 \)
5. \ (0,33,0,67 \)
Упражнение \ (\ PageIndex {11} \)
- Создайте собственное уравнение, которое можно решить, извлекая корни. Поделитесь им и решением на доске обсуждений.
- Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.2} с одной стороны уравнения, сохраняя константы с противоположной стороны. После этого следующий очевидный шаг — извлечь квадратные корни из обеих сторон и найти значение x. Всегда добавляйте символ \ pm, когда вы получаете квадратный корень из константы.
Умножение биномов с помощью метода FOIL: Мнимые числа: Решение квадратных уравнений с использованием квадратичной формулы: Решение квадратных уравнений: Алгебра: Порядок операций: Деление комплексных чисел: Полиномы: Внешний вид полиномиального уравнения: Стандартная форма прямой: Положительная Интегральные делители: деление дробей
Решение линейных уравнений методом перекрестного умножения.Решение одношаговых уравнений. Решение квадратных уравнений путем факторизации. Решение квадратных уравнений по формуле корней квадратного уравнения. Решение квадратных уравнений, заполнив квадрат. Природа корней квадратного уравнения. Сумма и произведение корней квадратного уравнения Алгебраический …
Умножение биномов с помощью метода FOIL: мнимые числа: решение квадратных уравнений с использованием квадратичной формулы: решение квадратных уравнений: алгебра: порядок операций: деление комплексных чисел: многочлены: Внешний вид полиномиального уравнения: стандартная форма линии: положительные интегральные делители: деление дробей
Решение квадратных уравнений — метод 3 — заполнение квадрата Этот метод решения квадратных уравнений прост, но требует определенной последовательности шагов.Вот процедура: Пример: Решите 3×2 + 4x — 7 = 0, заполнив квадрат 1. Изолируйте x2 и x-члены на одной стороне =, применяя свойство сложения равенства.
Квадратное уравнение — это уравнение, которое может быть записано как ax 2 + bx + c = 0, когда 0. Существует три основных метода решения квадратных уравнений: факторизация, использование формулы квадратичного преобразования и завершение квадрата.
Создатель листов квадратного уравнения сгенерирует распечатываемый рабочий лист задач и ключ ответа.Выберите свои параметры в форме ниже и нажмите кнопку «Создать рабочий лист». Мы откроем новое окно, содержащее ваш рабочий лист пользовательских квадратных уравнений. Если вам понравился рабочий лист, вы можете распечатать его прямо из браузера.
Подсказка кроется в решениях уравнения x 2 — 2x — 15 = 0 (называемого квадратным уравнением). Если мы разложим квадрат на множители, уравнение можно записать как (x — 5) (x + 3) = 0. Но произведение двух множителей может быть равно нулю только в том случае, если один или другой множитель равен нулю.


 При этом возникли дробные коэффициенты.
При этом возникли дробные коэффициенты.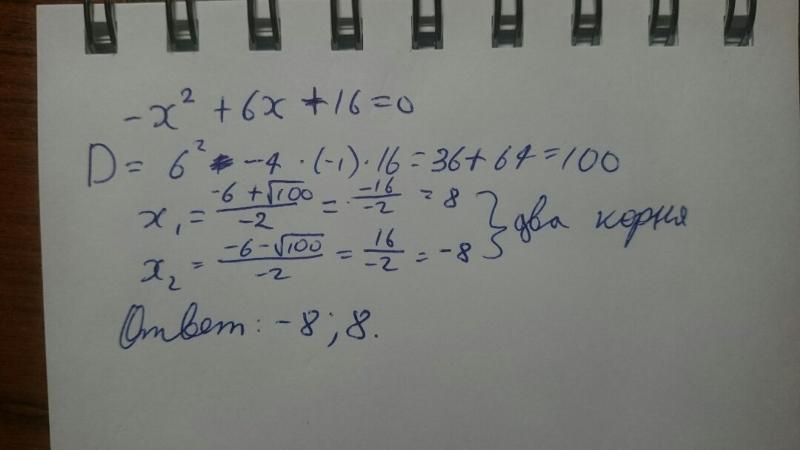
 Но мы это сейчас исправим, разделив обе стороны уравнения на коэффициент a = 3. Получим: x2 + 11x + 10 = 0.
Но мы это сейчас исправим, разделив обе стороны уравнения на коэффициент a = 3. Получим: x2 + 11x + 10 = 0. е. коэффициент при x2 равен 1;
е. коэффициент при x2 равен 1;
 Вариант 6 (без производной)
Вариант 6 (без производной)