Розв язання системи рівнянь: Методи розв’язання систем рівнянь — урок. Алгебра, 11 клас.

Системи рівнянь. Метод підстановки та додавання

Сьогодні розберемо готові приклади на системи рівнянь (СР), які Ви мали би вміти розв’язувати при проходженні ЗНО тестів для вступу у ВУЗи. Всього таких прикладів понад 40, всіх помістити в одну статтю не вийде, тому далі розберемо прості завдвння. Складніші системи рівнянь з логарифмами, показниковими функціями та модулями будуть розписані в наступних публікаціях.

Приклад 20.1 Розв’язати систему рівнянь {x+3y=14;2y-x=6}
і знайти добуток компонентів розв’язку.

Обчислення: Розв’яжемо систему рівнянь методом додавання:
поміняємо порядок доданків другого р-ня, а далі

додамо почленно обидва рівняння, отримаємо
(x-x)+(3y+2y)=14+6,
5y=20,
y=20:5=4
У перше рівняння системи підставимо значення y=4 і знайдемо «ікс» x:
x+3•4=14,
x+12=14,
x=14-12=2.
Отже, (2;4) — розв’язок системи рівнянь.
Тоді 2•4=8 — добуток компонентів розв’язку.
Відповідь: 8 – В.

Складні системи рівнянь часто вирішують числовим або графічним методом. Для прикладу, система рівнянь {x+3y=14;2y-x=6} задає дві прямі на декартовій площині, щоб їх побудувати виразимо з системи «ігрик» як функцію від «ікс» {y=14/3-x/3, y=x/2+3} та побудуємо графіки прямих в Мейпл
Точка перетину прямих за фізичним змістом і є шуканим розв’язком розглянутої системи рівнянь.

 

Приклад 20.2 Дано систему 2 рівнянь {x+y=3; 2x-3y=-4}. Яке утвориться рівняння, якщо з першого рівняння виразити змінну y через x, і отриманий вираз підставити у друге рівняння замість y?

Обчислення: Розв’яжемо систему 

методом підстановки:

підставимо перше рівняння у друге, отримаємо
2x-3•(3-x)=-4,
2x-9+3x=-4,
звідси
5x-9=-4.
Це і є відповідь до ЗНО тесту, додатково можемо знайти
x=1 і y=2 – розв’язок системи рівнянь.
Відповідь: 5x-9=-4 – Д.

 

Приклад 20.3 Знайти суму компонентів x₀+y₀+z₀ розв’язку системи трьох лінійних рівнянь
{x+y=-2, y+z=-11, x+z=1}

Обчислення: Обчислимо систему 3 рівнянь методом підстановки:

підставимо перше і третє рівняння у друге кінцевої системи, отримаємо

Звідси, (5;-7;-4) розв’язок заданої системи рівнянь.
Тоді x₀+y₀+z₀=5+(-7)+(-4)=-6.
Відповідь: -6 – А.

 

Приклад 20.4 Розв’язати систему рівнянь
{3x+4y=-20, 5x+2y=-10}

Обчислення: Обчислимомо систему рівнянь методом додавання, для цього помножимо друге рівняння системи на -2:

додамо почленно обидва рівняння, отримаємо
(3x-10x)+(4y-4y)=-20+20,
-7x=0,
x=0.
У перше рівняння системи підставимо значення x=0 і знайдемо y:
3•0+4y=-20,
4y=-20,
y=-20:4=-5.
Точка (0;-5) — розв’язок СР.
Відповідь: (0;-5) – Б.

 

Приклад 20.5 Знайти середнє арифметичне для значень чисел x та y, які є розв’язками системи рівнянь {3x+2y=7; -x+3y=16}.

А	Б	В	Г	Д
3	2	1	4	3,5

Обчислення: Розв’яжемо систему рівнянь

методом додавання, для цього помножимо друге рівняння  на 3:

додамо почленно обидва рівняння, отримаємо
(3x-3x)+(2y+9y)=7+48,
11y=55,
y=55:11=5.
У перше рівняння системи підставимо значення y=5 і знайдемо x:
3x+10=7,
3x=-3,
x=-1.
В підсумку, (-1;5) — розв’язок заданої системи рівнянь.
Тоді (x+y)/2=(-1+5)/2=2 – середнє арифметичне для значень чисел x та y.
Відповідь: 2 – Б.

Від систем лінійних рівнянь переходимо до тих, що містять обернені функції, корені, квадратичні та показникові функції.

Приклад 20.6 Знайти компонент x0 розв’язку (x0;y0) системи рівнянь

А	Б	В	Г	Д
3	1/3	147	91	1 I 6/7

Обчислення: Оскільки невідомі містяться в знаменниках дробів, то виписуємо обмеження на область допустимих значень (ОДЗ): {x≠0;y≠0}.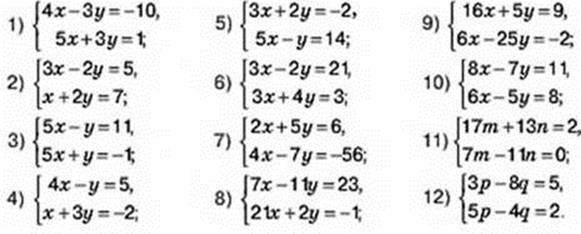
Розв’яжемо систему рівнянь методом додавання, для цього помножимо перше рівняння на 3 і додамо почленно до другого рівняння:

(1/3;-1/2) — розв’язок СР, в умові потрібно знайти x0.
Відповідь: 1/3 – Б.

 

Приклад 20.7 Скільки розв’язків має система рівнянь
?

А	Б	В	Г	Д
Один	два	три	чотири	жодного

Обчислення: Розпишемо систему рівнянь методом додавання, для цього помножимо перше рівняння на 2 і додамо почленно до другого рівняння:

Число під квадратом може приймати як додатне так і від’ємне значення, пам’ятайте про це, тому комбінації правильних розв’язків наступні

Всього чотири розв’язки (1;2), (-1;2), (1;-2) і (-1;-2) — заданої СР. (x-y)=0,25} і вказати компонент x₀ її розв’язку (x₀;y₀).

А	Б	В	Г	Д
0	-1	1	2	-2

Обчислення: Зведемо систему показникових рівнянь до однієї основи в р-нях

При однакових основах прирівнюємо степені та переходимо до обчислення системи 2 лінійних рівнянь методом додавання.

(1;2) — розв’язок СР, звідси x₀=1 – перший компонент розв’язку.
Відповідь: 1 – В.

 

Приклад 20.21 Скільки розв’язків має система рівнянь {xy=6; yz=8; zx=12}
?

А	Б	В	Г	Д
Один	два	три	чотири	жодного

Обчислення: Задано систему трьох рівнянь з трьома невідомими, для її розкриття виразимо «ікс» та «зет» з перших двох рівнянь, та підставимо в третє.

Підстановкою «ігриків» знаходимо (3;2;4) і (-3;-2;-4) — два розв’язки системи рівнянь.
Відповідь: два – Б.

Приклад 20.26 Установити відповідність між системами рівнянь (1–4) та рівняннями (А–Д), які утворюються з цих систем при їх розв’язуванні способом підстановки.

Системи рівнянь із ЗНО підготовки розв’яжемо методом підстановки. Детальні пояснення самостійно проаналізуйте з таблиці

 

Приклад 20.27 Установити відповідність між системами рівнянь (1–4) та першими компонентами x₀ розв’язків (x₀;y₀) цих систем (А–Д).
Дане завдання містить системи обернених, степеневих, кореневих та логарифмічних функцій. Для розв’язування систем рівнянь використовуємо властивості вказаних функцій.

 

Приклад 20.40 Розв’язати систему рівнянь

У відповідь записати найбільшу суму x0+y0+z0, де (x0;y0;z0) — розв’язок системи.
Обчислення: Маємо систему трьох рівнянь з трьома невідомими, з перших двох рівнянь виражаємо x, z та підставляємо у третє

Отримаємо два розв’язки СР
(2;0,5;4) і (-2;-0,5;-4).
Обчислимо найбільше значення x0+y0+z0:
x₀+y₀+z₀=2+0,5+4=6,5.
Відповідь: 6,5.

Решта із 44 готових прикладів на системи рівнянь чекає вашої уваги в наступних уроках. Пояснення, що ми підготували, дозволять Вам вивчити самостійно усі можливі технічні прийоми, що потрібні для розв’язування найважчих систем рівнянь.

Що таке система рівнянь? | House of Math

Енциклопедія>Алгебра>Рівняння та нерівності>Рівняння>Системи рівнянь>Що таке система рівнянь?

Система рiвнянь — це, просто кажучи, множина рiвнянь. Дотепер ми працювали з одним рiвнянням з однiєю змiнною (одним невiдомим). Тепер навчимося розв’язувати два рiвняння з двома змiнними (двома невiдомими).

Загалом системи рiвнянь можуть мати скiльки завгодно невiдомих, але для того, щоб отримати однозначну вiдповiдь, нам потрiбно мати стiльки рiвнянь, скiльки маємо невiдомих. У математицi iснує цiла галузь — лiнiйна алгебра, яка вивчає системи рiвнянь.

То навiщо потрiбнi системи рiвнянь? Вiдповiдь проста: часто кiлька об’єктiв залежать один вiд одного, i тодi потрiбен iнструмент, який це враховуватиме. Прикладом може бути одночасне придбання дитячих i дорослих квиткiв. Ми знаємо загальну вартiсть квиткiв i скiльки квиткiв придбали, але скiльки фактично коштують два рiзних типи квиткiв?

Ти познайомишся з трьома методами розв’язування систем рiвнянь: розв’язування за допомогою графiка, метод пiдстановки i метод виключення. Усi цi методи мають однакову мету: розв’язати два рiвняння з двома змiнними. Насправдi не має значення, який метод використовувати для розв’язування задач, проте очiкується, що ти знатимеш усi три. Найпростiший метод — це розв’язування за допомогою графiка, тому з нього й почнемо. Але перш нiж знайомитися з рiзними методами, потрiбно з’ясувати декiлька питань.

Правило

Важливi аспекти двох рiвнянь iз двома змiнними

1.

Розв’язки лiнiйних систем рiвнянь складаються з двох значень: значення x i значення y.

2.

Цi два значення — це перша та друга координати перетину двох графiкiв, побудованих за двома рiвняннями.

3.

Заданi рiвняння можна переписати у виглядi функцiй, якi можна зобразити у формi графiкiв у системi координат.

4.

Хоч який метод застосовується — метод пiдстановки чи метод виключення — у розв’язку буде два значення. Цi два значення завжди розглядаються як координати перетину двох графiкiв.

No related posts.