Онлайн калькулятор: Дискретное преобразование Фурье онлайн
Этот калькулятор позволяет поиграться с дискретным преобразованием Фурье произвольного сигнала, заданного набором значений. Калькулятор ограничивается вещественным дискретным преобразованием Фурье, то есть дискретным преобразованием Фурье, которое использует вещественные числа для представления входного и выходного сигналов. Дискретное преобразование Фурье является одним из преобразований Фурье, то есть операций, раскладывающих исходную функцию на элементарные составляющие — гармонические колебания с разными частотами. Данный калькулятор позволяет удовлетворить любопытство в части того, как же для заданного сигнала выглядит набор представляющих его гармоник и как выглядит восстановленный с их помощью сигнал.
По умолчанию дискретный сигнал, который раскладывается на гармоники и затем восстанавливается из них состоит из 32 отсчетов, все из которых имеют значение ноль, за исключением второго, который имеет значение 5.
Для заданного сигнала калькулятор показывает графики его действительных и мнимых значений, а также графики магнитуды и фазы. Также калькулятор отображает все гармоники и их суммарный сигнал.
Теперь немного теории. Применение преобразований Фурье основано на идее о том, что сигнал может быть представлен в виде суммы гармонических составляющих с разными частотами. Есть несколько типов преобразований Фурье: для непериодического непрерывного сигнала (собственно, преобразование Фурье), для периодического непрерывного сигнала (ряд Фурье), для непериодического дискретного сигнала (дискретное во времени преобразование Фурье), для периодического дискретного сигнала (дискретное преобразование Фурье). Все эти преобразования работают с сигналами продолженными в бесконечность. В области цифровой обработки сигналов мы имеем дело с конечным набором значений. Поэтому при использовании преобразований Фурье мы подразумеваем, что наше конечное число значений повторяется до бесконечности как справа, так и слева от заданных значений. Таким образом как бы имеем дело с периодическим дискретным сигналом — и используем для его разложения дискретное преобразование Фурье. Зачем нужно повторять сигнал, а не представить, например, что все остальные значения равны нулю? Потому что в таком случае мы будем иметь дело с непериодическим дискретным сигналом, и для его представления нам понадобится бесконечное число гармоник.
Таким образом как бы имеем дело с периодическим дискретным сигналом — и используем для его разложения дискретное преобразование Фурье. Зачем нужно повторять сигнал, а не представить, например, что все остальные значения равны нулю? Потому что в таком случае мы будем иметь дело с непериодическим дискретным сигналом, и для его представления нам понадобится бесконечное число гармоник.
Стоит заметить, что каждое из преобразований Фурье есть в двух видах: вещественном и комплексном. Преобразование, работающее с вещественными числами, проще, так как использует, соответственно, вещественные числа для входных и выходных величин. Его и использует калькулятор ниже.
Дискретное преобразование Фурье превращает N отсчетов входного сигнала в два набора из N/2+1 отсчетов выходного сигнала — которые являются амплитудами синусоидальных и косинусоидальных волн. Например, для того, чтобы представить 32 отсчета, нам нужно 17 синусоидальных волн и 17 синусоидальных волн.
При этом если входной сигнал является функцией времени (временным рядом), то преобразование Фурье превращает его в функцию частоты (частотный спектр), то есть разлагает функцию на гармонические составляющие на различных частотах.
Процесс отображения сигнала в частотный спектр называется декомпозицией сигнала, анализом сигнала, прямым дискретным преобразованием Фурье или просто дискретным преобразованием Фурье. Обратный процесс называется синтезом или обратным дискретным преобразованием Фурье.
Введем обозначения:
Входной сигнал — функцию времени — обозначаем буквой x в нижнем регистре, т.е. x[ ], функцию частоты — буквой X в верхнем регистре, т.е. X[ ]. Две части выходного сигнала, вещественную и мнимую, соответственно, Re X[ ] и Im X[ ]. Значения Re X[ ] это амплитуды косинусоидальных волн, а значения Im X[ ] — амплитуды синусоидальных волн. Несмотря на то, что в названии есть слово «мнимая», это просто амплитуда синусоидальной волны, а термин пришел из обобщенного преобразования, которое работает с комплексными числами.
Синусоидальные и косинусоидальные волны с единичной амплитудой называются базисными функциями дискретного преобразования Фурье. Они имеют следующие уравнения:
,
где i меняется от 0 до N-1, k меняется от 0 до N/2.
Каждое значение амплитуды Re X и Im X может быть перемножено с соответствующей базисной функцией и результат может быть просуммирован для того, чтобы восстановить входной сигнал.
Это уравнение синтеза, которое выглядит следующим образом:
Таким образом, значение любого отсчета входного сигнала из N точек может быть восстановлено путем сложения N/2+1 значений косинуcoидальных составляющих и N/2+1 значений синусоидальных составляющих в данной точке.
Обратите внимание на черту над X в формуле выше. Это нормализованное значение амплитуды, которое должно применяться при синтезе. Масштабирование частотного спектра выполняется следующим образом:
,
с двумя специальными случаями:
Далее, вещественные и мнимые части могут быть представлены в полярных координатах, используя следующее соотношение:
M и тета называются магнитудой and фазой и могут быть получены из Re и Im с использованием следующих формул:
Таким образом, в полярной нотации результат дискретного преобразования Фурье сигнала из N отсчетов можно представить в виде N/2+1 косинусоидальных волн с указанной амплитудой и фазой. Иногда графики магнитуды и фазы более выразительны, чем графики вещественной и мнимой составляющей.
Иногда графики магнитуды и фазы более выразительны, чем графики вещественной и мнимой составляющей.
Как же найти вещественные и мнимые составляющие сигнала? Если мы посмотрим на уравнение синтеза
то мы увидим, что Im X[0] и Im X[N/2] всегда равны нулю. Таким образом для N точек мы имеет N уравнений с N неизвестными. Причем это линейные уравнения — мы просто имеем систему линейных алгебраических уравнений с N неизвестными. Ее, в принципе, можно решать, например, методом Гаусса, но, конечно, для больших N это очень медленно. Поэтому для нахождения значений Re и Im используется быстрое преобразование Фурье.
Однако, быстрое преобразование Фурье работает для более общего, комплексного дискретного преобразования Фурье (когда N комплексных точек входного сигнала преобразуются в N комплексных точек выходного сигнала), поэтому нам надо учесть это каким-то образом при использовании его для вещественного дискретного преобразования Фурье.
К счастью, это довольно просто. N вещественных точек входного сигнала преобразуются в N комплексных точек, где мнимая часть равна нулю. Далее применяется быстрое преобразование Фурье, а результат получается из первых N/2+1 точек вещественной части и первых N/2+1 точек мнимой части результата.
N вещественных точек входного сигнала преобразуются в N комплексных точек, где мнимая часть равна нулю. Далее применяется быстрое преобразование Фурье, а результат получается из первых N/2+1 точек вещественной части и первых N/2+1 точек мнимой части результата.
Калькулятор ниже позволяет «поиграться» с дискретным преобразованием Фурье. Вы можете задать входной сигнал, калькулятор применит к нему дискретное преобразование Фурье (используя javascript реализацию быстрого преобразования Фурье от Project Nayuki) и отобразит графики Re X[ ], Im X[ ], Mag X[ ], Phase X[ ], а также графики синтезированного оригинального сигнала — суммированием синусоидальных и косинусоидальных волн, и суммированием косинусоидальных волн соответствующих магнитудам и фазам.
Дискретное преобразование Фурье
Набор значений сигнала
| Порядковый номер | Числовое значение | ||
|---|---|---|---|
51020501001000
Набор значений сигнала
Порядковый номер
Числовое значение
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: 50;-50. 5
5
Загрузить данные из csv файла
Точность вычисления
Знаков после запятой: 2
Набор значений сигнала
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Re X[ ]
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Im X[ ]
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Магнитуда X[ ]
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Фаза X[ ]
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Синтез (cos + sin)
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Синтез (сумма cos + sin)
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Синтез (магнитуда + фаза)
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.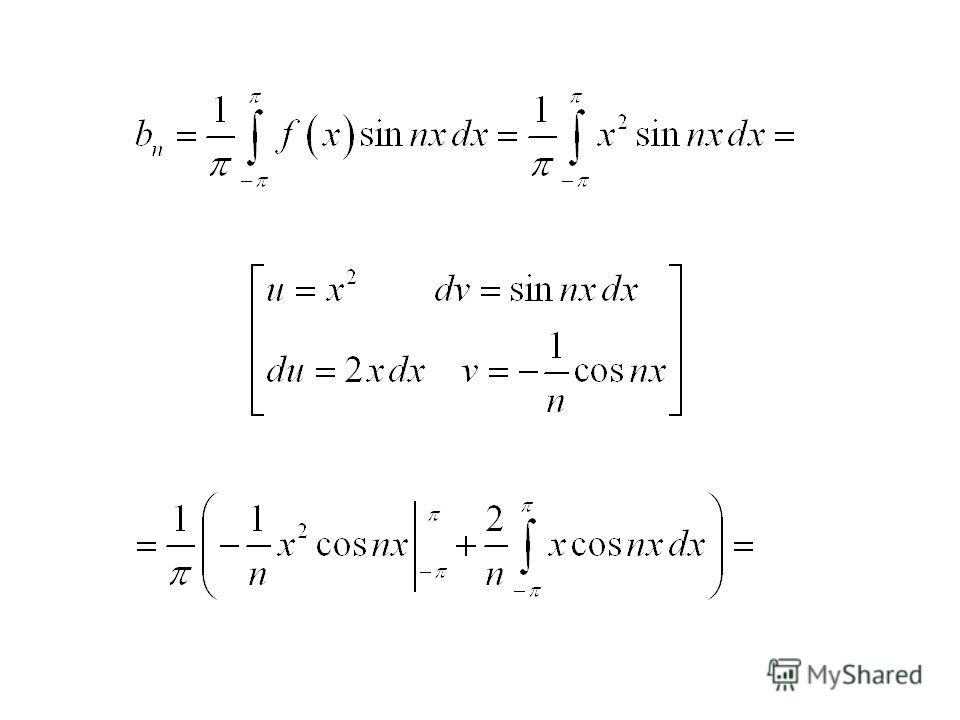
Синтез (сумма магнитуда + фаза)
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
DFT DSP FFT быстрое преобразование Фурье дискретное преобразование Фурье Матанализ песочница преобразование Фурье цифровая обработка сигналов
Ряд Фурье. Контрольные онлайн
Образовательные онлайн сервисы: теория и практика
- Главная
- Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика
- Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование.
 Методы оптимизации
Методы оптимизации
- Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика - Другое
- Контакты
Полезные материалы:
- Учебники
- Справочники
- Онлайн калькуляторы
- Помощь в решении
- Онлайн занятия в Zoom
Ряд Фурье
Определение. Коэффициентами Фурье функции называются числа и , определяемые формулами
,
Ряд называется рядом Фурье функции .
В случае разложения в ряд Фурье функции, заданной в интервале , где — произвольное число, формулы принимают вид:
, Пример1 Разложить в ряд Фурье функцию на отрезке . Решение.
Подставим найденные значения коэффициентов ряда Фурье в формулу:
Пример2 Разложить в тригонометрический ряд Фурье функцию
Решение
Если функция задана на интервале , то её ряд Фурье имеет вид ,
где , , .
Заданная функция определена на интервале , следовательно, и ряд Фурье для функции будет иметь вид ,
где , , .
Вычислим коэффициенты ряда Фурье для заданной функции.
Проинтегрировав по частям, получим
Проинтегрировав по частям, получим
Таким образом, в точках дифференцируемости функции
Читать методичку Ряды и интегралы Фурье (pdf)
Задать вопрос
Заказать помощь
Отзывы
+7-911-7987704
vk.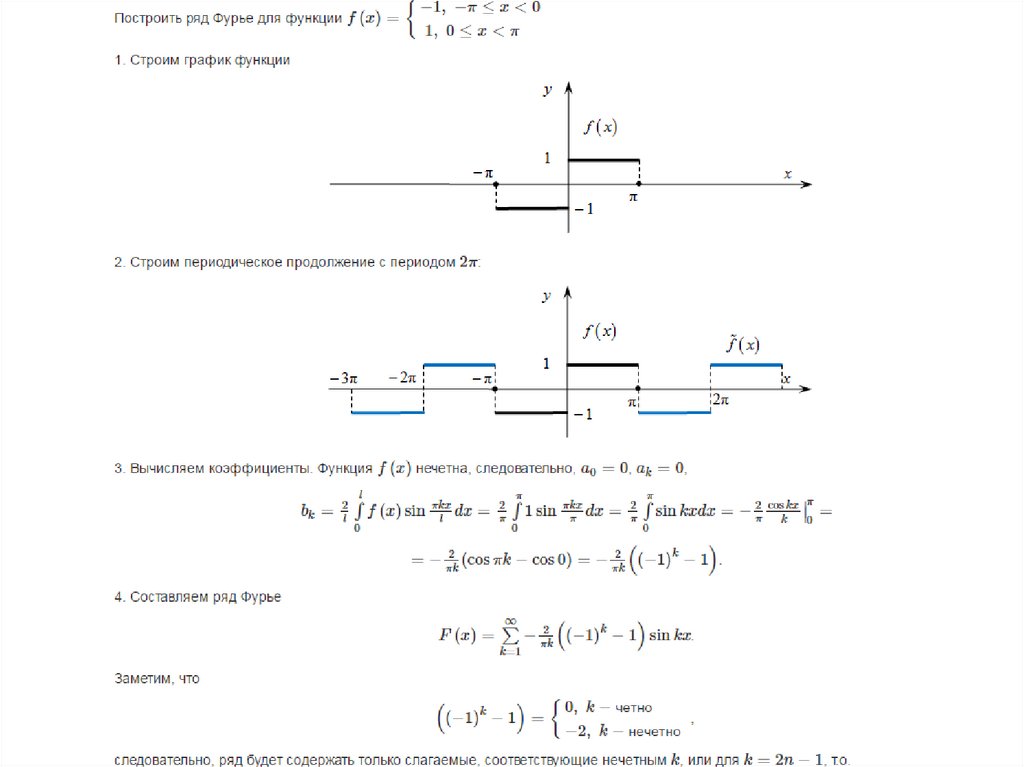
Написать в Whatsapp
Написать в Viber
@matem96
Skype: matem96.ru
Калькулятор ряда Фурье — Определение разложения ряда Фурье
Онлайн-калькулятор ряда Фурье предназначен исключительно для расчета ряда Фурье заданной периодической функции. Теперь мы решили начать с некоторой базовой теории!
Читайте прямо сейчас!
Что такое ряд Фурье?
В математике
« Разложение периодической функции по бесконечным суммам синусов и косинусов называется рядом Фурье».
9Lf\left(x\right)\sin \left(\frac{n\pi x}{L}\right)dx,\:\quad \:n>0 $$С помощью калькулятора коэффициентов Фурье , вы можете легко найти значения этих коэффициентов.
Ряды Фурье четных и нечетных функций:
В некоторых задачах, с которыми мы сталкиваемся в отношении рядов Фурье, коэффициенты Фурье a_{0} , a_{n} или b_{n} могут стать равными нулю после завершения интеграции. Это означает, что если мы попытаемся найти нулевые коэффициенты, это действительно может занять много времени, и его следует избегать. Но если у нас есть надлежащие знания о четных и нечетных функциях, нам становится легко предсказать нулевые коэффициенты до того, как мы начнем интегрирование. 9{\infty \:}a_n\cdot \cos \left(\frac{n\pi x}{L}\right) $$
Это означает, что если мы попытаемся найти нулевые коэффициенты, это действительно может занять много времени, и его следует избегать. Но если у нас есть надлежащие знания о четных и нечетных функциях, нам становится легко предсказать нулевые коэффициенты до того, как мы начнем интегрирование. 9{\infty \:}a_n\cdot \cos \left(\frac{n\pi x}{L}\right) $$
Всякий раз, когда вы сталкиваетесь с четной функцией, вы можете использовать наш бесплатный онлайн-калькулятор косинусного ряда Фурье. .
Нечетные функции:
В общем случае функция f(x) называется нечетной, если;
f(-x) = -f(x)
Для получения дополнительных сведений щелкните Четная или нечетная функция.
Если нечетная функция определена в течение периода -L, L и имеет период времени 2L 9{\infty \:}b_n\cdot \sin \left(\frac{n\pi x}{L}\right) $$
Калькулятор ряда синусов Фурье — лучший способ найти ряд Фурье нечетной функции данный.
Свойства четных и нечетных функций:
Имея дело с рядом Фурье, мы должны иметь правильное представление об основных элементах четных и нечетных функций, которые включают:
Дополнительные свойства:
- Сумма двух четных функций всегда является четной функцией
- Сумма двух нечетных функций тоже нечетна.
- Сумма четной функции и нечетной функции не является ни четной, ни нечетной (если только одна функция не равна нулю)
Свойства умножения:
- Произведение двух нечетных функций всегда четно
- Произведение двух четных функций равно
- Если мы умножим четную функцию на нечетную, мы получим нечетную функцию.
Бесплатный калькулятор разложения в ряд Фурье автоматически предсказывает тип функции и вычисляет коэффициенты, необходимые для получения ряда Фурье.
Как вычисляется ряд Фурье?
Определение ряда Фурье заданной функции может оказаться лихорадочной и длительной практикой. Вот почему мы запрограммировали наш бесплатный онлайн-калькулятор рядов Фурье для мгновенного и точного определения результатов. Но чтобы понять правильное использование рядов Фурье, давайте решим пару примеров.
Вот почему мы запрограммировали наш бесплатный онлайн-калькулятор рядов Фурье для мгновенного и точного определения результатов. Но чтобы понять правильное использование рядов Фурье, давайте решим пару примеров.
Пример № 01:
Вычислить ряд Фурье от приведенной ниже функции:
$$ f\left( x \right) = L – x on – L \le x \le L $$ 9{2}}{3} $$
Однако для получения более точных результатов используйте наш бесплатный онлайн-калькулятор коэффициентов ряда Фурье.
Как работает калькулятор рядов Фурье?
Всякий раз, когда вы сталкиваетесь со сложными функциями, наш бесплатный онлайн-калькулятор рядов Фурье поможет вам определить точные результаты. Воспользовавшись нашим калькулятором, вы получите правильный сценарий расчетов.
Давайте посмотрим, что вам нужно сделать:
Ввод:
- Сначала напишите свою функцию в выпадающем списке
- После этого выберите переменную, по которой необходимо определить разложение в ряд Фурье
- Ввод нижнего и верхнего пределов
- Нажмите «Рассчитать»
Вывод:
Калькулятор разложения Фурье вычисляет:
- Ряд Фурье заданной функции
- Коэффициенты Фурье функции f: a_{0}, a_{n} и b_{n}
- Пошаговые расчеты, задействованные в процессе
Часто задаваемые вопросы:
Является ли ряд Фурье уникальным?
Да, для любого числа n ряд Фурье всегда уникален.
Какая польза от ряда Фурье?
В рядах Фурье используется отношение ортогональности функций синусов и косинусов.
Все ли функции имеют ряд Фурье?
Если у нас есть какая-либо функция, определенная на всей прямой и периодическая, считается, что она имеет ряд Фурье. Однако наш бесплатный онлайн-калькулятор рядов Фурье поможет вам определить, содержит ли данная функция ряды Фурье или нет.
Укажите основную причину использования ряда Фурье.
Основное использование ряда Фурье заключается в том, что мы можем легко анализировать сигнал в другой подходящей области, а не в исходной области.
Заключение:
Ряды Фурье имеют очень широкие перспективы в области техники и технологий, поскольку они очень важны в обработке сигналов, акустике, теории оболочек, квантовой механике и обработке изображений, где широко используется бесплатный онлайн-калькулятор рядов Фурье. выполненный. Не только это, вы также можете легко решить сложные проблемы, изменив домены сигналов. При этом главное преимущество анализа Фурье заключается в том, что в процессе преобразования сигнала теряется очень мало информации.
При этом главное преимущество анализа Фурье заключается в том, что в процессе преобразования сигнала теряется очень мало информации.
Литература:
Из источника Википедии: Сходимость, Ряд Фурье на квадрате, Интерпретация гильбертова пространства, Свойства, лемма Римана–Лебега, лемма Римана–Лебега.
Из источников академии хана: Коэффициенты Фурье, Интеграл от sin(mt) и cos(mt), Интеграл от произведения синусов.
Из источника изучения люмена: Синусоида, Произвольная волна, Волновое уравнение.
Серия Фурье Он-лайн калькулятор — Серия Фурье
Основные понятия и принципы
Онлайн-калькулятор ряда Фурье — это интерактивное приложение для расчета коэффициентов ряда Фурье (до 10000 элементов) для определяемых пользователем кусочных функций, например, до 5 штук.
\( f(x) = \left\{\begin{matrix} 0 & x \in [-1,0)\\ x+1 & x \in [0,1] \end{matrix}\right . \)
Выдает результат
Обратите внимание, что функция должна находиться в пространстве интегрируемых функций или L1 на выбранном интервале, как мы показали в разделах теории.
Калькулятор рядов Фурье вычисляет коэффициенты Фурье, аналитические и числовые интегралы, и его удобно использовать для построения графиков функций с одной переменной и их рядов Фурье на общем заданном пользователем интервале.
Щелкните здесь для доступа к Калькулятору ряда Фурье
Расширенная теория
Точность расчетов во многом зависит от введенного размерного интервала и количества выбранных коэффициентов для расчета.
Использование его заключается в следующем.
1) Запишите нижнюю границу диапазона в текстовом поле с надписью Limit inf.
2) Введите верхний диапазон в текстовое поле с надписью Limit Sup.
3) Напишите функцию в текстовом поле с функцией метки.
В случае кусочной функции действуйте следующим образом
2) Введите верхний диапазон в текстовое поле с надписью Limit Sup.

3) Напишите первую функцию в текстовом поле с функцией метки .
4) Введите верхний поддиапазон в текстовое поле с надписью Подинтервал 1.
5) Запишите функцию, как определено в первом подинтервале в текстовом поле, помеченном как подинтервал 1. .
Например, предположим, что у нас есть кусочная функция
\( f(x) = \left\{\begin{matrix} 0 & x \in [-1,0)\\ x+1 & x \in [0,1] \end{matrix}\right . \)
9{\ pi} f (x) sin nx dx \)В случае с коэффициентами Фурье существует несколько методов расчета, запрограммированных здесь владельцами Mathstools .
Чтобы вычислить производную функции: использует суровые численные методы для вычисления.
Для вычисления примитивной функции: применяются методы численного интегрирования, описанные в разделе численных методов .
Обратите внимание, что при численном анализе ошибки возникают из-за конкретных методов, а также из-за ограничений арифметического компьютера.

 Методы оптимизации
Методы оптимизации