Симметричен график четной функции: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Четная функция | это… Что такое Четная функция?

ТолкованиеПеревод

Четная функция

f(x) = x — пример нечётной функции.

f(x) = x² — пример чётной функции.

f(x) = x³, нечётная

f(x) = x³ + 1 ни чётная, ни нечётная

Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

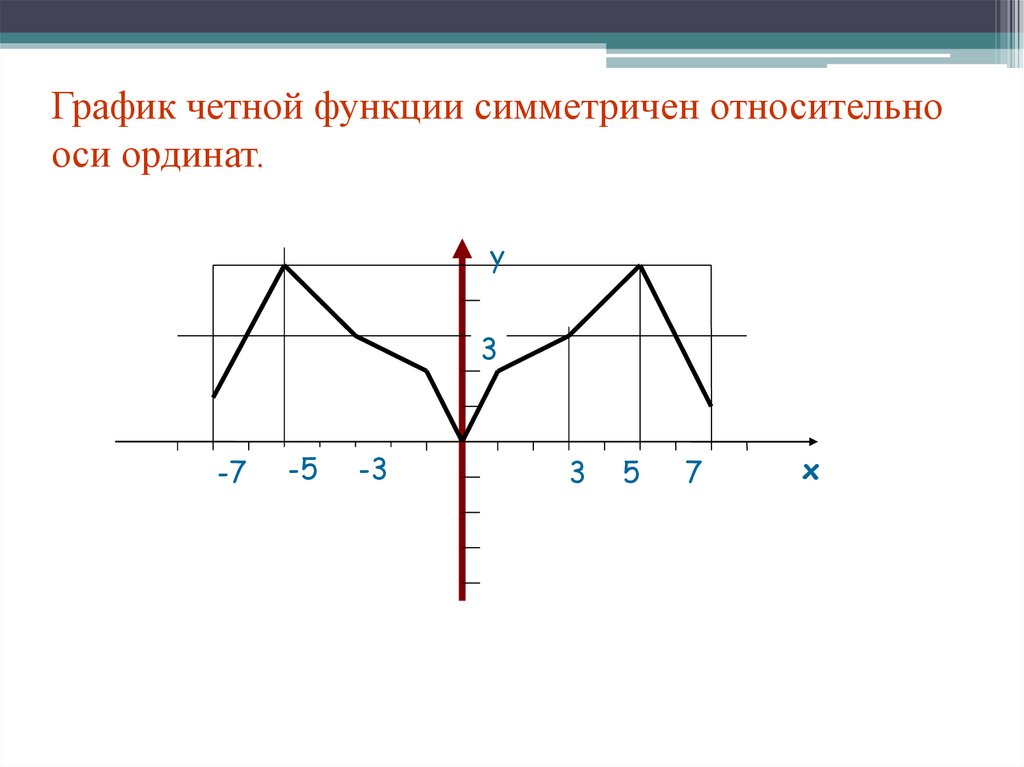
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание 1 Определения 2 Свойства 3 Примеры 3. 1 Нечётные функции 3.2 Чётные функции 4 Вариации и обобщения

Определения

• Функция называется нечётной, если справедливо равенство

• Функция f называется чётной, если справедливо равенство

• Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.

Свойства

• График нечётной функции симметричен относительно начала координат O.
• График чётной функции симметричен относительно оси ординат Oy.
• Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:

f(x) = g(x) + h(x),

где

• Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Произведение или дробь двух нечётных функций чётно.
• Произведение или дробь двух чётных функций чётно.
• Произведение или дробь нечётной и чётной функций нечётно.
• Композиция двух нечётных функция нечётна.
• Композиция двух чётных функций чётна.
• Композиция чётной функции с нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот).
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка сохраняет чётность.

Примеры

Нечётные функции

• Нечётная степень где  — произвольное целое число.
• Синус .
• Тангенс .

Чётные функции

• Чётная степень где  — произвольное целое число.
• Косинус .

Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

Wikimedia Foundation. 2010.

Игры ⚽ Поможем сделать НИР

• Четность (математика)
• Четмэн Вернон

Полезное

Четность и нечетность функции | Онлайн калькулятор

Все калькуляторы

/

Учеба и наука

/

Математика

/   Четность и нечетность функции

Данный калькулятор предназначен для определения четности и нечетности функции онлайн. Четность и нечетность функции определяет ее симметрию.

Функция y=f(x) является четной, если для любого значения x∈X выполняется следующее равенство: f(-x)=f(x). Область определения четной функции должна быть симметрична относительно ноля. Если точка b принадлежит области определения четной функции, то точка –b также принадлежит данной области определения. x

: Log[a, x]

: Log[x]

: cos[x] или Cos[x]

: sin[x] или Sin[x]

: tan[x] или Tan[x]

: cot[x] или Cot[x]

: sec[x] или Sec[x]

: csc[x] или Csc[x]

: ArcCos[x]

: ArcSin[x]

: ArcTan[x]

: ArcCot[x]

: ArcSec[x]

: ArcCsc[x]

: cosh[x] или Cosh[x]

: sinh[x] или Sinh[x]

: tanh[x] или Tanh[x]

: coth[x] или Coth[x]

: sech[x] или Sech[x]

: csch[x] или Csch[е]

: ArcCosh[x]

: ArcSinh[x]

: ArcTanh[x]

: ArcCoth[x]

: ArcSech[x]

: ArcCsch[x]

[19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)

×

Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Скачать калькулятор

Select rating12345

Рейтинг: 3.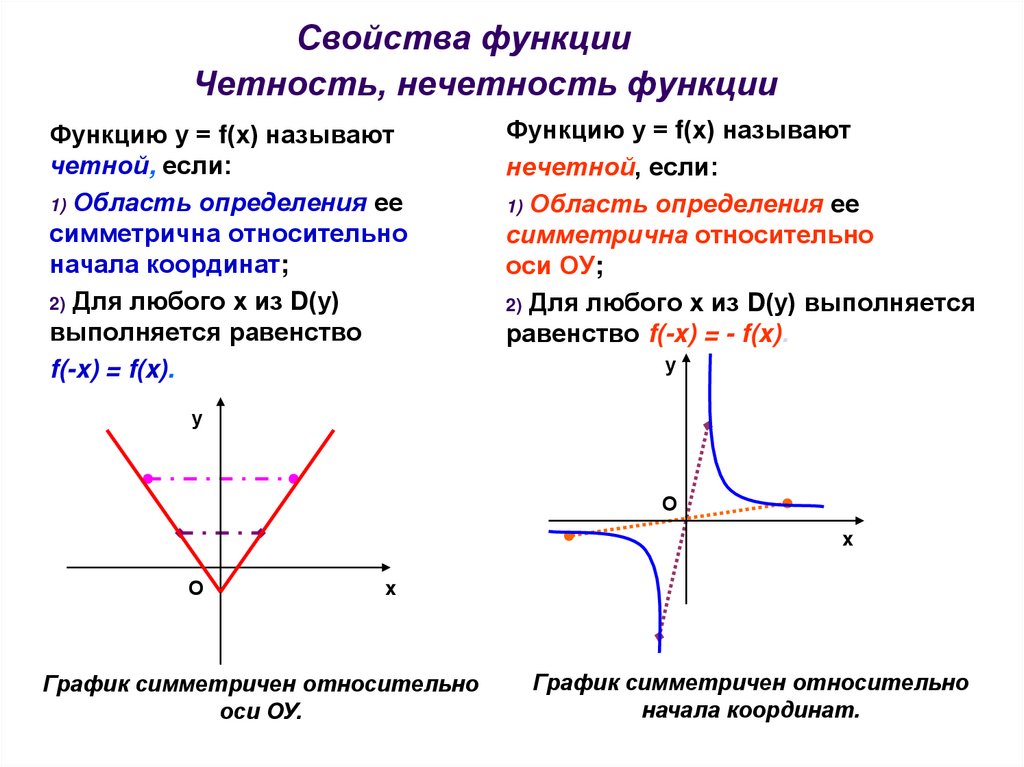 1 (Голосов 111)

Сообщить об ошибке

Смотрите также

Симметрия функции: тестирование для

Решение проблем >

Содержание:

1. Что такое симметричная функция?
2. Ось симметрии
3. Центр симметрии
4. Как проверить симметрию функции

«Симметрия функции» обычно относится к симметрии графика функции . Четные и нечетные функции симметричны:

• Четные функции симметричны относительно вертикальной оси Y. График в правой части (квадрант 1) является зеркальным отображением графика в левой части (квадрант 2). Четная функция симметрична относительно вертикальной оси.
• Нечетные функции симметричны относительно начала координат. Математически это определяется как f(-x) = x для каждого x в области. График симметричной нечетной функции.

Некоторые специфические полиномиальные функции называются «симметричными» не потому, что их график симметричен, а потому, что полиномы остаются прежними, если вы переставляете их корни. См.: Симметричные полиномиальные функции

Функция слева симметрична оси y; Функция справа симметрична началу координат. Синяя пунктирная линия — это число 9.0005 ось симметрии.

Ось симметрии (также называемая линией симметрии ) представляет собой линию, которая образует две стороны: каждая сторона является зеркальным отражением.

Для парабол осью симметрии является вертикальная линия, проведенная через вершину (самую высокую или самую низкую точку графика). Уравнение для оси симметрии представляет собой x-значение координат вершины. Например, если вершина параболы равна (1, 2), формула для оси симметрии будет x = 1,9.0003

Две точки симметричны относительно центра симметрии (точки), если они лежат на одной прямой и находятся на одинаковом расстоянии от центра симметрии. Две точки связаны друг с другом поворотом на 180°.

Полезным фактом о многочленах является то, что они симметричны относительно оси y, когда каждый член либо является константой, либо имеет четный показатель степени.

Что касается других функций, вы можете просто изобразить их на графике, чтобы проверить симметрию. Однако увидеть симметрию на графике может быть непросто. Например, следующий график симметричен относительно начала координат, но его сложно увидеть из-за диких колебаний:

Лучший способ проверить симметрию функции, используя немного алгебры. Все, что вам нужно сделать, это пройтись по списку из трех возможных вариантов:

• Заменить x на -x. Если вы получаете ту же функцию, то эта функция симметрична относительно оси Y.
• Заменить у на -у. Если вы получаете ту же функцию, то эта функция симметрична относительно оси X.
• Заменить x на -x и y на -y . Если вы получаете ту же функцию, то эта функция симметрична относительно начала координат.

Пример вопроса : Является ли y = 2x ³ – x симметричным?

Решение:

• Замените x на -x и затем упростите:
  • у = 2х ³ – х →
  • у = 2(-х) ³ – (-х) →
  • у = 2 х ³ + х

  Это дает другую функцию, поэтому y = 2x ³ – x не симметричен оси y.

• Заменить у на -у.
  • у = 2х ³ – х →
  • -у = 2 х ³ – х

  Это также дает другую функцию, поэтому y = 2x ³ – x также не симметричен относительно оси x.

• Замените x на -x и y на -y.
  • у = 2х ³ – х →
  • Замена x и y: -y = 2(-x) ³ -(- x) →
  • Упрощение: -y = -2x ³ + x→
  • Умножить на -1: y = 2x ³
  Это приводит к той же функции, поэтому y = 2x ³ – x симметричен относительно начала координат.

Ссылки

Ларсон, Р. и Эдвардс, Б. (2018). Исчисление: ранние трансцендентальные функции. Cengage Learning.
Графики, нарисованные с помощью Desmos.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Симметрия функции: тестирование для» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www. statisticshowto.com/symmetry-of-a-function/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .

Симметрия функций | Исчисление I

Результаты обучения 93-4x[/latex] показано на рисунке 13(b). Если мы возьмем график и повернем его на 180° вокруг начала координат, новый график будет выглядеть точно так же. В этом случае мы говорим, что функция имеет симметрию

относительно начала координат.

Рис. 13. (a) График, симметричный относительно оси [latex]y[/latex]. (b) Граф, симметричный относительно начала координат.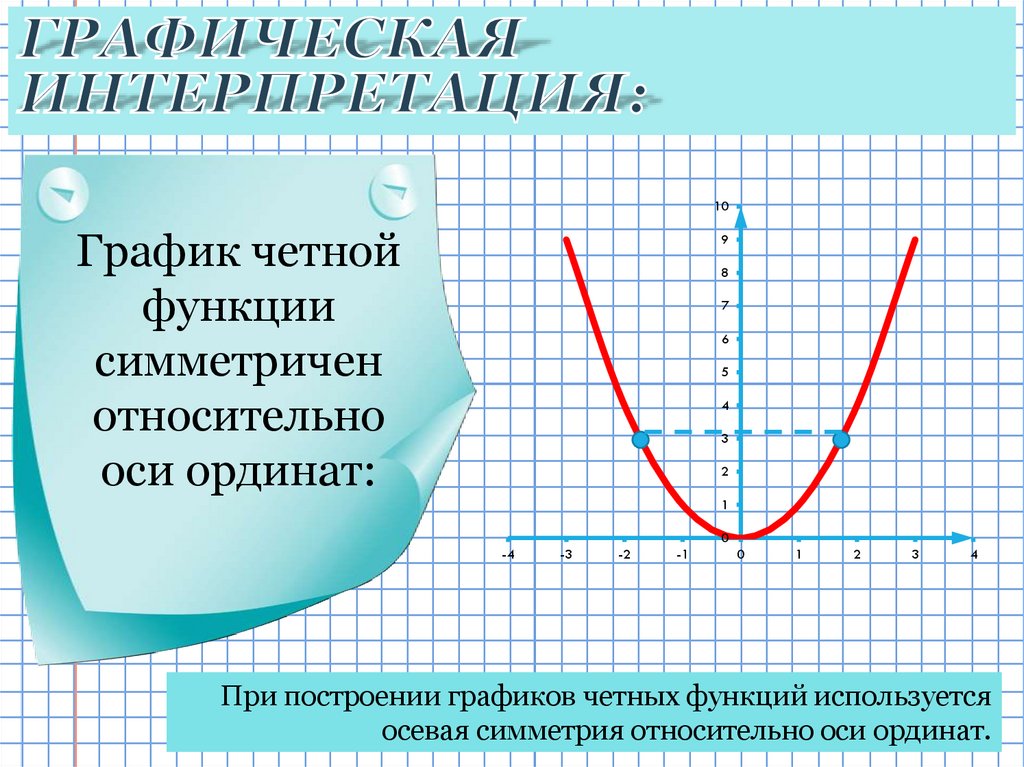

Если нам дан график функции, легко увидеть, обладает ли график одним из этих свойств симметрии. Но как без графика алгебраически определить, обладает ли функция [latex]f[/latex] симметрией? Снова взглянув на рисунок 13(a), мы видим, что поскольку [latex]f[/latex] симметричен относительно оси [latex]y[/latex], если точка [latex](x,y)[/latex ] находится на графике, точка [латекс](−x,y)[/латекс] находится на графике. Другими словами, [латекс]f(−x)=f(x)[/латекс]. Если функция [latex]f[/latex] обладает этим свойством, мы говорим, что [latex]f[/latex] является 93=-f(x)[/латекс].

 

Определение

---

Если [latex]f(-x)=f(x)[/latex] для всех [latex]x[/latex] в домене [latex]f[/latex], тогда [latex]f[/latex] — четная функция. Четная функция симметрична относительно оси [latex]y[/latex].

Если [latex]f(-x)=-f(x)[/latex] для всех [latex]x[/latex] в домене [latex]f[/latex], тогда [latex]f[ /latex] — нечетная функция. Нечетная функция симметрична относительно начала координат.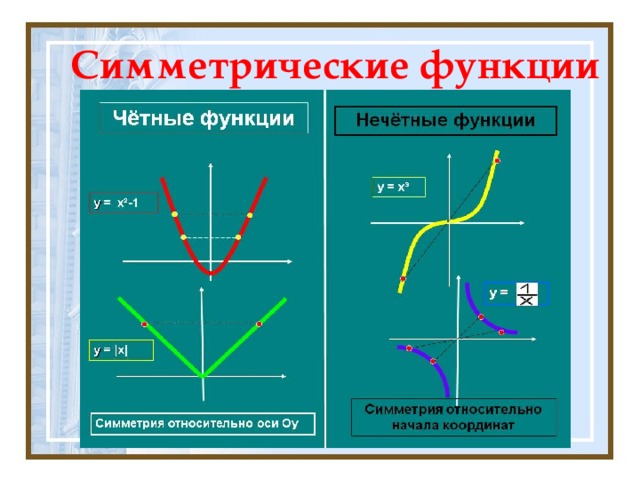

Пример: четные и нечетные функции 93-5x[/latex] — это четное, нечетное или ни то, ни другое.

 

 

Показать решение

Одной из часто встречающихся симметричных функций является функция абсолютного значения , которая записывается как [латекс]|х|[/латекс]. Функция абсолютного значения определяется как

[латекс]f(x)=\begin{cases} x, & x \ge 0 \\ -x, & x < 0 \end{cases}[/latex]

 

Некоторые студенты описывают эту функцию, заявляя, что она «делает все положительным». По определению функции абсолютного значения мы видим, что если [латекс]х<0[/латекс], то [латекс]|х|=-х>0[/латекс], и если [латекс]х>0[ /латекс], затем [латекс]|x|=x>0[/латекс]. Однако для [латекса]x=0, \, |x|=0[/латекс]. Следовательно, точнее будет сказать, что для всех ненулевых входных данных выход положительный, но если [latex]x=0[/latex], выход [latex]|x|=0[/latex]. Мы заключаем, что диапазон функции абсолютного значения составляет [латекс]\{у|у\ге 0\}[/латекс].

No related posts.