Симплекс-метод решения задачи линейного программирования
Симплекс-метод решения
задачи линейного
программирования
КТН, доцент
Манкевич Александр Валерьевич
Учебные вопросы:
1. Вычислительные методы решения
задач линейного программирования.
2. Сущность симплекс – метода.
3. Примеры решения с использованием
симплекс-метода.
Учебный вопрос № 1
Вычислительные методы решения задач
линейного программирования
Вычислительные методы решения задач линейного
программирования
Геометрическая интерпретация, при решении задач
линейного программирования, перестает быть пригодной
для этой цели при числе свободных переменных n — m > 3,
а затруднительна уже при n — m = 3. Для нахождения
решения задачи линейного программирования в общем
случае
(при
переменных)
произвольном
применяются
вычислительные
методы.
числе
не
Из
свободных
геометрические,
них
а
наиболее
универсальным является так называемый симплексметод.
Вычислительные методы решения задач линейного
программирования
Симплекс-метод
—
оптимизационной
задачи
программирования
путём
выпуклого
многогранника
алгоритм
(ОЗ)
линейного
перебора
в
решения
вершин
многомерном
пространстве. Метод был разработан американским
математиком Джорджем Данцигом (George Dantzig) в
1947 году.
Википедия
Учебный вопрос № 2
Сущность симплекс-метода
Сущность симплекс-метода
Идея симплекс-метода относительно проста. Пусть в
задаче
линейного
программирования
имеется
n
переменных и m независимых линейных ограничений,
заданных в форме уравнений. Известно, что оптимальное
решение (если оно существует) достигается в одной из
опорных точек (вершин ОДР), где по крайней мере k = n — m
из переменных равны нулю. Выберем какие-то k
переменных в качестве свободных и выразим через них
остальные m базисных переменных. Пусть, например, в
качестве свободных выбраны первые k = n — m
переменных х1, х2, …, хk, а остальные m выражены через
них:
хk+1 = α k+1,1 х1 + α k+1,2 х2 + … + α k+1,k хk + β k+1;
хk+2 = α k+2,1 х1 + α k+2,2 х2 + … + α k+2,k хk + β k+2;
…
хn= α n1 х1 + α n2 х2 + … + α nk хk + β n.
(1)
Сущность симплекс-метода
Предположим, что все свободные переменные
х1, х2, …, хk равны нулю.
При этом получим:
хk+1 = β k+1;
хk+2 = β k+2;
…
х n= β n .
Это
решение
может
быть
допустимым
или
недопустимым. Оно допустимо, если все свободные
члены β k+1, β k+2, … , β n неотрицательны. Предположим, что
это условие выполнено. Тогда мы получили опорное
решение. Но является ли оно оптимальным? Чтобы
проверить это, выразим целевую функцию F через
свободные переменные х1, х2, …, хk :
F = γ0 + γ1х1 + γ2х2 + … + γk хk .
(2)
Сущность симплекс-метода
Очевидно, что при х1 = х2 = … = хk =0, F = γ0.
Проверим, может ли быть улучшено решение, т. е.
получено уменьшение функции F c увеличением какихнибудь из переменных х1, х2, …, хk (уменьшать их мы не
можем, так как все они равны нулю, а отрицательные
значения
переменных
недопустимы).
Если
все
коэффициенты γ1, γ2, … , γk в (2) положительны, то
увеличение каких-либо из переменных х1, х2, …, хk не
может уменьшить F; следовательно, найденное опорное
решение является оптимальным.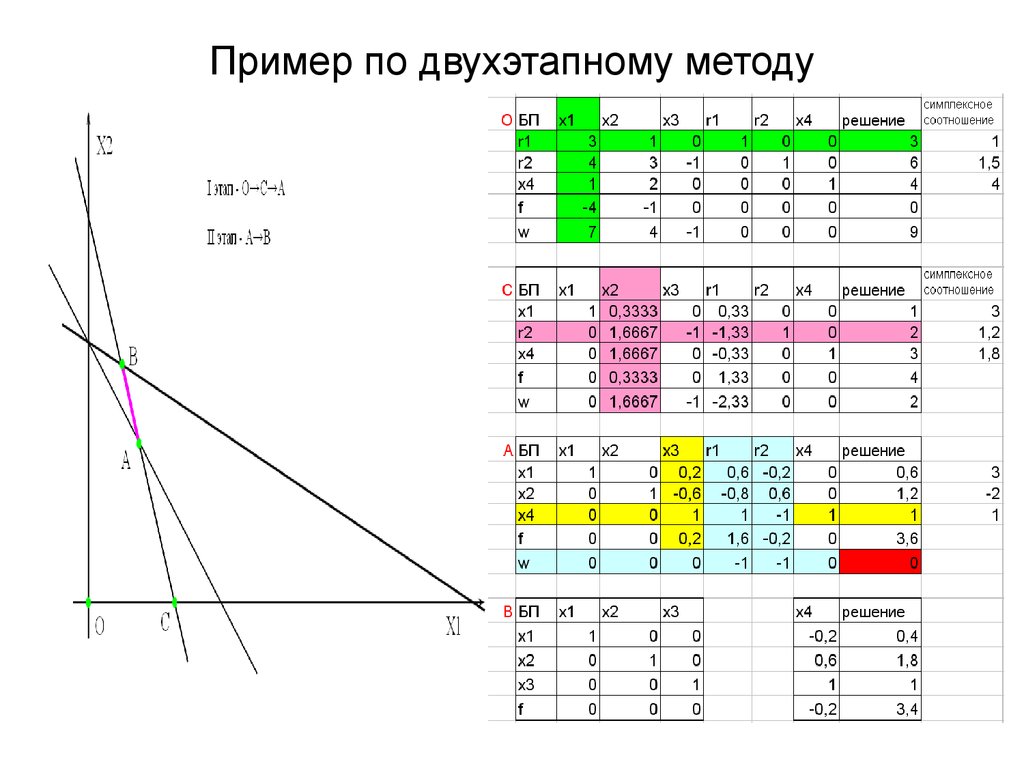
Если же среди
коэффициентов γ1, γ2, … , γk есть отрицательные, то,
увеличивая некоторые из переменных х1, х2, …, хk (те,
коэффициенты при которых отрицательны), можно
улучшить решение.
Сущность симплекс-метода
Пусть, например, коэффициент γi в (2) отрицателен.
Значит, есть смысл увеличить х1, т. е. перейти от данного
опорного решения к другому, где переменная х1 не равна
нулю, а вместо нее равна нулю какая-то другая. Однако
увеличивать х1 следует с осторожностью, так чтобы не
стали отрицательными другие переменные хk+1,хk+2, … , хn
выраженные через свободные переменные, в частности
через х1 формулами (1).
Например,
если
коэффициент
при
х1
в
соответствующем хi уравнении (1) отрицателен, то
увеличение х1 может сделать хi отрицательным.
Наоборот, если среди уравнений (1) нет уравнения с
отрицательным коэффициентом при х1 то величину х1
можно увеличивать беспредельно, а, значит, линейная
функция F не ограничена снизу и оптимального решения
ОЗ не существует.
Сущность симплекс-метода
Допустим, что это не так и что среди уравнений (1) есть
такие, в которых коэффициент при х1 отрицателен. Для
переменных, стоящих в левых частях этих уравнений,
увеличение х1 опасно — оно может сделать их
отрицательными.
Возьмем одну из таких переменных х1 и посмотрим, до
какой степени можно увеличить х1, пока переменная хi не
станет отрицательной. Выпишем i-е уравнение из
системы (1):
х i = αi 1 х 1 + α i 2 х 2 + … + α i k х k + β i
Здесь свободный член β
отрицателен.
i
≥ 0, а коэффициент αik
Сущность симплекс-метода
Если оставить х2 = х3 = … = хk =0, то х1 можно
увеличивать только до значения, равного (– βi / α1i), а при
дальнейшем увеличении х1 переменная хi станет
отрицательной.
Выберем ту из переменных хk+1, хk+2, … , хn, которая
раньше всех обратится в нуль при увеличении х1 т. е. ту,
для которой величина (– βi / α1i) наименьшая. Пусть это
будет хr . Тогда имеет смысл разрешить систему
уравнений
(1)
относительно
других
базисных
переменных, исключая из числа свободных переменных
х1 и переводя вместо нее в группу свободных
переменных хr .
Перейдём от опорного решения,
задаваемого равенствами х1 = х2 = … = хk = 0, к опорному
решению, в котором уже х1 ≠ 0, а х2 = … = хk = хr = 0.
Сущность симплекс-метода
Первое опорное решение получим, положив равными
нулю все прежние свободные переменные х1 , х2 , … , хk
второе ‒ если обратим в нуль все новые свободные
переменные
Базисными переменными при этом будут
х1 , хk+1 , хk+2 , … , хr‒1 , хr , хr+1 , … , хn
Сущность симплекс-метода
Предположим, что уравнения типа (1) для нового
набора базисных и свободных переменных составлены.
Тогда можно выразить через новые свободные
переменные и линейную функцию F. Если все
коэффициенты при переменных в этой формуле
положительны, то значит найдено оптимальное решение:
оно получится, если все свободные переменные
положить равными нулю. Если среди коэффициентов при
переменных
есть
отрицательные,
то
процедура
улучшения решения продолжается: система вновь
разрешается относительно других базисных переменных,
и так далее, пока не будет найдено оптимальное решение,
обращающее функцию F в минимум.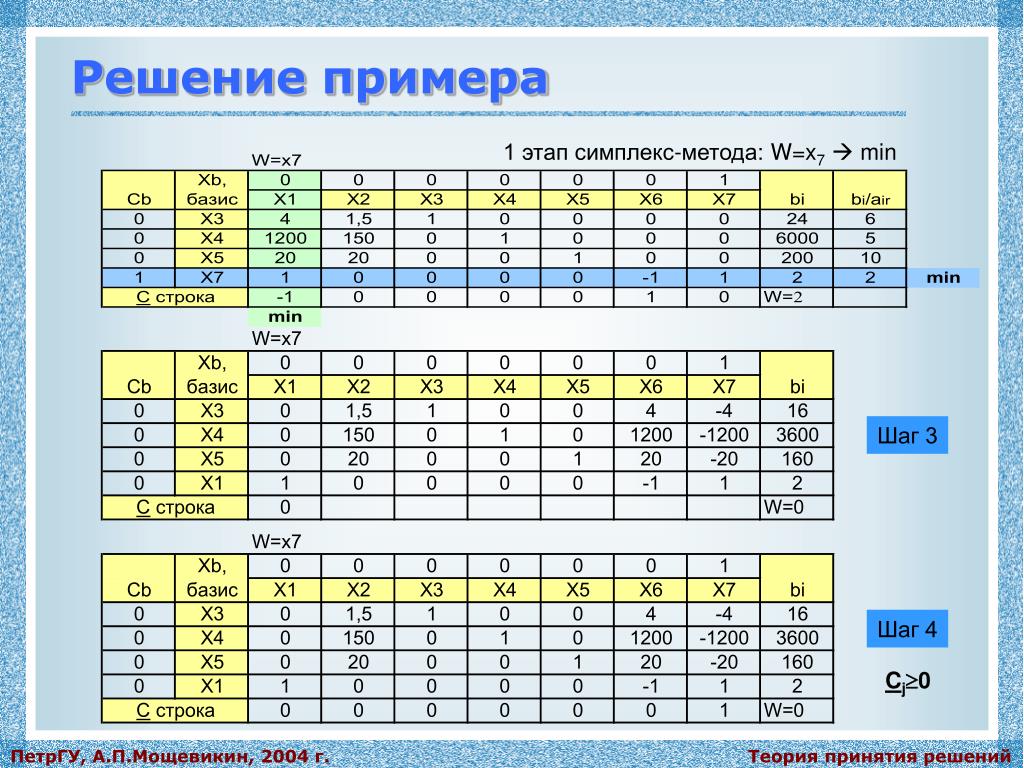
Учебный вопрос № 3
Примеры решения с использованием
симплекс-метода
Пример
Пример.
Пусть
имеется
задача
линейного
программирования с ограничениями-неравенствами:
– 5х1 – х2 + 2х3 ≤ 2;
– х1 + х3 + х4 ≤ 5;
– 3х1 + 5 х4 ≤ 7.
(3)
Требуется минимизировать линейную функцию
F = 5х1 – 2х3
Пример (продолжение)
Приводя неравенства к стандартному виду (≥ 0) и
вводя добавочные переменные у1, у2, у3, переходим к
условиям-равенствам:
у1 = 5х1 + х2 – 2х3 + 2;
у2 = х1 – х3 – х4 + 5;
у3 = 3х1 – 5 х4 + 7.
(4)
Число переменных (n = 7) на 4 превышает число
уравнений (m = 3). Значит, четыре переменные могут
быть выбраны в качестве свободных.
Пример (продолжение)
Пусть в качестве свободных переменных выступают
х1, х2, х3, х4. Положим их равными нулю и получим
опорное решение:
х1 = х2 = х3 = х4 = 0;
у1 = 2, у2 = 5, у3 = 7.
При этих значениях переменных F = 0.
Это решение не оптимально, поскольку в линейной
функции F коэффициент при х3 отрицателен.
Значит,
увеличивая х3, можно уменьшить F.
Попробуем увеличивать х3 . Из выражений (4) видно,
что в у1 и у2 переменная входит с отрицательным
коэффициентом,
значит,
при
увеличении
х3
соответствующие
переменные
могут
стать
отрицательными.
Пример (продолжение)
Определим, какая из этих переменных (у1 или
у2)
раньше обратится в нуль при увеличении х3. Очевидно,
что это у1: она станет равной нулю при х3 = 1, а величина
у2 — только при х3= 5.
Выбирается
переменная
у, и вводится в число
свободных вместо х3. Чтобы разрешить систему (4)
относительно х3, у2, у3 необходимо:
Разрешить первое уравнение (4) относительно новой
базисной переменной х3:
5
1
5
х3 х1 х2 у1 1
2
2
2
Пример (продолжение)
Это выражение подставляется вместо х3 во второе
уравнение:
5
1
5
х
х
х
у
1
;
3
1
2
1
2
2
2
3
1
1
у2 х1 х2 у1 х4 4;
2
2
2
у3 3 х1 5 х4 7.
(5)
Пример (продолжение)
Что касается третьего уравнения, то оно, как не
содержащее х3 не изменится. Система (4) приведена к
виду со свободными переменными х1, х2, у1, х4 и
базисными х3, у2, у3.
Выразим
функцию
F
через
новые
свободные
переменные:
F = 5х1 – 5х1 – х2 + у1 – 2 = – х2 + у1 – 2
(6)
Положим теперь свободные переменные равными
нулю. Функция приобретает значение F = – 2, что меньше
(лучше), чем прежнее значение F = 0.
Пример (продолжение)
Это решение все еще не оптимально, так как
коэффициент при х2 в выражении (6) отрицателен, и
переменная х2 может быть увеличена. Это увеличение,
как это видно из системы (5), может сделать
отрицательной у2 (в первое уравнение х2 входит с
положительным коэффициентом, а в третьем —
отсутствует).
Поменяем местами переменные х2 и у2 — первую
исключим из числа свободных, а вторую — включим. Для
этого разрешим второе уравнение (5) относительно х2 и
подставим х2 в первое уравнение.
Получим следующий
вид системы (4): х х у х 5;
3
1
2
4
(7)
у2 3х1 2 у2 у1 2 х4 8;
у 3х 5 х 7.
1
4
3
Пример (продолжение)
Выразим F через новые свободные переменные:
F = 3х1 + 2у2 – у1 + 2х4 – 8 + у1 – 2 = 3х1 + 2у2 + 2х4 – 10 (8)
Полагая , что 3х1 + 2у2 + 2х4 = 0, получим F = – 10.
Это решение является оптимальным, так как
коэффициенты при всех свободных переменных в
выражении (8) неотрицательны. Итак, оптимальное
решение ОЗ найдено:
х 1 0, х 2 8, х 3 5, х 4 0; у 1 0, у 2 0, у 3 7.
При таких значениях переменных линейная функция F
принимает минимальное значение:
Fmin= – 10.
Пример (продолжение)
В
рассмотренном
примере
не
пришлось
искать
опорное решение: оно сразу же получилось, когда
положили свободные переменные равными нулю. Это
объясняется тем, что в уравнениях (4) все свободные
члены были неотрицательны и, значит, первое же
попавшееся решение оказалось опорным.
Если это
окажется не так, можно будет прийти к опорному решению
с
помощью
такой
же
процедуры
обмена
местами
некоторых базисных и свободных переменных, повторно
решая уравнения до тех пор, пока свободные члены не
станут неотрицательными.
Пример
ЗАДАНИЕ. Компания производит полки для ванных
комнат двух размеров – А и В. Агенты по продаже
считают, что в неделю на рынке может быть реализовано
до 550 полок. Для каждой полки типа А требуется 2 м2
материала, а для полки типа В – 3 м2 материала. Компания
может получить до 1200 м2 материала в неделю. Для
изготовления одной полки типа А требуется 12 мин.
машинного времени, а для изготовления одной полки
типа В – 30 мин; машину можно использовать 160 час в
неделю. Если прибыль от продажи полок типа А
составляет 3 денежных единицы, а от полок типа В – 4
ден. ед., то сколько полок каждого типа следует
выпускать в неделю?
Пример
РЕШЕНИЕ. Составим математическую модель задачи.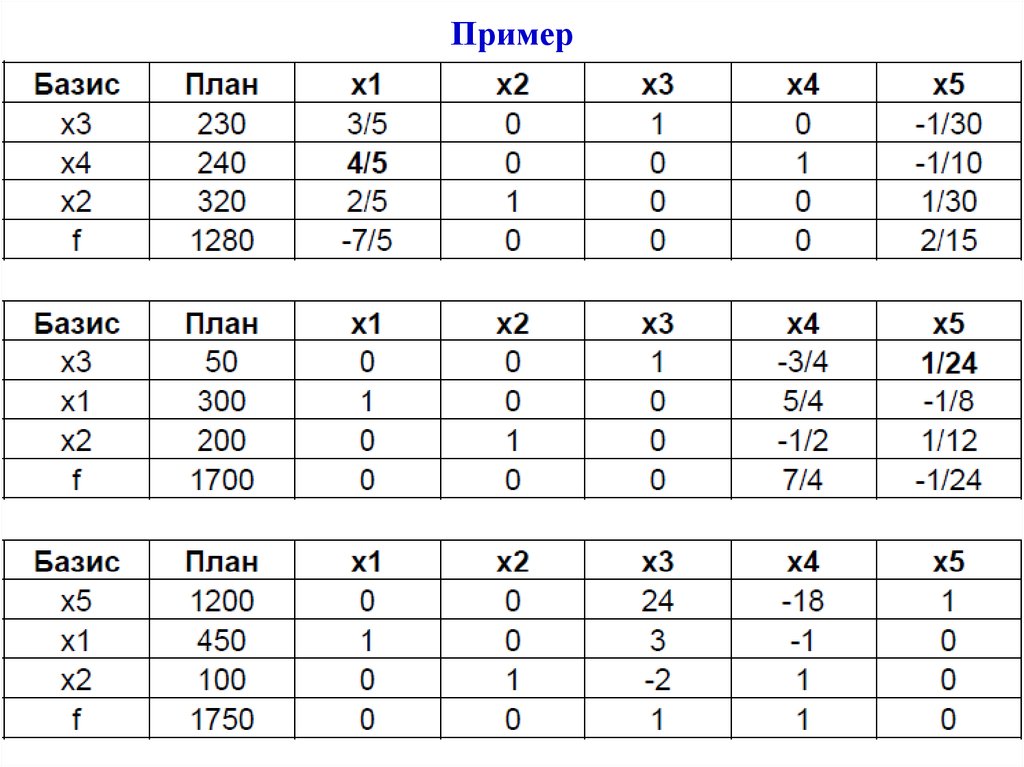
Пусть х1 – количество полок вида А, х2 – количество
полок вида В, которые производятся в неделю (по
смыслу задачи эти переменные неотрицательны).
Прибыль от продажи такого количества полок составит
3х1 + 4х2, прибыль требуется максимизировать.
Выпишем ограничения задачи.
х1 + х2 ≤ 550 – в неделю на рынке может быть
реализовано до 550 полок.
Затраты материала: 2х1 + 3х2 ≤ 1200
Затраты машинного времени: 12х1 + 30х2 ≤ 9600.
Пример
Таким образом,
программирования.
приходим
к
задаче
линейного
Решим
ее
симплекс-методом.
Введем
три
дополнительные переменные x3, x4, x5 и придем к задаче
Пример
В
качестве
опорного
плана
выберем
X0=(0,0,550,1200,9600). Составим симплекс-таблицу.
В последней оценочной строке есть отрицательные
оценки, поэтому нужно делать шаг симплекс-метода.
Выбираем столбец с наименьшей оценкой, а затем
разрешающий элемент – по наименьшему отношению
свободных членов к коэффициентам столбца (последний
столбец).
Результат
шага
запишем
в
таблицу
(разрешающий элемент будем выделять жирным).
Аналогично будем повторять шаги, пока не придем к
таблице с неотрицательными оценками.
Пример
Пример
В
последнем
плане
строка
f
не
содержит
отрицательных значений, план x1 = 450, x2 = 100
оптимален, целевая функция принимает значение 1750.
Таким образом, чтобы получить максимальную прибыль,
предприятию необходимо производить 450 полок вида А
и 100 полок вида В, при этом прибыль составит 1750 ден.
ед., а останется неиспользованными 1200 минут (20
часов) машинного времени.
Пример
ЗАДАНИЕ. Решить задачу линейного программирования
симплекс-методом.
РЕШЕНИЕ. Будем решать эквивалентную задачу
Пример
Введем дополнительные переменные, чтобы привести
задачу к каноническому виду:
Так
как
нет
единичных
искусственный базис:
векторов,
вводим
Пример
Получили расширенную задачу с опорным планом
(0,0,0,0,0,0,8,2,1).
Составим cимплекс-таблицу:
В последней оценочной строке есть отрицательные
оценки (смотрим на коэффициенты при М, пока
искусственный базис не выйдет), поэтому нужно делать
шаг симплекс-метода. Выбираем столбец с наименьшей
оценкой, а затем разрешающий элемент – по
наименьшему
отношению
свободных
членов
к
коэффициентам столбца (последний столбец). Результат
шага запишем в таблицу (разрешающий элемент будем
выделять жирным). Аналогично будем повторять шаги.
Пример
Пример
Искусственный базис выведен, но в единственном
столбце с отрицательной оценкой (Х2) все коэффициенты
отрицательны, то есть функция не ограничена на
множестве допустимых решений, оптимальный план
найти невозможно.
Симплекс-метод. Пример решения задачи. | Презентация к уроку на тему:
Опубликовано 24.03.2018 — 20:57 — Ковалева Елена Вячеславовна
В презентации рассматривается решение задачи линейного программирования симплекс-методом.
В процессе решения задача приводится к каноническому виду и вводятся искуственные переменные. Решение осуществляется с помощью симплек таблиц.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Пример решения задачи Симплекс — метод ФГБОУ ВО МГУТУ им. К.Г. Разумовского (ПКУ) УКИТ Ковалева Елена Вячеславовна
Слайд 2
Общая постановка задачи и каноническая форма
Слайд 3
СП БП Х 1 Х 2 Св. члены Х 3 — 1 1 1 Х 4 1 -1 1 Х 5 1 1 2 Z min 6 -7 -3 СП БП Х 4 Х 2 Св. члены Х 3 Х 1 Х 5 Z min СП БП Х 1 Х 2 Св. члены Х 3 — 1 1 1 Х 4 1 -1 1 Х 5 1 1 2 Z min 6 -7 -3 СП БП Х 4 Х 2 Св. члены Х 3 1 0 2 Х 1 1 -1 1 Х 5 -1 2 1 Z min -6 -1 -9
Слайд 4
Искусственный базис
Слайд 5
СП БП Св.ч х1 х2 х4 х5 Х3 1 3 -5 2 0 У1 4 -2 2 -1 1 У2 5 -1 3 -2 1 Zmin 0 -1 -2 0 0 Fmin 9 -3 5 -3 2
Слайд 6
СП БП Св.ч х1 х2 х4 х5 Х3 1 3 -5 2 0 У1 4 -2 2 -1 1 У2 5 -1 3 -2 1 Zmin 0 -1 -2 0 0 Fmin 9 -3 5 -3 2 СП БП Св.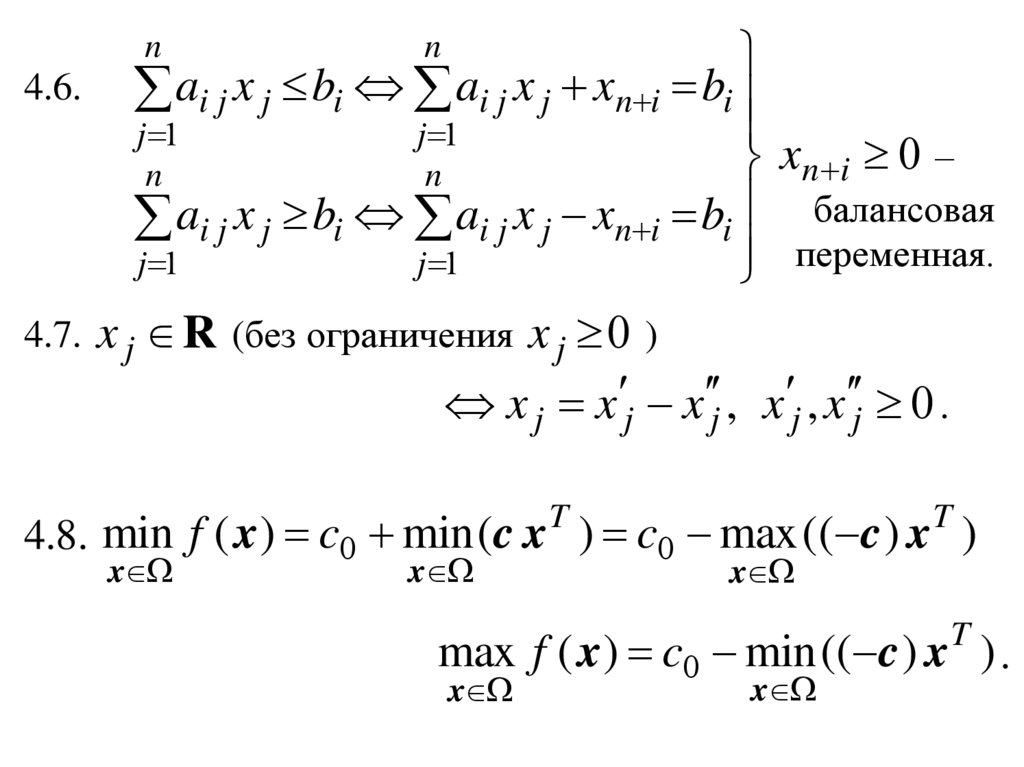
ч х1 х2 х4 y1 Х3 x5 У2 Zmin Fmin СП БП Св.ч х1 х2 х4 y1 Х3 1 3 5 2 0 x5 4 -2 2 -1 1 У2 1 1 1 -1 -1 Zmin 0 -1 -2 0 0 Fmin 1 1 1 -1 -2
Слайд 7
СП БП Св.ч х1 х2 х4 y1 Х3 1 3 5 2 0 x5 4 -2 2 -1 1 У2 1 1 1 -1 -1 Zmin 0 -1 -2 0 0 Fmin 1 1 1 -1 -2 СП БП Св.ч х1 y 2 х4 y1 Х3 6 8 5 -3 -5 x5 2 -4 -2 1 3 x 2 1 1 1 -1 -1 Zmin 2 1 2 -2 -2 Fmin 0 0 -1 0 -1
Слайд 8
СП БП Св. члены Х 1 Х 4 Х 3 6 8 -3 Х 5 2 -4 1 Х 2 1 1 -1 Z min 2 1 -2 СП БП Св. члены Х 3 Х 4 Х 1 Х 5 5 -0,5 Х 2 Z min
По теме: методические разработки, презентации и конспекты
Применение свойств модуля при решении задач и построении графиков функции.
ВведениеСущественной характеристикой числа, как в действительной, так и в комплексной области, является понятие его абсолютной величины или модуля.Это понятие имеет широкое распространение в раз…
Mетодическое пособие по «Теории вероятностей и математической статистике». Примеры решения задач.
Методическая разработка…
Симплекс-метод
Презентация по учебной дисциплине «Математические методы» по теме «Линейное программироване: Симплекс-метод решения задач ЛП».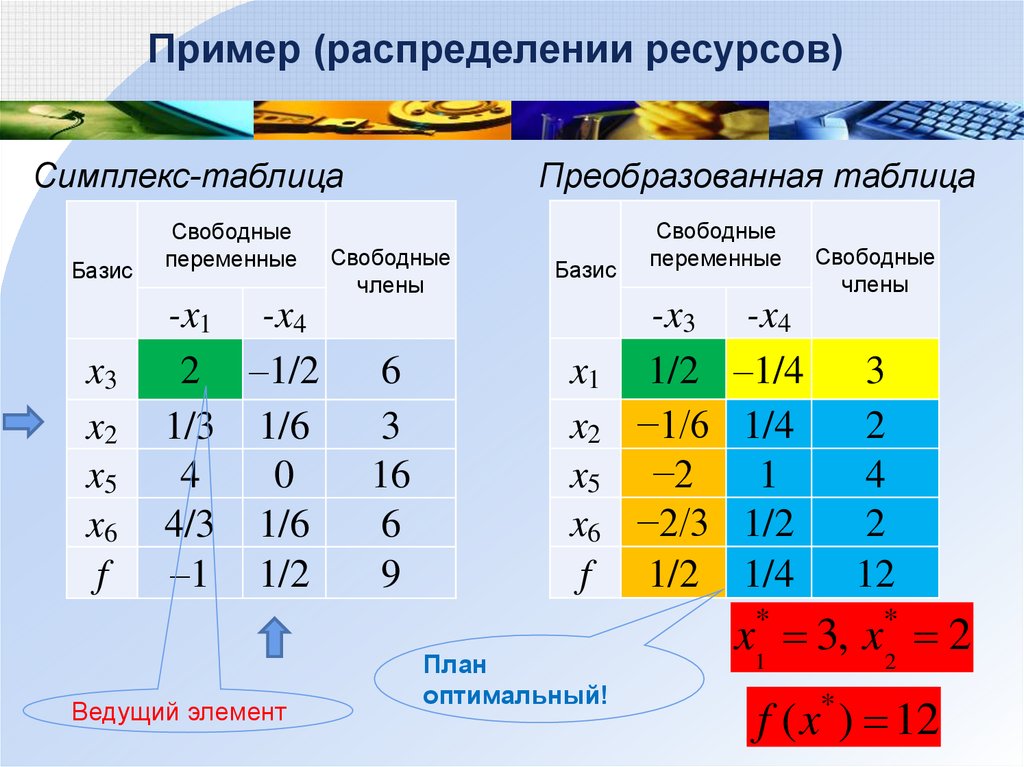
..
Формирование профессиональных и общих компетенций на примере решения ситуационной профессиональной задачи
Формирование профессиональных и общих компетенций выпускников в процессе решения ситуационных задач…
Тема: комплексный подход к решению задач воинского, патриотического, правового, нравственного и эстетического воспитания обучающихся на примере участия нахимовцев 1 роты в проекте «Незабытые адмиралы»
ДокладТема: комплексный подход к решению задач воинского, патриотического, правового, нравственного и эстетического воспитания обучающихся на примере участия нахимовцев 1 роты в проекте «Незабытые адм…
Битва под Москвой в примерах и задачах по математике», посвященный 75 лет битве за Москву.
Битва под Москвой в примерах и задачах по математике», посвященный 75 лет битве за Москву….
Конспект урока по математике в 1 «Б» классе Тема: « Решение примеров и задач в пределах 10»
Урок по математике в 1 «Б» классе Тема: Решение примеров и задач в пределах 10Цели: — тренировать детей в решении примеров и задач;— учить ребят правильно ставить знаки: больше.
..
Поделиться:
Начало работы с алгоритмом симплекс-метода | Программа инженерного образования (EngEd)
Симплекс-метод представляет собой алгоритм линейного программирования, используемый для определения оптимального решения для данной задачи оптимизации.
Этот метод используется, когда задача линейной оптимизации подвергается ограничениям неравенства. В этой статье мы рассмотрим, как работает этот алгоритм.
Предпосылки
Для дальнейшего чтения считыватель должен иметь следующее:
- Python установлен на вашем компьютере.
- Знание метода исключения Гаусса Жордана в линейной алгебре.
Чтобы понять, как работает этот алгоритм, рассмотрим следующую задачу:
Производитель велосипедов производит туристические, гоночные и модельные велосипеды. Эти велосипеды изготовлены из алюминия и стали. Компания имеет 91800 стальных единиц и 42000 алюминиевых единиц.
Настройка симплексного метода
Теперь многие проблемы оптимизации, с которыми мы столкнемся, имеют форму операторов. Отсюда нам потребуется правильно сформулировать уравнения оптимизации. Поэтому мы выбрали именно такую задачу, а не уже разработанную, чтобы вы могли научиться систематически разрабатывать задачу, которую мы потом оптимизируем. Это даст возможность делать s9 в будущем самостоятельно.
Первое, что нам нужно сделать, это определить наши переменные. Мы определяем их следующим образом:
R: Количество гоночных велосипедов.
T: Количество туристических велосипедов.
M: Количество горных велосипедов.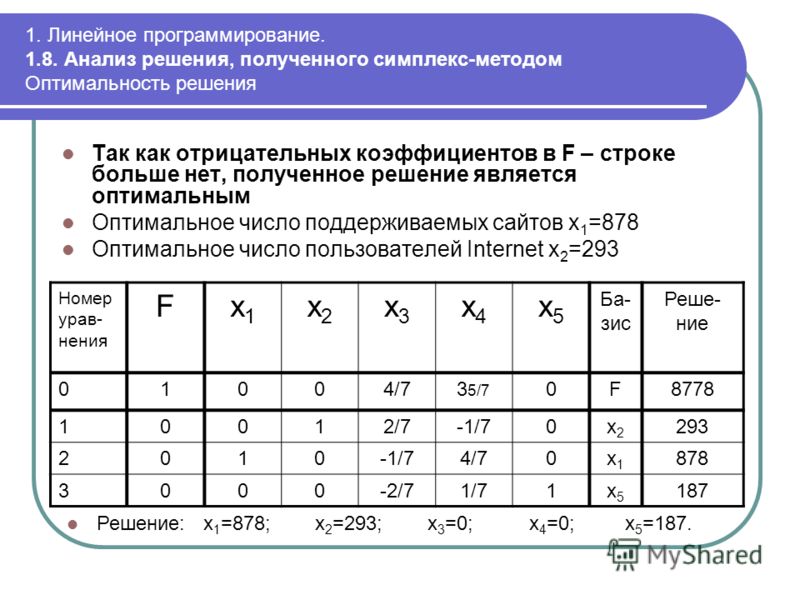
Следующее, что нужно сделать, это понять, для чего мы оптимизируем задачу. Из вопроса нас просят найти максимальную прибыль. Поэтому мы оптимизируем функцию прибыли.
Еще из вопроса, функция прибыли:
P = 8R + 12T + 22M
Теперь у нас есть наша целевая функция. Следующее, что нужно выяснить, на какие ограничения накладывается эта функция. Например, все производства могут использовать только доступные ресурсы. Следовательно, из этого мы можем реализовать наше первое ограничение.
Поскольку у нас есть две категории ресурсов с соответствующим возможным количеством производственных единиц, изготовленных из них, у нас будет два ограничения.
Эти ограничения:
$$17R+27T +34M\le91800$$ $$12R+21T +15M\le42000$$
Кроме того, мы должны понимать, что любой произведенный продукт может быть либо равен нулю, когда ничего не производится, либо больше нуля, когда производится хотя бы одна единица. Поэтому в дополнение к двум вышеупомянутым ограничениям мы также добавим следующее:
$R\ge0, T\ge0,M\ge0$
Теперь мы можем объединить следующее и разработать следующую задачу оптимизации:
Это оптимизация, которую нам нужно решить.
Для начала возьмем в целевом уравнении все переменные и поместим их слева, т. е.
.
Следовательно, наша задача будет переписана так:
Это стандартная форма нашей задачи. Из этих уравнений мы получаем нашу исходную таблицу как:
Следующее, что нужно сделать, это определить опорный столбец, то есть столбец с самым отрицательным значением в целевой строке. Как мы видим, опорным столбцом является M. Из этого столбца нам нужно определить опорное значение.
Базовое значение находится следующим образом:
$min,(91800/34, 42000/15) = min,(91800/34, 42000/15) = 91800/34 = 2700$
Поскольку 34 — это значение опорного столбца, соответствующее наименьшему частному, оно является опорным значением. Теперь нам нужно сделать это значение единичным значением. Для этого мы умножаем сводную строку на $1/34$.
Это даст следующую таблицу:
Следующим шагом будет обнуление всех значений ниже и выше опорного значения.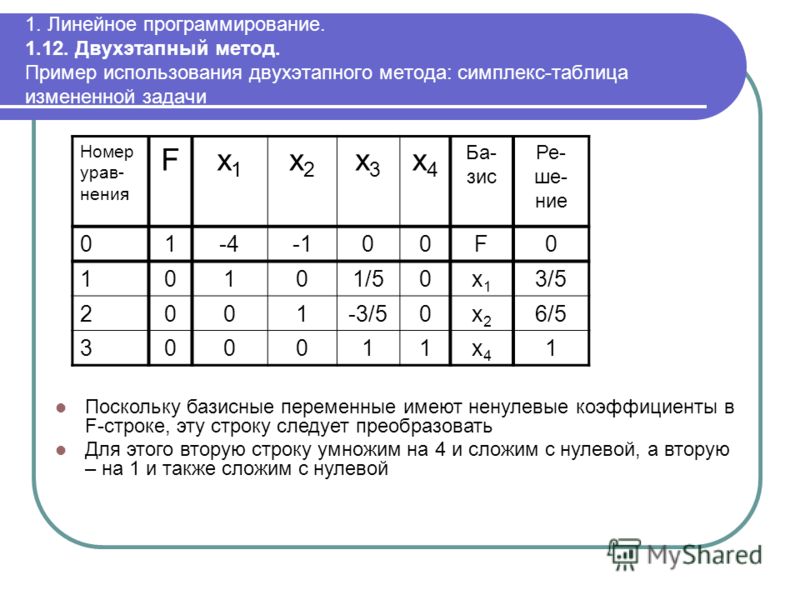
Для этого нам необходимо выполнить следующие операции:
Замените $R_2$ на $R_2 = -15R_1 + R_2$
Заменить $R_3=$ на $R_3=22R_1+R_3$
Эта операция даст следующую таблицу:
Мы достигли оптимального решения без отрицательного значения в нашей целевой строке, что указывает на то, что у нас есть оптимальное решение. Из этого решения мы замечаем, что M и $S_2$ являются базовыми переменными (принимают форму единичной матрицы), а остальные небазисными. Поэтому мы устанавливаем все неосновные переменные равными нулю.
Отсюда следует, что наше решение будет следующим:
$Р = 0$ $Т = 0$ $М=2700$ $P = 59400$
Следовательно, оптимальным решением будет производство не гоночного велосипеда, не туристического велосипеда и 2700 горных велосипедов, чтобы получить максимальную прибыль в размере 59 400 долларов США.
Как видим, эта задача быстрее сходилась к оптимальному решению. Однако бывают случаи, когда этого не произойдет.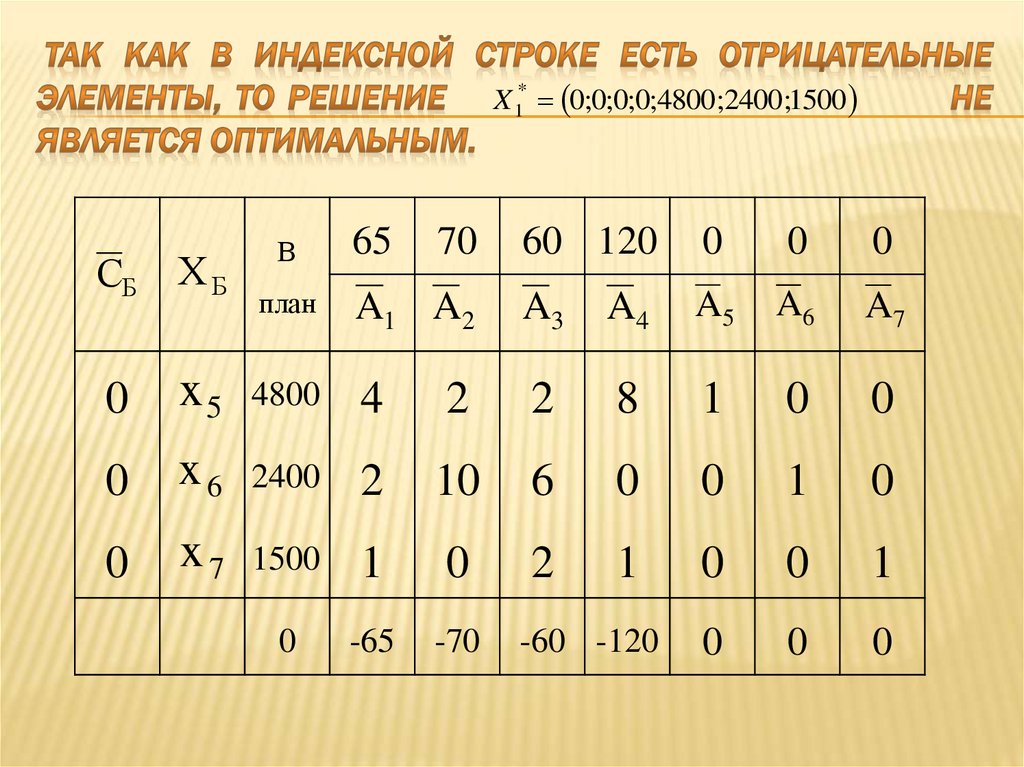
{th}$. Если мы это сделаем, сводной колонкой, также известной как входящая переменная, будет $y$.
Из этого столбца найдем опорное значение, т. е. значение, соответствующее минимальному частному в опорном столбце. Где частные рассчитываются следующим образом:
- $50/1$
- $75/1$
- $90/2$
Как видно из приведенных выше коэффициентов, 45 — это минимум всех вопросов. Таким образом, опорное значение равно 2. Нам нужно применить технику редукции строк методом исключения Гаусса-Джордана. Это сделает опорное значение равным единице, в то время как все остальные элементы будут выше или ниже нуля. 9{th}$ ряд, это решение не является оптимальным. Опять же, мы идентифицируем опорный столбец из текущей таблицы и повторяем все шаги, начиная с определения опорного столбца и опорного значения. Применяя метод исключения Гаусса Джордана, мы делаем опорное значение единичным значением, а все остальные элементы в том же столбце — нулями.
Затем мы проверяем, является ли наша целевая строка оптимальной (не имеет отрицательного значения).
th$ строка не станет оптимальной. 9{th}$ строки, и, таким образом, решение является оптимальным. Вот как работает алгоритм
Реализация алгоритма Simplex на Python
Мы можем запустить два приведенных выше примера на Python и посмотреть, получим ли мы тот же результат. Мы рассмотрим, как мы создали наши входные массивы из первой задачи, а затем последует вторая проблема.
Случай 1
### Импорт необходимых библиотек
импортировать numpy как np
импортировать scipy как sp
# Получить матрицы
с = [-8, -12, -22]
А = [[17, 27, 34], [12, 21, 15]]
б = [91800, 42000]
# определяем верхнюю и нижнюю границы
R = (0, нет)
Т = (0, Нет)
М = (0, Нет)
# Реализация симплексного алгоритма
из scipy.optimize импортировать linprog
# Решаем задачу Симплекс-методом в Оптимизации
res = linprog(c, A_ub=A, b_ub=b, bounds=(R, T, M), method='simplex', options={"disp": True}) # линейное программирование p[проблема
print(res) # распечатать результаты
Эта программа возвращает:
Оптимизация успешно завершена.Текущее значение функции: -59400.000000 Итерации: 3 против: массив ([], dtype = float64) весело: -59400.0 сообщение: «Оптимизация успешно завершена». нит: 3 слабина: массив ([ 0., 1500.]) статус: 0 успех: правда х: массив ([ 0., 0., 2700.])
Текущее значение функции: -59400.000000
Итерации: 3
против: массив ([], dtype = float64)
весело: -59400.0
сообщение: «Оптимизация успешно завершена».
нит: 3
слабина: массив ([ 0., 1500.])
статус: 0
успех: правда
х: массив ([ 0., 0., 2700.])
Из этого вывода становится ясно, что оптимальное действие — построить 0 туристических велосипедов, 0 гоночных велосипедов и 2700 горных велосипедов. Если это действие будет осуществлено, компания получит оптимальную прибыль в размере 59 400 долларов.
Теперь приступим к решению второй задачи.
Задача оптимизации:
Из этой задачи у нас могут быть следующие три массива:
Мы реализуем эти матрицы в Python и решим нашу задачу. Ниже приведен код Python, который выполняет эти операции.
Случай 2
### Импорт необходимых библиотек импортировать numpy как np импортировать scipy как sp # Получить матрицы с = [-30, -40] А = [[1, 1], [4, 2], [50, 100]] б = [50, 150, 4500] # определяем верхнюю и нижнюю границы х = (0, нет) у = (0, нет) # Реализация симплексного алгоритма из scipy.optimize импортировать linprog # Решаем задачу Симплекс-методом в Оптимизации res = linprog(c, A_ub=A, b_ub=b, bounds=(x, y), method='simplex', options={"disp": True}) # линейное программирование p[проблема print(res) # распечатать результаты
Выполнение этой программы дает:
Оптимизация успешно завершена.
Текущее значение функции: -1900.000000
Итерации: 3
против: массив ([], dtype = float64)
удовольствие: -1900.0
сообщение: «Оптимизация успешно завершена».
нит: 3
слабина: массив ([ 0., 30., 0.])
статус: 0
успех: правда
х: массив ([10., 40.])
В результате значение целевой функции, т. е. удовольствие, равно -1900. Это значение вычисляется для задачи минимизации. В случае задачи максимизации мы опускаем знак минус. Следовательно, решение для нашей максимизации равно 19.00. Также из результатов видно, что значения x и y , которые приведут к оптимальному решению, равны 10 и 15 соответственно.
Результат, который мы получили от наших двух вышеприведенных реализаций, аналогичен соответствующим ручным задачам, которые мы решали ранее. Таким образом, симплексная задача была успешно решена.
Заключение
В этом уроке мы теоретически рассмотрели симплекс-метод и его реализацию в Python. Помимо решения самой задачи оптимизации, мы показали вам, как разумно вывести функцию оптимизации из данной задачи.
Удачного кодирования!
Рецензирование Вклад: Джерим Каура
Пример симплекс-метода — построение симплекс-таблицы
Основные понятия и принципы
Формулировка задачи линейного программирования
В этом разделе мы увидим практический пример решения типичной задачи максимизации. Иногда бывает трудно поднять линейное программирование, после этого мы будем использовать методы, изучаемые в разделах теории математики: симплексные, двойные и двухфазные методы.
Начнем с постановки задачи оптимизации
Задача линейного программирования
Горнодобывающая компания производит бурый уголь и антрацит.
На данный момент она способна продать весь добытый уголь, получив прибыль на тонну лигнита и антрацита 4 и 3 денежные единицы соответственно.
На переработку каждой тонны бурого угля требуется 3 часа работы углерезальной машины и еще 4 часа на промывку.
Ежедневное время, отведенное на каждое из этих действий (стрижка и мытье), составляет 12 и 8 часов соответственно. Кроме того, желательно ежедневно производить не менее 4 тонн угля.
1) Представьте задачу линейного программирования, чтобы определить количество тонн лигнита и антрацита, которое необходимо производить ежедневно, чтобы максимизировать прибыль.
2) Использование симплекс-алгоритма для решения задачи двухфазным методом
Приступаем к пониманию задачи. Для этого составим следующие таблицы
Во-первых, это стоимость или, в данном случае, таблица выигрышей.
| Material | Gains produced (monetary units /Tn) |
| Lignite | 4 |
| Anthracite | 3 |
| Material | Cutting hours (по Tn) | Время промывки (по Tn) |
| Бурый уголь | 3 | 4 |
| Anthracite | 4 | 2 |
Attached to this table, we have the constraint of time available for each machine daily
| Process | Hours available daily |
| Промывка | 8 |
| Резка | 12 |
и, наконец, у нас есть цель производить не менее 94 тонн угля ежедневно0003
Расширенная теория
С этими данными у нас есть то, что нужно для постановки задачи линейного программирования.
Действуем следующим образом:
Lets
x1=Тонн произведенного лигнита
x2=Тонн произведенного антрацита
Мы хотим максимизировать прибыль, т.е. максимизировать функцию 4×1 +3×2, это будет наша целевая функция.
теперь ограничения на строительство
Начнем с процесса стирки, учтите, что на каждый день у нас
3×1+ 4×2 ≤ 12
Так как на каждый день количество доступных часов стирки равно 12.
Аналогично у нас есть для процесса резки
4×1+ 2×2 ≤ 8
Потому что 8 — это количество часов, доступных для резки.
Наконец, последнее из ограничений — наша цель тонн продукции
x1 + x2 ≥ 4
Сложив все вместе, мы получим задачу линейного программирования 12
4×1 + 2×2 ≤ 8
x1 + x2 ≥ 4
x1, x2 ≥ 0
Теперь мы можем решить задачу линейного программирования, используя симплексный или двухфазный метод, если необходимо, как мы видели в разделах теории
В этом случае мы используем наш знаменитый калькулятор задач линейного программирования Usarmos калькулятор симплексного метода.