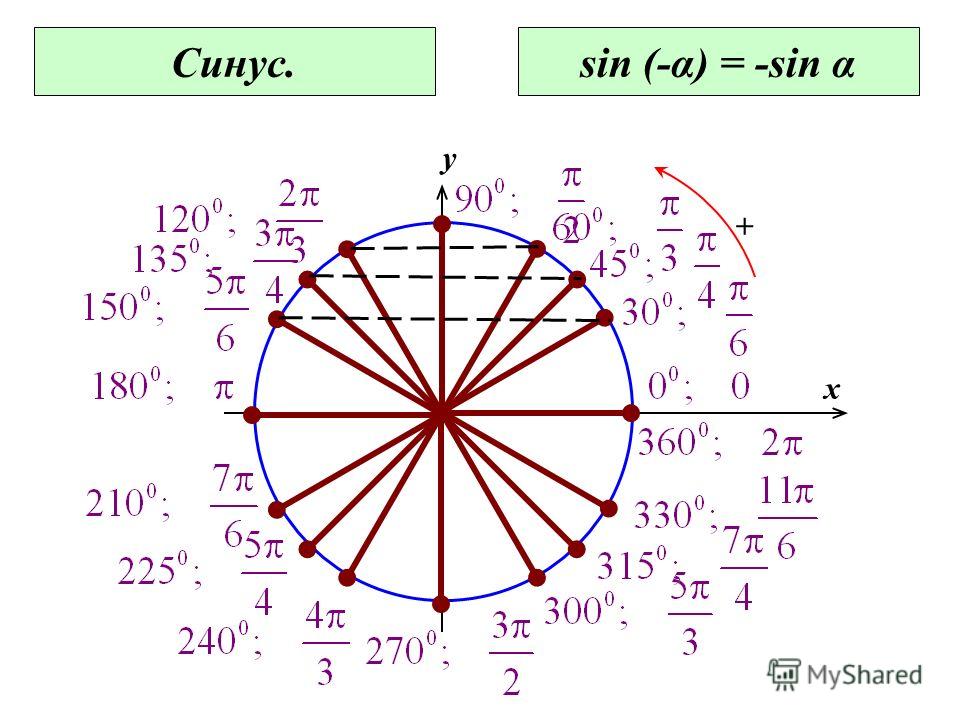
Sin 0 почему равен 0
Обновлено: 03.11.2022
Добрый день!
У меня возникли проблемы с решением уравнений, и да, jzb снова тригонометрические. Мне дано по условию следующее: sin x = 0. Надеюсь, хоть Вы сможете мне это объяснить. Точнее объяснить, как понимать такое задание, чтоб суметь его решить
Да, я понимаю, что это Вам ничем не помогло, но находить будет легче. Для подобных уравнений есть определённое правило решения, которое принимает всегда вот такой общий вид:
Как только мы разобрались с общим решением, то с лёгкостью можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что , или же . Возьмём с Вами второй вариант.
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Sin 0 почему равен 0
Новые вопросы в Математика
252. Найдите наибольший общий делитель и наименьшее общее кратное a3bcd и у а?ь?с?, ab2c ; 4) х = a4b4c2d4 и y = a*b*c2d. 2) x хиу, если: 1) х = abcd … и у 3) х = ab3c3 и у abcd; ;
2) x хиу, если: 1) х = abcd … и у 3) х = ab3c3 и у abcd; ;
6 ACTIVATE Look again at the dialogue in exercise 1. Choose a group of people you know from the box. Imagine that you are a photo of the group to a fr … iend. Practise your new dialogue with a partner. showing classmates uncles and aunts cousins brothers and sisters friends family помогите пожалуйста.
Таблица умножения-это таблица, в каждой клетке которой записано произведение номера столбца и номера строки. Четыре слона стоят в углах некоторого кле … тчатого прямоугольника в таблице умножения. Каждый из них сделал ход внутрь прямоугольника-все на одинаковое расстояние. Докажите, что сумма чисел под ними не изменилась
26 баллов Используя условия этого задания рассмотрите числа 1)902)1083)82Читайте внимательно
sin 0 градусов
Здравствуйте!
Помогите! Чему равен sin 0 градусов? Как его вычислить? Хочу научиться вычислять значения тригонометрических функций.
Спасибо!
Среди методов вычисления значений тригонометрических функций рассмотрим три наиболее распространенных.
Способ, с которым нас изначально знакомят в школе – это использование таблиц значений тригонометрических функций. В этой таблице представлены чаще всего четыре основные функции, причем синус является одной из них, и значения этих функций от определенного набора углов.
На пересечении строки с функцией синус и нужного нам угла 0 градусов получим значение 0. То есть синус 0 равен 0:
sin 0 = 0.
Способ, который осваивают уже более продвинутые знатоки математики – это использование единичной или тригонометрической окружности (что одно и то же).
Точка на окружности, которая соответствует 0 градусов, лежит на оси Ох. Значения синусов содержатся на оси Оу. Таким образом, для рассматриваемой точки координата у равна нулю. Из этого вытекает, что синус 0 равен 0.
Также удобно использовать график синуса.
Находим на оси Ох точку, отвечающую значению 0. Координата у точки графика с абсциссой равной 0, также равна нулю. Другими словами, нужно найти координату у точки графика, координата х которой равна нулю. Так как график синуса проходит через начало координат, то синус 0 равен 0.
Так как график синуса проходит через начало координат, то синус 0 равен 0.
Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
sin 0 равен
Здравствуйте!
Помогите! Чему sin 0 равен? Как его вычислить? Хочу научиться вычислять значения тригонометрических функций.
Спасибо!
Чаще всего при решении тригонометрических задач использую три основных математических метода вычисления значений тригонометрических функций.
Самым простым из них является вычисление с помощью таблиц значений тригонометрических функций от основных углов. В ней необходимо найти столбик со значением аргумента (в нашем случае 0), и строку с функцией (в нашем случае sin) и получить значение на их пересечении. Итак, согласно таблице sin 0 равен 0.
Другим не намного сложнее способом является применение тригонометрической окружности.
Главное, что нужно помнить при использовании окружности, что значения синусов находятся на оси ординат, а косинуса – на оси абсцисс, сами же углы находятся на кривой окружности.
Найдем точку на кривой окружности, которая будет соответствовать углу 0 градусов. Эта точка совпадет с точкой 1, которая лежит на оси Ох. Так как значения синусов находятся на оси Оу, то нужно получить соответствующее значение с помощью проекции полученной точки на эту ось. Итак, получим, значение 0:
sin 0 = 0.
Не менее простым является и использование графика функции синус. На оси Ох графика несложно найти точку, которая отвечает значению 0, и тем более несложно получить соответствующее значение кривой графика на оси Оу. Таким образом, снова подтвердилось, что синус 0 равен 0.
Каждый из способов прост, а каким удобнее пользоваться, скорее всего, зависит от ситуации.
Пожалуйста, зарегистрируйтесь или войдите, чтобы добавить ответ.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
Читайте также:
- Как призвать безглазого джека в майнкрафт
- Чем отличается crysis 2 от crysis 2 maximum edition
- Сколько гусей было в стае у нильса с дикими гусями
- Как менялся соник и его жизненный цикл в гта 5
- Pci express native control что это
Синус 0 градусов, sin 0
Синус нуля градусов равняется нулю. На картинке синуса это выглядит так:
Вы, конечно, спросите: «А где же, собственно, сам синус на этой картинке?» А нет его, он в дырочку от нолика спрятался. Как мышонок в норку. Чтобы увидеть мышонка, нужно его выманить из норки. В мультиках утверждают, запах сыра очень помогает в этом деле. Синус сыром не поманишь. Но есть одна штучка, которая на синус действует безотказно. Называется эта волшебная приманка для синусов — угол. Не тот, в который деток ставят, а тот, который в градусах или радианах измеряется.
Нет у нас угла (угол равняется нулю) — нет и синуса.
sin 0° = sin 0π = 0
Теперь попробуем поманить синус самым маленьким уголком. Посмотрим, как отреагирует синус на угол в ноль градусов, ноль минут, одну тысячную секунды:
sin (0° 0′ 0,001″) = 0,00000000484813681109
Видите, из норки показался самый кончик любопытного носика? Попробуем увеличить в десять раз нашу приманку и возьмем угол в одну сотую секунды.
sin (0° 0′ 0,01″) = 0,00000004848136811095
Количество ноликов перед циферками сократилось на один, а в конце показалась пятерка. Конечно, в норке прячется еще очень много циферок, которые при желании можно увидеть. Это скорее удав с длинню-ю-ю-ю-ющим хвостом из цифр. Еще в десять раз увеличим угол.
sin (0° 0′ 0,1″) = 0,00000048481368110954
Вы заметили, что циферки после ноликов совсем не меняются? Это не означает, что синус, как и угол, увеличивается ровно в десять раз. Где-то там, в дали от запятой, цифры меняются — мышонок шевелит хвостиком, но мы этого не видим. Мы наблюдаем только за первыми двадцатью цифрами после запятой.
Где-то там, в дали от запятой, цифры меняются — мышонок шевелит хвостиком, но мы этого не видим. Мы наблюдаем только за первыми двадцатью цифрами после запятой.
Вот теперь у нас появилась уникальная возможность полюбоваться синусом одной секунды во всей его красе (точнее, его первых двух десятков цифр):
Дальше посмотрим, как меняются первые десять цифр после запятой для 10, 20, 30, 40 и 50 секунд (совершенно естественно, что лишний хвостик мы округляем):
sin (0° 0′ 10″) = 0,0000484814
sin (0° 0′ 20″) = 0,0000969627
sin (0° 0′ 30″) = 0,0001454441
sin (0° 0′ 40″) = 0,0001939255
sin (0° 0′ 50″) = 0,0002424068
Можно считать, что ради одной минуты синус уже полностью покидает свою норку и начинает резво носиться по окрестностям. Вы только посмотрите на синус 10, 20, 30, 40 и 50 минут:
sin (0° 1′) = 0,0002908882
sin (0° 10′) = 0,0029088780
sin (0° 20′) = 0,0058177314
sin (0° 30′) = 0,0087265355
sin (0° 40′) = 0,0116352658
sin (0° 50′) = 0,0145438977
Надеюсь, теперь вы понимаете, что когда угол достигает всего одного градуса, синус становится совсем большим.
sin 1° = 0,017452
sin 2° = 0,034899
sin 3° = 0,052336
sin 4° = 0,069756
sin 5° = 0,087156
sin 6° = 0,104528
sin 7° = 0,121869
sin 8° = 0,139173
sin 9° = 0,156434
sin 10° = 0,173648
Некоторые значения синуса угла альфа по заявкам посетителей:
sin 17° = 0,292372
Если вам еще не надоели наблюдения за синусом, тогда предлагаю перейти на страницу синус 30 градусов. Там его можно не только увидеть, но и потрогать руками, при желании.
На этой странице вы найдете ответы на следующие вопросы по тригонометрической функции синус:
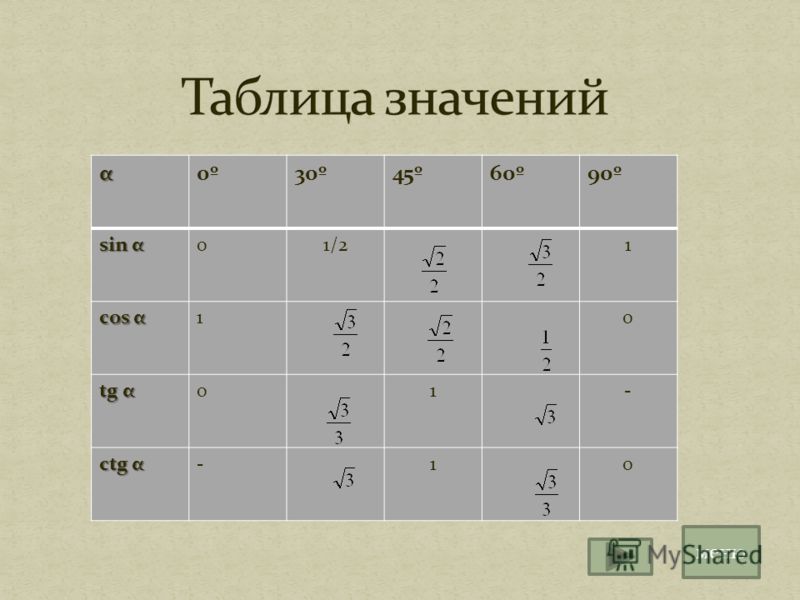
Sin 0 градусов — Найдите значение Sin 0 градусов
LearnPracticeDownload
Значение sin 0 градусов равно 0 . Sin 0 градусов в радианах записывается как sin (0° × π/180°), т. е. sin (0π) или sin (0). В этой статье мы обсудим способы нахождения значения sin 0 градусов на примерах.
- Sin 0°: 0
- Грех (-0 градусов): 0
- Sin 0° в радианах: sin (0π) или sin (0 . . .)
Каково значение Sin 0 градусов?
Значение sin 0 градусов равно 0. Sin 0 градусов также может быть выражено с использованием эквивалента заданного угла (0 градусов) в радианах (0 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 0 градусов = 0° × (π/180°) рад = 0π или 0 . . .
∴ sin 0° = sin(0) = 0
Объяснение:
Для sin 0 градусов угол 0° лежит на положительной оси x. Таким образом, значение sin 0° = 0
Таким образом, значение sin 0° = 0
Поскольку функция синуса является периодической функцией, мы можем представить sin 0° как sin 0 градусов = sin(0° + n × 360°), n ∈ Z.
⇒ sin 0° = sin 360° = sin 720° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-0°) = -sin(0°) = 0.
Методы нахождения значения Sin 0 градусов
Значение sin 0° задается как 0. Мы можем найти значение sin 0 градусов по:
- Используя тригонометрические функции
- Использование Unit Circle
Sin 0° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 0 градусов как:
- ± √(1-cos²(0°))
- ± тангенс 0°/√(1 + тангенс²(0°))
- ± 1/√(1 + раскладушка²(0°))
- ± √(сек²(0°) — 1)/сек 0°
- 1/косек 0°
Примечание. Поскольку 0° лежит на положительной оси x, конечное значение sin 0° будет равно 0.
Мы можем использовать тригонометрические тождества, чтобы представить sin 0° как
- sin(180° — 0°) = sin 180°
- -sin(180° + 0°) = -sin 180°
- cos(90° — 0°) = cos 90°
- -cos(90° + 0°) = -cos 90°
Sin 0 градусов с использованием единичной окружности
Чтобы найти значение sin 0 градусов с помощью единичной окружности:
- Нарисуйте радиус единичной окружности r, чтобы образовать угол 0° с положительной осью x. Мы также знаем, что для греха 0° угол 0° соответствует точке (1, 0) на единичной окружности (поскольку это точка на единичной окружности на оси x).
- Синус 0 градусов равен координате y(0) точки пересечения(1, 0) единичной окружности и r.
Отсюда значение sin 0° = y = 0
☛ Также проверьте:
- sin 40 градусов
- грех 53 градуса
- грех 556 градусов
- грех 750 градусов
- грех 9 градусов
- грех 43 градуса
Примеры использования Sin 0 градусов
Пример 1.
 Найдите значение 5 sin(0°)/7 sin(90°).
Найдите значение 5 sin(0°)/7 sin(90°). Решение:
Используя тригонометрические значения, мы знаем, что значение sin(0°) = 0 и sin(90°) = 1.
⇒ значение 5 sin(0°)/7 sin(90°) = 0Пример 2: Упростить: 2 (sin 0° + sin 360°)
Решение:
Мы знаем sin 0° = sin 360° = 0
⇒ 2 (sin 0° + sin 360°) = 2(0) = 0Пример 3: Найдите значение cosec 0°, используя значение sin 0°.
Решение:
Так как sin 0° = 1/csc 0°
⇒ csc 0° = 1/0 = не определено (∞)
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 0 Degrees
Что такое Sin 0 Degrees?
Sin 0 градусов — значение тригонометрической функции синуса для угла, равного 0 градусов. Значение sin 0° равно 0.
Значение sin 0° равно 0.
Как найти значение Sin 0 градусов?
Значение sin 0 градусов можно рассчитать, построив угол 0° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности. Значение sin 0° равно координате y (0). ∴ sin 0° = 0,
Каково значение Sin 0° в единицах Sec 0°?
Поскольку функцию синуса можно представить с помощью функции секанса, мы можем записать sin 0° как √(sec²(0°) — 1)/sec 0°. Значение sec 0° равно 1.
Как найти Sin 0° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 0° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(0°))
- ± тангенс 0°/√(1 + тангенс²(0°))
- ± 1/√(1 + раскладушка²(0°))
- ± √(сек²(0°) — 1)/сек 0°
- 1/косек 0°
☛ Также проверьте: таблицу тригонометрии
Каково значение Sin 0 градусов в пересчете на Cos 0°?
Используя тригонометрические тождества, мы можем записать sin 0° через cos 0° как sin(0°) = √(1-cos²(0°)). Здесь значение cos 0° равно 1.
Здесь значение cos 0° равно 1.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядная учебная программа
Sin 0 Степень — значение, расчет, вывод, методы и часто задаваемые вопросы
Формальное определение функции Sin может быть выражено в форме отношения длин противоположной стороны и гипотенузы любого данного треугольника. На самом деле функция синуса записывается как , когда угол прямоугольного треугольника задается как ноль градусов. В прямоугольном треугольнике с нулевым градусом длина противоположной стороны равна нулю.
Тригонометрия — раздел математики и подраздел алгебры, связанный с измерением определенных функций углов и их применением в вычислениях. Примером тригонометрии, который легко понять, является то, что архитекторы используют для расчета любых конкретных расстояний.
Алгебра и тригонометрия — две основные области математики. Алгебра включает в себя изучение математики с использованием определенных формул, правил, уравнений и других переменных.
Основные функции угла
Шесть основных функций угла, которые обычно используются в тригонометрии:
котангенс (cot),
секанс (сек) и
косеканс (CSC).
Значение греха 0
Немного о тригонометрии и тригонометрических соотношениях-
Тригонометрические соотношения в тригонометрии получаются из трех сторон прямоугольного треугольника, в основном гипотенузы, основания (прилегающего ) и перпендикуляр (противоположный).
В соответствии с тригонометрическими соотношениями в математике существуют три основных или первичных тригонометрических соотношения, также известных как тригонометрические тождества.
 9{\circ}} Value = \theta\]
9{\circ}} Value = \theta\]Вот основные тригонометрические функции!
Основными тригонометрическими функциями являются косинус, синус и тангенс. Значение Sin 0 градусов и другие тригонометрические отношения используются для общих углов, таких как 0 °, 30 °, 45 °, 60 °, 90 °, которые используются в тригонометрических уравнениях и расчетах.
Наименование
Аббревиатура
Связь 902
- 301
Sine
Sin
\[Sin (\theta)\]= Opposite/Hypotenuse
CoSine
Cos
\[Cos (\theta) \] = Прилегающая/гипотенуза
Tangent
TAN
\ [TAN (\ THETA) \] = противоположный/соседний Треугольник есть?
Рассмотрим прямоугольный треугольник ABC, у которого три стороны, а именно противолежащая, прилежащая и гипотенуза.
 В прямоугольном треугольнике мы обычно ссылаемся на три стороны в соответствии с их отношением к углу. Маленький прямоугольник в правом углу треугольника, приведенного ниже, обозначает прямой угол, равный 90°.
В прямоугольном треугольнике мы обычно ссылаемся на три стороны в соответствии с их отношением к углу. Маленький прямоугольник в правом углу треугольника, приведенного ниже, обозначает прямой угол, равный 90°.(Изображение будет обновлено в ближайшее время)
Три стороны прямоугольного треугольника следующие:
Сторона, противоположная прямому углу, является самой длинной стороной треугольника, которая известна как гипотенуза (H ). 9{2}\]
Поскольку наш угол интереса равен Sin 0. Соответственно, функция Sin угла или Sin 0 градусов равна отношению длины противоположной стороны к длине гипотенузы (самая длинная сторона ).
Формула Sin 0 —
Значение Sin 0 = Противоположная сторона/Гипотенуза проверьте координаты точек на плоскости x и y. Sin 0 означает, что значение координаты x равно 1, а значение координаты y равно 0, то есть координаты (x, y) равны (1, 0), что означает, что значение Когда мы размещаем значения в отношении Sin для θ = 0 °, заменив перпендикулярную сторону = 1 и гипотенузу = 0,
Получаем,
Sin 0⁰ = 0/1
Или
Sin 0⁰ = 0
Теперь, когда мы записываем обратное значение Sin Degrees, мы получаем значения cos Degrees.

Как мы знаем, Sin θ = 1/Cos θ
Следовательно, теперь мы можем записать значения Sin и cos под разными углами.
SIN 0 ° = COS 90 ° = 0
SIN 30 ° = COS 60 ° = ½
SIN 30 °.0003
SIN 60 ° = COS 30 ° = √3/2
SIN 90 ° = COS 0 ° = 1
10003
. мы получаем значения cos и Sin Degrees.
Как мы знаем, что значение TAN θ = sin θ / cos θ
Следовательно,
TAN 0 ° = SIN 0 ° / COS 0 ° = 0 0003
8888888888888888888888888888888888888888888888888889 гг. Tan 30°=Sin 30°/Cos 30°= 1/√3 TAN 45 ° = SIN 45 °/COS 45 ° = 1
TAN 60 ° = SIN 60 °/COS 60 ° = √3
88888888888888888999999999999999999999999999999999999999999999999999999999989998989н.  90°/Cos 90°=не определено
90°/Cos 90°=не определеноТаблица, показывающая различные значения Sin, Cos и Tan для разных углов.
Angles in Degrees
0⁰
30⁰
45⁰
60⁰
90⁰
Sin
0
1/2
1/√2
√3/2
1
Cos
1
√3/2
1/√2
1/2
0
Tan
0
1/√3
1
√ 3
Not defined
Cosec
Not defined
2
√ 2
2/√ 3
1
Sec
1
2/√3
√ 2
2
Not defined
Cot
Not defined
√3
1
1/√3
0
Таблица, показывающая различные значения Sin, Cos и Tan по отношению к радианам.

Angle
0⁰
30⁰
45⁰
60⁰
90⁰
180⁰
270⁰
360⁰
Radian
0
π/6
π/4
π/3
29292929299 2 9292929292999π/3
- 29292929292929299
.0003
π
3π/2
2π
Вопросы.
Соль. Поскольку мы знаем, что значение Sin 90⁰ = 1
А значение Cos 90⁰ = 0
Подставляя значения Sin 90⁰ и Cos 90⁰ ,
Следовательно, Sin 90⁰ + Cos 90⁰ = 1 + 0
- 301
2. Чему равно Sin 270⁰ + 2 Tan 45⁰.
Чему равно Sin 270⁰ + 2 Tan 45⁰.
Соль. Поскольку мы знаем, что значение Sin 270⁰ = -1
А значение Tan 45⁰ = 1
Подставляя значения Sin 270⁰ и Tan 45⁰ ,
Следовательно, Sin 270⁰ + 2Tan 45⁰ = -1+2×1 = -1+2 = 1
Забавные факты
Синус, обратный, обозначается как Sin-1, а также может быть записан как arcSin или синус
Гиппарх известен как отец тригонометрии. Величина дуги и хорды для ряда углов была открыта им
Применение тригонометрии, которое вам необходимо знать-
Тригонометрические отношения помогают нам найти недостающие углы и недостающие стороны треугольника.
Тригонометрия широко используется строителями для измерения высоты и расстояния до здания с его точки зрения.

Он также используется учащимися для решения вопросов по тригонометрии.
Время викторины
1. Если x и y считать дополнительными углами, то какое из следующих утверждений верно?
а. Tan x = Tan y
b. Sin x=Sin y
c. Cos x= Cos y
d. Sec x= Cosec y
Ответ: Вариант d
2. Каково будет значение Sin 150°?
1/5
2
1/2
1
ANS: опция C 903
- 1112
ANS: опция C 903
1112ANS: опция C 903
91112ANS: опция C 903
1112ANS: опция 9023 9022
ANS.

 Найдите значение 5 sin(0°)/7 sin(90°).
Найдите значение 5 sin(0°)/7 sin(90°).  9{\circ}} Value = \theta\]
9{\circ}} Value = \theta\] В прямоугольном треугольнике мы обычно ссылаемся на три стороны в соответствии с их отношением к углу. Маленький прямоугольник в правом углу треугольника, приведенного ниже, обозначает прямой угол, равный 90°.
В прямоугольном треугольнике мы обычно ссылаемся на три стороны в соответствии с их отношением к углу. Маленький прямоугольник в правом углу треугольника, приведенного ниже, обозначает прямой угол, равный 90°.
 90°/Cos 90°=не определено
90°/Cos 90°=не определено