Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
03.14
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В гараже в одном ряду было 25 машин,а в другом -32.
cos(-2x)=-3/2
Задача
задача
Пользуйтесь нашим приложением
Divinity: Original Sin 2
Previous Next
Добавляй новости, загружай моды и читы, пиши обзоры и гайды, задавай вопросы на форуме, загружай арты и скриншоты в галерею.
Получай за это бонусы, которые можно тратить на ценные призы.
40 ЧИТОВ для Divinity: Original Sin 2 в категориях Исправления, Редакторы, Сохранения, Таблицы, Трейнеры
, Чит-моды| Кино и сериалы
По словам Джеймса Ганна, Disney не вмешивалась в создание «Стражей Галактики 3»
| Трейлеры
Улучшенную версию The Witcher 3 сравнили с демоверсией на E3 2014
| Кино и сериалы
Хью Джекман подтвердил временную линию «Дэдпула 3» и рассказал о реакции режиссера «Логана»
| Трейлеры
Разработка Granblue Fantasy Re:Link почти завершена, а новая информация появится в январе 2023 года
Для Kingdom Come: Deliverance наконец-то выйдет «родная» озвучка
| Скриншоты
Новый скриншот Atomic Heart показывает жуткую зимнюю атмосферу
| Индустрия
Factorio продалась тиражом в 3,5 миллиона копий
| Кино и сериалы
Создатель «Истории игрушек» раскритиковал мультфильм «Базз Лайтер»
| Индустрия
Elden Ring официально стала главной игрой 2022 года, заработав 106 наград от критиков и геймеров
Завтра покажут новый геймплейный трейлер S.
| Кино и сериалы
«Достать ножи: Стеклянная луковица» стал настоящим хитом на Netflix
| Индустрия
Разработчики Dead Island 2 рассказали, почему не стали менять сеттинг в игре
Создатели Cyberpunk: Edgerunners представили новую иллюстрацию в честь приближающихся праздников
| Индустрия
Японские разработчики раскрыли планы на 2023 год: Множество долгожданных анонсов от Konami и новости о Dragon’s Dogma 2
| Трейлеры
Новый геймплей S.T.A.L.K.E.R. 2: Heart of Chornobyl
Илон Маск стал первым человеком в мире, потерявшим 200 миллиардов долларов
| Кино и сериалы
Кевин Смит готовится наконец-то снять фильм «Челюсти лося»
2(C)=2\sin(A)\sin(B) \cos(C)$, если $A+B+C=180$ градусовспросил
Изменено 7 лет, 1 месяц назад
Просмотрено 24к раз
$\begingroup$
Смиренно прошу помощи в этом вопросе.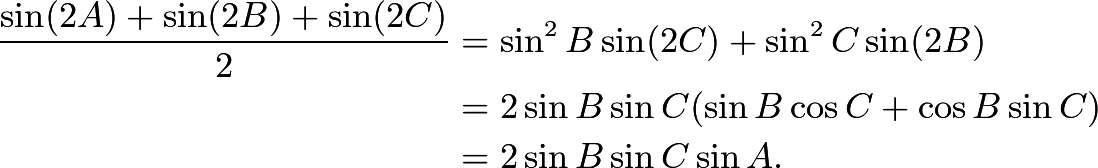
- тригонометрия
$\endgroup$
3
$\begingroup$
Это тождество можно вывести из сочетания закона синусов и закона косинусов.
Закон синусов гласит, что для трех углов $A$, $B$, $C$ треугольника с противоположными сторонами $a$, $b$, $c$ имеем $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = d. $$ Последнее равенство просто определяет $d$, и его можно опустить, но все равно будет формулировка закона синусов. Обычное значение $d$ на самом деле является диаметром описанной окружности. 92 С $$ и есть ваша личность.
Это все еще оставляет проблему, как доказать закон синусов и закон косинусов. И если вы хотите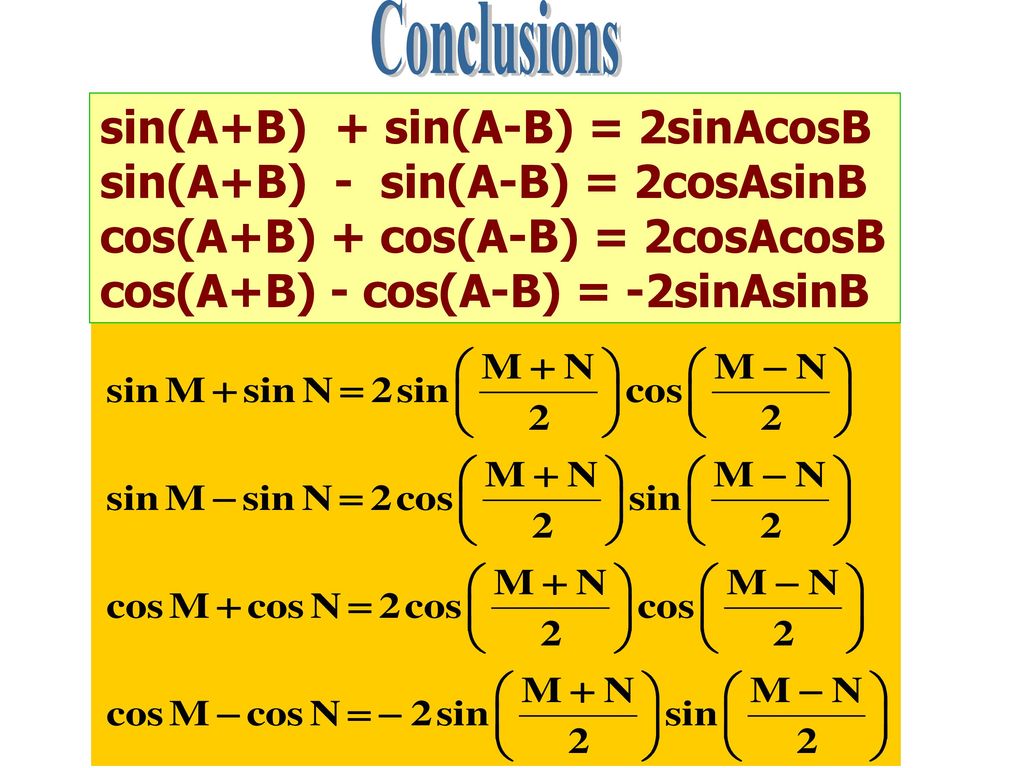 
Но если вы можете считать, что два закона уже установлены, то это делает это.
$\endgroup$
3
$\begingroup$ 92A+\sin{A} \sin(B-C)$
$=\sin{A}(\sin{A}+\sin(B-C))$
$=\sin{A}(\sin(B+) C)+\sin(B-C))$ заменив $\sin{A}$ на $\sin(B+C)$
$=\sin{A}(2\sin{B}\cos{C}) $
$ = 2 \ грех {A} \ грех {B} \ cos {C} $
$\endgroup$
3
$\begingroup$
Возможно, это не кратчайший путь, но он достаточно систематичен и не требует никаких хитростей. Во-первых, мы исключаем углы $C$ из уравнения, используя то, что $C = 180 — A — B$. Мы пишем $\sin(C) = \sin(180 — A — B) = \sin(A + B)$ и $\cos(C) = \cos(180 — A — B) = -\cos( A + B)$, и вам нужно доказать, что
$$\sin^2A + \sin^2B — \sin^2(A + B) = -2\sin A\sin B \cos(A+B)$$
Вставив сюда формулы сложения синуса и косинуса, то, что вам нужно доказать, становится
$$\sin^2A + \sin^2B — (\sin A\cos B + \cos A \sin B)^2 = -2\sin A \sin B(\cos A \cos B — \sin A \ грех Б)$$
Записывая это, становится
$$\sin^2A + \sin^2B — \sin^2 A\cos^2 B — 2\sin A \cos A \sin B \cos B -\cos^2 A \sin^2B$$
$$ = -2\sin A\sin B \cos A \cos B + 2\sin^2 A \sin^2 B$$
Отменяя условия, ваша цель — доказать
$$\sin^2A + \sin^2B — \sin^2 A\cos^2 B-\cos^2 A \sin^2B = 2\sin^2 A \sin^2 B$$
Эквивалентно,
$$\sin^2A(1 — \cos^2B) + \sin^2B(1 — \cos^2A) = 2\sin^2 A \sin^2 B$$
Последнее равенство верно, поскольку $1 — \cos^2 = \sin^2$.