Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Идеальный пружинный маятник совершает колебания так, как показано на рисунке, последовательно проходя положения « 1 », « 2 », « 3 », « 4 » и « 5 ». Заполни пропуски в утверждениях, выбрав и отметив
Заполни пропуски в утверждениях, выбрав и отметив
При взаимодействии водяных паров объемом 16.8 л (н.у)с раскаленным железом получился водород 12л (н.у),а второй продукт-оксид железа 2. Вычислите выход водорода (в%) от теоретически возможного.
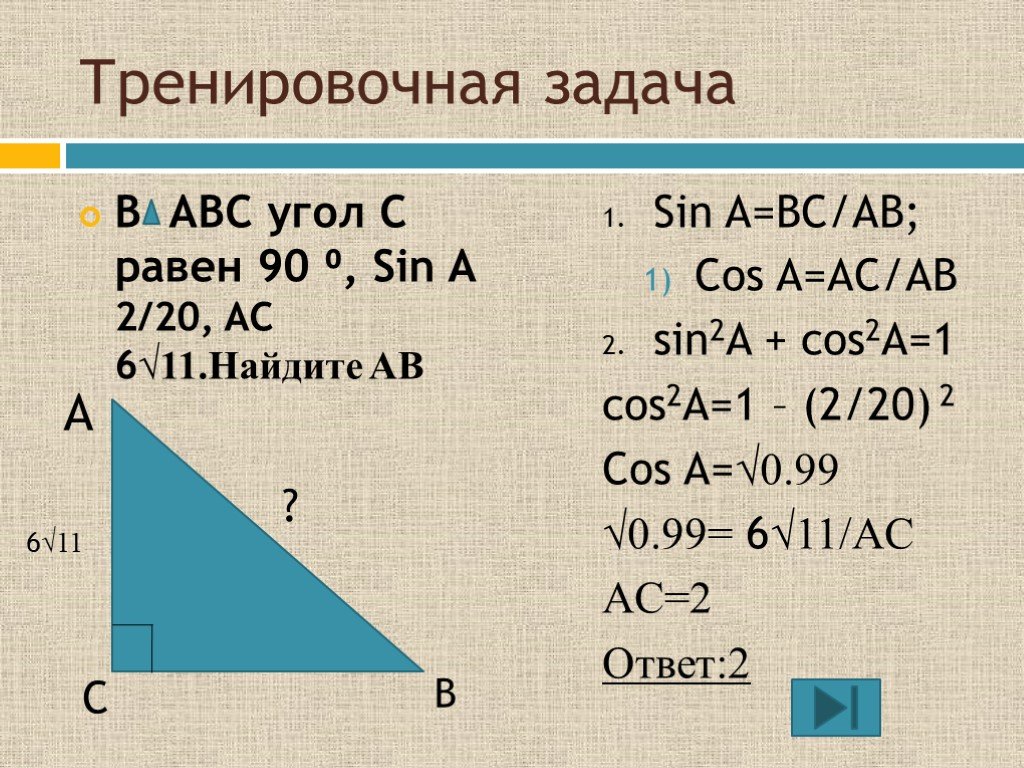
Две стороны треугольника равны 7 и 8 см, а угол между ними равен 120 градусам. Найти третью сторону треугольника.
Решено
В треугольнике ABC известно что AB=3 BC=8 AC=7. Найдите косинус (COS) угла ABC. Помогите пожалуйста с решением-очень очень нужно. Спасибо.
AB//CD Mn=12 см Ac=4 см BD =6 см.найдите отрезок MB
Пользуйтесь нашим приложением
как вычислить двойной угол синуса :: SYL.ru
Зимой комнатным цветам нужна помощь. Как подкормить растения
Двойное омбре на ногтях: как самостоятельно сделать завораживающий маникюр
Помада телесного цвета: пять шагов к более полным губам и утонченному макияжу
Не навязанные обществом, а собственные: как определить жизненные ценности
Челка-шторка идеально сочетается с любой стрижкой: 10 идей для женщин 60+
“Многие желания рождаются и тухнут”: Зоя Яровицына рассказала о своих привычках
Панк и гранж: каким будет новогодний макияж в этом году (свежие тренды)
Трендовые короткие стрижки 2023: правила выбора прически для круглого лица
Отменить изменения не получится: о чем многие забывают, делая химическую завивку
Любителям стиля бохо: организуйте уголок для чтения на полках цвета шалфея
Автор Надежда
Тригонометрия – один из разделов математики, в центре изучения которого находятся углы и взаимосвязи между ними. Основы науки закладываются в школьные годы, когда вводятся определения функций угла. В дальнейшем полученная база используется при освоении астрономии, приборостроения, архитектуры и других областей знаний. Как и любая точная наука, тригонометрия не обходится без формул. Практическое применение нашли выражения для определения двойного аргумента. Например, прибегая к соответствующему уравнению, легко можно узнать двойной угол синуса.
Основы науки закладываются в школьные годы, когда вводятся определения функций угла. В дальнейшем полученная база используется при освоении астрономии, приборостроения, архитектуры и других областей знаний. Как и любая точная наука, тригонометрия не обходится без формул. Практическое применение нашли выражения для определения двойного аргумента. Например, прибегая к соответствующему уравнению, легко можно узнать двойной угол синуса.
Тригонометрическое выражение для расчёта
Выражение просто записывается и запоминается: синус двойного угла вычисляется как двукратное произведение синуса и косинуса одинарного аргумента.
Эта формула выводится на основе выражения синуса суммы углов (Q1 + Q2):
sin(Q1 + Q2) = sin Q1 * cos Q1 + sin Q2 * cos Q2.
Полагая, что заданные углы равны друг другу, формула записывается в привычной форме.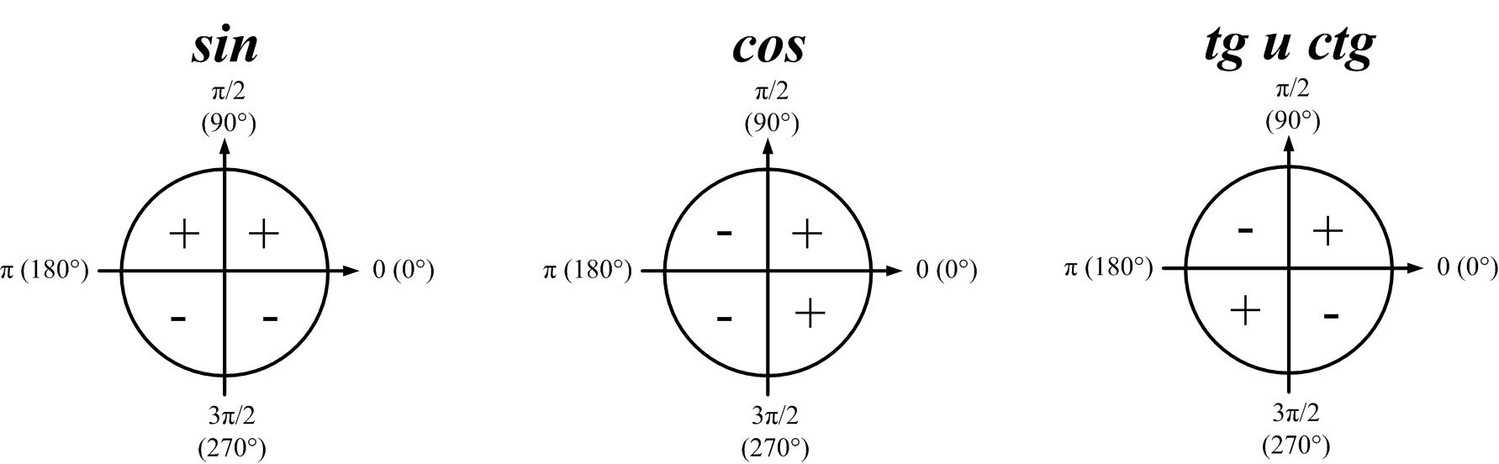
Использовать выражение можно при любых значениях аргумента функции. Вычислить двойной угол синуса по ней достаточно просто, убедиться в этом помогут примеры ниже.
Пример использования
Вот несколько иллюстраций применения полученной формулы. Пусть требуется рассчитать значение тригонометрической функции синуса угла равного 60 градусам. Соответствующий одинарный угол составит 30 градусов. Поскольку величины синуса и косинуса угла в 30 градусов известны, двойной угол синуса составит sin 60 = 2 * sin 30 * cos 30.
Формула используется не только для вычисления «вручную», найти значения по ней можно и с помощью математических пакетов или таблиц MS Excel.
Несмотря на простоту тригонометрического тождества, оно вызывает затруднения у выпускников школы. Именно на это рассчитывают разработчики заданий ЕГЭ, предлагая тесты на проверку основных формул. Вывод – формулу, чтобы подсчитать двойной угол синуса, нужно знать наизусть!
Похожие статьи
- Тригонометрия с нуля: основные понятия, история
- Что такое синус и косинус в тригонометрии?
- Четыре формулы, по которым можно вычислить площадь ромба.
 Свойства ромба
Свойства ромба - Закон преломления света: формулировка и практическое применение
- Как найти гипотенузу: 4 способа поиска ответа
- Площадь трапеции: формулы и методика вычислений
- Линейка логарифмическая – забытое счетное устройство из прошлого?
Также читайте
Аналитическая тригонометрия двухугольных тождеств
- Home /
- Pre-Calculus /
- Аналитическая тригонометрия /
- Темы /
- Триг-идентификаторы /
- Двойной угла идентификации
- .
- Введение
- Темы
- Графические тригонометрические функции
- Периодичность и симметрия
- Обратные тригонометрические функции
- Формулы триг.

- В реальном мире
- Примеры
- Упражнения
- Викторины
- Условия
- Раздаточный материал
- Лучшее из Интернета
- Содержание
- НАЗАД
- СЛЕДУЮЩИЙ
- НАЗАД
- СЛЕДУЮЩИЙ
- Формулы двойного угла являются тождествами.
 То есть они всегда верны .
То есть они всегда верны .
Перед каждым из них можно было бы написать: «Для всех действительных чисел $\,x\,$…» - Напомним соглашение об использовании обозначения функций
с многобуквенными именами функций (например, ‘$\,\sin\,$’ и ‘$\,\cos\,$’):
скобки можно опустить, если нет путаницы в порядке операций.Таким образом, вы обычно видите ‘$\,\sin 2x\,$’ (без скобок) вместо ‘$\,\sin(2x)\,$’ (со скобками).
Оба ‘$\,\sin 2x\,$’ и ‘$\,\sin(2x)\,$’ представляют одно и то же:
- имя функции ‘$\,\sin\,$’ (произносится как «sine», длинное i)
- вход в функцию $\,2x\,$ 92 x — 1\,$
версия с участием только косинус Обратите внимание, что эти описания относятся к тому, что происходит в правой части формул.
Вывод формул двойного угла
Формулы двойного угла доказываются просто, как только формулы сложения для синуса и косинуса будут на месте.
Для всех действительных чисел $\,x\,$:$\sin 2x$ $=$ $\sin(x+x)$ (переименовать $\,2x\,$ в $\,x + x\,$) $=$ $\sin x\,\cos x + \cos x\,\sin x$ (формула сложения синуса) $=$ $2\sinx\,\cosx$ (добавьте похожие термины) $\cos 2x$ $=$ 92 х — 1} $$Геометрическое доказательство формул двойного угла для малых углов
Для наброска и вывода ниже предположим, что $\,x\,$ измеряется в градусах, а $\,2x Это другая «укладка» треугольников, чем в предыдущий урок, показать альтернативные подходы к доказательству.

- Начните с прямоугольного треугольника $\,\треугольник ABC\,$ (желтый).
Он имеет острый угол $\,x\,$ и гипотенузу длины $\,1\,$.
Таким образом:- нижняя часть: $\,\cos x\,$
- боковая нога: $\,\sin x\,$
- Сложите прямоугольный треугольник $\,\треугольник ACD\,$ (в основном зеленый)
на гипотенузе желтого треугольника.
Он также имеет острый угол $\,x\,$.
Нижняя ножка имеет длину $\,1\,$.- Поскольку $\,\cos x = \frac{\text{ADJ}}{\text{HYP}} = \frac{1}{\text{HYP}}\,$,
гипотеза имеет длину $\,\frac{1}{\cos x}\,$.
- Таким образом, боковая сторона равна $\,\frac{1}{\cos x}\cdot \sin x = \frac{\sin x}{\cos x}\,$.
- Поскольку $\,\cos x = \frac{\text{ADJ}}{\text{HYP}} = \frac{1}{\text{HYP}}\,$,
- синий прямоугольный треугольник:
- поскольку $\,\overline{EC}\, ||\, \overline{AB}\,$,
$\,\угол ACE = x\,$
(чередование внутренних углов) 92 х}{\cos х}\,$
- поскольку $\,\overline{EC}\, ||\, \overline{AB}\,$,
$\,\угол ACE = x\,$
- боковая нога: $\,\frac{\sin x}{\cos x}(\cos x) = \sin x\,$
Снова используя правый $\,\треугольник AFD\,$, получаем формулу синуса двойного угла: $$ \cssId{s119{\ грех 2x} \ \cssId{s120}{=\ \frac{\text{OPP}}{\text{HYP}}} \ \cssId{s121}{=\ \frac{\sin x +\sin x}{1/\cos x}} \ \cssId{s122}{=\ 2\sin x\,\cos x} $$Обзор: Определяет ли $\,\cos x\,$ однозначно $\,\sin x\,$? Нет!
Напомним, что каждое ненулевое действительное число однозначно определяется двумя вещами:
- его размер (расстояние от нуля)
- его знак (плюс-минус)
Этот факт часто имеет решающее значение при работе с тригонометрическими выражениями.

Часто зная значение тригонометрического выражения (например, $\,\cos x\,$) 90 156 позволяет правильно определить размер других тригонометрических выражений, но не знак .
Для получения правильного знака необходимо предоставить дополнительную информацию.Например, предположим, что вы знаете, что $\,\cos x = \frac 45\,$, и ничего больше .
Позволяет ли это нам однозначно определить $\,\sin x\,$?
Нет!
Это дает размер $\,\sin x\,$, но не знак , как показано ниже:- Знание $\,\cos x = \frac 45\,$ помещает конечную точку для $\,x\,$ в любой квадрант I (точка $\,A\,$)
или квадрант IV (точка $\,B\,$), как показано справа. 92} \
\cssId{s144}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s145}{=\ \frac{9}{25}}
$$
Таким образом, $\sin x = \pm \frac{3}{5}\,$.
92} \
\cssId{s144}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s145}{=\ \frac{9}{25}}
$$
Таким образом, $\sin x = \pm \frac{3}{5}\,$.
Размер $\,\sin x\,$ равен $\,\frac 35\,$. Знак неизвестен (без дополнительной информации).Существует различная дополнительная информация, которая может быть предоставлена определить знак $\,\sin x\,$. 
Вот несколько примеров:информация: следствие: информация: следствие: $\,x\,$ находится в квадранте I $\,\sin x\,$ положителен $\,x\,$ находится в квадранте IV $\,\sin x\,$ отрицательно $\csc х > 0$ косеканс есть величина, обратная синусу;
если косеканс положительный, то и синус;
$\,\sin x\,$ положителен$\csc х косеканс есть величина, обратная синусу;
если косеканс отрицательный, то и синус;
$\,\sin x\,$ отрицательно$\tan x > 0$ тангенс представляет собой синус над косинусом;
если косинус положительный
и тангенс положительный, тогда:
$\,\sin x\,$ положителен$\загар х тангенс представляет собой синус над косинусом;
если косинус положительный
, а тангенс отрицательный, то:
$\,\sin x\,$ отрицательноПример: использование формул двойного угла
Предположим, что $\displaystyle\,\cos x = \frac 45\,$ и $\,\csc x Найдите $\,\sin 2x\,$, $\,\cos 2x\,$ и $\,\tan 2x\,$.
 2} \
\cssId{s183}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s184}{=\ \frac{9{25}}\,$
2} \
\cssId{s183}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s184}{=\ \frac{9{25}}\,$
поэтому $\displaystyle\, \sin x = \pm \frac{3}{5}\,$.- Поскольку $\displaystyle\,\csc x := \frac{1}{\sin x}
- Вместе $\,\displaystyle\sin x = -\frac{3}{5}\,$.
- $\displaystyle \cssId{s1892 — 1} \ \cssId{s196}{=\ 2\cdot\frac{16}{25} — \frac{25}{25}}\ \cssId{s197}{=\ \frac{7}{25}}$
(можно использовать любую из трех формул косинуса двойного угла.
Выбранный здесь вариант является «наиболее безопасным», поскольку он использует только с учетом «не вычисленной» информации.)- $\displaystyle \cssId{s200}{\загар 2x} \ \cssId{s201}{:=\ \frac{\sin 2x}{\cos 2x}}\ \cssId{s202}{=\ \frac{-\frac{24}{25}}{\frac{7}{25}}\cdot \frac{25}{25}}\ \cssId{s203}{=\ -\frac{24}{7}}$
Сложная дробь — это выражение, включающее «дроби внутри дробей», например $\,\displaystyle\frac{-\frac{24}{25}}{\frac{7}{25}}\,$.

Маленькие вопросы могут привести к большим событиям. Спросите своего друга: «Как прошел твой день сегодня?» может привести к 20-минутному разглагольствованию о пороках капитализма и о том, что их менеджер, в частности, является самым извращенным деспотом по эту сторону Саурона.
Вот еще один вопрос, который кажется достаточно простым: что произойдет, если мы попытаемся добавить угол самому себе? Это кажется простым, но приводит нас прямо к двухугольные тождества .
sin (α + α) = sin α cos α + cos α sin α = 2sin α cos α
Или, чтобы получить фактический двойной угол:
sin (2α) = 2sin α cos α
Вот так, серьезно. Самое простое доказательство, верно? Точно так же и косинус:
cos (2α) = cos (α + α) = cos α cos α – sin α sin α
= cos 2 α – sin 2 α
О, эй, треугольник в квадрате функции. Помните, что триггер 2 α точно такой же, как (триггер α) 2 . Но это не то же самое, что триг (α 2 ). Понятно?
Легкая череда открытий подряд не может длиться вечно, не так ли? Если кто-то и собирается это разрушить, так это по касательной. Тангент похож на профессионального организатора вечеринок.
Тангенс должен быть на разрыве или что-то в этом роде, потому что тождество двойного угла для тангенса тоже легко.
Мы не жалуемся.
Пример задачи
Найдите точное значение sin (120°).
Мы знаем все о синусе и косинусе 60°, поэтому давайте воспользуемся ими, а также нашей блестящей новой формулой двойного угла для синуса, чтобы получить sin (120°):
sin (120) = sin (2(60)) = 2sin (60) cos (60)
Обратите внимание, что это фактически то же самое значение, что и sin 60°. Что может стоять за таким совпадением? Как всегда, наша первая мысль — инопланетяне. Наша вторая мысль состоит в том, что опорный угол для 120° равен 60°, и что синус положителен в квадранте II.
Может быть, это и объясняет. Если инопланетяне были замешаны, они, должно быть, были супер хитрыми и супер бесполезными. Они даже ничего не сделали. Как лениво.
Процитировать эту страницу
Формулы двойного угла для синуса и косинуса
Формулы двойного угла для синуса и косинуса рассказывают, как найти синус
и косинус дважды угол ($\,2x\,$),
через синус и косинус исходного угла ($\,x\,$):

 02.21
02.21 Свойства ромба
Свойства ромба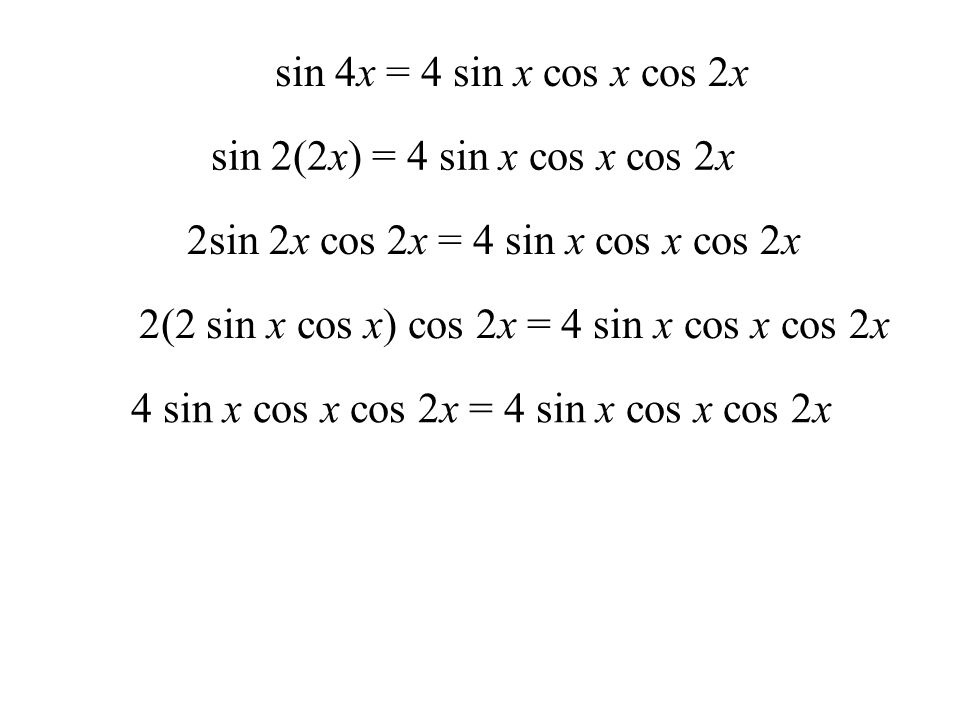
 То есть они всегда верны .
То есть они всегда верны . 





 2} \
\cssId{s183}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s184}{=\ \frac{9{25}}\,$
2} \
\cssId{s183}{=\ \frac{25}{25} — \frac{16}{25}}\
\cssId{s184}{=\ \frac{9{25}}\,$