Тригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки
В каждой профессии существуют свои инструменты, обеспечивающие решение и качественное выполнение определенных задач. Математики применяют тригонометрический круг, позволяющий легко и быстро вычислить значение какой-либо функции. Однако не все могут им правильно пользоваться, поскольку не понимают основных понятий.
Содержание
- Общие сведения
- Углы и их классификация
- Информация о функциях
- Тригонометрический круг
- Построение «инструмента»
- Готовый макет
- Правила использования
Общие сведения
Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.
Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.
Углы и их классификация
Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:
- Острые.
- Прямые.
- Тупые.

- Развернутые.
- Выпуклые.
- Полные.
К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).
Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла.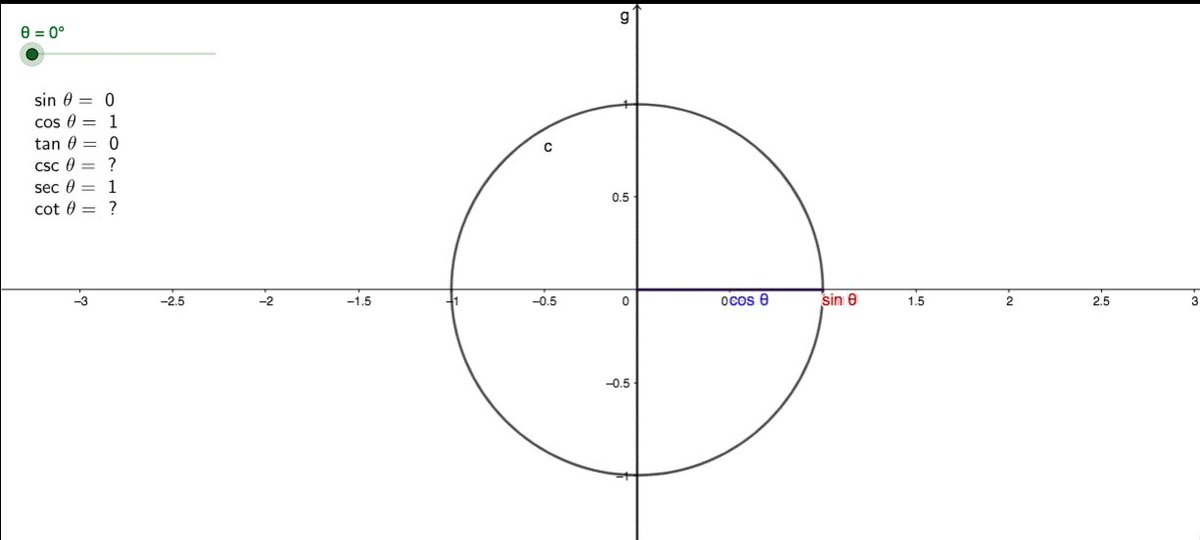 Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.
Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.
Информация о функциях
Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.
Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.
Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.
Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.
Тригонометрический круг
Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.
Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:
- a + b = 180.
- cos(a) = sin(b).
- cos(b) = sin(a).
- tg(a) = ctg(b).
- tg(b) = ctg(a).
- tg(a) = 1 / ctg(a).
- tg(b) = 1 / ctg(b).
Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.
Построение «инструмента»
Построить окружность, которая ускорит процесс решения задач, довольно просто.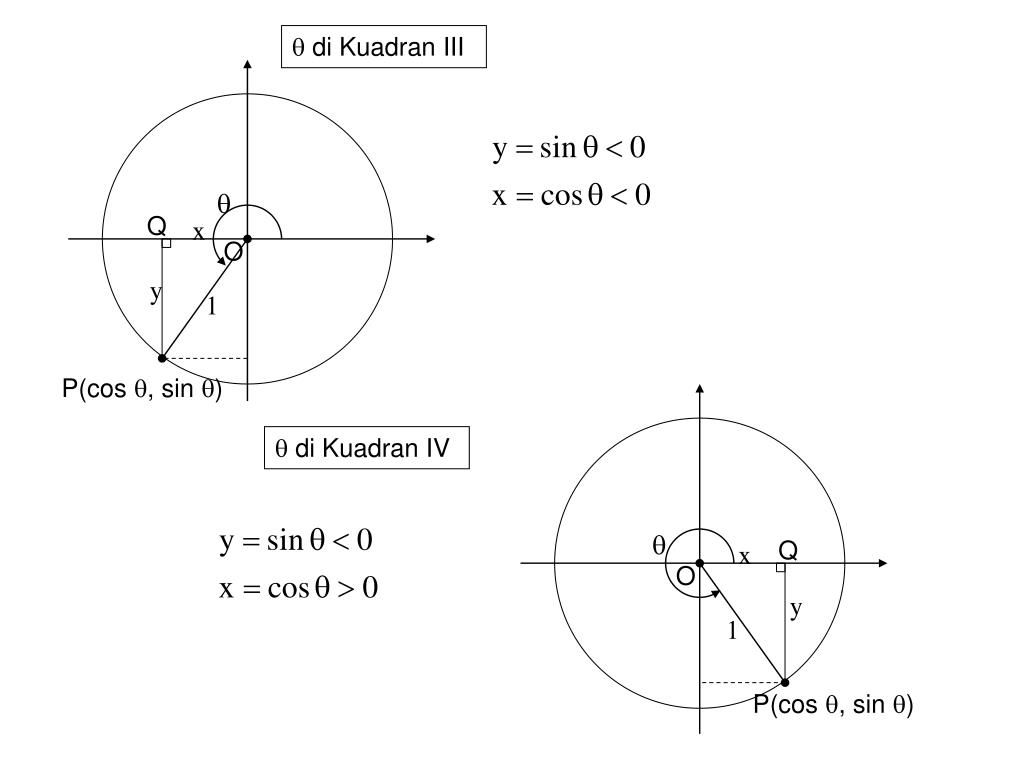 Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).
Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.
Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями.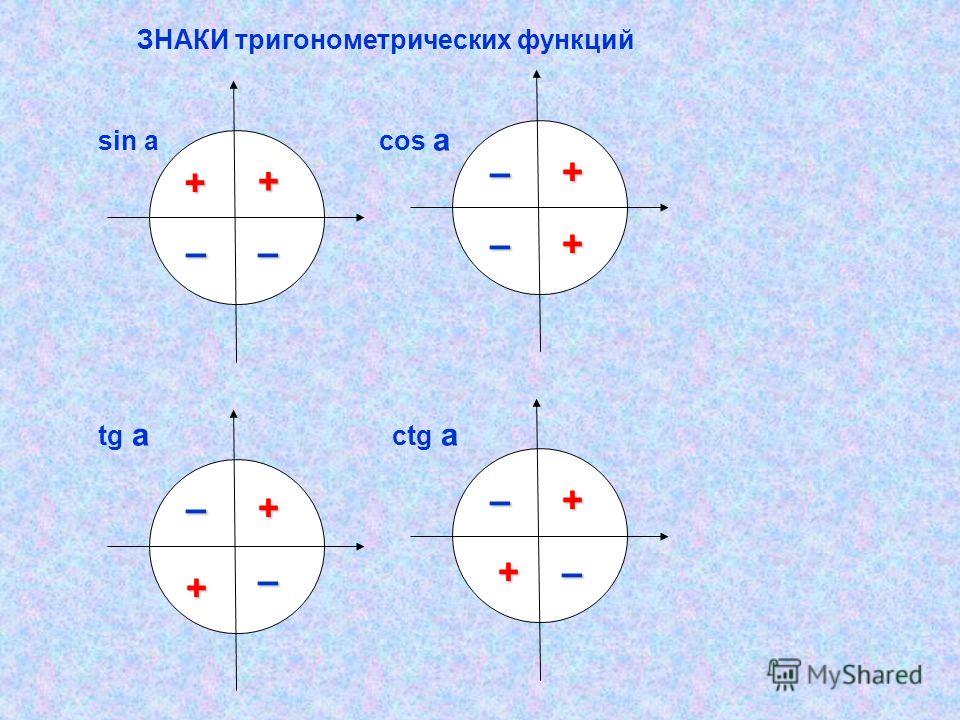 Их четыре:
Их четыре:
- Первая состоит из положительных координат по х и у.
- Вторая имеет по х отрицательные и положительные по у.
- Третья — только отрицательные значения.
- Четвертая — положительные значения по х и отрицательные по у.
Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).
Готовый макет
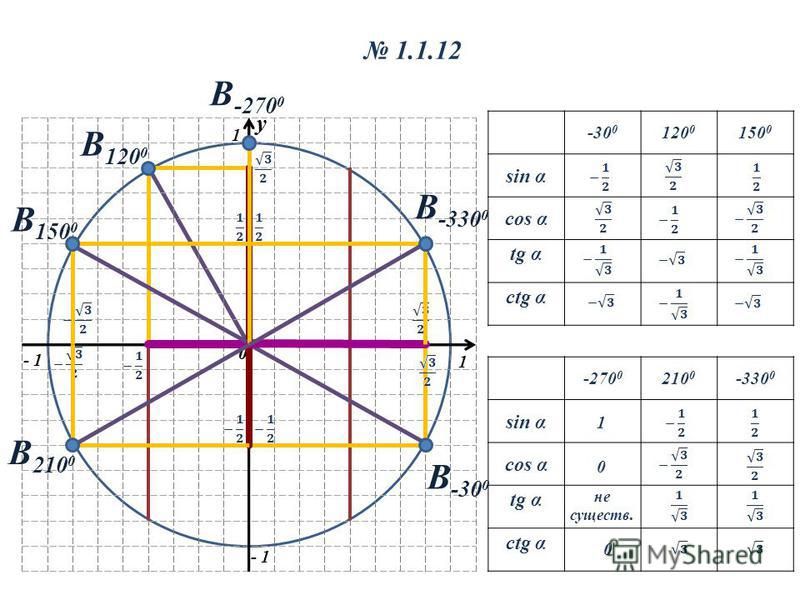
Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. 2] = sqrt(3) / 2.
2] = sqrt(3) / 2.
Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:
- Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
- Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).
Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:
- Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
 2 = 1.
2 = 1. - sin(45) + cos(45) = sqrt(2) / 2.
Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.
Правила использования
Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:
- Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
- На оси синусов значение составляет -1 (точка лежит на оси).
Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6).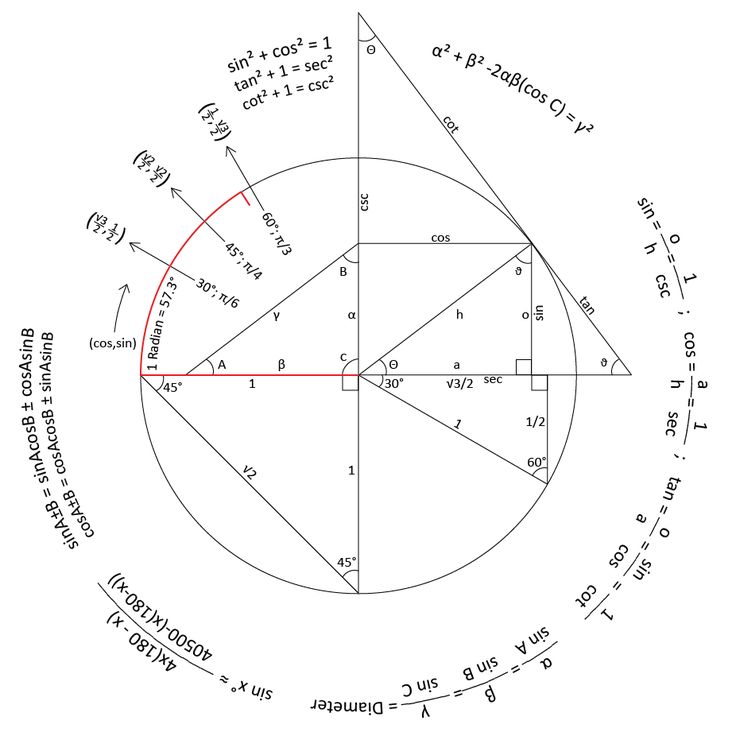 В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).
Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.
Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.
Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.
Предыдущая
АлгебраКак найти область определения функции заданной формулой, примеры и способы решения 10 класс, ручной и автоматизированный методы, онлайн-калькулятор
Следующая
АлгебраКак найти наибольшее и наименьшее значение функции алгоритм вычисления и нахождения наименьшего и наибольшего значения функции на отрезке, луче, промежутке, интервале
Ось синусов и косинусов.
 Тригонометрический круг. Основные значения тригонометрических функций
Тригонометрический круг. Основные значения тригонометрических функцийТригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень.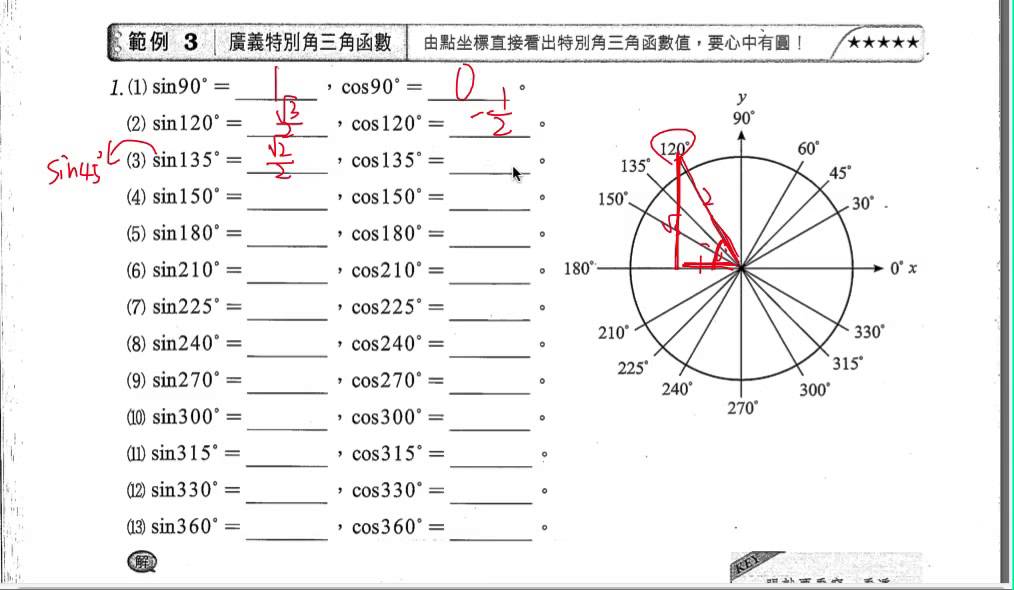 Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, углом какой координатной четверти является α . Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α .
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I
, II
, III
и IV
координатной четверти».
Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.
По определению синус угла α — это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.
В свою очередь косинус угла α — это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1 к абсциссе, а котангенс – отношение абсциссы точки A 1 к ординате. Тогда из правил деления чисел
с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1 одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1 различны. Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А
всегда будем попадать в точку А 1
на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1
.
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α — угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.
Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1
– точка, полученная в результате поворота начальной точки А(1, 0)
вокруг точки O
на угол α
, а точка А 2
– это результат поворота точки А
на угол −α
, противоположный углу α
.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб.
 для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7 - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора.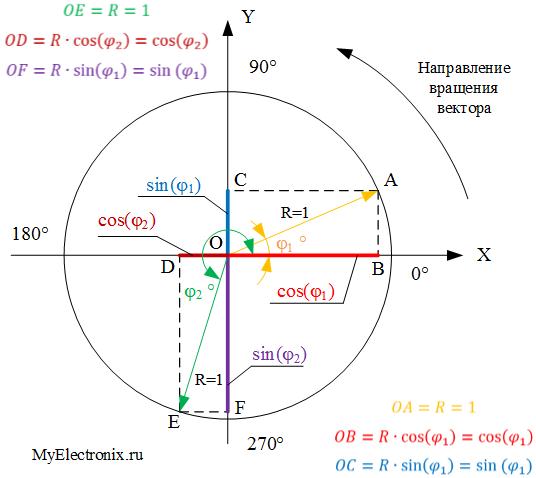 Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°.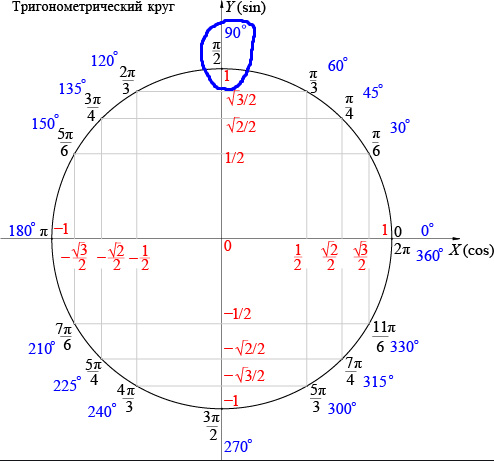 При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто.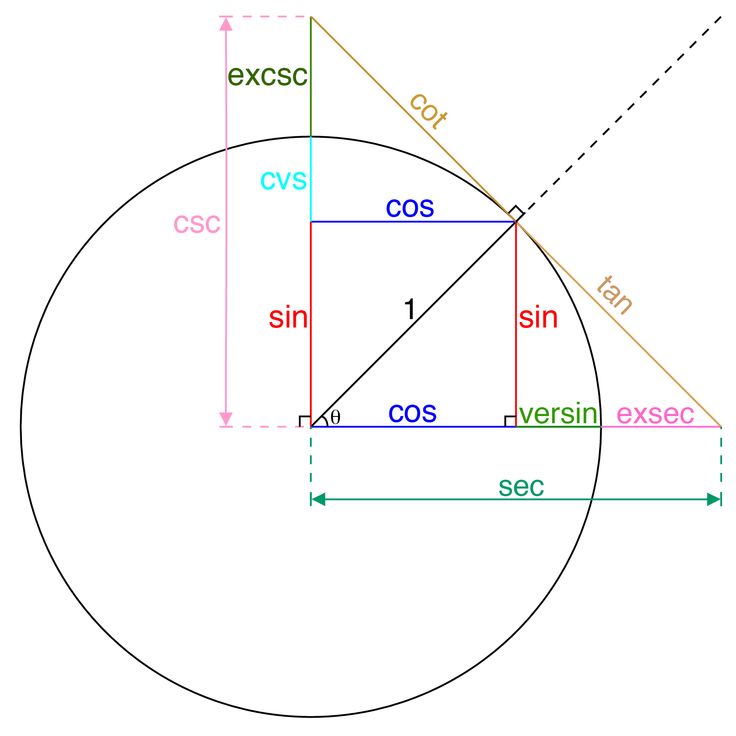 Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.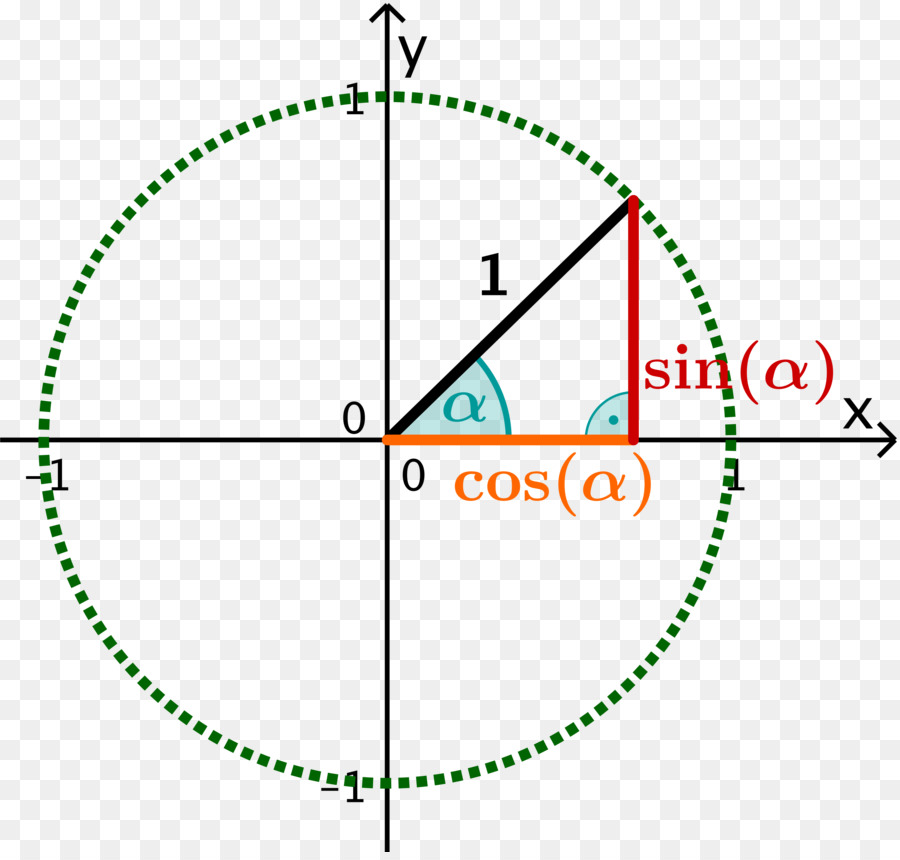
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Прежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.
Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).
Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).
Таким образом, наши формулы обретают иной вид.
Так как b = y , a = x , c = R, то:
y x
sin t = — , cos t = —.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y /x ,
ctg = x /y .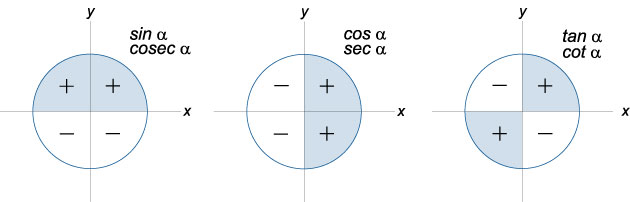
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = — = y ,
1
x
cos t = — = x .
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
Из формул тангенса и котангенса следует еще одна формула:
Уравнения числовой окружности.
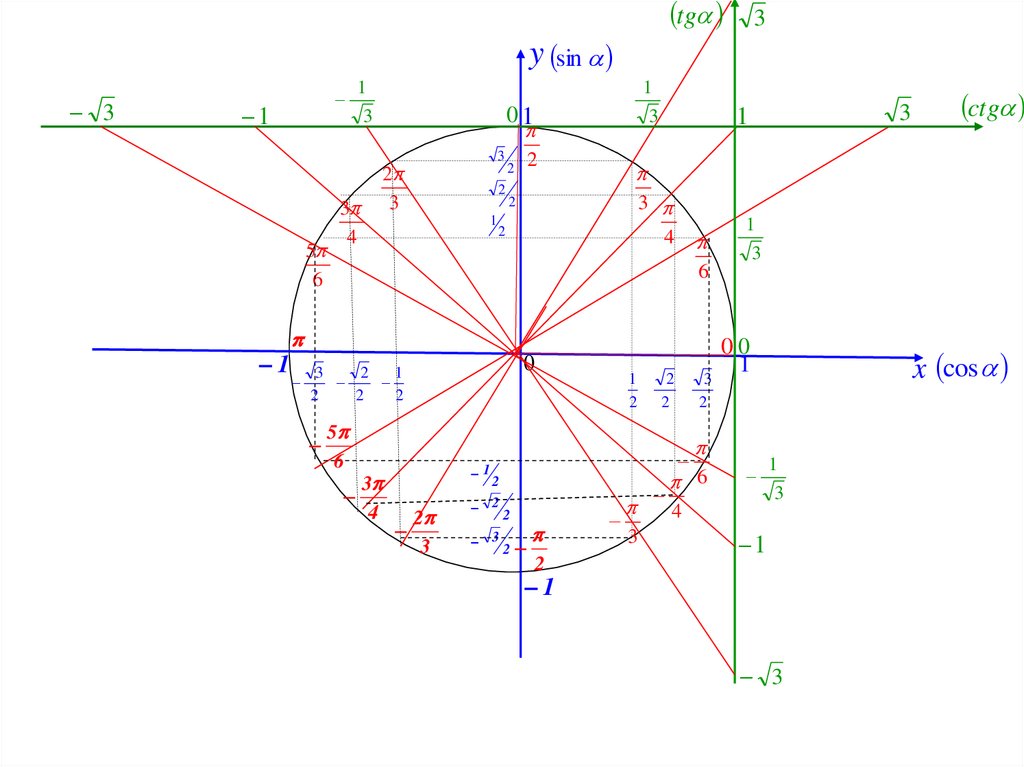
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть | |
Косинус и синус основных точек числовой окружности:
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; -; —; —; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси х ), разумеется, косинусы равны модулю 1 , а синусы равны 0.
На концах оси синусов (оси у ) синусы равны модулю 1 , а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.
И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.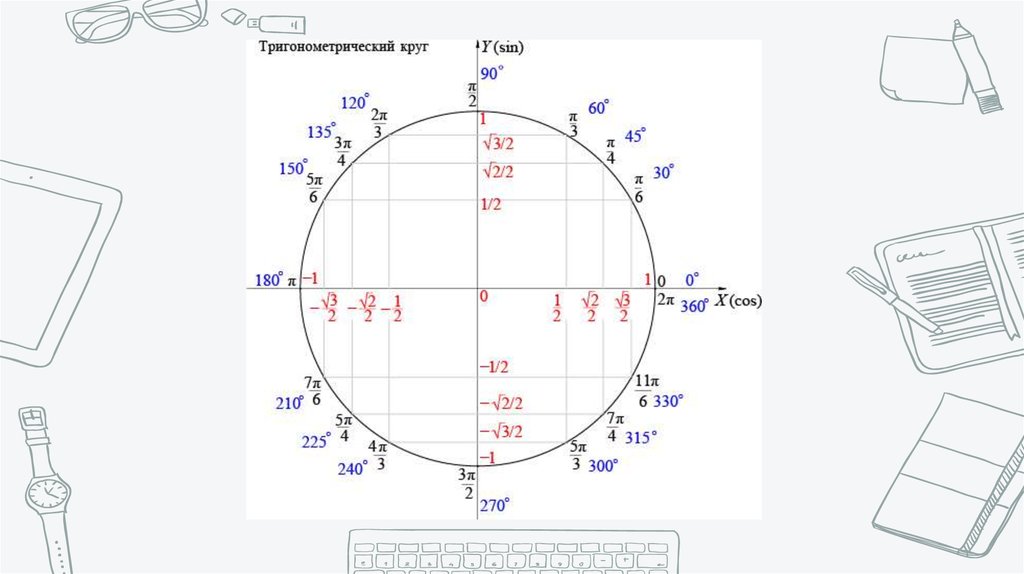
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать :
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).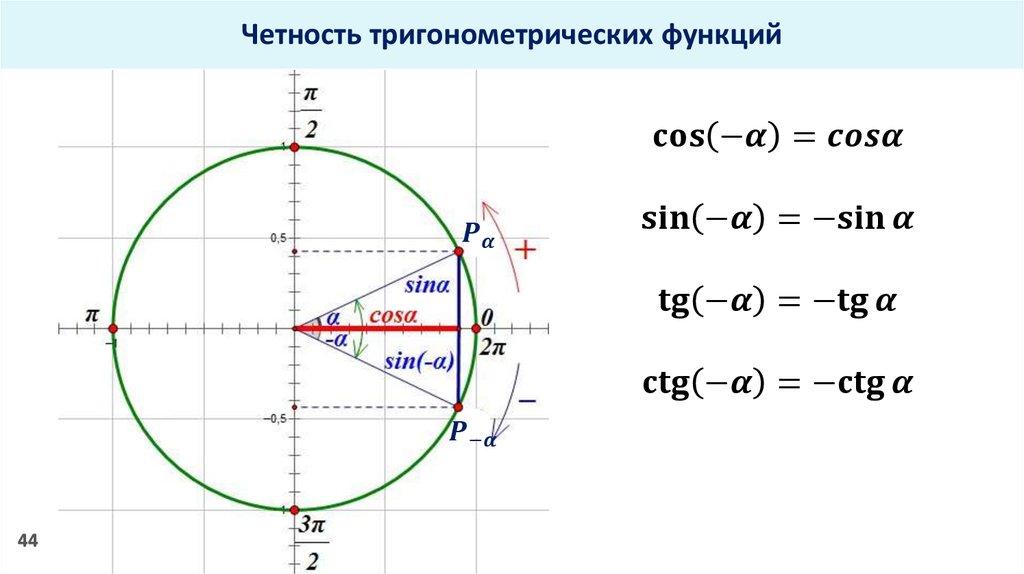
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; —; —; -; 0; – -; – —; – —; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
Тангенс и котангенс основных точек числовой окружности.
Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.
ПРИМЕЧАНИЕ : В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.
Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.
Как запомнить, где прочерки, а где нули? Поможет правило.
Тангенс – это отношение синуса к косинусу. На концах оси синусов (ось у ) тангенс не существует.
Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х ) котангенс не существует.
В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:
1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.
2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.
3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.
Не ошибитесь со знаками – и вы большой знаток.
Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см. числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.
числовую окружность выше или раздел «Возрастание и убывание тригонометрических функций»). Тогда еще лучше будет понятен и порядок чередования значений тангенса и котангенса.
Тригонометрические свойства чисел числовой окружности.
Представим, что определенная точка М имеет значение t.
Свойство 1 :
| | | |
Пояснение . Пусть t = –60º и t = –210º.
cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º и 60º равны как по модулю, так и по знаку: cos –60º = cos 60º.
cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.
cos (– t) = cos t.
sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.
sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.
Таким образом, мы доказали, что sin (– t) = – sin t.
Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.
Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.
Свойство 2: Так как t = t + 2πk , то:
| |
Пояснение
: t и t + 2πk – это одна и та же точка на числовой окружности. Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t. Значит, и равенства, изложенные в этой таблице, очевидны.
Значит, и равенства, изложенные в этой таблице, очевидны.
Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.
| | | |
Пояснение
: Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности.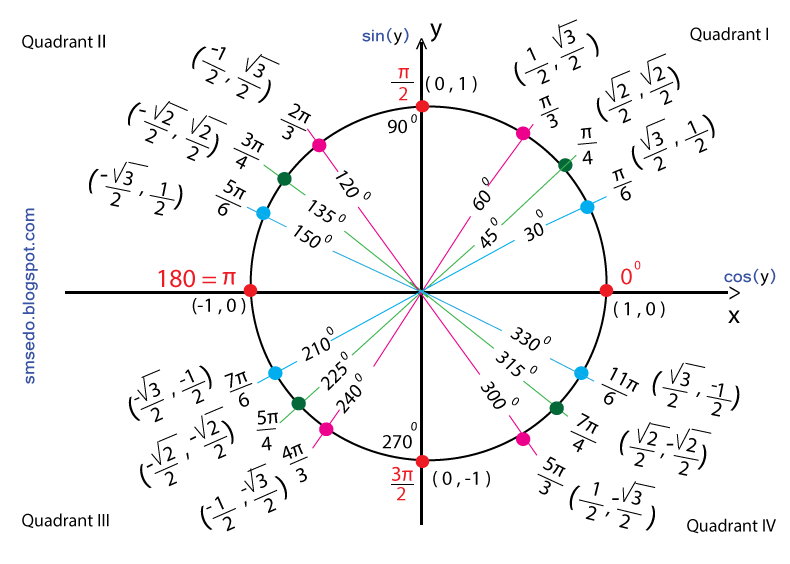 Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:
–sin t
tg (t + π) = —- = tg t
–cos t
–cos t
ctg (t + π) = —- = ctg t
–sin t
Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.
Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.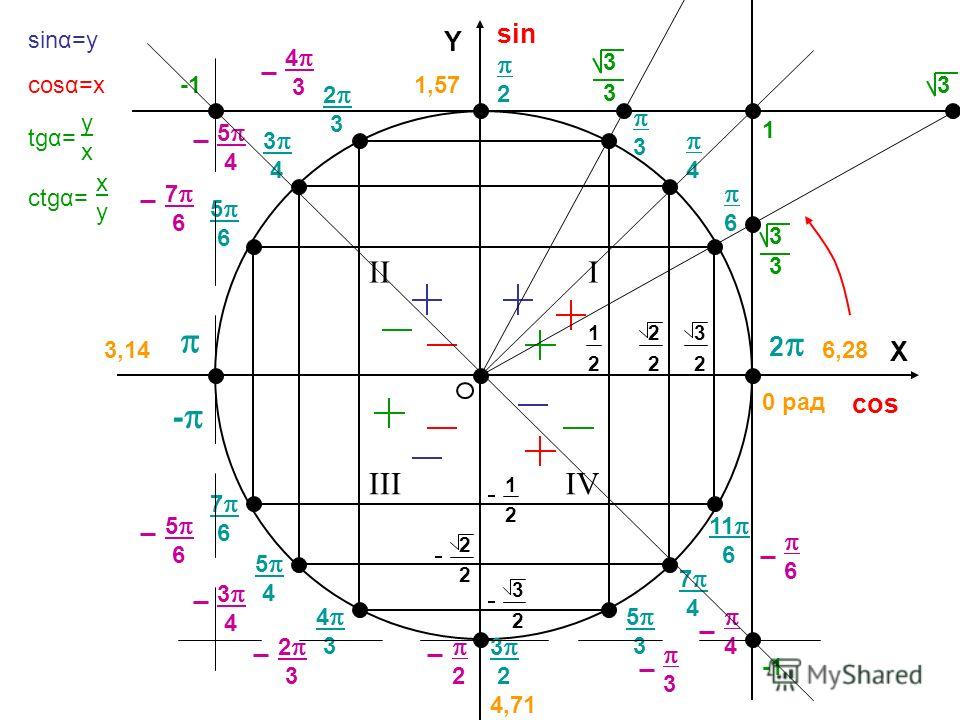
π | π |
Тригонометрический круг — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
у
1
Тригонометрический круг
Тригонометрический круг – это круг с радиусом равным
единице и с центром в начале координат.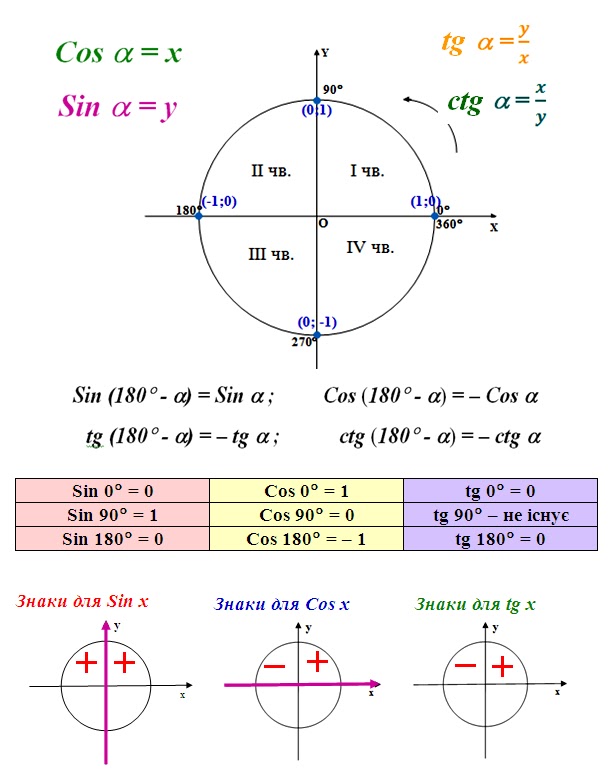
1
х
у
(0;1)
(1;0) х
(-1;0)
(0;-1)
Радиус R = 1
Градусная мера углов
Четверти круга
90
180
0
360
270
2
1
3
4
Углы
на тригонометрическом круге
у
Угол на круге определяется поворотом радиуса
+
х
—
За нулевое положение радиуса принято его положение на
положительном направлении оси Х.
Угол поворота радиуса отсчитывается от положительного направления оси Х: с
плюсом — против часовой стрелки, с минусом — по часовой стрелке.
у
у
х
х
Координаты положения радиуса
У
ордината
У
(х0;у0)
Х
Х
абсцисса
У
У
Х
Х
Радианная мера угла
Один радиан – это центральный угол, опирающийся на дугу равную радиусу
Длина окружности 2πR
В окружности 2πR : R = 2π радиан
2π соответствуют 360°
2π ————— 360°
90° = 180° /2 = π /2
π ————— 180°
270° = 90°· 3 = 3π /2
Радианная мера углов в круге
1,57
π /2
π
0
Так как π = 3,14…, то
3,14
0
6,28
2π
3π /2
4,71
Перевод градусов в радианы
Для перевода в радианы удобно пользоваться пропорцией.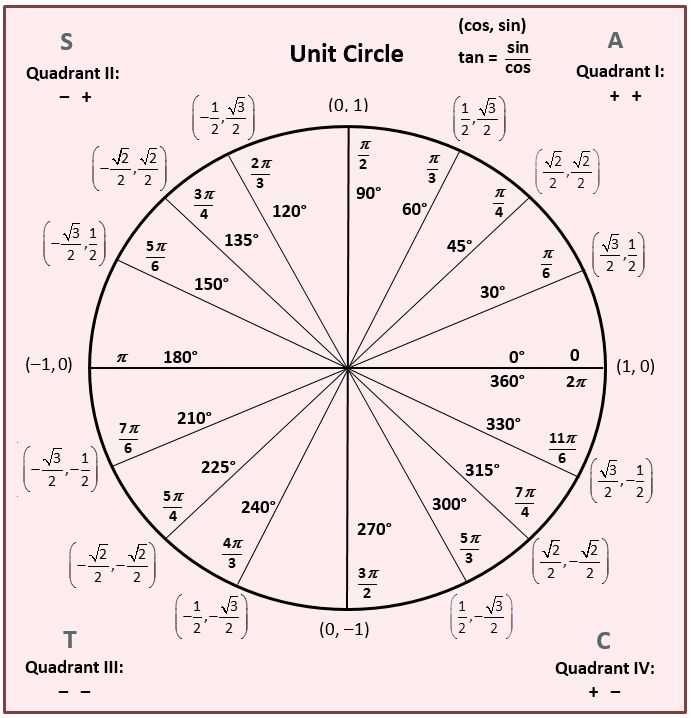
π ————— 180°
Перевести 120 в радианы.
180
120 х
Запомните!
2
120
x
180
3
30° = π /6
2
x
3
45° = π /4
60° = π /3
Перевод радиан в градусы
Подставьте вместо π 180° и сократите
Перевести 3π /4 в градусы.
3 3 180
135
4
4
Определение тригонометрических
функций
Повторение
α
У
α
В
противолеж.катет
sin
гипотенуза
ордината
А
О
sinα
Х
Заметим, ОА = R = 1
AB
sin
AB
OA
Синусом угла является ордината точки А на круге,
получающаяся при повороте радиуса на угол .
Синус угла α – это ордината (у) угла α
Определение тригонометрических
функций
Повторение
α
У
В
прилеж.катет
cos
гипотенуза
Заметим, ОА = R = 1
А
О
cosα
Х
OB
cos
OB
OA
абсцисса
Косинусом угла является абсцисса точки А на круге,
получающаяся при повороте радиуса на угол .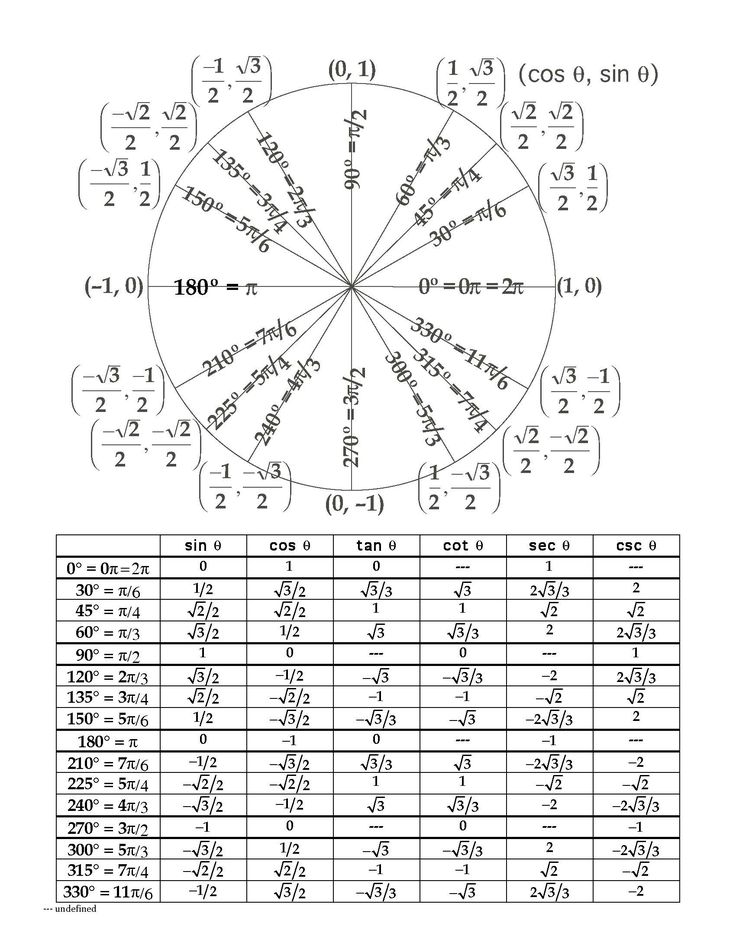
Косинус угла α – это абсцисса (х) угла α
Определение тригонометрических
функций
tgα, ctgα
Повторение
противолеж.катет
tg
прилеж.катет
прилеж.катет
ctg
противолеж.катет
α
У
А
О
В
Х
AB sin
tg
OB cos
OB cos
сtg
AB sin
У
М
Sin
Sin
Х
M
Запомни! Синус – это ордината (y)
cosα
У
Х
Абсцисса — cosα
2) Косинусом угла является абсцисса точки М на тригонометрическом круге,
получающаяся при повороте радиуса на угол .
У
М
cos
cos
Х
M
Запомни! косинус – это абсцисса (x)
tgα
Ось тангенсов, х = 1
У
В
Х
В
3) Тангенсом угла является ордината точки В на оси тангенсов ( х = 1 ),
получающаяся при пересечении продолжения радиуса с осью тангенсов при
повороте радиуса на угол .
3)tgα =
tgα =
сtgα
В
У
В
Ось котангенсов, у = 1
Х
4) Котангенсом угла является абсцисса точки В на оси котангенсов ( у = 1 ),
получающаяся при пересечении продолжения радиуса с осью котангенсов при
повороте радиуса на угол .
4)ctgα =
ctgα =
Значения тригонометрических функций
Диаметральные углы
(0;1)
π
(-1;0)
3π/2
0
π/2
π
3π/2 2π
у
0
1
0
-1
0
0 (1;0)
х
1
0
-1
0
1
2π
sin
y
0
1
0
cos
x
tg
1
0
—
0 -1 0 1
— 0 — 0
0 — 0 —
π/
2
(0;-1)
Красная линия — это плюс
Синяя – это минус
сtg
sin
tg
cos
-1 0
cos
сtg
sin
Значения тригонометрических функций
π/6
π/4
π/3
1
2
2
2
3
2
π/6
sin
2
2
3
2
cos
3
2
3
3
2
2
1
2
3
3
сtg
1
2
π/4
2
2
π/3
3
3
1
Ряд тангенса
Для косинуса поменяйте крайние значения
π/6
π/3
1
2
tg
Зап
омн
и!
π/4
1
Табличные значения
Ряд синуса
π/6
3
3
3
2
π/4
π/3
1
3
Для котангенса поменяйте крайние значения
π/6
π/4
π/3
3
3
1
3
Свойства триг.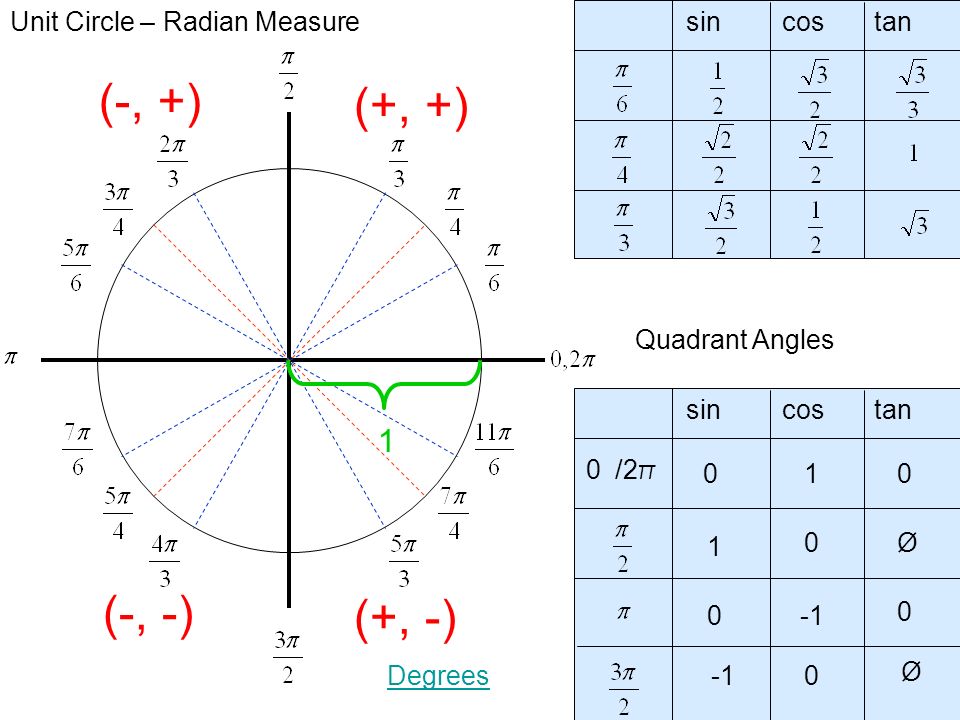 функций
функций
Знать
Уметь
1. Знаки по четвертям
Синус: знаки
соответствуют
знакам по оси У,
косинус –по оси Х
Тангенс и котангенс
в 1 четв.- плюс,
далее знаки
чередуются
π/
2
Sin
0
π
2π
3π/2
Красная линия — это плюс
Синяя – это минус
1. Определять четверть нахождения
угла; 2. Определить знак функции.
+ +
— —
Cos
Tg, ctg
— +
— +
— +
+ —
sin315º < 0, т.к угол 3 четв.
tg5π/6 <0, угол 2 четв.
cos2 11π/4 > 0, т.к Cos2
5. Множество значений
функций
-1 ≤ sin х ≤ 1, или |sinx | ≤ 1,
-1 ≤ cos х ≤ 1, или |cosx | ≤ 1,
y = 3 -2sinx. E(y) = (1;5)
sinx = -1, y = 3+2 = 5
sinx = 1, y = 3-2 = 1
tgx € R, ctgx € R,
π/
2
|sinx | ≤ 1
|cosx | ≤ 1
Уметь находить множество
значений функции, выражения
1
-1
π
1
2π
3π/2
-1
Период
Период
– это число, при прибавлении которого к
аргументу значение функции не изменяется.
f(x +Т) = f(x)
Если Т – период, то Tn для n € Z тоже период. Считается Т –
наименьший период
Так как f(x
sin, cos
+Тn) = f(x), то Tn можно опустить
Т = 2π
tg, ctg
Примеры
1. sin 390º = sin (360º + 30º) = sin 30º = ½
2. sin 790º = sin (2·360º + 30º) = sin 30º = ½
3
3. tg 210º = tg (180º + 30º) = tg 30º = 3
4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½
5. cos (2π – β) = cos (-β) = cos β
6. sin (6π – 2α) = sin (-2α) = — sin 2α
Т=π
Четность, нечетность
Синус, тангенс, котангенс – функции
нечетные.
Минус у угла можно вынести за знак функции
Косинус – функция
четная.
Минус у угла можно опустить
Примеры
1. sin ( – х) = — sin х
2. sin ( π/4 – х) = — sin ( х — π/4 )
3. tg (- π/6) = — tg π/6 = —
3
3
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α — π/2) = — ctg (π/2 — 2α )
Область определения
Синус, косинус
D(y) = R
Функции непрерывны на R
Tангенс
π/2
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
3π/2
Котангенс
D(y) = R, x ≠ πn
x = πn – горизонтальная асимптота
π
0
ctgx – определен при sinx ≠ 0
English Русский Правила
Тригонометрический круг | Презентация к уроку:
Слайд 1
Владикавказское художественное училище имени Азанбека Джанаева Тригонометрический круг Выполнила: Созиева З.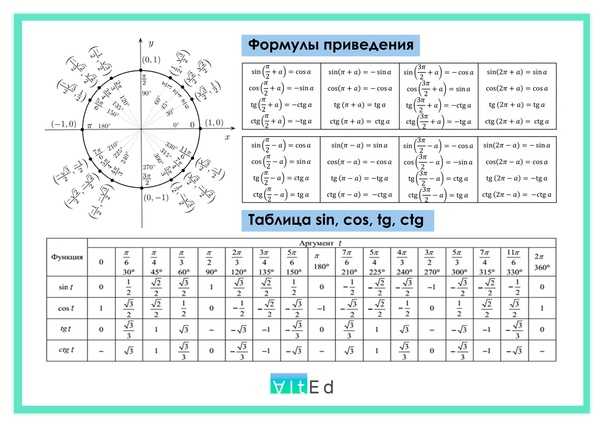 С.
С.
Слайд 2
Тригонометрический круг Радиус R = 1 х у 1 1 Тригонометрический круг – это круг с радиусом равным единице и с центром в начале координат. х у (1;0) (0;1) (-1;0) (0;-1)
Слайд 3
0 ° 90 ° 180 ° 270 ° Градусная мера углов 360 ° Четверти круга 1 2 3 4
Слайд 4
Углы на тригонометрическом круге х у Угол на круге определяется поворотом радиуса За нулевое положение радиуса принято его положение на положительном направлении оси Х. Угол поворота радиуса отсчитывается от положительного направления оси Х: с плюсом — против часовой стрелки, с минусом — по часовой стрелке. + — х у х у
Слайд 5
Координаты положения радиуса У Х ордината (х 0 ;у 0 ) абсцисса У Х У Х У Х
Слайд 6
Радианная мера угла Один радиан – это центральный угол, опирающийся на дугу равную радиусу Длина окружности 2πR В окружности 2πR : R = 2π радиан 2π соответствуют 360° 2π ————— 360° π ————— 180° 90° = 180° /2 = π /2 270° = 90°· 3 = 3π /2 0 ° π /2 π 3 π /2 Радианная мера углов в круге 2 π 0 ° 1,57 3,14 4,71 6,28 Так как π = 3,14…, то
Слайд 7
Перевод градусов в радианы Перевести 120° в радианы. Для перевода в радианы удобно пользоваться пропорцией. π ————— 180° 180°−−−−−−−−−−−− π 2 3 120° −−−−−−−−−−−− х 30° = π /6 45° = π /4 60° = π /3 Перевод радиан в градусы Подставьте вместо π 180° и сократите Перевести 3π /4 в градусы.
Для перевода в радианы удобно пользоваться пропорцией. π ————— 180° 180°−−−−−−−−−−−− π 2 3 120° −−−−−−−−−−−− х 30° = π /6 45° = π /4 60° = π /3 Перевод радиан в градусы Подставьте вместо π 180° и сократите Перевести 3π /4 в градусы.
Слайд 8
Определение тригонометрических функций Повторение α У Х ордината О А В Заметим, ОА = R = 1 Синусом угла α является ордината точки А на круге, получающаяся при повороте радиуса на угол α. Синус угла α – это ордината (у) угла α sinα α
Слайд 9
Определение тригонометрических функций Повторение α У Х абсцисса О А В Заметим, ОА = R = 1 Косинусом угла α является абсцисса точки А на круге, получающаяся при повороте радиуса на угол α. Косинус угла α – это абсцисса (х) угла α cosα
Слайд 10
Определение тригонометрических функций Повторение α У Х О А В tgα, ctgα
Слайд 11
У Х М Sin α Sin α M Синус – это ордината ( y )
Слайд 12
cosα 2) Косинусом угла α является абсцисса точки М на тригонометрическом круге, получающаяся при повороте радиуса на угол α. У Х Абсцисса — cosα
У Х Абсцисса — cosα
Слайд 13
У Х М cos α cosα M Запомни! косинус – это абсцисса (x)
Слайд 14
3) Тангенсом угла α является ордината точки В на оси тангенсов ( х = 1 ), получающаяся при пересечении продолжения радиуса с осью тангенсов при повороте радиуса на угол α. tgα У Х Ось тангенсов, х = 1 В В
Слайд 15
4) Котангенсом угла α является абсцисса точки В на оси котангенсов ( у = 1 ), получающаяся при пересечении продолжения радиуса с осью котангенсов при повороте радиуса на угол α. сtgα У Х Ось котангенсов, у = 1 В В
Слайд 16
π/2 0 π/2 π 3π/2 2π 3π/2 Красная линия — это плюс Синяя – это минус 0 1 0 0 π/2 π 3π/2 2π у х sin cos tg сtg 1 0 -1 -1 0 0 1 y x 0 1 0 -1 0 1 0 -1 0 1 0 — 0 — 0 — 0 — 0 — Значения тригонометрических функций (1;0) (0;1) (-1;0) (0;-1) Диаметральные углы
Слайд 17
Табличные значения π/6 π/4 π/3 sin cos tg сtg Значения тригонометрических функций 1 1 Ряд синуса π/6 π/4 π/3 Для косинуса поменяйте крайние значения π/6 π/4 π/3 Ряд тангенса π/6 π/4 π/3 Для котангенса поменяйте крайние значения π/6 π/4 π/3
Слайд 18
Свойства триг.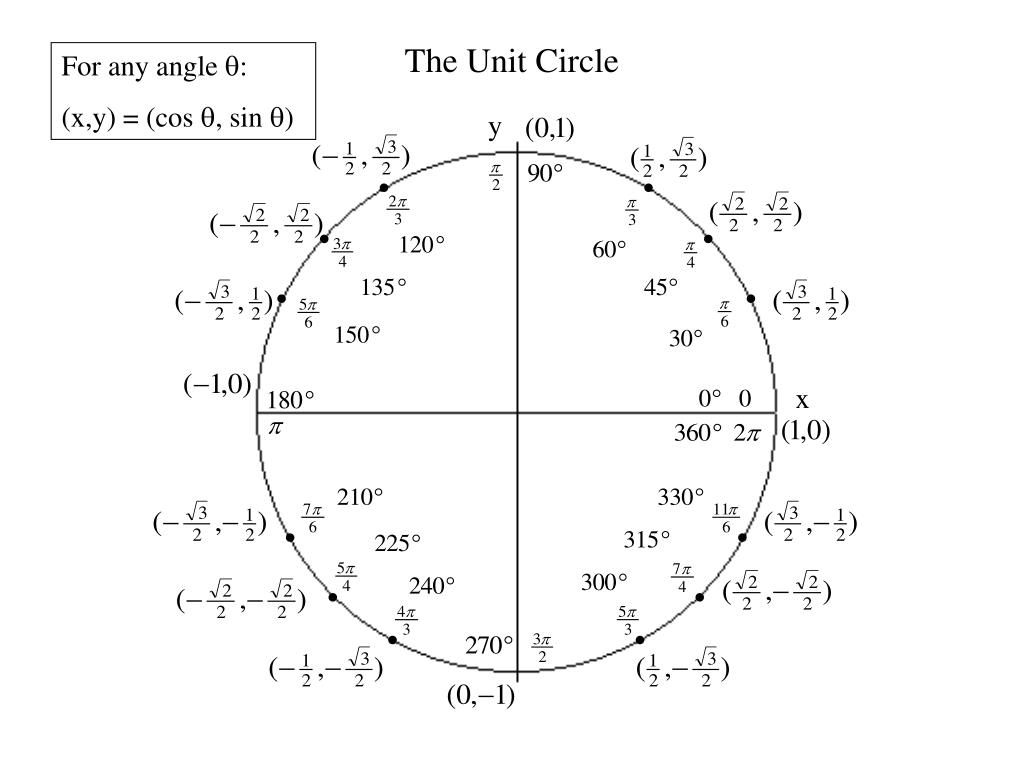 функций 1. Знаки по четвертям Синус: знаки соответствуют знакам по оси У, косинус –по оси Х Тангенс и котангенс в 1 четв.- плюс, далее знаки чередуются 1. Определять четверть нахождения угла; 2. Определить знак функции. sin315º 0, т.к Cos 2 π/2 0 π/2 π 3π/2 2π 3π/2 Красная линия — это плюс Синяя – это минус Sin Cos Tg, ctg + — + — + — + — + — + —
функций 1. Знаки по четвертям Синус: знаки соответствуют знакам по оси У, косинус –по оси Х Тангенс и котангенс в 1 четв.- плюс, далее знаки чередуются 1. Определять четверть нахождения угла; 2. Определить знак функции. sin315º 0, т.к Cos 2 π/2 0 π/2 π 3π/2 2π 3π/2 Красная линия — это плюс Синяя – это минус Sin Cos Tg, ctg + — + — + — + — + — + —
Слайд 19
5. Множество значений функций tgx € R, ctgx € R, -1 ≤ sin х ≤ 1, или |sinx | ≤ 1, — 1 ≤ cos х ≤ 1, или |cosx | ≤ 1, Уметь находить множество значений функции, выражения y = 3 -2sinx. E(y) = (1;5) sinx = -1 , y = 3+2 = 5 sinx = 1 , y = 3-2 = 1 π 3π/2 2π 3π/2 π/2 1 -1 1 -1 |sinx | ≤ 1 |cosx | ≤ 1
Слайд 20
Период Период – это число, при прибавлении которого к аргументу значение функции не изменяется. f(x +Т) = f(x) Если Т – период, то Tn для n € Z тоже период. Считается Т – наименьший период Так как f(x +Тn) = f(x), то Tn можно опустить Примеры 1. sin 390º = sin (360º + 30º) = sin 30º = ½ 2. sin 790º = sin (2∙360º + 30º) = sin 30º = ½ 3. tg 210º = tg (180º + 30º) = tg 30º = 4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½ 5. cos (2π – β) = cos (-β) = cos β 6. sin (6π – 2α) = sin (-2α) = — sin 2α sin, cos Т = 2π tg, ctg Т = π
tg 210º = tg (180º + 30º) = tg 30º = 4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½ 5. cos (2π – β) = cos (-β) = cos β 6. sin (6π – 2α) = sin (-2α) = — sin 2α sin, cos Т = 2π tg, ctg Т = π
Слайд 21
Четность, нечетность Синус, тангенс, котангенс – функции нечетные. Минус у угла можно вынести за знак функции Примеры 1. sin ( – х) = — sin х 2. sin ( π/4 – х) = — sin ( х — π/4 ) 3. tg (- π/6) = — tg π/6 = — 4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½ 5. cos (-β) = cos β 6. ctg ( 2α — π/2) = — ctg (π/2 — 2α ) Косинус – функция четная. Минус у угла можно опустить
Слайд 22
Область определения Синус, косинус D(y) = R Функции непрерывны на R Tангенс D(y) = R, x ≠ π/2 + πn x = π/2 + πn – вертикальная асимптота Котангенс D(y) = R, x ≠ πn x = πn – горизонтальная асимптота tgx – определен при cosx ≠ 0 ctgx – определен при sinx ≠ 0 π/2 3π/2 0 π
Как определить знак sin cos tg ctg
Обновлено: 25.09.2022
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».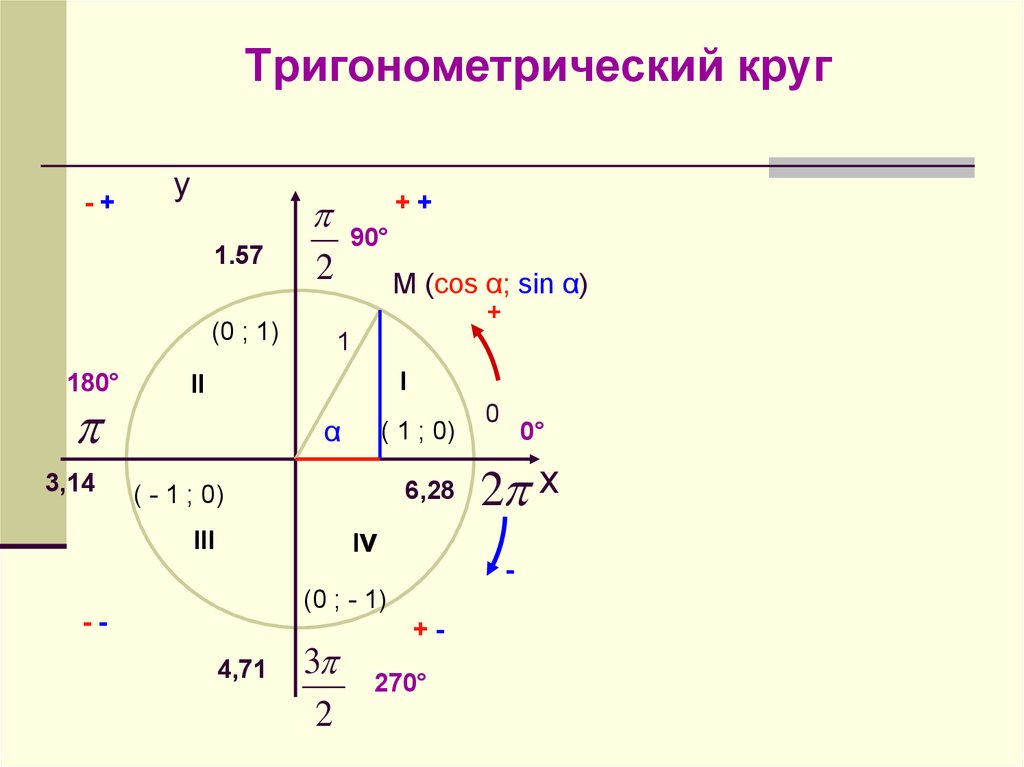
- Синус угла – отношение противолежащего катета к гипотенузе;
- Косинус угла – отношение прилежащего катета к гипотенузе;
- Тангенс угла – отношение противолежащего катета к прилежащему;
- Котангенс угла – отношение прилежащего катета к противолежащему.
Или в виде формул:
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.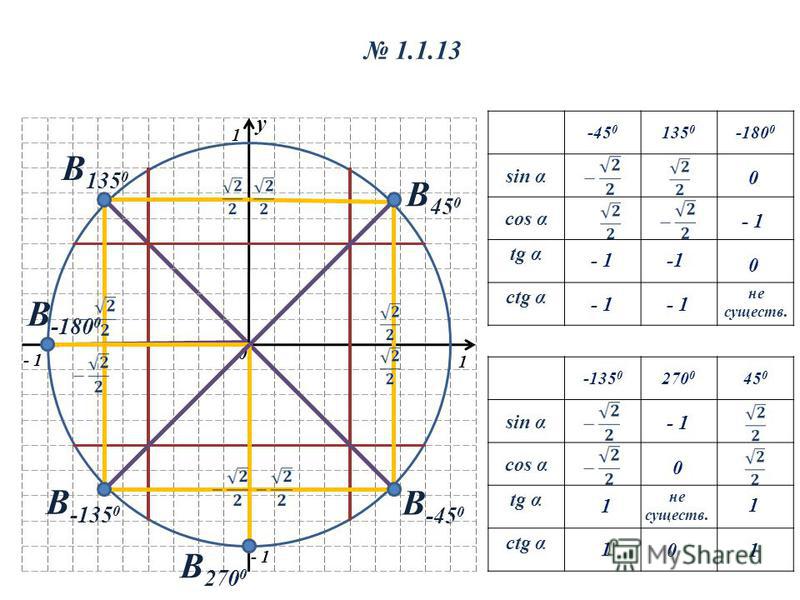
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Например, значения тригонометрических функций для углов 270° и -90° равны.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Геометрия. Урок 1. Тригонометрия
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрический круг
Углы в радианах
Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.
Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан.
Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π .
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Знаки тригонометрических функций .
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Прямые тригонометрические функции.
Другие тригонометрические функции.
В современном мире есть 6 базовых тригонометрических функций, которые ниже в таблице указаны вместе с уравнениями, которые связывают их.
Функция
Соотношение
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Значения тригонометрических функций.
Значения sin, cos, tg, ctg, sec и cosec для определенных углов указаны в таблице. («∞» обозначает, что функция в данной точке не определена, а в её окрестности стремится к бесконечности).
0°
30°
π/6
45°
π/4
60°
π/3
90°
π/2
180°
270°
3π/2
360°
2π
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.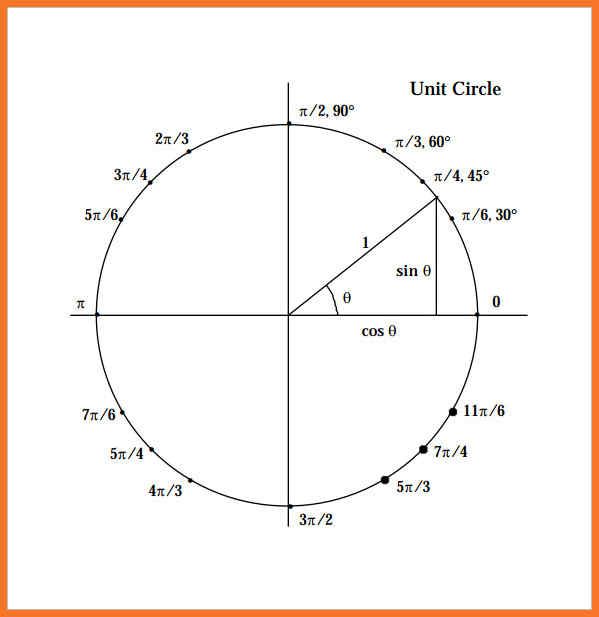
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Производные тригонометрические функции.
Тригонометрические функции. Значение тригонометрических функций.
Тригонометрические функции — это периодические функции с периодами для sin, cos, sec и cosec, и для tg и ctg.
Зачастую тригонометрические функции обозначают отношением сторон прямоугольного треугольника либо длины конкретных отрезков в единичной окружности.
Урок 10. Тригонометрические функции. Тригонометрические уравнения и их системы. Теория
На этом уроке мы рассмотрим основные тригонометрические функции, их свойства и графики, а также перечислим основные типы тригонометрических уравнений и систем. Кроме этого, укажем общие решения простейших тригонометрических уравнений и их частные случаи.
Данный урок поможет Вам подготовиться к одному из типов задания В5 и С1.
Читайте также:
- Как стать магом в майнкрафте без модов и без командных блоков
- Breathedge транспортный отсек где найти
- Dayz epoch что это
- Как восстановить exodus кошелек
- Где щенячий патруль музыка
Разбираем алгоритмы компьютерной графики. Часть 6 — Анимация «Плазма» / Хабр
Разновидностей алгоритмов генерации «плазм» столько же, сколько, наверное, звезд на небе. Но связывает их вместе принцип плавного формирования перехода цветов.
Для бесшовного формирования цвета очень часто используются тригонометрические функции. Во-первых, потому что они периодические, т.е. через определенный промежуток значения функции повторяются, а во-вторых, они возвращают непрерывные значения, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Благодаря этому можно используя простые комбинации функций получать плавное возрастание и убывание цветов.
Я попробую рассмотреть один из вариантов, который использует функции синуса и косинуса.
Сначала произведем небольшую оптимизацию. Вычисления тригонометрических функций довольно накладное для процессора занятие. А поскольку таких вычислений на каждом кадре анимации придется делать по нескольку штук, то желательно нужные нам значения рассчитать заранее.
Еще раз напомню, что функции синуса и косинуса – периодические. Их наименьший интервал, через который они начинают повторять значения, это 360 градусов или 2 * Пи.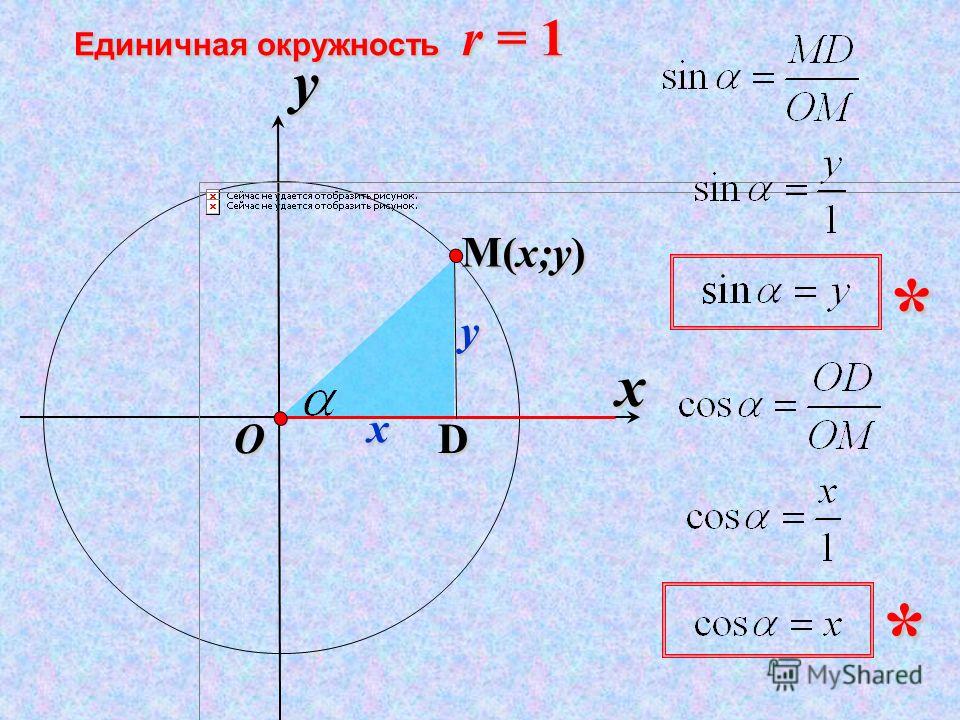
Поэтому, чтобы запомнить только уникальные значения (все остальные можно вычислить на их основе) достаточно рассчитать кусочек от 0 до 2 * Пи.
Нужный нам кусочек из общего графика функции sin и cosСделаем по 255 значений для каждой из функций. Для этого создадим два списка по 255 значений в каждом.
sintab = [] # Таблица заранее просчитанных значений синусов
costab = [] # и косинусов.
# Заполняем начальными значениями таблицы sin и cos
for index in range(0, 255):
sintab.append(math.sin(index * Pi2 / 255.0))
costab.append(math.cos(index * Pi2 / 255.0))Для того чтобы значения синуса и косинуса были в диапазоне от 0 до 1, разделим наш счетчик index на 255. А чтобы внутри массива получился только один период значений функций — умножим аргумент еще на 2 * Пи.
Теперь внутри массивов мы имеем кусочки синусоиды и косинусоиды по одному полному колебанию.
Подобный подход к работе с тригонометрическими функциями, очень часто используется при программировании демо-работ, для оптимизации скорости выполнения программ.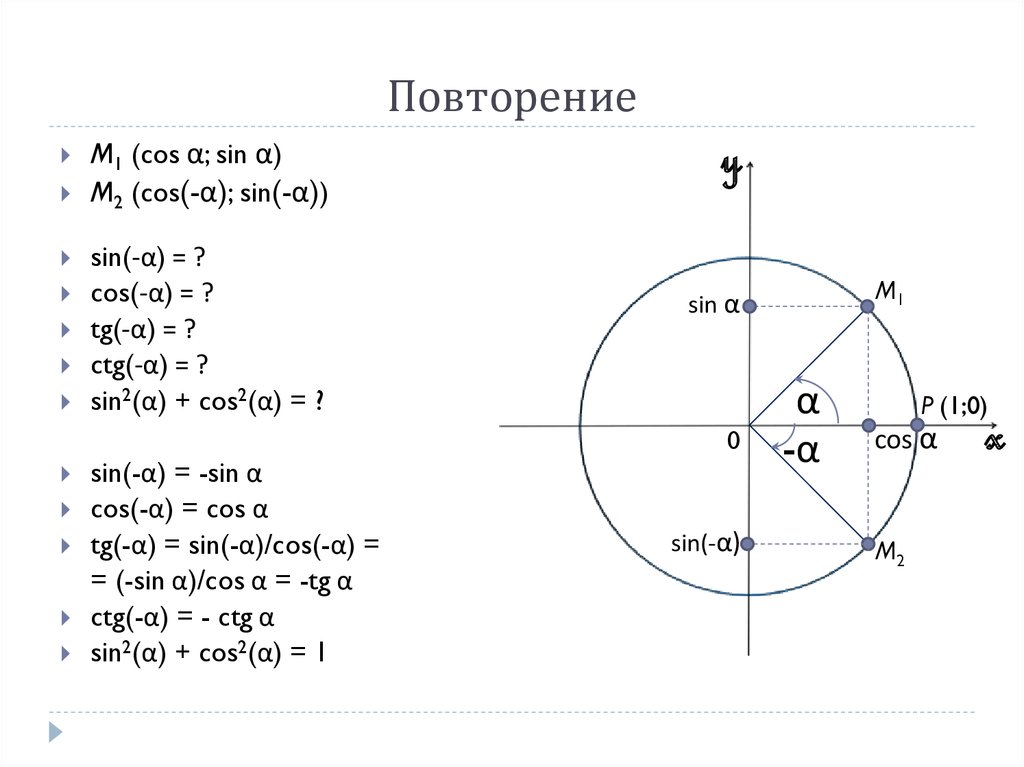
Дополнительно сделаем обратную процедуру, напишем функцию, которая по значению на вход, будет возвращать индекс из нашего массива, который бы соответствовал входному значению, но после получения остатка от деления на длину нашего массива. Звучит очень сложно, но попробую объяснить на пальцах, ну или на картинках:
Пусть у нас есть массив из трех элементов:
Есть число 5, которое мы хотим применить к нашему массиву и понять как бы оно расположилось на нашем массиве, если взять от него остаток от деления по длине нашего массива. Число 5 можно представить, как еще один массив:
Уберем из нашего второго массива длину первого:
Остается два элемента:
И пытаемся их совместить с нашим первоначальном массивом:
Таким образом наше число 5, попадает на ячейку с номером 2.
Вот кратко суть функции по высчитыванию индекса в массиве. В нашем случае будем вычислять индекс для диапазона от 0 до 2 * Пи.
def getInd(num):
return int(((255.0 * (num % Pi2) / Pi2)))Функция вернет целое значение в диапазоне от 0 до 255, получая на вход какое-то число и подставляя его в диапазон от 0 до 2 * Пи, который разбит на 255 частей.
А вот дальше уже пойдет почти «магия», поскольку мы начнем получать цветовые характеристики точек по формулам с использованием тригонометрических функций. Почему «магия»? Потому, что объяснить некоторые вещи не до конца получается, во всяком случае у меня. Просто при каких-то сочетаниях функций и арифметических действий — результат будет довольно красивым. И здесь зачастую приходится действовать эмпирическим путем.
Но обо всем по порядку.
Плазма не должна быть статичной! Чтобы этого добиться, нужно на каждой итерации обновления экрана и генерации кадра изображения, добавлять какую-то динамическую составляющую в расчет картинки.
Создадим переменную t (по умолчанию равная 0), в которой будет накапливаться сдвиг для генерации изображения. Пусть эта переменная, на каждом кадре изменяется на значение delta:
Пусть эта переменная, на каждом кадре изменяется на значение delta:
И как только переменная t превысит значение 2 * Пи, то будем сбрасывать ее в 0. Т.е. она по кругу будет проходить через 255 значений, пока не доберется до 2 * Пи.
Приступаем к генерации изображения, сначала размещу часть кода, затем поясню:
for i in range(0, MY):
y = i / MY
for j in range(0, MX):
x = j / MX
# Вычисляем цветовые коэффициенты и затем сами цветовые составляющие
a1 = 8.0 * sintab[getInd(x + t)]
a2 = 7.0 * costab[getInd(x + t)]
a3 = 6.0 * sintab[getInd(x + t)]
r = int(100 * abs(sintab[getInd(a1 * x + t)] + costab[getInd(a1 * y - t)]))
g = int(100 * abs(costab[getInd(a2 * x - t)] + sintab[getInd(a2 * y + t)]))
b = int(100 * abs(sintab[getInd(a3 * x + t)] + costab[getInd(a3 * y - t)]))
pygame.draw. rect(screen, (r, g, b), (i*scale, j*scale, scale, scale))
rect(screen, (r, g, b), (i*scale, j*scale, scale, scale))Итоговая анимация плазмы будет вот такая:
Цвета на gif немного искажены, в True color у меня не удалось ее сделатьУ нас есть два вложенных цикла. Первый проходит по строкам изображения, второй по колонкам. Пересечение этих циклов — это обрабатываемая точка на экране с координатой i,j. Формируем для каждой из этих координат, ее аналог, но выравненный по диапазону от 0 до 1. Делается это просто делением на ширину первоначального диапазона, для y, это i / MY, для x, это j / MX.
Теперь добавим «хаоса» в генерацию изображения. Сделаем три коэффициента для трех составляющих цвета: a1 для красного (red), a2 для зеленого (green), a3 для синего (blue).
Вычисляем их по следующему принципу: получаем значение индекса для координаты x + t и получаем значение синуса или косинуса для этого индекса. Полученное значение умножаем на произвольный коэффициент. На самом деле это число поможет нам изменять количество волн на экране.
Полученное значение умножаем на произвольный коэффициент. На самом деле это число поможет нам изменять количество волн на экране.
Например:
a1 * 18a2 * 17a3 * 16Все три коэффициента умноженные на значения перечисленные выше, одновременноКак видите, здесь можно играть коэффициентами как угодно, результат аналитически просчитать заранее сложно.
Но это мы пока вычисляли коэффициенты, теперь используем их при вычислении цветов r, g, b.
Мы опять применим сочетания синусов и косинусов взятые из таблиц, но с учетом добавления туда коэффициентов a. Что именно использовать cos или sin не сильно принципиально, просто их смещение в разных сочетаниях дает интересные результаты.
Умножение на 100 здесь служит для того, чтобы дробное значение цвета привести к диапазону от 0 до 255, в котором его обрабатывает библиотека PyGame.
Советую «поиграться» коэффициентами, расположением функций sin и cos. Получаются очень примечательные картины.
Получаются очень примечательные картины.
Итоговый код:
import pygame
import math
MX = MY = 256 # Размер массива с плазмой
Pi2 = math.pi * 2.0 # Просто константа 2 * Пи для простоты и скорости
scale = 4 # Масштаб точек для вывода на экран
SX = MX * scale # Размер экрана исходя из размера плазмы и ее масштаба
SY = MY * scale
pygame.init()
screen = pygame.display.set_mode((SX, SY))
running = True
sintab = [] # Таблица заранее просчитанных значений синусов
costab = [] # и косинусов.
# Заполняем начальными значениями таблицы sin и cos
for index in range(0, 255):
sintab.append(math.sin(index * Pi2 / 255.0))
costab.append(math.cos(index * Pi2 / 255.0))
t = 0 # Сдвиг для получения анимации
delta = Pi2 / 255.0 # Шаг нашего сдвига, на каждом кадре анимации
# -------------------------------------------------------------------------------------------------------
# Возвращаем индекс в диапазоне от 0 до 255, которое занимало бы число num, если бы его располагали от
# 0 до (2 * Пи)
# -------------------------------------------------------------------------------------------------------
def getInd(num):
return int(((255. 0 * (num % Pi2) / Pi2)))
# -------------------------------------------------------------------------------------------------------
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
for i in range(0, MY):
y = i / MY
for j in range(0, MX):
x = j / MX
# Вычисляем цветовые коэффициенты и затем сами цветовые составляющие
a1 = 8.0 * sintab[getInd(x + t)]
a2 = 7.0 * costab[getInd(x + t)]
a3 = 6.0 * sintab[getInd(x + t)]
r = int(100 * abs(sintab[getInd(a1 * x + t)] + costab[getInd(a1 * y - t)]))
g = int(100 * abs(costab[getInd(a2 * x - t)] + sintab[getInd(a2 * y + t)]))
b = int(100 * abs(sintab[getInd(a3 * x + t)] + costab[getInd(a3 * y - t)]))
pygame.draw.rect(screen, (r, g, b), (i*scale, j*scale, scale, scale))
t += delta # "Двигаем" анимацию
if t >= Pi2:
t = 0
pygame.
0 * (num % Pi2) / Pi2)))
# -------------------------------------------------------------------------------------------------------
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
for i in range(0, MY):
y = i / MY
for j in range(0, MX):
x = j / MX
# Вычисляем цветовые коэффициенты и затем сами цветовые составляющие
a1 = 8.0 * sintab[getInd(x + t)]
a2 = 7.0 * costab[getInd(x + t)]
a3 = 6.0 * sintab[getInd(x + t)]
r = int(100 * abs(sintab[getInd(a1 * x + t)] + costab[getInd(a1 * y - t)]))
g = int(100 * abs(costab[getInd(a2 * x - t)] + sintab[getInd(a2 * y + t)]))
b = int(100 * abs(sintab[getInd(a3 * x + t)] + costab[getInd(a3 * y - t)]))
pygame.draw.rect(screen, (r, g, b), (i*scale, j*scale, scale, scale))
t += delta # "Двигаем" анимацию
if t >= Pi2:
t = 0
pygame. display.flip()
pygame.quit()
display.flip()
pygame.quit()Ссылка на предыдущую статью: Разбираем алгоритмы компьютерной графики. Часть 5 – Анимация «Shade Bobs»
В следующий раз рассмотрим алгоритм искажений на плоскости, например эффект линзы.
Тангенциальная функция
Горячая математикаКасательная функция представляет собой периодический функция, которая очень важна в тригонометрии.
Самый простой способ понять функцию касательной — использовать единичную окружность. Для заданной угловой меры θ нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной как положительной Икс -ось. Икс -координата точки пересечения другой стороны угла с окружностью потому что ( θ ) и у -координата грех ( θ ) .
Есть несколько значений синуса и косинуса, которые следует запомнить, основываясь на
30
°
−
60
°
−
90
°
треугольники и
45
°
−
45
°
−
90
°
треугольники. Основываясь на них, вы можете определить соответствующие значения тангенса.
Основываясь на них, вы можете определить соответствующие значения тангенса.
грех ( θ ) | потому что ( θ ) | загар ( θ ) |
| грех ( 0 ° ) знак равно 0 | потому что ( 0 ° ) знак равно 1 | загар ( 0 ° ) знак равно 0 1 знак равно 0 |
| грех ( 30 ° ) знак равно 1 2 | потому что ( 30 ° ) знак равно 3 2 | загар ( 30 ° ) знак равно 1 2 ⋅ 2 3 знак равно 3 3 |
| грех ( 45 ° ) знак равно 2 2 | потому что ( 45 ° ) знак равно 2 2 | загар ( 45 ° ) знак равно 2 2 ⋅ 2 2 знак равно 1 |
| грех ( 60 ° ) знак равно 3 2 | потому что ( 60 ° ) знак равно 1 2 | загар ( 60 ° ) знак равно 3 2 ⋅ 2 1 знак равно 3 |
| грех ( 90 ° ) знак равно 1 | потому что ( 90 ° ) знак равно 0 | загар
(
90
°
)
знак равно
1
0
знак равно
недеф
. |
Обратите внимание, что:
- для углов с конечным плечом в квадранте II, поскольку синус положительный, а косинус отрицательный, тангенс отрицательный.
- для углов с конечным плечом в квадранте III, поскольку синус отрицательный, а косинус отрицательный, тангенс положительный.
- для углов с конечным плечом в квадранте IV, поскольку синус отрицательный, а косинус положительный, тангенс отрицательный.
Вы можете нанести эти точки на координатную плоскость, чтобы показать часть функции, часть между 0 а также 2 π .
Для значений θ меньше, чем 0 или больше, чем 2 π можно найти значение θ с использованием опорный угол .
График функции на более широком интервале показан ниже.
Обратите внимание, что областью определения функции является вся действительная линия, а диапазон
−
∞
≤
у
≤
∞
.
Единичный круг (в градусах и радианах) – определение, уравнение, диаграмма
Что такое единичный круг
Единичный круг – это круг единичного радиуса, что означает, что его радиус равен 1 единице. Обычно его представляют в декартовой системе координат. Единичный круг имеет центр в начале координат (0, 0).
Основная цель единичного круга состоит в том, что он упрощает другие функции математики. Например, в тригонометрии для единичного круга под любым углом используются значения синуса и косинуса.
Квадранты единичной окружностиУравнение единичной окружности
Единичная окружность обладает всеми свойствами окружности, и ее уравнение также выводится из уравнения окружности.
Общее уравнение окружности в стандартной форме (x – h) 2 + (y – k) 2 = r 2 , который представляет собой окружность с центром (h, k) и радиусом r.
Приведенное выше уравнение можно упростить, представив уравнение единичного круга. Так как единичный круг имеет центр в (0, 0) и радиус 1 единицу, подставляя значения в приведенное выше уравнение, мы получаем
Так как единичный круг имеет центр в (0, 0) и радиус 1 единицу, подставляя значения в приведенное выше уравнение, мы получаем
(x – 0) 2 + (y – 0) 2 = 1 2
x 2 + y 2 = 1
Уравнение единичной окружностиПриведенное выше уравнение удовлетворяет всем точкам, лежащим на окружности во всех четырех квадрантах.
Нахождение углов тригонометрических функций с помощью единичной окружности: Sin, Cos, Tan
Мы можем вычислить тригонометрические функции синуса, косинуса и тангенса с помощью единичной окружности. Здесь мы будем использовать теорему Пифагора в единичном круге, чтобы понять тригонометрические функции.
Возьмем точку P на окружности единичного круга с координатами (x, y). Будучи единичным кругом, его радиус «r» равен 1 единице, что является расстоянием между точкой P и центром круга. Проведя радиус и перпендикулярную линию из точки P к оси x, мы получим прямоугольный треугольник, помещенный в единичный круг в плоскости декартовых координат. Радиус единичной окружности — это гипотенуза прямоугольного треугольника, который составляет угол θ с положительной осью x. Длины двух сторон (основания и высоты) имеют значения x и y соответственно.
Радиус единичной окружности — это гипотенуза прямоугольного треугольника, который составляет угол θ с положительной осью x. Длины двух сторон (основания и высоты) имеют значения x и y соответственно.
Итак, у нас есть прямоугольный треугольник со сторонами, равными 1, x, y. Применяя эти значения в тригонометрии, мы получаем
sin θ = высота/гипотенуза = y/1
cos θ = основание/гипотенуза = x/1
tan θ = высота/основание = y/x
cosec θ = 1 /sin θ = Гипотенуза/ Высота = 1/y
с θ = 1/cos θ = Гипотенуза/ Основание = 1/x
cot θ = 1/tan θ = Основание/ Высота = x/y
Поскольку, уравнение единичной окружности задается как x 2 + y 2 = 1, где x = cos θ и y = sin θ , получаем важное соотношение:
sin 2 θ + cos 2 θ = 1
Знак тригонометрической функции тригонометрическая функция зависит от квадранта, в котором находится угол. Чтобы помочь вспомнить, какие из тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «
A ll S tudents T ake C alculus» или All Sin Tan, Cos (ASTC). Правила единичного круга
Правила единичного кругаКаждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, то есть «А», все тригонометрические функции положительны. В квадранте II, «Smart», только синус положительный. В квадранте III положительный только тангенс «Trig». Наконец, в квадранте IV «Класс» положителен только косинус.
Если мы внимательно посмотрим на единичный круг, мы обнаружим, что значения sin и cos углов колеблются между -1 и 1. Они принимают значение 0, а также положительные и отрицательные значения трех чисел √3 /2, √2/2 и ½. Идентификация эталонных углов поможет нам выявить закономерность в этих значениях. Обратитесь к нашим
Значение углов в тригонометрических функциях
Значение θ может быть выражено как в градусах, так и в радианах. Важно помнить значения sin, cos и tan для некоторых конкретных углов. Эти углы называются опорными углами.
В единичной окружности мы имеем косинус в качестве координаты x и грех в качестве координаты y. Найдем их значения для θ = 0° и θ = 90°.
Найдем их значения для θ = 0° и θ = 90°.
Для θ = 0° координата x равна 1, а координата y равна 0. Таким образом, cos 0° = 1 и sin 0° = 0. Опять же, для θ = 90 °, cos 90 ° = 1 и sin 90 ° = 1. Точно так же мы можем найти значения тригонометрических функций для некоторых конкретных значений θ, таких как 30 °, 60 ° и 90 °. Эти углы, называемые специальными углами, используются для упрощения вычислений, связанных с тригонометрическими функциями с разными углами. Их значение всегда находится между 0 и 90° при измерении в градусах или 0 и π/2 при измерении в радианах. Опорный угол всегда использует ось x в качестве системы отсчета.
Значения специальных углов всех тригонометрических функций представлены в виде таблицы, приведенной ниже.
Таблица единичных окружностейПодготовка полной диаграммы единичных окружностей
Вся единичная окружность представляет собой полный угол в 360°, который равен 2π при выражении в радианах.
Таким образом, математически
2π радиан = 360°
Это означает, что 1 радиан = 360°/2π = 180°/π
Это соотношение используется для преобразования углов из радианов в градусы.
Единичный круг разделен на четыре квадранта, образующих углы 90°, 180°, 270° и 360° (в градусах) или π/2, π. 3π/2 и 2π (в радианах) соответственно.
Угол на единичной окружности всегда измеряется от положительной оси x с вершиной в начале координат. Его начальная сторона лежит на оси абсцисс, а луч, начинающийся в начале координат и совпадающий с точкой на единичной окружности, образует конечную сторону. Угол имеет положительное значение, если он измеряется против часовой стрелки от оси x.
Таким образом, значение sin (x) и косинуса (y) любого угла основано на координате, которой он принадлежит. Ниже приведен список:
Квадрант 1 – (0 – 90°(π/2)) : X положительный, Y положительный
Квадрант 2 – (90°(π/2) – 180°(π)) : X положительный отрицательный, Y положительный
Квадрант 3 – (180°(π) – 270°(3π/2)) : X отрицательный, Y отрицательный
Квадрант 4 – (270°(3π/2) – 360°(2π) ): X отрицательное, Y отрицательное
Далее мы представляем некоторые часто встречающиеся углы вместе со специальными углами на единичной окружности в виде диаграммы, объединенной вместе в градусах и в радианах.
Приведенная выше диаграмма единичного круга также может быть представлена отдельно в градусах и в радианах для простоты. Они приведены ниже.
Единичная окружность Градусы Единичная окружность РадианыКак использовать единичную окружность
Лучший способ использования единичной окружности — найти неизвестный угол тригонометрических функций. Позвольте нам решить некоторые проблемы, чтобы еще лучше прояснить вашу концепцию.
Найдите значение sin 4π/3.
Решение:
Поскольку заданная тригонометрическая функция является синусоидальной, нам достаточно найти, в каком квадранте она находится, чтобы понять, будет ответ положительным или отрицательным.
3π/2 ˃ 4π/3 ˃ π
Таким образом, 4π/3 лежит в третьем квадранте, и поскольку синус обозначает координату y, 4π/3 отрицательно.
Теперь найдем значение sin 4π/3 = -√3/2
Найдите значение sin (150°), используя единичный круг.
Решение:
Поскольку значение sin положительно во втором квадранте и обозначается координатой y, мы возьмем вторую координату в единичной окружности.
Таким образом, sin (150°) = ½
Найдите точное значение тангенса 210°, используя единичный круг.
Решение:
Как мы знаем,
тангенс 210° = sin 210°/cos 210°
Используя диаграмму единичного круга, мы получаем
sin 210° = -1/2
cos 210° = -√3 /2
Таким образом,
=> тангенс 210° = -1/2/-√3/2
=> tan 210° = 1/3
Графические функции синуса, косинуса и тангенса
Функции синуса и косинуса связывают вещественные значения с координатами x и y точки на единичной окружности. Теперь давайте узнаем, как они выглядят на графике в координатной плоскости?
Для построения графика функции синуса давайте начнем с функции синуса: y =sin x
Мы можем создать таблицу, а затем нанести значения на график. Даны некоторые значения синусоидальной функции на единичной окружности, где координата x представляет собой угол в радианах, а координата y представляет собой sin x.
Даны некоторые значения синусоидальной функции на единичной окружности, где координата x представляет собой угол в радианах, а координата y представляет собой sin x.
(0, 0), (π/6, ½), (π/4, √2/2), (π/3, √3/2), (π/2, 1), (2π/3 , √3/2), (3π/4, √2/2), (5π/6, 1/2), (π, 0)
Наносим точки из таблицы и продолжаем вдоль оси x, чтобы получить форма синусоидальной функции.
Sine Graph Unit CircleОбратите внимание, что значения синуса положительны между 0 и π, что соответствует значениям функции синуса в квадрантах I и II на единичной окружности, а значения синуса отрицательны между π и 2π, что соответствует значения функции синуса в квадрантах III и IV на единичной окружности.
Аналогично, для построения графика функций косинуса, давайте посмотрим на функцию косинуса: y = cos x
Мы будем следовать тем же процедурам, что и функция синуса: создадим таблицу значений и используем их для построения графика. Ниже приведены значения функции косинуса на единичной окружности от 0° до 180°, где координата x представляет собой угол в радианах, а координата y равна cos x:
(0, 1), (π/ 6, √3/2), (π/4, √2/2), (π/3, 1/2), (π/2, 0), (2π/3, -1/2), (3π /4, -√2/2), (5π/6, -√3/2), (π, -1)
Подобно синусоидальной функции, мы можем построить заданные точки, чтобы получить график косинусной функции.
Для построения графика функций тангенса для специальных углов мы не можем использовать единичную окружность. Вместо этого нам нужно применить формулу tan x = sin x/cos x, чтобы определить тангенс каждого значения. Его можно изобразить, нанеся (x, f(x)) точки.
Давайте посмотрим на графическое поведение функции тангенса и их значения для некоторых особых углов. Ниже приведены значения для функции тангенса, для которых координаты x представляют собой углы в радианах, а координаты y равны тангенсу x:
(-π/2, не определено), (-π/3, -√3), (-π/4, -1), (-π/6, -√3/3), (0, 0) , (π/6, √3/3), (π/4, 1), (π/3, -√3), (π/2, не определено)
Приведенные выше точки помогут нам построить наш график, но нам нужно определить, как граф ведет себя там, где он не определен.
Рассмотрим последние четыре пункта. Мы можем видеть, что значение y увеличивается, когда x увеличивается по мере приближения к π/2. Точно так же значение y уменьшается по мере приближения к -π/2. Теперь есть несколько значений x, которые дают cos x = 0, и это именно те точки, в которых tan x не определен. В точках, где tan x не определен, на графике будут разрывы. При таких значениях (x = π/2 и x = – π/2) касательные функции имеют вертикальные асимптоты.
Теперь есть несколько значений x, которые дают cos x = 0, и это именно те точки, в которых tan x не определен. В точках, где tan x не определен, на графике будут разрывы. При таких значениях (x = π/2 и x = – π/2) касательные функции имеют вертикальные асимптоты.
Единица окружности и тригонометрические функции sin(x), cos(x), tan(x)
Используя единичную окружность , вы сможете изучить и получить глубокое понимание некоторых свойств, таких как домен, диапазон, асимптоты (если есть) тригонометрических функций .
| Отношения между графиками (в прямоугольных координатах) sin(x), cos(x) и tan(x) и координатами точки на единицы окружности исследуются с помощью апплета. Определения 1- Пусть x будет действительным числом, а P(x) точкой на единичной окружности такой, что угол в стандартном положении, конечная сторона которого является сегментом OP, равен x радианам.(O является источником используемой системы координат). 2- Мы определяем sin(x) как координату y точки P(x) на единичной окружности . 3- Мы определяем cos(x) как x-координату точки P(x) на блок круг . 4- Мы определяем tan(x) как отношение координаты y и координаты x точки P(x) на единичной окружности . Интерактивное учебное пособие с использованием апплетов Две возможности изучения тригонометрической функции с помощью единичного круга. 1) Использование апплета HTML5 Unit Circle
Дополнительные ссылки на единичный круг и тригонометрические функции . http://analyzemath.com/unitcircle/unit_circle_video_1.html
|
Как использовать единичный круг в тригонометрии?
Единичная окружность определяется как окружность, радиус которой равен 1 единице, центр находится в начале координат, а длина окружности равна 2π, поскольку r = 1. Здесь длина дуги эквивалентна величине центрального угла, пересекающего дуга. Тригонометрические функции, синус и косинус, имеют особое значение при рассмотрении единичного круга. Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно.
Например, для любой точки на конце окружности угла в стандартном положении значение свойства синуса такого угла эквивалентно координате y точки. Кроме того, косинус такого угла эквивалентен координате x этой точки соответственно.
Единица окружности в тригонометрии
Формула единичной окружностиНиже приводится общее уравнение для окружности:
(x – h) 2 + (y – k) 1 1 2 9 9 1 1 1 2 90 90
где,
- r — радиус окружности
- (h, k) — координаты центра круг можно лучше использовать для понимания тригонометрических функций. Для этого рассмотрим прямоугольный треугольник, помещенный внутри единичного круга в декартовой координатной плоскости. Если мы заметим, радиус этой окружности обозначает гипотенузу прямоугольного треугольника. Радиус окружности образует вектор. Это приводит к образованию угла, скажем, θ с положительной осью x. Предположим, что x — длина основания, а y — длина высоты прямоугольного треугольника соответственно.
Кроме того, координаты конечных точек радиус-вектора равны (x, y) соответственно.
Прямоугольный треугольник содержит стороны 1, x и y соответственно. Теперь можно вычислить тригонометрическое отношение следующим образом:
Теперь,
sin θ = y,
cos θ = x
Вычисления, tan θ = sin θ /cos θ = y/x.
Подставляя значения θ, мы также можем получить главные значения. Аналогично вычисляются значения всех остальных тригонометрических функций.
Тригонометрическое представление единичной окружности
Единичная окружность с отношениями Sin, Cos и TanЛюбая точка на единичной окружности с координатами (x, y), которые равны тригонометрическим тождествам (cosθ, sinθ). Координаты углов радиуса представляют собой косинус и синус значений θ для конкретного значения θ и линии радиуса. Имеем cos θ = x, а sin θ = y. Есть четыре части круга, каждая из которых лежит в одном квадранте, образуя углы 90°, 180°, 270° и 360°.
Единичные окружности и тригонометрические тождестваЗначения радиуса находятся в диапазоне от -1 до 1 соответственно. Кроме того, значения sinθ и cosθ лежат между 1 и -1 соответственно.
Тригонометрические тождества единичных окружностей для котангенса, секанса и косеканса можно вычислить, используя тождества для sin, cos и tan. В итоге получаем прямоугольный треугольник со сторонами 1, x и y соответственно. Вычисление тождеств единичного круга может быть выражено как
Таблица единичных окружностейsin θ =
cos θ =
tan θ =
sec θ =
cosec θ =
9θ0002 cot0003Тригонометрические отношения, используемые в таблице единичных окружностей, используются для перечисления координат точек на единичной окружности, которые соответствуют общим углам.
Angles in Degree
0 o
30 o
45 o
60 o
90 o
sin
0
1
cos
1
0
TAN
0017 0
1
Not Defined
csc
Not Defined
2
1
СЕД
1
\
2
0003 2
Not Defined
cot
Not Defined
1
0
We can find the secant, cosecant , и функции котангенса, также использующие эти формулы:
secθ =
cosecθ =
cotθ =
Мы обсудили единичный круг для первого квадранта.
Решенные примеры для формулы единичной окружностиТочно так же мы можем расширить и найти радианы для всех квадрантов единичной окружности. Числа 1/2, 1/√2, √3/2, 0 и 1 повторяются вместе со знаком во всех 4 квадрантах.
Задача 1. Докажите, что точка Q лежит на единичной окружности.
Решение:
Согласно уравнению единичного круга, которое:
Отсюда заключаем, что точка Q не лежит на единичной окружности.
Задача 2: Вычислить tan 30 o , используя значения sin и cos единичного круга.
Решение:
Вычисление TAN 30 O Использование SIN и COS значений,
С.
Следовательно,
, мы имеем
SIN 30 O =
COS,
SIN 30 O =
COS,
SIN 30 O =
COS,
SIN 30 O =
COS,
SIN 30 .
o =
Следовательно,
Итого,
Tan 30 o =
Задача 3. Проверить, лежит ли точка P(2/3, 3/2) на единичной окружности.
Решение:
Согласно уравнению единичного круга, которое равно:
x 2 + y 2 = 1
Подстановка значений x и y в уравнение (4*4)+(9*4))/36 = 1
= (16 +36)/36 = 1
= 52/36 = 1
= 13/9 = 1
Таким образом, 13/ 9≠ 1
Следовательно, точка P не лежит на единичной окружности.
Задача 4. Проверить, лежит ли точка Q(1/3, 1) на единичной окружности.
Решение:
Часто задаваемые вопросы о формуле единичного кругаСогласно уравнению единичного круга, то есть:
x 2 + Y 2 = 1
Здесь мы имеем
x = 1/3
Y = 10003 здесь.
Теперь,
Подстановка значений x и y в уравнение
=> (1/3) 2 + (1) 2 = 1
=> 1/9 + 1 = 1
=> 10/9 = 1
Таким образом, 10/9 ≠ 1.
Следовательно, точка Q не лежат на единичной окружности.
Вопрос 1. Что означает термин единичный круг?
Решение:
Единичная окружность определяется как расположение точки на расстоянии одной единицы от фиксированной точки. Его центр находится в точке (0,0), а значение его радиуса равно 1,9.0003
Вопрос 2. Каково значение единичной окружности в тригонометрии?
Решение:
Единичный круг полезен, потому что он позволяет нам найти синус, косинус или тангенс любого количества градусов или радианов. Знание круговой диаграммы особенно полезно, когда необходимо найти конкретное значение тригонометрии.
Вопрос 3. Как проверить, лежит ли точка на единичной окружности или нет?
Решение:
Любая точка, лежащая в двумерной плоскости и имеющая форму (x, y), помещается в уравнение единичной окружности x 2 + y 2 = 1, чтобы проверить, лежит ли она на окружности или нет.
Вопрос 4. Каково значение sin θ cos θ для точки (x, y) на единичной окружности?
Решение:
Что касается точки (x, y), sin θ = y и cos θ = x, значение sin θ cos θ становится xy.
SIN И COS
SIN И COSВ последнем разделе была представлена идея периодических функций. В этом разделе мы разовьем эту идею и рассмотрим две конкретные периодические функции — синус и косинус. Рисунки, показанные ниже, дают вам представление о графике функции синуса (слева) и графике функции косинуса (справа).
alt=»Ваш браузер понимает тег
График синусоиды
График косинуса

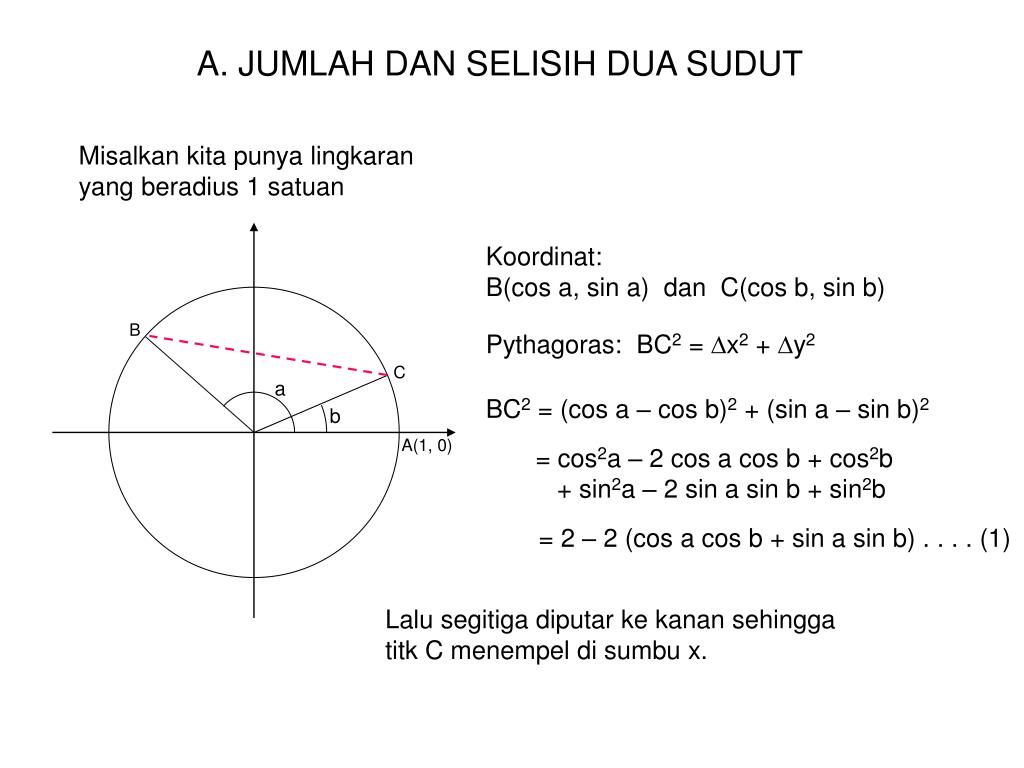
 2 = 1.
2 = 1.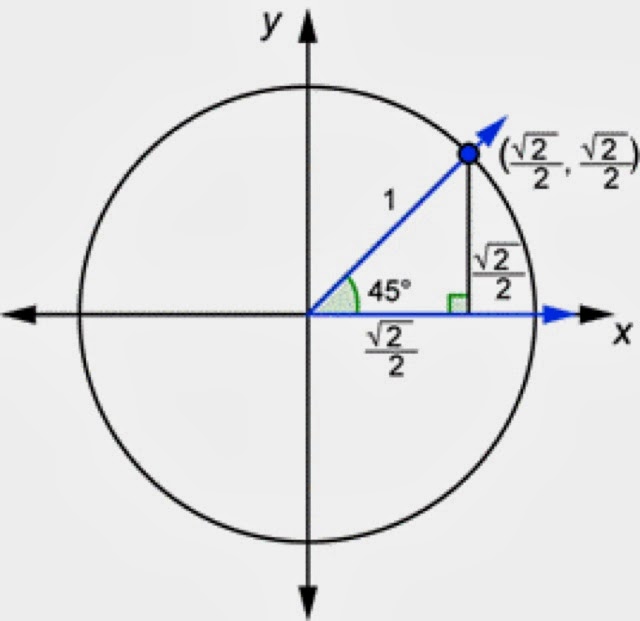 для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7