Первый корень:
`sinx=-1`;
`x=-pi/2+2pin, n in Z`;
Второй корень:
`sinx=(sqrt(2))/2`;
`x=pi/4+2pin, n in Z`;
`x=(3pi)/4+2pin, n in Z`.
С учетом ОДЗ остаются следующие корни (см. тригонометрическую окружность ниже):
`x=-pi/2+2pin, n in Z` и `x=(3pi)/4+2pin, n in Z`.
б) С помощью числовой окружности отберем корни, принадлежащие промежутку `[-(11pi)/2; -4pi]`.
Получились следующие корни: `-(21pi)/4; -(9pi)/2`.
Решение №2 (скан):
$IMAGE3$Ответ: а) `-pi/2+2pin; (3pi)/4+2pin, n in Z`;
б) `-(21pi)/4; -(9pi)/2`.
Формулы для решения простейших тригонометрических уравнений
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Содержание статьи:
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число.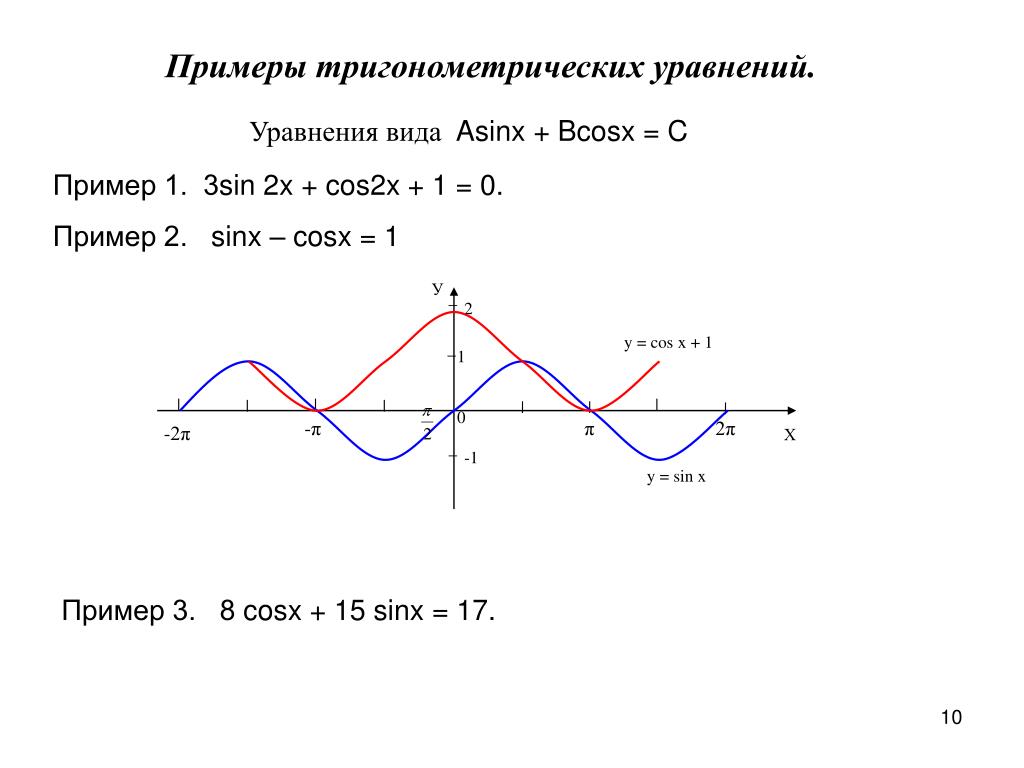
Таблица арксинусов
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Таблица арккосинусов
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
Таблица арктангенсов
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Таблица арккотангенсов
Формулы корней тригонометрических уравнений в таблице
Для синуса:Для косинуса:Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Материалы по теме:
Поделиться с друзьями:
Загрузка. ..
..Простейшие тригонометрические уравнения с косинусом и синусом. Часть 1
Ключ к решению простейших тригонометрических уравнений – в отличном знании тригонометрического круга. Если вы знаете значения стандартных точек и их синусы и косинусы, то проблем с уравнениями не будет. А если пробелы все-таки есть, то восполнить их можно в статье «Как запомнить тригонометрический круг?».
Эта статья состоит из двух частей:
Решение простейших уравнений с косинусом
Решение простейших уравнений с синусомАлгоритм решения простейших уравнений с косинусом
Любой алгоритм проще всего понять на конкретных примерах, поэтому сразу с них и начнем.
Пример №1. Решить уравнение \(\cosx=\frac{1}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2. Отметить на оси косинусов значение, которому косинус должен быть равен.

Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению для каждой из полученных точек на круге. Для уравнений с косинусом значения в верхней и нижней точках всегда будут отличаться только знаком.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn,n∈Z\) (подробнее о формуле в этом видео), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Возможно, у вас возник вопрос, почему мы в ответ добавляем \(+2πn\), \(n∈Z\). Дело в том, что у каждой точки на тригонометрическом круге есть множество значений, и каждое значение будет решением уравнения, а значит все они обязательно должны быть в ответе.
Но проблема в том, что значений этих бесконечно много, и просто в строчку их не запишешь.
 Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Пример №2. Решить уравнение \(\cosx=-\frac{\sqrt{3}}{2}\).
С 1-3 шагом всё понятно, а вот над 4 шагом надо подумать. Как найти значения полученных точек? Можно заметить, что дуга между точкой со значением \(π\) и найденной точкой равняется π/6 (см. картинку ниже). И чтоб из точки π прийти к верхней найденной точке надо пройти в отрицательную сторону расстояние \(\frac{π}{6}\), то есть значение верхней точки равно \(π-\frac{π}{6}=\frac{5π}{6}\). Значит значение нижней \(-\frac{5π}{6}\).
Пример №3. Решить уравнение \(\cosx=1\).
Видно, что в этом случае у косинуса только одна точка на круге будет решением, и эта точка совпадает с нулём на окружности.
 Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Пример №4. Решить уравнение \(\cosx=-\frac{7}{6}\).
Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Пример №4. Решить уравнение \(\cosx=-\frac{7}{6}\).Значения косинуса (как и синуса) для любого аргумента всегда лежат между \(-1\) и \(1\) включительно, поэтому равняться \(-\frac{7}{6}\) косинус никак не может. Значит такое уравнение не имеет решений.
Вот так решаются простейшие тригонометрические уравнения вида \(\cosx=a\). Для наглядности мы все рассказанное выше объединили на одной инфографике — взглянув на нее вы сразу вспомните суть. Пользуйтесь на здоровье.
Алгоритм решения простейших уравнений с синусом
Пример №5. Решить уравнение \(\sinx=\frac{\sqrt{3}}{2}\).
Шаг 1. Построить окружность и оси синусов и косинусов.
Шаг 2.
 Отметить на оси синусов, значение, которому синус должен быть равен.
Отметить на оси синусов, значение, которому синус должен быть равен.
Шаг 3. Провести перпендикуляр и отметить точки пересечения перпендикуляра и круга. Если пересечений нет, то уравнение не имеет решений.
Шаг 4. Найти по одному значению каждой из полученных точек на круге. Для уравнений с синусом значение второй точки можно найти, если вычесть из π значение первой точки.
Шаг 5. Записать все значения каждой точки используя формулу \(x=t_0+2πn\), \(n∈Z\), где \(t_0\) – как раз те значения точек, которые вы нашли в шаге 4.
Пример №6. Решить уравнение \(\sinx=-\frac{\sqrt{2}}{2}\).
Так как суть, думаю, вам уже ясна, дальнейшие объяснения мы опускаем.
Пример №7. Решить уравнение \(\sinx=0\).

В уравнениях с \(0\), главное не перепутать к какой оси надо проводить перпендикуляр. Ось синусов – вертикальная, соответственно перпендикуляр будет горизонтален.
Пример №8. Решить уравнение \(\sinx=\frac{\sqrt{5}}{2}\).
Вот в принципе и всё. Как обычно, в конце – инфографика для наглядности.
Смотрите также:
Синус
Косинус
Решение уравнений \(tg\;x=a\) и \(ctg\;x=a\)
Тригонометрические уравнения§ 19. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
cos x = a, sin x = a, tg x = a, ctg x = a .

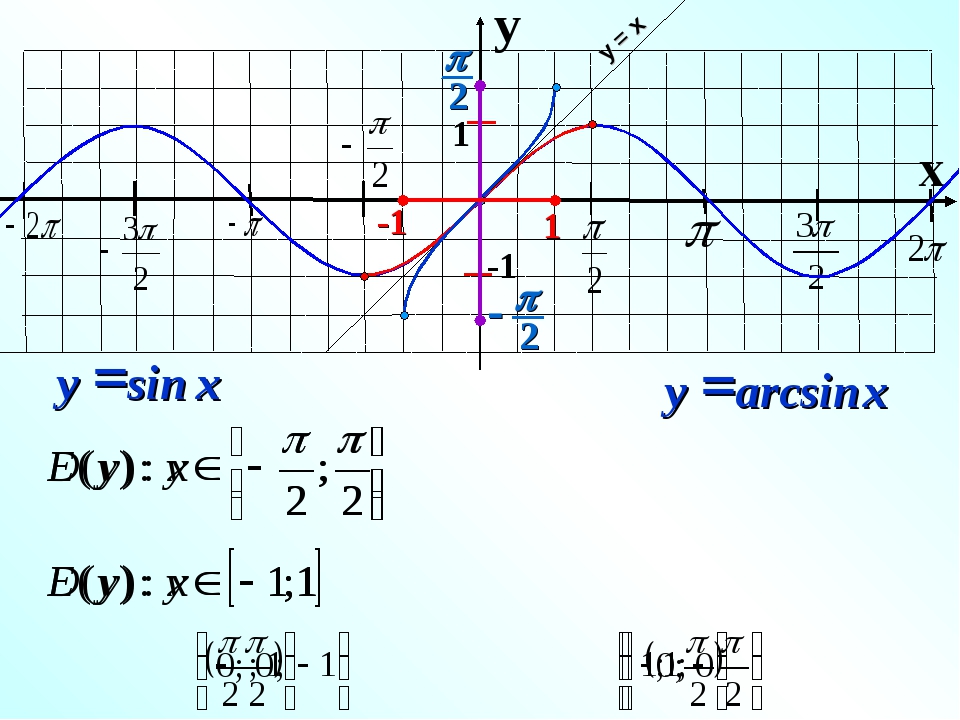
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Таблица 1
Объяснение и обоснование
- Корни уравнения cos x = a.
При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a < -1 не пересекает график функции y =
Пусть | a | ≤ 1. Тогда прямая y = a пересекает график функции y = cos x (рис.
 из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).
из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).Косинус – четная функция, поэтому на промежутке [-π; 0] уравнение cos x = a также имеет только один корень – число, противоположное x1, то есть x2 = — arccos a.
Таким образом, на промежутке [-π; π] (длиной 2π) уравнение cos x = a при |a| ≤ 1 имеет только корни x = ±arccos a.
Функция y = cos x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных на 2πn (n ∈ Z).
 Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:
Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:x = ±arccos a + 2πn, n ∈ Z (1)
- Частые случаи решения уравнения cos x = a.
Полезно помнить специальные записи корней уравнения cos x = a при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка А или точка В (рис.
 из пункта 2 табл. 1). Тогда
из пункта 2 табл. 1). ТогдаАналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка С, следовательно, x = 2πk, k ∈ Z.
Также cos x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, x = п + 2πk, k ∈ Z
Примеры решения задач
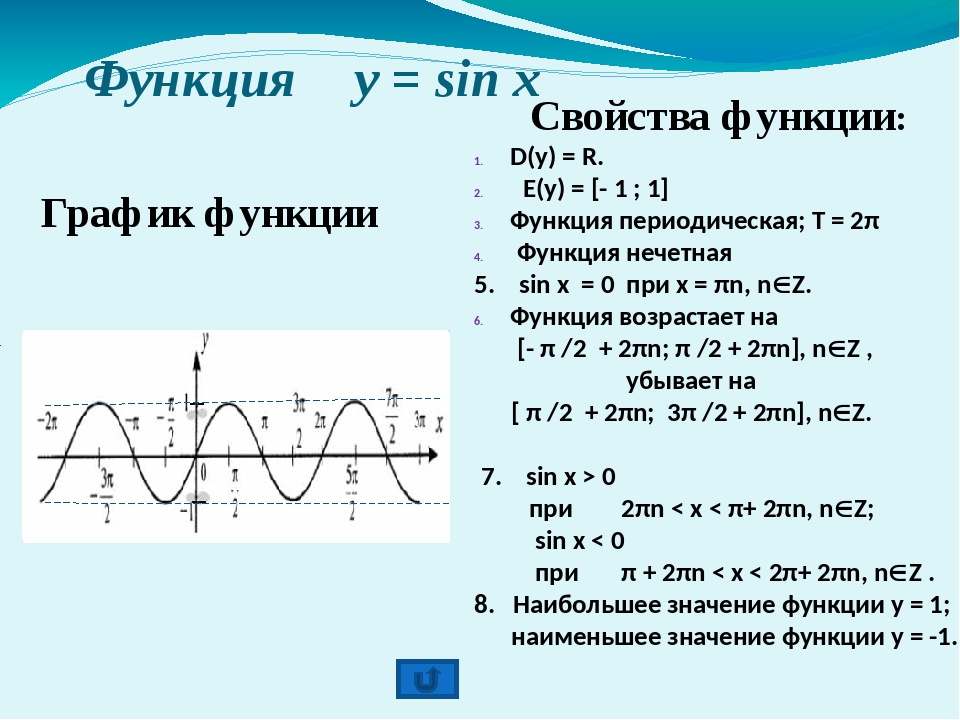
19.2. Уравнение sin x = a
Таблица 2
Объяснение и обоснование
1.
 Корни уравнения sin x = a.
Корни уравнения sin x = a.При |a| > 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a < -1 не пересекает график функции y = sin x).
Рисунок 1
Пусть |a| ≤ 1. Тогда прямая y = a пересекает график функции y = sin x (рис. 1). На промежутке функция y = sin x возрастает от -1 до 1. Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень, который по определению арксинуса равен: x1 = arcsin a (и для этого корня sin x = a).

На промежутке функция y = sin x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение sin x = a имеет на этом промежутке только один корень x2 = π — arcsin a (рис. 1). Для проверки правильности записи значения второго корня x2 заметим, что x2 = π — x1, тогда sin x2 = sin (π- x1) = sin x1 = a. То есть x2 – корень уравнения sin x = a.
Таким образом на промежутке (длиной 2π) уравнение sin x = a при |a| ≤ 1 имеет только корни x1 = arcsin a, x2 = π — arcsin a.

Функция y = sin x периодическая с периодом 2π, поэтому все остальные корни отличаются от найденных 2πk (k ∈ Z). Получаем следующие формулы корней уравнения sin x = a при |a| ≤ 1:
x=arcsin a + 2πk, k ∈ Z. (1)
x= π — arcsin a + 2πk, k ∈ Z. (2)
Все значения корней уравнения sin x = a при |a| ≤ 1, которые дают формулы (1) и (2), можно записать с помощью одной формулы
x=(-1)n arcsin a + 2πn, n ∈ Z (3)
Действительно, из формулы (3) при четном n = 2k получаем x = arcsin a + 2πk – формулу (1), а при нечетном n = 2k +1 – формулу x= — arcsin a + π(2k+1)= π — arcsin a + 2πk, то есть формулу (2).

2.Частые случаи решения уравнения sin x = a.
Рисунок 2
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
Примеры решения задач
Замечание.
 Ответ к задаче 1 часто записывают в виде:
Ответ к задаче 1 часто записывают в виде:19.3. Уравнения tg x = a и ctg x = a
Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.

Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞).
 Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
При a = 0
таким образом, уравнение ctg x = 0 имеет корни
Примеры решения задач
Вопросы для контроля
- Какие уравнения называют простейшими тригонометрическими?
- Запишите формулы решения простейших тригонометрических уравнений.
 В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам? - Выведите формулы решения простейших тригонометрических уравнений.
- Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение (1-11)
Найдите корни уравнения на заданном промежутке (12-13)
Внеклассный урок — Формулы двойного аргумента
Формулы двойного аргумента (двойного угла)Выражения sin 2x, cos 2x, tg 2x можно выразить через sin x, cos x, tg x. Эти преобразующие формулы называются формулами двойного аргумента (или двойного угла).
Логику преобразования можно понять на примере выражения sin 2x.
Представим это выражение в виде sin (x + x).

Тогда мы легко можем применить формулу синуса суммы аргументов:
sin (x + x) = sin x cos x + cos x sin x = 2 sin x cos x.
Мы получили первую из формул двойного аргумента. А вот все формулы:
sin 2x = 2 sin x cos x
cos 2x = cos2x – sin2x
cos 2x = 1 – 2 sin2x
2 tg x
tg 2x = ————
1 – tg2xВ первых строках мы показали, как была получена первая формула из таблицы. Вычислим остальные три.

2) cos 2x = cos2x – sin2x.
Здесь так же представляем 2х в виде х + х и применяем формулу косинуса сложения аргументов:
cos 2x = cos (x + x) = cos x cos x – sin x sin x = cos2x – sin2x.
3) cos 2x = 1 – 2 sin2x.
Здесь мы просто продолжим преобразовывать предыдущую формулу.
Используем для этого основное тригонометрическое тождество cos2x + sin2x = 1.
Из этого тождества следует, что cos2x = 1 – sin2x. Итак, выпишем предыдущую формулу, вставим значение cos2x, сведем подобные члены и получим результат:cos 2x = cos2x – sin2x = 1 – sin2x – sin2x = 1 – 2sin2x.

2 tg x
4) tg 2x = ————
1 – tg2xСпособов, как прийти к такому тождеству, два.
Первый способ. Здесь нам поможет формула тангенса сложения аргументов. Для этого представим tg 2x в виде tg (x + х). Итак:
tg х + tg х 2 tg х
tg 2x = tg (x + х) = —————— = —————
1 – tg х tg х 1 – tg2хВторой способ. Он сложнее. Сначала применяем формулы синуса и косинуса сложения аргументов:
sin (x + х) sin x cos х + cos x sin х
tg 2x = tg (x + х) = —————— = ———————————
cos (x + х) cos x cos х – sin x sin хТеперь, чтобы упростить выражение, делим все его части на cos x cos х, сокращаем подобные члены и приходим к решению:
sin x cos х cos x sin х 2 sin х
————— + ————— —————
cos x cos х cos x cos х 2 cos х 2 tg x
———————————— = ——————— = —————
cos x cos x sin x sin х sin2x 1 – tg2x
————— – ————— 1 – ————
cos x cos x cos x cos х cos2xПРИМЕЧАНИЕ:
При решении конкретных задач важно помнить, что задача имеет смысл лишь в том случае, если в процессе решения знаменатели нигде не оказываются равны нулю.

Теперь для наглядности решим несколько примеров по теме.
Пример 1. Упростить выражение:
sin 2α
———
sin α
Решение:sin 2α 2 sin α cos α
——— = —————— = 2 cos α
sin α sin αПример 2. Пусть tg α = 3/4 и 180º < α < 270º.
Найти sin 2α.
Решение.
В первую очередь, отмечаем, что угол находится в третьей четверти. Значит, синус будет со знаком минус.
1
1) Значение синуса мы могли бы найти через формулу 1 + ctg2 α = ———.
sin2 αЗначит, нам надо сначала вычислить значение котангенса. Мы знаем, что tg α · ctg α = 1. Следовательно:
1 1 4
ctg α = —— = —— = ——
tg α 3/4 3
2) Теперь находим значение синуса:1 1 1 1 9
sin2 α = ————— = ————— = ———— = —— = ——
1 + ctg2 α 1 + (4/3)2 1 + 16/9 25/9 253
sin α = – ——
53) Мы знаем, что sin 2α = 2 sin α cos α.
 Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:9 16
cos2 α = 1 – sin2 α = 1 – —— = ——
25 254
cos α = – ——
54) Осталось применить формулу двойного угла:
3 4 2 · 3 · 4 24
sin 2α = 2 · (– ——) · (– ——) = ———— = —— = 0,96.
5 5 5 · 5 25Пример решен.
Пример 3: Вычислить
π π
cos2 — – sin2 —
8 8Решение.
Это выражение соответствует правой части формулы косинуса двойного
аргумента (cos 2x = cos2x – sin2x). Значит, просто приравняем его к левой части. Для этого замечаем, что
Значит, просто приравняем его к левой части. Для этого замечаем, чтоπ
х = —
8Остается ввести в формулу это значение х и решить уравнение:
π π π 2π π √2
cos2 —— – sin2 —— = cos 2 ∙ —— = cos —— = cos —— = —— .
8 8 8 8 4 2Пример решен.
Отвод компрессионный для ПЭ d. 63 х 1 1/2″ (п) (черн/син) (20шт) ТМ «RTP»
Фитинг ПЭ это основной элемент для соединения труб из полиэтилена низкой и высокой плотности. Обычное применение таких труб — транспортировка питьевой воды и других жидкостей в магистралях с давлением до 16 бар. Материалы, из которых изготовляются фитинги, имеют высокую химическую стойкость в т. ч. и к ультрафиолетовому излучению.Корпус из полипропилена (РР-В) устойчивый к УФ излучению.Уплотнитель из нитриловой резины (NBR).Втулка из полипропилена(РР-В) устойчивая к УФ излучению.Фальцевое кольцо (цанга) из ацетальной смолы.Крышка-гайка из полипропилена (РР-В).
Обычное применение таких труб — транспортировка питьевой воды и других жидкостей в магистралях с давлением до 16 бар. Материалы, из которых изготовляются фитинги, имеют высокую химическую стойкость в т. ч. и к ультрафиолетовому излучению.Корпус из полипропилена (РР-В) устойчивый к УФ излучению.Уплотнитель из нитриловой резины (NBR).Втулка из полипропилена(РР-В) устойчивая к УФ излучению.Фальцевое кольцо (цанга) из ацетальной смолы.Крышка-гайка из полипропилена (РР-В).Данные о ценах и остатках товара находятся в тестовом режиме. Уточняйте точную стоимость и наличие товара у оператора по тел. 15-05.
Отзыв не может быть пустым.

Ваш отзыв будет опубликован после проверки модератором.
Тригонометрические уравнения в 10 классе, примеры и решения
Дата публикации: .
Урок и презентация на тему: «Решение простейших тригонометрических уравнений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Тригонометрические уравнения (PPTX)Что будем изучать:
1. Что такое тригонометрические уравнения?
2. Простейшие тригонометрические уравнения.
3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.Что такое тригонометрические уравнения?
Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс.
 n – минус один в степени n.
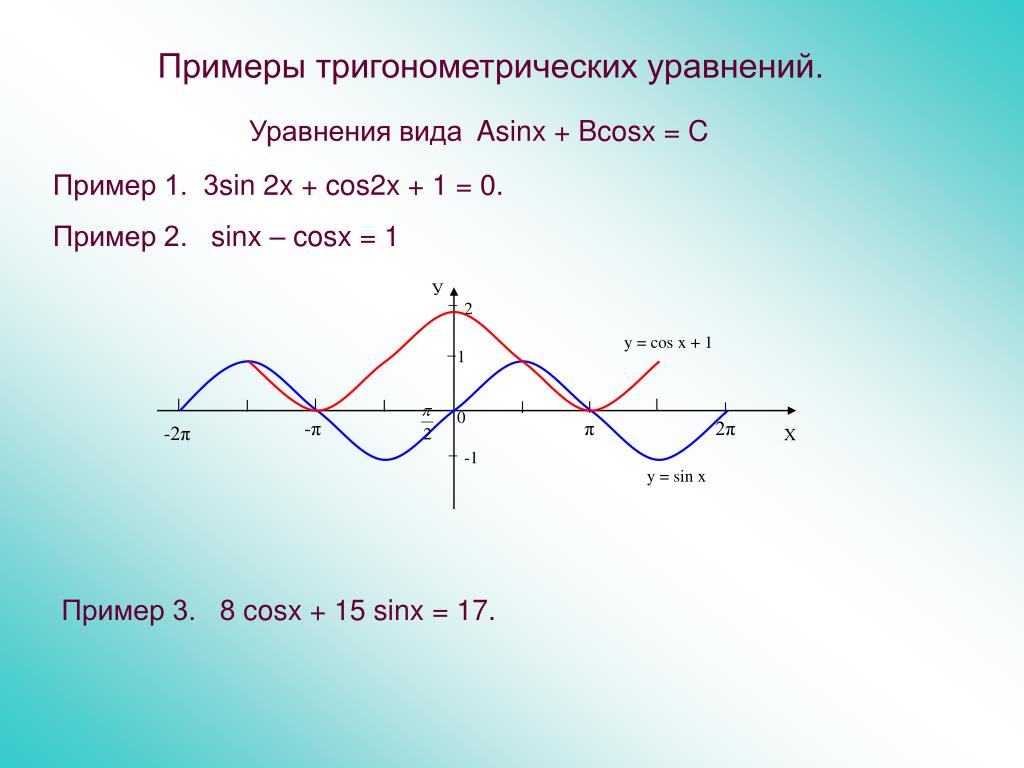
n – минус один в степени n.Ещё примеры тригонометрических уравнений.
Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3Решение:
а) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:
x/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk
Ответ: x=5πk, где k – целое число.
б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3
3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3
Ответ: x=2π/9 + πk/3, где k – целое число.
Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке [0; π].
Решение:
Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk
4x= ± π/4 + 2πk;
x= ± π/16+ πk/2;
Теперь давайте посмотрим какие корни попадут на наш отрезок. При k При k=0, x= π/16, мы попали в заданный отрезок [0; π].
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.
Ответ: x= π/16, x= 9π/16
Два основных метода решения.
Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.Решим уравнение:
Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).В результате замены получим: t2 + 2t -1 = 0
Найдем корни квадратного уравнения: t=-1 и t=1/3
Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.
x=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.
Ответ: x= -π/4+πk; x=arctg(1/3) + πk.
Пример решения уравнения
Решить уравнений: 2sin2(x) + 3 cos(x) = 0
Решение:
Воспользуемся тождеством: sin2(x) + cos2(x)=1
Наше уравнение примет вид:2-2cos2(x) + 3 cos (x) = 0
2 cos2(x) — 3 cos(x) -2 = 0
введем замену t=cos(x): 2t2 -3t — 2 = 0
Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2
Тогда cos(x)=2 и cos(x)=-1/2.

Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.
Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk
Ответ: x= ±2π/3 + 2πk
Однородные тригонометрические уравнения.
Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.Уравнения вида
однородными тригонометрическими уравнениями второй степени.Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.Решить уравнение:
Пример: cos2(x) + sin(x) cos(x) = 0Решение:
Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0
Тогда нам надо решить два уравнения:
cos(x)=0 и cos(x)+sin(x)=0
cos(x)=0 при x= π/2 + πk;
Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):
1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk
Ответ: x= π/2 + πk и x= -π/4+πk
Однородные тригонометрические уравнения второй степени
Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда!1.
 Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:
Делаем замену переменной t=tg(x) получаем уравнение:Решить пример №:3
Решить уравнение:
Решение:Разделим обе части уравнения на косинус квадрат:
Делаем замену переменной t=tg(x): t2 + 2 t — 3 = 0Найдем корни квадратного уравнения: t=-3 и t=1
Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk
tg(x)=1 => x= π/4+ πk
Ответ: x=-arctg(3) + πk и x= π/4+ πk
Решить пример №:4
Решить уравнение:
Решение:
Преобразуем наше выражение:
Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πkОтвет: x= — π/4 + 2πk и x=5π/4 + 2πk
Решить пример №:5
Решить уравнение:
Решение:
Преобразуем наше выражение:
Введем замену tg(2x)=t:22 — 5t + 2 = 0Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2
Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/22x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2
Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2
Задачи для самостоятельного решения.

1) Решить уравнениеа) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7
2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].
3) Решить уравнение: ctg2(x) + 2ctg(x) + 1 =0
4) Решить уравнение: 3 sin 2(x) + √3sin (x) cos(x) = 0
5) Решить уравнение:3sin2(3x) + 10 sin(3x)cos(3x) + 3 cos2(3x) =0
6)Решить уравнение:cos2(2x) -1 — cos(x) =√3/2 -sin2(2x)
ВыпущенXils-Lab Syn’X 2 v2.5 (мультитембральная эмуляция Synthex)
Syn’X 2 v2.5 Выпущен(начальная цена 99 евро вместо 169 евро)
В то время как наш MiniSyn’X — это «всего лишь» эмуляция Synthex высокого класса, представленная в XXI веке со всеми преимуществами Современная технология, ее старший брат, Syn’X 2.5, поднимает аналоговый синтез до новых высот и стандартов.
Две клавиатуры, объединяющие 8 полностью независимых слоев с максимальной мультитембральной гибкостью: до 72 осцилляторов, 8 великолепных многомодовых фильтров Zdf, 32 огибающих; 32 LFO, 8 слайдов и более 500 возможных модуляций, жестко зашитых или настраиваемых ……….
 ЗА ПАТЧ !!!
ЗА ПАТЧ !!!А для версии 2.5 мы добавили : новый блок реверберации, настраиваемую маршрутизацию эффектов, межслойные модуляции, новый менеджер предустановок, обновленный графический интерфейс / пользовательский интерфейс, больше предустановок и встроенную дополнительную панель Help Hood
8 слоев и True Unison в сочетании : начните с обдумывания режима Unison, в котором вы можете формировать не только количество осцилляторов, но и небольшие модуляции для каждого параметра из сотен, включая фильтры, огибающие, LFO, стереопозицию, Sync, RM, FM и т. Д.Теперь расширите концепцию до совершенно разных слоев: сложные многослойные звуки, такие как большие анимированные пэды. Огромные соло и басы. Клавиши, в которых каждый компонент по-разному реагирует на скорость. Сплиты, сочетающие арпеджио, басы, клавиши.
Что нового Подробная информация:
- Новый эффект реверберации : Блок старинной реверберации с естественным звучанием, с фильтром HPF
- Пользовательский путь для всех эффектов и клавиатуры.
 : Хорус реверберация или хорус, а затем реверберация? Разделение нижних басов переходит в хорус, а верхний пэд — в фазер, а затем реверберацию.Вам решать !
: Хорус реверберация или хорус, а затем реверберация? Разделение нижних басов переходит в хорус, а верхний пэд — в фазер, а затем реверберацию.Вам решать ! - New One Window Integrated Preset Manager : Найдите нужный патч за секунды, управляйте пресетами, звуковыми банками и создавайте свои собственные теги.
- Обновленный графический интерфейс / UI с простыми и сложными режимами.
- Межслойная модуляция : Уровень X теперь может передавать модуляции из других слоев. Очень могущественный.
- Еще заводские пресеты , в разных стилях и вкусах
- Встроенный механизм справки : Описание блоков и областей под дополнительным капотом.
- Catalina : Mac OS 10.15 Совместимость с Catalina
Подробнее: Xils-Lab Syn’X 2
Примечание. Обновление бесплатно для всех владельцев Syn’X 1 / Syn’X 2.XILS Labs Syn’x 2 Политембральный синтезатор
Syn’x 2 — это политембральный синтезатор, вдохновленный для синтезирующей части легендарным итальянским синтезатором 80-х годов, а его многослойная карточная архитектура вдохновлена сложными аппаратными аналоговыми монстрами, такими как Oberheim Matrix 12.

The Sound : он предлагает поразительную комбинацию четких и энергичных DCO с режущими многомодовыми аналоговыми фильтрами, подобными его предку, одному из последних винтажных полифонических аналоговых синтезаторов и кусочкам истории синтеза, включая знаменитый BBD Chorus!
А поскольку он мультитембральный, вы можете использовать до 16 осцилляторов, 8 аналоговых фильтров 0df, 32 огибающих DADSR и матрицы модуляции, обращаясь к любому из 132 возможных мест назначения для создания ваших собственных патчей, когда 300 заводских пресетов библиотеки будет недостаточно
Это синтезатор Xils-Lab, поэтому мы добавили БОЛЬШЕ.Назову несколько :- Осцилляторы с совокупными формами сигналов (до 40 на патч)
- Новый алгоритм 0DF PWM / Hard Sync
- Уникальный Lfos с совокупными формами волны (до 50 на патч)
- Дополнительные огибающие D-ADSR и матрицы модуляции (для каждого уровня)
- Унисон, 2 арпеджиатора, 2 зоны клавиатуры, гитарный мультитембральный режим
- Множество монофонических и полифонических режимов воспроизведения
- PolySequencer (также действует как источник модуляции)
- Простое создание звука с помощью нашей уникальной технологии Smart Load
- Винтажные звуковые эффекты: хорус, фазер, задержка, аналоговый эквалайзер.
 Настоящая стереотехнология.
Настоящая стереотехнология. - И двойная среда программирования, которая предлагает вам два разных режима редактирования (простой и расширенный).
Easy Mode позволяет использовать мощную, но интуитивно понятную и оптимизированную среду программирования, аналогичную дуотембральному синтезатору miniSyn’X , но с дополнительной мощностью дополнительных огибающих, LFO и т. Д.
Расширенный режим раскрыл всю мощь Syn’X 2 для создания толстых, сложных и никогда не слышных патчей при полностью обновленном и быстром рабочем процессе.
Все это делает Syn’X 2 одним из самых мощных и сложных виртуальных аналоговых синтезаторов современной эпохи и предлагает вам лучшее из обоих миров: винтажный звук в современном стиле и невиданные возможности
Характеристики:
.
Syn’X 2 — это мультитембральный синтезатор, предлагающий 8 слоев (полностью независимых синтезаторов), которые имеют общую 16-голосную полифонию и могут быть свободно назначены на любую из двух клавиатур. Он поставляется с 300 пресетами, разработанными профессиональными звукорежиссерами
Он поставляется с 300 пресетами, разработанными профессиональными звукорежиссерамидля каждого слоя / параметров синтезатора (до 8 слоев на патч)
Генераторы
- 2 генератора без наложения спектров с кумулятивными формами волны (пила / двойная пила / треугольник / синус / импульс / квадрат)
- Кольцевая модуляция, широтно-импульсная кросс-модуляция между генераторами
- Жесткая синхронизация между осцилляторами.Новый алгоритм 0df Cm / HardSync
- Модуль Advanced Glide / Portamento
Фильтры
- Один многомодовый аналогово смоделированный фильтр 0df (12/24 низких частот, 6/12 полосовых фильтров, 12 фильтров высоких частот) на основе эмуляции микросхемы CEM 3320
- Автоколебательный фильтр во всех режимах
- Приводной модуль до / после
Модуляторы
- 4 свободно назначаемых генератора огибающей (DADSR) с синхронизируемой задержкой.

- 2 полифонических LFO, синхронизируемых с несколькими формами волны (с собственной матрицей модуляции)
- 1 эксклюзивный Chaotic LFO (с собственной матрицей модов)
- 1 эксклюзивный Rhythm LFO (с собственной матрицей модов)
- Матрица модуляции на 6 слотов с более чем 15 источниками и 130 адресами
на параметры клавиатуры (до 2 клавиатур на патч)
- 1 Монофонический / полифонический арпеджиатор
- 8 моно / полифонических режимов воспроизведения + гитарный режим (1 MIDI-канал на слой)
- Полифония до 8 слоев и 16 голосов на клавиатуру
- Режим воспроизведения Mono / Unison / Poly с полифонией до 16 голосов
- Диапазон клавиатуры (низкие и высокие ноты)
Глобальные параметры и эффекты для каждого патча
- Двойная среда программирования (простой и расширенный режимы)
- Полисеквенсор 128 шагов (4 строки)
- 1 Global Sine монофонический LFO (джойстик)
- Аналоговый хорус, фазер, задержка и эквалайзер.

- Аналоговая ручка-распылитель
- Все параметры управляются по MIDI через встроенную карту Midi.
Осцилляторы:
- 7 осциллограмм. (Треугольник, Треугольник ШИМ, Пила, Пила ШИМ, Квадрат, Импульс ШИМ). Сигналы треугольной и пилообразной формы
- также могут принимать ШИМ. Новый режим кросс-модуляции ШИМ с нулевой задержкой обратной связи. Кольцевой модулятор и жесткая синхронизация между генераторами.
- Для каждого осциллятора можно выбрать одновременно несколько форм сигналов (до 40 на патч)
Многомодовый фильтр:
На основе эмуляции микросхемы CEM 3320 многомодовый фильтр Syn’X обеспечивает 6 типов фильтров: 12 и 24 дБ низких частот, 6 и 12 дБ полосовых частот и 12 дБ высоких частот.Автоколебания для всех типов. Перед фильтром или после него можно использовать специальную схему повышающей передачи. Этот фильтр использует наш запатентованный «алгоритм обратной связи с нулевой задержкой», обеспечивающий потрясающий аналоговый символD-ADSR:
- Доступно 4 специальных конверта
- Добавлен к стандартному Attack-Decay-Sustain-Release, Syn’X предлагает сегмент синхронизированной задержки MIDI, полезный, например, для запуска синхронизированных по темпу модуляций или для открытия фильтра через несколько миллисекунд после усилителя, давая некоторые взрывные эффекты.
 .
. - С помощью этой функции можно создавать широкий спектр новых звуков.
Полифонический LFO:
- 2 LFO с широкими возможностями, которые могут модулировать высоту и ширину генератора, частоту фильтра и уровень усилителя, а также могут использоваться в качестве источников в матрицах модуляции.
- Частота может быть синхронизирована с темпом хост-приложения. Модуляция также может быть сброшена с клавиатуры или в автономном режиме, и доступна функция плавного увеличения.
Chaox:
- Этот дополнительный уникальный LFO вдохнет реальную жизнь в механизм (ы) синтеза.
- Этот модуль вычисляет в двухмерном пространстве движение точки. Каждая из двух осей может модулировать любое из множества доступных пунктов назначения.
- Можно установить скорость модуляции и задержку перед применением модуляции.
- Параметр сглаживания позволяет уменьшить вариации модуляции, а параметр уровня хаотичности позволяет увеличить или уменьшить хаотический аспект движения.

- Можно выбрать 4 хаотических функции: Flying Fly, Bow Tie, Rainbow и Butterfly.
Ритмический LFO:
- 5 уникальных LFO для ритмических эффектов.
- 5 модуляций могут выполняться одновременно, и каждая может быть назначена любому из 132 возможных мест назначения.
- Модуляция может быть отложена, а параметр фазы может регулировать начало цикла.
- Octo : импульс в 8-й части цикла.
- Hexa : импульс в 16-й части цикла.
- Terna : импульс в 6-й части цикла.
- Hoover : рампа в 16-й части цикла.
- Stutter : 5 маленьких пил в 16-й части цикла.
Multi-Layer Две клавиатуры и режим гитары:
- Syn’X предлагает две MIDI-клавиатуры (верхнюю и нижнюю), подходящие для разделенных и наложенных инструментов, и специальный режим гитары, в котором все слои могут быть назначены на независимые MIDI-каналы.

- Каждая клавиатура имеет свои собственные независимые параметры точки разделения, унисон и режим воспроизведения, а также простой, но мощный полифонический арпеджиатор.
- На каждой клавиатуре можно использовать до 8 слоев / 16 голосов, выбираемых по своему усмотрению, чтобы получить максимальную пользу от многоуровневых функций Syn’X.
- Syn’X предлагает до 16 голосов полифонии, сгруппированных по два голоса (1–9, 2–10, 3–11,…), для полностью независимого управления 8 уровнями.
Guitar Mode:
- Syn’X предоставляет особый режим голосов / слоев, изначально изобретенный для гитаристов Midi.
- На каждый MIDI-канал можно назначить два голоса (т. Е. По одному на гитарную струну). Играть разные звуки на каждой гитарной струне еще никогда не было так просто.
- Эту функцию также могут использовать барабанщики, подключив MIDI-пэды к этим записям.
Технические характеристики:
- Mac OSX 10.
 5 и новее: VST, Audio Unit, RTAS (Protools 7.0 и новее), AAX (32- и 64-битные, собственные)
5 и новее: VST, Audio Unit, RTAS (Protools 7.0 и новее), AAX (32- и 64-битные, собственные) - Windows XP, Vista и 7,8,10; VST, RTAS (Protools 7.0 и новее), AAX (32- и 64-битные, собственные)
PLaneT> synx> maker.plt
Этот пакет недоступен в репозитории 3xx. Вместо этого показаны версии пакетов, доступные для всех репозиториев.
Пакеты в других репозиториях Эти пакеты недоступны в репозитории 3xx, но они доступны для других версий Racket.
Версия PLaneT Внешняя версия Источник DL Документы Треб.PLT Дата добавления (2 0) — 116
[нет]
[нет] 35 9033 9039 load: (require (planet «main. rkt» («synx» «maker.plt» 2 (= 0))))
rkt» («synx» «maker.plt» 2 (= 0))))Доступно в репозиториях: 4.x Maker
This Модуль имеет удобные инструменты для создания вещей, не пытаясь навязать вам еще одну совершенно новую парадигму.
(1 2) — 153
[нет]
[нет] 2010-05-21 для загрузки: (требуется main.ss «(» synx «» maker.plt «1 (= 2)))) Доступно в репозиториях: 4.x Maker
В этом модуле есть удобные инструменты для изготовления вещей , не пытаясь навязать вам еще одну совершенно новую парадигму.
(1 1) — 7
[нет]
[нет] 2009-11-15 Для загрузки: (требуется main.  ss «(» synx «» maker.plt «1 (= 1))))
ss «(» synx «» maker.plt «1 (= 1))))Доступно в репозиториях: 4.x Maker
В этом модуле есть удобные инструменты для изготовления вещей , не пытаясь навязать вам еще одну совершенно новую парадигму.
(1 0) — 1
[нет]
[нет] 2009-11-11 Для загрузки: (требуется (требуется main.ss «(» synx «» maker.plt «1 (= 0)))) Доступно в репозиториях: 4.x Maker
В этом модуле есть удобные инструменты для изготовления вещей , не пытаясь навязать вам еще одну совершенно новую парадигму.
Характеристика и фитнес-тестирование штамма synX.
 (A) Дизайн …
(A) Дизайн …Контекст 1
… последовательность synX была создана in silico с помощью пакета редактирования генома BioStudio, начиная с нативной последовательности хромосомы X (8-10) (рис. S1 ). Модификации в synX (рис. 1А) включают делецию ретротранспозонов, субтеломерных повторов и интронов. Кроме того, 24 гена тРНК были удалены, а однокопийный ген тРНК, tR (CCU) J (11), был перемещен в локус HO (таблица S1).Все стоп-кодоны TAG были заменены на TAA. Всего 490 пар синонимичных последовательностей при открытом чтении …
Контекст 2
… последовательность synX была создана in silico с помощью набора для редактирования генома BioStudio, начиная с нативной последовательности хромосомы X (8 -10) (рис. S1). Модификации в synX (рис. 1А) включают делецию ретротранспозонов, субтеломерных повторов и интронов. Кроме того, 24 гена тРНК были удалены, а однокопийный ген тРНК, tR (CCU) J (11), был перемещен в локус HO (таблица S1).
 Все стоп-кодоны TAG были заменены на TAA. Всего 490 пар синонимичных последовательностей в открытых рамках считывания (ORF) или PCRTags обслуживали …
Все стоп-кодоны TAG были заменены на TAA. Всего 490 пар синонимичных последовательностей в открытых рамках считывания (ORF) или PCRTags обслуживали …Контекст 3
… фрагментов ДНК размером ~ 5 т.п.н. Все мини-чанки были синтезированы поставщиками синтеза ДНК и использованы для поэтапного включения для замены нативной хромосомы X (рис. S2 и таблица S2) (10,14). Анализ PCRTag подтвердил наличие всех синтетических ампликонов и соответствующее отсутствие ампликонов дикого типа, что соответствует полному включению (рис.1B и рис. …
Контекст 4
… отлаженный штамм synX yYW0115 проявлял фенотипы, очень похожие на фенотипы дикого типа (BY4741) в различных условиях культивирования (фиг. 1C). Примечательно, что штамм synX yYW0115 демонстрирует удлиненную клеточную морфологию. Однако после обратного скрещивания эндоредупликации с диким типом морфология клеток synX стала сходной с таковой дикого типа (рис. S8). Чтобы обнаружить более тонкие различия в свойствах роста, мы реализовали тест конкурентного роста, чтобы охарактеризовать приспособленность synX.
 ..
..Контекст 5
… штамм yYW0115 показал удлиненную клеточную морфологию. Однако после обратного скрещивания эндоредупликации с диким типом морфология клеток synX стала сходной с таковой дикого типа (рис. S8). Чтобы обнаружить более тонкие различия в свойствах роста, мы реализовали тест конкурентного роста, чтобы охарактеризовать приспособленность synX с высокой чувствительностью (рис. 1D) (17). Клетки, кодирующие synX (yYW0115) и нативный chrX (BY4741), отслеживали по экспрессии красного флуоресцентного белка (RFP) и зеленого флуоресцентного белка (GFP) соответственно.После инокуляции при соотношении клеток 1: 1 два штамма поддерживали постоянное соотношение популяций в течение 72-часового периода совместного культивирования (рис. 1D), что свидетельствует об идентичном росте …
Контекст 6
… пригодность synX с высокой чувствительностью (рис. 1D) (17). Клетки, кодирующие synX (yYW0115) и нативный chrX (BY4741), отслеживали по экспрессии красного флуоресцентного белка (RFP) и зеленого флуоресцентного белка (GFP) соответственно.
 После инокуляции при соотношении клеток 1: 1 два штамма поддерживали постоянное соотношение популяций в течение 72-часового периода совместного культивирования (рис.1D), предполагая идентичные свойства роста в условиях конкурентного роста …
После инокуляции при соотношении клеток 1: 1 два штамма поддерживали постоянное соотношение популяций в течение 72-часового периода совместного культивирования (рис.1D), предполагая идентичные свойства роста в условиях конкурентного роста …Контекст 7
… несколько областей на synX с амплификациями сложной структуры (рис. 4B). qPCR для оценки количества копий генов, расположенных в каждой из трех повторяющихся областей, предположил, что они возникли во время трансформации с помощью мегачанка C (фиг. 4C). Анализ последовательностей соединений предположил тандемную дупликацию для структуры тройных областей (рис. 4B и рис.S10A). Аберрантные соединения, лежащие в основе амплификаций, и их положение относительно входящих фрагментов во время интегративной трансформации предполагают, что в одном случае гомологичная рекомбинация произошла на почти концевых сайтах loxPsym, а негомологичная рекомбинация произошла в сайтах Not I на концах миничанка в другом …
Контекст 8
… что гомологичная рекомбинация произошла на почти концевых сайтах loxPsym в одном случае, а негомологичная рекомбинация произошла на сайтах Not I на концах миничанка в другом случае.Другие структуры амплификации в мегачанках D и E также были проанализированы, и количественная ПЦР показала, что дупликации произошли во время трансформации мегачанка E (рис. S10, B и C). Структурные перестройки, опосредованные сайтами loxPsym и липкими концевыми окончаниями, также наблюдались в synII и synV …
Контекст 9
… был сконструирован в качестве селектируемого маркера, вставленного между областями синтетического и дикого типа. Синтетический мегачанк F (~ 50 т.п.н.) служил гомологичной областью для кроссовера двух хромосом X.После скрещивания двух штаммов и споруляции из тетрад отбирали споры, неспособные расти на среде без урацила и среде без лейцина (фиг. S10D). В одной из четырех тетрад наблюдались перекрестные события в интересующей области. Удаление амплифицированной области было подтверждено с помощью праймеров соединений и анализа гель-электрофореза в импульсном поле (фиг. 4, A и E, и фиг. S10E). Наконец, одна из шести Ura-Leu -спор имела все синтетические ПЦР-теги, и секвенирование генома …
Context 10
… Два штамма и спорулирующие споры, неспособные расти на среде без урацила и среде без лейцина, были отобраны из тетрад (рис. S10D). В одной из четырех тетрад наблюдались перекрестные события в интересующей области. Удаление амплифицированной области было подтверждено с помощью праймеров соединений и анализа гель-электрофореза в импульсном поле (фиг. 4, A и E, и фиг. S10E). Наконец, одна из шести Ura-Leu -спор имела все синтетические ПЦР-метки, и секвенирование генома подтвердило наличие однокопии ДНК во всех ранее амплифицированных…
Context 11
… был произведен in silico с помощью набора для редактирования геномных данных BioStudio (рис. S1) (10). Три принципа дизайна были определены следующим образом: во-первых, синтетическая хромосома должна приводить к (почти) фенотипу дикого типа и приспособленности; во-вторых, в синтетической хромосоме не должно быть дестабилизирующих элементов, таких как гены тРНК или транспозоны; и в-третьих, синтетическая хромосома должна обладать генетической гибкостью, чтобы облегчить будущее …
Synx — быстрое приспособление для старых / неподдерживаемых проектов XCode | Автор: Петр Кориенев
Это статья №3 цикла « Все об инструментах ». Итак,
Недавно мне дали задание проанализировать проект iOS и подготовить описательную документацию, чтобы оценить объем работы, необходимой для подготовки клона Android. Несмотря на то, что это определенно не лучший способ сделать оценку, требовалось сделать клон Android как можно ближе к архитектуре приложения iOS — чтобы оба приложения поддерживались предсказуемо.
Я начал смотреть на проект, и мне показалось, что он имеет довольно регулярную структуру (пока что это очень хорошо):
Первое, что я обычно делаю, это очень эмпирически оцениваю сложность, исходя из количества написанного кода.Я использую cloc (который также является простым, но мощным инструментом) для этого:
имя_компьютера: имя_каталога petr $ cloc TargetName
517 текстовых файлов.
501 уникальный файл.
105 игнорируемых файлов. Github.com/AlDanial/cloc v 1,74 T = 4,69 с (87,8 файлов / с, 10433,4 строк / с)
-------------------- ------------------------------------------------
Язык файлы пустой комментарий код
--------------------------------------------- -----------------------
Swift 333 7380 4814 34714
JSON 78 0 0 2025
Заголовок C / C ++ 1 2 5 1
----- -------------------------------------------------- -------------
СУММА: 412 7382 4819 36740
----------------------------- ---------------------------------------Хорошо, 333 файла Swift с 34714 SLOC.Следующее, что я хотел бы показать, — это разделение кода между различными разделами приложения.
имя_компьютера: имя_каталога petr $ cloc TargetName
0 текстовых файлов.
0 уникальных файлов.
0 файлов проигнорировано.1 ошибка:
Невозможно прочитать: TargetName / Screens
su-macbook-2e23: ios_for_sigma petr $Странно, проверяю фактический каталог и вижу:
ls -la TargetName | wc -l
429Гоша! Структура папок для проекта отсутствует — присутствуют только группы XCode. Это не та ситуация, с которой легко жить, но, к счастью, у нас есть synx — простое в использовании исправление структуры папок проекта XCode.
gem install synx # на случай, если вы еще не сделали это
synx * .xcodeprojНу вот!
ls -la TargetName | wc -l
44
cloc TargetName / Screens
22 текстовых файла.
22 уникальных файла.
1 файл проигнорирован. Github.com/AlDanial/cloc v 1,74 T = 0,20 с (105,1 файлов / с, 44861,2 строк / с)
-------------------- ------------------------------------------------
Язык файлы пустой комментарий код
--------------------------------------------- -----------------------
Swift 21 1420 572 6970
-------------------- ------------------------------------------------
СУММ : 21 1420 572 6970
-------------------------------------------- ------------------------Мы видим 21 файл Swift с 6970 SLOC для подклассов
UIViewController, поэтому сразу легко получить начальную подсказку Размер UI для проекта.Я рекомендую использовать Synx регулярно, особенно если вы не можете убедиться, что 100% кода проекта проходит экспертную оценку ИЛИ вы хотите быстро организовать «устаревший» проект. Однако для новых проектов, созданных с нуля в XCode, это не так актуально — XCode теперь по умолчанию создает папки для групп.
Спасибо за чтение и надеюсь, что это поможет 😃
Synx
Применяя глубокое обучение и компьютерное зрение, мы можем добиться более быстрой диагностики, что приводит к оптимизации лечения пациентов на протяжении всего процесса и принятию решений врачом. .Abstract
Мы разработали систему автоматического скрининга / диагностики диабетической ретинопатии с использованием ансамбля глубоких нейронных сетей, за которыми следует случайный лесной классификатор. Наша система имеет чувствительность 95% и специфичность 65%. // Пример ответа API{ "label": "Нет DR", «сумма_р»: 0,000285714285714285, «sum_y»: 0,018857143, "red_alert": ложь, "yellow_alert": ложь, "probs": { «здоровый»: 0,7143, «мягкий»: 0,0722857143, «умеренный»: 0,0185714286, «тяжелый»: 0.000285714286, г. «пролиферативный»: 0 } }
Обзор проблемы
Диабетическая ретинопатия (ДР), серьезное микрососудистое осложнение диабета, оказывает значительное влияние на мировые системы здравоохранения. Только в Мексике этим заболеванием страдают более 11 миллионов человек [1]. Во всем мире число людей с ДР вырастет со 126,6 миллиона в 2010 году до 191,0 миллиона к 2030 году, и, по оценкам, число людей с угрожающей зрению диабетической ретинопатией (VTDR) увеличится с 37,3 миллиона до 56.3 миллиона, если не будут приняты оперативные меры.Несмотря на растущее количество доказательств, подтверждающих эффективность рутинного скрининга ДР и раннего лечения, ДР часто приводит к плохому зрительному функционированию и представляет собой ведущую причину слепоты среди населения трудоспособного возраста. Во многих странах с низкими доходами DR игнорировалась в исследованиях и планировании здравоохранения, где доступ к квалифицированным офтальмологам и специализированным офтальмологическим услугам может быть недостаточным. Спрос на услуги, а также их предложение могут стать проблемой.Показатели соблюдения режима приема лекарств от диабета и ежегодных обследований глаз могут быть низкими, и причины этого многофакторные [2].
Мотивация
С намерением разработать автоматическую диагностическую систему для скрининга пациентов с возможной диабетической ретинопатией, мы использовали последние достижения в области компьютерного зрения и глубокого обучения для обучения ансамбля нейронных сетей для выявления этого заболевания и уровня его прогрессирования.Обзор модели
Данные
Для обучения и проверки мы использовали 85 000 изображений с высоким разрешением, каждое из которых состояло из захвата цифровой щелевой лампы, помеченного правильным диагнозом (сделанным врачом, оценившим тяжесть заболевания).Каждое изображение помечено как [0] отсутствие DR, [1] легкое DR, [2] умеренное DR, [3] тяжелое DR или [4] пролиферативное DR. Представление для каждого класса в наборе данных выглядит следующим образом:
Данные были случайным образом разделены между тренировочным (90%) и тестовым (10%) наборами.Результаты тестирования использовались для ранней остановки во время обучения и для выбора некоторых метапараметров нейронных сетей. Пример изображения из исходных данных. Пример изображения из исходных данных.Класс Количество изображений Нет DR 62,920 Mild DR 5650 3Тяжелая ЛР 2,020 Пролиферативная ЛР 1,690 Предварительная обработка
Глаз обнаруживается, и изображение масштабируется и настраивается так, чтобы глаз всегда находился в центре с фиксированным размером. Каналы RGB локально нормализованы с помощью движущегося гауссова ядра, чтобы подчеркнуть локальную изменчивость изображения. Это позволяет модели не зависеть от общей интенсивности света и других факторов в зависимости от конкретной используемой камеры.Пример изображения из исходных данных. Это изображение представляет собой окончательное изображение из исследования пролиферативного DR, используемого для обучения нейронной сети.Neural Networks
Несколько нейронных сетей были обучены с использованием разных архитектур (InceptionV3, Resnet50). В обучении использовалось трансферное обучение из модели Imagenet и проводилось поэтапно с самых верхних уровней, постепенно снижая скорость обучения. Для обучения каждой модели использовались две недели серверов с 2 GPU. Пример изображения из исходных данных.После обучения нейронная сеть способна оценивать предварительно обработанные изображения, это изображение показывает тепловую карту, на которой обнаружено повреждение у пациента с пролиферативным DR.Случайный лес
Мы обучили случайный лес объединить результаты разных нейронных сетей на обоих глазах пациента с другой статистикой изображений, чтобы предсказать окончательные вероятности того, что конкретное изображение соответствует определенному уровню DR. На этом этапе каждому изображению присваивается вектор с вероятностями каждого класса.Агрегация меток
Большинство руководств рекомендуют ежегодный скрининг для людей без ретинопатии или легкой диабетической ретинопатии; каждые 6 месяцев при умеренной диабетической ретинопатии и направление к офтальмологу для оценки лечения в течение нескольких недель или месяцев при тяжелой или пролиферативной диабетической ретинопатии [3].Следуя другим исследованиям, таким как [3], мы определяем отрицательный случай как без ДР или умеренный ДР, а положительный случай как ДР средней, тяжелой или пролиферативной формы. Таким образом, вектор вероятностей упрощается до вероятности того, что это положительный случай DR.Теперь мы можем создать кривую ROC, чтобы выбрать порог для нашего прогноза. Семейство моделей с разной чувствительностью и спецификой. На рисунке X мы видим различные возможности. Среди них мы выбрали модель с чувствительностью 95% и соответствующей специфичностью 65%, чтобы она служила хорошим первым скрининговым слоем в диагностическом конвейере.
Аналогичным образом мы создали красную тревогу, используя только тяжелую и пролиферативную DR в качестве положительных случаев и ища чувствительность 0.9. Эти два предупреждения, желтый и красный, имеют следующую статистику:
Класс Желтое предупреждение Красный сигнал Нет DR 18% 1% Mild DR 57% 2% Умеренный DR 90% 38% Тяжелый DR 98% 89% 903 Нет DR или легкая DR 35% (общая специфичность = 65%)
1% Средняя, тяжелая или пролиферативная 95% (общая чувствительность)
50% Тяжелая или пролиферативная 98% 90%
Вероятность срабатывания желтых или красных предупреждений, когда у пациента есть определенный класс ретинопатии.Мы видим, что красная тревога может сработать только при умеренном, тяжелом или пролиферативном DR; в то время как Yellow alert более консервативен и способен выявлять 95% всех положительных случаев. В сочетании оба предупреждения могут быть чрезвычайно полезны для раннего выявления диабетической ретинопатии.Дальнейшие шаги по повышению производительности модели:
- Более надежная маркировка в соответствии с примером [3] определенно уменьшит ошибку прогнозирования. Для этого мы будем сотрудничать с командой офтальмологов для систематической надежной диагностики и локализации ран.
- На этапе случайного леса включение дополнительных данных о пациентах (таких как уровень глюкозы, возраст и т. Д.) Было бы очень полезным.
- В настоящее время в модели используется ансамбль из 3 нейронных сетей. Если бы мы использовали хотя бы 10, мы могли бы повысить точность модели. Кроме того, работа с изображениями большего размера (с более высоким разрешением) может позволить нам обнаруживать более мелкие раны. И увеличенный ансамбль нейронной сети, и изображения с более высоким разрешением подразумевают большую мощность во время обучения.
Свитер Synx 1 с капюшоном | Черный
Свитер Synx 1 с капюшоном | Черный | G-Star RAW® Нажмите клавишу ВВОД, чтобы перейти на нашу страницу контактов, или позвоните в службу поддержки клиентов напрямую по номеру 888-933-3301. Нажмите Enter, чтобы перейти к основному содержанию {{ampiencePreviewTime}} Скопировать URL-адрес предварительного просмотра Выйти из предварительного просмотра G-Star Raw поискEN
Выберите пункт назначения и язык
Ваша сумка будет пуста, когда вы измените настройки страны.
авторизоватьсяСвитер Synx 1 с капюшоном
€ 99,95 включая НДС
В настоящее время этот товар недоступен
Калибр
Рост модели 1,78 м, размер S (грудь 85 см, талия 68 см, бедра 92 см). См. Руководство по размеру
Характеристики
Калибр
Модель 1.78 м, размер S (грудь 85 см, талия 68 см, бедра 92 см). См. Руководство по размеру
Детали
Цвет
Инструкция по стирке
30 ° мягкий процесс
Изобразительное искусство.номер: 95000E-4698-990
{{/ DiscountSigning}} {{#productSignings}}{{{метка}}}
{{/ productSignings}}{{name}}
{{#hasDiscountPrice}} {{#formattedFromPrice}} {{formattedFromPrice}} {{/ formattedFromPrice}} {{/ hasDiscountPrice}} {{#formattedBasePrice}} {{formattedBasePrice}} {{/ formattedBasePrice}}
{{цвет}} {{#availableStyleVariantsSorted}} {{/ availableStyleVariantsSorted}} {{/продукты}} Вернуться наверх .

 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.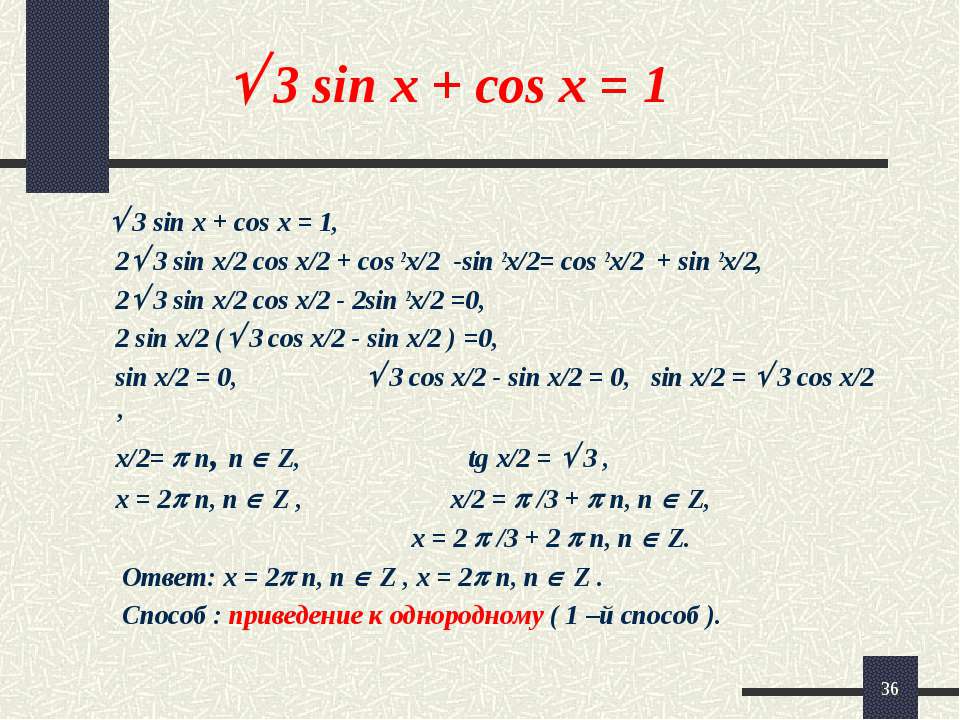 ..
..
 Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
Поэтому и придумали такую формулу записи, в которой содержатся все значения одной точки на тригонометрическом круге (подробнее смотрите в этом и этом видео).
 Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
Т.е. по формуле получим \(x=0+2πn\), \(n∈Z\). Однако добавление нуля ничего не меняет, поэтому ответ можно записать проще: \(x=2πn\), \(n∈Z\).
 Отметить на оси синусов, значение, которому синус должен быть равен.
Отметить на оси синусов, значение, которому синус должен быть равен.

 из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).
из пункта 1 табл. 1). На промежутке [0; π] функция y = cos x убывает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = a имеет на этом промежутке только один корень, который по определению арккосинуса равен: x1 = arccos a (и для этого корня cos x = a).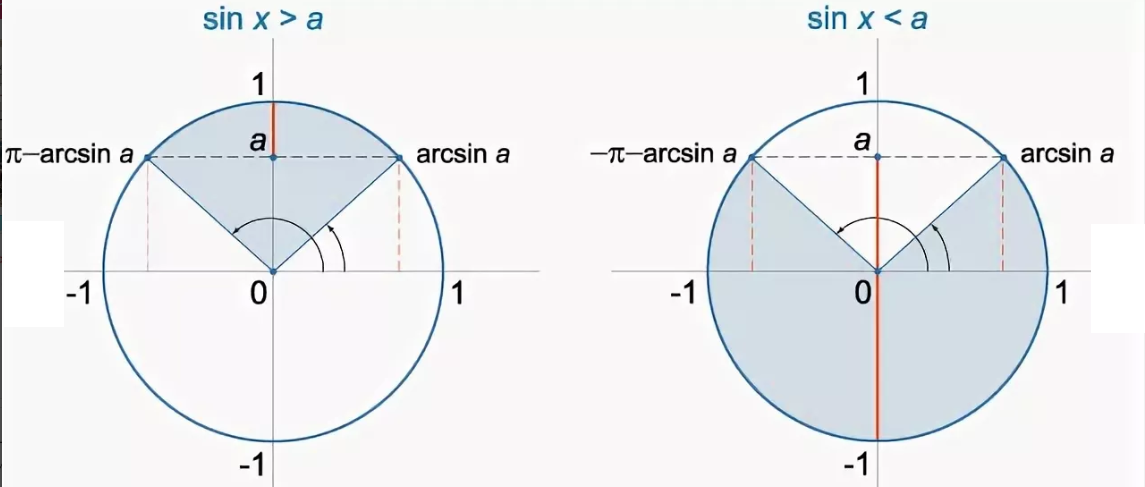 Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1:
Получаем следующую формулу корней уравнения cos x = a при |a| ≤ 1: из пункта 2 табл. 1). Тогда
из пункта 2 табл. 1). Тогда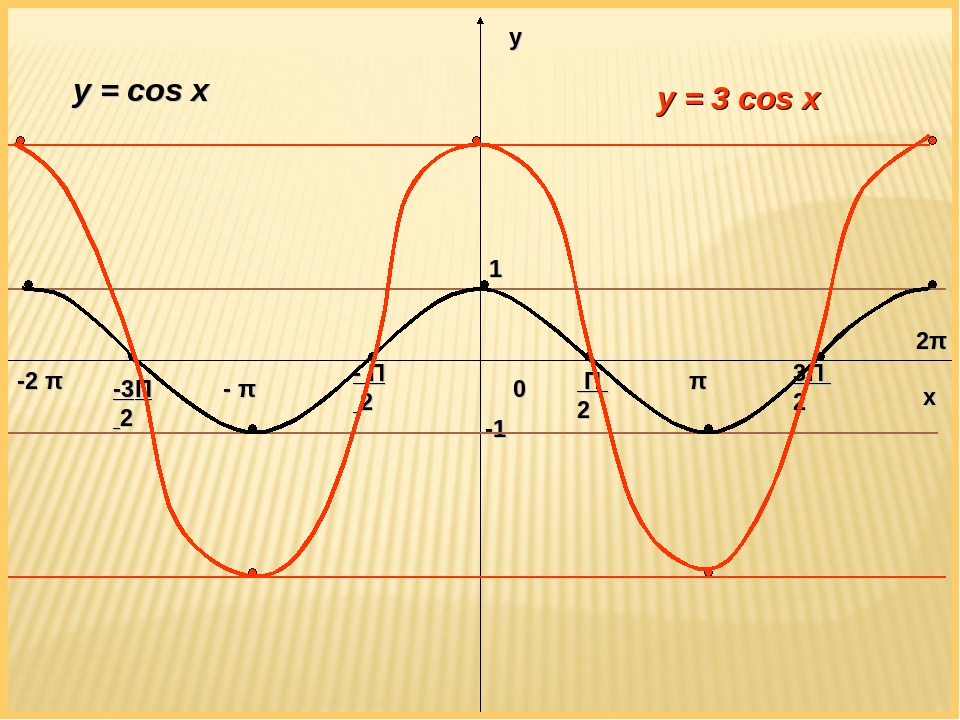 Корни уравнения sin x = a.
Корни уравнения sin x = a.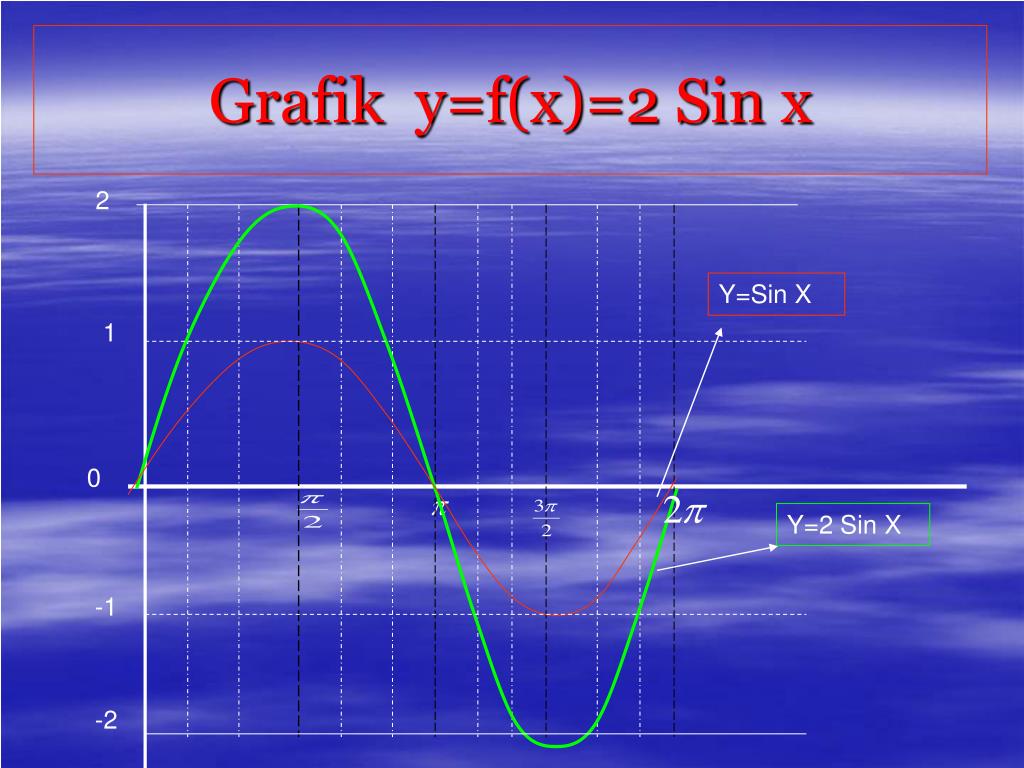
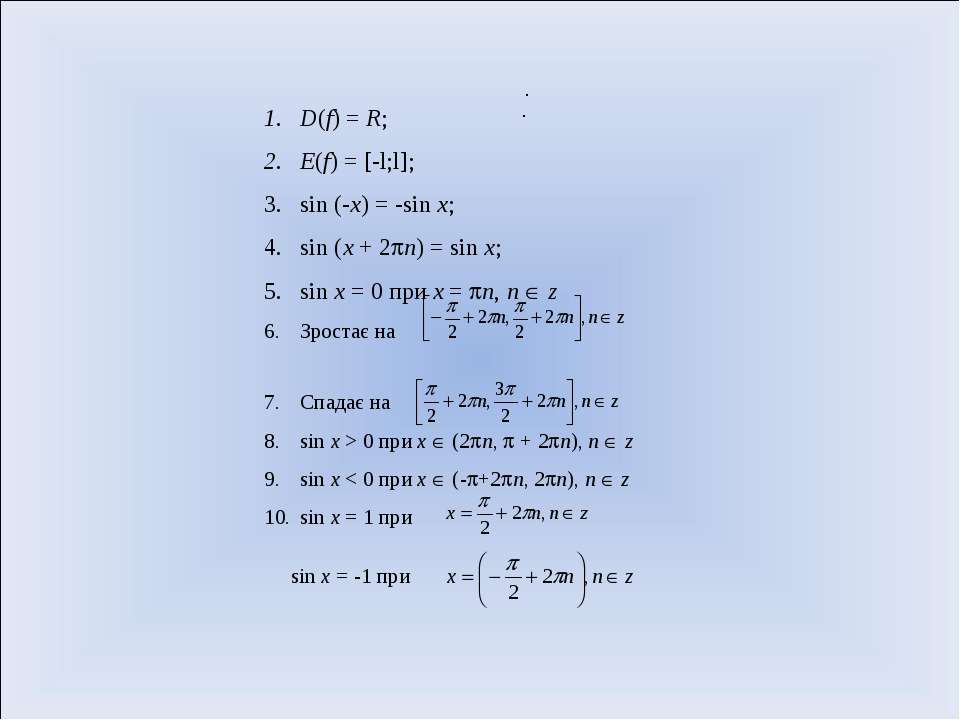

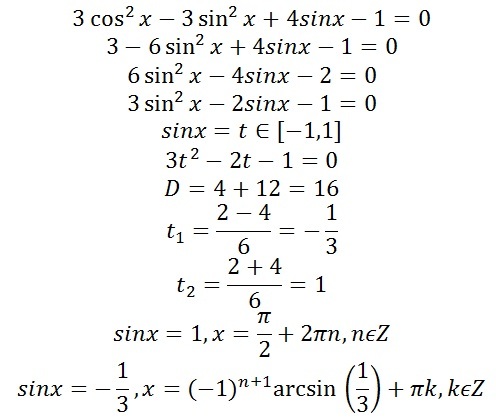 Ответ к задаче 1 часто записывают в виде:
Ответ к задаче 1 часто записывают в виде:
 Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?


 Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак:
Значит, находим еще косинус (по формуле cos2 α + sin2 α = 1). При этом опять не забываем, что угол – в третьей четверти и косинус должен быть со знаком минус. Итак: Значит, просто приравняем его к левой части. Для этого замечаем, что
Значит, просто приравняем его к левой части. Для этого замечаем, что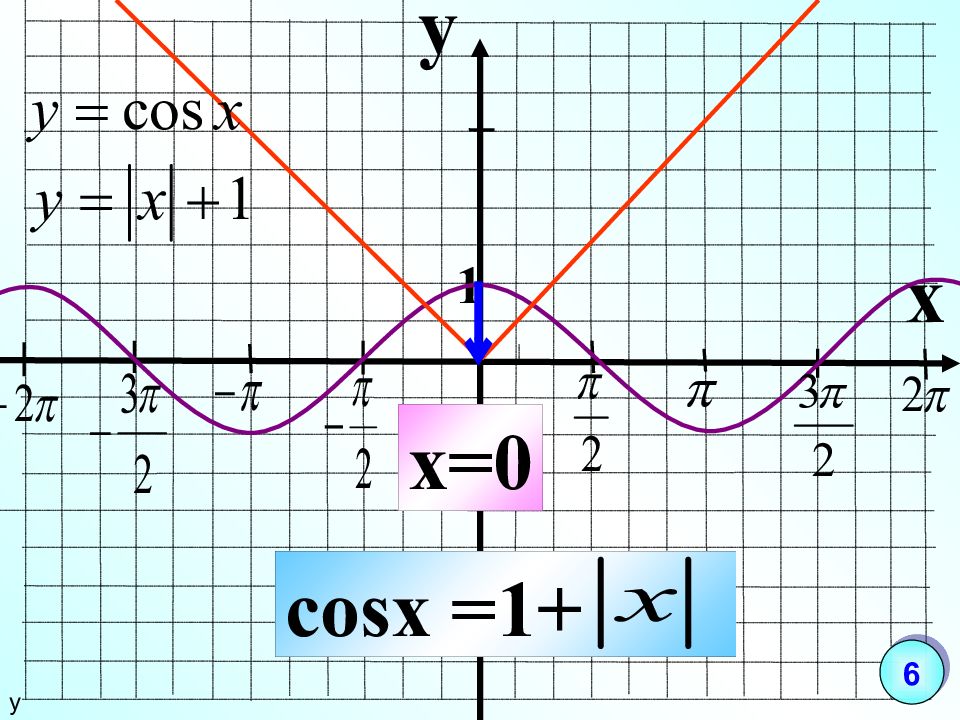 Обычное применение таких труб — транспортировка питьевой воды и других жидкостей в магистралях с давлением до 16 бар. Материалы, из которых изготовляются фитинги, имеют высокую химическую стойкость в т. ч. и к ультрафиолетовому излучению.Корпус из полипропилена (РР-В) устойчивый к УФ излучению.Уплотнитель из нитриловой резины (NBR).Втулка из полипропилена(РР-В) устойчивая к УФ излучению.Фальцевое кольцо (цанга) из ацетальной смолы.Крышка-гайка из полипропилена (РР-В).
Обычное применение таких труб — транспортировка питьевой воды и других жидкостей в магистралях с давлением до 16 бар. Материалы, из которых изготовляются фитинги, имеют высокую химическую стойкость в т. ч. и к ультрафиолетовому излучению.Корпус из полипропилена (РР-В) устойчивый к УФ излучению.Уплотнитель из нитриловой резины (NBR).Втулка из полипропилена(РР-В) устойчивая к УФ излучению.Фальцевое кольцо (цанга) из ацетальной смолы.Крышка-гайка из полипропилена (РР-В).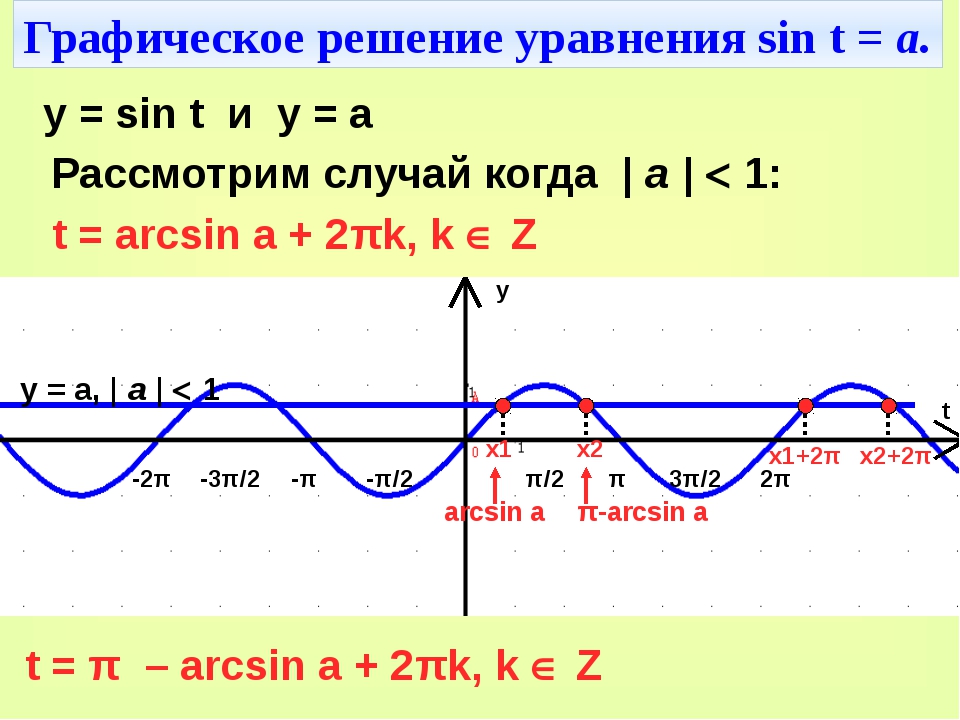
 n – минус один в степени n.
n – минус один в степени n.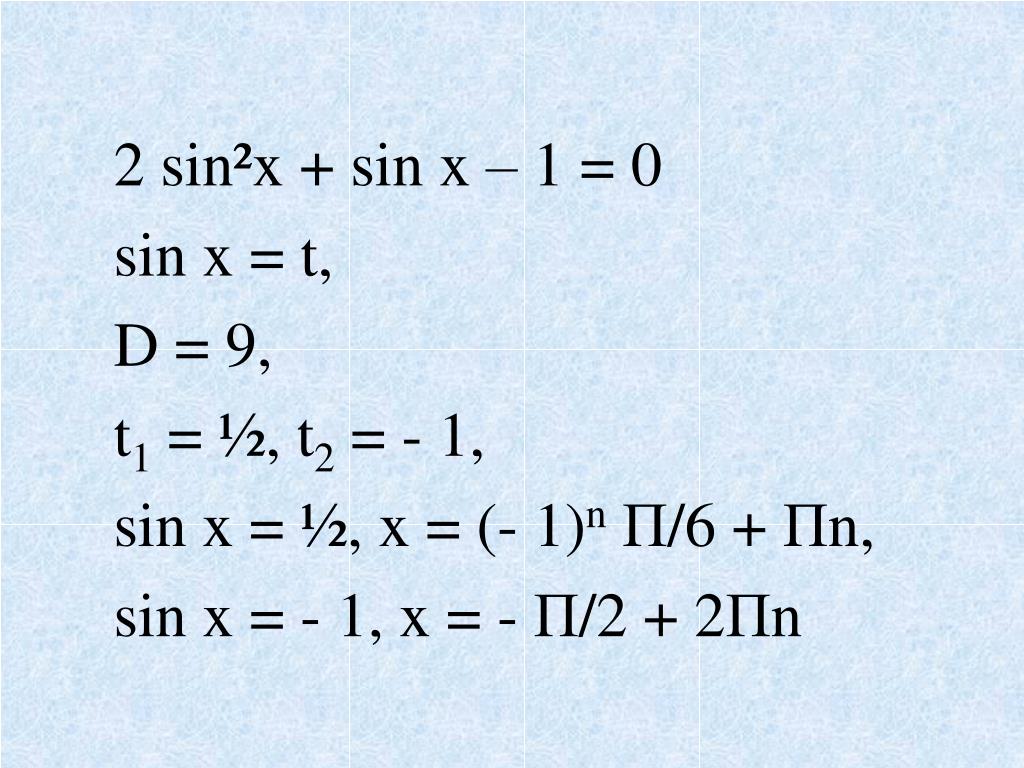

 Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде
 ЗА ПАТЧ !!!
ЗА ПАТЧ !!! : Хорус реверберация или хорус, а затем реверберация? Разделение нижних басов переходит в хорус, а верхний пэд — в фазер, а затем реверберацию.Вам решать !
: Хорус реверберация или хорус, а затем реверберация? Разделение нижних басов переходит в хорус, а верхний пэд — в фазер, а затем реверберацию.Вам решать ! 
 Настоящая стереотехнология.
Настоящая стереотехнология. Он поставляется с 300 пресетами, разработанными профессиональными звукорежиссерами
Он поставляется с 300 пресетами, разработанными профессиональными звукорежиссерами

 .
.

 5 и новее: VST, Audio Unit, RTAS (Protools 7.0 и новее), AAX (32- и 64-битные, собственные)
5 и новее: VST, Audio Unit, RTAS (Protools 7.0 и новее), AAX (32- и 64-битные, собственные) rkt» («synx» «maker.plt» 2 (= 0))))
rkt» («synx» «maker.plt» 2 (= 0)))) ss «(» synx «» maker.plt «1 (= 1))))
ss «(» synx «» maker.plt «1 (= 1))))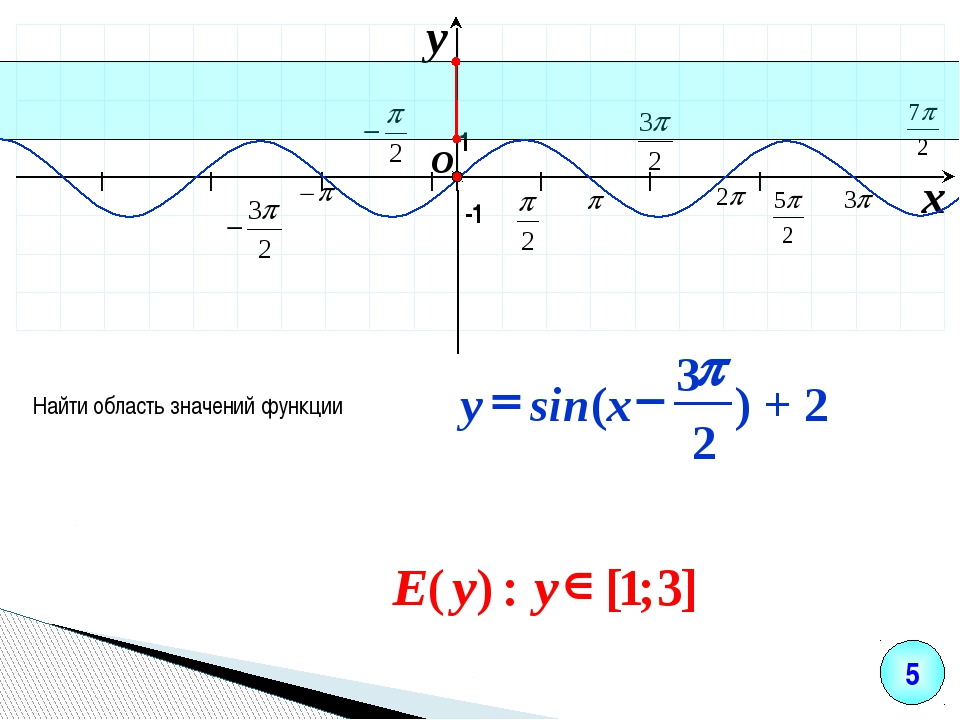 (A) Дизайн …
(A) Дизайн … Все стоп-кодоны TAG были заменены на TAA. Всего 490 пар синонимичных последовательностей в открытых рамках считывания (ORF) или PCRTags обслуживали …
Все стоп-кодоны TAG были заменены на TAA. Всего 490 пар синонимичных последовательностей в открытых рамках считывания (ORF) или PCRTags обслуживали … ..
..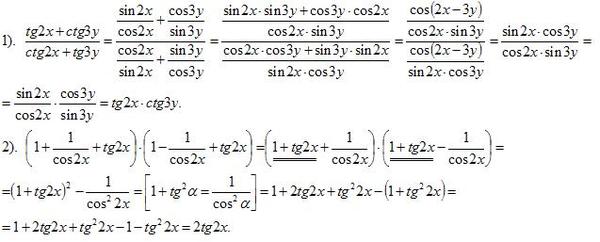 После инокуляции при соотношении клеток 1: 1 два штамма поддерживали постоянное соотношение популяций в течение 72-часового периода совместного культивирования (рис.1D), предполагая идентичные свойства роста в условиях конкурентного роста …
После инокуляции при соотношении клеток 1: 1 два штамма поддерживали постоянное соотношение популяций в течение 72-часового периода совместного культивирования (рис.1D), предполагая идентичные свойства роста в условиях конкурентного роста …