Дифференциальные уравнения (варианты)
Решение
Это уравнение вида — линейное дифференциальное уравнение I порядка. Такое уравнение можно решать методом Бернулли с помощью подстановки где u и v две неизвестные функции. Подставляя в исходное уравнение получим
или
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение . Получим откуда
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие . Тогда , Окончательно
Ответ:
Решение
Составим характеристическое уравнение Его корни
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид .
Частное решение неоднородного уравнения будем искать в виде , тогда , . Подставим в исходное , . Приравнивая коэффициенты при одинаковых степенях х в левой и правой части получим систему:
Тогда частное решение
Общее решение неоднородного примет вид:
Решение
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения и с помощью второго уравнения системы, получим
, ,
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение имеет корни и . Следовательно, общее решение для х будет .
Частное решение неоднородного уравнения будем искать в виде , тогда , .
Подставим в исходное , , . Приравнивая коэффициенты при одинаковых степенях х в левой и правой части получим систему:
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Решение
Данное уравнение – уравнение с разделяющимися переменными.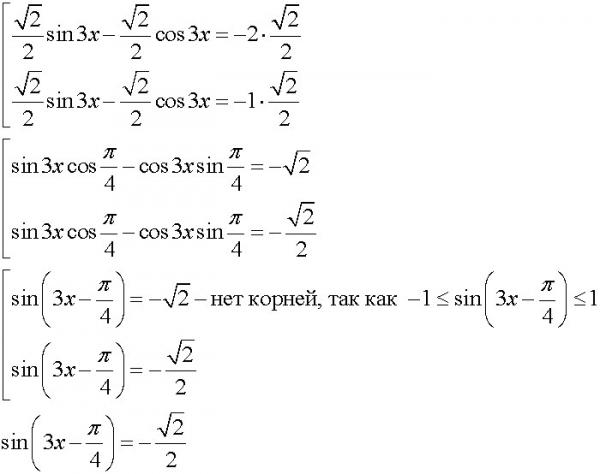 Разделим переменные: . Интегрируем:
Разделим переменные: . Интегрируем:
Посчитаем интегралы отдельно:
Тогда: или
Ответ:
Решение
Это уравнение вида — линейное дифференциальное уравнение I порядка. Такое уравнение можно решать методом Бернулли с помощью подстановки где u и v две неизвестные функции. Подставляя в исходное уравнение получим
или
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение . Получим откуда
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие . Тогда , Окончательно
Ответ:
Решение
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки , тогда .
Отсюда — линейное дифференциальное уравнение. Приведём к виду: ,
Замена где u и v две неизвестные функции. Подставляя в исходное уравнение получим
или
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение . Получим
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решение
Решим соответствующее однородное уравнение
Составим характеристическое уравнение Его корни
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид .
Частное решение неоднородного уравнения будем искать в виде , тогда , . Подставим в исходное , . Приравнивая коэффициенты при одинаковых степенях х в левой и правой части получим систему:
Тогда частное решение
Общее решение неоднородного примет вид:
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3-3r2+4= 0
(r + 1)(r2 — 4r + 4)=0
Корни характеристического уравнения:
R1 = -1 и корень характеристического уравнения r2 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e-x, y2 = e2x, y3 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = (2•x-3)•e-x
Уравнение имеет частное решение вида:
Вычисляем производные:
Y’ =
Y» =
Y»’ =
которые подставляем в исходное дифференциальное уравнение:
-3+4=
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r3 — 16r = 0
Корни характеристического уравнения:r1 = -4, r2 = 0, r3 = 4
Следовательно, фундаментальную систему решений составляют функции:
Y1 = e-4x, y2 = e0x, y3 = e4x
Общее решение однородного уравнения имеет вид:
Правая часть F(x) = e2•x+3cos2x-sinx
Будем искать отдельно частные решения для F1(x) = e2•x, F2(x) = 3cos2x, F3(x) = — sinx
Рассмотрим правую часть: F1(x) = e2•x
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 0.
Следовательно, число α + βi = 2 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Вычисляем производные:
Y’ = 2•A•e2x
Y» = 4•A•e2x
Y»’ = 8•A•e2x
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•e2x) -16(2•A•e2x) = e2•x или -24•A•e2x = e2•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-24A = 1
Решая ее, находим: A = -1/24;
Частное решение имеет вид: y* = -1/24e2x
Рассмотрим правую часть: F2(x) = 3•cos(2•x)
Поиск частного решения.
Уравнение имеет частное решение вида:y* = Acos(2x) + Bsin(2x)
Вычисляем производные:
Y’ = 2•B•cos(2x)-2•A•sin(2x)
Y» = -4(A•cos(2x)+B•sin(2x))
Y»’ = 8•A•sin(2x)-8•B•cos(2x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (8•A•sin(2x)-8•B•cos(2x)) -16(2•B•cos(2x)-2•A•sin(2x)) = 3•cos(2•x)
или 40•A•sin(2x)-40•B•cos(2x) = 3•cos(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
40A = 0
-40B = 3
Решая ее, находим: A = 0;B =-3/40;
Частное решение имеет вид:
Y* = -3/40*sin(2x)
F3(x) = — sin(x)
Поиск частного решения.
Уравнение имеет частное решение вида: y* = Acos(x) + Bsin(x)
Вычисляем производные:
Y’ = B•cos(x)-A•sin(x)
Y» = — A•cos(x)-B•sin(x)
Y»’ = A•sin(x)-B•cos(x)
Которые подставляем в исходное дифференциальное уравнение:
Y»’ -16y’ = (A•sin(x)-B•cos(x)) -16(B•cos(x)-A•sin(x)) = — sin(x)
или 17•A•sin(x)-17•B•cos(x) = — sin(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
17A = -1
-17B = 0
Решая ее, находим: A = -1/17;B = 0;
Частное решение имеет вид: y* = -1/17cos(x) + 0sin(x) или y* = -1/17cos(x)
Окончательно, общее решение данного уравнения
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -6 r + 8 = 0
Корни характеристического уравнения: r1 = 2, r2 = 4
Следовательно, фундаментальную систему решений составляют функции: y1 = e4x, y2 = e2x
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Для этого решим систему:
Тогда окончательно
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 -4 r + 4 = 0
Корни характеристического уравнения:
Корень характеристического уравнения r1 = 2 кратности 2.
Следовательно, фундаментальную систему решений составляют функции: y1 = e2x, y2 = xe2x
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = e2•x•sin(5•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 1, Q(x) = 0, α = 2, β = 5.
Следовательно, число α + βi = 2 + 5i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = e2x(Acos(5x) + Bsin(5x))
Вычисляем производные:
Y’ = e2x((2•B-5•A)•sin(5x)+(2•A+5•B)•cos(5x))
Y» = — e2x((20•A+21•B)•sin(5x)+(21•A-20•B)•cos(5x))
Которые подставляем в исходное дифференциальное уравнение:
Y» -4y’ + 4y = (-e2x((20•A+21•B)•sin(5x)+(21•A-20•B)•cos(5x))) -4(e2x((2•B-5•A)•sin(5x)+(2•A+5•B)•cos(5x))) + 4(e2x(Acos(5x) + Bsin(5x))) = e2•x•sin(5•x)
или -25•A•e2x•cos(5x)-25•B•e2x•sin(5x) = e2•x•sin(5•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-25A = 0
0A -25B = 1
Решая ее, находим: A = 0;B = -1/25;
Частное решение имеет вид: y* = e2x(0cos(5x) -1/25sin(5x)) илиy* =-1/25 e2x sin(5x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Решение
Характеристическое уравнение исходного дифференциального уравнения имеет мнимые корни .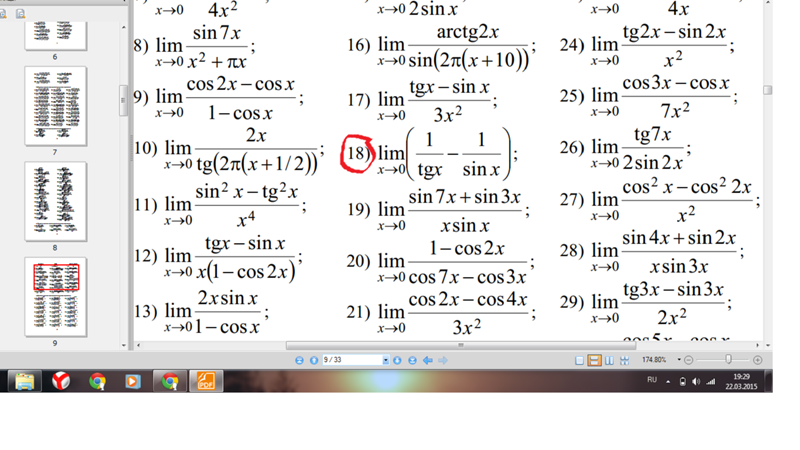 Следовательно, общее решение дифференциального уравнения . Тогда . Подставляем в первое граничное условие
Следовательно, общее решение дифференциального уравнения . Тогда . Подставляем в первое граничное условие
. Тогда .
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому и — собственные значения
— собственные векторы
Решение
Метод исключения неизвестных.
Продифференцируем по х первое уравнение
Исключая с помощью второго уравнения , получим ,
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Характеристическое уравнение имеет корни и . Следовательно, общее решение для х будет .
Частное решение неоднородного уравнения будем искать в виде , тогда , . Подставим в исходное ,
Тогда частное решение
Общее решение неоднородного примет вид:
Из первого уравнения
Ответ:
Решение
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения , получим
, ,
Таким образом, задача свелась к линейному неоднородному уравнению с постоянными коэффициентами второго порядка. Решим соответствующее однородное уравнение.
Решим соответствующее однородное уравнение.
Характеристическое уравнение имеет корни и . Следовательно, общее решение для х будет .
Частное решение неоднородного уравнения будем искать в виде , тогда , . Подставим в исходное , . Приравнивая коэффициенты при одинаковых степенях х в левой и правой части получим систему:
Тогда частное решение
Общее решение неоднородного примет вид:
Из второго уравнения
Ответ:
Решение
Данное уравнение – уравнение с разделяющимися переменными. Разделим переменные: . Интегрируем:
Посчитаем интегралы отдельно:
Тогда: или
Ответ:
Решение
Это уравнение вида — линейное дифференциальное уравнение I порядка. Такое уравнение можно решать методом Бернулли с помощью подстановки где u и v две неизвестные функции. Подставляя в исходное уравнение получим
или
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Первое уравнение – дифференциальное уравнение с разделяющимися переменными. Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение . Получим откуда
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Используем условие . Тогда , Окончательно
Ответ:
Решение
Данное уравнение не содержит у, следовательно понизить его порядок можно с помощью подстановки , тогда .
Отсюда — линейное дифференциальное уравнение. Приведём к виду: ,
Замена где u и v две неизвестные функции. Подставляя в исходное уравнение получим
или
Так как одна из неизвестных функций может быть выбрана произвольно, возьмем в качестве v одно из частных решений уравнения
Тогда исходное дифференциальное уравнение примет вид
Рассмотрим каждое из получившихся уравнений. Первое уравнение – дифференциальное уравнение с разделяющимися переменными.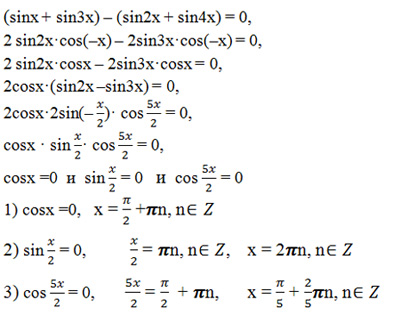 Разделяем переменные:
Разделяем переменные:
Интегрируя, находим
Подставим найденную функцию v во второе уравнение . Получим
Это дифференциальное уравнение с разделяющимися переменными. Решая его, находим функцию и:
Возвращаясь к функции у, получим
Ответ:
Решение
Решим соответствующее однородное уравнение
Составим характеристическое уравнение Его корни
Так как его корни действительные и есть кратные, общее решение однородного уравнения имеет вид
.
Частное решение неоднородного уравнения будем искать в виде , тогда , . , , .
Подставим в исходное , . Приравнивая коэффициенты при одинаковых степенях х в левой и правой части получим систему:
Тогда частное решение
Общее решение неоднородного примет вид:
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 — r= 0
Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 — r= 0
Вынесем r за скобку. Получим: r(r-1) = 0
Корни характеристического уравнения:r1 = 0, r2 = 1
Следовательно, фундаментальную систему решений составляют функции: y1 = e0x, y2 = ex.
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) =
Уравнение имеет частное решение вида:
Вычисляем производные:
которые подставляем в исходное дифференциальное уравнение:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Частное решение имеет вид:
Таким образом, общее решение дифференциального уравнения имеет вид:
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
Корни характеристического уравнения:(комплексные корни): r1 = 4i, r2 = -4i
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 16•cos(4•x)-16•e4x, будем искать отдельно частные решения для f1(x)= 16•cos(4•x) и для f2(x)= 16•e4x
Для f1(x) = 16•cos(4•x) имеем
Уравнение имеет частное решение вида: y ч1* = x (Acos(4x) + Bsin(4x))
Вычисляем производные:
Y’ = Acos(4x)+Bsin(4x)-4Axsin(4x)+4Bxcos(4x))
Y» = -4Asin(4x)+4Bcos(4x)-16Axcos(4x)-4Asin(4x)+4Bcos(4x))-16Bxsin(4x))=
=-8Asin(4x)+8Bcos(4x)-16Axcos(4x)-16Bxsin(4x))
Которые подставляем в исходное дифференциальное уравнение:
-8Asin(4x)+8Bcos(4x)-16Axcos(4x)-16Bxsin(4x))+16xAcos(4x)+16xBsin(4x))=
=16cos(4x)
или -8Asin(4x)+8Bcos(4x)=16cos(4x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-8A = 0
8B = 16
Решая ее, находим: A = 0;B = 2;
Частное решение имеет вид: yч1* = x (0cos(4x) + 2sin(4x)) или y ч1* = 2xsin(4x)
Для f2(x) = 16•e4x
Частное решение ищем в виде y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 16, Q(x) = 0, α = 4, β = 0.
Следовательно, число α + βi = 4 + 0i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида:
Вычисляем производные:
Y’ = 4•A•e4x
Y» = 16•A•e4x
Которые подставляем в исходное дифференциальное уравнение:
Y» + 16y = (16•A•e4x) + 16(Ae4x) = 16•e4•x или 32•A•e4x = 16•e4•x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
32A = 16
Решая ее, находим: A = 1/2;
Частное решение имеет вид: y*ч2 = 1/2e4x
Таким образом, общее решение дифференциального уравнения имеет вид:
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 9 = 0
Корни характеристического уравнения: r1 = -3i, r2 = 3i
Общее решение однородного уравнения имеет вид:
Для поиска частного решения воспользуемся методом вариации произвольных постоянных. Для этого решим систему:
Для этого решим систему:
Тогда окончательно
Решение
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами: r2 + 1 = 0
Корни характеристического уравнения:(комплексные корни): r1 = i,
Следовательно, фундаментальную систему решений составляют функции:
,
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть: f(x) = 2•cos(3•x)-3•sin(3•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида: R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
Имеет частное решение y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
Где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 2, Q(x) = -3, α = 0, β = 3.
Следовательно, число α + βi = 0 + 3i не является корнем характеристического уравнения.
Уравнение имеет частное решение вида: y* = Acos(3x) + Bsin(3x)
Вычисляем производные:
Y’ = 3•B•cos(3x)-3•A•sin(3x)
Y» = -9(A•cos(3x)+B•sin(3x))
Которые подставляем в исходное дифференциальное уравнение:
Y» + y = (-9(A•cos(3x)+B•sin(3x))) + (Acos(3x) + Bsin(3x)) = 2•cos(3•x)-3•sin(3•x)
или -8•A•cos(3x)-8•B•sin(3x) = 2•cos(3•x)-3•sin(3•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-8A = 2
-8B = -3
Решая ее, находим: A = -1/4;B = 3/8;
Частное решение имеет вид: y* = -1/4cos(3x) + 3/8sin(3x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Используем начальные условия
Тогда окончательно,
Решение
Характеристическое уравнение исходного дифференциального уравнения имеет мнимые корни . Следовательно, общее решение дифференциального уравнения . Подставляем в первое граничное условие
Следовательно, общее решение дифференциального уравнения . Подставляем в первое граничное условие
. Тогда .
Подставляем во второе граничное условие
При А=0 и В=0 – тривиальное решение у=0
Поэтому и — собственные значения
— собственные векторы
Решение
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения и с помощью второго уравнения системы, получим
,
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение имеет корни . Следовательно, общее решение для будет .
Из второго уравнения
Ответ:
Решение
Найдём сначала общее решение соответствующей однородной системы
Продифференцируем по х второе уравнение
Исключая с помощью первого уравнения и с помощью второго уравнения системы, получим
,
Таким образом, задача свелась к линейному однородному уравнению с постоянными коэффициентами второго порядка. Характеристическое уравнение имеет корни . Следовательно, общее решение для будет .
Характеристическое уравнение имеет корни . Следовательно, общее решение для будет .
Из второго уравнения Общее решение однородной системы:
Принимаем частное решение первоначальной системы в виде:
Тогда
Решаем данную систему по формулам Крамера, получим два дифференциальных уравнения первого порядка:
Тогда
Окончательно,
Или
Или
Ответ:
| < Предыдущая | Следующая > |
|---|
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как вы можете доказать, что sin3x = sinx(3cos^2x — sin^2x).
 Есть ли личность, которую можно использовать? 92х). Есть ли идентификатор, который можно использовать?» eNotes Editorial , 25 мая 2015 г., https://www.enotes.com/homework-help/how-can-you-prove-sin3x-sinx-3cos-2x-sin -2х-там-480044.
По состоянию на 7 декабря 2022 г.
Есть ли личность, которую можно использовать? 92х). Есть ли идентификатор, который можно использовать?» eNotes Editorial , 25 мая 2015 г., https://www.enotes.com/homework-help/how-can-you-prove-sin3x-sinx-3cos-2x-sin -2х-там-480044.
По состоянию на 7 декабря 2022 г.Ответы экспертов
Сначала вы можете использовать закон сложения синусов:
Где «a» равно 2x, а «b» равно x. Итак, у нас будет:
sin(2x+x) = sin2x cosx + sinx cos2x
Затем мы используем формулы двойного угла для sin и cos:
sin(2x) = 2 sinx cosx 92x)
…
См.
Этот ответ сейчас
Запустите 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Сначала вы можете использовать закон сложения синусов:
Где «a» равно 2x, а «b» равно x. Итак, у нас будет:
Итак, у нас будет:
sin(2x+x) = sin2x cosx + sinx cos2x 92x)
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы педагога
Математика
Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.
Решите для b2:A= 1/2h (b1+b2)
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г.
