progressive_plots или ускоряем построение графиков / Хабр
Здравствуйте, меня зовут Николай Стрекопытов и большую часть карьеры я работал на стыке R&D и Deep Learning и в задачах возникающих в этих нишах часто невозможно написать какие-то автотесты и не всегда понятно где вообще может быть проблема поэтому нужно визуально исследовать графики каких-то алгоритмически-заданных функций или показаний с девайса при разных параметрах, а хочется эти графики изучить в максимально детализированном варианте, что почти всегда занимает неприлично большое количество времени.
Я подумал, что можно вычислять значения функции в узлах не в порядке «перебираем каждую строчку столбца, а затем переключаемся на следующий столбец», а в каком-то более хитром порядке И выводить результат не через часы вычислений, а по мере извлечения информации, а в точках, в которых еще не была вычислена функция показывать результат интерполяции. Собственно в этой статье я хочу описать как я разработал прототип библиотеки, которая решает эту задачу и в комментариях с удовольствием вычитаю дельные замечания.
Как можно упорядочить узлы эффективнее?
Идея строится на том, что если достаточно разумно выбрать порядок узлов, то большая часть артефактов графика будет заметна уже на 30-70% вычислений, но какие есть варианты упорядочивания узлов? Далее вас ждут то ли сырые, то ли свежие идеи о том как это можно сделать, придумывал по пути, аналогов не нашел за короткий срок поиска, если кто-то что-то знает о такой задаче или близких, то я жду вас в комментариях
Независимо от функции
Следующая точка максимизирует расстояния до всех уже имеющихся точек с условием принадлежности множеству (отрезок если график функции одной переменной и прямоугольник если график функции двух переменных)
В зависимости от функции
Методов такого типа значительно больше из-за вычислительных нюансов и сегодня мы будем рассматривать подход только первого типа, но формула может быть, например, такой
гдеприближениепостроенное на узлахто есть каждый следующий узел это точка, в которой приближение хуже всего себя ведет.

Эти точки оказались Парето-оптимальными (при изменении координат нельзя увеличить ни один из функционалов не уменьшив хотя бы один). И, что замечательно, они высчитываются без сложных оптимизационных алгоритмов, а простым усреднением некоторых пар предыдущих элементов последовательности.
Оказалось, что алгоритм оптимального упорядочивания узлов по сути является построением бинарного дерева заданной глубины.
import numpy as np v = np.random.rand(6) # Задаем функцию, график которой хотим исследовать. # Случайная частичная сумма ряда Фурье (3 первых члена) def f(x): phi = np.array([np.sin(x), np.cos(x), np.sin(2 * x), np.cos(2 * x), np.sin(3 * x), np.cos(3 * x)]) return np.dot(v, phi) depth = 8 # Задаем глубину дерева или меру разрешения итогового графика a, b = 0, 8 * np.pi # Задаем отрезок length = 2 ** depth # Вычисляем количество узлов x_arr = np.linspace(a, b, length) # Задаем узлы y_arr = np.full_like(x_arr, np. nan, dtype=np.double) # Задаем хранилище значений и заполняем nan
mask = np.full_like(x_arr, False, dtype=bool) # Задаем маску маркирующую вычисленные узлы (их индексы)
# Вычисляем на границах
y_arr[0] = f(x_arr[0])
mask[0] = True
update(x_arr[mask], y_arr[mask])
y_arr[-1] = f(x_arr[-1])
mask[-1] = True
update(x_arr[mask], y_arr[mask])
prev_nodes = [(0, -1 + 2 ** self.depth)] # Список пар узлов, в которых уже было вычислена функция и внутри отрезка которых нет точек, в которых была вычислена функция
curr_nodes = []
for _ in range(self.depth):
for node in self.prev_nodes:
c = sum(node) / 2
curr_nodes.extend([(node[0], c), (c, node[1])])
index = int(c)
y_arr[index] = f(x_arr[index])
mask[index] = True
update(x_arr[mask], y_arr[mask])
self.prev_nodes = list(self.curr_nodes)
self.curr_nodes = []
nan, dtype=np.double) # Задаем хранилище значений и заполняем nan
mask = np.full_like(x_arr, False, dtype=bool) # Задаем маску маркирующую вычисленные узлы (их индексы)
# Вычисляем на границах
y_arr[0] = f(x_arr[0])
mask[0] = True
update(x_arr[mask], y_arr[mask])
y_arr[-1] = f(x_arr[-1])
mask[-1] = True
update(x_arr[mask], y_arr[mask])
prev_nodes = [(0, -1 + 2 ** self.depth)] # Список пар узлов, в которых уже было вычислена функция и внутри отрезка которых нет точек, в которых была вычислена функция
curr_nodes = []
for _ in range(self.depth):
for node in self.prev_nodes:
c = sum(node) / 2
curr_nodes.extend([(node[0], c), (c, node[1])])
index = int(c)
y_arr[index] = f(x_arr[index])
mask[index] = True
update(x_arr[mask], y_arr[mask])
self.prev_nodes = list(self.curr_nodes)
self.curr_nodes = []
Выше приведен полупсевдокод, функция update не объявлена, а она отвечает за обновление графика и интерполяцию, которая в текущей версии библиотеки полностью возложена на плечи matplotlib.
 Рабочий код можно посмотреть здесь github.com/nstrek/progressive_plots/
Рабочий код можно посмотреть здесь github.com/nstrek/progressive_plots/Для простоты в этой версии узлы жестко заданы и мы варьируем только порядок их вычисления, но и узлы, и их количество может задаваться алгоритмически, на основе какого-то правила. Например, количество узлов, а то есть глубину дерева можно увеличивать до тех пор пока отклонение графика с глубиной d от графика с глубиной d+1 больше чем delta.
В итоге такой алгоритм дает следующий процесс:
Слева процесс постепенного увеличения разрешения графика через добавление узлов в интерполяцию, а справа «истинный» график. Число сверху — количество уже вычисленных узлов из 256. Красная точка указывает на то в каком узле сейчас произведено вычисление.
Итоги
Как видно по анимации, гипотеза подтвердилась, уже с ~50% узлов видны почти все особенности графика. Представьте насколько это внушительно если количество узлов от 10 000 и функция вычисляется хотя бы 2 секунды, а ведь при увеличении количества узла еще и доля необходимая для насыщаемости будет падать.

Жду ваши предложения и замечания в комментариях. А также приглашаю в мой блог, в котором я пишу о своих идеях и наблюдениях на стыке R&D и DL — https://t.me/research_and_deep_learning
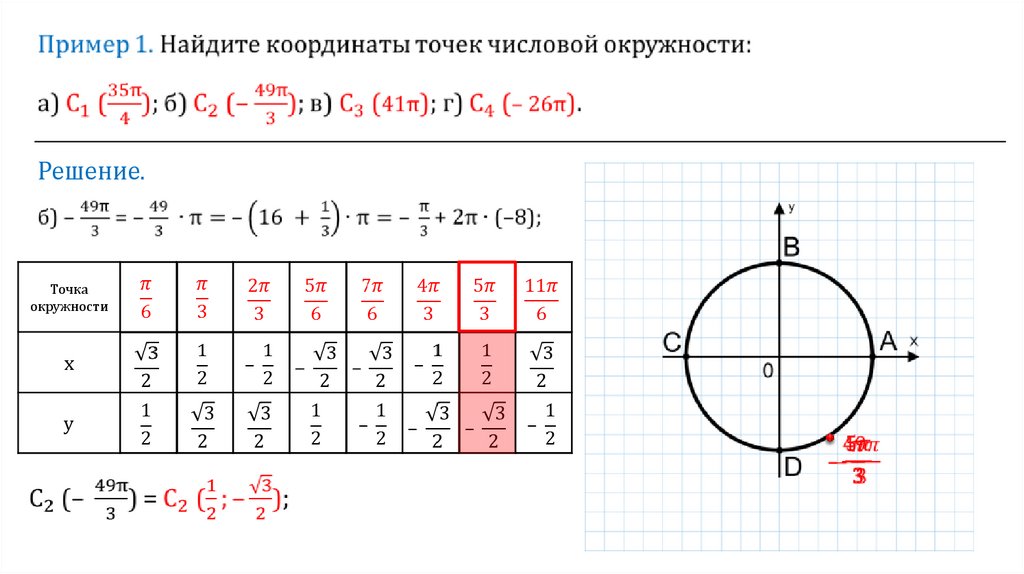
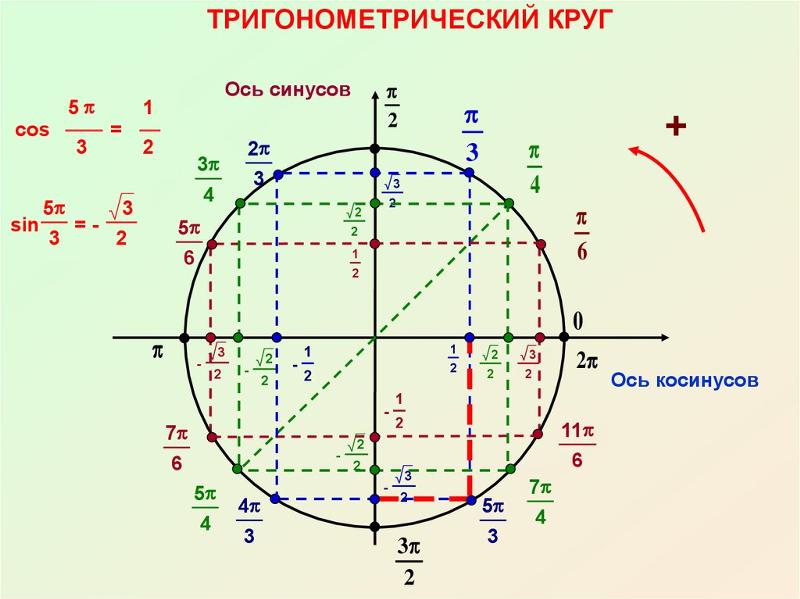
2(3pi/8)=?- задачи по тригонометрии
Ваш ответ
Ваше имя для отображения (необязательно): Напишите мне по этому адресу, если мой ответ выбран или прокомментирован: Напишите мне, если мой ответ выбран или прокомментирован Конфиденциальность: Ваш адрес электронной почты будет использоваться только для отправки этих уведомлений.
Проверка на спам: Чтобы избежать этой проверки в будущем, пожалуйста, войдите или зарегистрируйтесь.

1 Ответ
Расчет значений X и Y с помощью графика | Графические калькуляторы TI-83 Plus и TI-84 Plus
Ответ: 2.
МЕТОД
3π/8=π-5π/8. потому что (π-5π/8)=-cos(5π/8)=cos(3π/8).
грех(π-5π/8)=sin(5π/8)=sin(3π/8). 94 к стандартной форме, почему оба этих ответа отрицательные?
спросил 23 июля 2015 г. в ответах по тригонометрии к анонимный | 619 просмотров
- задачи по тригонометрии
1 ответ
Вычислить sin 5pi/6
спросил 4 августа 2013 г. в ответах по тригонометрии к анонимный | 2,2 тыс. просмотров
- тригонометрические задачи
1 ответ
как cos 3pi/4 равняется -1/корень 2?
спросил 2 марта 2015 г. в ответах по тригонометрии к икра коакаб Пользователь 1-го уровня (120 баллов) | 413 просмотров
- тригонометрические задачи
1 ответ
если sin(X)=-1/3 и pi/x/3pi/2, то каково значение tan(x)?
спросил 31 октября 2017 г. в ответах по тригонометрии
к
Хейли
| 2.1k просмотров
в ответах по тригонометрии
к
Хейли
| 2.1k просмотров- задачи по тригонометрии
- решение тригонометрических уравнений
1 ответ
если tanx=12/5 и Pi
задан вопрос 5 ноября 2015 г. в ответах по тригонометрии к анонимный | 2.7k просмотров
- задачи тригонометрии
- тождества с двумя углами
- решение тригонометрических уравнений
1 ответ
упростить sin(x+3pi/2)cosx
спросил 8 мая 2013 г. в ответах по тригонометрии к анонимный | 1.4k просмотров
- тригонометрические задачи
2 ответа
Преобразование функции y = sin(x -3pi/4)
вопрос 10 апреля 2013 г. в ответах по тригонометрии к анонимный | 2,6 тыс. просмотров
- задачи по тригонометрии
- решение уравнений
1 ответ
Учитывая Sec(x)= 3/2 при 3pi/2 < x < 2pi, найти sin (x/2).

спросил 17 ноября 2011 г. в ответах по тригонометрии к анонимный | 688 просмотров
- тригонометрические задачи
1 ответ
покажи как решить cos (5pi/6)
спросил 27 апр. 2014 г. в Word ответы на задачи к анонимный | 992 просмотра
- решение тригонометрических уравнений
- обратные тригонометрические функции
- задачи тригонометрии
- вычисление тригонометрических функций
1 ответ
tan (-17pi/12)
спросил 25 ноября 2012 г. в ответах по тригонометрии к анонимный | 1.1k просмотров
- тригонометрические задачи
1 ответ
каковы период, сдвиг по горизонтали, сдвиг по вертикали и отражение y=sec(1/2x+3pi)?
спросил 13 марта 2015 г. в ответах по тригонометрии к Реба | 385 Просмотров
- Проблемы тригонометрии
- Проблемы с алгеброй
- Период
- ПРОБЛЕМЫ ПРЕДУПРЕЖДЕНИЯ
1 Ответ
Уравнение 24 февраля 2014 г.
 в ответах по тригонометрии
к
спешка 76
| 500 просмотров
в ответах по тригонометрии
к
спешка 76
| 500 просмотров- задачи тригонометрии
- тригонометрические уравнения
1 ответ
Если sin a=4/5 и cos b=5/13, докажи, что cos a-b/2=8/65
спросил 4 июня 2013 г. в ответах по тригонометрии к анонимный | 595 просмотров
- тригонометрические задачи
1 ответ
Sin x = 1/2 √3, Cos x = -1/2 √3, Tan x = √3, X =…
спросил 11 июля 2022 г. в ответах по тригонометрии к Арселия | Тригонометрия ).
спросил 14 мая 2020 г. в ответах по тригонометрии к анонимный | 1 ответ 9 марта 2020 г. в ответах по тригонометрии к М | 991 просмотр
- тригонометрические задачи
1 ответ
cos(x-20)=sin(2x+32)
спросил 2 сентября 2019 г.в ответах по тригонометрии к Кельвин | 1.1k просмотров
- тригонометрические задачи
1 ответ
tan θ (cos θ + cot θ) = sin θ + 1
спросил 5 фев.
 2019 г.
в ответах по тригонометрии
к
йса
| 684 просмотра
2019 г.
в ответах по тригонометрии
к
йса
| 684 просмотра- тригонометрические задачи
- доказательство тригонометрических тождеств
2 ответа
доказать, что cos(A+B)+sin(AB)=2sin(45+A)cos(45+B)4 задано 27 июня 2017 г. в ответах по тригонометрии к Паула | 1,6 тыс. просмотров
- доказательство тригонометрических тождеств
- тригонометрическое тождество
- тригонометрических задач
- математических задач
1 ответ
Предположим, что sin2(t)=7/5 в первом квадранте. Найдите cos(t).
спросил 1 апр. 2017 г. в ответах по тригонометрии к анонимный | 624 просмотра
- cos
- sin
- квадрант
- задачи тригонометрии
- Все категории
- Pre-Algebra Answers 12,7к
- Алгебра 1 ответы 26.3k
- Алгебра 2 Ответы 10.8k
- Геометрия Ответы 5.5k
- Тригонометрические ответы
2.
 8k
8k - Исчисление Ответы 6.6k
- Статистика Ответы 3.3k
- Ответы на задачи Word 10.6k
- Другие математические темы 7.5k
сообщите об этом объявлении
сообщите об этом объявленииСправка по тригонометрии
Студенты, нуждающиеся в помощи по тригонометрии, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по тригонометрии. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы мгновенно получите много помощи по тригонометрии. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по тригонометрии.
После того, как вы успешно закончите курсы алгебры и геометрии в средней школе, вы будете готовы к изучению тригонометрии. Этот раздел математики занимается изучением треугольников.
 В частности, он рассматривает отношения между сторонами треугольника и углами, а также функции различных углов. Но в тригонометрии есть нечто большее, чем теорема Пифагора. Вы также изучите такие понятия, как синусы, косинусы, радианы и тождества углов, которые закладывают основу для дальнейшей работы по исчислению и другим математическим вычислениям. Понятия, введенные в тригонометрию, также полезны в ряде профессий, таких как архитектура, радиология и навигация.
В частности, он рассматривает отношения между сторонами треугольника и углами, а также функции различных углов. Но в тригонометрии есть нечто большее, чем теорема Пифагора. Вы также изучите такие понятия, как синусы, косинусы, радианы и тождества углов, которые закладывают основу для дальнейшей работы по исчислению и другим математическим вычислениям. Понятия, введенные в тригонометрию, также полезны в ряде профессий, таких как архитектура, радиология и навигация.Подготовка к тригонометрии, доступная в учебных пособиях Varsity Tutors Learn by Concept, обеспечивает всестороннюю помощь в обучении. Инструмент настроен как учебная программа класса с рядом категорий, которые разветвляются на более конкретные темы. Интерактивный формат позволяет щелкнуть любую категорию или тему; Это приведет вас к ряду примеров вопросов. Каждый из этих вопросов представлен в формате множественного выбора, с проблемой и несколькими возможными ответами. Вы можете просмотреть ответы перед тем, как приступить к решению задачи, а затем выбрать то, что, по вашему мнению, является правильным ответом.
 Фактический ответ также предоставляется, что позволяет вам проверить и увидеть, правильно ли вы его поняли.
Фактический ответ также предоставляется, что позволяет вам проверить и увидеть, правильно ли вы его поняли.Но Learn by Concept делает больше, чтобы быть полезным, чем предоставление примеров вопросов. Независимо от того, дали ли вы ответ правильно или неправильно, вы можете ознакомиться с подробным объяснением процесса, использованного для получения правильного ответа. Каждый шаг, каким бы маленьким он ни был, включен в это объяснение, что позволяет вам увидеть каждую применимую концепцию. Если вы ответили правильно, вы можете подтвердить, что выполнили работу правильно, а не просто повезло. Если вы дали неверный ответ, вы можете найти точную точку, в которой вы сбились с пути, и выяснить, на чем вам, возможно, нужно сосредоточиться, чтобы не сбиться с пути в будущем.
Инструмент Learn by Concept можно использовать в качестве учебного пособия по тригонометрии в течение года, в качестве тестового обзора или даже просто для закрепления одной конкретной темы. Охвачены все широкие категории тригонометрии, включая углы, треугольники, тригонометрические функции и графики, а также единичный круг.
 Вы также можете получить в специфике в каждой категории. Доступны тысячи примеров вопросов. Почти все возможные темы, которые могут возникнуть на вашем уроке тригонометрии, рассматриваются в инструменте «Узнай по концепции».
Вы также можете получить в специфике в каждой категории. Доступны тысячи примеров вопросов. Почти все возможные темы, которые могут возникнуть на вашем уроке тригонометрии, рассматриваются в инструменте «Узнай по концепции».Хотя инструмент «Обучение по концепции» полезен сам по себе, существует ряд других доступных средств обучения. Вы можете пройти бесплатный полноценный практический тест, чтобы узнать, какие области вы уже знаете, а в каких вам может понадобиться помощь. Практические тесты по тригонометрии сосредоточены на более конкретных областях, что позволяет вам уделить больше времени этому материалу или просмотреть свой прогресс. В дополнение к примерам вопросов по тригонометрии «Узнай по концепции» вы можете работать с бесплатными карточками «Средства обучения» по тем же темам. Практические тесты и карточки можно настроить в соответствии с вашими учебными потребностями. Ежедневное использование инструмента «Вопрос дня» поможет вам проверить свои общие знания по тригонометрии с помощью рандомизированных вопросов по всем темам.


 nan, dtype=np.double) # Задаем хранилище значений и заполняем nan
mask = np.full_like(x_arr, False, dtype=bool) # Задаем маску маркирующую вычисленные узлы (их индексы)
# Вычисляем на границах
y_arr[0] = f(x_arr[0])
mask[0] = True
update(x_arr[mask], y_arr[mask])
y_arr[-1] = f(x_arr[-1])
mask[-1] = True
update(x_arr[mask], y_arr[mask])
prev_nodes = [(0, -1 + 2 ** self.depth)] # Список пар узлов, в которых уже было вычислена функция и внутри отрезка которых нет точек, в которых была вычислена функция
curr_nodes = []
for _ in range(self.depth):
for node in self.prev_nodes:
c = sum(node) / 2
curr_nodes.extend([(node[0], c), (c, node[1])])
index = int(c)
y_arr[index] = f(x_arr[index])
mask[index] = True
update(x_arr[mask], y_arr[mask])
self.prev_nodes = list(self.curr_nodes)
self.curr_nodes = []
nan, dtype=np.double) # Задаем хранилище значений и заполняем nan
mask = np.full_like(x_arr, False, dtype=bool) # Задаем маску маркирующую вычисленные узлы (их индексы)
# Вычисляем на границах
y_arr[0] = f(x_arr[0])
mask[0] = True
update(x_arr[mask], y_arr[mask])
y_arr[-1] = f(x_arr[-1])
mask[-1] = True
update(x_arr[mask], y_arr[mask])
prev_nodes = [(0, -1 + 2 ** self.depth)] # Список пар узлов, в которых уже было вычислена функция и внутри отрезка которых нет точек, в которых была вычислена функция
curr_nodes = []
for _ in range(self.depth):
for node in self.prev_nodes:
c = sum(node) / 2
curr_nodes.extend([(node[0], c), (c, node[1])])
index = int(c)
y_arr[index] = f(x_arr[index])
mask[index] = True
update(x_arr[mask], y_arr[mask])
self.prev_nodes = list(self.curr_nodes)
self.curr_nodes = []
 Рабочий код можно посмотреть здесь github.com/nstrek/progressive_plots/
Рабочий код можно посмотреть здесь github.com/nstrek/progressive_plots/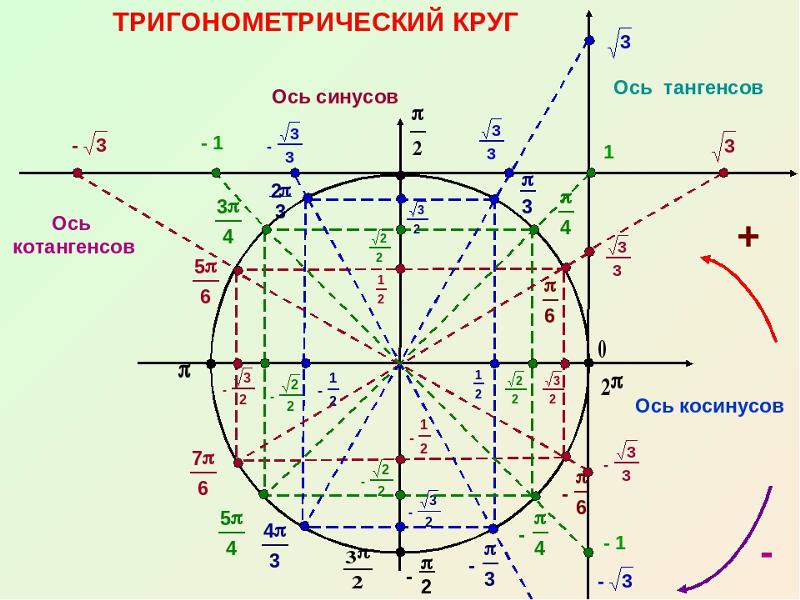

 в ответах по тригонометрии
к
Хейли
| 2.1k просмотров
в ответах по тригонометрии
к
Хейли
| 2.1k просмотров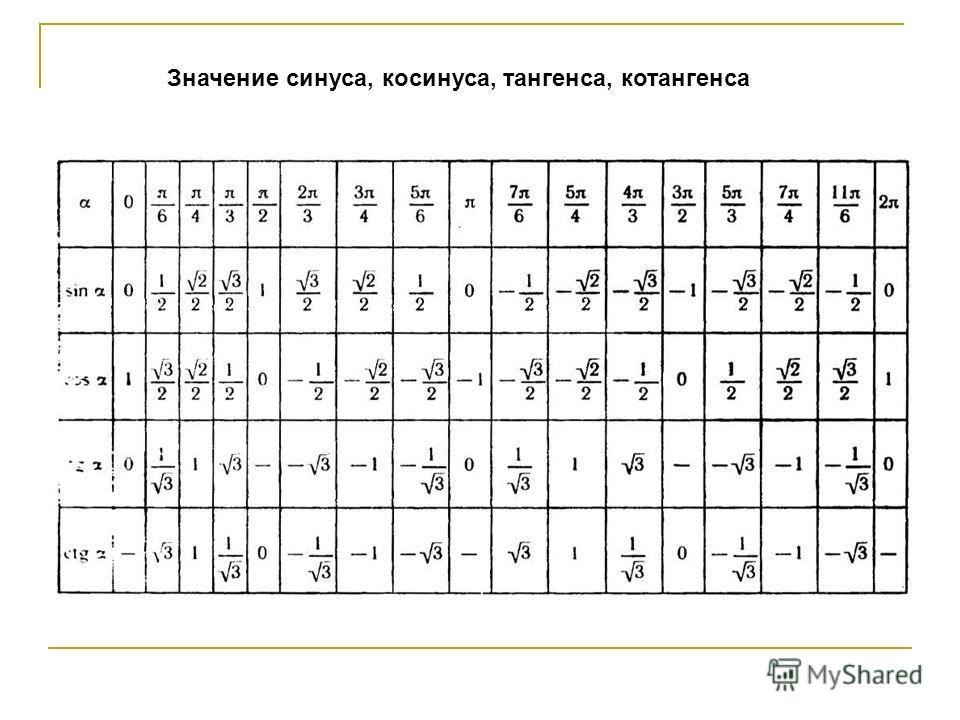
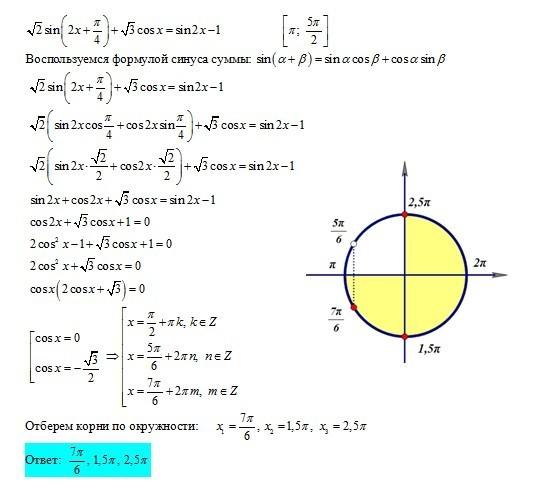 в ответах по тригонометрии
к
спешка 76
| 500 просмотров
в ответах по тригонометрии
к
спешка 76
| 500 просмотров 2019 г.
в ответах по тригонометрии
к
йса
| 684 просмотра
2019 г.
в ответах по тригонометрии
к
йса
| 684 просмотра 8k
8k В частности, он рассматривает отношения между сторонами треугольника и углами, а также функции различных углов. Но в тригонометрии есть нечто большее, чем теорема Пифагора. Вы также изучите такие понятия, как синусы, косинусы, радианы и тождества углов, которые закладывают основу для дальнейшей работы по исчислению и другим математическим вычислениям. Понятия, введенные в тригонометрию, также полезны в ряде профессий, таких как архитектура, радиология и навигация.
В частности, он рассматривает отношения между сторонами треугольника и углами, а также функции различных углов. Но в тригонометрии есть нечто большее, чем теорема Пифагора. Вы также изучите такие понятия, как синусы, косинусы, радианы и тождества углов, которые закладывают основу для дальнейшей работы по исчислению и другим математическим вычислениям. Понятия, введенные в тригонометрию, также полезны в ряде профессий, таких как архитектура, радиология и навигация. Фактический ответ также предоставляется, что позволяет вам проверить и увидеть, правильно ли вы его поняли.
Фактический ответ также предоставляется, что позволяет вам проверить и увидеть, правильно ли вы его поняли. Вы также можете получить в специфике в каждой категории. Доступны тысячи примеров вопросов. Почти все возможные темы, которые могут возникнуть на вашем уроке тригонометрии, рассматриваются в инструменте «Узнай по концепции».
Вы также можете получить в специфике в каждой категории. Доступны тысячи примеров вопросов. Почти все возможные темы, которые могут возникнуть на вашем уроке тригонометрии, рассматриваются в инструменте «Узнай по концепции».