Алгебра и начала анализа. (10 класс)
Похожие презентации:
Начала тригонометрии
Тригонометрические формулы. 10 класс
Тригонометрические формулы. 10 класс
Тригонометрия. Леонард Эйлер
Формулы приведения. 10 класс
«Тригонометрические уравнения» 10 класс
Градусная и радианная меры угла. Вращательное движение. Синус, косинус, тангенс и котангенс
Тригонометрия. Формулы приведения. (10 класс)
Тригонометрические функции. Пособие для учащихся 10 классов
Алгебра и начала математического анализа
Что означает название предмета «Алгебра и начала анализа?»
Алгебра – один из разделов математики, изучающий свойства
величин, выраженных буквами, независимо от их конкретного
числового значения.
Математический анализ – это совокупность частей математики,
в которых главным объектом исследования является функция, а
оперативная часть опирается на выполнение операций
дифференцирования и интегрирования.
Основоположники математического анализа:
Тригономе́трия (от греч. τρίγονο (треугольник) и греч.
μετρειν (измерять),
то есть измерение треугольников) — раздел математики,
в котором изучаются тригонометрические функции и их
приложения к геометрии.
Данный термин впервые появился в 1595 г. как название
книги немецкого математика Бартоломеуса Питискуса
(Bartholomäus Pitiscus, 1561—1613),
а сама наука ещё в глубокой древности использовалась для
расчётов в астрономии, геодезии и архитектуре.
Эти ученые внесли свой вклад в развитие тригонометрии
Архимед
Жозеф Луи
Лагранж
Фалес
Тригонометрия возникла и развивалась в древности как
один из разделов астрономии, как ее вычислительный
аппарат, отвечающий практическим нуждам человека. С ее
помощью можно определить расстояние до недоступных
предметов и существенно упрощать процесс геодезической
съемки местности для составления географических карт.
Общепринятые понятия тригонометрии, а также
обозначения и определения тригонометрических функция
сформировались в процессе долгого исторического развития.
Тригонометрические сведения были известны древним
вавилонянам и египтянам, но основы этой науки заложены в
Древней Греции встречающиеся уже в III веке до н.э.
в работах великих математиков– Евклида, Архимеда,
Апполония Пергского. Древнегреческие астрономы успешно
решали вопросы из тригонометрии, связанные с астрономией.
Тригонометрия – математическая дисциплина,
изучающая зависимость между сторонами и углами
треугольника.
Тригонометрические вычисления применяются
практически во всех областях геометрии, физики и
инженерного дела, при измерении расстояний до
недалёких звёзд в астрономии, между ориентирами в
географии, при контроле системы навигации, в теории
музыки, акустике, оптике, электронике, теории
(включая ультразвуковое исследование (УЗИ) и
компьютерную томографию), фармацевтике, химии,
сейсмологии, метеорологии, океанологии, картографии,
архитектуре, экономике, электронной технике,
машиностроении, компьютерной графике.
Вспомним:
0 90
с
а
a
sin
с
b
cos
c
a
tg
b
в
Синус острого угла в прямоугольном треугольнике —
отношение противолежащего катета к гипотенузе.
Косинус — отношение прилежащего катета к гипотенузе.
Тангенс — отношение противолежащего катета к
прилежащему.
В XVIII веке Леонард Эйлер
дал современные, более
общие определения,
расширив область
определения этих функций
на всю числовую ось.
угол _ поворота
R
у
1
0
х
1
у
1
0
х
1
Рассмотрим в прямоугольной системе координат
окружность единичного радиуса и отложим от
горизонтальной оси угол
(если величина угла положительна, то откладываем против
часовой стрелки, иначе по часовой стрелке). Точку
пересечения построенной стороны угла с окружностью
у
обозначим Р.
0
Р
1
0
1
х
1
0
Р90
у
Р60
Р45
Р30
Р180
хР0
1
0
1
Р270
Р360
cos
у
1
P ( x; y )
у
sin
1
0
P (1;0)
х 0
1
х
1
sin y
Синус угла определяется как ордината
точки P
cos x
Косинус — абсцисса точки P
y
tg
Тангенс – отношение
ординаты к абсциссе
точки P x
x
Котангенс – отношение
абсциссы
к
ординате
ctgточки
P
y
Понятие синуса встречается уже в III в.
до н. э.и имел название джива (тетева лука) ,
джайб (выпуклость) , XII в. заменено на латинское
синус (изгиб, кривизна) .
Косинус – это дополнительный синус.
Тангенс переводится с латинского
как «касающийся»
Р90
у
Р60
1
Р45
sin
45
0,7
Р30
cos45 0,7
1
2
-1
1
sin 30
2
cos 30 0,9
Р180
хР0
1
0
1
1
2
1
Р360
sin 60 0,9
1
cos 60
2
-1
Р270
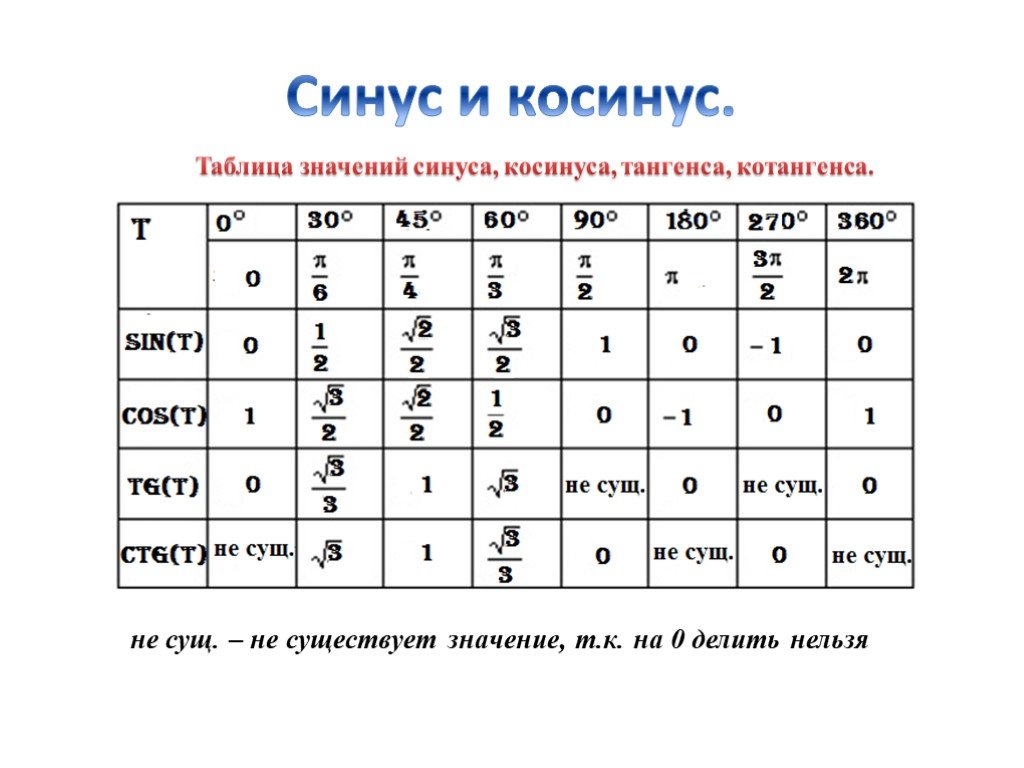
Запомним !
cos
tg
ctg
45
60
1
2
2
2
3
2
3
2
2
2
1
2
30
sin
1
3
3
3
3
1
3
1
1
3
3
3
Р90
у
Р0 (1; 0)
Р90 (0; 1)
Р180
хР0
1
0
1
Р360
Р180 (-1; 0)
Р270
Р270 (0;-1)
Проверим:
180
270
0
-1
0
0
-1
0
1
0
—
0
—
0
—
0
—
0
—
sin
0
0
90
1
cos
1
tg
ctg
360
Знаки синуса, косинуса, тангенса, котангенса
в координатных четвертях
у
у
+ +
х
1
— —
0
1
— +
+ 1
1
х
— +
+ 1
1
0
sin68 0
cos 76 0
sin 153 0
cos 236 0
sin 249 0
tg127 0
sin 315 0
ctg195 0
у
0
— +
— +
1
1
0
у
х
х
Четность, нечетность синуса, косинуса,
тангенса, котангенса
sin( ) sin
tg ( ) tg
ctg ( ) ctg
Нечетные функции
cos( ) cos
Четная функция
Периодичность тригонометрических
функций
При изменении угла на целое число оборотов
значения синуса, косинуса, тангенса, котангенса
не изменяются
у
sin
sin( 360 )
sin( 2 360 )
у
sin( n 360 )
cos
1
0
cos( 360 )
х
1
х
cos( 2 360 )
cos( n 360 )
tg
tg ( n 180 )
ctg
ctg ( n 180 )
у
3
sin 60
2
cos 60
2
3
2
60
1
0
1
420 ?
sin 780
х
1
2
1
2
cos420
cos780 ?
sin
sin 780
420
sin( 60
2 360 )
sin( 60 360 )
sin 60
sin 60
3
2 23
cos 780
cos
420
cos(
360 ))
cos(60
60 2360
11
cos
60
cos 60
22
sin 765
cos1110
sin( 45 2 360 )
cos(30 3 360 )
2
sin 45
2
3
cos 30
2
1
sin( 1470 ) sin 1470 sin( 30 4 360 ) sin 30
2
1
cos( 1140 ) cos1140 cos(60 3 360 ) cos 60
2
sin( 810 ) sin 810 sin( 90 2 360 ) sin 90 1
cos( 1170 ) cos1170 cos(90 3 360 ) cos 90 0
Радианная мера угла
R
С
центральный угол
R – радиус
С – длина дуги
Если R = C,
то центральный угол равен
одному радиану
Радианной мерой угла называется
отношение длины соответствующей дуги
к радиусу окружности
1 рад 57
180
n
n 60
n
180
60
180
3
60
3
180
n
4
180
180
180
n 4
45
4
4
45
4
Градусная и радианная меры углов
Угол
в
градусах
n
0 30 45 60
Угол
в
радианах
0
6
4
3
90 180 270 360
2
3
2
2
sin( ) sin
4
4
2
2
sin 2,5 sin( 0,5 2 ) sin 0,5 sin
2
1
9
1
2
cos( ) cos( 2 ) cos( 2 ) cos 4
4
4
4
2
13
1
3
tg
tg (2 ) tg ( 2 ) tg
6
6
6
6
3
7
1
ctg ( ) ctg (2 ) ctg ( 2 ) ctg 3
3
3
3
3
English Русский Правила
План-конспект урока алгебры и начал математического анализа в 10 классе по теме «Синус, косинус, тангенс углов а и -а».
Главная / Старшие классы / Алгебра
Скачать
37.29 КБ, 515186.docx Автор: Демьяненко Ирина Николаевна, 21 Мар 2015
Материал содержит методическую разработку плана-конспекта урока алгебры и начал математического анализа в 10 классе по теме «Синус, косинус, тангенс углов а и -а».
Автор: Демьяненко Ирина Николаевна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|---|---|---|
| документ | Методическая разработка урока алгебры и начал математического анализа в 11 классе по теме: «Степенная функция». | Власова Надежда Васильевна | 21 Мар 2015 |
| презентация, документ | Конспект урока алгебры и начал анализа в 10 классе по теме «Производные тригонометрических функций» | Серёгина Людмила Александровна | 21 Окт 2015 |
| разное | Урок математики в 8 классе по теме: «Синус, косинус и тангенс острого угла прямоугольного треугольника» | Крынина Светлана Ивановна | 4 Апр 2015 |
| документ | Урок алгебры и начал анализа в 10 классе по теме «Формулы двойного аргумента» | Татчин Ульяна Вирославовна | 1 Апр 2015 |
| документ | Конспект урока по математике на тему: «Решение задач по теме: «Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника»» | 31 Мар 2015 | |
| документ | Урок алгебры и математического анализа в 10 классе | Калинина Лариса Евгеньевна | 28 Фев 2016 |
| документ | Технологическая карта урока Синус, косинус и тангенс угла | Хафизова Фанзеля Кашбеевна | 19 Мар 2016 |
| документ | Самостоятельная работа по теме «Синус, косинус, тангенс угла» в 9 классе | Федькова Галина Юрьевна | 4 Ноя 2015 |
| презентация | Синус, косинус, тангенс и котангенс угла. Задачи по теме.9 класс. | Еремина Людмила Евгеньевна | 1 Апр 2015 |
| презентация | Синус, косинус и тангенс угла | Сидорова Анна Викторовна | 21 Мар 2015 |
| презентация | Синус, косинус и тангенс острого угла прямоугольного треугольника | Кузменкова Наталья Андреевна | 21 Мар 2015 |
| разное | Синус,косинус и тангенс угла. | Ананьева Ольга Владимировна | 31 Мар 2015 |
| разное | синус, косинус и тангенс угла | Зырянова Ирина Юрьевна | 4 Апр 2015 |
| презентация | Синус, косинус и тангенс острого угола прямоугольного треугольника | Борисова Ольга Анатольевна | 23 Сен 2015 |
| документ | Карточки-задания по различным разделам алгебры и начал анализа, 10 класс | Казанцева Светлана Борисовна | 21 Мар 2015 |
| разное | Рабочая программа и тематическое планирование курса алгебры и начал анализа в 11 классе | Волик Татьяна Геннадьевна | 1 Апр 2015 |
| документ | Урок обобщения и систематизации знаний по алгебре и началам математического анализа в 10-м классе по теме «Решение простейших тригонометрических уравнений». | Абросимова Елена Николаевна | 21 Мар 2015 |
| документ | Первообразная. Математический диктант к уроку алгебры и начал анализа в 11 классе | Сазонова Галина Васильевна | 1 Апр 2015 |
| презентация, документ | План-конспект урока в 10-м классе по алгебре и начала анализа на тему: « Возрастание и убывание функций. Экстремумы » | Галимова Гулия Рашитовна | 6 Дек 2015 |
| документ | Свойства и графики тригонометрических функций. Разработка урока алгебры и начала анализа в 10 классе. | Юшко Любовь Леонидовна | 12 Апр 2015 |
| документ | Конспект урока алгебры в 9 классе по теме «Функции, их свойства и графики» | Суханова Светлана Николаевна | 10 Апр 2015 |
| разное | материал по теме Синус и косинус | Павлова Татьяна | 21 Мар 2015 |
| разное | решебник по алгебре и начала математического анализа 10 класс | tronarukeh2980 | 11 Мая 2015 |
| разное | решебник по алгебра и начала математического анализа 10 класс | moukhfeduking1973 | 11 Мая 2015 |
| презентация | 8 класс Геометрия Синус, косинус и тангенс острого угла прямоугольного треугольника | Каримова Сания Рахимовна | 21 Мар 2015 |
| документ | План — конспект обобщающего урока алгебры в 10 классе школы глухих по теме “Функции” | Богданова Вера Ивановна | 1 Апр 2015 |
| документ | Планирование учебного материала по алгебре и началам математического анализа в 10 классе на 3 часа в неделю по учебнику под ред. Колмогорова А.Н. | Новикова Мария Александровна | 4 Апр 2015 |
| презентация, документ | Семинар на тему: «Решение нестандартных задач в рамках итогового повторения курса алгебры и начал анализа» | Залыгина Тамара Игоревна | 1 Апр 2015 |
| документ | План-конспект урока по алгебре «Логарифмические уравнения» Колмогоров А.Н.Алгебра и начала математического анализа. Учебник для 10-11 кл.,2008 Цыпкин А.Г., Пинский А.И. Справочное пособие по методам решения задач по математике. — М. | Бушева Инга Николаевна | 5 Мая 2015 |
| документ | Синус и косинус числа. 10 класс | Шишкина Людмила Емельяновна | 1 Апр 2015 |
| документ | Рабочая программа учебного курса «Алгебра и начала математического анализа» в 10 классе | Люлёва Ольга Васильевна | 12 Апр 2015 |
| документ | Урок алгебры и начала анализа по теме: «Обобщение знаний по разделу тригонометрия», 10 кл. | Байдуганова Лилия Ивановна | 1 Апр 2015 |
| документ | Урок алгебры и начала анализа в 10 классе. Решение логарифмических уравнений | Базакина Анна Васильевна | 20 Ноя 2015 |
| документ | План — конспект урока по литературе в 10 классе по теме: «Федор Михайлович Достоевский. Этапы биографии и творчества» | Куракина Ольга Васильевна | 2 Мар 2016 |
| разное | решебник по алгебре и начала математического анализа профильный уровень 10 класс мордкович | moukhfeduking1973 | 11 Мая 2015 |
| разное | решебник по алгебре 10 класс мордкович алгебра и начала математического анализа | ropipinla1979 | 11 Мая 2015 |
| документ | Тесты по алгебре и началам математического анализа 10 класс | Мулдашева Алия Рахметдуллаевна | 1 Апр 2015 |
| документ | Развернутое тематическое планирование по алгебре и началам математического анализа в 10 – 11 классах | Шангина Ирина Евгеньевна | 20 Мар 2015 |
| разное | решебник алгебра и начало математического анализа 10 класс | tronarukeh2980 | 11 Мая 2015 |
| разное | решебник алгебра и начала математического анализа 10 класс мордкович | ropipinla1979 | 11 Мая 2015 |
Разница между тригонометрией и геометрией
Математика имеет различные важные разделы, такие как алгебра, геометрия, вероятность, тригонометрия, арифметика и многое другое.
Мы знаем, что геометрия — это изучение различных форм, размеров и положений различных фигур в зависимости от количества сторон, углов и так далее. Принимая во внимание, что тригонометрия — это подмножество геометрии, которое имеет дело со свойствами одной из фигур в геометрии, называемой «треугольником». И тригонометрия, и геометрия кажутся связанными друг с другом, но это не одно и то же.
В этой статье давайте обсудим разницу между геометрией и тригонометрией с некоторыми подробными пояснениями.
Раздел математики, в котором изучаются соотношения между углами и отношениями сторон прямоугольных треугольников, известен как тригонометрия. Соотношения, используемые для изучения этих отношений, которые включают тангенс, синус, косинус, секанс, котангенс и косеканс, известны как тригонометрические отношения. Мы используем тригонометрию, чтобы найти неизвестные размеры любого прямоугольного треугольника, используя формулы и тождества.
Раздел математики, в котором изучаются принципы, связанные с углами, узорами, пройденными расстояниями, площадями и объемами, известен как геометрия.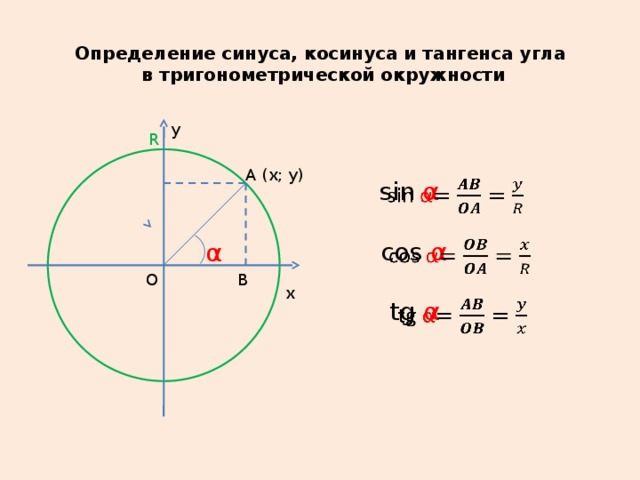
Геометрия включает в себя изучение всех понятий, связанных с пространственным и визуальным. Геометрию можно разделить на три типа: евклидову, эллиптическую и гиперболическую.
Геометрия, в которой мы изучаем свойства плоской поверхности и объемных фигур, основанные на теоремах и аксиомах, известна как евклидова геометрия. В то время как геометрия, в которой не выполняются параллельные постулаты Евклида, известна как эллиптическая геометрия. Геометрия, в которой мы изучаем гиперболические поверхности, известна как гиперболическая геометрия.
Давайте посмотрим на разницу между геометрией и тригонометрией.
В чем разница между тригонометрией и геометрией?
Тригонометрия
Тригонометрию можно рассматривать как подмножество геометрии. В современной математике огромную роль играет тригонометрия. Тригонометрия в основном связана с изучением различных свойств треугольников, длин и углов.
Однако он также имеет дело с волнами и колебаниями.
В тригонометрии мы в основном изучаем отношения между длинами сторон и углами прямоугольного треугольника. Существует шесть тригонометрических соотношений. Три основные, называемые синус, косинус и тангенс, объединены вместе с секансом, косекансом и котангенсом.
Предположим, что у нас есть прямоугольный треугольник. Тремя сторонами будут соответственно высота, основание и гипотенуза. Тогда мы можем определить основные тригонометрические соотношения следующим образом:
sin A=(высота)/(гипотенуза)
cos A=(основание)/(гипотенуза)
tan A=(высота)/(основание)
Cosec , Sec и Cot также могут быть определены как величины, обратные синусу, косинусу и тангенсу соответственно. Тригонометрия — это не просто изучение простых плоских фигур. У него есть ветвь, называемая сферической тригонометрией, изучающая треугольники в трехмерных пространствах.
Геометрия
Геометрия определяется как изучение различных размеров, форм и свойств пустых пространств заданного количества измерений, таких как 2D или 3D. Евклид, великий математик, внес огромный вклад в область геометрии. Поэтому он известен как отец геометрии. Геометрию можно разделить на следующие категории:
Плоская геометрия имеет дело с двумерными геометрическими объектами, такими как точки, линии, кривые и различные плоские фигуры, такие как круги, треугольники и многоугольники. Геометрия тела изучает трехмерные объекты, такие как различные многогранники, сферы, кубы, призмы, пирамиды и т.д. Сферическая геометрия также изучает трехмерные объекты, такие как сферические треугольники и сферические многоугольники.
Геометрию также можно разделить на евклидову геометрию, изучающую плоские поверхности, и риманову геометрию, в которой основным предметом является изучение искривленных поверхностей.
Тригонометрия и геометрия: разница
Тригонометрия | Геометрия |
IT A Spank of Geometry. | Это основной раздел математики. |
Изучаются свойства треугольников. | Изучаются свойства фигур. |
Занимается измерением углов. | Он касается свойств углов и суммы углов. |
Он касается отношений между углами треугольников и их сторонами. | Он касается пространственных отношений. |
Найдите расстояние между двумя кораблями. 
Гиппарх, греческий математик, изобрел тригонометрию.
Благодарю вас!
Используйте теорему Пифагора для вычисления сторон a и b
Найдите длины сторон а, b, угол бета, если с = 5, и угол альфа = А = 35 градусов.