Урок геометрии по теме «Соотношения между сторонами и углами в прямоугольном треугольнике»
Цели урока:
- обобщение понятия синус, косинус, тангенс острого угла в прямоугольном треугольнике;
- формирование умений и навыков в применении соотношений между сторонами и углами прямоугольного треугольника;
- развитие познавательного интереса;
- воспитание самостоятельности, аккуратности;
- коррекция внимания при выполнении тестовых заданий.
Эпиграф: (Слайд № 1) (Приложение 4)
«Человек подобен дроби: в знаменателе – то,
что он о себе думает, в числителе – то, что он
есть на самом деле. Чем больше знаменатель,
тем меньше дробь».
Лев Толстой
Ход урока
1. Организационный момент. (Слайд № 2)
Учитель: для того, чтобы повторять материал по теме «Соотношения между сторонами и углами треугольника».
Мотивация урока. (Слайд № 3)
Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная…»
У вас может возникнуть вопрос: Почему в геометрии особое внимание уделяется прямоугольному треугольнику, хотя не часто встречаются предметы подобной формы?
Как в химии изучают вначале элементы, а затем – их соединения, в биологии – одноклеточные, а потом – многоклеточные организмы, так и в геометрии – точки, отрезки и треугольники, из которых состоят другие геометрические фигуры.
2. Устный счет (Слайд № 4)
- Чему равен синус угла В (отношение противолежащего катета к гипотенузе)? (0,6)
- Чему равен косинус угла В (Отношение прилежащего катета к гипотенузе)? (0,8)
- Чему равен тангенс угла В (Отношение противолежащего катета к прилежащему)? (0,75)
3. Актуализация опорных знаний.
Актуализация опорных знаний.
Блиц-опрос с последующей взаимопроверкой (Слайд № 5)
(Слайд № 6)
|
Вариант 1 |
Вариант 2 |
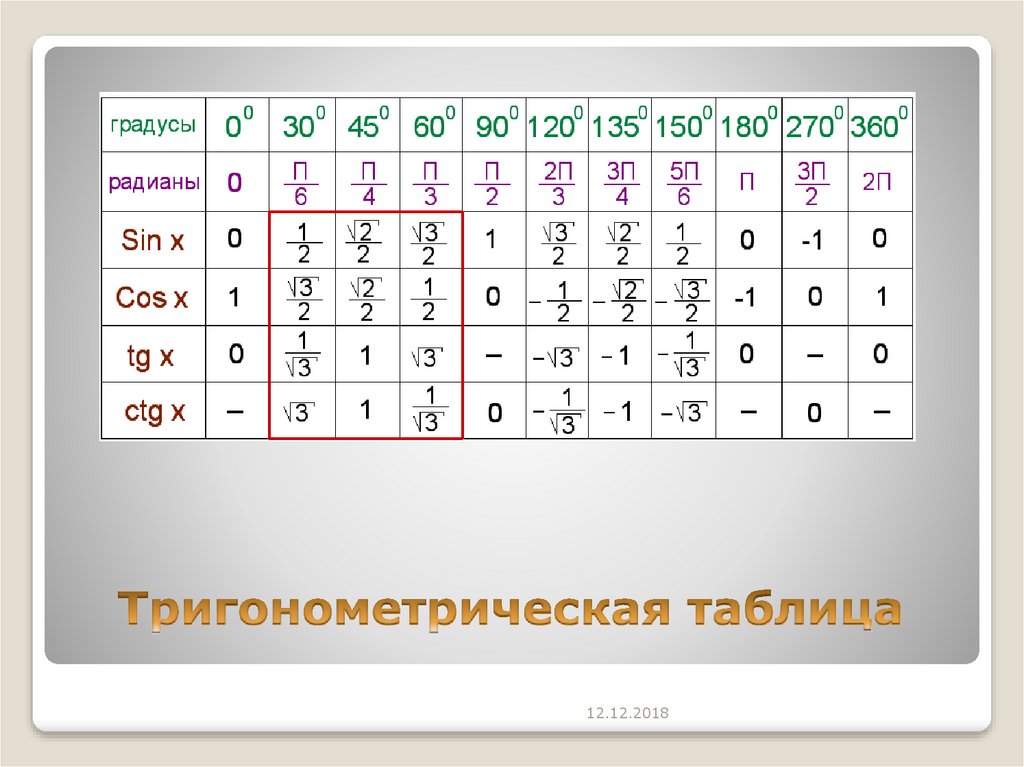
1. Запишите, используя обозначения косинус 60° равен 1/2 |
1. Запишите, используя обозначения синус 45° равен √2/2 |
2.Запишите основное тригонометрическое тождество |
2. Запишите формулой, чему равен тангенс угла А |
3. Может ли синус острого угла равняться 1,01? |
3. Тангенс острого угла прямоугольного треугольника равен единице. Какого вида этот треугольник? |
Чему равен? |
Чему равен? |
4. |
4. Cos 30° |
5. Cos45° |
5. Sin45° |
Ответы. (Слайд № 7)
|
Ответы 1 |
Ответы 2 |
1. cos60°=1/2; |
1. sin45°= √2/2; |
2. sin2A + cos2A = 1; |
2.tgA=sinA/cosA; |
3. Нет; |
3. Равнобедренный; |
4. √3/2; |
4. √3/2; |
5. √2/2. |
5. |
4. Решение задач
Задача 1 (Слайд № 8)
Пирамиды Древнего Египта (египетские пирамиды) — величайший архитектурный памятник Древнего Египта, одно из «Семи чудес света».  Скорее всего, именно таков и был замысел архитектора этой пирамиды, Имхотепа. Он разработал способ кладки из тёсаного камня. Впоследствии, египтяне глубоко почитали зодчего первой пирамиды, и даже обожествили его. Он считался сыном бога Птаха, покровителя искусств и ремёсел. Сама пирамида Джосера расположена в Саккаре, неподалёку от древнего Мемфиса.
Скорее всего, именно таков и был замысел архитектора этой пирамиды, Имхотепа. Он разработал способ кладки из тёсаного камня. Впоследствии, египтяне глубоко почитали зодчего первой пирамиды, и даже обожествили его. Он считался сыном бога Птаха, покровителя искусств и ремёсел. Сама пирамида Джосера расположена в Саккаре, неподалёку от древнего Мемфиса.
(Слайд № 9)
Ученые решили найти высоту пирамиды Джосера. Вначале они смогли измерить только длину её основания – 55,5 м. и длину боковой грани – 32 м. Затем им удалось измерить угол между этими отрезками – 60 градуса, после чего возник вопрос, а какова же высота пирамиды? Провести измерения высоты на местности не было никакой возможности, тогда на помощь археологам пришла математика, и они вычислили эту высоту.
Решение данной задачи (Слайды №№ 10, 11)
Наводящие вопросы:
Итак, нам известна гипотенуза и острый угол В в прямоугольном треугольнике, а так же определения синуса, косинуса и тангенса острого угла.
Почему именно синус? (Он связывает вместе гипотенузу, угол и искомый катет)
Как? (Гипотенузу умножим на синус 60 градусов)
Чему равен синус 60 градусов?
Итак, какова высота пирамиды Джосера?
Физминутка.
Мы немножко отдохнем,
Встанем, глубоко вздохнем,
Руки в стороны, вперед.
Дети по лесу гуляли,
За природой наблюдали
Вверх на солнце посмотрели
И их все лучи согрели.
Чудеса у нас на свете:
Стали карликами дети.
А потом все дружно встали,
Великанами мы стали.
5. Самостоятельная работа. (Слайд № 12)
Раздаем карточки (Учитель оказывает помощь слабым учащимся)
Вариант 1 |
Вариант 2 |
1. а) 5/4; б) 4/5; в) 3/5; г) 5/3. |
1. Найдите косинус угла В ∆АВС, угол С=90°, если ВС=3, АВ= 5. а) 5/3; б) 4/5; в) 3/5; г) 5/4. |
2.Дано: ∆АВС, ВС = 5 см угол С=90°, угол А = 41° Найти: АС а) 5* cos41°; б) 5:tg41°; с) 5* tg41°; г) 5: sin41°. |
2. Дано: ∆АВС, ВС = 9 см, угол С = 90°, угол В = 49° Найти: АС а) 9: tg49°; б) 9*cos49°; в) 9: sin49°; г) 9* tg49°. |
3. sin260° — 3* tg45° а) -2,25; б) -1,25; в) -0,75; г) -1,5. |
3. а) -2; б) -3; в) -1,5; г) -2,5. |
6. Рефлексия. (Слайд № 13)
Учащимся раздаются карточки (Приложение 3), на которых они отмечают свое настроение.
7. Подведение итогов. Выставление оценок
8. Домашнее задание. (Слайд № 14)
Письменно № 599
Повторить п. 66.
– Спасибо урок окончен. До свидания!
Дополнительные задачи (Приложение 2)
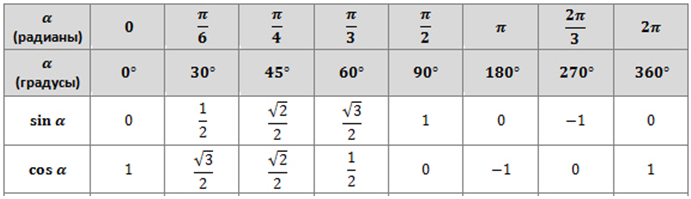
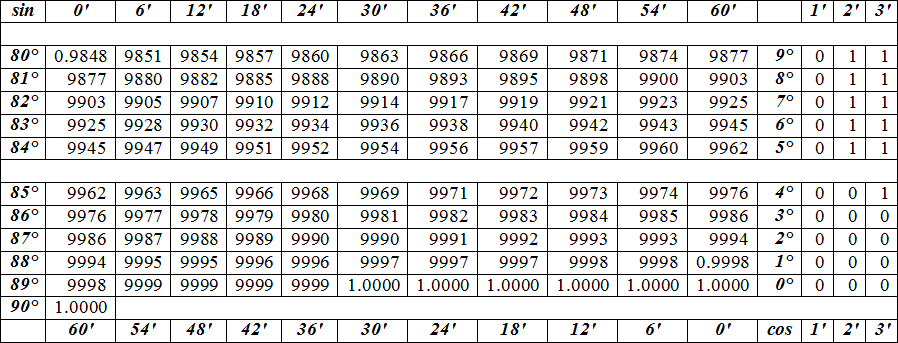
Справочный материал (Приложение 1)
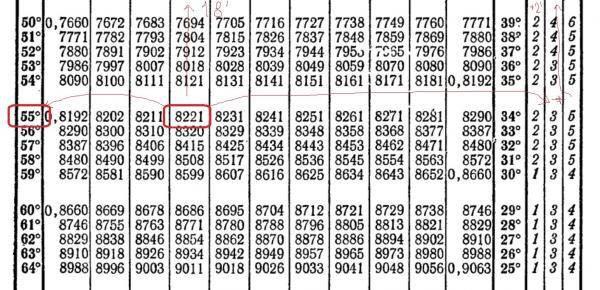
Малые углы
В принципе можно было бы мерить все углы в радианах. На практике широко используется и градусное измерение углов, хотя с чисто математической точки зрения оно неестественно. При этом для малых углов используются специальные единицы: угловая минута и угловая секунда. Угловая минута — это 1/60 часть градуса; угловая секунда — это 1/60 часть угловой минуты. Если, например, величина угла равна 129 градусам, 34 минутам и 16 секундам, то пишут: 129◦3401600.
Угловая минута — это 1/60 часть градуса; угловая секунда — это 1/60 часть угловой минуты. Если, например, величина угла равна 129 градусам, 34 минутам и 16 секундам, то пишут: 129◦3401600.
Задача 4.1. На какой угол поворачивается за одну секунду:
а) часовая стрелка часов;
б) минутная стрелка часов;
в) секундная стрелка часов?
Решение. Разберем только пункт а). Полный оборот часовая стрелка делает за 12 часов; стало быть, за час она поворачивается на 360/12 = 30◦. Следовательно, за минуту часовая стрелка повернется на угол, в 60 раз меньший, чем за час, то есть на 300;
всвою очередь, за секунду стрелка повернется на угол, в 60 раз меньший, чем за минуту, то есть на 3000. Теперь вы видите, на-
сколько мала угловая секунда: ведь даже угол, в тридцать раз больший (поворот часовой стрелки за секунду времени) мы не
всостоянии заметить.
Представление об угловой минуте дает такой факт: «разрешающая способность» человеческого глаза (при стопроцентном зрении и хорошем освещении) равна примерно одной угловой минуте. Это означает, что две точки, которые видны под углом 10 или меньше, на глаз воспринимаются как одна.
Это означает, что две точки, которые видны под углом 10 или меньше, на глаз воспринимаются как одна.
Посмотрим, что можно сказать о синусе, косинусе и тангенсе малых углов. Если на рис. 4.2 угол α мал, то высота BC, дуга BD и отрезок BE, перпендикулярный AB, очень близки. Их длины — это sin α, радианная мера α и tg α. Стало быть, для малых углов синус, тангенс и радианная мера приближенно равны друг другу:
15
Рис. 4.1. Разрешающая способность.
|
|
|
|
|
|
|
|
| Рис. 4.2. Малые углы. |
| |
Если α — малый угол, измеренный в радианах, то sin α ≈ α; tg α ≈ α.
Задача 4.2. Запишите приближенные формулы для синуса и тангенса малых углов, считая, что угол измеряется в градусах.
Ответ. sin α◦ ≈ πα/180.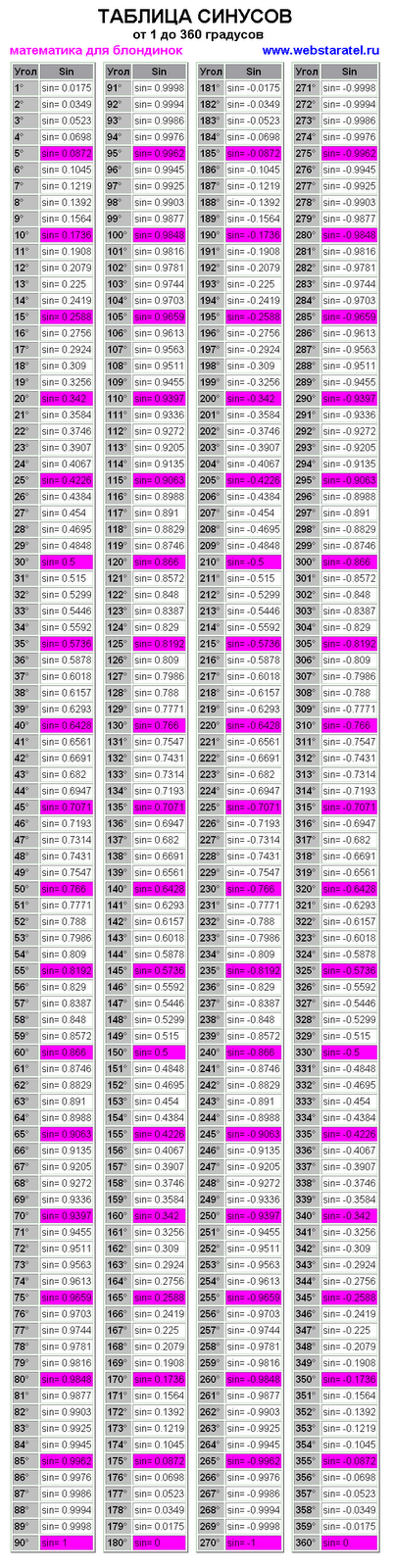
Видно, что формулы сложнее, чем для радианной меры — еще один довод в ее пользу!
Задача 4.3. Под каким углом видно дерево высотой 10 метров с расстояния в 800 метров? Дайте ответ: а) в радианах; б) в угловых минутах.
Задача 4.4. Чему равно расстояние, равное одной минуте дуги земного меридиана? Радиус Земли равен примерно 6370 .
Расстояние, о котором идет речь в этой задаче, примерно равно морской миле (именно так и появилась эта мера длины).
16
Рис. 4.3. Парсек.
Рис. 4.4. Формула тысячных.
Задача 4.5. В астрономии применяется единица измерения расстояний, называемая парсек. По определению, расстояние в 1 парсек — это расстояние с которого радиус земной орбиты1 виден под углом 100 (рис. 4.3). Сколько километров в одном парсеке? (Радиус земной орбиты равен примерно 150 миллионам километров.)
Задача 4.6. Военные пользуются единицей измерения углов, называемой «тысячная». По определению, тысячная — это 1/3000 развернутого угла. Такое измерение углов военные применяют в следующей формуле для определения расстояния до удаленных предметов: = (/) · 1000.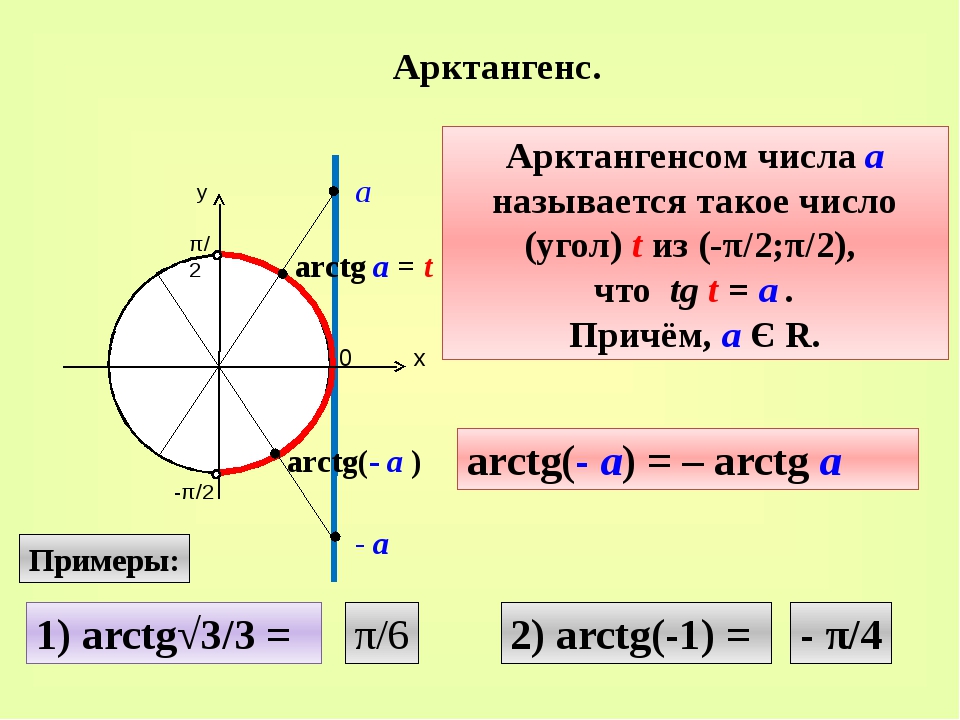 Здесь — расстояние до предмета, — его высота, — угол, под которым он виден, измеренный в тысячных (рис. 4.4). Точна ли эта формула? Почему ей можно пользоваться на практике? Чему равно число π, по мнению военных?
Здесь — расстояние до предмета, — его высота, — угол, под которым он виден, измеренный в тысячных (рис. 4.4). Точна ли эта формула? Почему ей можно пользоваться на практике? Чему равно число π, по мнению военных?
Мы видим, что формулы sin α ≈ α, tg α ≈ α верны с хорошей точностью для малых углов. Посмотрим, что произойдет,
1Астрономы поправили бы нас: не радиус (орбита Земли — не круг, а эллипс), а большая полуось (половина расстояния между наиболее удаленными друг от друга точками орбиты).
17
если угол не столь мал. Для угла в 30◦ точное значение синуса равно 0,5, а радианная мера равна π/6 ≈ 0,52. Ошибка (или, как еще говорят, погрешность), которую дает формула sin α ≈ α, равна примерно 0,02, что составляет 4% от значения синуса. Можно сказать, что относительная погрешность при таком вычислении (отношение погрешности к значению синуса) составляет 4%. Для углов, меньших 10◦, относительная погрешность формулы sin α ≈ α меньше одного процента. Чем меньше угол α, тем меньше относительная погрешность формулы sin α ≈ α.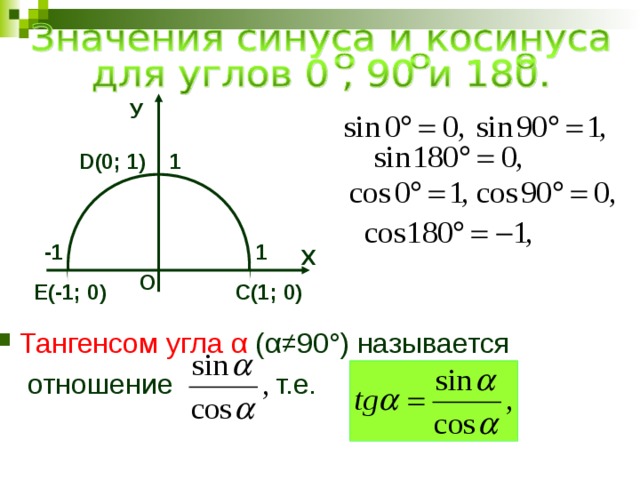
Существуют и другие формулы, позволяющие вычислять синусы и тангенсы — и не только малых углов — с хорошей точностью. Например, формула sin α ≈ α − α3/6 (напоминаем, что α измеряется в радианах!) дает относительную погрешность менее 1% уже для всех углов, не превосходящих 50◦. Позднее мы увидим, как оценить погрешность наших формул.
Задача 4.7. Пусть α — острый угол, измеренный в радианах. Докажите неравенство cos α > 1 − α2.
Указание. Воспользуйтесь формулой cos α = | 1 − sin2 α, нера- | |||
√ |
| 0 < t < 1 | ). | |
венством sin α < α и неравенством t > t (для p |
| |||
Задача 4.8. Для косинусов малых углов в качестве приближенного значения можно брать 1.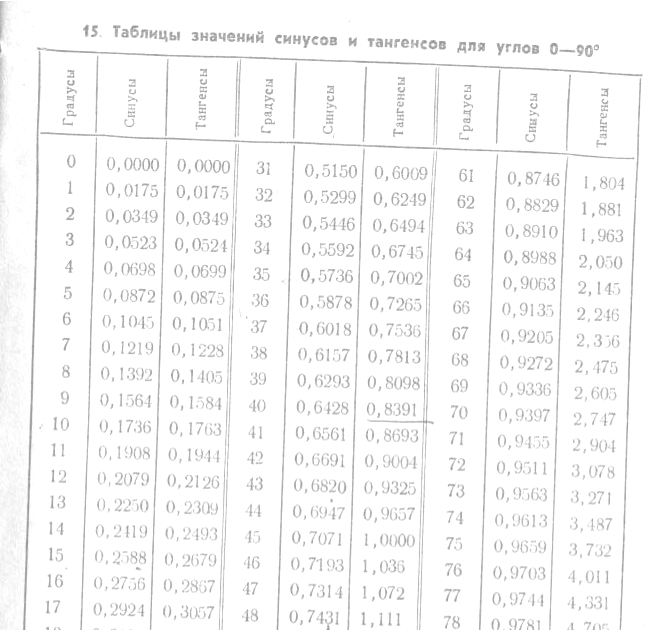 Докажите, что при величине угла менее 5◦ относительная погрешность этого приближения будет менее 1%.
Докажите, что при величине угла менее 5◦ относительная погрешность этого приближения будет менее 1%.
18
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.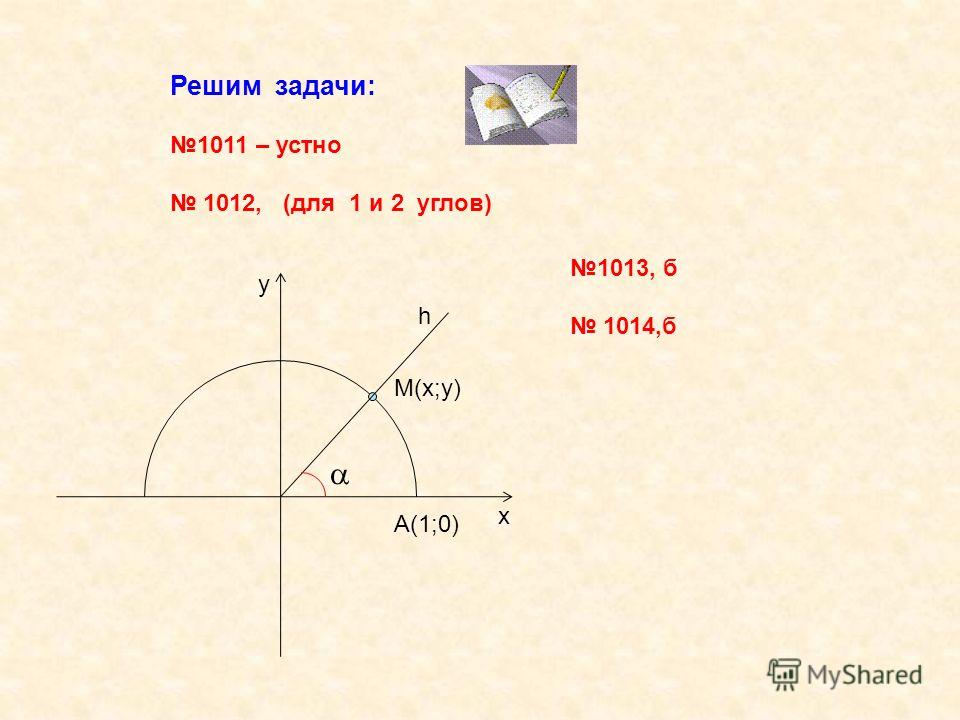 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — sin(0.
 6) — Solumaths
6) — SolumathsГрех, онлайн-исчисление
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.
sin online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x)`
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x)`
- Производная синуса
- Первообразная синуса
- Свойства функции синуса
- Уравнение с синусом
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс : косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.

Синус вычисляет угол в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.
После этого можно приступать к расчетам.
Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градианах
Для вычисления синуса угла в градианах необходимо сначала выбрать нужную единицу измерения
нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значения общего синуса :
| sin(`2*pi`) | `0` | |||||||||||||||||||||||||||||||
| sin(`pi`) | `0` | |||||||||||||||||||||||||||||||
sin(`pi/90 `2`)
`AA x в RR, k в ZZ`, Производная синуса равна cos(x). Первообразная синуса равна -cos(x). Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии. Калькулятор имеет решатель, который позволяет решать уравнение с синусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или же `2*sin(x)=sqrt(2)` с этапами расчета. Синтаксис:sin(x), где x — мера угла в градусах, радианах или градах. Примеры:sin(`0`), возвращает 0 Производный синус:Чтобы дифференцировать синус функции онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции синуса производная sin(x) является производной(`sin(x)`)=`cos(x)` Синус первообразной : Калькулятор первообразных позволяет вычислить первообразную функции синуса. Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)` Предел синуса :Калькулятор предела позволяет вычислять пределы функции синуса. предел sin(x) is limit(`sin(x)`) Обратная функция синуса :обратная функция синуса это функция арксинуса, отмеченная как arcsin. График синуса :Графический калькулятор может отображать синусоидальную функцию в заданном интервале. Свойство функции синуса:Функция синуса является нечетной функцией. Расчет онлайн с sin (синусом) См. также Список связанных калькуляторов: |

 Sin60°
Sin60°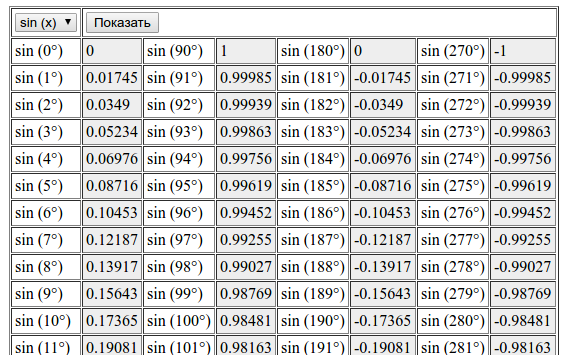 √2/2.
√2/2. Найдите синус угла А ∆АВС, угол С=90°, если ВС=4, АВ= 5.
Найдите синус угла А ∆АВС, угол С=90°, если ВС=4, АВ= 5. cos245° — 4* sin30°
cos245° — 4* sin30°
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.