Основные тригонометрические формулы синуса, косинуса, тангенса и котангенса. Тригонометрия 9. Ч13
12+
2 недели назад
Математика от Баканчиковой81 подписчик
Тригонометрия 9 класс. Основные тригонометрические формулы. Как получаются основные тригонометрические формулы? Какие формулы получаются из основных тригонометрических формул, и как с ними работать? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Тригонометрические функции в геометрии», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. В заключение урока мы покажем Вам 20 основных тригонометрических формул, которые нужно запомнить. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:47 Тригонометрические формулы тангенса и котангенса. Как они получаются?
04:34 Умножим тангенс на котангенс. tg α * ctg α = ?
07:14 Прибавим 1 к квадрату тангенса и квадрату котангенса. 2 α = ?
16:34 Итого получили 20 формул тригонометрии.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°.
2 α = ?
16:34 Итого получили 20 формул тригонометрии.
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Тригонометрические функции в геометрии. Что это такое. Сколько тригонометрических функций и почему. Геометрия 9 класс. Часть 1. https://rutube.ru/video/b99256c0e2a5f1411c87731142e2a822/
Как запомнить формулы тригонометрических функций. Стандартные обозначения этих функций, треугольника и длин его сторон. Тригонометрические функции в геометрии. Часть 2. Геометрия 9 класс. https://rutube.ru/video/cb235fc7ef53f468f18b151435d18c77/
Как найти sin, cos, tg и ctg угла по двум сторонам треугольника. Как построить угол по sin, cos или tg. Тригонометрические функции в геометрии. Часть 3. Геометрия 9 класс. https://rutube.ru/video/3c8642f0072caa41866cb44fe5cf1eb2/
Как найти значение тригонометрических функций тремя способами. Тригонометрические функции в геометрии. Часть 4. Геометрия 9 класс. https://rutube.ru/video/70f16a0f13b974194b59d3327a03a403/
Как найти значения sin, cos, tg и ctg для углов в 30°, 45° и 60°.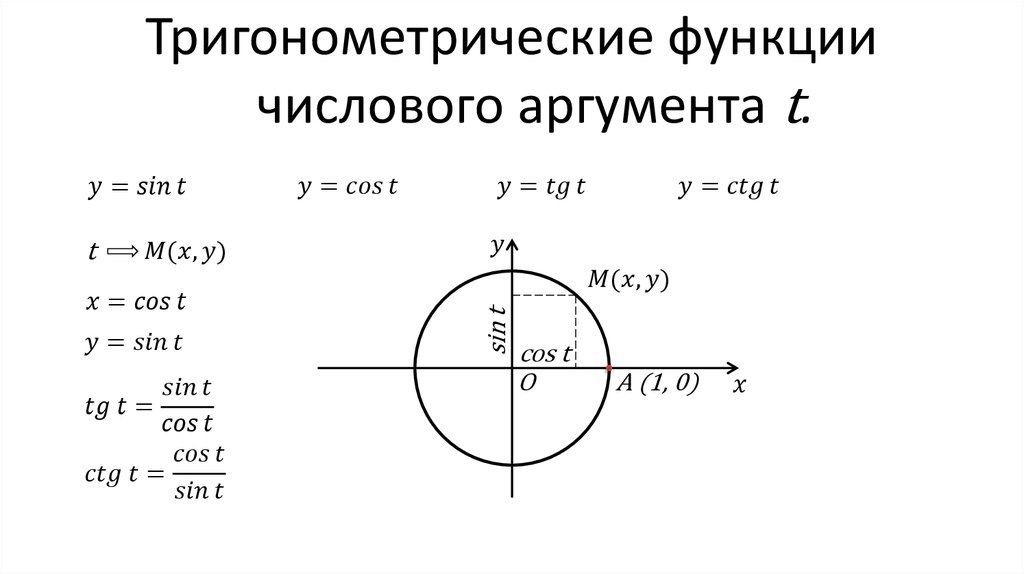

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Косинус в геометрии
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.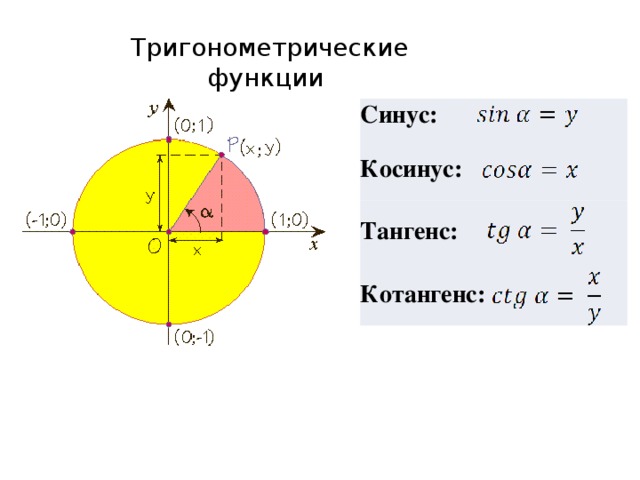
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x, y ).
Определение дается через координаты точки A 1 ( x, y ).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 ( x, y ). sin α = y
Косинус угла поворота α — это абсцисса точки A 1 ( x, y ). cos α = х
Тангенс угла поворота α — это отношение ординаты точки A 1 ( x, y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x, y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.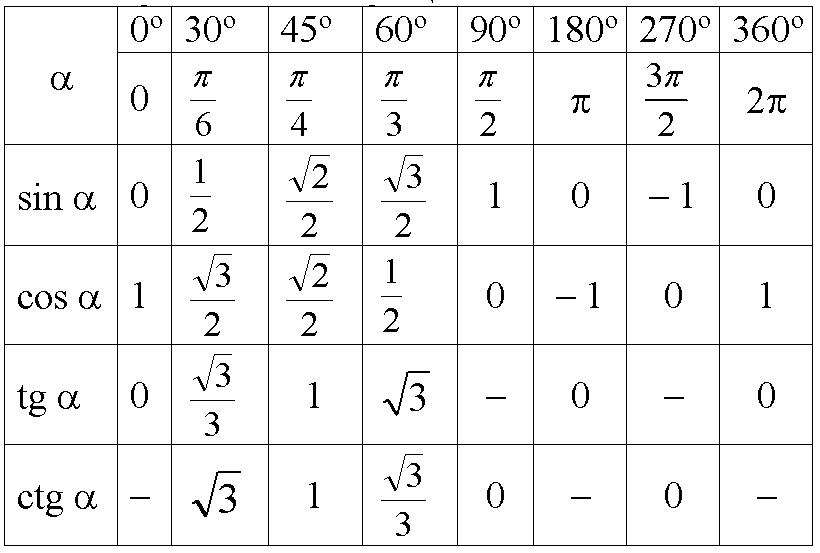
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа T называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в T радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу T ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами ( 1 , 0 ).
Положительному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу T соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа T — ордината точки единичной окружности, соответствующей числу T. sin t = y
Косинус числа T — абсцисса точки единичной окружности, соответствующей числу T. cos t = x
Тангенс числа T — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу T. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу T, совпадает с точкой, в которую переходит начальная точка после поворота на угол T радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k, k ∈ Z ( α = π 2 + π · k, k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k, k ∈ Z ( α = π · k, k ∈ Z ).
Можно сказать, что sin α, cos α, t g α, c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу T соответствует определенное значение синуса или косинуса числа T. Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Всем числам, отличным от π 2 + π · k, k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k, k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x, y ) перпендикуляр к оси абсцисс.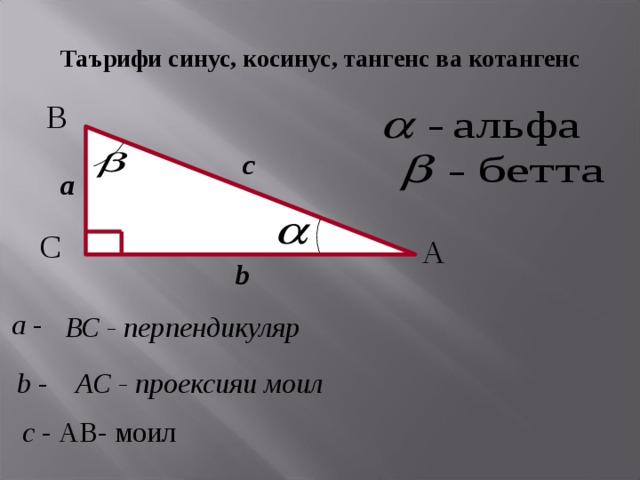 В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α, длина катета O H равна абсциссе точки A 1 ( x, y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x, y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
Sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Определение дается через координаты точки A 1 x, y.
Zaochnik. com
25.07.2018 15:59:32
2018-07-25 15:59:32
Источники:
Https://zaochnik. com/spravochnik/matematika/trigonometrija/sinus-kosinus-tangens-i-kotangens/
Функция косинуса: онлайн калькулятор, формулы, график | » /> » /> . keyword { color: red; }
keyword { color: red; }
Косинус в геометрии
Косинус — тригонометрическая функция, которая геометрически определяется как соотношение прилежащего катета к гипотенузе. Как и все тригонометрические функции, косинус нашел широчайшее применение в науке.
История вопроса
Тригонометрия как наука возникла еще в Древней Индии, когда ученые разработали таблицу соотношений катетов и гипотенуз и их численных значений для основных углов. Термин «косинус» — сравнительно молодой, так как изначально ученые пользовались только синусом и тангенсом угла. Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Геометрически косинус — это соотношение прилежащего катета к гипотенузе. Прилежащий катет — это сторона прямоугольного треугольника, которая вместе с гипотенузой образует рассматриваемый угол. Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Определение косинуса
Итак, есть прямоугольный треугольник, катеты которого обозначаются как A и B, а гипотенуза как C. Из определения косинуса мы получаем, что для заданного угла AC его соотношение прилежащего катета и гипотенузы будет равно cosAC = A/C. Изначально косинусы рассчитывались только для прямоугольных треугольников, однако с развитием математической науки косинусы прочно вошли в расчеты и сейчас используются для любых треугольников. Одним из таких примеров является теорема косинусов — теорема евклидовой геометрии, которая расширяет теорему Пифагора на любые плоские треугольники.
Теорема косинусов
Для любого треугольника справедливо равенство:
A 2 = b 2 + c 2 — 2b × c × cosA,
Где угол A — это угол, противолежащий стороне a.
Данное уравнение правдиво для любых плоских треугольников и при помощи него легко определить угол или одну из сторон. Если угол A — прямой, то выражение 2b×c×cosA обращается в ноль, так как cos90 = 0. Следовательно, напротив прямого угла лежит наибольшая сторона или гипотенуза, а теорема косинусов превращается в классическую теорему Пифагора:
Где a — гипотенуза.
Использование косинусов
В повседневной жизни тригонометрические функции не находят применения. Вся бытовая математика находится на уровне математических познаний древних греков, когда для простейших расчетов используются элементарные арифметические функции и рациональные соотношения. Однако большая часть современных технологий функционирует с использованием различных тригонометрических функций. К примеру, для определения мощности электротехнических приборов используется косинус фи — косинус угла между векторными значениями тока и напряжения. Еще пример: через тригонометрические функции легко перевести геодезические углы в привычные нам координаты на земной поверхности.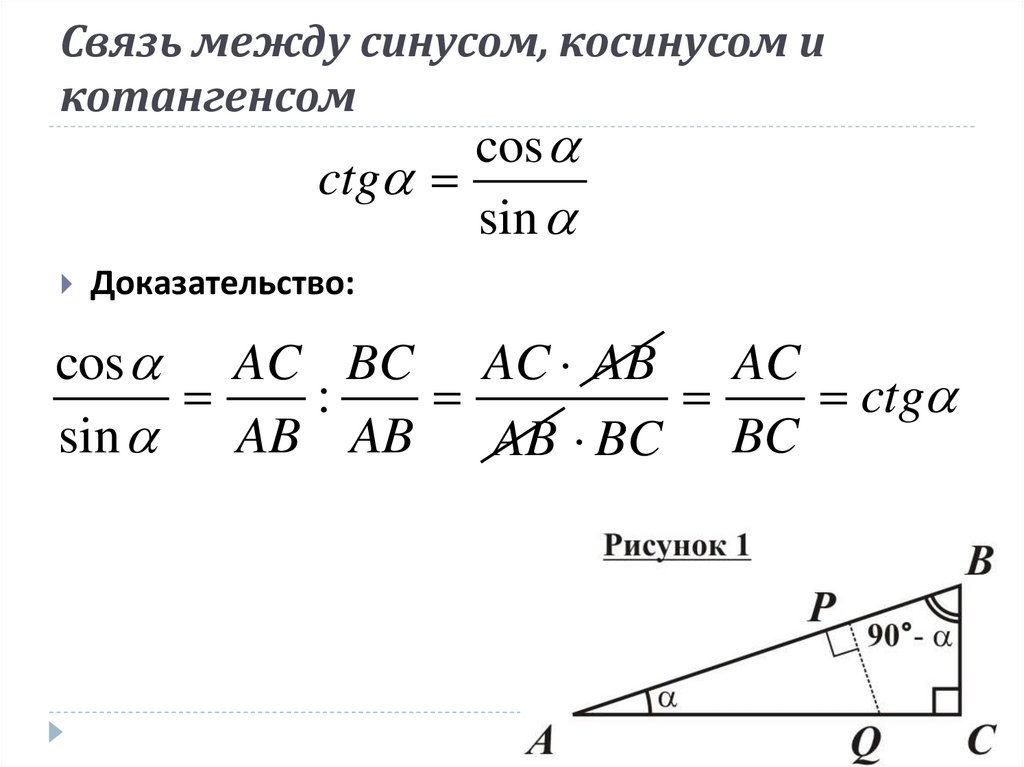
Наша программа представляет собой онлайн-калькулятор, который позволяет рассчитывать значения основных тригонометрических функций углов, выраженных в градусах или радианах. Для использования калькулятора требуется выбрать в меню программы требуемую функцию и ввести величину угла в градусах. Калькулятор вычисляет и обратную функцию арккосинуса. Если требуется определить угол по известному значению косинуса, введите значение функции в ячейку «Косинус» и выполните расчет. Программа мгновенно выдаст значение угла. Рассмотрим пару примеров использования калькулятора.
Примеры из жизни
Вычисление углов
Пусть в задаче по геометрии дан треугольник со сторонами A = 3 см, B = 4 см и C = 5 см. Требуется найти значения всех углов. На первый взгляд это сложная задача, однако мы знаем, что 3, 4 и 5 — это классическая пифагорова тройка, следовательно, известны значения катетов и гипотенуз. Очевидно, что угол AB = 90 градусов, так как катеты всегда образуют прямой угол. Теперь мы можем найти углы AC и BC.
- cosAC = A/C = 3/5 = 0,6; cosBC = B/C = 4/5 = 0,8.
Теперь определим соответствующие углы при помощи нашего калькулятора. Углы с такими значениями косинусов равны соответственно 53,13 и 36,87 градуса. Правильность решения легко проверить, сложив величины углов:
90 + 53,13 + 36,87 = 180.
Расчет косинусов
Прямая задача определения численных значений функций — это вычисление косинуса в зависимости от величины угла. Для такой задачи можно использовать таблицу Брадиса — четырехзначные таблицы значений тригонометрических функций для целочисленных величин углов. Вычислим значения косинусов для основных углов. Для этого введем значения в ячейки «Косинус»:
- cos30 = 0,866; cos45 = 0,707; cos60 = 0,5; cos90 = 0; cos120 = –0,5; cos150 = — 0,866; cos180 = — 1.
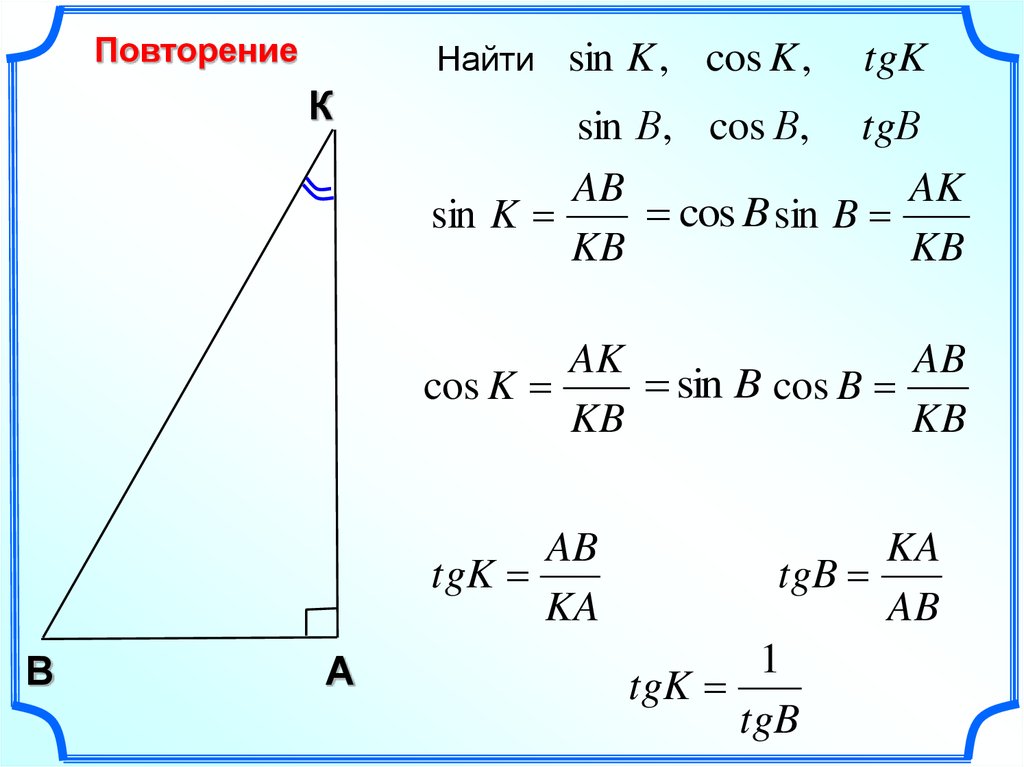
Это основные значения косинусов для стандартных величин углов треугольника. В целом значения тригонометрических функций периодически повторяются каждые 360 градусов.
Заключение
Тригонометрия — определенно важный раздел математики, функции которого повсеместно используются в современных технологиях. Наши калькуляторы прекрасно подходят для элементарных расчетов по геометрии и тригонометрии.
Косинус — тригонометрическая функция, которая геометрически определяется как соотношение прилежащего катета к гипотенузе. Как и все тригонометрические функции, косинус нашел широчайшее применение в науке.
Тригонометрия как наука возникла еще в Древней Индии, когда ученые разработали таблицу соотношений катетов и гипотенуз и их численных значений для основных углов. Термин «косинус» — сравнительно молодой, так как изначально ученые пользовались только синусом и тангенсом угла. Complementry sinus, он же дополнительный синус, он же косинус — это просто синус угла, смещенного на 90 градусов. Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Именно поэтому для расчета соотношений прилежащего к углу катета и гипотенузы использовался синус смещенного угла, что упрощало расчеты.
Геометрически косинус — это соотношение прилежащего катета к гипотенузе. Прилежащий катет — это сторона прямоугольного треугольника, которая вместе с гипотенузой образует рассматриваемый угол. Как и любая тригонометрическая функция, изначально косинус рассчитывался только для углов. Для любого значения угла косинус имеет строго определенное значение и никогда не изменяется. С развитием математической науки тригонометрические функции были расширены на всю числовую ось, и сегодня легко взять косинус не только целого числа, но также вещественного и даже комплексного.
Геометрически косинус это соотношение прилежащего катета к гипотенузе.
Bbf. ru
28.07.2017 23:25:25
2017-07-28 23:25:25
Источники:
Https://bbf. ru/calculators/170/#:~:text=%D0%9A%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81%20%E2%80%94%20%D1%82%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F%20%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F%2C%20%D0%BA%D0%BE%D1%82%D0%BE%D1%80%D0%B0%D1%8F%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%20%D0%BE%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D1%8F%D0%B5%D1%82%D1%81%D1%8F%20%D0%BA%D0%B0%D0%BA,%D0%BA%D0%BE%D1%81%D0%B8%D0%BD%D1%83%D1%81%20%D0%BD%D0%B0%D1%88%D0%B5%D0%BB%20%D1%88%D0%B8%D1%80%D0%BE%D1%87%D0%B0%D0%B9%D1%88%D0%B5%D0%B5%20%D0%BF%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20%D0%B2%20%D0%BD%D0%B0%D1%83%D0%BA%D0%B5. 2-22м+8=0
2-22м+8=0
М1=4/9 не подходит так как м натуральное
М2=2
Ответ 2
А+б+с+д+в+равно 56 изиизи
2 Равны по двум углам и стороне между ними.
Yznay. com
05.05.2020 4:31:02
2020-05-05 04:31:02
Источники:
Https://yznay. com/geometriya/kak-najti-sinus-sin-i-kosinus-co-18201896
Тригонометрия | Синусы Косинусы Тангенс Котангенс, Формулы
Тригонометрия
Что такое тригонометрия?
Тригонометрия как сам мир от греческого, что означает измерение треугольника. Этот раздел математики изучает взаимосвязь между длинами сторон и углами треугольников.
Как мы видим, тригонометрия — это решение треугольника, что означает нахождение всех недостающих частей треугольника, в основном всех длин сторон и углов.
Как мы собираем треугольники?
Мы знаем, как решить треугольник, когда известны длины двух сторон в прямоугольном треугольнике, используя знаменитую « теорему Пифагора».
Также мы знаем, как найти недостающий угол, когда мы знаем острый угол прямоугольного треугольника, просто применяя правило, согласно которому сумма углов треугольника равна 180°.
Но как нам решить прямоугольный треугольник, если мы знаем только одну длину стороны и один угол?
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник — это тип треугольника, у которого прямой угол равен 90°.
По острому углу назовем стороны прямоугольного треугольника.
Мы знаем, что самая длинная сторона прямоугольного треугольника называется гипотенуза.
Сторона, в которой лежит известный нам угол, всегда будет называться прилежащей.
Сторона перед углом будет называться противоположная.
В зависимости от угла, который нам дан, эти две стороны меняют маркировку.
Предположим, что наш угол помечен ϴ.
Стороны:
Гипотенуза – самая длинная сторона.
Смежная – сторона, в которой лежит угол ϴ.
Напротив – перед углом ϴ.
Как тригонометрия помогает нам решить прямоугольный треугольник, как в случае выше?
Давайте изучим все возможные соотношения между длинами сторон нашего треугольника выше.
Все отношения таковы: Для нашего угла Ѳ:
1. $\displaystyle \frac{противоположная}{гипотенуза}$
2. $ \displaystyle \frac{adjacent}{гипотенуза}$
3. $ \displaystyle \frac{opossite}{adjacent}$
4. $ \displaystyle \frac{hypotenuse}{opposite}$
5. $ \displaystyle \frac{hypotenuse}{adjacent}$
6. $ \displaystyle \frac {adjacent}{opposite}$
Эти 6 найденных нами соотношений представляют собой шесть тригонометрических функций любого угла в прямоугольном треугольнике. В нашем случае тригонометрические функции нашего угла Ѳ.
Первые три соотношения являются самыми основными и используются в тригонометрии. Мы называем их синус, косинус, тангенс и обозначаем их как sin, cos и tan данного угла.
Три других отношения называются косеканс, секанс, котангенс, и мы обозначаем их как csc, sec, cot данного угла.
cscΘ = $ \displaystyle \frac{гипотенуза}{напротив}$
cscΘ = $ \displaystyle \frac{гипотенуза}{adjacent}$
cotΘ = $ \displaystyle \frac{adjacent}{напротив}$
Простой способ напомнить три основные тригонометрические функции — напомнить известное слово «СОХКАТОА»
Мы делим слово на три слова по 3 буквы.
SOH, CAH и TOA
– Первая буква каждого слова представляет название функции.
— вторая буква обозначает знак соотношения.
— Третий представляет то, что находится внизу знака соотношения.
Пишем:
sinΘ = $ \displaystyle \frac{\text{Наоборот}}{\text{Гипотенуза}}$
cosΘ = $ \displaystyle \frac{Adjacent}{\text{Гипотенуза}}$
tanΘ = $ \displaystyle \frac{Opposite}{Adjacent}$
Пример 1. Вычисление значения синуса, косинуса и тангенса угла ϴ на треугольнике ниже.
Решение: сначала обозначьте стороны, исходя из угла Ѳ.
6 — Противоположная
8 — Соседняя
10 — Гипотенуза
Во-вторых, запишите отношения синуса, косинуса и тангенса нашего угла.
sinΘ = $ \displaystyle \frac{\text{Наоборот}}{\text{Гипотенуза}}$
cosΘ = $ \displaystyle \frac{Adjacent}{\text{Гипотенуза}}$
tanΘ = $ \displaystyle \frac{Opposit}{Adjacent}$
В-третьих, примените функции, основанные на длинах сторон, которые данный.
sinΘ = $ \displaystyle \frac{6}{10}=\frac{3}{5}$
cosΘ = $ \displaystyle \frac{8}{10}=\frac{4}{5}$
tanΘ = $ \displaystyle \frac{6}{8}=\frac{3}{4}$
Пример 2. Найдите x, используя правильную тригонометрическую функцию.
Решение: Основываясь на рисунке, мы знаем гипотенузу и угол 30° и должны найти противоположное значение (30°). 9{\circ }}\cdot 14$
$ \displaystyle x=\frac{1}{2}\cdot 14$
x = 7
Следовательно, значение x=7.
Пример 3: Угол захода на посадку авиалайнера составляет 3°. Если самолет находится на высоте 305 метров над землей, как далеко он должен быть от аэродрома? Решение. Мы видим, что правильной функцией является тангенс функции.
$ \displaystyle \tan \theta =\frac{Opposite}{Adjacent}$
tan3° = $ \displaystyle =\frac{305}{x}$
x ⋅ tan3° = 305
9{\circ }}=0,052$x = $\displaystyle \frac{{305}}{{0,052}}=5865,38$
x $\displaystyle \ приблизительно $
5866 Copyright © Math OriginalПредварительное исчисление: тригонометрические функции: тигонометрические уравнения
Тригонометрическое уравнение – это любое уравнение, содержащее тригонометрическую
функция. Существует два основных типа тригонометрических уравнений:
тождества и условные уравнения. Тождества — это уравнения, которые выполняются
для любого угла. Условные уравнения — это уравнения, которые решаются только
определенные углы.
Существует два основных типа тригонометрических уравнений:
тождества и условные уравнения. Тождества — это уравнения, которые выполняются
для любого угла. Условные уравнения — это уравнения, которые решаются только
определенные углы.
Существуют десятки важных тригонометрических тождеств. Помните, приведенные ниже тождества верны для любого угла .
Восемь фундаментальных идентичностей
основной
| csc ( θ ) = . |
| сек ( θ ) = . |
| детская кроватка ( θ ) = . |
тангенс ( θ ) = . |
| детская кроватка ( θ ) = . |
| (sin( θ )) 2 + (cos( θ )) 2 = 1. |
| 1 + (загар( θ )) 2 = (сек( θ )) 2 . |
1 + (кроватка( θ )) 2 = (csc( θ )) 2 .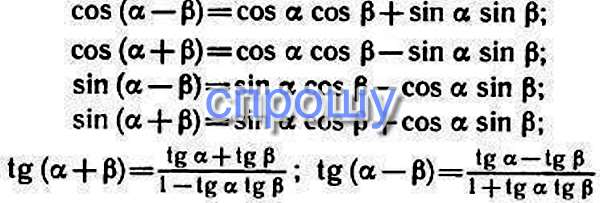 |
Кофункциональные тождества
кофункция
| sin(-x) = cos(x). |
| потому что (- х ) = грех ( х ). |
| загар(- х ) = детская кроватка( х ). |
| детская кроватка (- х ) = коричневый ( х ). |
csc (- x ) = сек ( x ).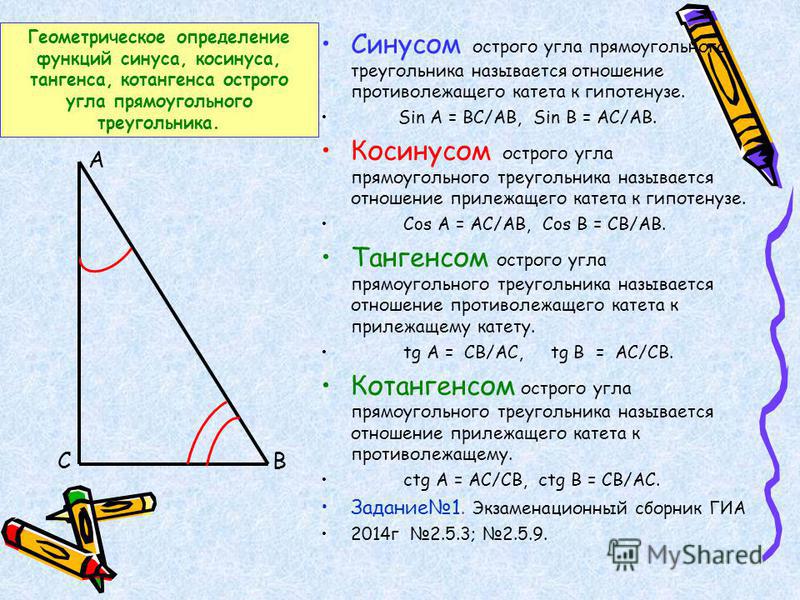 |
| сек(- х ) = csc( х ). |
Тождества с отрицательным углом
Синус, тангенс, косеканс и котангенс странные функции. косинус и секанс четные функции. Эти характеристики очевидны в тождествах с отрицательным углом.
отрицательный
| sin(- θ ) = — sin( θ ). |
| cos(- θ ) = cos( θ ). |
желтовато-коричневый (- θ ) = — загар ( θ ). |
| csc(- θ ) = — csc( θ ). |
| сек(- θ ) = сек( θ ). |
| детская кроватка(- θ ) = — детская кроватка( θ ). |
Формулы двойного угла
двойной
| sin(2 x ) = 2 sin( x )cos( x ). |
COS (2 x ) = COS 2 ( x ) — SIN 2 ( X ) = 1 -2 SIN 2 ( x ) = 1 -2 ( x ) = 1 -2 9 ( x ) = 1 -2 ( x ) = 1 -2 2 ( x ) = 1 -24999 ( x ) = 1 2 ( x ).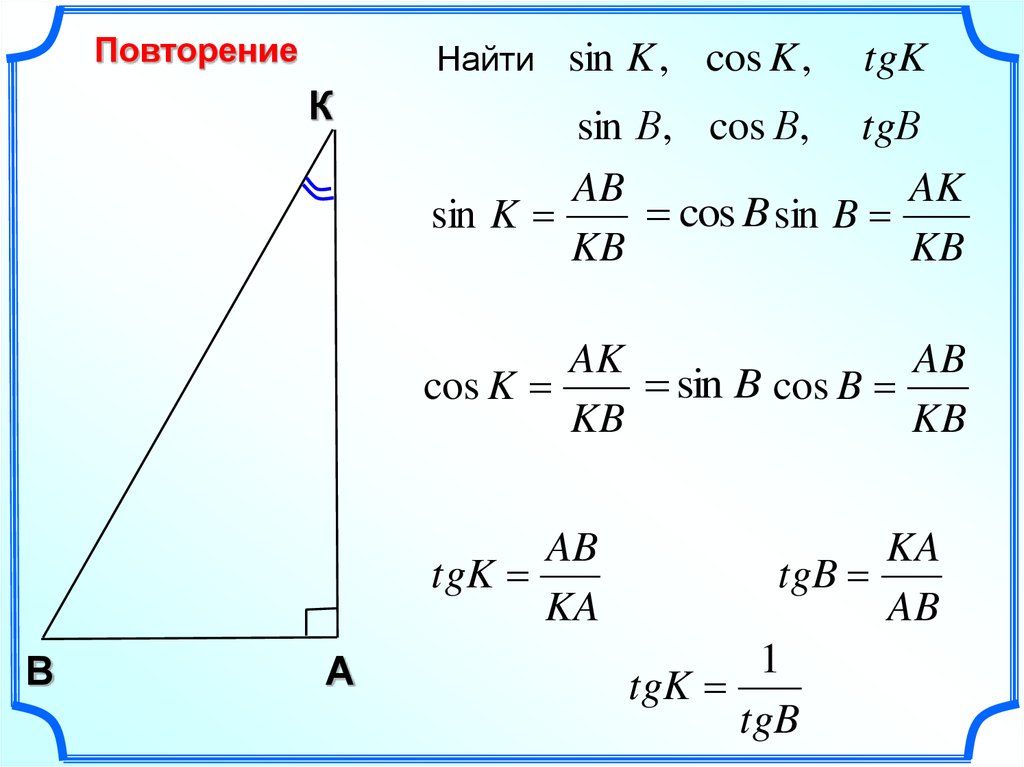 cos 2 ( x ) — 1. cos 2 ( x ) — 1. |
| тан(2 x ) = . |
Формулы половинного угла
половина
| sin() = ±. |
| cos() = ±. |
| тангенс() = ± = = . |
Формулы сложения
дополнение
sin( α + β ) = sin( α )cos( β ) + cos( α )грех( β ). |
| COS ( α + β ) = COS ( α ) COS ( β ) -SIN (72) COS ( β ). |
| тангенс( α + β ) = . |
Формулы вычитания
вычитание
| грех( α — β ) = sin( α )cos( β ) — cos( α )sin( β ). |
COS ( α — β ) = COS ( α ) COS ( β ) + SIN (72) COS ( β ) + SIN (72). |
| тан( α — β ) = . |
Формулы продукта
товар
| sin( α )sin( β ) = — (cos( α + β ) — cos( α — β 9). |
| cos( α )cos( β ) = (cos( α + β ) + cos( 1 β α ) ). |
sin( α )cos( β ) = (sin( α + β ) + sin( α — β )). |
| cos( α )sin( β ) = (sin( α + β ) — sin( α ) 1 β 1 β ). |
Формулы суммы и разности
суммаразность
| sin( α ) + sin( β ) = 2 sin(cos(. | ) |
| cos( α ) + cos( β ) = 2 cos(cos(. | ) |
sin( α ) — sin( β ) = 2 cos(sin(. | ) |
| cos( α ) — cos( β ) = — 2 sin(sin(. | ) |
Единого метода решения тригонометрических уравнений не существует. Несколько техник хоть пригодится. 1) Разложим все на синус и косинус, то отмените все что можно. 2) Манипулировать уравнением с факторингом и другие алгебраические методы для создания тригонометрических тождеств, которые могут быть упрощенный. 3) Если решение не может быть найдено, попробуйте изобразить уравнение в виде графика. реши.
Во всяком тригонометрическом уравнении либо не будет решений, либо
бесконечное количество решений. Причина этого в том, что тригонометрический
функции периодические. принято
перечислите только решения x , где 0≤ x < 2 Π или, если указанный период
отличается от 2 Π , чтобы описать все решения.
