Синус угла альфа: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Рисунок \(\PageIndex{1}\): определение высоты флагштока (рисунок не в масштабе)

Тригонометрические функции и прямоугольные треугольники

Мы видели, как мы определяем значения тригонометрических функций угла \(\theta\), помещая \(\theta\) в стандартное положение и позволяя \((x, y)\ ) — точка пересечения конечной стороны угла \(\theta\) с окружностью радиуса \(r\). Затем

1. \(\cos(\theta) = \dfrac{x}{r}\)
2. \(\sin(\theta) = \dfrac{y}{r}\)
3. \(\tan(\theta) = \dfrac{y}{x}\), если \(x \neq 0\)
4. \(\sec(\theta) = \dfrac{r}{x}\), если \(x \neq 0\)
5. \(\csc(\theta) = \dfrac{r}{y}\) если \(y \neq 0\)
6. \(\cot(\theta) = \dfrac{x}{y}\), если \(y \neq 0\)

В нашей работе с прямоугольными треугольниками мы будем использовать только функции синуса, косинуса и тангенса.

Теперь мы увидим, как связать тригонометрические функции с углами в прямоугольных треугольниках. Предположим, у нас есть прямоугольный треугольник со сторонами длины \(x\) и \(y\) и гипотенузой длины \(r\). Пусть \(\theta\) будет углом, противоположным стороне длины \(y\), как показано на рисунке \(\PageIndex{2}\). Теперь мы можем разместить наш треугольник так, чтобы угол \(\theta\) находился в стандартном положении на плоскости, а треугольник вписывался в окружность радиуса \(r\), как показано справа на рисунке \(\PageIndex{3). }\).

По определению наших тригонометрических функций имеем

\[\cos(\theta) = \dfrac{x}{r}\]

\[\sin(\theta) = \dfrac{y}{ r}\]

\[\tan(\theta) = \dfrac{y}{x}\]

Если вместо \(x\), \(y\) и \(r\), мы обозначаем \(y\) как длину стороны, противоположной острому углу \(\theta\), \(x\) как длину стороны, прилегающей к острому углу \(\theta\), и \( г\) как длину гипотенузы, получим следующую цифру:

Рисунок \(\PageIndex{2}\): Прямоугольный треугольник

Рисунок \(\PageIndex{3}\): Прямоугольный треугольник в стандартном положении

Итак, мы видим, что

\[\sin (\ theta) = \dfrac{длина \пространство \пространство стороны \пространство напротив\пространство \theta}{длина \пространство \пространство гипотенузы} \space\space \sin(\theta) = \dfrac{противоположный}{гипотенуза }\]

\[\cos(\theta) = \dfrac{длина \пространства \пространства стороны \пространства, примыкающего\пространства к \пространству \theta}{длины \пространства \пространства гипотенузы} \space\space \cos (\ тета) = \ dfrac {смежный} {гипотенуза} \]

\[\tan(\theta) = \dfrac{длина \пространство \пространство стороны \пространство напротив\пространство \theta}{длина \пространство \пространство стороны \пространство примыкает\пространство к \пространству \theta} \пространство \space \tan(\theta) = \dfrac{opposite}{adjacent}\] ​​

Уравнения справа представляют собой удобные сокращения правильных уравнений слева.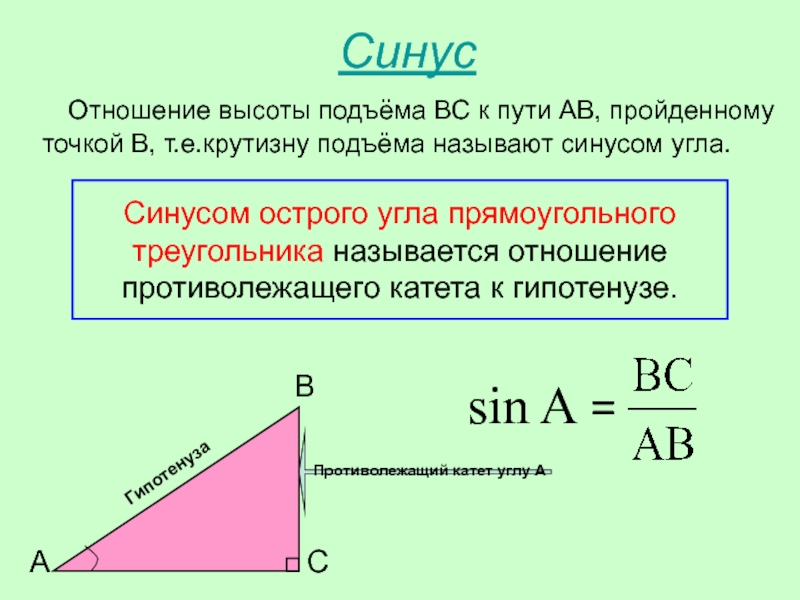 \circ\] \[\gamma = 9\circ\) и что длина стороны, примыкающей к этому углу, равна 8 дюймам. Определить другой острый угол прямоугольного треугольника и длины двух других сторон.

Раствор

Первое, что мы делаем, это рисуем треугольник. (Картинка не обязательно должна быть идеальной, но она должна разумно отражать предоставленную информацию.) При построении диаграммы мы также должны обозначить неизвестные части треугольника. Один из способов сделать это показан на схеме.

9{2} \ок. 95,379 \номер\]

Итак, мы видим, что наша работа согласуется с теоремой Пифагора.

Решение прямоугольных треугольников

В примере \(\PageIndex{1}\) мы сделали то, что называется решением прямоугольного треугольника . Обратите внимание, что эта фраза вводит в заблуждение, потому что на самом деле вы не можете «решить» треугольник. К сожалению, эта фраза укоренилась в просторечии тригонометрии, поэтому мы будем продолжать ее использовать. Идея состоит в том, что если нам дано достаточно информации о длинах сторон и размерах углов в прямоугольном треугольнике, то мы можем определить все остальные значения. Следующая проверка прогресса также является примером «решения прямоугольного треугольника».

Упражнение \(\PageIndex{2}\)

Длина гипотенузы прямоугольного треугольника равна \(17\) футам, а длина одной стороны этого прямоугольного треугольника равна \(5\) футам. Определите длину другой стороны и два острых угла этого прямоугольного треугольника.

Подсказка : Нарисуйте картинку и обозначьте третью сторону прямоугольного треугольника переменной, а два острых угла обозначьте как \(\альфа\) и \(\бета\).

Ответить

9{2}\]

и таким образом мы видим, что \(b = \sqrt{264} \приблизительно 16,2481\) футов.

Применение прямоугольных треугольников

Как показано в приведенных выше примерах, при работе над задачами, связанными с прямоугольными треугольниками (включая прикладные задачи), мы должны:

• Нарисовать схему задачи.
• Определите, что вы знаете о ситуации. Если уместно, включите эту информацию в свою фотографию.
• Определите количество, которое необходимо определить, и присвойте этому количеству имя переменной. При необходимости включите эту информацию в свою диаграмму.
• Найдите уравнение, связывающее известное с тем, что необходимо определить. Это часто будет включать тригонометрическую функцию или теорему Пифагора.
• Решите уравнение относительно неизвестного. Затем подумайте об этом решении, чтобы убедиться, что оно имеет смысл в контексте проблемы.
• Если возможно, найдите способ проверить результат.

Вернемся к примеру, приведенному во введении к этому разделу на стр. 179. В этом примере мы использовали термин угол места . Это общий термин (так же, как угол наклона ) в задачах, связанных с треугольниками. Мы можем определить угол возвышения объекта как угол, начальная сторона которого горизонтальна и имеет поворот так, что конечная сторона находится над горизонталью.

Ответить

Первое, что мы делаем, это рисуем схему. На диаграмме пусть \(h\)

Рисунок \(\PageIndex{6}\): Определение высоты флагштока (рисунок не в масштабе)

— высота флагштока, \(x\) — длина тени, а \(\theta\) — угол возвышения. Нам даны значения для \(x\) и \(\theta\), и мы видим, что

\[\tan(\theta) = \dfrac{h}{x}\] \[x\tan(\theta) = h\] 9\circ\] \[h \приблизительно 29,1208 \пространственных футов\]

Высота флагштока составляет около \(29,12\) футов или \(29\) футов, \(1,4\) дюймов.

Упражнение \(\PageIndex{3}\)

Компании необходимо построить пандус, доступный для инвалидных колясок, к своему входу. В Руководстве Закона об американцах с ограниченными возможностями для зданий и сооружений для пандусов говорится: «Максимальный уклон пандуса в новом строительстве должен составлять \(1:12\)».

1. Директива \(1:12\) означает, что на каждый 1 фут подъема пандуса должно приходиться \(12\) футов пробега. Каков угол подъема (в градусах) такой рампы?
2. Если въезд компании находится \(7,5\) футов над уровнем земли, используйте тригонометрию для приблизительной длины пандуса, который компании необходимо будет построить с использованием максимального уклона. Объясните свой процесс.

Ответить

При подъеме на \(1\) фут на каждые \(12\) футов пробега мы видим, что если мы допустим \(\theta\) угол подъема, то

\[\тангенс(\тета) = \dfrac{1}{12}\]

\[\theta = \arctan(\dfrac{1}{12})\] 9\цирк\]

Длина пандуса будет гипотенузой прямоугольного треугольника. Итак, если мы возьмем \(h\) за длину гипотенузы, то

\[\sin(\theta) = \dfrac{7.5}{h}\]

\[h = \dfrac{7.5}{\sin(\theta)}\]

\[ч \около 90,3120\]

Длина гипотенузы приблизительно равна \(90,3\) фута. Мы можем проверить наш результат, определив длину третьей стороны, которая составляет \(7,5 \cdot 12\) или \(90\) футов, а затем проверив результат теоремы Пифагора. Мы можем убедиться, что 9{2}.\]

Упражнение \(\PageIndex{4}\)

Это вариант примера 3.19. Предположим, что флагшток находится на вершине холма и мы не можем напрямую измерить длину тени от флагштока, как показано на рис. 3.19.

Некоторые величины отмечены на диаграмме. Углы \(\alpha\) и \(\beta\) — это углы подъема к вершине флагштока из двух разных точек на ровной поверхности. Эти точки находятся на расстоянии \(d\) футов друг от друга и находятся прямо на одной линии с флагштоком. Проблема 9\circ\] \[d = 22,75 фута\]

Обратите внимание, что значение для \(x\) не указано, потому что это расстояние от первой точки до воображаемой точки непосредственно под флагштоком и даже на ровной поверхности.

Имейте в виду, что, вероятно, проще писать формулы в терминах \(\alpha\), \(\beta\) и \(\gamma\) и ждать до конца, чтобы использовать числовые значения. Например, мы видим, что \[\tan(\alpha) = \dfrac{h}{x}\] и \[\tan(\beta) = \dfrac{h}{d + x}\]

In уравнения (1), обратите внимание, что мы знаем значение \(\альфа\). Это означает, что если мы можем определить значение либо \(x\), либо \(h\), мы можем использовать уравнение (1) для определения значения другого. Сначала определим значение \(x\).

1. Решите уравнение (1) для h, а затем подставьте его в уравнение (2). Назовите это уравнение (3).
2. Один из членов уравнения (3) имеет знаменатель. Умножьте обе части уравнения (3) на этот знаменатель.
3. Теперь решите полученное уравнение относительно \(x\) (в терминах \(\alpha\), \(\beta\) и \(\gamma\)).
4. Подставьте данные значения вместо \(\alpha\), \(\beta\) и \(\gamma\), чтобы определить значение \(x\) и

   , затем используйте это значение и уравнение (1) для определения значения \(h\).

5. Есть ли способ проверить правильность результата?

Ответить

1. \(h = x\tan(\alpha)\). Итак, \[\tan(\beta) = \dfrac{x\tan(\alpha)}{d + x}\]

2. \(\tan(\beta)(d + x) = x\tan(\alpha)\)

3. Мы можем перейти к решению для x следующим образом:

\[d\tan(\beta) + x\tan(\beta) = x\tan(\alpha)\]

\[d\tan(\beta) = x\tan(\alpha) — x\tan(\beta)\] 9\цирк\]

Другой метод проверки результатов заключается в использовании синуса \(\alpha\) или \(\beta\) для определения длины гипотенузы одного из прямоугольных треугольников, а затем проверки с помощью теоремы Пифагора.

Резюме

В этом разделе мы изучили следующие важные концепции и идеи:

Имея достаточно информации о длинах сторон и мерах углов в прямоугольном треугольнике, мы можем определить все остальные значения, используя следующие соотношения:

\[\sin(\theta) = \dfrac{opposite}{гипотенуза}\]

\[\cos(\theta) = \dfrac{adjacent}{гипотенуза}\]

\[\tan (\ тета) = \ dfrac {напротив} {смежный} \]

Эта страница под названием 3. 2: Right Triangles публикуется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Тедом Сандстромом и Стивеном Шликером (ScholarWorks @Grand Valley State University) с использованием исходного контента, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Тед Сандстром и Стивен Шликер

   Лицензия

   СС BY-NC-SA

   Версия лицензии

   3,0

   Показать страницу TOC

   нет

2. Теги

   1. угол возвышения
   2. гипотенуза
   3. прямоугольных треугольников
   4. источник@https://scholarworks. gvsu.edu/books/12

Формулы сложения синусов — Задача 3

Мы говорим о формулах сложения синусов, вот особенно сложный пример. В нем говорится, что если косинус альфа равен 7 больше 25, а альфа находится между 3 пи больше 2 и 2 пи, а синус бета равен 3/5 с бета между пи больше 5 и пи, найдите синус альфа минус бета и синус альфа плюс бета.

Чтобы решить эту проблему, мне нужно будет использовать единичный круг, потому что мне нужно больше, чем просто косинус альфа и синус бета.

Итак, начнем с альфы. Угол альфа находится между 3 пи на 2 и 2 пи, поэтому альфа находится в четвертом квадранте 3 пи на 2, 2 пи прямо здесь, а косинус альфа равен 7 на 25, так что это означает, что первая координата моей точки на единичном круге 7 на 25, так что я поставлю это прямо здесь, и я не знаю координату y, но я найду ее второй, так что это альфа.

Теперь помните, что это единичный круг, а единичный круг имеет уравнение x² плюс y² равно 1, поэтому каждая точка на единичном круге удовлетворяет этому уравнению, включая это, и это означает, что 7 на 25² плюс y² это y² равно 1.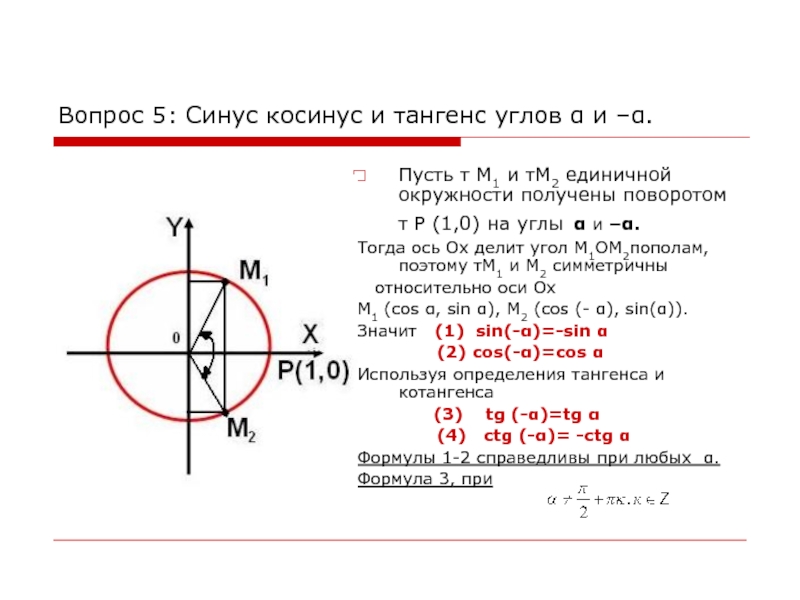 Возведем в квадрат это мы получаем 49больше 625 плюс y² равно 625 больше 625, и мы вычитаем y² равно чему-то больше 625. 625 минус 49, 625 минус 50 будет 575, поэтому минус 49 будет 576, и получается, что это оба идеальные квадраты, 576 это 24² и 625 равно 25², так что это плюс или минус 24 на 25. Итак, мы должны решить, плюс это или минус, но в четвертом квадранте координата y должна быть отрицательной, поэтому она должна быть отрицательной, -24 на 25. Хорошо, что позаботится об альфе.

Теперь мы знаем косинус альфа и синус альфа, а бета? Что ж, бета находится между пи больше 2 и пи, а его синус равен 3/5, поэтому между пи больше 2 и пи поместите бета во второй квадрант этого квадранта, и если синус равен 3/5, это означает, что значение y точки на этом круге равно будет 3/5 ну это примерно здесь так что-то 3/5.

Так что это может быть бета-версия моего угла. Чтобы найти координату x, я проделал тот же трюк, что и здесь, я использовал уравнение x² плюс y² равно 1, поэтому я получаю x² плюс 3/5 в квадрате равно 1, и это означает, что x² плюс 9 на 25 равно 25 на 25, поэтому я вычитаю x² равно 16 на 25, а затем извлеките корни, чтобы получить плюс или минус 4/5.

Теперь координата x должна быть отрицательной, потому что мы находимся во втором квадранте, поэтому ответ будет -4/5, 3/5, и это даст мне косинус и синус моего угла бета, и теперь это все, что мне нужно, чтобы найти синус альфа минус бета и синус альфа плюс бета.

Теперь запомните формулу синуса и разности, это синус, косинус, косинус, синус альфа-бета, альфа-бета, альфа-бета, а затем, когда у вас есть знак минус с формулой синуса, она остается неизменной, поэтому я просто заполняю в ценностях. Синус альфа-24 больше 25, а косинус 7 больше 25, поэтому -24 и 7 больше 25, а как насчет бета? Косинус бета равен -4/5, синус бета равен 3/5, -4/5, 3/5.

Итак, у нас есть -24 на 25, умноженное на -4 на 5, два отрицательных числа сокращаются, наш знаменатель будет 125 25 на 5, а числитель 24 на 4, 24 на 2 будет 48, умножить на 2, а еще 2 на 9.6, а затем минус знаменатель все еще 125, я получаю 21 сверху, так что в основном это 96 минус 21, это 75. Итак, 75 на 125, что очень хорошо сокращается до 3/5, и это мой ответ для синуса альфа минус бета.