Синус углов: Синус, косинус угла треугольника

описание формул, примеры и решение / Справочник :: Бингоскул

Синусы углов и как их сравнивать: описание формул, примеры и решение

добавить в закладки удалить из закладок

Содержание:

Одним из видов тригонометрических функций является синус. Данная функция рассчитывается для любых углов, находящихся в окружности. Прямоугольный треугольник применяется для определения значения sin острых углов. Если угол имеет обозначение Х, алгебра предполагает использование выражения sinХ. Перед тем, как сравнивать синусы, необходимо определить тип угла, создать окружность, установить четверть этой окружности.

Как сравнивать синусы углов –

sin острого угла и пример расчета

Острый угол – угол меньше 90 градусов. Для расчета синуса необходимо рассчитать соотношение противолежащих сторон. Сравнивается катет с гипотенузой. 

Катет представляет собой одну из сторон в прямоугольном треугольнике. \propto } = 2 ( — 1 ) 2 + 22 = 25 = 255

Итог: \sin  = 25 \sqrt 5

Как сравнить синусы углов – анализ значений

Синусом называют функцию угла. Он находится в окружности, разделенной на 4 четверти. Для сравнения sin используется следующая таблица:
 

Угол	Значение
00	Всегда = 0
300	0,5
600	\sqrt {3}/2 \approx 1, 7/2 \approx 0,9
900	1

Важно запомнить: если угол находится в первой четверти, его sin будет возрастать до 90 градусов. Убывание значения отмечается во второй части окружности. Он стремится от 1 к 0. В третьей и четвертой четверти значение sin отрицательное. Для третьей части характерно стремление от нуля к -1, для 4 четверти – от -1 к 0.

Рассмотрим сравнение синусов на примерах:

1. Нужно установить соотношение между sin 195° и sin 200° . Для этого используется окружность. Местоположение 195, 200 находится на этой окружности. Это свидетельствует о том, что sin 195° > sin 200° , так как расположен ниже.
2. Определить отношение между sin 734° и sin -1066° .

Диаметр цельного круга составляет 360 градусов, двух окружностей – 720 градусов. Отсюда следует, что 734° включает два круга и 14 градусов. Если обойти три раза по кругу в обратную сторону, получится -360 х 3 = -1080 градусов. Получается, что точка -1066 – это три окружности и еще 14 градусов. Синусы точек с одинаковой градусной мерой равные. sin 734°= sin -1066°  

Поделитесь в социальных сетях:

29 июня 2021, 16:29

Математика

Could not load xLike class!

Значения тригонометрических функций разных углов

Рассмотрим значения тригонометрических функций углов от 0° до 360°. Углы изобразим на единичной окружности с радиусом единица. Одна сторона угла всегда будет совпадать с положительным направлением оси абсцисс, а другая будет перемещаться при росте угла против часовой стрелки.

Синус

Синус угла — это высота, на которой оказалась точка пересечения второй стороны угла с единичной окружностью.

Для изображённого угла высота этой точки — 0,6. Значит синус этого угла равен 0,6.

При изменении угла от 0° до 360° синус изменяется. Когда угол равен нулю, его стороны схлопываются, как книжка, и совпадают с положительным направлением оси абсцисс, и вторая сторона пересекает единичную окружность на высоте 0, т.е. синус 0° равен 0. С увеличением угла синус возрастает, и синус 90° равен 1. Затем синус начинает уменьшаться, и синус 180° уже снова равен 0. Потом синус продолжает уменьшаться, и синус 270° уже равен –1. А после этого с дальнейшим увеличением угла синус обратно возрастает до нуля, и синус 360° уже равен 0.

Косинус

Косинус угла — это абсцисса точки пересечения второй стороны с единичной окружностью.

Косинус изображённого угла равен 0,7.

При изменении угла от 0° до 360° значение косинуса изменяется. Если угол равен нулю, то обе его стороны совпадают с положительным направлением оси абсцисс и пересекает единичную окружность в самой правой точке, у которой абсцисса равна единице. Т.е. косинус 0° равен 1. При росте угла косинус уменьшается, и косинус 90° уже равен 0. Потом косинус уменьшается ещё дальше при увеличении угла, и косинус 180° равен –1. Затем косинус снова увеличивается, и косинус 270° уже равен 0. Косинус продолжает увеличиваться, и косинус 360° уже снова равен 1.## ТангенсТангенс — это синус делённый на косинус. Чтобы найти значение тангенса, нужно построить дополнительную прямую, которая называется ось тангенсов. И масштаб на этой прямой выбирается такой же, как и на оси синусов и косинусов, т.е. отрезок, равный радиусу окружности, принимается за 1. Так вот тангенс угла — это высота, на которой продолжение 2й стороны угла пересекает ось тангенсов.

Для изображённого угла тангенс равен примерно 1,4.

В отличие от синуса и косинуса тангенс не ограничен плюс и минус единицей, и может принимать любые значения от минус до плюс бесконечности.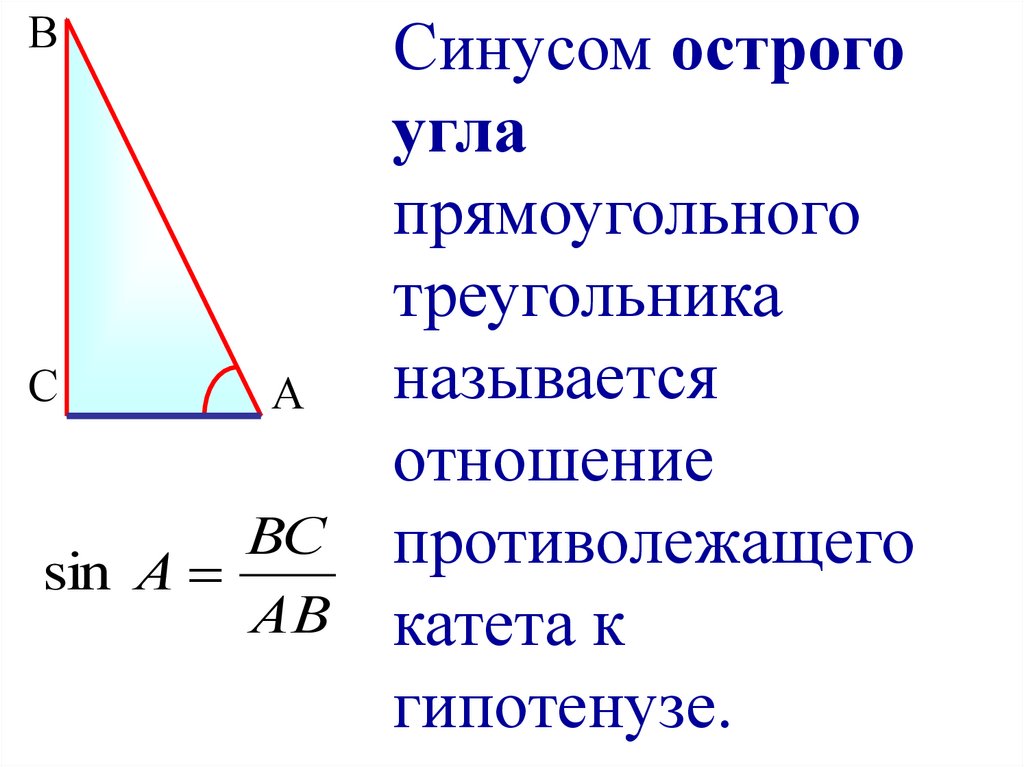 Посмотрим, как изменяется тангенс при изменении угла от 0° до 360°. Если угол равен нулю, то вторая сторона его так же, как и первая, пересекает ось тангенсов на высоте 0, и тангенс 0° равен 0. При увеличении угла тангенс всегда возрастает. И в первой четверти до 90° он возрастает от 0 до +∞. И наконец, тангенс 90° не определён, потому что продолжение стороны не пересекает ось тангенсов. А когда угол увеличивается снова, то сторону нужно продолжать в другом направлении. Тангенс продолжает возрастать уже от –∞ до 0, и наконец тангенс 180° равен 0. Снова возрастает угол и снова возрастает тангенс уже от 0 до +∞ и тангенс 270° опять не определён. И при увеличении угла тангенс снова возрастает от –∞ до 0, и тангенс 360° равен нулю.## КотангенсКотангенс — это косинус деленный на синус. Чтобы определить значение котангенса, нужно построить дополнительную прямую. Она называется ось котангенсов. И масштаб на этой прямой выбирается так же, как и на оси синусов и косинусов — отрезок, равный радиусу окружности, принимается за 1. 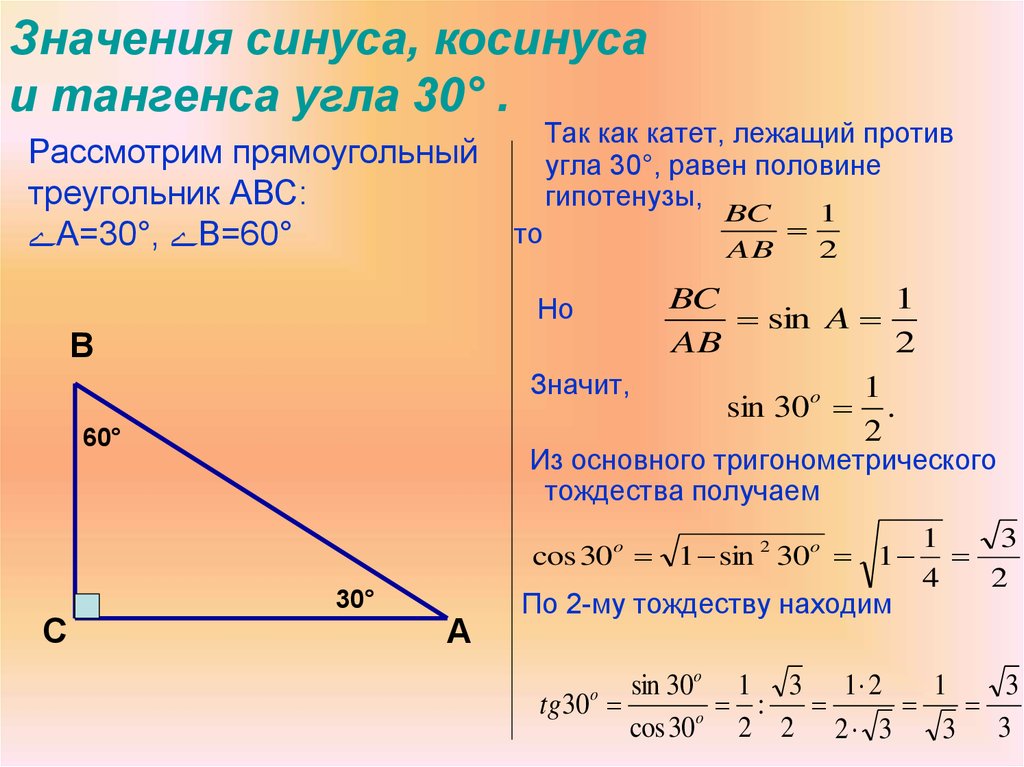Так вот котангенс угла это абсцисса, на которой продолжение 2й стороны пересекает ось котангенсов. И для изображённого угла котангенс равен примерно 1,3.

Посмотрим как меняется котангенс при изменении угла от 0° до 360°. И сразу возникает особенность — когда угол равен нулю, обе его стороны совпадают с положительным направлением оси абсцисс, и вторая сторона не пересекает ось котангенсов, и котангенс 0° не определён. При возрастании угла котангенс всё время убывает, и в первой четверти котангенс убывает от +∞ до 0. И котангенс 90° равен 0. При возрастании угла котангенс продолжает убывать уже от 0 до –∞, и котангенс 180° снова не определён. Опять возрастает угол и опять убывает котангенс уже от +∞ до 0. И котангенс 270° равен 0. И снова возрастает угол и снова убывает котангенс уже от 0 до –∞ и котангенс 360° градусов снова не определён.

← Предыдущий урок

Оглавление

Следующий урок →

функций — Проблемы с пониманием синуса, косинуса углов больше $90$ градусов

спросил 3 года 9 месяцев назад

Изменено 3 года, 9 месяцев назад

Просмотрено 2к раз

$\begingroup$

Недавно я узнал о тригонометрических функциях углов больше 9 долларов.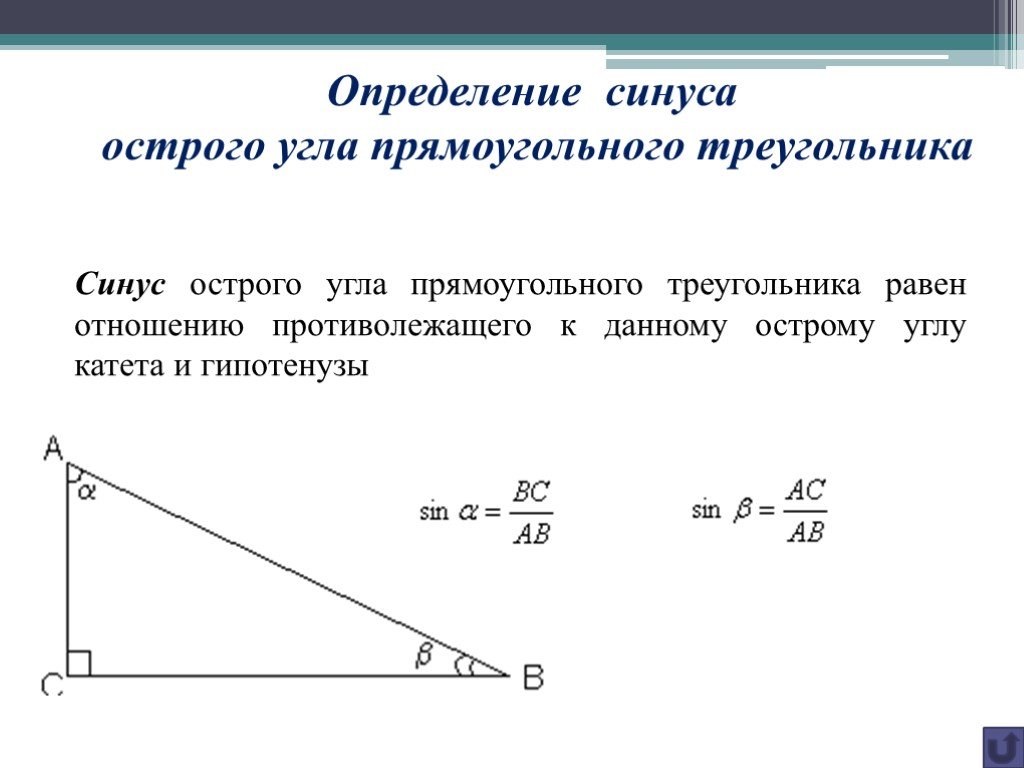 0$ градусов, и мне трудно понять концепцию.

Мы работали с такой диаграммой:

Мой учитель рассказал классу, что синус угла $\theta$ равен отношению между противолежащим катетом ($y$) и гипотенузой ($r $).

Я не совсем понимаю эту логику. Я знаком с тригонометрическими функциями, но насколько я их помню, они применялись к углам внутри прямоугольного треугольника, а не к углу вне его. Это кажется мне контринтуитивным.

Не должен ли коэффициент синуса (или косинуса, если на то пошло) представлять угол $180 — \theta$, расположенный внутри прямоугольного треугольника, а не вне его? Объяснение было бы очень признательно, так как это ключевая часть нашего текущего подразделения.

• функции
• тригонометрия

$\endgroup$

6

$\begingroup$

Когда тригонометрические функции, такие как синус и косинус, применяются к ситуациям, когда мы имеем дело с углами, которые больше или равны 9\circ$), как на вашей картинке. По сути, вы все еще как бы используете идею прямоугольного треугольника, но теперь вы должны принять во внимание тот факт, что стороны треугольника могут иметь отрицательные значения, потому что вся идея о том, что угол может быть больше или равен 90 градусам, возникает от единичного круга, с которым мы работаем в декартовой системе координат. Следовательно, когда $x$ отрицательно, длина соответствующей ветви имеет отрицательное значение. Когда $y$ отрицательно, длина соответствующей ветви также будет отрицательной. Имеет ли это смысл для вас?

Если мое объяснение покажется вам запутанным, вот более конкретная версия: забудьте об определении прямоугольного треугольника для углов, больших или равных 90 градусам. Это действительно не работает. Теперь вы работаете в декартовой системе координат, где гипотенуза равна $1$, $\cos\theta$ — координата x, а $\sin\theta$ — координата y.

$\endgroup$

7

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Функция синуса

Синус

• Сводка
• Синтаксис
• Аргументы
• Возвращаемое значение
• Использование
• Примеры
• Интерактивный
• Пояснение
• Определение
• Ссылки

Резюме

Функция синуса возвращает синус угла в радианах. В геометрических терминах функция возвращает вертикальную составляющую точки, образованной углом на единичной окружности.

Синтаксис

 грех(θ) 

Аргументы

Имя	Описание
θ (тета)	Угол в радианах

Возвращаемое значение

Возвращает синус угла в радианах.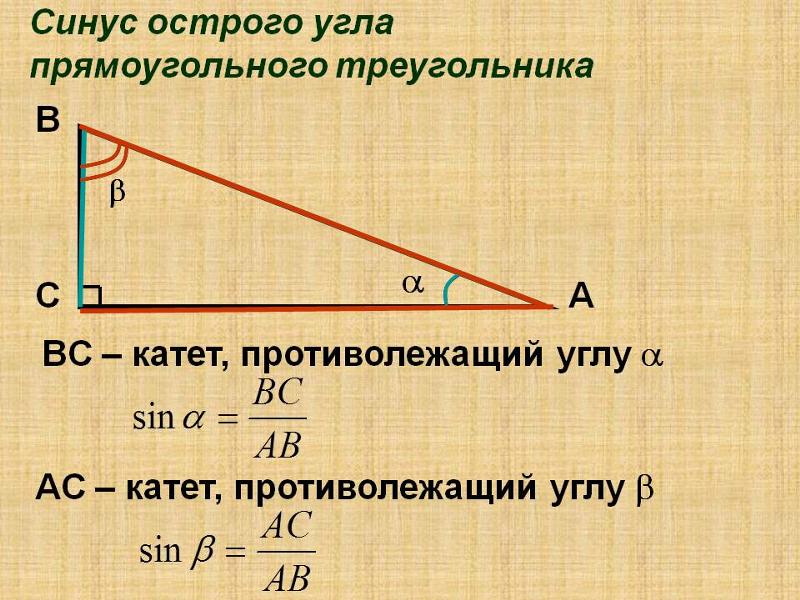

Применение

Функция синуса возвращает синус числа, указанного в радианах. В геометрических терминах функция возвращает вертикальную составляющую точки, образованной соответствующим углом (тета) на единичной окружности. Например, при заданном угле в радианах (треть оборота) функция возвращает значение .

Визуально возвращаемое значение равно Y-компоненте точки на единичной окружности, соответствующей углу в радианах. Это показано на рисунке ниже, на котором показана единичная окружность в координатной плоскости XY , а угол выделен красным цветом, а вертикальная составляющая точки — синим.

Примеры

В этих примерах показано возвращаемое значение синуса для некоторых распространенных углов, образованных делением единичного круга на равные части. Обратите внимание, что постоянная окружности (тау) представляет собой полный оборот в радианах.

В этих примерах показано возвращаемое значение синуса для некоторых распространенных углов, образованных делением единичного круга на равные части.

 грех(0*ТАУ/8) = 0
 

 sin(1*TAU/8) = 0,7071... // sqrt(2)/2
 

 грех(2*ТАУ/8) = 1
 

 sin(3*TAU/8) = 0,7071... // sqrt(2)/2
 

Интерактивный

Интерактивное изображение выше визуализирует геометрическое отношение синуса к единичной окружности. Нажмите и перетащите любую из двух контрольных точек, чтобы посмотреть изменение ввода и вывода. Ввод выделен красным цветом и представляет входной угол в радианах. Выход выделен синим цветом.

Пояснение

Функция синуса является частью группы тригонометрических функций, которые возвращают отношения, связанные с геометрией окружности. Функция синуса является одной из трех основных функций: синуса, косинуса и тангенса, которые принимают угол в качестве входных данных и возвращают отношение в качестве выходных данных. График функции синуса показан ниже, который демонстрирует возможный выход функции синуса для области до , где .