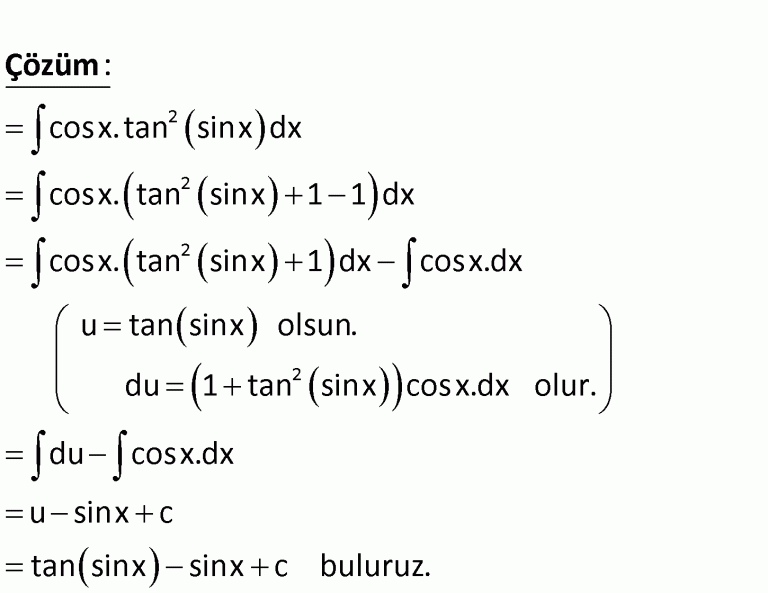§ 4. Интегрирование тригонометрических функций
1. Интегралы вида , где R— рациональная функция.
Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки tg(x/2) = t.
В результате этой подстановки имеем:
1472. Найти интеграл
Решение.
Подынтегральная функция рационально зависит от sin x и cos x; применим подстановку tg(x/2) = t, тогда и
Возвращаясь к старой переменной, получим
▲
1473. Найти интеграл
Решение.
Полагая tg(x/2) = t, получим
▲
Универсальная подстановка tg(x/2)=t во многих случаях приводит к сложным вычислениям, так как при ее применении sin x и соsx: выражаются через t в виде рациональных дробей, содержащих t2.
В некоторых частных случаях нахождение интегралов вида может быть упрощено.
1. Если R(sinx, cos x) —
нечетная функция относительно sinx, т. е. если R(—sin x, cosx)
=— R (sin x, cosx),
то интеграл рационализируется подстановкой cosx = t.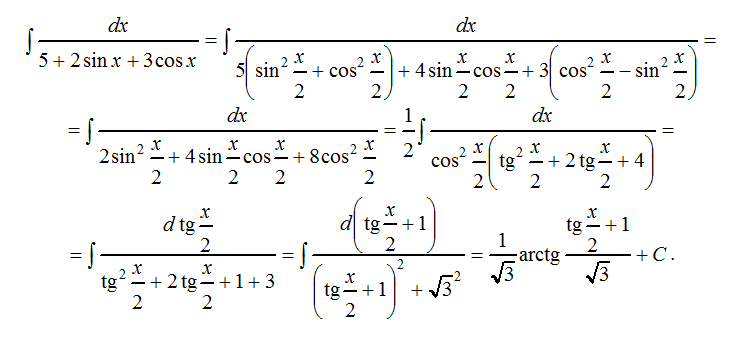
2. Если R(sinx, cosx)—нечетная функция относительно cosx, т. е. если R(sinx, —cosx) = —R (sin x, cos x), то интеграл рационализируется с помощью подстановки sin x = t.
3. Если R (sin x, cos x) — четная функция относительно sin x и cosx, т. е. если R(—sinx, — cosx) = R (sin x, cosx), то к цели приводит подстановка tgx = t.
1474. Найти интеграл
Решение. Так как подынтегральная функция нечетна относительно синуса, то полагаем cosx
Таким
образом,Следовательно
Отметим, что в рассматриваемом случае интеграл всегда может быть записан виде
▲
1475. Найти интеграл .
Решение.
Здесь подынтегральная функция является нечетной относительно косинуса. Поэтому применяем подстановку sinx = t; тогда cos2x= 1 — sin2 x = 1— t2
, cosxdx = dt. Следовательно,Так как
то
Окончательно получаем
Отметим,
что в рассматриваемом случае интеграл
всегда может быть записан в виде .
▲
1476. Найти интеграл
Решение.
Подынтегральная функция четна относительно синуса и косинуса. Полагаем tgx = t; тогда
Отсюда
,
Далее имеем
и, следовательно,
Заметим,
что нахождение интеграла можно упростить,
если в исходном интеграле разделить
числитель в знаменатель на cos
▲
2. Интегралы вида . Мы выделим здесь два случая, имеющие особенно важное значение.
С л у ч а й 1. По крайней мере одни из показателей т или n —нечетное положительное число.
Если п —
нечетное положительное число, то
применяется подстановка sinx=t;
если же т —
нечетное положительное число, —
подстановка cosx = t.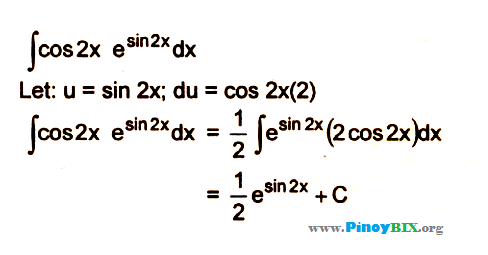
1477. Найти интеграл .
Решение.
Полагая sinx=t, cosxdx = dt, получим
▲
1478. Найти интеграл
Решение.
Имеем
Полагая cos x = t , — sin x dx = dt, получим
▲
С л у ч а й 2. Оба показателя степени т и n — четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью формул
, (1)
, (2)
. (3)
1479. Найти интеграл
Решение.
Из формулы (1) следует, что
Применив теперь формулу (2), получаем
.
Итак,
▲
1480. Найти интеграл
Решение. Используя формулу (3), получим
=
=
=
=
=
1481. Найти интеграл
Решение. Имеем
3. Интегралы вида tgm x dx и ctgm x dx, где m — целое положительное число.
При
нахождении таких интегралов применяется
формула tg 2 x = sec2 x —
1 (или ctg2 x = cosec2 x — 1), с
помощью которой последовательно
понижается степень тангенса или
котангенса.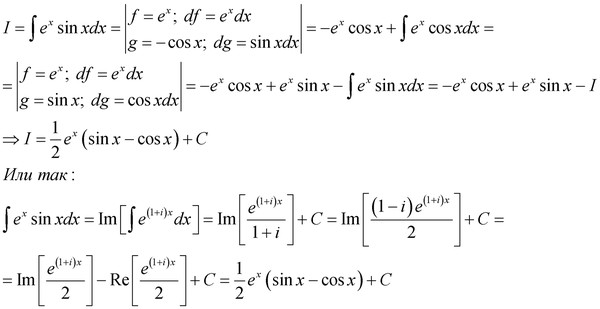
1482. Найти
интеграл
Решение. Имеем
1483. Найти интеграл
Решение. Имеем
=
=
4. Интегралы вида и , где п — четное положительное число. Такие интегралы находятся аналогично рассмотренным в п. 3 с помощью формулы
sec2x
1484. Найти интеграл.
Решение. Имеем
1459. Найти интеграл
Решение. Имеем
=
5.
Интегралы вида и .
Интегралы
от нечетной положительной степени
секанса или косеканса проще всего
находятся по рекуррентным формулам:
(1)
(2)
1460. Найти интеграл
Решение. Применяя рекуррентную формулу (2) при 2n+1=5, т. е. при n = 2, получим
полагая теперь 2n+1=3, т. е. n=1, по той же формуле имеем
нo
Следовательно,
Интегрирование тригонометрических выражений R(sinx,cosx)непарных по sinx — Мегаобучалка
Неопределенный интеграл
Если , то и , где — произвольная функция, имеющая непрерывную производную
Из определения интеграла следуют две важные формулы:
Интергирование по частям.
Примеры
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
для определённого:
Для неопределённого интеграла
Функции и гладкие, следовательно, возможно дифференцирование:
Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:
Операция интегрирования обратна дифференцированию:
После перестановок:
Примеры
Таблица интегралов
5. Рациональные дроби,правильные,не правильные,примеры
прав,не прав
Непр.—-выделяем целую часть +прав дробь(раскладываем на целую дробь)
Прав.
Дробь—-в знаменатели-раскладываем на множители—à
Примеры:
х=0
1=5А В=1/5,С=-4А
Рациональные дроби.Разложение.Метод неопределенных коэффициентов.
Разложение дроби
подынтегральной функции на простейшие дроби , все сводится к достаточно простым интегралам
Метод неопределенных коэффициентов
Разложить дробь на простейшие.
Решение:
Комбинированный метод определения коэффициентов разложения рациональных дробей
Найдем коэффициенты разложения комбинированным методом :
Таким образом,
Интегрирование дробей 3 типа
Для начала представляем неопределенный интеграл в виде суммы:
Первый интеграл берем методом подведения под знак дифференциала:
Поэтому,
У полученного интеграла преобразуем знаменатель:
Следовательно,
Формула интегрирования простейших дробей третьего типа принимает вид:
Пример.
Найдите неопределенный интеграл .
Используем полученную формулу:
Если бы у нас не было этой формулы, то как бы мы поступили:
- Интегрирование простейших дробей четвертого типа
Первый шаг – подводим под знак дифференциала:
Второй шаг – нахождение интеграла вида . Интегралы подобного вида находятся с использованием рекуррентных формул
Интегрирование тригонометрических примеров
находятся с помощью тригонометрических формул
11..Интегрирование тригонометрических примеров
n-нечетная
Если n-четная—> понижаем степень
|
Понижение степени
| |||||
|
Интегрирование тригонометрических выражений R(sinx,cosx)непарных по sinx
Специальные подстановки
1) Если R (-sin x, cos x) = -R (sin x, cos x), то рационализует подстановка cos x = t.
2) Если R (sin x, -cos x) = -R (sin x, cos x), то рационализует подстановка sin x = t.
3) Если R (-sin x, -cos x) = R (sin x, cos x), то рационализует подстановка tg x = t.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Интеграция продуктов и возможностей sinx и cosx
Результаты обучения
- Решение задач интеграции, связанных с продуктами и возможностями [latex]\sin{x}[/latex] и [latex]\cos{x}[/latex ]
Ключевая идея стратегии, используемой для интеграции комбинаций произведений и степеней [латекс]\sin{x}[/латекс] и [латекс]\cos{х}[/латекс], заключается в переписывании этих выражений в виде сумм и разностей.
{j}x\sin {x}dx[/латекс]. Переписав эти интегралы, мы вычисляем их с помощью 9{4}x\cos{x}dx[/латекс].
Показать раствор
Посмотрите следующее видео, чтобы увидеть работающее решение вышеизложенного. Попробуйте
Для субтитров откройте видео на исходной странице, щелкнув логотип Youtube в правом нижнем углу видеодисплея. На YouTube видео начнется с той же начальной точки, что и этот клип, но будет воспроизводиться до самого конца.
Вы можете просмотреть стенограмму этого сегментированного клипа «3.2 Тригонометрические интегралы» здесь (откроется в новом окне). 9{2}xdx[/латекс].
Показать раствор
Посмотрите следующее видео, чтобы увидеть работающее решение для описанного выше Попробуйте
.
Для субтитров откройте видео на исходной странице, щелкнув логотип Youtube в правом нижнем углу экрана видео. На YouTube видео начнется с той же начальной точки, что и этот клип, но будет воспроизводиться до самого конца.
Вы можете просмотреть стенограмму этого сегментированного клипа «3.2 Тригонометрические интегралы» здесь (откроется в новом окне). 9{2}\влево(3x\вправо)dx[/латекс].
Показать раствор
В некоторых областях физики, таких как квантовая механика, обработка сигналов и вычисление рядов Фурье, часто необходимо интегрировать продукты, которые включают [латекс]\sin\left(ax\right)[/latex], [ латекс]\sin\left(bx\right)[/latex], [латекс]\cos\left(ax\right)[/latex] и [латекс]\cos\left(bx\right)[/latex] .
Эти интегралы оцениваются путем применения тригонометрических тождеств, как указано в следующем правиле.
9Правило 1065: Интегрирование произведений синусов и косинусов разных углов /latex], [latex]\cos\left(ax\right)[/latex] и [latex]\cos\left(bx\right)[/latex], используйте замены
[латекс]\sin\ влево(ах\вправо)\sin\влево(bx\вправо)=\frac{1}{2}\cos\влево(\влево(a-b\вправо)x\вправо)-\frac{1}{2}\ cos\left(\left(a+b\right)x\right)[/latex]
[латекс]\sin\left(ax\right)\cos\left(bx\right)=\frac{1} {2}\sin\left(\left(a-b\right)x\right)+\frac{1}{2}\sin\left(\left(a+b\right)x\right)[/latex]
[латекс]\cos\left(ax\right)\cos\left(bx\right)=\frac{1}{2}\cos\left(\left(a-b\right)x\right)+\ frac{1}{2}\cos\left(\left(a+b\right)x\right)[/latex]
Эти формулы могут быть получены из формул суммы углов для синуса и косинуса.
Пример: вычисление [латекс]\displaystyle\int \sin\left(ax\right)\cos\left(bx\right)dx[/latex]
Вычисление [латекс]{\displaystyle\int}\sin\ влево(5x\вправо)\cos\влево(3x\вправо)dx[/латекс].