Системы счисления уравнения: Решите уравнение, найдите основание системы счисления – как решать

Карточка для практической работы по теме «Уравнения и системы счисления» | Учебно-методический материал по информатике и икт (8, 9, 10, 11 класс):

Опубликовано 22.05.2020 — 8:24 — Нестерова Оксана Александровна

В карточке подробно разобраны различные примеры решения уравнений в разных системах счисления. Далее ребятам предлагаются аналогичные задания для самостоятельного решения и напоследок подборка заданий на повторение предыдущих тем. Часть заданий взята с сайта Константина Юрьевича Полякова 

Скачать:

Предварительный просмотр:

Системы счисления

1. Изучите способы решения уравнений и законспектируйте в тетрадь все примеры

Пример 1

Решите уравнение 425+х=11223.Ответ запишите в четверичной системе счисления.

Решение:

Переведем все числа в десятичную систему счисления

1 0            3 2 1 0

425+х=11223

4*51+2*50+х=1*33+1*32+2*31+2*30

22+х=44

х=22

Переведем ответ из десятичной системы счисления в четверичную

22   4

20   5  4

  2   4  1

       1

х=1124

Ответ: 1124

Пример 2

Решите уравнение.  104х+20х=8410. Ответ запишите в двоичной системе счисления.

Решение:

Переведем все числа в десятичную систему счисления

 2 1 0     1 0

104х+20х=8410

1*х2+0*х1 + 4*х0+2*х1+0*х0=84

х2+2*х-80=0

х1=8,   х2=-10 (не подходит)

Переведем ответ из десятичной системы счисления в двоичную

х=8 = 10002

Ответ: 10002

Пример 3

В системе счисления с некоторым основанием десятичное число 47 записывается в виде 52. Укажите это основание.

Решение:

Пусть основание равно х

Составим уравнение:

52х=47

Решим это уравнение:

5*х1+2*х0=47

5х+2=47

х=9

Ответ: 9

Пример 4

Запись числа 658 в некоторой системе счисления выглядит так: 311N. Найдите основание системы счисления N.

Решение:

Составим уравнение:

311N=658

Решим это уравнение:

3*N2+1*N1+1*N0=6*81+5*80

3N2+N+1=53

3N2+N-52=0

D=12+4*3*52=625

x1=4

x2 не подходит, т.к.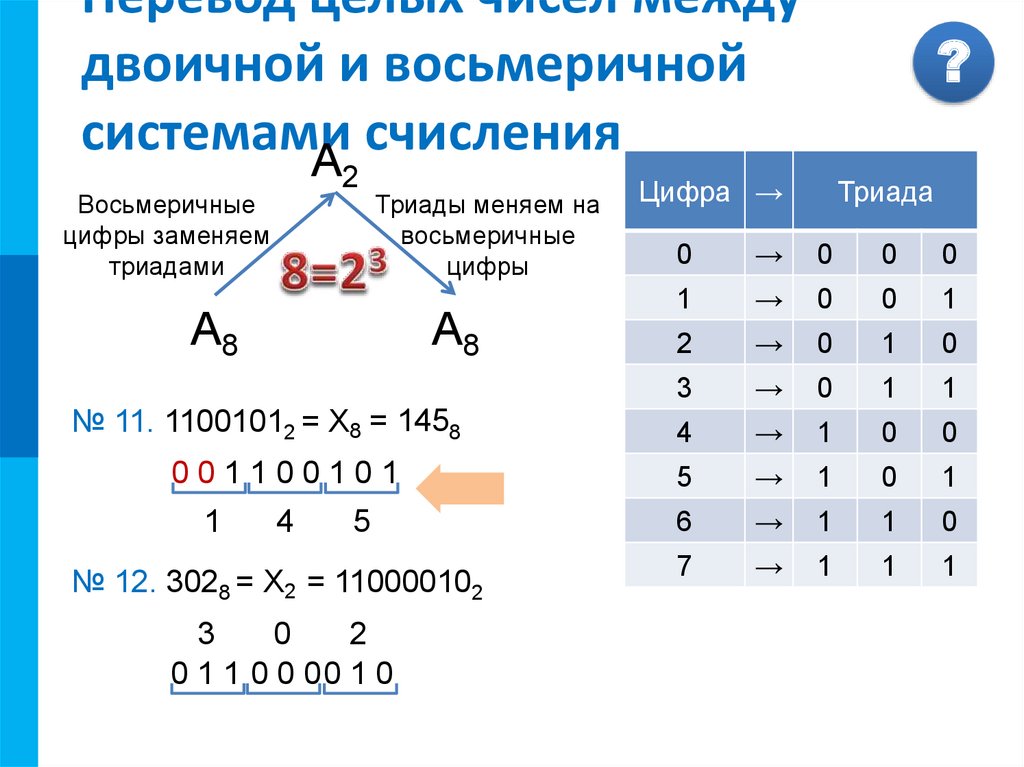 отрицательный

Ответ: 4

2. Решите уравнение 608+х=1207. Ответ запишите в шестеричной системе счисления.
3. Решите уравнение . Ответ запишите в троичной системе счисления.
4. В системе счисления с некоторым основанием десятичное число 12 записывается в виде 110. Укажите это основание.
5. Решите уравнение . Ответ запишите в шестеричной системе счисления.
6. В системе счисления с некоторым основанием десятичное число 49 записывается в виде 100. Укажите это основание.
7. Запись числа 578 в некоторой системе счисления выглядит так: 2DN. Найдите основание системы счисления N.
8. Решите уравнение . Ответ запишите в десятичной системе счисления.
9. Десятичное число 70 в некоторой системе счисления записывается как 64. Определите основание системы счисления.
10. Определите число N, для которого выполняется равенство 143N + 256 = 138N+1.
11. Запись числа 2B16 в некоторой системе счисления выглядит так: 111N. Найдите основание системы счисления N.
12. Известно, что X = 124 + 45 + 1012. Чему равно число X в десятичной системе счисления?
13. Выполните арифметические операции:

1. 72158-6768
2. D1C16+AF9516
3. 10111012·11002
4. 54148+4358
5. 101011002+1100012
6. B8D4F16-BA7616
7. 100101012-110001002

14. Перевести:

1. 10234=X7
2. 25417=X3

15. Вычислите сумму чисел x и y при x = D216, y = 378. Результат представьте в двоичной системе счисления.

По теме: методические разработки, презентации и конспекты

Практическая работа «Компьютерные словари и системы машинного перевода текста»

Практическая работа«Компьютерные словари и системы машинного перевода текста»1.       Открыть Электронный словарь на сайте www.ver-dict.ru или по выбору.2….

Инструктивная карточка к практической работе по теме «спирты»

Инструктивная карточка к практической работе по теме «свойства спиртов», 10 (11) класс, органическая химия. Данная карточка позволяет оптимизировать проведение практической работы по органической хими…

Проверочная работа по по теме «Системы счисления»

Проверочная работа по по теме «Системы счисления» предназначения для проверки знаний учащихся 9 классов. В работе  представлены  3 варианта….

Инструктивные карточки к практическим работам по химии

Представлены инструктивные карточки к практическим работам по химии за курс 8-11 класс….

Контрольная работа по теме «Информация. Системы счисления»

Материал контрольной работы в 2-х вариантах с ответами. Используются как тестовые задания, так и задания, требующие приведения решения….

инструктивная карточка к практической работе 9 класс

инструктивная карточка к практической работе 9 класс…

Практическая работа «Строение атома. Периодическая система химических элементов»

Задание1. Дать характеристику химическому элементу №39  по плану:Название, символ _______________________Порядковый номер______________________Атомная масса__________________________Ме, неМе, пер. ..

Поделиться:

 

Системы счисления. Подготовка к ЕГЭ

1. Подготовка к ЕГЭ: системы счисления

Автор: Мочалова Марина Владимировна,
учитель информатики
ГБОУ лицей №144 Калининского р-на
г.Санкт-Петербург
Задание 1 (Демо-2015, задание 4)
Сколько единиц в двоичной записи числа 519?
Вариант 1 (прямой перевод):
переводим число 519 в двоичную систему: 519 = 10000001112
Ответ: 4
Вариант 2 (разложение на сумму степеней двойки):
519 = 512 + 4 + 2 + 1 = 29 + 22 + 21 + 20
Ответ: 4
Вариант 3 (определение количества нечетных чисел при
последовательном делении на 2 исходного числа и
получаемых частных):
519 → 259 → 129 → 64 → 32 → 16 → 8 → 4 → 2 → 1
1
1
1
Ответ: 4
Проверь себя!
Задание 2 (http://ege.yandex.ru)
Сколько единиц в троичной записи десятичного числа 243?
Ответ: 1
Задание 3 (http://ege.yandex. ru)
Сколько единиц в двоичной записи десятичного числа 242?
Ответ: 6
Задание 4 (http://ege.yandex.ru)
Сколько единиц в троичной записи десятичного числа 242?
Ответ: 0
Задание 5 (http://ege.yandex.ru)
Даны 4 числа, они записаны с использованием различных систем счисления. Укажите
среди этих чисел то, в двоичной записи которого содержится ровно 5 единиц. Если
таких чисел несколько, укажите наибольшее из них.
1) 1510
2) 778
3) 3458
4) FA16
Решение:
Для решения задачи необходимо перевести в двоичную систему счисления все числа.
Первое число переводим любым методом, поскольку оно небольшое. Например,
разложим его на сумму степеней двойки:
15 = 8 + 4 +2 + 1 =23 + 22 +21 + 20 = 11112
Три следующих числа переводим, используя таблицы соответствия двоичнойвосьмиричной и двоичной-шестнадцатиричной (таблицы соответствия систем
счисления, родственных двоичной).
778 = 111 1112
3458 = 11 100 1012
FA16 = 1111 10102
Как видим, два числа имеют в двоичной системе счисления 5 единиц – число 1510 =
11112 и число 3458 = 11 100 1012. В нашем случае в ответе требуется указать
наибольшее из них – это число 3458
Ответ: 3)
Проверь себя!
Задание 6
Даны 4 числа, они записаны с использованием различных систем счисления.
Укажите среди этих чисел то, в двоичной записи которого содержится ровно
4 единицы. Если таких чисел несколько, укажите наибольшее из них.
1) 1410
2) 3418
3) 718
4) F716
Ответ: 2)
Задание 7
Даны 4 числа, они записаны с использованием различных систем счисления.
Укажите среди этих чисел то, в двоичной записи которого содержится ровно
6 единиц. Если таких чисел несколько, укажите наибольшее из них.
1) FA16
2) 2510
3) 3458
4) 778
Ответ: 1)
Задание 8
Даны 4 числа, они записаны с использованием разных систем счисления.
Укажите среди них то число, двоичная запись которого содержит ровно
шесть «1». Если таких чисел несколько, укажите наибольшее из них.
1)6310*410
2)3338
3)F816 + 110
4)111001112
Ответ: 1)
Задание 9 (ФИПИ, открытый банк заданий)
Укажите наибольшее основание системы счисления, в
которой запись числа 15 имеет ровно 3 значащих разряда.
Решение:
Поскольку по условию задачи запись числа 15 в системе
счисления с основанием р имеет три значащих разряда, то
можно записать
100р ≤ 15 < 1000р или р2≤ 15<р3
Решаем первую часть неравенства: р2≤ 15. Получаем: р < 4.
Поскольку имеем строгое неравенство, ответом не может
быть р=4. Поэтому ответом будет р=3.
Проверяем вторую часть неравенства для р=3:
р3 > 15
33>15
27>15
Ответ: 3
Проверь себя!
Задание 10 (ФИПИ, открытый банк заданий)
Укажите наименьшее основание системы счисления, в которой
запись числа 19 имеет ровно 3 значащих разряда. (3)
Задание 11
Укажите наименьшее основание системы счисления, в которой
запись числа 65 имеет ровно 3 значащих разряда.
Ответ: 5
Задание 12
Укажите наименьшее основание системы счисления, в которой
запись числа 130 имеет ровно 4 значащих разряда.
Ответ: 5
Задание 13
Укажите наименьшее основание системы счисления, в которой
запись числа 65 имеет ровно 3 значащих разряда.
Ответ: 5
Задание 14 (ФИПИ открытый банк заданий)
Укажите наименьшее основание системы счисления, в которой
запись числа 97 имеет ровно 3 значащих разряда.
Ответ: 6
Задание 15 (ФИПИ открытый банк заданий)
В системе счисления с некоторым основанием десятичное число
16 записывается как 100. Укажите это основание
Решение:
Запишем условие задачи: 16 = 100р (р – искомое основание
системы счисления).
Решаем уравнение: 16 = р2 и получаем р=4
Ответ: 4
Задание 16
Десятичное число 65 в некоторой системе счисления
записывается как 230. Определите основание системы
счисления.
Решение
По условию задачи: 65 = 230р, где р – искомое основание
системы счисления.
Представим это равенство в десятичной системе счисления:
65 = 2*р2 + 3*р
Получаем квадратное уравнение 2р2 + 3р — 65 = 0
Находим его корни, учитывая, что основание системы
счисления р – натуральное число (p>=2).
Получаем р=5.
Ответ: 5
Проверь себя!
Задание 17
В системе счисления с некоторым основанием десятичное число 26 записывается
как 101. Укажите это основание.
Ответ: 5
Задание 18
В системе счисления с некоторым основанием десятичное число 27 записывается
как 1000. Укажите это основание.
Ответ: 3
Задание 19
В системе счисления с некоторым основанием десятичное число 37записывается
как 101. Укажите это основание.
Ответ: 6
Задание 20
В системе счисления с некоторым основанием десятичное число 37 записывается
как 123. Укажите это основание.
Ответ: 5
Задание 21
Решите уравнение 1D16 + 728 = X2. Основание системы
счисления в ответе не указывать.
Решение
Как видно из условия, все числа в задании представлены в
системах счисления, родственных двоичной (8-ричной и 16ричной).
Искомое число записано в двоичной системе счисления,
поэтому для решения нужно все числа записать в двоичной
системе счисления, затем выполнить их сложение.
1D16 = 111012
728 =1110102
Собирая всё в одно уравнение, получаем
X2 = 111012 +1110102
Выполняем сложение, получаем результат: X2 =10101112
Ответ: 1010111
Задание 22
Решите уравнение 121x + 1 = 1017 . Ответ дайте в троичной
системе счисления.
Решение
Переведём все числа в десятичную систему счисления:
121х = 1·х2 + 2·х + 1
1017 = 1·72 + 0·71 +1·70=50
Собираем всё в одно уравнение, получаем
х2 + 2х + 1 +1 + 50
х2 + 2х – 48 = 0
Это уравнение имеет два решения, х=6 и х= -8; основание
системы счисления – натуральное число, поэтому ответ х= 6
Переводим ответ в троичную систему: 6 = 2·31 = 203.
Ответ: 203
Проверь себя!
Задание 23
Решите уравнение 425 + x = 11234. Ответ дайте в
шестиричной системе счисления. Основание системы
счисления не указывать.
Ответ: 153
Задание 24
Решите уравнение 123 + 12x = 128
Ответ: 3
Задание 25
Решите уравнение 1007 + x = 2305
Ответ: 16
Задание 26
Решите уравнение 215 + 113 = 120x
Ответ: 3
Задание 27
Найдите наименьшие значения x и y, при которых существует
равенство 147 + x = 14y. Ответ запишите в троичной системе
счисления через запятую. Основание системы счисления
указывать не нужно.
Решение:
1)запишем равенство в десятичной системе счисления:
1*7 + 4 + х = y + 4
11 + x = y + 4
2) Из условия следует, что y>=5 (т.к. число 14y в системе
счисления с основанием у содержит значащие цифры 1 и 4).
Минимальное значение уmin = 5.
3) Минимальное значение хmin получается при минимальном
значении уmin .
4) При уmin=5 получаем хmin=2 .
5) Переводим 2 и 5 в троичную систему счисления: 2 =23 5=123.
Ответ: 2,12
Проверь себя!
Задание 28
Решите уравнение 425 + x = 11234 Ответ дайте в
шестиричной системе счисления. основание системы
счисления не указывать.
Ответ: 153
Задание 29
Решите уравнение 123 + 12x = 128
Ответ: 3
Задание 30
Решите уравнение 1007 + x = 2305
Ответ: 16
Задание 31
Решите уравнение 215 + 113 = 120x
Ответ: 3
Задание 32
Даны числа а = 9216 и b = 2248. Для какого двоичного числа с
выполняется неравенство a<c<b?
1) 10010011 2) 10001110
3) 10001010
4) 10001100
Решение: необходимо все числа перевести в одну и ту же систему
счисления.
Вариант 1 (через десятичную систему счисления):
а=9*16+2=146 b=2*64+2*8+4=148
1) 147 2) 142
3) 138
4) 135
Находим значение с, лежащее в интервале от а до b.
Ответ: 1)
Вариант 2 (через двоичную систему счисления):
а=100100102 b=100101002
Находим значение с, лежащее в интервале от а до b.
Ответ: 1)
Решать задачу через переводы чисел в восьмиричную или
шестнадцатиричную системы счисления – нерационально, хотя для
любителей оных – пожалуйста!
Проверь себя!
Задание 33 – (ФИПИ)
Даны числа а = 3D16 и b = 778. Для какого двоичного числа с
выполняется неравенство a<c<b?
1) 111101
2) 111110
3) 111111
4) 111010
Ответ: 2)
Задание 34 – (ФИПИ)
Даны числа а = 5D16 и b = 1378. Для какого двоичного числа с
выполняется неравенство a<c<b?
1) 1011110
2) 1001101
3) 1001111
4)
1011100
Ответ: 1)
Задание 35
Даны числа а = 8B16 и b = 2158. Для какого двоичного числа с
выполняется неравенство a<c<b?
1) 10010011 2) 10001100
3) 10001010
4) 10001100
Ответ: 2)
Задание 36 (http://ege. yandex.ru)
Сколько есть систем счисления, в которых запись числа 22 оканчивается
на 2?
Решение:
по условию число 22 в некоторой системе счисления с основанием р
оканчивается на 2, значит, его можно записать в виде 22 = k*p + 2, где k
=1,2,3,… Получаем k*p = 20, т.е. значения р являются делителями числа 20.
Это числа 4,5,10,20, всего их 4.
Ответ: 4
Задание 37 (ФИПИ)
Укажите в порядке возрастания все основания систем счисления, в
которых запись числа 22 оканчивается на 4?
Решение:
по условию число 22 в системах счисления с основанием р должно
оканчиваться на 4, значит, его можно записать в виде 22 = k*p + 4, где k
=1,2,3,… Получаем k*p = 18, т.е. значения р являются делителями числа 18.
Это числа 2,3,6,9,18, всего их 5. Но в двоичной и троичной системах счисления
нет цифры 4. Значит, ответом будут три основания р=6, р=9 и р=18
Ответ: 6,9,18
Задание 38 — http://ege.yandex.ru
В системах счисления с основанием р запись числа 77
оканчивается на 0, а запись числа 29 – на 1. Чему равно это
число?
Решение:
1)поскольку число 77 в р-ричной системе счисления
оканчивается на 0, то основание р является делителем числа
77, т.е. возможны значения р=7, р=11, р=77
2) поскольку число 29 в р-ричной системе счисления
оканчивается на 1, то основание р является делителем числа
28, т.е. возможны значения р=2, р=4, р=7, р=14, р=28
3)общим основанием для обоих чисел является р=7
Ответ: 7
Проверь себя!
Задание 39 (ФИПИ)
Укажите в порядке возрастания все основания систем
счисления, в которых запись числа 24 оканчивается на 3?
Ответ: 7,21
Задание 40 (ФИПИ)
Сколько существует систем счисления, в которых запись
числа 71 оканчивается на 7?
Ответ: 4
Задание 41 (ФИПИ)
Сколько существует систем счисления, в которых запись
числа 28 оканчивается на 4?
Ответ: 4

Натуральные, Целые, Рациональные, Иррациональные, Действительные и т. д.

Натуральные числа

Натуральные (или считая ) Числа равны 1,2,3,4,5 и т. д. много натуральных чисел. Набор натуральных чисел {1,2,3,4,5,…}, иногда пишется N для краткости.

целых чисел являются натуральными числами вместе с 0.

(Примечание: некоторые учебники не согласны и говорят, что натуральные числа включают 0.)

Сумма любые два натуральных числа также являются натуральным числом (например, 4+2000=2004), а произведение любых двух натуральных чисел — натуральное число (4×2000=8000). Этот однако это неверно для вычитания и деления.

Целые числа

целых чисел представляют собой набор действительных чисел, состоящий из натуральных чисел, их аддитивных инверсий и нуля.

{…,−5,−4,−3,−2,−1,0,1,2,3,4,5,…}

Набор целых чисел иногда написано J или Z для краткости.

сумма, произведение и разность любых двух целых чисел также являются целыми числами. Но это неверно для деления… просто попробуйте 1÷2.

Рациональные числа

рациональных чисел те числа, которые могут быть выражены как отношение между два целых числа. Например, дроби 13 и −11118 равны рациональное число. Все целые числа входят в число рациональных, так как любое целое число z может быть записано как отношение z1.

Все десятичные дроби, которые заканчиваются, являются рациональными числами (поскольку 8.27 можно записать как 827100). которые имеют повторяющийся шаблон после некоторого момента, также являются рациональными: например,

0,0833333….=112.

Множество рациональных чисел замкнуто относительно всех четырех основных операций, то есть для любых двух рациональных чисел их сумма, разность, произведение и частное также являются рациональными числами (если мы не делим на 0).

Иррациональные числа

Иррациональное число — это число, которое нельзя записать в виде отношения (или дроби). В десятичной форме оно никогда не заканчивается и не повторяется. древние греки обнаружили, что не все числа рациональны; там уравнения, которые нельзя решить, используя отношения целых чисел.

Первое такое уравнение для изучения было 2=x2. какая число, умноженное на себя, равно 2?

2 есть около 1,414, потому что 1,4142=1,999396, что близко к 2. Но вы никогда не попадете точно в квадрат дроби (или десятичный). Квадратный корень из 2 является иррациональным числом, т. десятичный эквивалент продолжается вечно, без повторяющегося шаблона:

2=1.41421356237309…

Другие известные иррациональные числа золотое сечение , число с большим значение для биологии:

1+52=1,61803398874989…

π (пи), отношение длины окружности к ее диаметру:

π=3,14159265358979…

и e, самое важное число в исчислении:

e=2,71828182845904…

Иррациональные числа могут быть далее подразделены на алгебраических чисел, которые являются решениями некоторых полиномиальных уравнений (таких как 2 и золотое сечение), и трансцендентных чисел, которые не являются решениями ни одного полиномиального уравнения.

π и e оба трансцендентны.

Вещественные числа

Вещественные числа — это набор чисел, содержащий все рациональные числа и все иррациональные числа. Настоящие числа — это «все числа» на числовой прямой. Существует бесконечно много действительных чисел, так же как бесконечно много чисел в каждом из других наборов чисел. Но можно доказать, что бесконечность действительных чисел равна 9.0005 больше бесконечность.

«Меньший», или исчисляемых бесконечностей целых чисел и рациональные числа иногда называют ℵ0 (алеф-ноль), и бесчисленных бесконечностей реалов называется ℵ1 (алеф-один).

Есть еще «большие» бесконечности, но для этого вам нужно пройти курс теории множеств!

Комплексные числа

Комплексные числа множество {a+bi | a и b — действительные числа}, где i — мнимая единица, −1. (нажмите здесь для подробнее о мнимых числах и операциях с комплексными числами).

Комплексные числа включают множество действительных чисел. Действительные числа в сложной системе записываются в виде a+0i=a. реальное число.

Этот набор иногда пишется как C для краткости. Набор комплексных чисел важно, потому что для любого многочлена p(x) с вещественными коэффициентами все решения p(x)=0 будут в C .

Beyond…

Есть наборы и побольше числа, которыми пользуются математики. кватернионов , открытые Уильямом Х. Гамильтоном в 1845 году, образуют систему счисления с тремя разные воображаемые единицы!

Системы счисления – определение, типы систем счисления, правила преобразования

Системы счисления – это системы в математике, которые используются для выражения чисел в различных формах и понимаются компьютерами. Число — это математическое значение, используемое для подсчета и измерения объектов, а также для выполнения арифметических вычислений. Числа имеют различные категории, такие как натуральные числа, целые числа, рациональные и иррациональные числа и так далее.

Точно так же существуют различные типы систем счисления, которые имеют разные свойства, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления.

В этой статье мы рассмотрим различные типы систем счисления, которые мы используем, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Мы изучим преобразования между этими системами счисления и решим примеры для лучшего понимания концепции.

1.	Что такое системы счисления?
2.	Типы систем счисления
3.	Двоичная система счисления
4.	Восьмеричная система счисления
5.	Десятичная система счисления
6.	Шестнадцатеричная система счисления
7.	Правила преобразования систем счисления
8.	Часто задаваемые вопросы о системах счисления

Что такое системы счисления?

Система счисления — это система представления чисел. Ее также называют системой счисления, и она определяет набор значений для представления количества. Эти числа используются как цифры, и наиболее распространенными из них являются 0 и 1, которые используются для представления двоичных чисел. Цифры от 0 до 9 используются для представления других типов систем счисления.

Системы счисления Определение

Система счисления определяется как представление чисел с помощью последовательного использования цифр или других символов. Значение любой цифры в числе может быть определено цифрой, ее положением в числе и основанием системы счисления. Числа представлены уникальным образом и позволяют нам выполнять арифметические операции, такие как сложение, вычитание и деление.

Типы систем счисления

Существуют различные типы систем счисления, в которых четыре основных типа следующие.

• Двоичная система счисления (основание — 2)
• Восьмеричная система счисления (основание — 8)
• Десятичная система счисления (основание — 10)
• Шестнадцатеричная система счисления (основание — 16)

Мы подробно изучим каждую из этих систем одну за другой после изучения следующей схемы системы счисления.

Таблица системы счисления

Ниже приведена таблица основных четырех типов системы счисления, которые мы используем для представления чисел.

Двоичная система счисления

В двоичной системе счисления используются только две цифры: 0 и 1. Числа в этой системе имеют основание 2. Цифры 0 и 1 называются битами, а 8 битов вместе составляют байт. Данные в компьютерах хранятся в виде битов и байтов. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее. Например: 10001 ₂ , 111101 ₂ , 1010101 ₂ — некоторые примеры чисел в двоичной системе счисления.

Восьмеричная система счисления

Восьмеричная система счисления использует восемь цифр: 0,1,2,3,4,5,6 и 7 с основанием 8. Преимущество этой системы в том, что в ней меньше цифр по сравнению с некоторыми другими системами, поэтому , было бы меньше вычислительных ошибок. Такие цифры, как 8 и 9, не входят в восьмеричную систему счисления. Как и двоичная, в миникомпьютерах используется восьмеричная система счисления, но с цифрами от 0 до 7. Например: 35

8 , 23 ₈ , 141 ₈ — некоторые примеры чисел в восьмеричной системе счисления.

Десятичная система счисления

Десятичная система счисления использует десять цифр: 0,1,2,3,4,5,6,7,8 и 9 с базовым числом 10. Десятичная система счисления — это система, которую мы обычно используем для представления чисел. в реальной жизни. Если какое-либо число представлено без основания, это означает, что его основание равно 10. Например: 723 ₁₀ , 32 ₁₀ , 4257 ₁₀ — некоторые примеры чисел в десятичной системе счисления.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления использует шестнадцать цифр/алфавитов: 0,1,2,3,4,5,6,7,8,9 и A,B,C,D,E,F с базовым числом 16. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Эта система используется в компьютерах для сокращения больших строк двоичной системы. Например, 7B3 ₁₆ , 6F ₁₆ , 4B2A ₁₆ — некоторые примеры чисел в шестнадцатеричной системе счисления.

Правила преобразования систем счисления

Число может быть преобразовано из одной системы счисления в другую с помощью формул системы счисления. Подобно тому, как двоичные числа могут быть преобразованы в восьмеричные числа и наоборот, восьмеричные числа могут быть преобразованы в десятичные числа и наоборот, и так далее. Давайте посмотрим, какие шаги необходимы для преобразования систем счисления.

Шаги для преобразования двоичной системы счисления в десятичную

Чтобы преобразовать число из двоичной в десятичную систему, мы используем следующие шаги.

• Шаг 1: Умножьте каждую цифру данного числа, начиная с самой правой, на показатели степени основания.
• Шаг 2: Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз, когда мы движемся справа налево.
• Шаг 3: Упростите каждый из вышеперечисленных продуктов и добавьте их.

Давайте разберемся с шагами с помощью следующего примера, в котором нам нужно преобразовать число из двоичной в десятичную систему счисления.

Пример: Преобразуйте 100111 ₂ в десятичную систему.

Решение:

Шаг 1: Определите основание данного числа. Здесь основание 100111 ₂ равно 2.

Шаг 2: Умножьте каждую цифру данного числа, начиная с самой правой, на показатели степени основания. Показатели должны начинаться с 0 и увеличиваться на 1 каждый раз, когда мы движемся справа налево. Поскольку основание здесь равно 2, мы умножаем цифры данного числа на 2 ⁰ , 2 ¹ , 2 ² и так далее справа налево.

Шаг 3: Мы просто упрощаем каждый из вышеперечисленных продуктов и добавляем их.

Здесь сумма является числом, эквивалентным данному числу в десятичной системе счисления. Или мы можем использовать следующие шаги, чтобы упростить этот процесс.

100111 = (1 × 2 ⁵ ) + (0 × 2 ⁴ ) + (0 × 2 ³ ) + (1 × 2 ² ) + (1 × 2 ¹ ) + (1 × 2 ⁰ )

= (1 × 32) + (0 × 16) + (0 × 8) + (1 × 4) + (1 × 2) + (1 × 1) )

= 32 + 0 + 0 + 4 + 2 + 1

= 39

Таким образом, 100111 ₂ = 39 ₁₀ .

Преобразование десятичной системы счисления в двоичную/восьмеричную/шестнадцатеричную систему счисления

Чтобы преобразовать число из десятичной системы счисления в двоичную/восьмеричную/шестнадцатеричную систему счисления, мы используем следующие шаги. Пошагово показано, как преобразовать число из десятичной системы в восьмеричную.

Пример: Преобразовать 4320 ₁₀ в восьмеричную систему.

Решение:

Шаг 1: Определите основание нужного числа. Поскольку мы должны преобразовать данное число в восьмеричную систему, основание искомого числа равно 8.

Шаг 2: Разделите данное число на основание требуемого числа и запишите частное и остаток в форма частно-остатка. Повторяем этот процесс (снова деля частное на основание), пока не получим частное меньше основания.

Шаг 3: Данное число в восьмеричной системе счисления получается простым чтением всех остатков и последнего частного снизу вверх.

Следовательно, 4320 ₁₀ = 10340 ₈

Преобразование из одной системы счисления в другую

Чтобы преобразовать число из одной из двоичных/восьмеричных/шестнадцатеричных систем в одну из других систем, мы сначала преобразуем его в десятичную систему, а затем мы преобразуем его в требуемые системы, используя вышеупомянутые процессы.

Пример: Преобразовать 1010111100 ₂ в шестнадцатеричную систему.

Решение:

Шаг 1: Преобразуйте это число в десятичную систему счисления, как описано выше.

Таким образом, 1010111100 ₂ = 700 ₁₀ → (1)

Шаг 2: Преобразуйте вышеуказанное число (которое находится в десятичной системе) в требуемую систему счисления (шестнадцатеричную).

Здесь мы должны преобразовать 700 ₁₀ в шестнадцатеричной системе, используя вышеупомянутый процесс.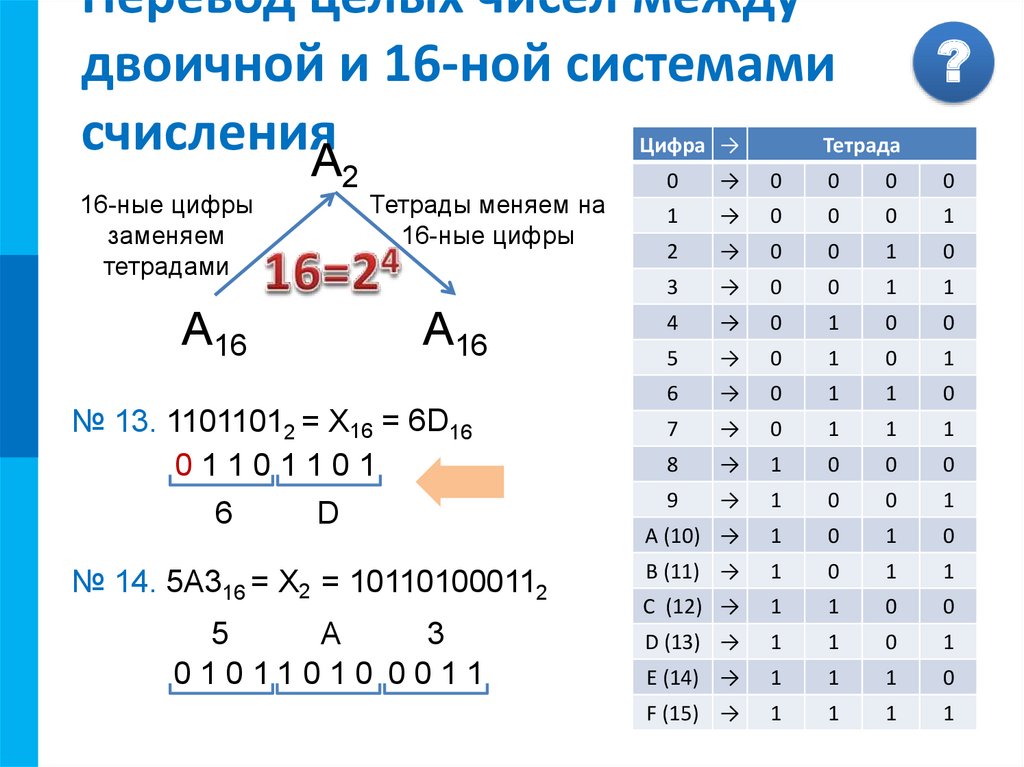 Следует отметить, что в шестнадцатеричной системе числа 11 и 12 записываются как B и C соответственно.

Таким образом, 700 ₁₀ = 2BC ₁₆ → (2)

Из уравнений (1) и (2) 1010111100 ₂ = 2BC 6 1 ☛ Похожие статьи

• Индийская система счисления
• Международная система счисления
• Двоичный калькулятор
• Преобразование двоичного кода в восьмеричный
• Восьмеричное в двоичное
• Преобразование десятичного числа в двоичное
• Двоичный код в десятичный
• Десятичный в шестнадцатеричный
• Шестнадцатеричный код в десятичный

Часто задаваемые вопросы о системах счисления

Что такое системы счисления с примерами?

Система счисления — это система записи или выражения чисел. В математике числа представлены в заданном наборе с помощью цифр или символов определенным образом. Каждое число имеет собственное уникальное представление, и числа также могут быть представлены в арифметической и алгебраической структуре. Существуют различные типы систем счисления, которые имеют разные свойства, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Некоторые примеры чисел в разных системах счисления: 10010 ₂ , 234 ₈ , 428 ₁₀ и 4BA ₁₆ .

Какие существуют 4 типа систем счисления?

Существует четыре основных типа систем счисления:

• Двоичная система счисления (основание — 2)
• Восьмеричная система счисления (основание — 8)
• Десятичная система счисления (основание — 10)
• Шестнадцатеричная система счисления (основание — 16)

Каковы правила преобразования систем счисления?

Чтобы преобразовать число из двоичной/восьмеричной/шестнадцатеричной системы счисления в десятичную систему счисления, мы используем следующие шаги:

• Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени основания.
• Показатель степени должен начинаться с 0 и увеличиваться на 1 при каждом движении справа налево.
• Упростите каждый из вышеперечисленных продуктов и добавьте их.

Чтобы преобразовать число из десятичной системы в двоичную/восьмеричную/шестнадцатеричную систему, мы используем следующие шаги:

• Разделите данное число на основание требуемого числа и запишите частное и остаток в «частном- форма «остаток».
• Повторяем этот процесс (снова деля частное на основание), пока не получим частное меньше основания.
• Данное число в десятичной системе счисления получается простым чтением всех остатков и последнего частного снизу вверх.

Чтобы преобразовать число из одной из двоичных/восьмеричных/шестнадцатеричных систем в одну из других систем:

• Сначала мы преобразуем его в десятичную систему.
• Затем конвертируем в нужную систему.

Каково использование каждой системы счисления?

Каждая система счисления предназначена для разных целей, например:

• Двоичная система счисления используется для хранения данных в компьютерах.
• Преимущество восьмеричной системы счисления состоит в том, что в ней меньше цифр по сравнению с некоторыми другими системами счисления, следовательно, будет меньше вычислительных ошибок.
• Десятичная система счисления — это система, которую мы используем в повседневной жизни.
• Шестнадцатеричная система счисления используется в компьютерах для сокращения больших строк двоичной системы счисления.

В чем важность систем счисления?

Системы счисления помогают представлять числа в небольшом наборе символов. Двоичные числа в основном используются в компьютерах, которые используют такие цифры, как 0 и 1, для вычисления простых задач. Системы счисления также помогают преобразовать одну систему счисления в другую.

Как классифицируются системы счисления?

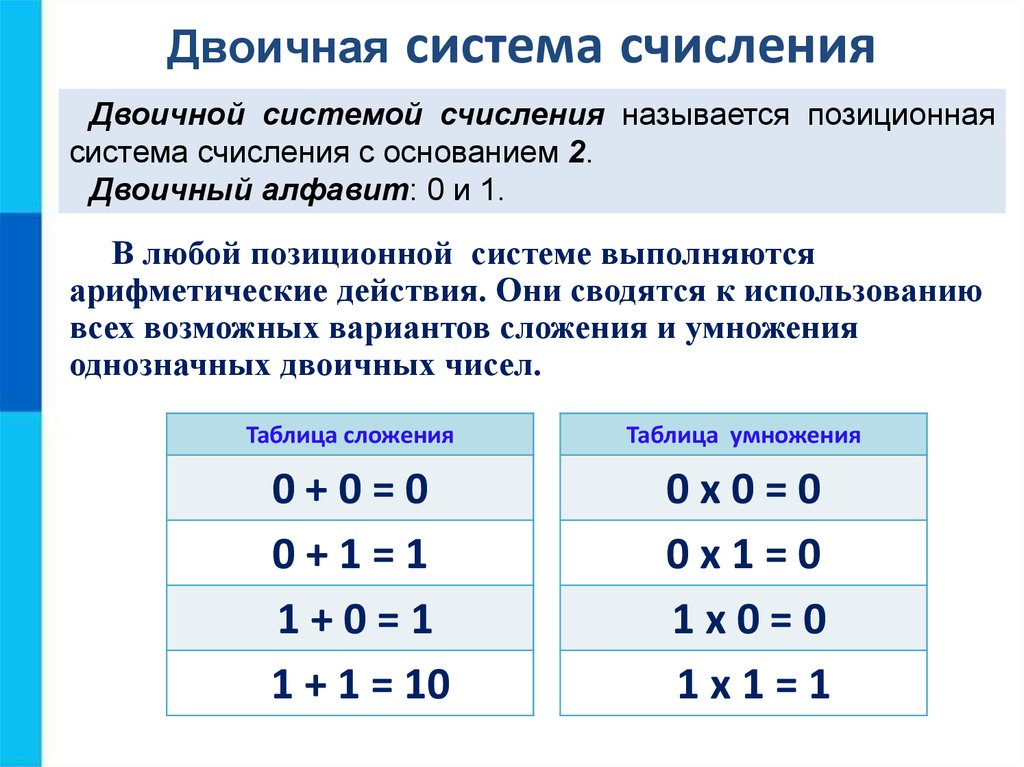
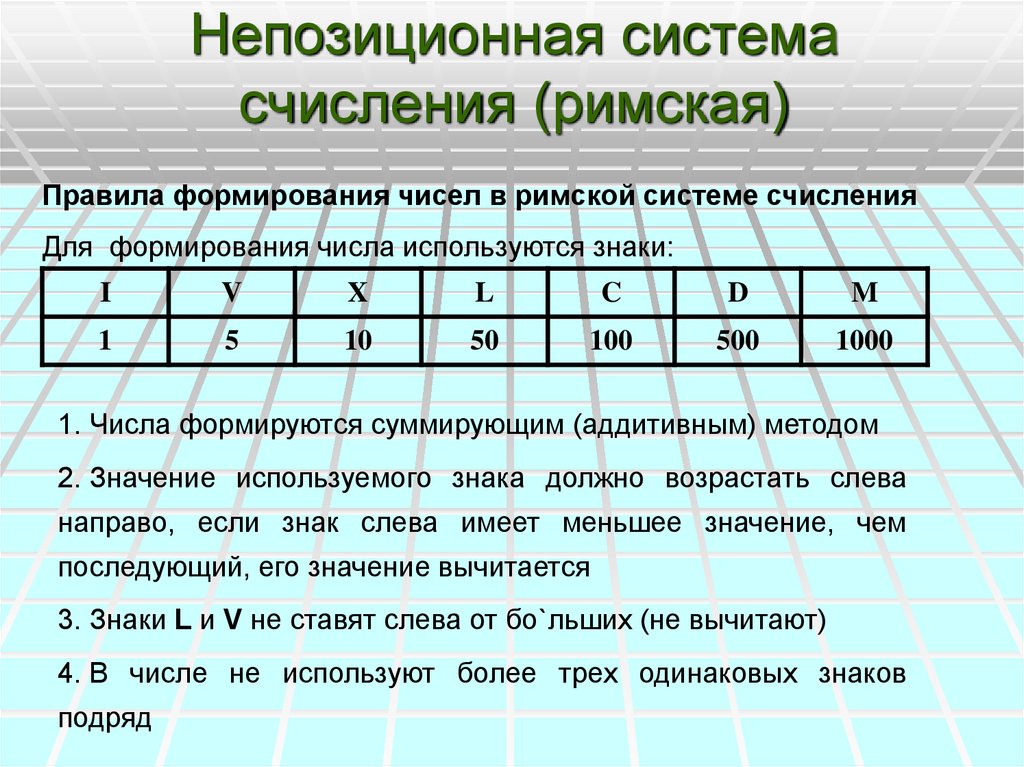
Системы счисления можно разделить в основном на две категории: позиционные и непозиционные системы счисления. В позиционных системах счисления каждая цифра связана с весом, и ее примерами являются двоичные, восьмеричные, десятичные и т.