Скалярное произведение векторов формулы: Скалярное произведение векторов, формулы и онлайн калькуляторы

{2}$ и называется скалярный квадрат.

3  Если $\overline{a} \neq \overline{0}$, то

4  Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.

5  $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$

6  $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$

7  $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$

Если векторы $\overline{a}$ и $\overline{b}$ заданы своими координатами: $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ , то их скалярное произведение вычисляется по формуле:

1

$(\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}$

Определение

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат. {\circ}$$

Читать дальше: векторное произведение векторов.

Умножение векторов, формулы и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Векторы Умножение векторов

Для векторов существует три вида умножения векторов: скалярное и векторное произведение двух векторов и смешанное произведение трех векторов. Результатом первого и последнего есть число, а результатом векторного произведения – вектор.

Скалярное умножение векторов

Замечание. Если один из векторов нулевой, то скалярное произведение равно нулю.

Замечание. Из определения скалярного произведения получаем, что угол (а точнее его косинус) между векторами-сомножителями вычисляется по формуле:

   

Скалярное произведение вектора на самого себя называется скалярным квадратом и обозначается .

Скалярный квадрат вектора равен квадрату его модуля:

   

Тогда длина вектора может быть найдена по формуле:

   

Скалярное произведение двух векторов положительно, если угол между векторами острый; и отрицательно, если угол тупой.

Критерий ортогональности векторов. Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, то есть когда эти векторы ортогональны (перпендикулярны):

   

Если векторы и заданы своими координатами, то их скалярное произведение равно сумме произведений соответствующих координат:

   

Векторное умножение векторов

Замечание. Таким образом, длина (модуль) вектора численно равна площади параллелограмма, построенного на векторах и :

   

Критерий коллинеарности векторов. Два вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулю:

   

Если векторы и заданы своими координатами в пространстве, то их векторное произведение определяется формулой:

   

Смешанное умножение векторов

Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами :

   

Критерий компланарности векторов. Если три вектора компланарны, то их смешанное произведение равно нулю.

Если векторы заданы в пространстве своими координатами: , то их смешанное произведение можно вычислить по формуле:

   

Понравился сайт? Расскажи друзьям!

Скалярный продукт — исчисление 3

Все ресурсы исчисления 3

6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая

1 2 3 4 5 6 7 8 9 … 17 18 Следующая →

Исчисление 3 Помощь » Векторы и векторные операции » Скалярный продукт

Вычислите скалярный продукт между , и .

Возможные ответы:

Правильный ответ:

Объяснение:

Все, что нам нужно сделать, это умножить подобные компоненты.

Сообщить об ошибке

Вычислить скалярное произведение , и .

Возможные ответы:

Правильный ответ:

Объяснение:

Все, что нам нужно сделать, это перемножить одинаковые компоненты и сложить их вместе.

Сообщить об ошибке

Найдите скалярное произведение следующих векторов:

Возможные ответы:

Правильный ответ:

Объяснение:

, чтобы найти точечный продукт между двумя векторами

Мы рассчитываем

Таким образом, для

Мы имеем

. Отчет о ошибке

Что на длину по длине по поводу вектора.

?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина  равна:

Сообщить об ошибке

Найдите скалярное произведение следующих векторов:

Возможные ответы:

Правильный ответ:

Объяснение:

, чтобы найти точечный продукт между двумя векторами

Мы рассчитываем

Таким образом, для

Мы имеем

. Отчет о ошибке

Что на длину по длине по поводу вектора.

?

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина  равна:

Сообщить об ошибке

Какое из следующих утверждений нельзя использовать в качестве определения скалярное произведение двух векторов с действительным знаком?

Возможные ответы:

Все они могут быть использованы

, где  это угол между .

Правильный ответ:

Объяснение:

 неверно. Это говорит о том, что нужно сложить вместе все компоненты двух векторов. Два других определения обычно используются при вычислении углов между векторами и другими объектами, а также могут быть получены друг из друга.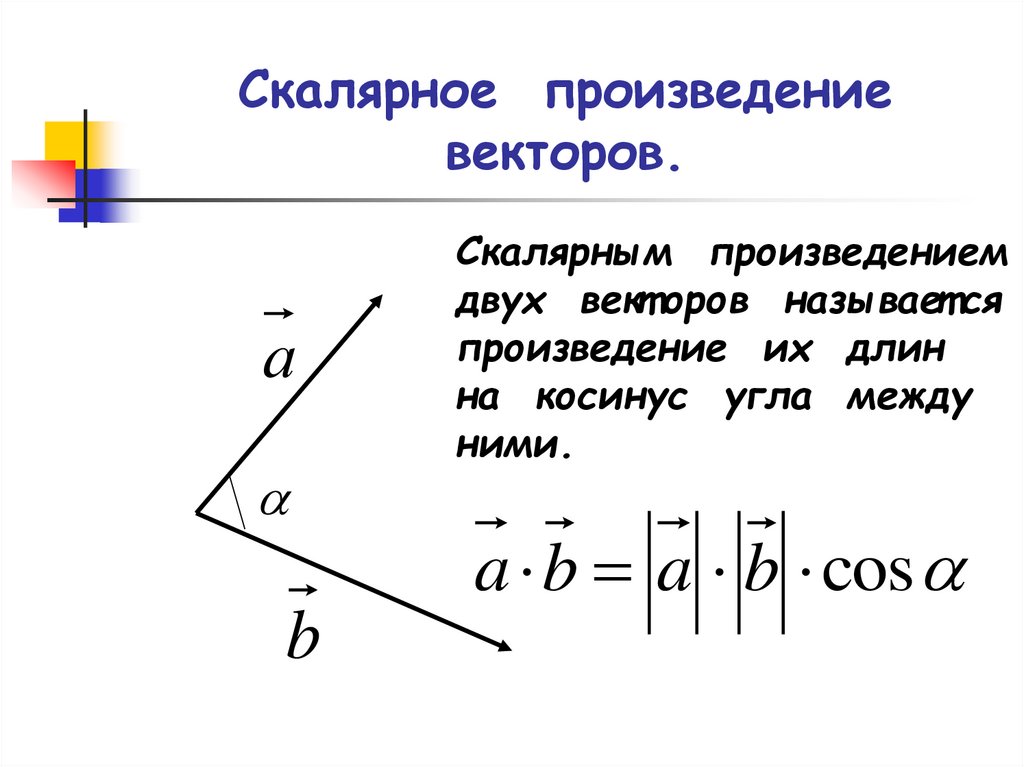

Сообщить об ошибке

Что из следующего верно относительно скалярного произведения двух векторов?

Возможные ответы:

 определен корректно, если каждый вектор имеет одинаковую размерность

Ни одно из других утверждений не верно.

Скалярное произведение двух векторов никогда не бывает отрицательным.

 тогда и только тогда, когда   ортогональны.

Скалярное произведение двух векторов никогда не является скаляром.

Правильный ответ:

тогда и только тогда, когда ортогональны.

Объяснение:

Это утверждение верно; его можно получить из определения, установив острый угол между векторами равным  ; требование ортогональности. Кроме того, если любой из векторов имеет длину, векторы по-прежнему называются ортогональными.

Сообщить об ошибке

Что такое скалярное произведение векторов  и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть вектор  представлен как   , а вектор   представлен как  .

 

Скалярное произведение векторов   и  равно .

В этой задаче

Сообщить об ошибке

Чему равно скалярное произведение векторов  и ?

Возможные ответы:

Не существует

Правильный ответ:

45

4 Объяснение:

Пусть вектор  представлен как   , а вектор   представлен как  .

 

Скалярное произведение векторов   и  равно .

В этой задаче

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 6 7 8 9 … 17 18 Следующая →

Уведомление об авторских правах

Все ресурсы исчисления 3

6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept

Калькулятор скалярного произведения

Создано Bogna Szyk и Wojciech Sas, PhD

Отредактировано Steven Wooding и Jack Bowater

Последнее обновление: 17 октября 2022 г.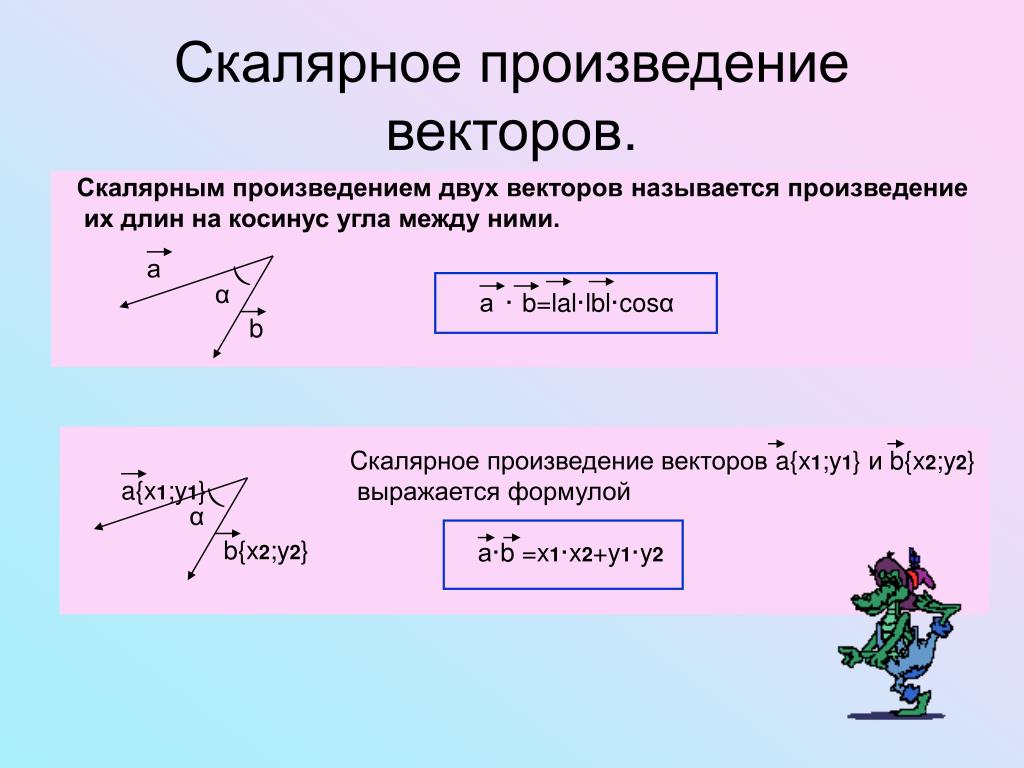

это формула скалярного произведения?

Определение векторного скалярного произведения

Скалярное произведение в сферических координатах

Матричное скалярное произведение

Скалярное произведение двух векторов – графическая интерпретация

Тройное произведение – как вычислить объем параллелепипеда?

Применение скалярного произведения

Калькулятор векторного скалярного произведения пригодится, когда вы решаете задачи на умножение векторов . Вместо того, чтобы вычислять скалярное произведение вручную, вы можете просто ввести компоненты двух векторов в этот инструмент, и пусть он сделает математику за вас.

Пожалуйста, продолжайте читать, чтобы узнать формулу скалярного произведения, которую использует наш калькулятор, как оценить скалярное произведение двух векторов и как обобщить формулу скалярного произведения матрицы. Вместе с калькулятором векторного произведения вы узнаете, что с векторной алгеброй не о чем беспокоиться!

Типы векторного умножения

Существует два основных типа векторного умножения: скалярное произведение (также называемое скалярным произведением), обозначаемое символом « · », и векторное произведение, обозначаемое символом « × «. Основное отличие состоит в том, что произведение точечной операции представляет собой одно число , а результат перекрестной операции — вектор.

Что такое формула скалярного произведения?

Предположим, что мы будем выполнить все наши вычисления в трехмерном пространстве . Это означает, что каждый вектор можно записать с использованием трех компонентов:

• a = [a₁, a₂, a₃]
• б = [б₁, б₂, б₃]

Геометрически скалярное произведение описывается как произведение модулей векторов на косинус угла между ними . Мы можем выразить это с помощью уравнения:

• a·b = |a| * |б| * cos α

Если вы не знаете, что такое модуль вектора или как его вычислить, перейдите к калькулятору единичных векторов для получения более подробной информации по этому вопросу.

Вы, наверное, заметили, что если угол между двумя векторами равен 90°, то скалярное произведение всегда будет равно 0, независимо от величины векторов. Точно так же, если угол равен 0 ° (векторы коллинеарны), скалярное произведение находится путем умножения только множеств. Другими словами, Чем больше относительный наклон между двумя векторами, тем выше значение скалярного произведения . Вы можете рассчитать наклон вектора с помощью калькулятора наклона.

Алгебраически скалярное произведение есть сумма произведений компонентов векторов. Для трехкомпонентных векторов формула скалярного произведения выглядит следующим образом:

a·b = a₁ * b₁ + a₂ * b₂ + a₃ * b₃

В пространстве, которое имеет более трех измерений, вам просто нужно добавить больше условий для суммирования. Если, с другой стороны, вы хотите умножить векторы в 2D-пространстве, вы должны опустить третий член формулы.

Калькулятор скалярного произведения также может работать как инструмент для нахождения угла между двумя векторами, для которых косинус является отношением между скалярным произведением и модулями векторов:

• cos α = a·b / (|a| * |б|) .

Чтобы узнать больше о коэффициентах, подобных этому, воспользуйтесь нашим калькулятором коэффициентов.

Определение векторного скалярного произведения

Итак, как же работает наш калькулятор векторного умножения? Следуйте этому пошаговому примеру, чтобы лучше понять принцип, лежащий в основе этого процесса.

1. Выберите свой вектор a . Например, возьмем a = [4, 5, -3].

2. Выберите свой вектор b . Предположим, что оно равно b = [1, -2, -2].

3. Вычислить произведение первого компонента каждого вектора. В данном случае он равен 4 * 1 = 4 .

4. Вычислить произведение второго (среднего) компонента каждого вектора. В данном случае он равен 5 * (-2) = -10 .

5. Вычислить произведение третьего компонента каждого вектора. В данном случае оно равно (-3) * (-2) = 6 .

6. Сложите всех этих результатов вместе, чтобы найти скалярное произведение векторов a и b .

   4 + (-10) + 6 = 0

Результат равен 0. Этот результат является скалярным произведением этих двух векторов. Это означает, что они перпендикулярны друг другу (угол между ними равен 90°).

Скалярное произведение в сферических координатах

Также можно вычислить скалярное произведение двух векторов, если они записаны в сферических координатах. Чтобы справиться с задачей, нам нужно выразить наши новые координаты с радиусом r и двумя углами θ , φ :

• x₁ = r₁ * sin φ₁ * cos θ₁ ;
• y₁ = r₁ * sin φ₁ * sin θ₁ ; и
• z₁ = r₁ * cos φ₁ .

И аналогично для x₂ , y₂ , z₂ . Тогда результат будет:

a·b = x₁*x₂ + y₁*y₂ + z₁*z₂ = r₁ * r₂ * sin φ₁ * cos θ₁ * sin φ₂ * cos θ₂ + r₁*r₂ * sin φ₂ * θ₁ * sin φ₂ * sin θ₂ + r₁*r₂ * cos φ₁ * cos φ₂ .

Если мы используем уравнение для косинуса разности углов, формула упрощается до: ) .

Скалярное произведение матрицы

На самом деле, операцию скалярного произведения можно производить не только для векторов, но и для более общих случаев – матриц . В результате получаем другую матрицу C , такую, что:

cij=ai1b1j+ai2b2j+…+ainbnj=∑kaikbkj\small \начать{выравнивать*} c_{ij} &= a_{i1}b_{1j}+a_{i2}b_{2j}+ … + a_{in}b_{nj} \\[1em] &= \sum_{k} a_{ik}b_{kj} \end{align*}cij​=ai1​b1j​+ai2​b2j​+…+ain​bnj​=k∑​aik​bkj​​

Аналог скалярного произведения простых векторов, но процедуру приходится повторять несколько раз для каждого элемента.

Однако перемножать можно не любые две матрицы. Если рассматривать A как матрицы m x n и B как матрицы k x l , то для полученной матрицы C = A·B , n должно быть равно k для матрицы 9 0 , а 4,1 D = B·A , l должно быть таким же, как m . Другими словами, количество столбцов левой матрицы должно совпадать с количеством строк во второй .

Как вы уже заметили, продуктов A·B и B·A в общем случае различны, а это означает, что скалярное произведение двух матриц некоммутативно . В частности, размеры результирующих матриц не совпадают.

Скалярное произведение двух векторов – графическая интерпретация

Рассмотрим подробно формулу скалярного произведения. Если мы нарисуем оба вектора, разделенные углом, а затем попытаемся найти образ скалярного произведения, мы поймем, что оно состоит из умножения двух частей: проекция одного вектора на направление второго и то же самое но для второго вектора. Поскольку они оба параллельны, результат является просто произведением их длин.

Как показано на картинке, мы можем выполнить операцию двумя способами , но результат всегда один и тот же. В заключение этого раздела можно сказать, что скалярное произведение есть произведение длин векторов, спроецированных в направлении одного из других.

Частным случаем является скалярное произведение вектора с самим собой, а² = а·а . Поскольку проекция и вектор — одно и то же, результатом является квадрат длины вектора. Другими словами, мы можем найти длину любого вектора, используя квадратный корень из следующего скалярного произведения: |a| = √(а·а) .

Тройное произведение – как вычислить объем параллелепипеда?

Помимо скалярного произведения и перекрестного произведения, есть еще один математический инструмент, который позволяет производить вычисления для трех векторов. Мы можем определить 9Тройное произведение 0015 (или смешанное произведение) как комбинация скалярного произведения и векторного произведения. Формула тройного произведения может быть выражена как:

V = a · (b × c) .

b × c — это вектор, что означает, что общий результат представляет собой скалярное произведение двух векторов и является просто числом. Буква V не случайна, потому что существует прямая зависимость между смешанным продуктом и объемом. Наш объем параллелепипедного калькулятора углубляется в эту тему.

Рассмотрим пример:

• Построить параллелепипед в декартовой системе координат.
• Обозначим его стороны как a , b , c — мы можем интерпретировать их как векторы, присоединенные в одной точке.
• Значение b × c = |b||c| sin α напоминает формулу площади параллелограмма. В результате мы получаем вектор, длина которого эквивалентна площади основания и перпендикулярна ему.
• Последним шагом является вычисление точечного произведения числа на . Как мы знаем из предыдущего раздела, это проекция на в направлении на , умноженная на на . Если мы посмотрим повнимательнее, то сможем понять, что эта проекция на самом деле является высотой нашего многогранника , а полученное произведение есть не что иное, как его объем!

Одно важное замечание: тройное произведение можно оценить несколькими эквивалентными способами:

a · (b × c) = b · (c × a) = c · (a × b)

Важно то, что порядок a-b-c-a-b-c-. .. должен сохраняться. В противном случае результат будет отрицательным. Мы всегда можем обойти эту проблему, вычислив объем как абсолютное значение тройного произведения.

Когда оба α и β равны 90°, результатом является не что иное, как объем прямоугольной призмы!

Применение скалярного произведения

Есть несколько областей, где скалярное произведение оказывается удобным.

1. Закон косинусов можно доказать с помощью скалярного произведения: если мы создадим треугольник из 3 векторов, мы можем написать, что c = b - a . Если мы хотим найти c² , мы можем расширить формулу следующим образом:

   c² = (b-a)·(b-a)
= b·b – b·a – a·b + a·a
= a² + b² - |b| * |а| * потому что - |а| * |б| * потому что
= а² + b² – 2 * |а| * |б| * cos α .

   Очевидно, что последний шаг возможен, поскольку умножение длин коммутативно.

   No related posts.