Зарисуй эти наборы С 9.№ 7 ГДЗ Математика 2 класс Моро М.И. – Рамблер/класс
Зарисуй эти наборы С 9.№ 7 ГДЗ Математика 2 класс Моро М.И. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
На столе лежат овощи:
Сколькими способами можно составить набор из
двух овощей? Зарисуй эти наборы в тетради.
ответы
Чтобы не пропустить ни одного варианта и не повто-
риться дважды, поступим так. Возьмём первый овощ
(свёклу) и будем присоединять к ней по порядку каж-
дый из остальных овощей: 1) свёкла, морковь, 2) свёк-
ла, огурец, 3) свёкла, помидор. Теперь возьмем второй
овощ (морковь) и присоединим к нему каждый из ос-
тальных овощей, расположенных справа от моркови:
1) морковь, огурец, 2) морковь, помидор. Осталось
взять третий овощ (огурец) и присоединить к нему по-
мидор (ещё один способ). Всего получилось 6 способов
(3 + 2 + 1 = 6).
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
5 класс
Репетитор
Химия
похожие вопросы 5
ГДЗ Русский язык 7 класс Часть 2 Львова.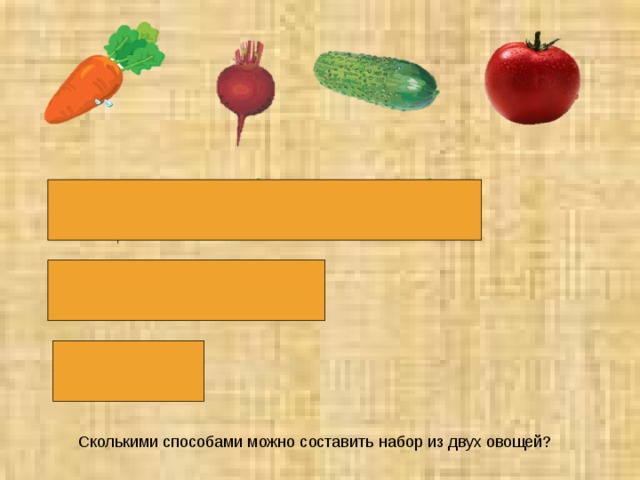
§ 28 Задание 616 Проведите морфологический разбор союзов
Кто выполнит? На уроке физики.
1. Спишите текст, раскрывая скобки и вставляя
пропущенные буквы. Объясните постановку (Подробнее…)
ГДЗРусский язык7 классЛьвова С.И.
ГДЗ. Математика. Базовый уровень ЕГЭ — 2017. Вар.№31. Зад.№7.Под руководством Ященко. Помогите найти корень уравнения.
Здравствуйте! Помогиет найти корень уравнения:
(Подробнее…)
ГДЗЭкзаменыМатематикаЯщенко И.В.
15. На прямой АВ взята точка М. Луч MD — бис- сектриса угла СМВ. Известно, что… ЕГЭ-2017 Математика Ященко И. В. ГДЗ. Вариант 27.
(Подробнее…)
ГДЗЕГЭМатематикаЯщенко И.В.
Как можно назвать С 4. № 8 ГДЗ Математика 2 класс Моро М.И.
1) Как можно назвать эти фигуры одним словом?
2) Почему каждую фигуру можно назвать лишней? (Подробнее…)
ГДЗМатематика2 классМоро М.И.
Сколько всего С 6.
№ 1 ГДЗ Математика 2 класс Моро М.И.
Скажи по-разному, сколько всего палочек на
каждом рисунке и сколько палочек разного
цвета (Подробнее…)
ГДЗМатематика2 классМоро М.И.
4.Элементы комбинаторики — метод пособие
ЛЕКЦИИ > 4.Элементы комбинаторики
|
При
бесповторной выборке все равно, каким образом осуществляется выбор: берутся все 
На место командира есть четыре
кандидата: a1, a2, a3, a4, на место инженера три — b1,
b2, b3, на место врача три – c1, c2, c3 . Проведенная проверка показала,
что a1 совместим с b1,
b2, c2,c3;
a2 совместим
с b1,
b2,c1,c2,c3; a3 совместим с b1 и
b2, c1, c3;
a4
совместим с b1, b2, b3, c2 ; b1
не совместим с c3 ; b2 не совместим с c1
; b3 не совместим с c2
. 
Давайте его посчитаем: C74=C73
по св-ву
1. C73 
Члены команды выбирают капитана и вратаря.
Сколькими способами это можно сделать?— Как найти все возможные комбинации набора опций?
Предположения и вопрос:
И вы можете иметь любой из этих вариантов, как вам нравится, и вы не можете иметь более одного одного и того же предмета.
Тогда каковы все возможные комбинации?
Окончательный ответ(а):
Ниже приведены все четыре возможных сценария с их формулами. Поскольку одно требование заключалось в том, что мы «не можем иметь более одного одного и того же элемента», то два сценария (из четырех возможных ниже), где «элементы не могут повторяться», являются допустимым ответом. У вас нет требования иметь значение порядка.
Таким образом, окончательный ответ либо 15, либо 64. Оба варианта верны. Желудки некоторых людей не согласятся с мороженым в неправильном порядке и могут вызвать кислотный рефлюкс. 🙂
Ключ:
A = пирог Б = Торт С = Маффин Д = Мороженое
Уникальные комбинации (порядок не имеет значения; элементы не могут повторяться):
уникальных комбинаций с 1 предметом 4 уникальные комбинации с 2 предметами 6 уникальные комбинации с 3 предметами 4 уникальные комбинации с 4 предметами 1
Формула:
Ссылка:
https://en.wikipedia.
org/wiki/Перестановка
n! / ((н-к)!к!) 4! / ((4-1)!1!) 4! / (3!1!) 24 / 6 4 4! / ((4-2)!2!) 4! / (2!2!) 24/4 6 4! / ((4-3)!3!) 4! / (1!3!) 24 / 6 4 4! / ((4-4)!4!) 4! / (0!4!) 4! / 4! 1
Вот перечисление:
1 элемент в списке = 4 А, Б, В, Г (1А, 1Б, 1С, 1Г) 2 элемента в списке = 6 АВ, АС, АД, БК, БД, КД (3А, 2Б, 1С, 0D) 3 элемента в списке = 4 (3А, 1Б) ABC, ABD, ACD, BCD 4 элемента в списке = 1 (4А, 0В, 0С, 0D) АВСD
ОТВЕТ:
15 уникальных комбинаций (порядок не имеет значения, элементы не могут повторяться)
Уникальные комбинации (порядок имеет значение; элементы не могут повторяться):
уникальных комбинаций с 1 предметом 4 уникальные комбинации с 2 предметами 4 * 3 = 12 уникальные комбинации с 3 предметами 4 * 3 * 2 = 24 уникальные комбинации с 4 предметами 4 * 3 * 2 * 1 = 24
Формула:
n! / (н-к)! 4! / (4-1)! 4! / 3! 24 / 6 4 4! / (4-2)! 4! / 2! 24/2 12 4! / (4-3)! 4! / 1! 24/1 24 4! / (4-4)! 4! / 0! 24
Вот перечисление:
1 элемент в списке = 4 А, Б, В, Г 1А, 1Б, 1С, 1Д 2 элемента в списке = 12 AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC 3А, 3Б, 3С, 3Д 3 элемента в списке = 24 DAB, DBA, DAC, DCA, CAD, CDA, ABC, ACB, ABD, ADB, ACD, ADC, BAD, CBA, BCA, BDA, CAB, BCD, BAC, BDC, CBD, CDB, DBA, DBC 6А, 6Б, 6С, 6Д 4 элемента в списке = 24 CDAB, CDBA, BDAC, BDCA, BCAD, BCDA, DABC, DACB, CABD, CADB, BACD, BADC, CBAD, DCBA, DBCA, CBDA, DCAB, ABCD, DBAC, ABDC, ACBD, ACDB, CDBA, ADBC 6А, 6Б, 6С, 6Д 94 = 4*4*4*4 = 256
ОТВЕТ:
340 уникальных комбинаций (порядок имеет значение; элементы повторяются)
Уникальные комбинации (порядок не имеет значения; элементы повторяются):
комбинаций с 1 предметом 4 комбинации из 2 предметов 10 комбинации из 3 предметов 20 комбинации из 4 предметов 35
Формула:
(k + n - 1)! / к!(п - 1)! (1 + 4 - 1)! / 1!(4 - 1)! 4! / 1!(3!) 24 / 6 4 (2+4-1)! / 2!(4 - 1)! 5! / 2!3! 120/12 10 (3+4-1)! / 3!(4 - 1)! 6! / 3!3! 6! / 36 20 (4+4-1)! / 4!(4 - 1)! 7! / 4!3! 5040/24*6 35
Перечисления:
1 элемент в списке = 4 А, Б, В, Г 2 элемента в списке = 10 AA, AB, AC, AD, BB, BC, BD, CC, CD, DD 3 элемента в списке = 20 AAA, AAB, AAC, AAD, ABB, ABC, ABD, ACC, ACD, ADD, BBB, BBC, BBD, BCC, BCD, BDD, CCC, CCD, CDD, DDD 4 элемента в списке = 35 AAAA, AAAB, AAAC, AAAD, AABB, AABC, AABD, AACC, AACD, AADD, ABBB, ABBC, ABBD, ABCC, ABCD, ABDD, ACCC, ACCD, ACDD, ADDD, BBBB, BBBC, BBBD, BBCC, BBCD, BBDD, BCCC, BCCD, BCDD, BDDD, CCCC, CCCD, CCDD, CDDD, DDDD ОТВЕЧАТЬ: > 69 уникальных комбинаций (порядок не имеет значения, элементы повторяются)
комбинаторика — Сколькими способами можно разделить набор из $2n$ элементов на два набора?
спросил
Изменено 5 лет, 5 месяцев назад
Просмотрено 3к раз
$\begingroup$
Предположим, $M=\{x_1,\ldots,x_{2n}\}$.